Stress shielding in the bony chain of leg in presence of varus or valgus knee

Abstract

Aims

The aim was to assess how the stress shielding can influence the integrity and resistance of bones in presence of a misalignment.

Methods

Three finite elements models have been developed: a normal one, and two varus and valgus knee ones.

Results

The obtained results reveal interesting consequences deriving by a wrong disposition of parts which compose the skeletal chain of the leg.

Conclusion

The most dangerous conditions occur in the contact interface between pelvis and hip of the femur, for the valgus knee configuration, and for the varus one, at the contact interface around the knee zone.

1. Introduction

Combined loading conditions during aggressive athletic activities have, however, not yet been measured, and could place large loads on the knee joint. Some sports such as football, running, and skiing are known to be responsible for thousands of knee injuries and related degenerative processes in many forms such as meniscal tear and, more particularly, ligamentous damage and rupture. It is realized that the ligaments of the knee help to guide the joint through normal motion and to provide the required stability by contributing to stiffness as well as flexibility of the joint. The principal mechanisms of injury of the human knee joint ligaments have been discussed in the literature.^15,17,5,49 Different stress and strain patterns cause different types of fractures. Under different tensile, compressive, torsional, bending and combined compressive forces the femoral cortical human bones showed specific fracture patterns according to the applied loading mode in the longitudinal direction. Injuries to the tibiofibular syndesmosis occur when the distal fibula is forcefully separated from the tibia. In literature are described three mechanisms that initiate partial or complete syndesmosis disruption: supination eversion or external rotation (SER), pronation–eversion or external rotation (PER), and pronation–abduction. Complete tibiofibular diastasis is traditionally associated with the PER mechanism and the associated proximal fibula fracture. The syndesmosis is usually torn secondary to a violent external rotation torque of the talus within the ankle mortise with simultaneous internal rotation of the leg. This can occur with a neutral, supinated, or pronated foot.⁴⁰ Boytim et al,¹¹ in a review of 98 ankle injuries in professional football players, found that external rotation was the most common cause of syndesmotic injury. Furthermore, they estimated that syndesmotic ankle sprains occur in 10% of all ankle injuries.^18,31 Other less common mechanisms leading to syndesmotic injury include excessive dorsi-flexion and abduction forces. Sudden dorsi-flexion of the talus within the ankle joint places excessive tension on the syndesmotic ligaments.^3,24,22 With the talus in a maximally dorsi flexed position, a severe abductory force places further stress on the syndesmotic ligaments. Fracture of the medial malleolus or deltoid ligament tear precedes syndesmotic injury with an abductory mechanism. Kelikian,²⁴ described two mechanisms of traumatic diastasis.²³ He described anterior tibiofibular diastasis as partial disruption of the syndesmosis that can be likened to the opening of a book. External rotation of the talus places a lateral and posterior stress on the fibular malleolus. The torque generated on the fibula places the greatest tension on the anterior syndesmotic ligaments. The posterior transverse tibiofibular ligament often remains intact and acts as a hinge, retaining its connection to the tibia and fibula with minimal separation.²⁴ However, with violent abduction or external rotation of the foot, a complete tibiofibular diastasis can occur.⁴⁸ Location of the joint below the centre of gravity of the body causes compressive loads acting on the tibiofemoral joint to be as high as 4–7 times the body weight during day-to-day activities such as walking, running or ascending stairs and even 24 times the body weight. The human knee joint is distinguished by its complex three dimensional geometry and multibody articulations that generate complex mechanical responses under physiological loads. The knee joint compliance and stability required for optimal daily function are provided by various articulations, menisci, ligaments and muscle forces. A proper understanding of knee joint biomechanics significantly improves the prevention and treatment of knee joint disorders and injuries. Knee joint mechanics have consequently been the subject of a large number of studies,^{1,20,36,42,25} majority of which are experimental and aim at the measurement of the gross multidirectional load–displacement response of the joint under both intact and perturbed measurements have also been reported on the biomechanical role of the ligaments and menisci, as well as the mechanism of load transfer and contact areas and pressures at the tibiofemoral^{14,7,21,41,19,4,28,34} and patellofemoral^{45,38,39,2,9,43,16,29,10,37} joints. In spite of the continuing accumulation of experimental results, it is recognized that measurements alone are not sufficient to delineate the detailed biomechanics of the human knee joint. Various applications in orthopaedic biomechanics have long demonstrated that realistic mathematical modelling is an appropriate tool for the simulation and analysis of complex biological structures such as the human knee joint. Such detailed investigation, however, requires the use of advanced computer techniques for both the geometric reconstruction and the subsequent stress analysis. The aim of this study is to assess how the stress shielding can influence the integrity and resistance of bones in presence of varus or valgus positioning of knee, and the obtained results reveal interesting consequences deriving by a wrong disposition of parts which compose the skeletal chain of the human leg.

2. Materials and methods

The geometrical data of the model developed herein were obtained by computerized tomography (CT) for bones coupled with a nuclear magnetic resonance (MRI) to better distinguish soft tissues, from a normal adult patient. The CT and MRI blocks consisted of parallel digital images separated at intervals of 1.5 mm in the sagittal, coronal and axial planes with the knee at 0° flexion. The contours of the pelvis, femur, patella, fibula, tibia, feet, articular cartilages, and ligaments. The manual segmentation was executed with an accuracy of 0.3 mm. These lines were transferred into the commercial code Hypermesh by Altair^® where the main surfaces and solid version of the model were reconstructed with an accuracy of 0.5 mm. Models consist of six bony structures: pelvis, femur, patella, fibula, tibia, and a simplified lump of the feet, their articular cartilage layers, were simulated by membranes of 3d tetrahedral elements. In particular 5758 elements and 1837 nodes were used for pelvis, 20096 elements and 1012 nodes in femur, 2567 elements and 687 nodes in patella, 2480 elements and 849 nodes in fibula, 17831 elements and 2032 nodes in tibia and 1120 elements and 412 nodes for the foot. On the upper zone, the ilio-femoral ligament, the ligament of the hip joint, which extends from the ilium to the femur in front of the joint, was modelled with 252 tetrahedral elements and 151 nodes. The knee joint constituted by the medial collateral ligament, which extends from the medial femoral epicondyle to the tibia, the lateral collateral ligament, which extends from the lateral femoral epicondyle to the head of the fibula, the anterior cruciate ligament which extends postero-laterally from the tibia and inserts on the lateral femoral condyle, and the posterior cruciate ligament which extends antero-medially from the tibia posterior to the medial femoral condyle were modelled with 529 tetrahedral elements and 296 nodes. On the lower zone, the foot joint, constituted by the plantar fascia, the medial and lateral ligaments were modelled with 366 tetrahedral elements and 187 nodes. Material properties were defined as nonlinear elastic materials for the structures, as reported in Fig. 1. In order to realize the different misalignments previously described, three numerical models of the complete lower limb were realized: the first one a normal reference one, and the second, a varus knee one, realized by choosing a centre of rotation on the femur, and clockwise rotating it of +4°. Successively a second centre of rotation was chosen on the tibia, and the normal reference fibula, tibia and feet were anti clockwise rotated of −4°. Finally the third configuration the valgus one was obtained by selecting the same rotational centres and switching the previous rotations, already described, for the varus configuration. A distributed, on 50 nodes, load of 700 N has been applied at the top of pelvis, as depicted in Fig. 1, while the tip of the feet, 460 nodes, were rigidly fixed. Contact interfaces were imposed at the ilio-femoral (femur-pelvis), knee (femur-patella, patella-tibia, fibula-tibia) and foot (tibia-feet) joints, defined using a penalty-based method with a weight factor, a coefficient of friction of 0.04 was chosen to be consistent. Nonlinear finite element analyses of the models were performed with Abaqus version 5.4 (Hibbitt, Karlsson and Sorensen, Inc., Pawtucket, RI) using the geometric nonlinearity and automatic time stepping options.

Fig. 1.

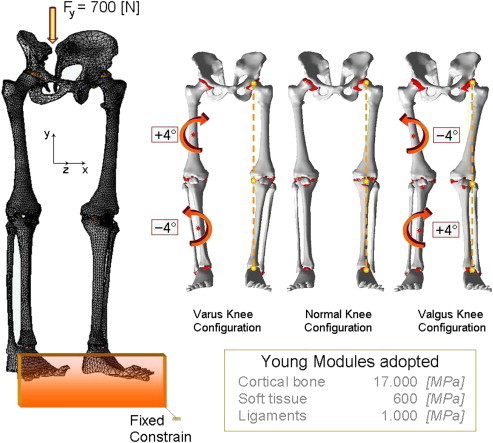
FE model and Young Modules adopted for the whole structure: pelvis, femur, patella, fibula, tibia, foot, and ligaments; with specifications about varus, normal and valgus configurations.

3. Results

A geometrical accurate 3D FE model of the human complete model of the leg was realised, taking into account three possible configurations inherent the special orientation of the knee: varus, normal, and valgus. The analysis of the entire chain allows to have a complete picture of the stress distribution and of the most stressed bones and soft tissues, but, more importantly can overcome problems connected with boundary conditions imposed at single bony components. In Table 1 are reported the obtained results in terms of maximum displacements and equivalent von Mises Stress, detailed for each part of the skeletal chain and related to the three different cases analysed. Also their relative percentage, respect to the reference normal knee configuration, was reported as well. As it is possible to notice by observing Fig. 2 and Table 1, the maximum total displacement is localised on the upper zone of the leg, concerning the pelvis and the femur, with values ranging from 12 to 9 mm, and percentages from −4% (femur in varus knee configuration), to +1% femur and femoral ligaments in valgus knee configuration. By going down, the lower part undergoes a minor effect, and displacements are of the order of 3 mm, localised in patella, knee, knee ligaments, tibia, and fibula. The maximum value of 2,95 mm is localised on the knee ligaments in the valgus knee configuration, which makes register the percentage values, around this area, higher than the normal knee one, from +6 calculated on the tibia, to +8% calculated on the fibula. On the contrary the varus knee configuration makes register the percentage values, around this area, lower than the normal knee one, from −3% calculated on the patella and knee ligaments, to −5% calculated on tibia and fibula, where the numerical value is of 2,32 mm. Interesting considerations can be done for the foot ligaments which are in both cases, varus and valgus knee configurations, much more unloaded (−67% and −56%). As it is possible to notice by observing Fig. 3 and Table 1, the maximum equivalent Von Mises Stress is localised, also in this case, on the upper zone of the leg. On the hip of the femur are localised stresses of about 30 MPa (+126%) in the valgus knee configuration, while in the varus one the femur is solicited with about 26 MPa (+91%). Pelvis and femur ligaments are identically stressed in the first case or even unloaded −48% for the varus knee configuration and −28% for the valgus one. The patella undergoes an increment of stress in valgus configuration +12% and a decrement in the varus one −13%, but stress are lower than 2 MPa. Knee ligaments, tibia and fibula suffer a significant increment of stress with values ranging from 19 to 26 MPa, and percentages ranging from 41 to 63%, localised maximally on the fibula of the varus knee configuration. The same area, also if in a lesser extent, for the valgus knee configuration is subjected to an increment of stress ranging from 12 to 22 MPa. Fibula results the more stressed part +36%, while tibia results unloaded of −11%. Foot ligaments make register an increment of +59% and a stress of 12 MPa in the valgus configuration, while in the other case the increment is only of the 14%. Finally the measured stress on the foot is about 5 MPa and +25%, in the valgus configuration and 3 MPa and −24% in the other case. The curves depicted in Figs. 4 and 5, total displacements and Equivalent Von Mises Stress vs. Position, have been calculated by choosing the average value for displacements and Eq. Von Mises Stress localised along perpendicular intercepting lines, drown every 5 mm starting from the pelvis and finishing to the feet, for each one of the three considered cases. As it is possible to notice the curves of Fig. 4, related to the displacements, exhibit a continuum trend decreasing from the pelvis to the feet, varus configuration shows the lower displacements, while the valgus one is almost equivalent to the normal reference one, except at 35 mm of position, that is the proximal femur, and in the zone under the knee in which displacements are higher till the proximal tibia and lower next to this zone. On the contrary the second curves, Fig. 5, related to the Eq. Von Mises Stress, exhibit a sinusoidal trend, with two significant peaks on the hip of the femur reached by the valgus, the higher, and varus configurations. Other two peaks are visible in the areas of proximal femur and knee ligaments, with higher stress reached by the varus case. The varus and valgus configuration curves maintain levels of stress higher than the normal one until the proximal tibia in which valgus curve shows a minor stress. Finally a peak on the foot ligaments is evidenced on the varus knee configuration. Fig. 6 represents the equivalent Von Mises contours maps, for the three considered cases, of the particulars in pelvis–femur, femur–tibia, and tibia–foot contacts in order to evidence which zones are much more stressed.

Table 1.

Maximum values of Total displacements and Eq. Von Mises Stresses localised on the different parts of the leg for the varus/normal/valgus knee configurations.

	Total displacements [mm]			Eq. Von Mises Stress [MPa]
	Varus	Normal	Valgus	Varus	Normal	Valgus
Pelvis	11,37 (−3%)	11,74	11,77 (0%)	17,04 (0%)	17,08	17,05 (0%)
Femural Lig.	9,11 (−3%)	9,44	9,56 (+1%)	6,76 (−48%)	13,00	9,35 (−28%)
Femur	8,95 (−4%)	9,29	9,41 (+1%)	25,61 (+91%)	13,38	30,26 (+126%)
Patella	2,65 (−3%)	2,72	2,88 (+6%)	1,18 (−13%)	1,35	1,51 (+12%)
Knee Lig.	2,69 (−3%)	2,76	2,95 (+7%)	25,85 (+44%)	18,00	21,53 (+20%)
Fibula	2,32 (−5%)	2,43	2,63 (+8%)	25,85 (+63%)	15,83	21,53 (+36%)
Tibia	2,50 (−5%)	2,64	2,81 (+6%)	18,37 (+41%)	13,02	11,62 (−11%)
Foot Lig.	0,03 (−67%)	0,09	0,04 (−56%)	8,86 (+14%)	7,75	12,34 (+59%)
Foot	0,01 (0%)	0,01	0,01 (0%)	3,15 (−24%)	4,12	5,17 (+25%)
Complete model	11,37 (−3%)	11,74	11,77 (0%)	25,85 (+44%)	18	30,26 (+68%)

Fig. 2.

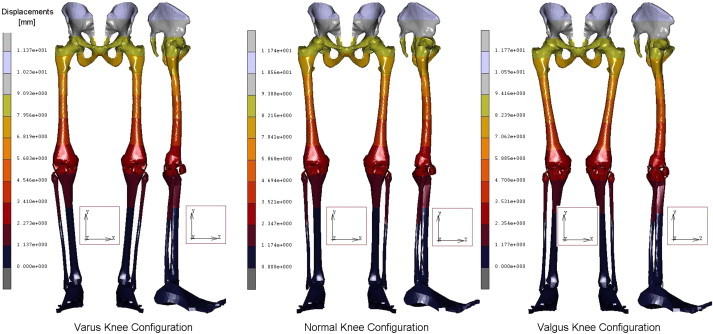
Contour maps of Displacements obtained for the three configurations of the knee.

Fig. 3.

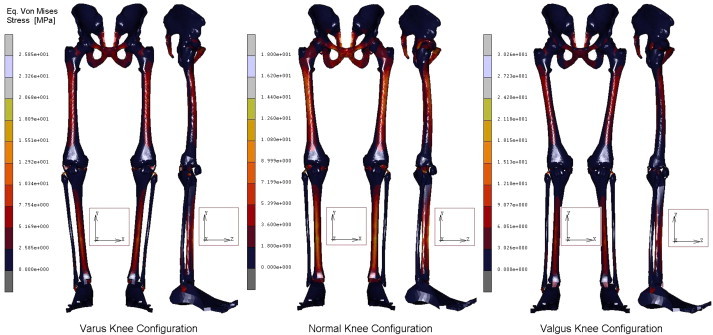
Contour maps of Eq. Von Mises Stress obtained for the three configurations of the knee.

Fig. 4.

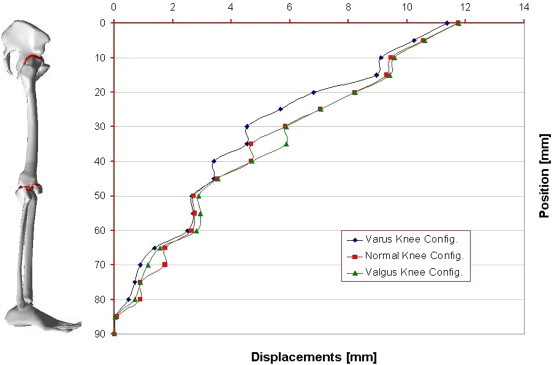
Curves of Displacements vs. Position (every 5 mm) calculated for the three configurations of the knee.

Fig. 5.

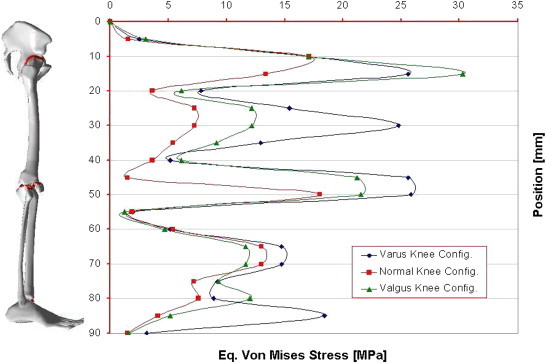
Curves of Eq. Von Mises Stress vs. Position (every 5 mm) calculated for the three configurations of the knee.

Fig. 6.

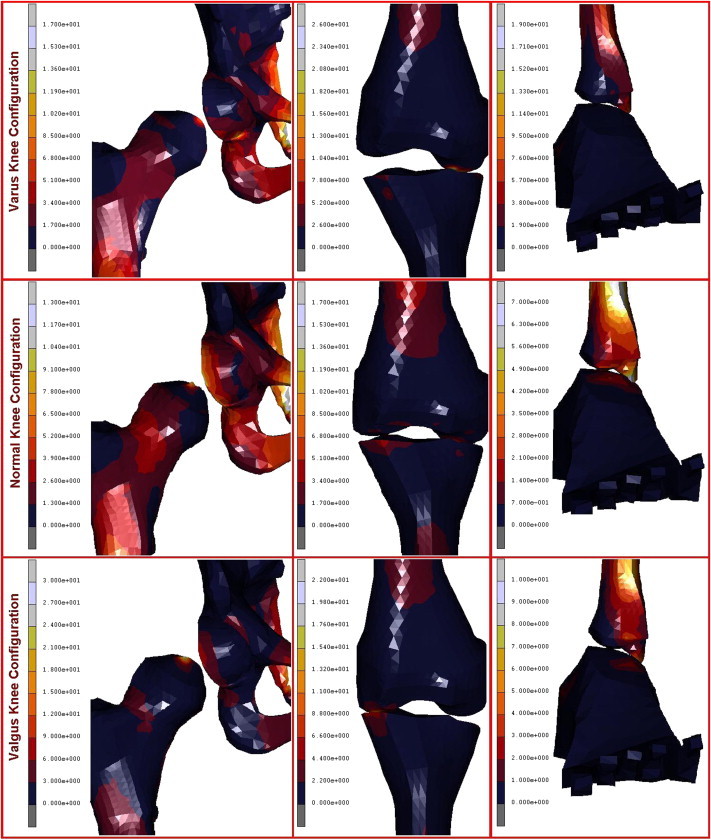
Particulars of femoral joint, femur-tibia contact, and tibia-feet contact obtained for the three considered cases.

4. Discussion

The basic deformity of a valgus knee consists of both bony and soft-tissue deformities that must be addressed. Potentially contracted lateral-sided structures, which may need to be released, include the ilio-tibial (IT) band, postero–lateral capsule, LCL, popliteus, and biceps femoris. Potentially lengthened medial-sided structures include the MCL and medial capsule. Common bony deformities include wear of the lateral femoral condyle both distally and posteriorly, as well as a central deformity of the lateral tibial plateau. The surgical challenges presented by these knees include correcting the angular deformity, properly rotating the femoral component, obtaining good patellofemoral tracking, and caring for the peroneal nerve both intra- and postoperatively. There have been many reports in the literature of techniques used to address these deformities in TKA, with varying degrees of complexity and success. Coronal and condylar malpositioning of the tibial and femoral components of knee may result in severe wear, the joints pressure and forces distribution, stress, of the bony and cartilaginous components. The difference in contact force on the medial and lateral condyles decreased in condition of valgus malalignment during the stance phase, while the strain distribution in the distal femur is related to the tibiofemoral contact force. For the situation of a prosthetic knee with a valgus inclination of 3°, in a patient weight of 75 kg, Orban et al 2013,³⁰ observed a maximum contact pressure of 19,3 MPa, and a contact pressure of 19,3 MPa on a balanced knee, upon the polyethylene surface with an almost symmetrical load distribution between the two compartments. Our results confirm an Eq. Von Mises Stress in that area of 22 MPa in the case of valgus malalignment, and 18 MPa in the normal reference one. Misalignment causes stress increase in both tibial bearing component and tibial tray, and a varus/valgus misalignment of 5° could increase maximum contact pressure for the fixed-bearing implant with 10.3 MPa (61%), ⁴⁴ Matsuda et al (1999),²⁷ determined that a 5° varus or valgus tilt increased the contact stresses by approximately 50% in five different knee implants. Bargren et al 1993,⁶ showed that, when the knee is loaded unequally, lift-off occurs on the unloaded side and collapse occurs on the eccentrically loaded side. Liau et al (2002),²⁶ compared the stresses of three kinds of prostheses (high conformity flat-on-flat, high conformity curve-on-curve and medium conformity flat-on-flat) subjected to different kinds of malalignment and under a load of 3000 N. When the femoral component was simulated as a maltranslation in the medial direction relative to the tibial component, the maximum contact stress and Von Mises Stress in the tibial component significantly increased in comparing with the neutral position, 27 MPa for a varus tilt of 3° in spite of 16,4 MPa, which are in good agreement with our results.

The greatest increase of contact stress and Von Mises Stress occurred in the high conformity flat-on-flat design of knee prosthesis under the severest malalignment condition. Comparing the malrotation to the maltranslation and varus tilt of the femoral component, the increase of stress in the tibial component was the smallest in malrotation condition. The malrotation of the femoral component would slightly increase the risk of polyethylene wear in tibial component. However, the malrotation of the femoral component would significantly increase the risk of patellofemoral complication after TKA.⁸ Perillo-Marcone et al (2000),³² demonstrated that valgus orientation of the prosthesis reduces the risk of cancellous bone failure. Using explicit finite element model, Perillo-Marcone and Taylor (2007),³³ reported investigation on the variations produced in bone strain distribution in the proximal tibia when the axial load is applied eccentrically. It has been reported that loosening of the femoral component may result from condylar osteoporosis.^35,46,47 Other studies have demonstrated stress shielding and bone loss in the anterior distal femur.^12,13 In two knees, with looser ligaments, an opposite medial to lateral load distribution was observed. With the simulated valgus alignment, the tibia would abnormally abduct and load the lateral compartment, conversely, with a varus alignment, the tibia would adduct and load the medial compartment.

Clinically, this amount of ad/abduction would not have been acceptable to a patient. This does suggest that an unacceptable amount of instability may occur and be associated with an uneven medial to lateral load distribution. Nicholas, and Yang, 2010,⁵⁰ demonstrated that the subject with varus alignment had the largest stresses at the medial compartment of the knee compared to the subjects with normal alignment and valgus alignment, suggesting that this subject might be most susceptible to developing medial compartment osteoarthritis (OA). In addition, the magnitude of stress and strain on the lateral cartilage of the subject with valgus alignment were found to be larger compared to subjects with normal alignment and varus alignment, suggesting that this subject might be most susceptible to developing lateral compartment knee OA.

In particular three subjects were studied: the first one with a Varus angle of 0,20° and a BW of 640 N; the second one, normal subject, with an angle of 7,67°and a BW of 725 N, and the third one angled of 10,34° with a BW of 704 N. The obtained results confirm a Normalized Compressive Stress, of 0,020 on the tibia, and 0,023 MPa/N on the femur of the valgus knee configuration. Our results show an Eq. Von Mises of 0,025 and 0,036 MPa/N on the same bony parts. In the normal case the values are of 0,017 and 0,020 MPa/N respectively on tibia and femur of the normal subject, ours results are of 0,024 and 0,018 MPa/N for the same case. Finally in the same components of the valgus subject, values are of 0,016 and 0,018 MPa/N, lower than ours which are of 0,031 and 0,03 in the same configuration. Obviously results are quite influenced by the geometrical characteristic such as distances, position, angulations, rather than loads, constrains interfaces etc.

5. Conclusions

The aim of this study was to assess how the stress shielding can influence the integrity and resistance of bones in presence of a misalignment of the bones. The analysis of the entire chain allows to have a complete picture of the stress distribution and of the most stressed bones, but, more importantly can overcome problems connected with boundary conditions imposed at single bony components, which deeply influence the obtained results. The obtained results reveal interesting consequences deriving by a wrong disposition of parts which compose the skeletal chain of the human leg. The most dangerous conditions occur in the contact interface between pelvis and hip of the femur, for the valgus knee configuration, and for the varus one, at the contact interface around the knee zone. Displacements vs. Position Curves, exhibit a continuum trend decreasing from the pelvis to the feet, varus configuration shows the lower values. On the contrary the Eq. Von Mises Stress vs. Position Curves, exhibit a sinusoidal trend, with two significant peaks on the hip of the femur reached by the valgus, the higher, and varus configurations.

The results suggest that under static loading, a tibial malposition of 4 or more angulations degrees in varus or valgus configuration can greatly alter the distribution of pressure and the load between the medial and lateral compartments. The change in the load distribution increases stresses in some regions and reduces them in others. If these changes are large enough they can lead to adaptive bone remodelling. Bone loss in the distal anterior femur can lead to loosening of the component and cause difficulties during a revision knee arthroplasty.

Conflicts of interest

The author has none to declare.