Skip to main content
PMC home page
Genome Research logoLink to Genome Research
letter
. 2004 Jul;14(7):1310–1314. doi: 10.1101/gr.2300204

Evolution and Topology in the Yeast Protein Interaction Network

Stefan Wuchty 1
PMCID: PMC442146  PMID: 15231746

Abstract

The integrity of the yeast protein–protein interaction network is maintained by a few highly connected proteins, or hubs, which hold the numerous less-connected proteins together. The structural importance and the increased essentiality of these proteins suggest that they are likely to be conserved in evolution, implying a strong relationship between the number of interactions and their evolutionary distance to its orthologs in other organisms. The existence of this coherence was recently reported to strongly depend on the quality of the protein interaction and orthologs data. Here, we introduce a novel method, the evolutionary excess retention (ER), allowing us to uncover a robust and strong correlation between the conservation, essentiality, and connectivity of a yeast protein. We conclude that the relevance of the hubs for the network integrity is simultaneously reflected by a considerable probability of simultaneously being evolutionarily conserved and essential, an observation that does not have an equivalent for nonessential proteins. Providing a thorough assessment of the impact noisy and incomplete data have on our findings, we conclude that our results are largely insensitive to the quality of the utilized data.

The recently uncovered scale-free topology of protein–protein interaction networks has focused our attention on the important role of a small subset of highly linked proteins, or hubs, that guarantee the functional and structural integrity of the network (Jeong et al. 2001; Park et al. 2001; Wagner 2001). The observed correlations between the essentiality and connectivity of a protein (Jeong et al. 2001; Wuchty 2002) suggest that hubs are likely maintained by evolution, implying the emergence of correlations between the number of interactions of a protein and its evolutionary conservation (Hurst and Smith 1999). Such a trend has been reported for Saccharomyces cerevisiae, concluding that proteins with a higher connectivity have a smaller evolutionary distance to their orthologs in Caenorhabditis elegans (Fraser et al. 2002). Yet, recent reanalyses (Jordan et al. 2002, 2003a,b) and alternative approaches (Hahn et al. 2002) rigorously questioned the strength of the available evidence, concluding the absence of distinctive correlations between the connectivity and evolutionary conservation of proteins. A recent reply to these objections (Fraser et al. 2003) argued that the utilization of incomplete and noisy sets of protein interactions, as well as inaccurately determined orthologs, are the reasons for the asserted absence of these trends. After carefully compiling interactions from all known high-throughput screens of proteins of S. cerevisiae (Uetz et al. 2000; Ito et al. 2001; Gavin et al. 2002; Ho et al. 2002) and determining their evolutionary distances to orthologs in Schizosaccharomyces pombe and Candida candidans by a novel phylogenetic estimation method (Wall et al. 2003), the highly disputed correlations ultimately were found.

Although the results were statistically significant, the sensitivity to the data sources remains a considerable weakness of the introduced method. Here, we contribute to the current debate by presenting an alternative approach, allowing us to uncover a significant and strong correlation that highly interacting proteins of S. cerevisiae have a far higher probability to be evolutionarily conserved in higher eukaryotes. Observing that the propensity of essential, highly connected proteins to be evolutionarily conserved is strongly correlated, we find that this trend does not have an equivalent for nonessential proteins. In addition, we provide a thorough assessment of the impact that the quality of the used data sets has on our ability of our method to determine these trends, and we conclude that our findings are largely insensitive to both incomplete and noisy protein interaction as well as ortholog data.

RESULTS AND DISCUSSION

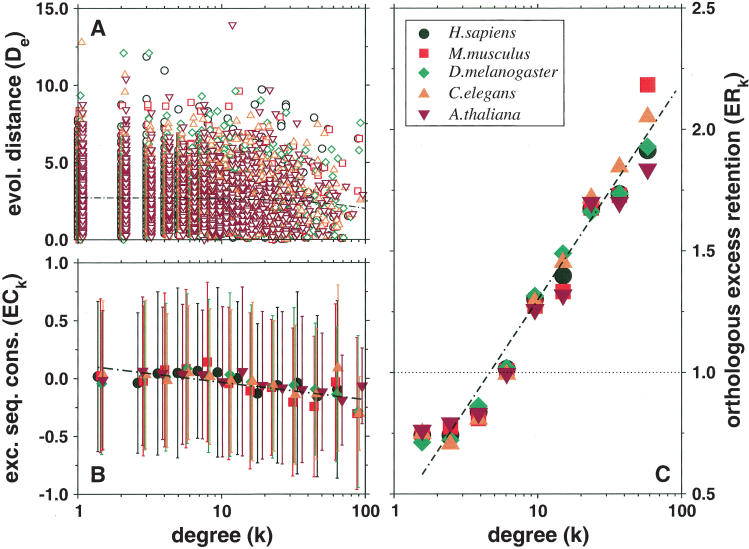
To build a source of ortholog data, we browsed protein clusters compiled in the InParanoid database (Remm et al. 2001), which provides sequence information of orthologous protein pairs between S. cerevisiae and five higher eukaryotes: Homo sapiens, Mus musculus, C. elegans, Drosophila melanogaster, and Arabidopsis thaliana. The connectivity of 3677 yeast proteins was inferred from a Web of 11,249 interactions assembled from the DIP database (Xenarios et al. 2002). Although the quality of interaction and ortholog data is still a matter of debate (Koski and Golding 2001, Goldberg and Roth 2003; Wall et al. 2003), we did not perform any quality checks, allowing us to assess the ability of our method to uncover the assumed trends from putatively flawed data. Using these data sets, the scatterplot in Figure 1A, depicting the evolutionary distance D (see Methods) of each yeast protein as a function of its connectivity k, fails to indicate convincing correlations. This is further indicated by low average values of the Pearson's correlation coefficient, r̄ = –0.045, P̄ = 0.137, and Spearman's rank coefficient 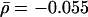Inline graphic, P̄ = 0.092 (for detailed values, see Supplemental material). The small average slope 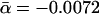Inline graphic of the best linear fit D ∼ αk supports previous conclusions that the dependence of the evolutionary distance D on the protein connectivity k is negligible (Jordan et al. 2003a,b; for detailed values, see Supplemental material). However, the observed correlations might be determined to a more enhanced level by accounting for the scale-free nature of the protein network. Indeed, the frequency of highly interacting proteins decays as a power-law (Jeong et al. 2001;Wagner 2001) P(k) ∼ k–γ, indicating that sparsely connected proteins significantly outnumber their highly linked counterparts. The uniform sampling used in Figure 1A does not account for differences between the number of proteins in the different connectivity groups. To guarantee balanced sampling for all k-values, we use logarithmic binning of the k-axis, a procedure that corrects for the skewed nature of the scale-free distribution (see Methods; Albert et al. 2000; Goldstein et al. 2004). Providing comparable numbers of proteins in each bin, we determine the mean excess sequence conservation, 〈ESCk〉 (see Methods). The distributions thus obtained (Fig. 1B) indicate statistically significant correlations between 〈ESCk〉 and k (average Pearson's r̄ = –0.775, P̄ = 2.6 × 10–3; average Spearman's 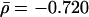Inline graphic, P̄ = 0.022), which best fit a logarithmic curve, 〈ESCk〉 ∼ βlog k, 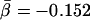Inline graphic. Although the fits indicate a stronger dependence, these result still seem to agree with earlier conclusions of a weak interdependence between the connectivity of a protein and its sequence conservation (Hahn et al. 2002; Jordan et al, 2003a).

Figure 1.

Figure 1

Open in a new tab

(A) Scatterplot showing for each yeast protein the evolutionary distance D to its orthologs in a higher eukaryote as a function of the proteins' number of interactions k. The thin black line corresponds to D ∼ αk with 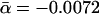Inline graphic. (B) By applying logarithmic binning to the horizontal k-axis, we obtain improved correlations of the excess sequence conservation ESCk on k (〈ESCk〉 ∼ βlog k, 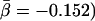Inline graphic. (C) The orthologous excess retention parameter ERk shown as a function of logarithmically binned ks indicates a statistically significant monotonic trend toward the conservation of the more connected proteins (ERk ∼ γlog k, 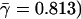Inline graphic). In each plot, the symbols correspond to the orthologs of S. cerevisiae identified in the higher organisms listed in the legends box of C.

However, an apparently weak correlation between sequence conservation and connectivity does not necessarily invalidate the original hypothesis, but is assumed to reflect the data dependence of the applied analytical framework (Fraser et al. 2003). To probe the initial assumption that more connected proteins have a higher tendency to be evolutionarily conserved, we introduce an alternative approach of separately identifying the fractions of orthologous proteins with k interactions. Dividing proteins into groups by logarithmically binning their connectivity k, we determine the respective fraction of the number of proteins having orthologs in the reference organisms and the total number of proteins in each bin. As a null hypothesis, we assume a random distribution of orthologs that is quantified by the fraction of the total number of proteins that have orthologs in a reference eukaryote and the total number of proteins present in the interaction network (see Methods). Defined as orthologous excess retention ERk, the ratio of the k-dependent and random fractions of orthologous proteins shows visually striking correlations with k (Fig. 1C). These results are further supported by distinct and statistically significant average Pearson's correlation coefficients r̄ = 0.892 (P̄ = 2 × 10–3) and Spearman's rank correlation coefficients 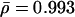Inline graphic (P̄ = 4 × 10–3). The linear dependence on a log-linear plot indicates that ERk ∼ γlog k with 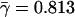Inline graphic, representing a clear trend toward the evolutionary conservation of the more connected proteins (for detailed values, see Supplemental material).

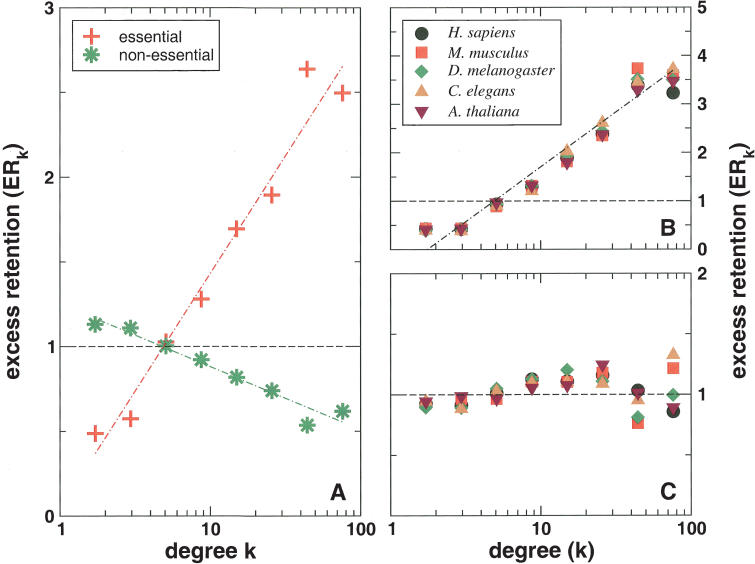
Similarly, we observe the same trend for the excess retention of essential proteins that we collected from the Bioknowledge library (Fig. 2A; Costanzo et al. 2001). As expected, we observe a dilution process of nonessential proteins with increasing levels of interactions. In both cases, the application of logarithmic binning uncovers sharp logarithmic trends, ERk ∼ γlog k (for detailed values, see Supplemental material), which are supported by distinctive and statistically significant Pearson's correlation coefficients (essential proteins: r = 0.868, P = 4.5 × 10–4, nonessential proteins: r = –0.848, P = 9.5 × 10–4) and Spearman's rank coefficients (essential proteins: ρ = 0.976, P = 9.8 × 10–3, nonessential proteins: ρ = 0.868, P = 4.5 × 10–3; for detailed values, see Supplemental material). Furthermore, we find that the excess retention of orthologous and essential proteins are not independent: Figure 2B shows a strong logarithmic, ERk ∼ γlog k, 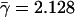Inline graphic, and statistically significant trend (average Pearson's r̄ = 0.909, P̄ = 7.1 × 10–4, average Spearman's 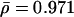Inline graphic, P̄ = 8.8 × 10–3) toward highly linked proteins which are simultaneously essential and evolutionarily conserved. In particular, proteins with less than ten interactions have an excess retention smaller than one (ERk < 1), indicating that a high fraction of the numerous weakly connected proteins has been discounted by evolution. Compared with the respective numbers of simple orthologous excess retention, the significantly higher excess retention for proteins with >10 links (ERk>10 > 1) suggests that these proteins are preferentially conserved in higher eukaryotes and essential for the survival of the cell. However, we do not find a comparable correlation for proteins that are both nonessential and evolutionarily conserved (Fig. 2C).

Figure 2.

Figure 2

Open in a new tab

(A) The essential and nonessential excess retention as a function of logarithmically binned connectivities of proteins shows statistically significant and monotonic trends (ERk ∼ γlog k, essential: γ = 1.386, nonessential: γ = –0.371). (B) The trend of excess retention of essential proteins is further enhanced if we focus on proteins that simultaneously have orthologs in higher eukaryotes (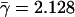Inline graphic). (C) However, proteins that have orthologs in the reference eukaryotes and are dispensable for the cell's survival fail to show any significant excess retention signal.

To estimate the potential influence of incomplete and noisy protein interaction data on our findings, we added (removed) up to 20% of interactions between randomly selected protein pairs, thereby mimicking false positives (negatives). Similarly, by simulating the presence of false-positive (negative) ortholog and/or essential (nonessential) signals, we randomly increased (decreased) the original sets of respective proteins by up to 20%. In each case, we generated 1000 different realizations of removal (addition) and repeated our assessment of essential/nonessential and/or orthologous excess retention. We find that the basic trends remain qualitatively unaltered, albeit the slopes of the actual curves gradually change, allowing us to conclude that the uncovered correlations are largely unaffected by data incompleteness (for details, see Supplemental material).

In summary, our results clearly indicate that highly connected proteins are far more likely to be essential and (simultaneously) conserved as orthologs in higher eukaryotes than are their less-connected counterparts. Focusing on the D-independent measure of the orthologous excess retention ERk and correcting for the scale-free statistics by applying logarithmic binning, we reduced the noise level and uncovered a significant trend between connectivity and evolutionary conservation in the underlying data sets. Although earlier approaches determining these trends have been severely impaired by the used data, our results suggest that our method is widely insensitive to the quality of the data sources, an observation that also holds for data inconsistencies and noise.

Our observations also allow a reappraisal of the conclusion that the dependence of the evolutionary distance D on protein connectivity k is negligible (Hahn et al. 2002; Jordan et al. 2003a). Because we found a logarithmic dependency of the excess retention on the proteins' connectivity, ERk ∼ log k, the assumption that any effect on the evolutionary distance D would also depend logarithmically on k, appears reasonable. Provided that the effect of the connectivity k on the evolutionary retention ERk is deemed large, the effect on the evolutionary distance D as exemplified by the mean excess sequence conservation 〈ESC〉 between orthologous sequences appears stronger than previously described. Therefore, the absence of distinctive correlations between the connectivity of a protein and its sequence conservation might be the result of the incorrect assumption that these distributions follow a linear instead a logarithmic trend.

Most importantly, the uncovered correlations indicate that the evolutionary conservation of a protein is affected not only by the protein's individual functional role but also by its topological and contextual placement in the cellular network. These trends are further enhanced by adding essential information to the sets of orthologous proteins. The fact that proteins are not essential for the survivability of the cell and yet are evolutionarily conserved is not a contradiction. However, we see that a protein core that ensures the cells survival has been strongly privileged by evolution.

METHODS

Protein Interactions

Large-scale two-hybrid screens that allow the identification of potential protein–protein interactions between open reading frames from the S. cerevisiae genomic sequence (Uetz et al. 2000; Ito et al. 2000, 2001) are an integral part of proteomics research. Yet, the quality of two-hybrid data is significantly affected by high rates of false positives and false negatives (von Mering et al. 2003), also indicated by the fact that the results that were obtained by different groups have limited overlap (Hazbun and Fields 2001). Moreover, many identified interactions merely rely on positive signals from a single technique and result from indirect observations. In our study, we used the database of interacting proteins (DIP), based on extensive literature searches and aims, to provide a well curated collection of all functional linkages of proteins obtained by experimental methods. The majority of protein–protein interaction data relies on yeast two-hybrid and coimmunoprecipitation experiments. Eighty-four percent of the interactions are detected by only one single experiment, whereas 16% are confirmed by more than one experimental method. DIP currently records 3677 proteins that are involved in 11,249 interactions (Xenarios et al. 2002).

Assignment of Orthology

The determination of orthologous pairs of sequences often employs pairwise BLAST comparisons of whole proteomes. Each protein represents a query against the entire proteome of the other species. Reciprocal best hits in these BLAST searches, emphasizing expectation values <10–3, are considered to be orthologous. Our choice of orthologous protein sequence information is the InParanoid database (Remm et al. 2001), which runs all-versus-all BLAST searches with two sets of sequences. Sequence pairs with mutual two-way best hits are detected and serve as central core ortholog pairs around which further orthologs from both species are clustered in later steps. The initial assumption is that sequences from the same species that are more similar to the main ortholog than to any sequence from other species are in-paralogs that belong to the same group of orthologs. The quality of the resulting orthologous clusters is examined and increased by a final bootstrap analysis. Furthermore, InParanoid provides comprehensive pairwise comparative orthologous information S. cerevisiae and H. sapiens, D. melanogaster, C. elegans, M. musculus and A. thaliana. In our study, we used those core pairs of each cluster that provide a confidence level of 100%. Thus, in the underlying interaction network, we found 1997 proteins that have orthologs in H. sapiens, 1757 in D. melanogaster, 1754 in M. musculus, 1489 in C. elegans and 1898 in A. thaliana.

Assignment of (non-)Essentiality

The Bioknowledge library (Costanzo et al. 2001) compiles scans of experimental literature to provide a comprehensive list of essential and nonessential proteins. Of the S. cerevisiae proteins appearing in the interaction network, 810 are assigned to be essential, 2704 are considered nonessential.

Evolutionary Distance

Assessing the number of substitutions per site, we define the evolutionary distance (Grishin 1997) D between a yeast protein and its orthologous sequences in a reference eukaryote as q = [ln(1 + 2D)]/2D, where q is the fraction of unchanged sites in a sequence alignment of protein pairs (Fraser et al. 2002, 2003; Jordan et al. 2003a,b).

Excess Sequence Conservation

To guarantee balanced sampling for all k-values, we grouped all proteins in bins of logarithmically increasing connectivity k. In each bin, we determine the mean excess sequence conservation,

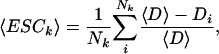graphic file with name M9.gif

where Nk is the number of proteins in the respective bin, and

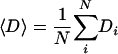graphic file with name M10.gif

is the mean evolutionary distance of the total number of N proteins.

Excess Retention

According to their degree k in the underlying yeast protein interaction network, we grouped all proteins in bins of logarithmically increasing connectivity k. In each bin, the ratio 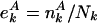Inline graphic represents a certain feature A, where 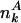Inline graphic is the number of proteins that have A (e.g., being essential or orthologous in a reference organism), and Nk is the total number of proteins. In the absence of a correlation between A and its position in the network, 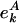Inline graphic has the general k-independent value e = n/N, where 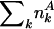Inline graphic is the total number of yeast proteins having feature A, and N = Σk Nk is the total number of yeast proteins in the underlying network. Thus, for each bin k, we define the evolutionary excess retention of a feature A as 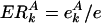Inline graphic, which should have the k-independent value ERk = 1 for a random assignment of A.

Logarithmic Binning

To guarantee balanced sampling for all k-values, we use logarithmic binning of the k-axis, a procedure for curve estimation that corrects for the skewed nature of the scale-free distribution. On a logarithmic scale, we define the bin size

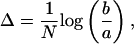graphic file with name M16.gif

where N corresponds to the selected number of bins. Values a and b refer to the minimal and maximal value of the connectivity ki,b = maxi (ki) and a = mini (ki). Thus,

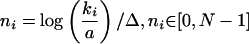graphic file with name M17.gif

reflects the number of the bin we assign a protein with k interactions. Representing the nith bin on the k-axis, we place kni at the end of each bin using kni = a eΔ(ni+1). The advantage of logarithmic binning is an elevated degree of noise reduction that is dependent on the bin size (Albert et al. 2000; Goldstein et al. 2004). Although this procedure causes a loss of accuracy, we still uncover the buried trends to a satisfying extent by applying our statistical methods on the binned data.

Acknowledgments

Research at the University of Notre Dame was supported by grants from the U.S. National Institutes of Health National Institute of General Medical Sciences), the Department of Energy Genomes to Life Program, and the National Science Foundation. Discussions with A.-L. Barabási and Z. Oltvai are gratefully acknowledged. Especially, we acknowledge P. Macdonald for carefully reading and editing the manuscript.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

E-MAIL swuchty@nd.edu; FAX (574) 631-5952.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2300204.

Footnotes

[Supplemental material is available online at www.genome.org.]

References

  1. Albert, R., Jeong, H., and Barabási, A.-L. 2000. Error and attack tolerance of complex networks. Nature 406: 378–382. [DOI] [PubMed] [Google Scholar]
  2. Costanzo, M., Crawford, M., Hirschman, J.E., Kranz, J.E., Olsen, P., Robertson, L.S., Skrzypek, M.S., Braun, B.R., Hopkins, K.L., Kondu, P., et al. 2001. YPD, PombePD and WormPD: Model organism volumes of the BioKnowledge Library, an integrated resource for protein information. Nucl. Acids Res. 29: 75–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Fraser, H., Hirsh, A., Steinmetz, L., Scharfe, C., and Feldman, M. 2002. Evolutionary rate in the protein interaction network. Science 296: 750–752. [DOI] [PubMed] [Google Scholar]
  4. Fraser, H., Wall, D., and Hirsh, A. 2003. A simple dependence between protein evolution rate and the number of protein–protein interactions. BMC Evol. Biol. 3: 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gavin, A., Boesche, M., Krause, R., Grandi, P., Marzioch, M., Bauer, A., Schultz, J., Rick, J.M., Michon, A.M., Cruciat, C.M., et al. 2002. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature 415: 141–147. [DOI] [PubMed] [Google Scholar]
  6. Goldberg, D. and Roth, F. 2003. Assessing experimentally derived interactions in a small-world. Proc. Natl. Acad. Sci. 100: 4372–4376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Goldstein, M., Morris, S., and Yen, G. 2004. Fitting to the power-law distribution. http://arxiv.org/abs/cond-mat/0402322.
  8. Grishin, N. 1997. Estimation of evolutionary distances from protein spatial structures. J. Mol. Evol. 45: 359–369. [DOI] [PubMed] [Google Scholar]
  9. Hahn, M., Conant, G., and Wagner, A. 2002. Molecular evolution in large genetic networks: Connectivity does not equal importance. SFI working paper, 02-08-039. [DOI] [PubMed]
  10. Hazbun, T. and Fields, S. 2001. Networking proteins in yeast. Proc. Natl. Acad. Sci. 98: 4277–4278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ho, Y., Gruhler, A., Heilbut, A., Bader, G.D., Moore, L., Adams, S.L., Millar, A., Taylor, P., Bennett, K., Boutilier, K., et al. 2002. Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature 415: 180–183. [DOI] [PubMed] [Google Scholar]
  12. Hurst, L. and Smith, N. 1999. Do essential genes evolve slowly? Curr. Biol. 9: 747–750. [DOI] [PubMed] [Google Scholar]
  13. Ito, T., Tashiro, K., Muta, S., Ozawa, R., Chiba, T., Nishizawa, M., Yamamoto, K., Kuhara, S., and Sakaki, Y. 2000. Towards a protein–protein interaction map of the budding yeast: A comprehensive system to examine two-hybrid interactions in all possible combinations between the yeast proteins. Proc. Natl. Acad. Sci. 97: 1143–1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ito, T., Chiba, T., Ozawa, R., Yoshida, M., Hattori, M., and Sakaki, Y. 2001. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl. Acad. Sci. 98: 4569–4574. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jeong, H., Mason, S., Barabási, A.-L., and Oltvai, Z. 2001. Lethality and centrality in protein networks. Nature 411: 41–42. [DOI] [PubMed] [Google Scholar]
  16. Jordan, I., Rogozin, I., Wolf, Y., and Koonin, E. 2002. Essential genes are evolutionary more conserved than are nonessential genes in bacteria. Genome Res. 12: 962–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Jordan, I., Wolf, Y., and Koonin, E. 2003a. Correction: No simple dependence between protein evolution rate and the number of protein–protein interactions: Only the most prolific interactors tend to evolve slowly. BMC Evol. Biol. 3. [DOI] [PMC free article] [PubMed]
  18. Jordan, I., Wolf, Y., and Koonin, E. 2003b. No simple dependence between protein evolution rate and the number of protein–protein interactions: Only the most prolific interactors tend to evolve slowly. BMC Evol. Biol. 3. [DOI] [PMC free article] [PubMed]
  19. Koski, L. and Golding, G. 2001. The closest blast hit is often not the nearest neighbor. J. Mol. Evol. 52: 540–542. [DOI] [PubMed] [Google Scholar]
  20. Park, J., Lappe, M., and Teichmann, A. 2001. Mapping protein family interactions: Intramolecular and intermolecular protein family interaction repertoires in the PDB and yeast. J. Mol. Biol. 307: 929–938. [DOI] [PubMed] [Google Scholar]
  21. Remm, M., Storm, C., and Sonnhammer, E. 2001. Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J. Mol. Biol. 314: 1041–1052. [DOI] [PubMed] [Google Scholar]
  22. Uetz, P., Giot, L., Cagney, G., Mansfield, T.A., Judson, R.S., Knight, J.R., Lockshon, D., Narayan, V., Srinivasan, M., Pochart, P., et al. 2000. A comprehensive analysis of protein–protein interactions of Saccharomyces cerevisiae. Nature 403: 623–627. [DOI] [PubMed] [Google Scholar]
  23. von Mering, C., Krause, R., Snel, B., Cornell, M., Oliver, S., Fields, S., and Bork, P. 2003. Comparative assessment of large-scale data sets of protein–protein interactions. Nature 417: 399–403. [DOI] [PubMed] [Google Scholar]
  24. Wagner, A. 2001. The yeast protein interaction network evolves rapidly and contains few redundant duplicate genes. Mol. Biol. Evol. 18: 1283–1292. [DOI] [PubMed] [Google Scholar]
  25. Wall, D., Fraser, H., and Hirsh, A. 2003. Detecting putative orthologs. Bioinformatics 19: 1710–1711. [DOI] [PubMed] [Google Scholar]
  26. Wuchty, S. 2002. Interaction and domain networks of yeast. Proteomics 2: 1715–1723. [DOI] [PubMed] [Google Scholar]
  27. Xenarios, I., Salwinski, L., Duan, X., Higney, P., Kim, S.-M., and Eisenberg, D. 2002. Dip, the database of interacting proteins: A research tool for studying cellular networks of protein interactions. Nucl. Acids Res. 30: 303–305. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES