The phase diagram and hardness of carbon nitrides

Abstract

Novel superhard materials, especially those with superior thermal and chemical stability, are needed to replace diamond. Carbon nitrides (C-N), which are likely to possess these characteristics and have even been expected to be harder than diamond, are excellent candidates. Here we report three new superhard and thermodynamically stable carbon nitride phases. Based on a systematic evolutionary structure searches, we report a complete phase diagram of the C-N system at 0–300 GPa and analyze the hardest metastable structures. Surprisingly, we find that at zero pressure, the earlier proposed graphitic-C₃N₄ structure () is dynamically unstable, and we find the lowest-energy structure based on s-triazine unit and s-heptazine unit.

The carbon-nitrogen (C-N) system was long believed to have materials harder than diamond¹. Recently, carbon nitrides attracted attention due to their potential applications in photocatalysis², photodegradation³ and photoelectrochemical anticorrosion⁴ technology. However, studies of carbon nitrides under pressure face a big problem: neither from theory, nor from experiment it is clear which compositions (i.e., which C/N ratios) will be stable at high pressure, and which compositions will have optimal properties, such as hardness.

Experiments face challenges related to metastability, selection of precursors, determination of the crystal structures and chemical compositions from tiny samples⁵,⁶,⁷; theoretical calculations suffer from assumptions of certain stoichiometries, e.g., C₃N₄¹, CN⁸, C₂N⁹,¹⁰, CN₂¹¹, C₁₁N₄¹², C₃N₂¹³, CN₆.... Some of them are meaningful, while most of them are probably not.

It is difficult to solve this problem because numerous compositions must be tested at each pressure point. For example, at P = 0 GPa, one needs to test compositions of 1:1, 1:2, 1:3,...; 2:1, 3:1, 4:1,...; 2:3, 2:5, 2:7,...... When the pressure changes, e.g. P = 5, 10, 20... GPa, this needs to be re-checked. Therefore, it becomes a major effort.

To solve this problem, we used the ab initio evolutionary algorithm USPEX¹⁴,¹⁵,¹⁶,¹⁷, which can simultaneously find stable stoichiometries and the corresponding structures in multicomponent systems. First, we carried out variable-composition calculations at pressures of 1 atm, 30, 60, 80, 100, 150, 200, and 300 GPa to find the stable and nearly stable compositions (found compositions: C₁₁N₄, C₂N, CN, C₃N₄, CN₂, CN₆). Then, for each of these compositions, we performed fixed-composition calculations with different numbers of formula units at different pressures. We not only obtained the stable compositions and structures at each pressure, we also analyzed the hardness of all the stable and metastable structures and found out the hardest structures and compositions, which provide a solid basis for future synthesis of promising ultrahard materials, stable or metastable. Moreover, we have three other novel findings:

• We uncovered three new superhard phases which are more stable than previous proposals.

• Graphitic-C₃N₄ (space group: , based on s-triazine unit)¹⁸,¹⁹,²⁰ was reported to be stable at ambient pressure and has rich potential applications in photocatalysis², photodegradation³ and photoelectrochemical anticorrosion⁴. However, we found graphitic-C₃N₄ is not dynamically stable and we uncovered two new structures based on s-triazine unit and s-heptazine unit, which are more stable at ambient pressure.

• We determined a complete pressure-composition phase diagram of the C-N system at 0–300 GPa, which provides basis to guide the future experimental synthesis of superhard C-N materials.

Results

Phase diagram

Detailed enthalpy calculations for the most stable structures allowed us to reconstruct the pressure-composition phase diagram (Fig. 1). The first thermodynamically stable carbon nitride, P4₂/m-CN, appears at the pressure of just 14 GPa. This is a superhard 3D-polymeric structure, as all the other stable carbon nitrides. The predicted phase diagram indicates that -CN₂ is stable at 59–298 GPa; P31c-C₃N₄ (i.e., α-C₃N₄) at 22–68 GPa; Cm-C₃N₄ at 68–98 GPa (reported for the first time); -C₃N₄ at 98–187 GPa (reported for the first time); -C₃N₄ (i.e., cubic-C₃N₄) at 187–231 GPa; Cmc2₁-C₃N₄ at 224–300 GPa (reported for the first time); P4₂/m-CN at 14–22 GPa; and Pnnm-CN, stable at 22–97 GPa (see Supplementary Table S1 online for details of structure detailed structural information). These stable structures have lower free energy than any isochemical mixture of other compounds or pure elements (see Supplementary Fig. S1 online). Their main features are the presence of only single C-C, C-N and N-N bonds, with fourfold (tetrahedral) coordination of all C atoms and threefold coordination of all N atoms. For all the stable structures, we computed phonons (see Supplementary Fig. S2 online) and elastic constants (see Supplementary Table S1 online) at ambient pressure, and found them to be dynamically and mechanically stable. Their band structures exhibit wide band gaps as a consequence of strongly localized electrons (see Supplementary Fig. S3 online). Remarkably, all of these phases have three-dimensional frameworks of short covalent bonds, which are responsible for their extreme hardness (Table 1).

Figure 1. (A) Pressure-composition phase diagram of the C-N system.

(B) Enthalpy curves (relative to α-C₃N₄) of the five earlier proposed structures¹⁸ and the newly predicted structures.

Table 1. Hardness (GPa), computed by microscopic models, enthalpy of formation (EF) (eV/atom), and atomic density (atoms/ų) for diamond and stable C-N phases at zero pressure.

Structures	EF	density	Hardness (GPa)
			Oganov	Šimůnek	Gao	Others
Diamond		0.176	89.2	90.7	93.0	93.6a
	0.813	0.167	85.6	89.0	82.2	77.4b
P31c-C3N4	0.504	0.161	78.1	81.3	72.0	82.7c
Cm-C3N4	0.571	0.165	75.5	82.0	71.7
	0.602	0.167	80.2	83.0	70.5
	0.710	0.173	83.8	86.8	75.1	92c
Cmc21-C3N4	0.644	0.167	79.1	76.1	72.7
P42/m-CN	0.395	0.155	58.3	70.5	54.7
Pnnm-CN	0.422	0.160	59.6	72.7	57.0	62.3d

^aReference³⁸. ^bReference¹¹. ^cReference²¹.^dReference³².

CN₂ is stable in the tetragonal structure at 59–298 GPa (Fig. 2a)¹¹. In this structure, each C atom is tetrahedrally bonded with four N atoms and each N atom is three-coordinate (2 C-N bonds and 1 N-N bond). Notably, under normal conditions, the 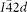-CN₂ structure has an atomic number density of 0.167 atoms/ų, which is just a little lower than that of diamond (GGA result: 0.176 atoms/ų; experimental result: 0.178 atoms/ų¹⁸) (Table 1). Moreover, its N-N bond length is only 1.359 Å, and C-N bond length is 1.480 Å. Both are shorter than the C-C bond length of diamond (1.547 Å) (Table 1).

Figure 2. Crystal structures of carbon nitrides.

(A) -CN₂. (B) P31c-C₃N₄. (C) Cm-C₃N₄. (D) -C₃N₄. (E) -C₃N₄. (F) Cmc2₁-C₃N₄. (G) P4₂/m-CN. (H) Pnnm-CN. Grey (large) and blue (small) spheres denote C and N atoms, respectively. -C₃N₄ structure is a vacancy-ordered derivative of the diamond structure.

C₃N₄ has attracted much attention for more than 20 years¹,¹⁸. It is not only because the predicted bulk modulus of the cubic-C₃N₄ structure is higher than that of diamond²¹,²², but also because of the rich potential applications of the graphitic-C₃N₄ in water splitting, organic photosynthesis and environmental remediation²³. The two most important graphitic carbon nitrides discussed in the literature are based on s-triazine²⁴ and s-heptazine (i.e. tri-s-triazine)²⁵ units. The graphitic-C₃N₄ (space group: , based on s-triazine unit) was reported to be stable at ambient conditions, and there are numerous reports in the literature that approach the synthesis of this material¹⁸,¹⁹,²⁰. Besides, many theoretical studies are based on this structure²⁶. However, we found it to be dynamically unstable (see Supplementary Fig. S2 online). This is in agreement with the prior prediction of Deifallah et al.²⁷ and Bojdys et al.²⁸, which reported a buckled-graphitic-C₃N₄ to be more stable than the planar graphitic-C₃N₄. In addition, we found the most stable structures based on s-triazine unit or s-heptazine unit are not just a buckled structure, all their layers are connected by one nitrogen atom with sp² C-N bonds²⁹, as shown in Supplementary Fig. S4. We found that the lowest-energy form of structures based on s-triazine unit and s-heptazine unit are almost the same. They have similar topology and belong to the same space group Cc (No. 9). The s-heptazine-based structures were postulated on the basis of density-functional calculations²⁵ and experiments²⁸ to be more stable at ambient conditions. Our predictions support this conclusion: Cc-C₃N₄ (s-heptazine) is lower in energy than Cc-C₃N₄ (s-triazine). Moreover, we have compared their energy with other theoretical proposals²⁵,²⁹, as shown in Supplementary Table S5 online. The newly found structures have lower energies than the previously proposed structures. We must emphasize that all calculations on zero-pressure phases of C₃N₄ took account of van der Waals interactions (see Methods).

At 22–68 GPa, the α-C₃N₄ structure is the most stable. The α-C₃N₄ structure is a three-dimensional framework, where each C atom has four inequivalent bonds to N atoms, and each N atom has three inequivalent bonds to C atoms (Fig. 2b). This kind of framework can very easily lead to an asymmetric charge distribution and weak piezoelectricity, which has been confirmed by our calculations (see Supplementary Table S2 online) and recent experimental work³⁰. At 68–98 GPa, the Cm-C₃N₄ structure is more stable than any other known C₃N₄ polymorph, and also consists of corner-sharing CN₄ tetrahedron (Fig. 2c). We also found another new structure at the same pressure range, Pmn2₁-C₃N₄ (see Supplementary Fig. S4 online), which is just 2 meV/atom higher in enthalpy than the Cm-C₃N₄ structure. The -C₃N₄ structure (Fig. 2d) is stable at 98–187 GPa. However, at pressures above 187 GPa this structure gives way to a high-density structure, cubic-C₃N₄, which is denser and less compressible (i.e. has higher bulk modulus) than diamond. Besides, it has the largest shear modulus and Young's modulus among all stable carbon nitrides (Table 2). At > 224 GPa (and at least to 300 GPa), the orthorhombic Cmc2₁-C₃N₄ structure, which has not been reported before, is stable. Its structure (Fig. 2f) can be described as an ABAB sequence of puckered graphitic-C₃N₄ layers with strong covalent bonds formed between the layers.

Table 2. Hardness (GPa), computed by the macroscopic Chen model, bulk modulus B (GPa), shear modulus G (GPa), Young's modulus E (GPa), k²G (k = G/B) and Poisson's ratio v for diamond and the stable C-N phases at zero pressure.

Structures	B	G	E	k 2 G	v	HChen
Diamond	434.9	520.6	1116.4	748.4	0.0722	92.9
	398.3	351.5	814.9	274.1	0.1589	50.3
P31c-C3N4	383.6	330.6	770.4	245.5	0.1653	47.0
Cm-C3N4	353.6	328.3	752.1	283.0	0.1455	51.4
	372.0	345.8	791.9	298.8	0.1452	53.1
	436.6	374.4	873.4	275.2	0.1666	50.5
Cmc21-C3N4	347.1	335.1	760.5	312.2	0.1348	54.6
P42/m-CN	326.8	272.7	640.1	189.8	0.1736	40.0
Pnnm-CN	338.6	327.0	742.2	305.0	0.1347	53.8

At 14–22 GPa, CN is stable in the P4₂/m-CN structure. When pressure is above 22 GPa, the Pnnm-CN structure is more stable (22–97 GPa), which is consistent with previous theoretical predictions⁸,³¹. The P4₂/m-CN structure has a three-dimensional network of covalent bonds composed of tetragonal C-N rings, connected by the C-C bonds (Fig. 2g), while the Pnnm-CN structure is composed of strongly puckered graphene layers of composition CN, connected to each other by C-C bonds (Fig. 2h). Both the P4₂/m-CN and Pnnm-CN structures have four-coordinate C atoms, connected with 3 N atoms and 1 C atom; and three-coordinated N, connected with 3 C atoms. The C-C bond lengths in the P4₂/m-CN and Pnnm-CN structures are 1.585 Å and 1.605 Å, respectively, i.e. longer than in diamond (1.547 Å). Interestingly, the P4₂/m-CN structure is similar to the host-guest structure recently predicted as a metastable form of carbon³².

Komatsu⁹ reported synthesis of sp³-bonded carbon nitride C₂N, but he did not provide the detail structural information. We have tried to find C₂N structures based on Komatsu's report, but all the structures that we found are not thermodynamically stable under pressure. Horvath-Bordon, Kroke, McMillan et al.³³, showed a nice work on the synthesis of crystalline carbon nitride imide phase, C2N2(NH) under high pressure and high temperature conditions, which indicated that hydrogen does help carbon nitrides to be stable and studying the ternary C-N-H system should be interesting.

Hardness

Hardness is one of the biggest factors that stimulated interest in carbon nitrides. To study their hardness, we have used the Oganov³⁴,³⁵, Šimůnek³⁶, and Gao³⁷ models that are based on microscopic parameters, and the Chen model³⁸ which is based on macroscopic parameters. All the results, including the Voigt-Reuss-Hill elastic moduli, are listed in Tables 1 and 2.

The hardest carbon nitride among the stable structures is -CN₂, based on all microscopic models. According to the hardness models of Oganov, Šimůnek, and Gao, its hardness is 85.6, 89.0 and 82.2 GPa, respectively. To our surprise, its hardness is very close to that of diamond (89.2, 90.7 and 93.0 GPa according to Oganov, Šimůnek, and Gao model). Moreover, its hardness is higher than that of cubic-C₃N₄, which was believed to be the hardest carbon nitride. Based on the microscopic models all the stable carbon nitrides are superhard. In addition, the three micro-models give similar values of hardness for every predicted structure, as can be seen in Table 1, because in all these models the hardness is determined by bond lengths and bond strengths, even though the models do differ mathematically and ideologically.

Based on the macroscopic Chen model, the hardest structure is Cmc2₁-C₃N₄ (Table 2). The hardness value in this model is determined by parameter k²G (k = G/B, G and B are shear and bulk moduli, respectively). We found that the Cmc2₁-C₃N₄ structure has the largest k²G among the stable structures (Table 2). This makes the Cmc2₁-C₃N₄ structure the hardest one among the stable structures according to the Chen model. Notably, the predicted Poisson's ratio of the Cmc2₁-C₃N₄ structure is 0.1348, almost the lowest among all the stable structures (v = 0 means that the material will not deform in a direction perpendicular to the applied load). According to the Chen model, all the stable structures are superhard, which is consistent with the prediction of the microscopic models. While the exact hardness values produced by the microscopic and macroscopic models are in this case rather different (which is unusual), the qualitative conclusions are similar. Note, on passing, that the bulk modulus of cubic-C₃N₄ is larger than that of diamond, in good agreement with theoretical studies²¹,²².

Metastable structures can often be synthesized by choosing appropriate precursors and/or controlling conditions such as the quench rate²⁰. If such a metastable phase has superior properties and can be depressurized to ambient conditions, it will be attractive for applications. For example, the hardest structure does not have to be the most stable one. For each structure/composition, its distance from the thermodynamic convex hull is the appropriate measure of its (meta)stability: the closer it is to the convex hull, the more stable it is. To find the hardest structure and the hardness-favored compositions in the C-N system, we also calculated the hardness and mechanical properties of metastable structures in a reasonable range of enthalpies (we have analyzed all structures within 0–0.2 eV/atom from the convex hulls at all pressures in the range 0–300 GPa). The five hardest structures in the C-N system, selected using the Oganov and Chen models, and their hardnesses, are listed in Supplementary Table S3 online. All of them are dynamically and mechanically stable at ambient conditions based on the computed phonon dispersions and elastic constants (see Supplementary Fig. S5 and Table S4 online).

According to the Oganov model, the five hardest structures in the C-N system are -CN₂, -CN₂, -CN₂, -C₁₁N₄ and -C₃N₄, with hardnesses 87.8, 86.0, 85.6, 83.8 and 83.8 GPa, respectively. Thus, compositions CN₂, C₁₁N₄, and C₃N₄ are hardness-favored based on the Oganov microscopic model. Strikingly, the hardest structure is -CN₂, with hardness of 87.8 GPa, just 1.4 GPa less than that of diamond (89.2 GPa based on the Oganov model).

According to the Chen model, the top five hardest structures of the C-N system are -C₁₁N₄, C2/m-C₂N, P2₁/c-C₂N, Cm-C₁₁N₄ and Pmn2₁-C₂N, with hardnesses of 74.1, 73.5, 72.6, 71.5 and 69.6 GPa, respectively. Consequently, compositions C₁₁N₄ and C₂N are hardness-favored based on the Chen macroscopic model. The hardest structure is -C₁₁N₄, with hardness of 74.1 GPa based on the Chen model. It is harder than the well-known superhard cubic-BN, which has a hardness of 62 GPa³⁹. This structure is a vacancy-ordered derivative of the diamond structure. The notable feature of the -C₁₁N₄ structure is that its shear modulus is much larger than its bulk modulus, similar to diamond. Besides, this structure has a very small Poisson's ratio (0.0985), which is one of the factors responsible for its superhardness.

Three-dimensional covalent bond network is one of key features of superhard materials. As shown in Figs. 3c, 3d and Supplementary Fig. S6 online, high electron localization is observed near midpoints of C-N, C-C and N-N bonds, indicating infinite three-dimensional covalent bond networks in all these phases. One can also see pronounced maxima of the electron localization function near N atoms, corresponding to the lone electron pair of the nitrogen atom.

Figure 3. Electronic structure of Cm-C₃N₄ and -C₃N₄ at 0 GPa.

Band structure and density of states (DOS) of (A) <>Cm-C₃N₄, and (B)<> 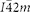-C₃N₄. E<>_F, Fermi energy. Electron localization function of (C) <>Cm-C₃N₄, and (D)<> -C₃N₄ at ELF = 0.85.

The widespread interest in carbon nitrides also arises from their predicted wide band gap, high atomic density and excellent thermal conductivity¹⁸. The calculated band gaps of the -CN₂, P31c-C₃N₄, Cm-C₃N₄, -C₃N₄, -C₃N₄, Cmc2₁-C₃N₄, P4₂/m-CN and Pnnm-CN structures are 3.57, 3.78, 3.74, 2.75, 2.91, 3.43, 3.81 and 3.71 eV, respectively. In all cases, the gap is found to be indirect, except -C₃N₄ (see Supplementary Table S2 online). One should keep in mind that DFT usually underestimates experimental band gaps by ~ 30%. All of these phases have predicted atomic densities approaching that of diamond (Table 1). On the basis of the high atomic density and bonding topology of these structures, they should be excellent thermal conductors¹⁸.

In summary, we have carried out a systematic search for stable phases in the C-N system in the pressure range 0–300 GPa using the ab initio evolutionary algorithm USPEX. We have predicted eight stable carbon nitride phases, three of them have never been reported. Carbon nitrides appear as stable phases at pressures above 14 GPa. All carbon nitrides that have stability fields are superhard wide-gap semiconductors or insulators, and remain dynamically and mechanically stable at zero pressure and thus can be quenched to ambient conditions. Among the stable carbon nitrides, the hardest one is -CN₂ (Cmc2₁-C₃N₄) based on the Oganov (Chen) models. Compositions C₁₁N₄, C₂N, CN₆ produce very low-enthalpy metastable states. Considering both stable and low-enthalpy metastable structures, the hardest structure is -CN₂ (-C₁₁N₄) based on the Oganov (Chen) models, and their hardnesses are close to that of diamond. At ambient pressure the lowest-energy form of C₃N₄ is Cc-C₃N₄ (s-heptazine), while another structure Cc-C₃N₄ (s-triazine) is a little higher in energy, but both s-heptazine and s-triazine units C₃N₄ could be synthesized using proper precursors. With respect to the synthesis of superhard materials, P4₂/m-CN is a good candidate, because it is thermodynamically stable at the lowest pressure of 14 GPa. In addition, CN₂ will be a promising compound to be synthesized in experiment, due to its stability over a wide pressure, and this phase has extremely high hardness.

Methods

Structure relaxations and energy calculations were performed using density functional theory (DFT)⁴⁰ within the generalized gradient approximation (GGA)⁴¹ as implemented in the VASP code⁴². The plane wave kinetic energy cutoff was set to 600 eV. Phonon dispersions were calculated by the supercell approach as implemented in the PHONOPY code⁴³. The elastic constants were calculated from the strain-stress relations⁴⁴, and hardness was computed using four different models: microscopic Oganov³⁴,³⁵, Šimůnek³⁶ and Gao³⁷ models and the Chen model³⁸, which is based on macroscopic parameters (elastic moduli). The enthalpy of formation of compounds C_xN_y is calculated by ΔH (per atom) = {H(C_xN_y)-[xH(C) + yH(N)]}/(x + y), where H(C_xN_y), H(C) and H(N) are enthalpies of C_xN_y (per formula), and of stable phases of carbon and nitrogen (per atom), respectively, at given pressure. Energies and phonon dispersion curves C₃N₄ structures at zero pressure were checked with the van der Waals corrections⁴⁵.

Supplementary Material

Supplementary Information

Supplementary Information for the phase diagram and hardness of carbon nitrides