Impact of metabolic heterogeneity on tumor growth, invasion, and treatment outcomes

Abstract

Histopathological knowledge that extensive heterogeneity exists between and within tumors has been confirmed and deepened recently by molecular studies. However, the impact of tumor heterogeneity on prognosis and treatment remains as poorly understood as ever. Using a hybrid multi-scale mathematical model of tumor growth in vascularized tissue, we investigated the selection pressures exerted by spatial and temporal variations in tumor microenvironment and the resulting phenotypic adaptations. A key component of this model is normal and tumor metabolism and its interaction with microenvironmental factors. The metabolic phenotype of tumor cells is plastic, and microenvironmental selection leads to increased tumor glycolysis and decreased pH. Once this phenotype emerges, the tumor dramatically changes its behavior due to acid-mediated invasion, an effect that depends on both variations in the tumor cell phenotypes and their spatial distribution within the tumor. In early stages of growth, tumors are stratified, with the most aggressive cells developing within the interior of the tumor. These cells then grow to the edge of the tumor and invade into the normal tissue using acidosis. Simulations suggest that diffusible cytotoxic treatments such as chemotherapy may increase the metabolic aggressiveness of a tumor due to drug-mediated selection. Chemotherapy removes the metabolic stratification of the tumor and allows more aggressive cells to grow towards blood vessels and normal tissue. Anti-angiogenic therapy also selects for aggressive phenotypes due to degradation of the tumor microenvironment, ultimately resulting in a more invasive tumor. In contrast, pH buffer therapy slows down the development of aggressive tumors, but only if administered when the tumor is still stratified. Overall, findings from this model highlight the risks of cytotoxic and anti-angiogenic treatments in the context of tumor heterogeneity resulting from a selection for more aggressive behaviors.

Major findings

Cancers commonly have altered metabolism, which involves excessive glucose consumption and acid production. This leads to acidification of the microenvironment that surrounds tumors. Because cancer cells are better adapted to acidic conditions than normal cells, they can damage and invade normal tissue. Acquisition of this invasive phenotype is complex and requires persistent evolutionary selection. Heterogeneity of metabolic phenotypes has an impact on tumor behavior. In this paper, we implement a cell-based mathematical model to investigate this heterogeneity and how it is modified as result of therapy. The model includes metabolic interrelationships that influence both tumor and normal cell fate and the microenvironment. The model recapitulates normal tissue homeostasis, tumor growth, evolution of invasive phenotypes and response to therapy, with many of the predictions directly validated with in vivo experimental results. Spatial, temporal and phenotypic heterogeneity have a significant impact on the behavior of the tumor, suggesting new methods for studying tumor growth.

Quick guide to model and major assumptions

0.1 Diffusible Molecules

For a molecule that diffuses across a domain x, the concentration C(x) is described by

$$\frac{\partial C}{\partial t}=D{\nabla }^{2}C+f(\mathbf{C},\mathbf{p}),$$ (0.1)

with diffusion constant D. Function f describes the production and consumption of the molecule depending on the concentrations of all extracellular molecules (C(x)) and parameters (p(x)) specific to the cell at position x. The three diffusible variables in the model are oxygen (O), glucose (G), and extracellular pH via production of protons (H).

0.2 Cellular Metabolism

Cells primarily produce energy (ATP) from glucose, using either an efficient aerobic pathway that requires oxygen, or using glycolysis, an inefficient anaerobic pathway. The model assumes that cells have a target level of ATP demand and that they meet this by using the aerobic pathway as much as possible. If oxygen levels are insufficient to support this level of ATP, then the difference is made up by increasing flux through the glycolytic pathway (i.e., the Pasteur effect).

Oxygen consumption f_O is determined by oxygen concentration, using Michaelis-Menten kinetics with a half-maximum of k_O,

$$f_o=-V_o\frac{O}{O+k_o}.$$ (0.2)

Glucose consumption is driven by the need to meet normal ATP demand, modified by a Michaelis-Menten term with a half-maximum of k_G, given by

$$f_G=-(\frac{p_G{A}_o}{2}+\frac{27f_o}{10})\frac{G}{G+k_G}.$$ (0.3)

The coefficient p_G is a multiplier representing the altered glucose metabolism seen in many tumor cells (i.e., the Warburg Effect). Normal cells have p_G=1. For tumor cells, p_G is variable, representing a continuum of metabolic phenotypes. For p_G>1, the tumor will consume more glucose than needed to meet normal ATP demand. This phenotype can be viewed as either a cell possessing constitutively activated glucose consumption, or the cell may be forced to increase consumption due to increased ATP demand from other abnormally activated cellular processes such as ion pumps. The actual ATP production rate for the cell is determined from nutrient consumption rates, given by

$$f_A=-(2f_G+\frac{27f_o}{5}).$$ (0.4)

Proton production is linked to the amount of glycolysis that does not feed the aerobic pathway, given by

$$f_H=k_H\left(\frac{29(p_G{V}_o+f_o)}{5}\right),$$ (0.5)

where parameter k_H accounts for proton buffering.

The functions f_O, f_G, and f_H are used for the corresponding reaction-diffusion functions f in Eq. 0.1. The ATP production rate (f_A) determines cell behavior.

0.3 Hybrid Cellular Automaton

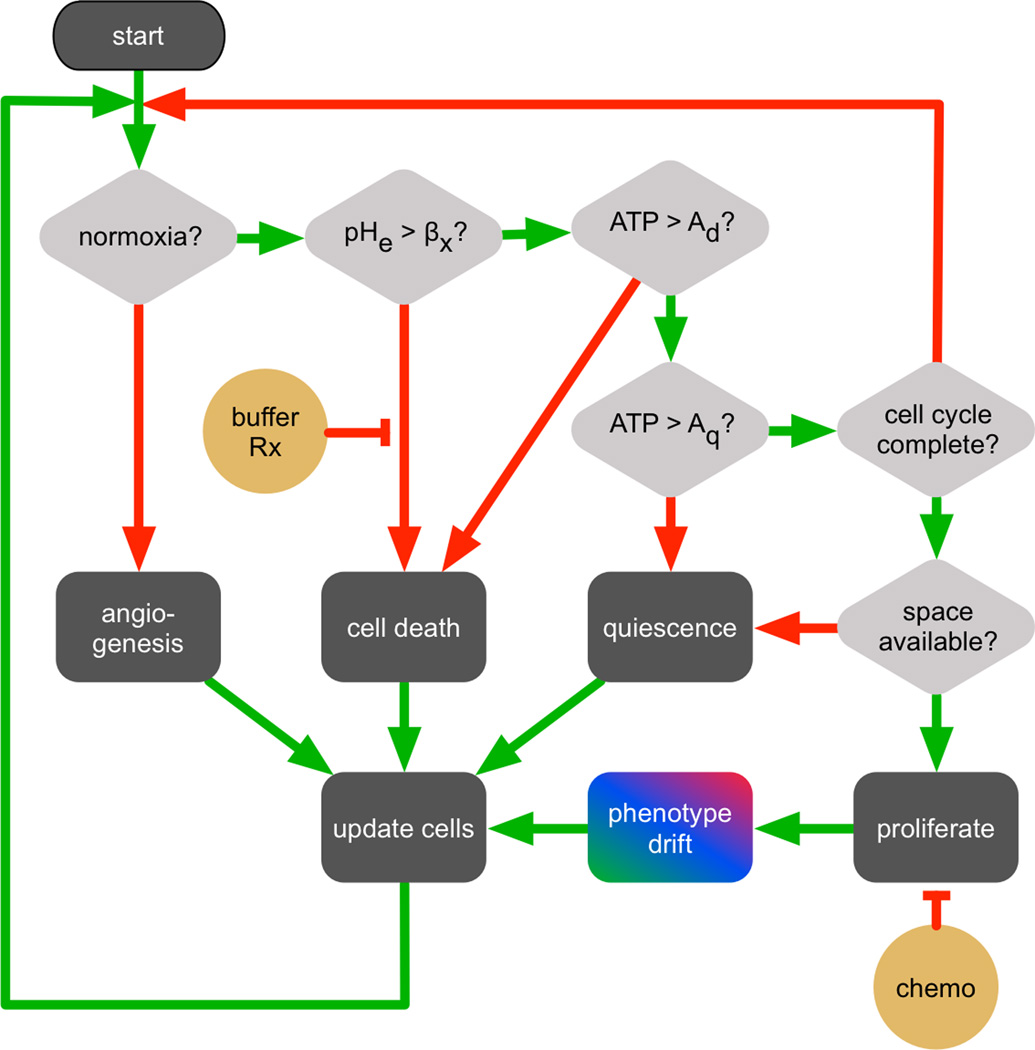
The metabolic program above is implemented into each cell of hybrid cellular automaton (HCA) model, simulated on a square lattice. One cell type is permitted per grid point, either a normal cell, tumor cell, necrotic cell, or blood vessel. For each time step dt, homeostatic cell death is calculated by selecting at random a fraction p_D of the cells and removing them from the grid, leaving empty space. Remaining cells are put through a decision process (Fig. 1) based on the metabolic state of each cell and the nutrient concentrations at that point. Between each step of the HCA, the reaction-diffusion partial differential equations (0.1) are solved over the domain of the HCA. The timescale of the HCA is on the order of hours or days, while the metabolic and diffusive processes operate on the order of seconds and minutes. Therefore, these can be simulated sequentially. Cells that have enough ATP production to meet the threshold of proliferation (A_q) will advance their cell cycle faster with higher ATP production rates (See Supplemental Information for details). This cell-cycle stretching as a function of microenvironment has been recently observed experimentally [1]. Cells that have completed the cell cycle will proliferate if there is adjacent space. The cycle is not advanced if the cell is quiescent due to lowered ATP production. Cells with production less than the death threshold (A_d) are removed. Nutrient-based cell-cycle mechanisms have been modeled in various ways in agent-based models [2, 3]. The present work does not include cell migration or mechanical effects. We have implemented the model in 2D in part because the primary experimental system used by our group to test and validate the predictions of our model is a dorsal wound chamber, which is a quasi-2D in vivo system [4].

Figure 1.

CA decision process for each cell, with diamonds representing decisions, green arrows meaning the condition is satisfied, and red meaning the condition is not met. Therapies are shown in yellow.

0.3.1 Phenotype variation and selection

Tumor cells in the model have two continuously variable, heritable traits: excess glucose consumption, p_G from Eq. 0.3; and resistance to low extracellular pH in the microenvironment [5], β_T . These traits are passed from a parent tumor cell to its two daughter cells with some small variation, chosen at random from an interval equally weighted in both directions to avoid biased drift. The model is agnostic with respect to specific biological mechanisms that underlie this drift, which could include gradual accumulation of mutations, regulation of gene transcription by epigenetics or aneuploidy, or changes in the number or structure of organelles, for example. The evolution of these phenotypes in time and space is an important consideration of this work.

0.3.2 Angiogenesis and vascular degradation

A point-source vasculature is used to simulate parallel blood vessels passing perpendicularly through the two-dimensional tissue slice. The primary function of the vasculature in this model is to spatiotemporally deliver nutrients and remove waste products. The field of vessels is seeded using a circle-packing algorithm based on vessel densities in vivo. This initial distribution can be altered by the creation of new vessels through angiogenesis, or by vessel degradation. To model angiogenesis, if an area of the simulation domain develops hypoxia, new vessels are added to the region until there is enough oxygen to remove the hypoxic state. Multiple mechanisms have been proposed for vessel loss in a tumor, including collapse due to mechanical stress [6]; loss of flow due to upstream remodeling [7]; and leaky vessels [8]. Here, vessels are degraded over time due to surrounding tumor growth until they are lost (see Supplement).

0.3.3 Administration of therapy

pH buffer therapy is approximated by increasing both the baseline pH in the blood (pH_o) by 0.2 units of pH and the diffusion constant of the protons D_H (increased by a factor of 3) during therapy, causing increased removal of protons. Chemotherapy is pulsed through the vasculature, diffusing through the tissue subject to Eq. (0.1). Cell death depends on the concentration of the drug at the cell position (see Supplement). The schedule is five pulses, two weeks apart. Anti-angiogenic therapy is simulated by preventing new blood vessels from forming during therapy.

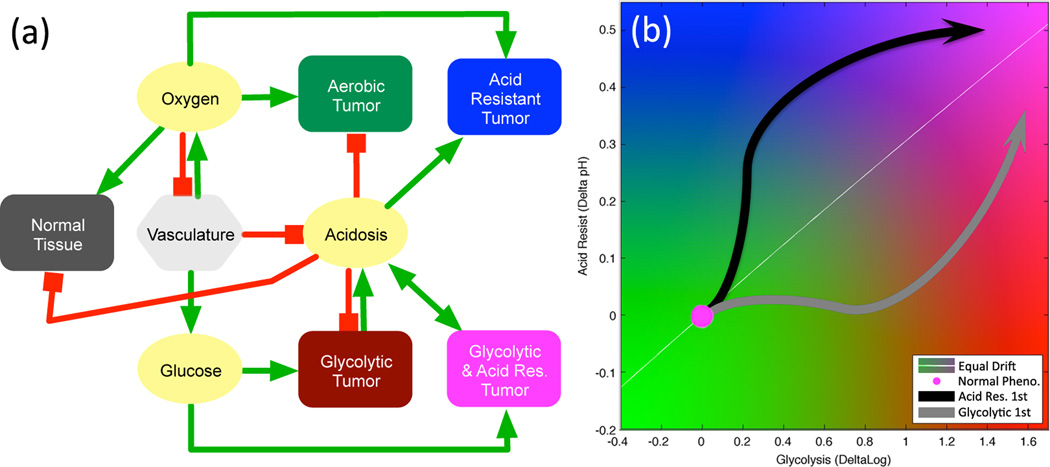
0.3.4 Interaction Network

A summary of the model interactions is shown in Figure 2a. Panel (b) shows the two dimensional tumor phenotype map used in the simulations. For clarity, axes are not labeled in subsequent figures, but have the same range as shown here. Parameters for the model are shown in Table 1.

Figure 2.

(a) Model interaction network for diffusible molecules (yellow), vasculature (light gray) , normal tissue (dark gray), and variable tumor phenotypes (colors). Red lines show negative or inhibitory interactions and green lines show positive or productive interactions. (b) A flow map of tumor phenotype space. The horizontal axis is the constitutively activated log-glycolytic capacity (log p_G), and vertical axis is the change in acid resistance (−Δβ_T) from normal, with higher resistance to acidic conditions being higher on the plot. The normal metabolic phenotype is at the origin (magenta circle), while the arrows represent two possible routes to reach the aggressive state of high glycolysis and high acid-resistance, as discussed in section 3.1. The white line shows the equal maximal variation, such that a cell acquiring maximal positive changes in glycolytic capacity and acid-resistance on each division would move along this line in phenotype space.

Table 1.

Parameter Values

Param.	Value	Unit	Description	Reference
δx	20	µm	Diameter of CA grid point	Model specific
pD	0.005	1/day	Normal tissue death rate	[42]
pδ	0.7	1/day	Death prob. in poor conditions	Model specific
pn	5×10−4	1/day	Necrotic turnover rate	Model specific
DO	1820	µm2/s	Diffusion rate of O2	[43]
DG	500	µm2/s	Diffusion rate of glucose	[44]
DH	1080	µm2/s	Diffusion rate of protons	[40]
DC	100	µm2/s	Diffusion rate of chemo	Model specific
Oo	0.056	mM	O2 concentration in blood	[45]
Go	5	mM	Glucose concentration in blood	[46]
pHo	7.4	pH	pH of blood	Physiologic pH
VO	0.012	mM/s	Max. O2 concentration	[45]
kO	0.005	mM	Half-max O2 consumption	[47]
kG	0.04	mM	Half-max glucose consumption	[47]
kH	2.5×10−4	—	Proton buffering coefficient	[40]
βN	6.65	pH	Normal acid resistance	[48]
βT,min	6.1	pH	Maximal acid resistance	[47]
pG,max	50	—	Maximal glycolytic phenotype	[49]
ΔH	0.001	—	Pheno. Variation rate (acid res.)	Model specific
ΔG	0.05	—	Pheno. Variation rate (glycolysis)	Model specific
Ad	0.3	—	ATP threshold for death	Model specific
Aq	0.8	—	ATP threshold for quiescence	Model specific
τmin	0.8	Day	Min. cell cycle time	[47]
σmin	80	µm	Min. vessel spacing	[50]
σmean	158	µm	Mean vessel spacing	[50]
ζO	[8,20]×10−4	mM	Hypoxic angiogenesis zone	Model specific
νmean	20	—	Vessel stability	Model specific
pang	0.3	—	Angiogenesis rate	Model specific
Co	1	—	Chemo concentration in blood	Model specific
Cd	0.25	—	Min chemo conc. half-max	Model specific

1 Introduction

Tumor heterogeneity at the genetic scale has been known for decades and until recently was largely viewed as a whole tumor metric. Historically, molecular techniques average genomic signals from large numbers of cells from single biopsies, thus smoothing and potentially hiding underlying variations. These average signatures have dominated the molecular era of cancer investigation and have driven biomarker development. However, a potential issue was recently highlighted by Swanton and colleagues [9], who showed that multiple biopsies from the same tumor display distinct genetic profiles and yet are phenotypically similar. This genotypic divergence and phenotypic convergence has previously been hinted at theoretically [10] and may be a predictable evolutionary consequence of the tumor ecosystem [11, 12]. The intricate dialogue between tumor cells and environment selects for clones that are best adapted phenotypically to survive, regardless of specific mutations that may facilitate tumor progression. Furthermore, this environment is temporally and spatially heterogeneous largely due to variations in blood flow, resulting in local fluctuations of nutrients, growth factors and other cellular populations (e.g. normal cells, stromal cells and immune cells). These dynamics occurring within the cancer ecosystem are almost impossible to dissect via experimentation alone.

A major open question in biology is how to connect genotype with phenotype. In many genetic diseases, a defect within a single gene manifests through observable changes that usually allows confident diagnosis of the specific mutation based on the phenotypic manifestations. In contrast, cancer cells frequently harbor thousands of mutations so that the connection to phenotype is less clear. Whilst we understand that the genotype to phenotype mapping is critical for integration of genetic information with a more functional understanding of the phenotypic behavior that it may facilitate, the practical reality is that its very difficult to quantify phenotypes and far easier to measure genotypes. Genetic heterogeneity within a tumor continues to be of great interest to the cancer community, with the advent of new tools to measure fewer cells in more detail, a serious effort is being put into quantifying this heterogeneity and understanding how it evolves as the tumor progresses and how it relates to overall outcome [13, 14, 15]. However, we are far from understanding how the microenvironment modulates this heterogeneity and drives the overall phenotypic behavior of the tumor cell population. We strongly believe that only through the integration of mathematical and computational models with careful experimentation can we hope to bridge the gene-centric and microenvironment-centric views of cancer progression. Here we focus on the phenotypic scale, as it allows us to circumvent much of the complexity observed at molecular scales and instead examine the functional outcome of mutation (be it genetic or epigenetic). Specifically, we consider the metabolic phenotype, in part because tumors are known to be metabolically very different from their normal tissue counterparts and in part because we believe metabolism contributes significantly to tumor progression.

Mathematical models of cancer progression have examined avascular growth [16, 17, 3], angiogenesis [18, 19], vascular growth [20, 21], invasion [22, 23] and metastasis [24, 25]; also see these reviews [26, 17, 27, 25]. Tumor metabolism, specifically glycolytic metabolism and its development has also been extensively studied [28, 2]. However, almost all of these models (with a few exceptions) ignore normal tissue and assume the tumor grows in a field of nutrients or extra cellular matrix. Fewer models explicitly consider phenotypic heterogeneity [22, 29] and those that do again ignore normal tissue. Our central focus here is to examine the interplay between cellular metabolism and the microenvironment (including normal cells), and how this leads to phenotypic heterogeneity within the tumor cell population. Understanding how this phenotypic heterogeneity develops through space and time [30] will allow us to better understand progression, treatment failure, and crucially lay the groundwork for novel therapies.

In our evolutionary model, tumors emerge from tightly regulated fields of cells in a largely normal tissue. At its simplest, homeostatic regulation of normal tissue ensures that cell death is balanced by birth. This homeostasis is not static but dynamic and remarkably robust to physical and chemical perturbation, e.g. wounding. Cancer cells both overcome and exploit these homeostatic mechanisms as they evolve strategies to maximize their proliferation [31].

We have previously examined metabolism [28, 2, 29] as a driver of tumor progression through the glycolytic pathway and associated acidosis. Extracellular pH (pH_e) is a potential treatment target, and we have recently published a series of experiments that validate this view [32, 33, 4]. Our intention here is to examine this work in light of the lens of metabolic and microenvironmental heterogeneity by reproducing observation and suggesting novel interpretation and treatment strategies. The focus of the work is on acid-mediated invasion, wherein tumor cells that have abnormally high glycolytic capacity acidify the local environment, causing the surrounding tissue to degrade and allow for tumor growth.

2 Materials and Methods

To investigate the effect of metabolism and the microenvironment on tumor growth and phenotype selection, a hybrid cellular automaton (HCA) in two dimensions is used to model cellular processes such as cell proliferation, death, and vascular remodeling. Metabolic activity of individual cells is calculated by solving a set of algebraic equations. The diffusion of molecules is calculated by solving a system of partial differential equations over the domain of simulation. The components of the model are described in the Quick Guide to Model section. Additional derivations and supporting algorithms of the model equations are given in the Supplemental Information.

3 Results

3.1 Tumors acquire acid-resistance followed by glycolytic capacity

In the absence of tumor cells, the dynamic equilibrium of the model is a homeostatic normal tissue with vasculature. The normal cells turnover, maintaining a cellular density that is determined by the choice of parameters for the proliferation algorithm. This homeostasis plays an important role in the model, competing with tumor cells for available space at the tumor edge. To illustrate the homeostatic properties of the normal tissue, two examples are shown in the Supplement.

There are two modes of tumor growth, depending on the activity of the normal tissue surrounding the tumor. The first is homeostatic-limited growth, where tumor growth is limited by the surrounding normal cells. Since the tumor can only grow into space relinquished by the normal cells at the tumor-normal interface, the growth rate is correlated with the normal tissue homeostatic death rate. Tissue which has a faster turnover rate relinquishes more empty space per unit of time, and therefore allows for faster tumor growth (see Supplement). The second mode of growth is invasive growth. This occurs when the tumor mass causes surrounding normal cells to die at a rate faster than the homeostatic death rate. This results in rapid availability of free space and subsequent tumor growth. There are two possible causes for induced cell death in the present model: nutrient deprivation and acidosis.

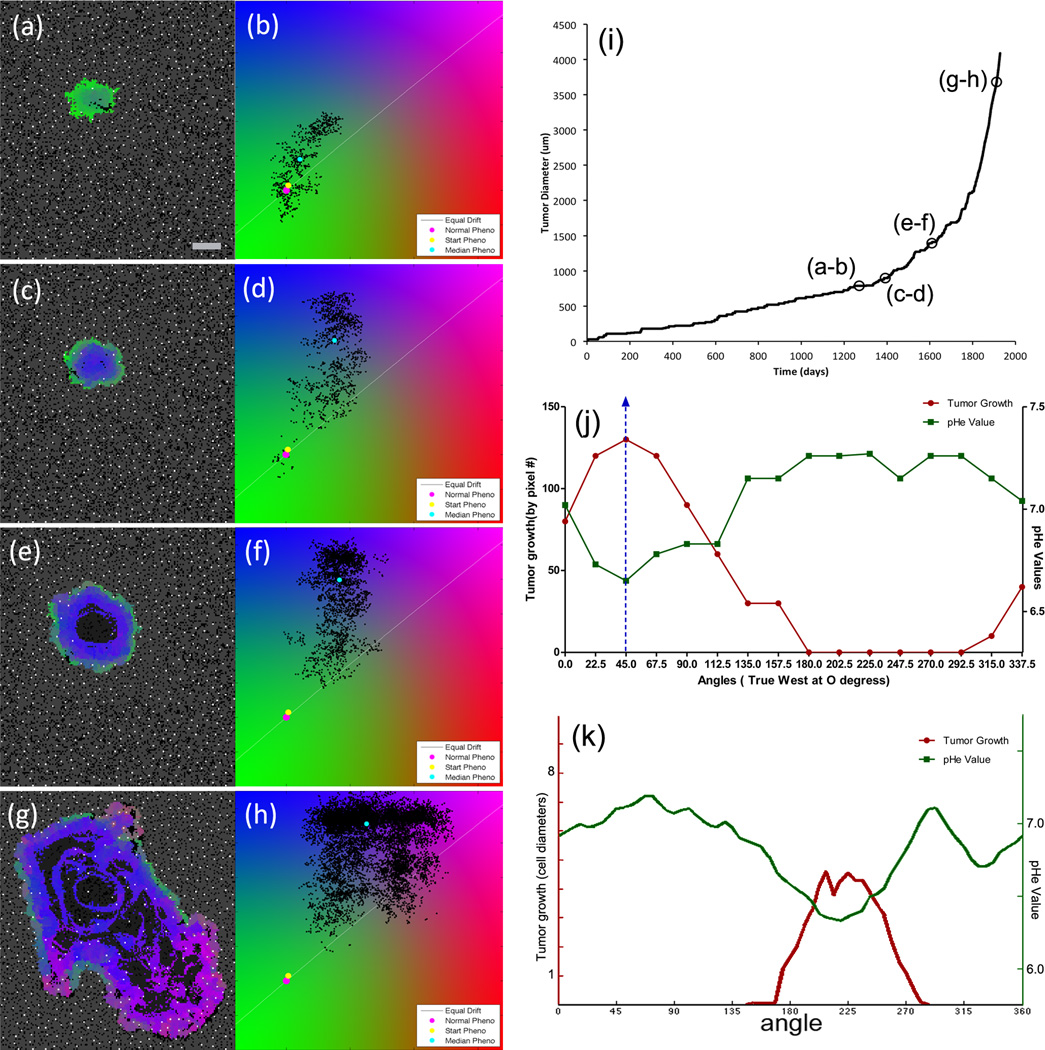
Fig. 3a–h shows a sequence of images taken from a representative simulation of tumor growth. In (a–b), the average tumor phenotype is still relatively normal. A slight shift towards acquired acid-resistance is due to intermittent hypoxia caused by blood vessel degradation followed by angiogenesis within the center of the tumor. Each short period of hypoxia-induced acidosis causes a slight selection pressure towards acid-resistant cells.

Figure 3.

(a–h) Representative simulation of tumor growth with time points (in days): (a/b)=1270, (c/d)=1392, (e/f)=1610, and (g/h)=1912. Scale bar is 400 microns. Video available on the online supplemental section (Video 1). (Left column): The 2D CA model output with vasculature (white), empty space (black), necrosis (dark gray), normal tissue (medium gray) and tumor cells labeled with colors corresponding with the cell position on the phenotype flow diagram of the right column. (Right column): Distribution of tumor cells along two phenotype axes, as described in Fig. 2, with starting (yellow) and median (cyan) tumor phenotype. (i) Growth curve for the simulation. (j) Radial pH_e and tumor growth from a murine dorsal window chamber [4]. The pH at the tumor edge was measured at multiples of 22.5 degrees and compared to the tumor growth at the same angular positions over 10 days. (k) Radial pH_e and tumor growth from the simulation by sampling the pH around the tumor edge and measuring the radial growth rate.

In (c–d), a sustained hypoxic central area leads to increased reliance on glycolysis by the tumor cells growing there. Since cells must develop resistance to increasing acidosis or perish, the central part of the tumor is acid-resistant (blue). This resistant population is surrounded by a metabolically-normal population of tumor cells (green). Since they are near to stable vasculature in the normal tissue, this surrounding buffer of metabolically benign cells exists because there is little selection pressure to acquire acid resistance on the tumor edge.

Panels (e–f) show the development of necrosis in the center of the tumor, and a few small pockets of glycolytic cells (magenta). The increased glycolysis in these cells causes a further decrease in pH_e, but the cells are not in sufficient number nor adjacent to acid-sensitive cells to allow for acid-mediated invasion to occur. There continues to be a buffer of tumor cells (green) between the aggressive phenotype and the acid-susceptible normal tissue.

Panels (g–h) show the tumor growing invasively via acid-mediated invasion. The acidosis produced by glycolytic cells affects the surrounding normal tissue. Several lobes of very aggressive glycolytic and acid-resistant cells have punctured through the edges of the tumor, growing into the space left open by normal tissue destroyed by acidosis. A thin zone of black empty space between the tumor and normal tissue is evident at the edge of the largest lobe on the lower right, a phenomenon seen in histological samples by Gatenby et al. [28].

This representative simulation offers several insights into the development of acid-mediated invasion. The growth curve for the simulation is shown in Figure 3i. The initial tumor growth has a shallow slope, representing homeostatic-limited growth. From t=0 to 1200 days, the average growth rate is about 0.2 mm per year. Here, the tumor takes advantage of space relinquished by normal cells during homeostatic turnover. The growth rate is correspondingly slow. Eventually, the tumor becomes invasive via self-produced acidosis and from t=1800 to t=1920 days, the average growth rate is about 6 mm per year, a thirty-fold change over the homeostatic-limited growth rate. Interestingly, there is no jump in phenotype that causes this sudden change in behavior. Unlike a genetic mutation model, where one could point to the acquisition of a key mutation shortly before a large behavioral change, this model only permits slow phenotype variation. Indeed, comparing the phenotype flow plots before and after invasive growth (third and fourth rows) shows only a slight shift in average phenotype. In order to understand this change in behavior, it is important to consider not only the specific phenotypes present, but also where they arise spatially and how they develop dynamically. Besides acquiring the invasive phenotype, three other key factors play a role in the development of acid-mediated invasion.

First, the cells must reach a critical mass of acid-producing cells. A single glycolytic, acid-resistant cell cannot sufficiently change the local pH_e to cause lethal acidosis to surrounding cells. Since the model assumes that phenotypes are passed on to daughter cells with some small random change, reaching critical mass is primarily a function of proliferating enough to create a group of similarly aggressive cells in the local microenvironment that can then have sufficient proton production, as a group, to significantly affect the pH_e of the surrounding tissue.

The second key development is that the invasive cells must be near to cells which are relatively acid-sensitive if invasion is to occur. If a highly glycolytic group of cells develops but is surrounded by acid-resistant, low-glycolytic cells, then the lowered pH_e that is caused by the glycolytic cells will have little effect on the surrounding cells and invasion will not occur. Therefore, the importance of the spatial buffer of relatively normal tumor cells on the edge of the tumor becomes clear. Unless the aggressive cells can invade through this protective barrier en masse, the acid-invasive phenotype will be contained interior to the tumor edge. To state it another way, the diffusion gradient of acidosis produced by a group of glycolytic cells must overcome the spatially-structured phenotype gradient that exists towards the edge of the tumor.

Finally, the presence of nearby blood vessels can contribute to decreased acidosis. A group of aggressive tumor cells that grows into a well vascularized region will be slowed by the increased buffering capacity of the vasculature. Invasion will only occur if the low pH_e produced by the mass of cells locally overcomes the ability of the vasculature to remove the acidosis through buffering.

The pathway to becoming a metabolically-aggressive cell is not a linear march through phenotype space. The diagonal line on the phenotype plots of Fig. 3b–d–f–h shows the direction of equal, maximal phenotypic variation. However, simulations show that the cells reaching the most aggressive phenotype tend to follow a non-linear path similar to the black arrow shown in Figure 2b. This path shows that acid resistance is selected first, after which high-glycolytic capacity develops. This observation is the opposite of the hypothesis that cells first acquire a glycolytic phenotype followed by acquisition of acid resistance [2], represented by the gray arrow of Figure 2b. The reason for the order of selection in the present model is that low pH_e naturally develops as a result of decreased or intermittent vascular density in the center of a growing tumor. Increased acid resistance is therefore a valuable trait to acquire early in the development of the tumor if vascular delivery is inconsistent or reduced. While increased glycolysis speeds up the cell cycle, this phenotype change has little advantage during homeostatic growth, since available space is freed on a time scale that is much longer than the cell-cycle time. Furthermore, unless critical mass is reached, acid-mediated invasion by an individual glycolytic cell is not possible.

Interestingly, because of the spatial structure of hypoxia and cell turnover, the most aggressive cells tend to develop in interior regions of the tumor where nutrient conditions are poor, selection pressures are great, and proliferation is more frequent because of cell death. However, in order to become invasive, these aggressive cells must come in contact with normal tissue, where the excess proton production can cause cell death. The ability of a mass of aggressive cells to penetrate the surrounding layer of less aggressive tumor cells depends in part on how acid-resistant the buffering cells are. If the phenotype gradient is steep, then the aggressive cells are more likely to invade and reach the normal tissue than if the intervening cells are already acid-resistant. Clearly vascular density is an important aspect of the progression of the tumor phenotypes in both space and time. Further exploration of the effect of vascular density is presented in the Supplemental Material.

The acid-mediated invasion seen in the model has been observed experimentally in a murine window-chamber model [4]. In that experiment, a droplet of tumor cells was cultured and implanted into a dorsal wound chamber. The pH_e and tumor growth rates were measured radially, and the direction of maximal growth was correlated with the direction of low pH_e, as seen in Figure 3j. A similar correspondence between pH_e at the tumor edge and radial growth was observed in the model, as seen in Figure 3k.

This representative simulation is produced consistently by the model with the same parameters. Additional repeats of the simulation are shown in the Supplemental Material, including further exploration of the impact of normal cell turnover rate and normal cell density. Simulations were also performed with larger CA domains (up to 1 cm) to explore slower rates of phenotypic drift (see Supplemental Material). Although the tumor takes more time to become invasive with a slow phenotypic drift rate, the qualitative nature of the evolution through phenotype space is the same as for simulations run in a smaller domain with faster evolution as described above. Since large domains become computationally expensive, we limit our present results and analysis to the CA domains of approximately 3 to 5 mm per side.

3.2 Effect of treatments on tumor growth and selection

3.2.1 Early application pH buffering therapy can significantly delay onset of tumor invasion

Recent experimental results from our group have shown that application of systemic pH buffers to mice can prevent or slow down tumor development and metastatic growth [32]. In a murine TRAMP model of spontaneous tumor growth, sodium bicarbonate has a preventative effect on tumor formation in these mice, but only if it is administered before a certain age [33].

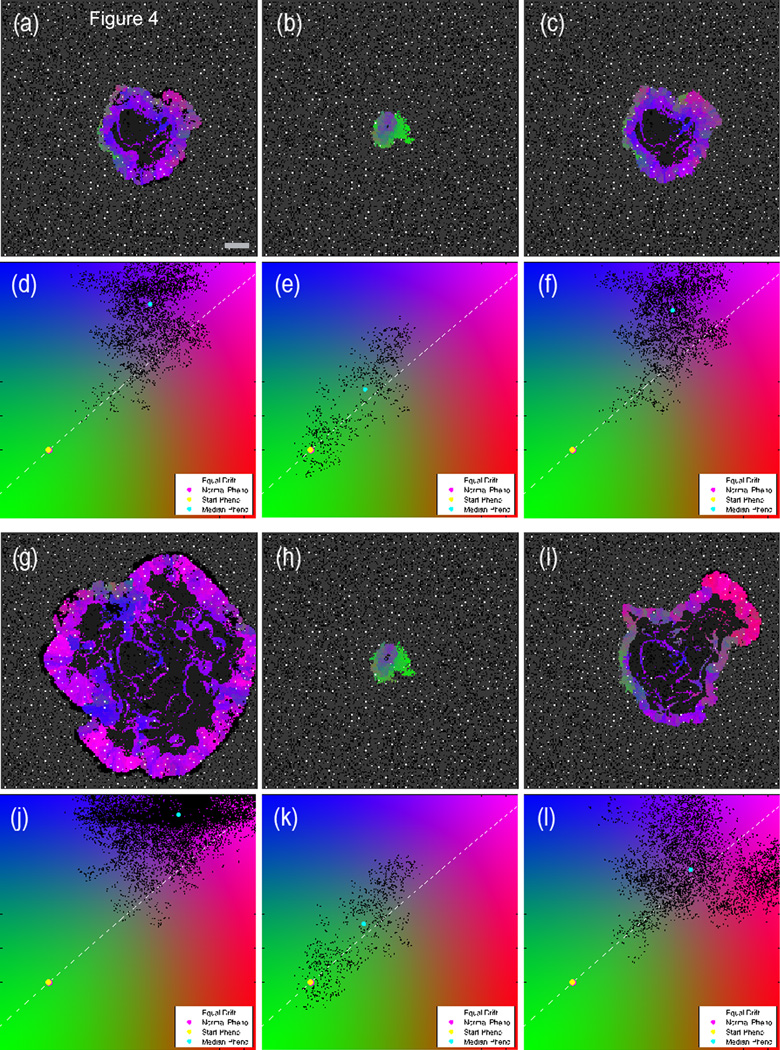
A generic pH buffering therapy has been simulated using the model (see Supplemental Material for discussion of the assumptions for implementation). In order to compare the simulation with the murine buffer study [33], an untreated control simulation is compared with same simulation treated at different time points (t_rel days). Figure 4 compares the untreated control with two buffer-treated simulations. The tumor that is treated earlier (central column, b–e–h–k) shows a significant delay in growth and acquisition of an invasive tumor phenotype compared to the untreated control (left column, a–d–g–j). On the other hand, the tumor treated at a later time point (right column, c–f–i–l) is only partly affected by the buffer. There is some slowing of the growth, but the invasive phenotype persists and the tumor growth rate is comparable to the untreated case. Supplemental Figure S11 shows the growth of the untreated tumor (black plot) and three different starting times for buffer therapy. The earlier the treatment is administered, the more delay of growth is observed.

Figure 4.

Comparison of three pH buffering simulations with identical initial conditions at two different time points. The left column is an untreated simulation; the central column is continuously treated with sodium bicarbonate starting at t_rel=0 days; the right column starts treatment at t_rel=75 days. The top panels (a–f) show the state of the three simulations at t_rel=78 days, i.e. shortly after the tumor in the right column has started the buffer therapy. The bottom set of panels (g–l) shows the state of the tumors at t_rel=142 days. Scale bar is 400 microns. Video available on the online supplemental section (Video 2).

These results suggest a possible mechanism for the preventative effect of early buffer treatment seen in the TRAMP model. If the therapy is administered prior to the protective layer of metabolically benign cells being breached (i.e., acid-mediated invasion has commenced), then the therapy can prevent the aggressive cells from reaching this invasive state for long periods. If the invasive state is already reached, however, the therapy has only a minimal effect. In order to test this hypothesis, we suggest that tumors from early and late treated mice be examined for metabolic signatures and phenotypic structure that could indicate the presence of acid-mediated invasion. The model also suggests that buffer therapy may be of limited use to patients with a primary tumor that is already glycolytic and exploiting acid-mediated invasion. However, buffer therapy may still be beneficial to these patients because micro-metastases that have yet to develop an invasive phenotype may be prevented by this systemic therapy. Even if the metastatic seed was highly glycolytic, if the micro-metastasis has not reached the critical mass needed to induce acid-mediated invasion, then the buffer therapy will further delay the acquisition of that invasive state by effectively raising the necessary threshold of critical mass. These results are also be consistent with the TRAMP mouse experiments where late-treated mice, in contrast to untreated mice, did not develop metastasis [4].

3.2.2 Anti-angiogenic therapy can promote the development of metabolically aggressive phenotypes

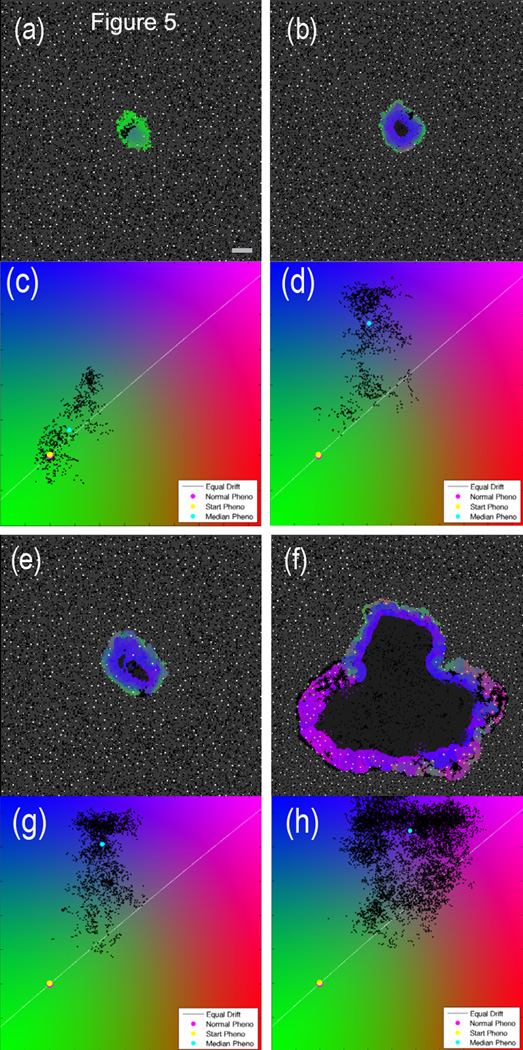
Anti-angiogenic therapy was developed on the premise that if a tumor is starved of nutrients, the tumor will grow slower, become quiescent, and perhaps die away. While this seems like a straightforward response to decreased nutrient availability, this nutrient-deprivation theory does not take into account the effect of waste products produced as a result of worsened metabolic conditions within a tumor. Specifically, reduction of perfusion with anti-angiogenic therapy will cause pockets of hypoxia, which in turn will lead to increased glycolysis in all cells and increased acidosis. The result of this sequence of events is that cells that may have previously developed acid-resistance due to an avascular tumor growth phase may suddenly be at an advantage when vascular density is decreased. The selection pressure due to therapy could have the effect of speeding up the development of the most aggressive subset of tumor cells at the time of treatment.

To illustrate this, we compare a simulation without any therapy with one in which anti-angiogenesis was started at a given time step. For simplicity we assume that anti-angiogenic therapy simply turns off the angiogenic aspect of the model: after the initiation of therapy, no new blood vessels are created. Existing blood vessels remain, and vessel degradation by the growing tumor continues. As expected, this leads to decreased vessel density within the tumor, so that nutrients will primarily diffuse from the surrounding vasculature within the normal tissue.

Figure 5 shows the comparison between treated and untreated cases for a representative simulation. The effect of the therapy is to greatly increase the selection pressure for acid-resistant cells and speed evolution by increased cellular turnover. This pressure drives the phenotype of the tumor cells towards a more aggressive state, and therefore acid-mediated invasion occurs much sooner than in the untreated simulation. The addition of therapy in this case is clearly a worse outcome than allowing the tumor to progress without therapeutic intervention. This result suggests a possible explanation for the historical failure of many anti-angiogenic therapies [34], including the recent withdrawals of anti-angiogenic therapies for both glioblastoma [35] and breast cancer [36]. It is of interest to note that shortly after therapy is applied, the number of tumor cells decreases, as cells that are far from the remaining blood vessels will be starved of nutrients. However, as the remaining cells adapt to the new environment, the tumor will grow back and become invasive sooner than the control.

Figure 5.

Comparison of untreated and anti-angiogenic therapy simulations with identical initial conditions at two different time points. The left column is untreated; the right column has anti-angiogenic treatment at t_rel=0 days. The top panels (a – d) show the state at t_rel=141 days, i.e. 141 days after the start of therapy in the right panel. The bottom set of panels (e – h) is at t_rel=285 days. Scale bar is 400 microns. Video available on the online supplemental section (Video 3).

3.2.3 The efficacy of cytotoxic therapy is dependent on spatial and phenotypic heterogeneity

The diffusible nature of therapies such as chemotherapy have implications for the spatial distribution of the drug, and therefore selection pressures on the tumor will vary depending on the position of a cell relative to nearby blood vessels. In principle, the most aggressive tumor cells tend to develop far from blood vessels. At the same time, these distal positions will be the hardest locations for the drug to reach by diffusion. These observations suggest that a cytotoxic agent may cause spatially-variable selection, an effect which can cause enhanced development of aggressive cells in certain circumstances.

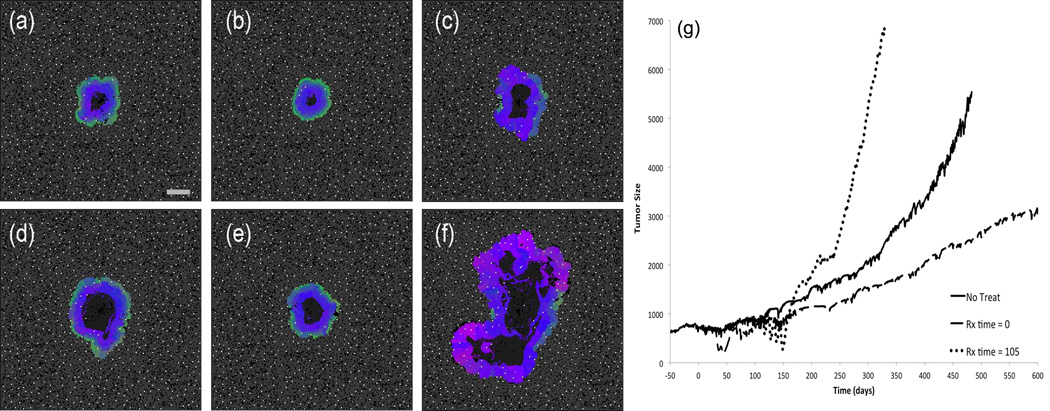
In order to test this prediction, we administered a diffusible cytotoxic drug into the model (see Supplemental Information for additional discussion of assumptions). Figure 6g shows the tumor size over time for three representative simulations. The solid black line is an untreated tumor. The dashed line is the result of starting the cytotoxic drug regimen at a relative time of t = 0, and the dotted line is the result of starting the regimen at t = 105. For the earlier treated case, the result is a significant decrease in the growth rate of the tumor, while the opposite is true for the later treated case: the tumor has grown faster than our untreated control.

Figure 6.

(a–f) Comparison of untreated and chemotherapy simulations with identical initial conditions at two different time points. The left column is an untreated simulation; the central column was pulsed with cytotoxic therapy starting at t_rel=0; the right column starts the identical treatment at t_rel=105. The top panels (a–c) show the state of the three simulations at t_rel=264, i.e. shortly after the tumor in the right column has finished the therapy. The bottom set of panels (d – f) shows the state of the tumors at t_rel=380. Scale bar is 400 microns. Video available on the online supplemental section (Video 4). (g) Growth curves for untreated (solid), early (dashed), and late (dotted) chemotherapy from (a–f). Tumor size on the vertical axis is the diameter in microns.

To understand the reason for this difference, key time points from the simulation are shown in Figure 6a–f. For the case of the early treatment, the therapy has decreased the size of the tumor and essentially set back the time course of growth. Furthermore, a subtle restructuring of the spatial heterogeneity of cell phenotypes has limited the ability of aggressive cells near the center to invade. However, in the later treated case, the therapy has allowed pre-existing aggressive cells in the center of the tumor to emerge and become active much sooner than in the other simulations. In the analysis of the untreated growth in section 3.1, it was noted that the metabolically benign cells (green) near the tumor boundary acted as a containment mechanism to prevent the more aggressive cells in the interior of the tumor from initiating acid mediated invasion. In the case of the late administration of chemotherapy, the spatial diffusion of the cytotoxic agent has stripped away this relatively benign protective layer of cells. The aggressive cells situated near the center of the tumor benefit from several advantages under this type of therapy. First, they are further from active blood vessels, and therefore the concentration of drug is decreased due to diffusion distances and consumption by cells closer to the vasculature. Second, limited space and nutrients near the center limits the division rate of these cells, and this also allows them to escape the effects of a drug that targets proliferation. Finally, once the outer layers of cells are stripped away by the drug, these aggressive cells find themselves in a perfect environment to initiate acid mediated invasion, since they can quickly reach critical mass through rapid proliferation post-therapy and then directly interface with normal tissue cells. This combination causes the tumor phenotype to quickly transform into the acid-mediated invasion type.

4 Discussion

The behavior of a cancer as a whole is the relevant clinical metric that informs prognosis and therapy decisions. The actions of a single malignant cell are only relevant if they lead to an aggressive cancer, and this can only happen in the context of the collective behavior of tumor cells, normal normal tissue, and surrounding microenvironment. Genetic, epigenetic, signaling, phenotypic, temporal, and spatial heterogeneity all play a role in shaping the dynamics of the complex system that drives tumor growth. Therefore tumor prognosis and response to therapy can only truly be understood if we consider their impact of these heterogeneity mechanisms as a spatially and temporally distributed system.

The results presented here attempt to elucidate how metabolic heterogeneity affects tumor progression and treatment outcome. First, development of localized hypoxia due to vascular instability leads to the selection of acid-resistant tumor cells, which is then followed by acquisition of the glycolytic phenotype. This non-linear trajectory through phenotype space is most clear in situations of prolonged hypoxia, in which the metabolic response of normal tissue is the Pasteur effect with subsequent acidification of the microenvironment. Extrapolating to in vivo situations, the case of prolonged hypoxia might be representative of ductal carcinomas, where angiogenesis is not possible in the initial stages of tumor growth due to the barrier of the basement membrane. On the other hand, a metastasis that immediately co-opts and disrupts the normal vasculature of a tissue may follow the profile of intermittent hypoxia. In both cases, however, the model predicts the same pathway through phenotype space.

Although the present work do not impose any costs on the different phenotypes, we have run simulations where we imposed a simple linear cost to the acquisition of acid resistance (results not shown). In this version of the model, tumors cells that increased their acid resistance had proportionally slower cell cycles. Various settings of the slope of this cost function had little impact on the overall evolutionary dynamic. The trajectory through phenotype space was conserved, and the cost only served to slow down the evolutionary pace. We hypothesize that this is because the competition between cells in hypoxic areas depends much more on the acquisition of acid-resistance rather than the ability to proliferate quickly, since the selection pressure is high while the turnover rate is relatively low. A full exploration of evolutionary costs is beyond the scope of the present work.

The simulations of treatments in the model offer some insights as to why these therapies may fail in some cases and be more successful in others. In aggregate, all of the results presented here argue for treatments that are aimed at maintaining the protective layer of less aggressive cells rather than eradicating them. Therapies which buffer the pH_e appear to be preventative rather than regressive. Indeed, there is no clear mechanism by which increasing extracellular pH should lead to cytotoxicity of tumor cells. Rather, the buffer changes the microenvironment so that the acid-meditated invasion phenotype cannot use its acid production against susceptible neighbors. However, the model suggests that there are limits to this preventative action that depend on both buffer dose and the mix of phenotypes in the tumor. A more detailed exploration of the interactions between the phenotypes of the tumor cells and the amount of buffering could perhaps define a quantifiable relationship between dose and growth delay, but this is beyond the scope of this work.

The results suggest that the effectiveness of cytotoxic therapies is strongly influenced by spatial heterogeneity of both the drug diffusion and the tumor structure. This may result in selective intratumoral lethality in which the drug kills less aggressive cells positioned adjacent to blood vessels but not the more malignant populations distant from blood vessels, therefore selecting for more resistant populations and removing a potential barrier to their proliferation by eliminating the perivascular cells. Alternative strategies to optimize the delivery of both dose and schedule to prevent the outgrowth of more aggressive clones post-therapy will be the subject of future work with the model, including drug combinations.

The model examined tumors grown from benign single cells. In the case of metastatic disease, the seeding cell may be of any phenotype present in the primary tumor. Bernards and Weinberg [37] have proposed that metastases arise early in the development of the primary and continue through the life of the tumor. This suggests that early disseminated cells will potentially be less aggressive, but will have more time to establish themselves in the metastatic niche. More aggressive cells, while arising later in the evolution of the primary, may reach invasiveness faster due to their phenotypic advantage. Future work will explore the trade-off between early but phenotypically benign metastases versus late, aggressive metastases.

All models incorporate limiting assumptions. We have developed the model in two dimensions, representing a slice through a tissue. While three-dimensional modeling has been useful for exploring the specifics of tumor morphology and blood vessel remodeling, our interest here is in the evolution of tumor phenotypic heterogeneity as a function of environmental selection. We expect that there would be little advantage to implementing the model in 3D with respect to the insights provided on acquisition of heterogeneity. However, the principles of the the model can be directly extended into three dimensions in the future.

The present work uses a lattice-based approach without mechanical deformation. Tumor cells are limited to grow only when there is space available in the lattice. Cells are not displaced volumetrically, as may be the case in a real tumor. This assumption imposes a strict limit on the growth of a tumor, whereas a deformable tissue may permit tumor growth through normal tissue even if available adjacent space is absent, thereby escaping the encapsulation and corresponding homeostatic growth phase. To investigate these effects, however, would require a significantly more complex model with mechanical forces and off-lattice modeling, and therefore is beyond the scope of the present work.

We have only considered acid-mediated invasion, and other forms of invasion such as MMP secretion and EMT transition are also important. The model can be extended to examine the effects of phenotypic changes on these additional axes in the future. Furthermore, cell migration without proliferation was not considered, and the effect of migration on spatial heterogeneity is likely to play a role in how the tumor develops. There have been previous models in relation to metabolism that incorporate these effects [22, 38, 39]. However, the effects of acid mediated invasion rely on critical mass, and dispersion of individual cells through the normal tissue due to migratory elements may not necessarily lead to faster development of the invasive phenotype. Clearly, one logical next step is to examine the influence of cell migration on the properties that lead to acid-mediated invasion. Escaping cells might be more likely to penetrate the protective shell of relatively benign tumor cells seen in the present work, but migration may also mean more cellular dispersion, which would spatially dilute the acid-production rate of a group of aggressive cells, limiting the effectiveness of acid-mediated invasion. Indeed, migration may be less important when trying to establish a niche, but more important in reaching that niche in the first place, such as with micrometastases.

In this work, we chose a point-source vasculature model. This is representative of a field of parallel blood vessels passing perpendicular to the two-dimensional tissue slice and is a simplification that has been considered before [40]. There is a significant amount of literature devoted to modeling angiogenesis and nutrient delivery [18, 19, 41]. However, including these complex mechanisms are beyond the scope of this work. We opted for a simply-defined vascular system that would deliver temporally and spatially heterogeneous nutrient and waste gradients with a minimal number of parameters. A dynamic point-source vasculature serves as a good surrogate for a more complicated model which would accomplish the same goal. Indeed, much of the behavior seen in this model is sensitive to localized nutrient gradients, and it is unlikely that a complex vasculature would produce gradient structures on a local level that are significantly different from a point source system.

For the present work, we confined the phenotypic variation to small unbiased changes occurring only at the time of division. Other methods of phenotypic variation can easily be implemented in the model in the future. For example, major mutations to key metabolic genes could be modeled by adding rare but large jumps in these parameters. Cells could also be allowed to alter their phenotype independently of proliferation.

In summary, we have developed a hybrid multiscale model of tumor growth within a normal, homeostatic tissue, and demonstrated the mechanisms by which phenotypic, temporal, and spatial heterogeneity affect growth of a tumor and the outcomes of treatments. The model predictions are consistent with clinical and experimental observations and provide insight into the mechanisms that result in treatment failure. This work highlights the importance of the phenotypic heterogeneity of tumor cells and how this heterogeneity varies in time and space. A key prediction of our model is that early stages of tumor development (either primary or metastatic) maintain a phenotypically spatially structured population, where less aggressive clones spatially suppress more aggressive counterparts. Importantly, we demonstrate that standard treatment modalities may selectively destroy this structured population and facilitate subsequent progression. Controlling tumor progression by maintaining rather than destroying this suppressive tumor layer appears to be more effective that conventional high dose density therapy that aims to kill the maximum possible number of tumor cells.