Bridging Levels of Understanding in Schizophrenia Through Computational Modeling

Abstract

Schizophrenia is an illness with a remarkably complex symptom presentation that has thus far been out of reach of neuroscientific explanation. This presents a fundamental problem for developing better treatments that target specific symptoms or root causes. One promising path forward is the incorporation of computational neuroscience, which provides a way to formalize experimental observations and, in turn, make theoretical predictions for subsequent studies. We review three complementary approaches: (a) biophysically based models developed to test cellular-level and synaptic hypotheses, (b) connectionist models that give insight into large-scale neural-system-level disturbances in schizophrenia, and (c) models that provide a formalism for observations of complex behavioral deficits, such as negative symptoms. We argue that harnessing all of these modeling approaches represents a productive approach for better understanding schizophrenia. We discuss how blending these approaches can allow the field to progress toward a more comprehensive understanding of schizophrenia and its treatment.

Schizophrenia is complex neuropsychiatric syndrome that profoundly affects perception, belief, and cognition (Lewis & Moghaddam, 2006) and is likely caused by distributed brain dysconnectivity (Stephan, Baldeweg, & Friston, 2006). Schizophrenia remains a leading cause of disability worldwide (C. J. L. Murray, Lopez, Harvard School of Public Health, World Health Organization, & World Bank, 1996) and is inadequately treated by available therapies (Krystal et al., 2003). This is especially true for disturbances in motivation and cognition that often accompany schizophrenia (Barch, 2005; Barch & Ceaser, 2012; Barch & Dowd, 2010). Studies of its pathophysiology initially focused on characterizing striatal dopaminergic hyperactivity (Guillin, Abi-Dargham, & Laruelle, 2007; Kapur, Mizrahi, & Li, 2005; Kegeles et al., 2010; Laruelle, Abi-Dargham, Gil, Kegeles, & Innis, 1999; Laruelle et al., 1996). This focus is now complemented by studies that have characterized altered glutamate neurotransmission in schizophrenia (Anticevic, Gancsos, et al., 2012; Corlett et al., 2006; Krystal & Moghaddam, 2011). An influential mechanistic hypothesis proposes a possible disruption in the balance of excitation and inhibition in the cortical microcircuitry resulting from hypofunction of the N-methyl-D-aspartate glutamate (NMDA) receptor (Krystal et al., 2003), which might affect cortical computations, thereby leading to large-scale dysconnectivity (Uhlhaas, 2013). However, such cellular-level hypotheses have yet to be systematically linked across levels of analyses to explain the complexity of schizophrenia symptoms. This objective is particularly daunting because it requires a multilevel understanding of complex phenomena across levels of experimental inquiry: from synapses, to cells, to neural circuits, to large-scale systems, and, ultimately, complex behavioral disturbances observed in schizophrenia.

One way to better understand how these disturbances scale across analysis levels involves blending clinical behavioral and neuroimaging studies with advances in computational and theoretical neuroscience. We argue that such a multidisciplinary/translational clinical science approach is vital to understand the staggering complexity of this neuropsychiatric syndrome. The fields of computational and theoretical neuroscience recently have made advances toward understanding neuroscientific observations across levels of analysis. For instance, in computational studies, researchers have articulated the synaptic and microcircuit mechanisms that produce complex cortical oscillations (X.-J. Wang, 2010), such as gamma rhythms. In a related set of investigations, researchers have proposed a theoretical foundation for how unique receptor contributions, at different timescales, can produce persistent and recurrent neuronal firing that gives rise to computations that support higher-level cognitive processes, such as working memory (WM). Furthermore, in system-level computational-modeling studies, researchers have proposed the role of specific neurotransmitters, such as dopamine (DA), for tuning of prefrontal cortical networks during cognitive operations (Cohen & Servan-Schreiber, 1992; Durstewitz, Kelc, & Gunturkun, 1999; Durstewitz & Seamans, 2002). Mathematical formalisms of behavior and brain-behavior relationships, such as associative learning or reward processing, have elucidated specific behavioral parameters that contribute to complex learning processes (Maia & Frank, 2011).

Consequently, such models generated predictions regarding specific disruptions that may occur in psychiatric illness (Maia & Frank, 2011), thereby informing experiments on neural data. Computation at each of these analysis levels is thought to be profoundly affected in schizophrenia, ranging from microcircuit disruptions (González-Burgos & Lewis, 2012; Lewis, Curley, Glausier, & Volk, 2012; Lewis & González-Burgos, 2008), to system-level perturbations in neurotransmission or connectivity (Anticevic, Cole, et al., 2014; Lisman, 2012; Lisman, Pi, Zhang, & Otmakhova, 2010; Woodward, Karbasforoushan, & Heckers, 2012), to complex behavioral alterations that include deficits in learning and motivation (Gold et al., 2012; Gold, Waltz, Prentice, Morris, & Heerey, 2008). Bridging each level of modeling with appropriate levels of experimental inquiry can provide a powerful interplay between experiment and theory to inform understanding of schizophrenia at a given level of analysis.

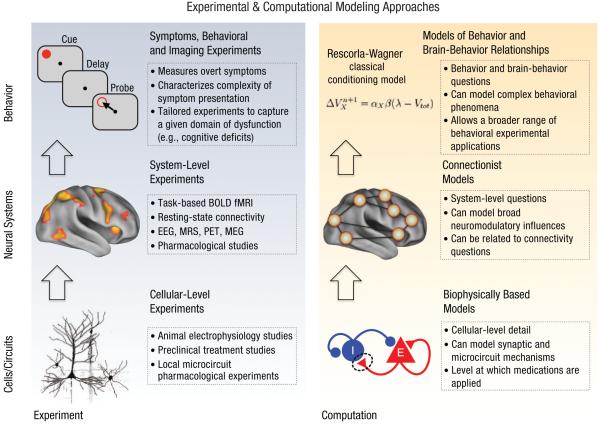
We propose that such an integrative computational modeling effort that spans levels of inquiry should encompass three broad complementary approaches, which span this continuum (see Fig. 1 for a conceptual illustration of computational modeling and experimental interplay across levels of analysis). The first approach uses biophysically based models that are informed by cellular-level detail to help constrain both preclinical and human pharmacological experiments targeting this level of analysis. The second uses connectionist models that inform neural-system-level hypotheses in schizophrenia but do not always commit to the same level of neurobiological detail as do biophysical models. Such models have the unique capacity to constrain neuroimaging studies that focus on both task-based activation and connectivity alterations in schizophrenia (Yang et al., 2014). And the third approach uses models of behavior and brain-behavior relationships that can characterize specific parameters that may govern complex symptoms in schizophrenia. The use of appropriate modeling across levels of analysis allows theory to interface with distinct experimental approaches, including (a) pharmacological (Krystal et al., 2003), animal electrophysiology, and other preclinical studies (Arnsten, 2011; Homayoun & Moghaddam, 2007; Moghaddam & Adams, 1998; Simen, DiLeone, & Arnsten, 2009; Verma & Moghaddam, 1996; M. Wang et al., 2013) that target synaptic and cellular-level questions; (b) connectivity- and task-based neuroimaging experiments in schizophrenia (Fornito, Yoon, Zalesky, Bullmore, & Carter, 2011; Fornito, Zalesky, Pantelis, & Bullmore, 2012; Repovs & Barch, 2012; Repovs, Csernansky, & Barch, 2011) designed to probe neural-system-level abnormalities; and (c) state-of-the-art behavioral and imaging studies designed to characterize behavioral and symptom disturbances in schizophrenia (Gold et al., 2012; Gradin et al., 2011; G. K. Murray et al., 2008; Schlagenhauf et al., 2014).

Fig. 1.

Conceptual illustration of computational modeling and experimental interplay across levels of analysis. The utility of computational modeling, particularly in the study of schizophrenia, is its ability to inform a given level of experimental study. Because we study abnormalities in schizophrenia from the cellular level (Lewis, Hashimoto, & Volk, 2005), at the neural-system level (Anticevic, Repovs, Corlett, & Barch, 2011), and, ultimately, at the level of behavior (Gold et al., 2012), we have to utilize our modeling approaches to best fit the experimental framework. For instance, as reflected in the bottom panels, cellular-level experiments use techniques and produce measurements that are best captured using models that contain the necessary level of biophysical realism. Such models can, for instance, inform synaptic processes that may govern the microcircuit phenomena under study, such as neural oscillations (X.-J. Wang, 2010). In turn, a number of neuroimaging studies have focused on characterizing system-level disturbances in schizophrenia using both task-based paradigms (Barch & Ceaser, 2012) and resting-state functional connectivity approaches (Fornito, Zalesky, Pantelis, & Bullmore, 2012). Such system-level cognitive neuroscience experiments are best informed by models that capture the relevant detail and complexity of larger-scale neural systems (as reflected in the middle panels). Such models can perhaps better inform the role of systemic pharmacological manipulations on BOLD fMRI (Honey & Bullmore, 2004) or can be used to predict results of functional connectivity studies in schizophrenia (Yang et al., 2014). Finally, schizophrenia produces complex and devastating behavioral symptoms, which can be measured via increasingly sophisticated behavioral paradigms (Gold et al., 2012; Waltz et al., 2009; Waltz & Gold, 2007). Here, the use of models that formalize complex behavior (as reflected in the top panels) can provide a powerful tool to quantitatively examine a given behavioral process in patients (e.g., reinforcement learning; Maia & Frank, 2011) as well as brain-behavior relationships (Gradin et al., 2011; G. K. Murray et al., 2008; Schlagenhauf et al., 2014). BOLD fMRI = blood-oxygen-dependent-level functional MRI; EEG = electroencephalography; MRS = magnetic resonance spectroscopy; PET = positron emission tomography; MEG = magnetoencephalography; E = excitatory cells; I = inhibitory cells.

We argue that precisely this type of multilevel approach has the potential to capture the complexity of schizophrenia (or other neuropsychiatric conditions more broadly). Specifically, different levels of modeling will provide more or less interface with different levels of experimental analysis, which allows for the interplay of theory and experiment uniquely relevant to a given level of observation. We suggest that a given computational model is not (and should not be) designed to explain all experimental observations (such a perfect model would be the human central nervous system itself). Instead, we argue that different levels of modeling are appropriate for different questions and the scope of experimental observation in a given study. Therefore, we discuss evidence across the three broad levels of modeling previously described and how they shed light on understanding of schizophrenia. This is not to say that all computational models fall within one of the three categories; instead, we use this “division” to highlight the utility of some models to interface with different levels of experimental inquiry.

First, we focus on models developed with explicit biological constraints guiding their design. We present evidence from basic physiology, clinical, and pharmacological experiments that interface with this level of modeling. Second, we turn to connectionist models designed to inform neural-system-level observations (although many generate complex behavioral predictions). We specifically focus on the role of DA in schizophrenia, its relevance for tuning prefrontal cortex (PFC) function and connectivity, and its role in executive deficits in this illness. This level of modeling has guided cognitive neuroscience studies in schizophrenia, although it does not specifically rely on stringent biological constraints. Last, we briefly describe mathematical models of complex behavior and brain-behavior relationships and how such models have informed understanding of schizophrenia symptoms. We argue that continued refinement of each of these approaches, and their continued interplay, represents an important objective in the field of clinical neuroscience.

Biophysically Based Models—Toward Understanding Circuit-Level Effects of Synaptic and Cellular Dysfunction

Biophysically based modeling refers to the modeling of neural circuits at the level of neurons and synapses on the basis of physiological characterization of neuronal and synaptic dynamics. In such models, the temporal evolution of neuronal and synaptic states is typically modeled through sets of differential equations. Such models can be grounded in basic neuroscience and constrained by multiple types of anatomical and physiological data from animal experiments (X.-J. Wang, 2010). The biophysical basis of the model specifically allows researchers to perturb certain parameters through the putative mechanisms of disease processes. In turn, hypotheses directly generated by such perturbation can be tested via pharmacological manipulations that target this very mechanism (Krystal et al., 1994). Because such models can possibly produce neural activity and behavior, they can be related to human neuroimaging and psychophysics in healthy and clinical populations. Biophysically based models could also inform rational design of pharmacotherapies, given that current medications for schizophrenia are predominantly designed to act at the synaptic and cellular levels (although there is evidence that targeted transcranial magnetic stimulation, TMS, could possibly alleviate some symptoms; Hoffman et al., 1999), thereby providing a theoretical platform for clinical translation that integrates findings across both basic and clinical neuroscience.

However, the level of biophysical detail included in the model critically depends on the questions under study. For example, models of a single synapse that include subcellular signaling pathways can be used to examine hypotheses about the preversus postsynaptic loci of dopaminergic dysregulation in schizophrenia (Qi et al., 2010). Conversely, a model of a cortical microcircuit may be composed of thousands of spiking neurons whose internal dynamics could be simplified to include only key channels and receptors (as opposed to more complex intracellular signaling pathways) to study phenomena that occur at the cortical network level, such as oscillations or persistent activity. Furthermore, biophysically based models are appealing in the study of functional consequences of neuropathology because perturbations can be implemented at the synaptic and neuronal levels. Modeling this detail currently has limitations in its application to system-level disturbances in schizophrenia; for instance, large-scale connectivity deficits in schizophrenia may at present be out of reach by biophysically based models, although in recent emerging studies, researchers have started to make strides in this direction (see later discussion; Yang et al., 2014). However, modeling synaptic phenomena in biologically plausible ways has the potential to link levels of analysis (e.g., synapses to network dynamics or even behavior).

Moreover, in recurrent networks, dynamical and functional consequences of a perturbation can be counterintuitive and difficult to parse without an explicit model. For example, neuromodulators, such as DA, change conductances on multiple sites in the prefrontal microcircuit (Seamans & Yang, 2004). In such instances, modeling this detail can strengthen intuition about the types of experiments that are needed to elucidate complex synaptic deficits in schizophrenia that involve a confluence of multiple neurotransmitter pathways whose complex dynamics cannot be readily intuited. Here, we focus on the role of biophysically based models to explain the dynamics of cortical microcircuits and their dysfunction in schizophrenia.

Microcircuit alterations in schizophrenia

Optimal cortical function depends on the balanced interaction of pyramidal excitatory (glutamatergic) and inhibitory (gamma-Aminobutyric acid, GABAergic) neurons (Shadlen & Newsome, 1994). Disruptions of this balance can have drastic behavioral consequences (Marin, 2012; Yizhar et al., 2011) relevant to serious mental illness, including schizophrenia and autism. Although microcircuit alterations in schizophrenia are complex, in many studies, researchers have converged on interneuron dysfunction as a key component of its pathophysiology (Marin, 2012; Nakazawa et al., 2012). An emerging hypothesis suggests a possibly parsimonious mechanism— namely, a deficit in the interaction between excitatory and inhibitory neurons (Benes, McSparren, Bird, SanGiovanni, & Vincent, 1991; Lewis et al., 2012; Lewis, Hashimoto, & Volk, 2005; Lewis & Moghaddam, 2006; Lewis, Volk, & Hashimoto, 2004; Marin, 2012). This hypothesis postulates a possible lack of inhibitory drive from GABA interneurons onto pyramidal neurons that results in disinhibition of pyramidal cells (Lewis et al., 2012; Marin, 2012). One line of evidence for abnormalities in this mechanism comes from postmortem investigations of dorsolateral PFC (DLPFC) in schizophrenia. These studies consistently have shown reduced levels of the messenger RNA for the 67-kilodalton isoform of glutamic acid decarboxylase (GAD67, encoded by GAD1), a key factor in optimal GABA levels, in the DLPFC of patients with schizophrenia (for review, see Lewis et al., 2005).

Pharmacological models of schizophrenia have offered complementary evidence. One such approach is to use NMDA receptor antagonists (e.g., ketamine), which transiently, safely, and reversibly induce cardinal schizophrenia symptoms in healthy volunteers. Leading hypotheses regarding ketamine’s effects on neural function also propose cortical “disinhibition” (Greene, 2001; Homayoun & Moghaddam, 2007; Kotermanski & Johnson, 2009; Krystal, Anand, & Moghaddam, 2002; Krystal et al., 2003). Specifically, it has been hypothesized that ketamine, and possibly other NMDA receptor antagonists, exerts its effects via preferential blockade of NMDA receptors on GABAergic interneurons in cortical microcircuits (Kotermanski & Johnson, 2009; for a detailed discussion, see Greene, 2001). Furthermore, proper functioning of GABA neurons has been linked to optimal WM function purportedly by virtue of GABA’s role in exerting lateral inhibition and synchronizing persistent firing of pyramidal cells in the DLPFC (Rao, Williams, & Goldman-Rakic, 2000). Therefore, it has been hypothesized that a disruption of excitation/inhibitory balance between pyramidal and GABA neurons may be one crucial pathophysiological mechanism operating in schizophrenia relevant to observed cognitive deficits and possibly system-level alterations in this illness (Anticevic, Cole, et al., 2014). Precisely this level of detail can be incorporated into biophysically based models to guide inferences regarding disruptions in more complex phenomena that can serve as biomarkers, such as cortical oscillations (Lisman, 2012).

Interpreting biomarkers in relation to modeling: Cortical oscillations

Understanding the mechanistic basis of neurophysiological biomarkers for schizophrenia could ultimately aid diagnosis and drug development by mapping the links between specific synaptic disruptions and network-level measurements. Biophysically based modeling provides a tool to link synapse-level parameters and emergent network-level dynamics. One area in which such links have been made is in the study of oscillations that emerge at the network level in recurrent cortical circuits (X.-J. Wang, 2010). This is relevant to schizophrenia because patients exhibit abnormal patterns of oscillatory activity, especially in the gamma (30–80 Hz) range (González-Burgos & Lewis, 2012; Lewis & González-Burgos, 2008; Uhlhaas, 2013; Uhlhaas & Singer, 2010). Computational models, in conjunction with physiological findings, support the idea that neocortical gamma oscillations arise from a feedback loop in a microcircuit of pyramidal cells reciprocally connected with perisomatic-targeting, parvalbumin-expressing interneurons (Buzsáki & Wang, 2012). In these models, gamma oscillations arise through a cycle of sequential activation in pyramidal cells and interneurons. Excitation leads pyramidal cells to fire, which recruits inhibitory interneurons to fire after a short delay. In turn, feedback inhibition suppresses firing, and after that inhibition subsides, the cycle begins again. Such oscillatory behavior arises naturally in dynamical systems with strong recurrent excitation and inhibition if there are delays or inhibition is slower than excitation. Understanding this basic cellular mechanism of oscillations can be directly applied to characterize deficits thought to occur in schizophrenia.

These models have been used to explore how gamma synchronization is affected by putative synaptic perturbations associated with schizophrenia, including reduced production of GABA and parvalbumin in interneurons (Vierling-Claassen, Siekmeier, Stufflebeam, & Kopell, 2008; Volman, Behrens, & Sejnowski, 2011), as described earlier. Also, experiments have demonstrated that abnormal levels of dopaminergic innervation (Kömek, Bard Ermentrout, Walker, & Cho, 2012) and antagonism of NMDA receptors on specific cell types are implicated in optimal microcircuit function (Rotaru, Yoshino, Lewis, Ermentrout, & González-Burgos, 2011; Spencer, 2009). In each case, the models have provided specific hypotheses for the physiological impact of synaptic manipulations. Biophysically constrained models can also drive inference in the other direction to infer the site of a synaptic perturbation from the pattern of changes in oscillation biomarkers. For instance, Neymotin et al. (2011) designed a detailed model of a hippocampal CA3 microcircuit with multicompartment pyramidal cells that are targeted by two types of inhibitory interneurons: soma targeting and dendrite targeting. The authors compared their simulation with in vivo recordings of local field potential changes in response to ketamine injection. They observed that the specific patterns of changes in power at gamma and theta frequency bands requires selective antagonism on NMDA receptors on the dendrite-targeting interneurons rather than on the other cell types. As these examples demonstrate, biophysically constrained computational modeling provides a means to interpret specific biomarkers and generate hypotheses that can be tested further with synapse-level and cellular-level measurements.

Biophysically based models of cortical oscillations have proven to be useful in linking synaptic perturbations to network-level biomarkers that can be measured in clinical populations and animal disease models. However, these models, although built explicitly to contain cellular-level detail, were not designed to inform a given cognitive process or specific symptoms (i.e., they are nonfunctional models). Extending these results to cognition remains a challenge but presents a key ongoing goal for schizophrenia research (which some models are explicitly designed to do, as reviewed in the final section). There is still controversy regarding whether oscillatory synchronization is fundamentally necessary for the computations performed by neocortical networks during cognition or whether oscillations are better understood as a mere signature of a particular network state. Here, computational studies are needed that posit specific roles for oscillations in cognitive processes (Börgers, Epstein, & Kopell, 2008; Dipoppa & Gutkin, 2013) and make specific predictions for how behavior could be impaired in disease states.

Models spanning from synapses to cognition: Focus on WM

Ultimately, a goal of neuropsychiatry is to explain how symptoms and cognitive deficits arise from synaptic pathologies. One area that has demonstrated productive interplay between theory and experiment is the study of WM, the ability to store and manipulate information on the timescale of a few seconds (Jonides et al., 2008). WM performance depends on a number of cortical areas, especially the PFC (Curtis, Rao, & D’Esposito, 2004). Single-neuron recording experiments showed that a neural correlate of WM in the PFC is stimulus-selective persistent activity, that is, elevated firing rates in a subset of neurons that spans the delay period in the absence of a stimulus (Funahashi, Bruce, & Goldman-Rakic, 1989).

A class of computational models called attractor networks have been applied to explain the mechanisms that allow a recurrent network of spiking neurons to maintain persistent activity during WM. In the mathematical formalism of dynamical systems, an attractor state is an activity pattern that is stable (i.e., the network will converge back to the attractor state after a small transient perturbation). An attractor network typically possesses multiple attractor states: a low-firing baseline state and multiple memory states in which a stimulus-selective subset of neurons are persistently active. In the attractor framework, strong synaptic connections among neurons support a stimulus-selective persistent activity pattern in the network (Amit & Brunel, 1997; X. J. Wang, 2001). Strong recurrent excitation among pyramidal cells with similar selectivity sustains persistent activation of those cells. Strong lateral inhibition, mediated by GABAergic interneurons, enforces selectivity of the WM representation, which prevents an unstructured spread of excitatory activity over time (Brunel & Wang, 2001; Compte, Brunel, Goldman-Rakic, & Wang, 2000). The stability of attractor dynamics also affords the network with an intrinsic resistance against distractors that intervene during the delay (Brunel & Wang, 2001; Compte et al., 2000), a key property of circuits that support goal-directed cognitive processing.

Using attractor models, researchers examined biophysical requirements for stability of both low-activity baseline state and stimulus-selective, high-activity memory state. As described earlier, a strongly recurrent network with recurrent excitation and inhibition is prone to oscillations, which can destabilize and destroy WM activity. X.-J. Wang (1999) found that such networks can be stabilized if the recurrent synaptic excitation is mediated primarily through slow NMDA receptors rather than through fast α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors so that excitation is slower than inhibition. These model predictions were confirmed by experiments on monkeys in which researchers combined electrophysiological recordings and pharmacological manipulation in the PFC: Blocking inhibition destroys selectivity (Rao et al., 2000), and NMDA receptors are crucial for stable persistent activity (M. Wang et al., 2013).

Within the attractor framework, Durstewitz, Seamans, and Sejnowski (2000) simulated dopaminergic modulation of multiple cellular and synaptic sites on both pyramidal cells and interneurons on the basis of physiological measurements from experiments in cortical slices. They found that strong stimulation of D1 receptors increases stability of both baseline and memory states in the network. Such a regime would be functionally beneficial during WM maintenance, given that the memory state is more robust to internal noise or external distractors. However, it may also be more difficult to flexibly reset the memory, thereby potentially generating perseverative errors. Conversely, low DA states have low stability for both regimes. This would be functionally beneficial during reset or encoding because it facilitates transitions between the states. However, during maintenance, the network would be vulnerable, given that noise or distractors could dislodge it from the memory state. Durstewitz and Seamans (2008) elaborated on this work to relate the model’s regimes to schizophrenia symptoms. They hypothesized that negative symptoms might correspond to the first, D1-dominated regime where the network can be stuck in a high-activity attractor state and not flexibly reset. This lack of flexibility in the D1-dominated regime could potentially drive perseverative behavior and prevent the PFC from being engaged by motivational signals for goal-directed behavior. Conversely, they hypothesized that positive symptoms might correspond to the second, D2-dominated regime where the network can spontaneously jump to a high-activity state as a result of internal noise, which potentially contributes to disorganized thought.

Other studies have focused on more generic changes to synaptic strengths on network dynamics and tried to relate those to specific behavioral impairments. This is a good example of where dynamical circuit models could be used to generate behavioral predictions, thereby highlighting the interplay across analysis levels. Loh, Rolls, and Deco (2007) decreased either the NMDA receptor conductance, the GABA conductance, or both onto pyramidal cells and interneurons in an attractor network. These manipulations instantiate two influential theories of the schizophrenia pathology: NMDA receptor hypofunction and interneuron dysfunction. Decreased NMDA conductance lowered memory-state stability and elevated distractibility because the memory state relies on strong recurrent excitation. Loh et al. proposed that this regime corresponds to cognitive and negative symptoms. In this regime, WM maintenance is compromised and noise can return the network to the baseline state. Decreased GABA conductance reduces baseline-state stability because strong feedback inhibition stabilizes the baseline state.

Moreover, Loh et al. (2007) found that decreased GABA conductance increases memory-state stability and decreases distractibility because it is more difficult to switch off the disinhibited pool of active pyramidal cells, which is somewhat in contrast to the behavior found in experimental observations in schizophrenia (J. Lee & Park, 2005; Park & Holzman, 1992). When both NMDA and GABA are reduced, the stability of both states is compromised, and the network undergoes noise-induced “wandering” among states. Similar to Durstewitz and Seamans (2008), Loh et al. proposed that this state corresponds to positive symptoms. The modeling studies described herein all focused primarily on the stability of the memory state, which suggests that its stability is associated with microcircuit changes in schizophrenia.

As noted, one key strength of WM models is that they make explicit predictions not just for neural activity but also for behavior, which can be tested experimentally in clinical populations or after pharmacological challenge. In that sense, models that were designed to inform a given level of analysis could scale across levels (which is also the case for connections/system-level models reviewed later). However, this translation from circuits to behavior is difficult because of the complexity behind behavioral deficits in schizophrenia. For instance, there are multiple functions required for WM that could be impaired: encoding, maintenance, robustness to distraction, precision, and capacity. There is still controversy regarding specific disruptions in each of these subprocesses in schizophrenia (Anticevic, Repovs, & Barch, 2013; Barch & Braver, 2007; Barch & Ceaser, 2012). Across many paradigms, the primary deficits appear at encoding rather than maintenance (J. Lee & Park, 2005; although there are relatively few studies in which researchers have formally manipulated delay length). For visuospatial WM, patients appear to exhibit deficits in encoding and maintenance of precision (Badcock, Badcock, Read, & Jablensky, 2008). In other visual paradigms, there appears to be reduced capacity but not necessarily precision (Hahn et al., 2010; Karlsgodt et al., 2009; Lencz et al., 2003). It is also possible that distinct neurophysiological mechanisms operate across WM modalities (e.g., verbal vs. spatial vs. object) that are differentially disrupted in schizophrenia.

Another complexity across behavioral studies is the stage of illness or chronicity of the patient population being studied. It may be possible that as the illness progresses, there are vital changes in the underlying neurobiology (e.g., glutamate function; Marsman et al., 2013) that could result in subtle but important differences in patterns of behavioral errors, which the models should incorporate into their design. Therefore, it will be critical to link multiple experimental modalities to computational models to better understand these discrepancies across studies.

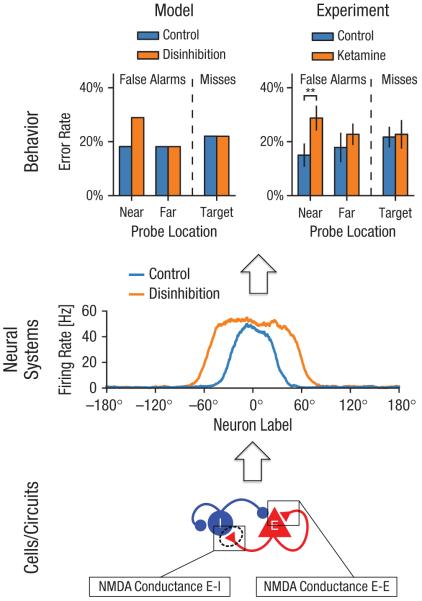
In one such study, J. D. Murray et al. (2014) examined the role of excitation-inhibition balance in the behavior of WM networks (see Fig. 2 for a schematic of how computational modeling can serve to bridge levels of analysis from circuits to behavior). As noted, cortical disinhibition has been strongly implicated in the pathophysiology of schizophrenia (Yizhar et al., 2011), but mechanistic links to cognitive and behavioral impairment remain tenuous. J. D. Murray et al. used a continuous attractor model developed for visuospatial WM (Compte et al., 2000) and implemented disinhibition through antagonism of NMDA receptors preferentially onto interneurons. In this model, disinhibition leads to a broadening in the neural-activity patterns that underlie WM maintenance. This neural change induced cognitive deficits by degrading WM precision, thereby leading to an increased vulnerability to distractors. In the continuous networks, a distractor can attract the memory if the two representations overlap. Because disinhibition broadens the WM-activity pattern, there is an increased range of distractors that can disrupt WM report. Note that this effect is distinct from the decreased vulnerability in a discrete model with no overlap between mnemonic and distractor representations (Loh et al., 2007).

Fig. 2.

Schematic of highlighted findings from a recent computational-modeling investigation. The bottom panel shows the manipulation of the N-methyl-D-aspartate glutamate (NMDA) receptor conductance on excitatory (E) and inhibitory (I) cells within a biophysically realistic computational model of working memory (complete details are presented in J. D. Murray et al., 2014). Because the model is able to capture effects at the microcircuit level (i.e., via firing traces), it generates a specific set of predictions that can be tested at the level of regions or neural systems. As shown in the middle panel, the specific prediction is a broadening of the working memory profile after decreased inhibitory drive onto E cells. This prediction could be tested with electrophysiology (M. Wang et al., 2013) or blood-oxygen-level-dependent functional MRI at the level of neural systems (Anticevic, Cole, et al., 2012; Anticevic, Gancsos, et al., 2012). Last, as shown in the top panel, the model generates a behavioral readout such that a specific profile of errors is predicted (top left), which can be tested with carefully optimized behavioral experiments (top right). Collectively, this approach has the potential to inform across-level understanding disturbances in schizophrenia from receptor to behavior. Nonetheless, this approach is limited because, at present, it can be extended to only a few well-characterized computational and behavioral processes, such as working memory (see main text for more extensive discussion). Asterisks indicate significance (***p < .001).

Because the model makes predictions at the level of behavior and neural activity, J. D. Murray et al. (2014) could experimentally test the model using human WM performance. The authors studied healthy human volunteers who performed a WM match-nonmatch task while undergoing a ketamine infusion during a functional neuroimaging experiment (Anticevic, Gancsos, et al., 2012). The model predicted a pattern of errors depending on whether the probe was similar to a target held in WM. Analysis of the behavioral data guided by the model revealed a similar specific pattern of errors under ketamine versus control conditions to that predicted by the computational model. This example demonstrates a utility of computational modeling, given that it inspired a more fine-grained behavioral analysis that, in turn, shed light on the specific cognitive deficits in this experiment. Using a similar model, Cano-Colino and Compte (2012) demonstrated that a stronger disinhibition can potentially destabilize the baseline firing state, thereby causing spontaneous emergence of random memory states. Critically, such different regimes can potentially be dissociated at the behavioral level by behavioral experiments that juxtapose competing model predictions. Put differently, the described microcircuit model can generate opposing behavioral predictions based on specific synaptic disturbances. Such models now need to be systematically applied to help guide analysis of behavioral data in schizophrenia.

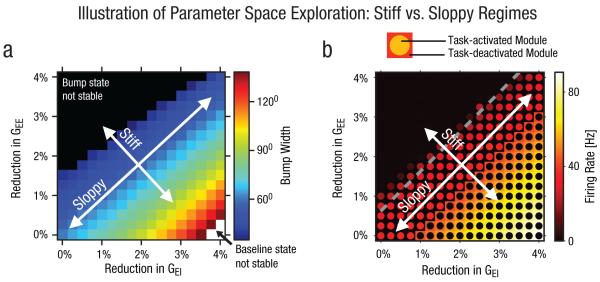
Modeling can also suggest what aspects of neural activity or behavior may be sensitive or robust to particular manipulations by disease or treatment. Changes in certain network parameters, or the combinations of parameters, have much stronger impact on model behavior than do changes in other parameter combinations (Gutenkunst et al., 2007). J. D. Murray et al. (2014) found that excitation/inhibition balance is a key parameter for optimal network function. This sensitivity to excitation/inhibition balance was also found in an extended model of reciprocal antagonism between a WM network and a task-deactivated network (see Fig. 3 for a schematic of parameter space exploration). Specifically, Anticevic, Cole, et al. (2012), Anticevic, Gancsos, et al. (2012), and Anticevic, Repovs, and Barch (2013) modeled the functional antagonism between the task-positive (frontoparietal) WM network and the task-deactivated default model network. Within the model, they implemented the alterations of excitation/inhibition balance by reducing the NMDA receptor contribution on the inhibitory interneurons. They compared their modeling results with neuroimaging experimental observations in which healthy volunteers underwent a ketamine infusion during WM performance. The authors found that NMDA receptor antagonism disrupted the anticorrelated functional properties of the two systems during WM, which is qualitatively similar to schizophrenia observations. They found that the excitation/inhibition balance manipulation within the model architecture qualitatively reproduced the experimental blood-oxygen-level-dependent (BOLD) responses. The authors also found that the model was robust to proportional excitation/inhibition changes that maintain the ratio, which is similar to the microcircuit model observations. Collectively, both modeling investigations, at the microcircuit and system levels, showed that excitation/inhibition balance is vital for optimal cognitive performance and neural-system-level operation. These modeling and experimental observations point to a “net effect” mechanism that could be operating in schizophrenia despite the underlying complexity of possible synaptic alterations.

Fig. 3.

Schematic of how modeling can serve to characterize synaptic parameter dependence. The graphs illustrate a parameter space of manipulating excitation (E) and inhibition (I) balance within circuit models of working memory (for complete details, see J. D. Murray et al., 2014). The purpose of this analysis was to illustrate how the model depends on level of perturbation of a given parameter. This example analysis illustrates a set of regimes along the diagonal (highlighted by the blue diagonal) where the model behavior was robust to manipulation of both E and I parameters. This parameter space illustrates that the model is robust as long as E/I balance is preserved (“sloppy” axis). In contrast, even subtle alterations in either E or I parameters (upper left and lower right quadrants) highlight that the model is sensitive along these parameters (“stiff” axis). That is, even a subtle alteration along these variables pushes the model out of a robust regime. This effect is captured in the graph in (a), which shows a biophysically based model at the microcircuit level (J. D. Murray et al., 2014), as well as in the graph in (b) when extended to model system-level interactions (Anticevic, Gancsos, et al., 2012; Yang et al., 2014). G_EE = recurrent excitation from excitatory (E) onto excitatory (E) cells; G_EI = feedback inhibition from excitatory (E) onto inhibitory (I) cells.

Another application of biophysically constrained modeling is the ability to test compensations that, in turn, could generate hypotheses about treatment mechanisms. The described models suggest that excitation/inhibition balance is the key parameter in determining network function. It is important that excitation/inhibition balance can be restored through compensations acting on multiple parameters. Specifically, J. D. Murray et al. (2014) tested two hypothesized mechanisms for pharmacological treatments: GABA_A-α2 agonism, implemented by strengthening the inhibition onto pyramidal cells; and mGluR_2/3 agonism, implemented by decreasing presynaptic glutamate release. They found that the GABAergic compensation required a small (2%) modification of parameters to reverse deficits. In contrast, the glutamatergic compensation required a large (25%) modification of parameters to restore behavior. The difference in modification magnitudes can be explained through their effects on excitation/inhibition balance: GABA_A-α2 agonism acts directly on inhibition to reduce the excitation/inhibition ratio, whereas mGluR_2/3 agonism in effect decreases both excitation and inhibition, thereby having a weaker impact on the excitation/inhibition ratio. This effect was a robust property of the model, irrespective of specific parameter starting points, which highlights excitation/inhibition balance as the key effective parameter. This example demonstrates how biophysically based modeling can provide a path for exploring potential treatments to ameliorate impairments that may exist in schizophrenia by targeting mechanisms that can restore optimal microcircuit function.

Future directions

One challenge for biophysically based modeling studies is the extension of this approach to large-scale distributed brain networks beyond the microcircuit level (Deco et al., 2013). The study of large-scale network models offers potential both in the interpretation of disease-related biomarkers and in understanding the neural-circuit basis of cognitive dysfunction across psychiatric conditions. Functional MRI studies have revealed patterns of cortical dynamics both at rest and during cognitive performance that are profoundly altered in schizophrenia (Anticevic, Cole, et al., 2014; Barch & Ceaser, 2012; Fornito et al., 2012).

As noted, there are a number of theoretical models that articulate that schizophrenia is a disorder of large-scale dysconnectivity (Friston & Frith, 1995; Stephan et al., 2006; Uhlhaas, 2013; Uhlhaas & Singer, 2010). Consistent with this hypothesis, results from resting-state functional connectivity studies have demonstrated coupling disruptions between brain areas in schizophrenia (Fornito et al., 2012), including PFC (Cole, Anticevic, Repovs, & Barch, 2011) and thalamo-cortical systems (Anticevic, Cole, et al., 2014; Woodward et al., 2012). There are ongoing efforts, however, to determine the specificity of these effects in relation to other severe mental illness (Anticevic, Brumbaugh, et al., 2012; Anticevic, Savic, et al., 2014; Anticevic, Yang, et al., 2014), such as bipolar disorder and autism (Anticevic, Cole, et al., 2013).

Similar large-scale alterations in resting-state functional connectivity have also been documented in pharmacological models, such as the NMDA receptor antagonist ketamine model (Driesen et al., 2013). During cognitive tasks, both schizophrenia and NMDA receptor pharmacological manipulations are associated with disrupted activation and deactivation across distributed cortical networks (Anticevic, Gancsos, et al., 2012). Large-scale biophysically based models could help to elucidate synaptic contributions to these large-scale network alterations, thereby helping to bridge levels of analysis (Anticevic, Gancsos, et al., 2012; Deco et al., 2013). Yang et al. (2014) recently have provided evidence that such biophysical dynamical models can be used to provide insight into large-scale neural-system disturbances observed during resting state in chronic patients with schizophrenia. Specifically, Yang et al. found that alterations in model connectivity either at local circuit level or across the entire network can effectively model elevated neural variability observed in schizophrenia. Such dynamical models of resting-state fluctuations have the potential to elucidate emerging neuroimaging biomarkers in schizophrenia (Anticevic, Cole, et al., 2013).

Another challenge is the extension of biophysically based models to more complex behavior and symptoms. Thus far, biophysically based models have been applicable to a limited repertoire of functions related to cognition, such as WM maintenance, primarily because such functions have been characterized through primate physiology experiments. One area of progress is in the domain of decision making. The neural-circuit bases of decision-making processes have been investigated in electrophysiological and computational-modeling studies (X.-J. Wang, 2008). Decision making, which is impaired in a range of psychiatric conditions in addition to schizophrenia, involves an extensive network of cortical and subcortical areas (D. Lee, 2013). To accurately capture adaptive cognitive behavior, researchers must incorporate multiple interacting brain areas into models that possess various distributed and modular computations. In this area, biophysically based modeling will be informed by other levels of modeling that are more abstract and removed from biophysical detail but that can be readily applied to modeling psychological processes and interactions among distributed neural systems. In the next section, we discuss the insights into more complex cognitive processes provided by connectionist models, whereas in the final section, we focus on select examples of modeling complex behavioral deficits in schizophrenia, which is currently out of reach for simple neural-circuit models.

Connectionist Models—Understanding System-Level Disturbances in Schizophrenia From Both a Psychological and a Neural Perspective

Another class of models used to examine the psychological and neurobiological mechanisms of schizophrenia stem from the connectionist or parallel-distributed-processing (PDP) framework (McClelland & Rumelhart, 1986; Rumelhart & McClelland, 1986). These models originated from a tradition that prioritized understanding the mechanisms driving cognition from a psychological perspective but using principles thought to capture computations as they might be carried out in the brain. In such models, each unit is a simple summing device that collects inputs from other model units and changes its output when the inputs change. Information in such models is represented as graded activity patterns over populations of these simple units in which processing takes place as the flow of activity from one set of units to another. Learning occurs through the modification of the connection strengths between these simple units. This learning is meant to capture some elements of the type of Hebbian learning known to govern changes in connection strength between neurons and is sometimes accomplished using algorithms referred to as “back-propagation” (Rumelhart, Hinton, & Williams, 1986). In back-propagation, the model is presented with an input pattern, and the output layer is allowed to settle into some response. The difference between the response generated by the model and the expected response (the target) is computed. In turn, these error signals are propagated back through the network toward the input layer, thereby adjusting the weights or connections between units. This is not precisely Hebbian learning, and at least in one sense, this is not a biologically plausible learning mechanism, given that we do not typically have access to the “correct” response in a way that can shape learning.

Another biological implausibility here stems from the lack of evidence for a mechanistic basis for back-propagating learning signals (but see O’Reilly’s, 1996, work in trying to generate a biologically plausible alternative to back-propagation). This is an example of how, at times, connectionist models, although capturing complex neural phenomena, may not map onto specific neurobiologically based mechanisms (in contrast to biophysically based models described earlier). Nevertheless, this approach captures the idea that learning occurs through a slow elimination of error by small changes in the connections between units, a phenomenon referred to as “gradient descent” (Cohen, Servan-Schreiber, & McClelland, 1992), which is thought to be disrupted in schizophrenia.

In such PDP models, the units are not meant to have one-to-one correspondence to individual neurons but, rather, to represent processing accomplished by neuronal assemblies that capture the general principles of neuronal information processing. Such models are typically simplified, capturing brain-style computation, without necessarily committing to the details of any particular neural system or subsystem (although see our later discussion for modifications that do try to make specific types of commitments and neurotransmitter modulations). Nonetheless, such connectionist models help to build bridges between understanding of low-level properties of neural systems and their participation in higher-level (system) behavior. They have the additional advantage of being able to capture a wide range of complex behaviors and neural-system interactions that cannot at present be modeled as effectively by biophysically based models (Cohen, Dunbar, & McClelland, 1990; Cohen & Servan-Schreiber, 1992; McClelland, 1991; McClelland & Elman, 1986; McClelland, St. John, & Taraban, 1989; Plaut, 1996; Plaut & Farah, 1990; Plaut, McClelland, Seidenberg, & Patterson, 1996; Plaut & Shallice, 1993).

Connectionist modeling of hallucinations and delusions in schizophrenia

Seminal models using such a framework were developed by Ralph Hoffman and colleagues in their examination of the impact of abnormal synaptic pruning in the cortex (Feinberg, 1982). Such models tested the effect of eliminating the connections between units (Hoffman & Dobscha, 1989). Hoffman and Dobscha (1989) found that when a sufficient number of connections were eliminated, the model developed what was referred to as “parasitic foci.” That is, they observed patterns of activity across units in the model that did not correspond to any learned memory but, instead, to the “state” to which the model kept returning. Hoffman and Dobscha likened these parasitic foci to delusions and hallucinations. Subsequently, Hoffman and McGlashan (1997) extended this framework to simulate speech perception and to compare effects of synaptic pruning with cell loss (elimination of whole units in the model). They used a type of PDP model referred to as an “Elman” network, which is a sequential recurrent network. Such networks consist of an input and an output layer connected by a “hidden layer” that computes internal processing. This Elman network included an additional layer connected to the hidden layer that could temporarily store information and was thought to support WM functions (temporary storage of information) during speech perception. They found that elimination of synapses in the WM subnetwork of the model initially improved speech perception. As the severity of the elimination increased, however, the model started to fail to detect words correctly and started to generate “hallucinations” or patterns of activity across the output layer that corresponded to words even if there was no structured input. In contrast to synapse elimination, a small of amount of “cell” removal (e.g., elimination of units) also initially improved speech perception, but greater cell loss did not generate hallucinations.

These early models were “proof-of-concept” examples of how various neurobiological changes might affect connectionist networks but did not explicitly simulate and match the model behavior with the experiment. Next, Hoffman and McGlashan (2001) examined the model’s ability to capture behavior produced by real patients. Specifically, they studied speech perception during babble among healthy individuals and schizophrenia patients with and without hallucinations. Consistent with the model, results showed that patients who experienced hallucinations made more errors in speech detection and had more misperceptions of words, although the nonhallucination patients experienced as many misperceptions at the highest noise levels. Furthermore, Hoffman and McGlashan examined the ability of repetitive TMS (rTMS) to reduce hallucinations, given that their modeling work predicted that the suppression of information flow should reduce misperceptions. This work was also based on prior imaging findings by Silbersweig et al. (1995), which indicated hyperactivity in auditory cortex during hallucinations. Consistent with the Silbersweig et al. model, suppressive rTMS significantly reduced hallucinations in schizophrenia patients compared with sham rTMS (Hoffman & McGlashan, 2001). Subsequently, Hoffman and McGlashan extended this model of speech perception to capture the potential influence of increased DA. Because of the putative role of DA in inhibition, they modeled increased DA by changing the bias onto the units in the WM module, thereby effectively requiring them to accumulate greater information to maintain information. This manipulation relates to only one aspect of the influence of DA on neuronal information processing, and by itself, it did not fully capture the data on speech perception. However, a combination of increased DA and synaptic pruning more successfully captured the performance of those patients who experienced hallucinations. In related work, Siekmeier and Hoffman (2002) used the same type of model to simulate semantic priming changes in schizophrenia and showed that reductions in connectivity could simulate the patterns of increased “automatic” semantic priming in schizophrenia as shown by Kwapil, Hegley, Chapman, and Chapman (1990).

Hoffman’s most recent work took a somewhat different approach. Here, Hoffman et al. (2011) used a connectionist model of narrative comprehension and recall called DISCERN (Miikkulainen & Dyer, 1991). DISCERN consists of a set of hierarchically organized modules that use a PDP framework that instantiates a lexicon of distributed input/output representations that can accomplish narrative text comprehension and recall of narrative components. Its development was not strongly driven by biological constraints; rather, the principles of processing are subsymbolic and capture brainlike processing. Hoffman et al. used this model to simulate eight different potential illness mechanisms in schizophrenia and their ability to capture the patterns of story recall shown by individuals with schizophrenia and control participants. These illness mechanisms varied in their level of analysis and ranged from a neural level (e.g., disconnection in WM-related brain networks, increased cortical noise, increased DA, increased neuronal arousal) to a more cognitive level (e.g., increased semantic priming, semantic network distortion) to hybrid mechanisms (increased learning due to exaggerated prediction error signals potentially resulting from altered DA function). Hoffman et al. found that the “hyperlearning” mechanism best captured recall patterns found in schizophrenia, including errors involving confusions of “who did what” that Hoffman et al. likened to the formation of delusional beliefs.

The models used by Hoffman (1997) and Carter and Neufeld (1999) used the brain-style computational principles embodied by PDP but did not make strong commitments to key aspects of neurobiology during model development. Nonetheless, they were critical steps to understand how neurobiological or cognitive deficits might contribute to the formation of core symptoms of psychosis, such as hallucinations and delusions. Although the models themselves did not produce behaviors with the same format and content as shown by human patients, the “in-principle” examples provided conceptual leverage to bridge the gap between biology and behavior and even extend to treatment recommendations in the case of the rTMS work conducted by Hoffman et al. (2011). Therefore, despite not committing to biological realism, connections models can guide neural/behavioral predictions that ultimately have treatment implications.

Connectionist modeling of cognition in schizophrenia

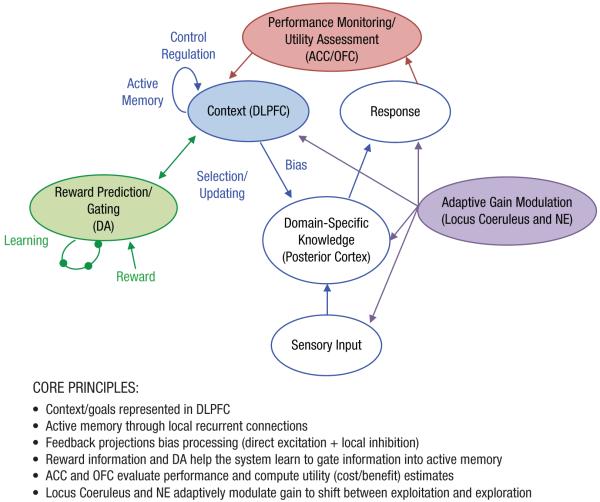
Another set of PDP models developed by Cohen and Servan-Schreiber (1992), and expanded by additional colleagues, made stronger commitments to neurobiological principles. The initial models developed by Cohen and Servan-Schreiber instantiated the hypothesis that cognitive control results from interactions between the DA neurotransmitter system and the PFC. These models suggested that goal-related information, or context information, was maintained in the PFC and used to bias stimulus-response mappings represented in the posterior cortex, thereby serving as a source of top-down support for controlling behavior (see Fig. 4 for a computational model of cognitive control). In these models, the “context” module was associated with the functions of the DLPFC. Active maintenance in the absence of external inputs was assumed to occur via recurrent excitation, as suggested by neurobiological data (Funahashi et al., 1989). This model assumed that feedback projections from the context/DLPFC module biased processing in posterior systems via direct excitation but that competition between representations within a processing stream occurred via lateral inhibition (Cohen et al., 1990; Cohen, Servan-Schreiber, & McClelland, 1992). Furthermore, the effects of DA were assumed to be modulatory rather than purely inhibitory, such that changes in DA activity could either increase or decrease activity depending on the nature of inputs that DA was modulating. Put differently, increases in DA were assumed to increase the signal-to-noise ratio of a unit’s activation value in relation to its input. With excitatory input, higher gain means that the same level of input leads to higher activation. Conversely, with inhibitory input, higher gain leads to more negative values and lower activation.

Fig. 4.

Computational model of cognitive control. Extensions to original model developed by Cohen and Servan-Schreiber (1992; model components in blue) that include roles for (a) dopamine (DA) in gating information into active memory (model components in green; Braver & Cohen, 1999), (b) anterior cingulate cortex (ACC) in monitoring for conflict and dynamically regulating cognitive control (model components in red; Botvinick, Braver, Barch, Carter, & Cohen, 2001), and (c) orbitofrontal cortex (OFC) in computing value/utility estimates and the locus coeruleus and norepinephrine (NE) in adaptive gain modulation to shift between exploitation and exploration (model components in purple; Aston-Jones & Cohen, 2005). DLPFC = dorsolateral prefrontal cortex.

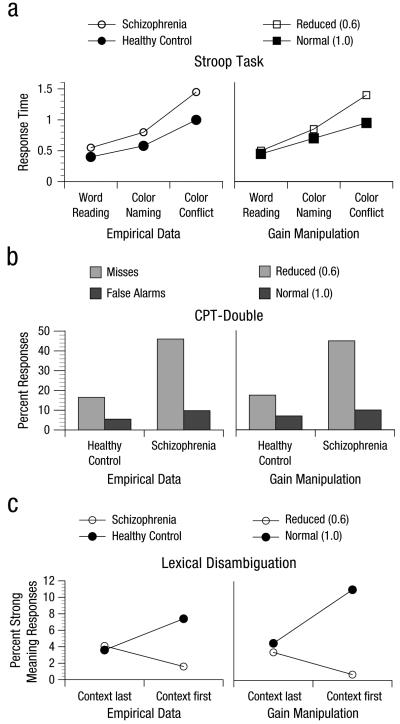
This basic Cohen and Servan-Schreiber (1992) model was used to capture the patterns of behavioral data shown by healthy individuals in three different tasks— the Stroop task, lexical disambiguation task, and continuous-performance task (CPT)—that were all thought to depend on the ability to represent and maintain context/goal information in DLPFC (see Fig. 5 for empirical and simulation results). In the Stroop task, individuals are presented with words in different-colored inks with the words themselves either color words or noncolor words. The color and the word can be congruent (e.g., red written in red) or incongruent (e.g., red written in green). Participants are typically asked to respond on the basis of the ink color and to ignore the word and are slower and less accurate if the word and the color conflict. The model assumes that this context/goal information (“respond to color, ignore the word”) is maintained in the context/DLPFC module and facilitates processing of the color information through feedback excitation. This allows the context module to effectively compete for response selection with the word information via lateral inhibition even though word reading is typically the dominant response. In the lexical disambiguation task, participants are presented with homophones (e.g., pen) that have a dominant meaning (writing instrument) and a subordinate meaning (fenced enclosure) and asked to interpret the meaning of the homophone. The homophones are accompanied by sentences that either bias the individual toward the dominant meaning (e.g., You can’t sign a check) or the subordinate meaning (e.g., You can’t keep chickens) of the word. Furthermore, this biasing context could come either before the homophone (e.g., You can’t keep chickens … without a pen) or after the homophone (e.g., Without a pen … you can’t keep chickens). The model assumed that when the biasing context preceded the homophone, it was maintained in the context/DLPFC module. This information could be used to bias the interpretation of the homophone pen toward the subordinate meaning, thereby allowing it to effectively compete against the dominant meeting.

Fig. 5.

Empirical and simulation results on the (a) Stroop task, (b) continuous-performance task (CPT-Double), and (c) lexical disambiguation task from Cohen and Servan-Schreiber (1992). See text for explanation of tasks and gain manipulation in model simulations.

Last, the CPT used was a version developed by Cornblatt, Lenzenweger, and Erlenmeyer-Kimling (1989) and Cornblatt, Risch, Faris, Friedman, and Erlenmeyer-Kimling (1988) called the CPT-Double, in which participants were required to respond “target” every time the current stimulus was the same as the immediately preceding stimulus. In the model, it was assumed that the preceding stimulus was maintained in the context/PFC module, and that, again, this information could bias interpretation of the next stimulus as either a target or a nontarget response. As shown in Figure 5, these models captured performance patterns across conditions in healthy individuals in all three tasks.

More important, these three models were used to test the hypothesis that reductions in DA input into DLPFC lead to impairments in the ability to represent and maintain context information in DLPFC and that this impairment in the representation of context leads to deficits in a range of cognitive tasks among individuals with schizophrenia. To test this hypothesis, Cohen and Servan-Schreiber (Cohen & Servan-Schreiber, 1993; Cohen, Servan-Schreiber, & McClelland, 1992; Cohen, Targ, Servan-Schreiber, & Spiegel, 1992; Servan-Schreiber, Cohen, & Steingard, 1996) modeled a reduction in DA inputs into DLPFC via a reduction in the gain parameter that modulates the signal-to-noise ratio of units in the context/DLPFC module. These researchers used the exact same manipulation to mimic reduced DA across all three models/tasks and found that the perturbed model captured all of the key aspects of performance changes among individuals with schizophrenia (see Fig. 5), including (a) overall slower performance on the Stroop task and increased interference on incongruent trials (in which the word and the color conflict), (b) increased misses and false alarms on the CPT-Double, and (c) an increase in interpretation of homophones as their dominant meaning. Furthermore, Cohen and Servan-Schreiber showed that a manipulation designed to mimic slowed processing speed (i.e., a change in cascade rate) did not recapitulate the pattern of performance shown by the individuals with schizophrenia on the Stroop task.

Using models to make predictions about cognitive function in schizophrenia

One important goal of computational models is to use modeling in a predictive fashion to test specific hypotheses about neurobiological or cognitive mechanisms that might lead to psychiatric impairments. Motivated by this goal, Cohen, Barch, Carter, and Servan-Schreiber (1999) used their initial modeling to create new versions of the CPT and the Stroop task to test model predictions regarding effects of reduced DA inputs into DLPFC on cognitive function in schizophrenia. Specifically, they modified a version of the AX-CPT, in which participants are presented with pairs of letters and instructed to respond “target” to the letter X, but only if it follows the letter A. To test hypotheses about a specific deficit in context processing, they made two modifications to the AX-CPT (Servan-Schreiber et al., 1996). For the first modification, they increased the frequency of target (AX) pairs to 70% and divided the remaining 30% evenly between three distractor conditions: a non-A followed by an X (BX condition), an A followed by a non-X (AY condition), and a non-A followed by a non-X (BY condition).

This frequency distribution creates two biases that can be used to probe context processing. First, it creates a bias to respond “target” to an X, given that this is the correct response for 87.5% of the trials in which X appears. This tendency has to be inhibited in the BX condition by using the context provided by the prior stimulus (non-A stimulus). Second, it creates a bias to prepare a target response after an A, given that the majority of the time the A will be followed by an X. Thus, on AY trials, individuals who are able to represent and maintain context should be slower and less accurate as the context leads them astray. The second manipulation was to vary the delay (1,000 or 5,000 ms) between the cue (A/non-A) and the probe (X/non-X) stimuli, with the hypothesis that deficits should be worse among individuals with schizophrenia at a longer delay because context information needs to be maintained.

Cohen et al. (1999) also made two modifications to the Stroop task. To increase reliance on context, they varied the task to be performed variably on each trial, signaled by a cue (context) that indicated whether the person should name the color or read the word. In addition, they varied the delay between the cue and the stimulus to examine whether individuals with schizophrenia have more difficulty using the cue (context) at longer delays to inhibit word reading (dominant response) on colornaming trials (subordinate response). Cohen et al. examined the model predictions with an independent sample of schizophrenia patients and healthy control participants on these modified AX-CPT and Stroop tasks, as well as on the lexical disambiguation task described earlier. Consistent with model predictions, results showed that schizophrenia patients made more errors in the AX and BX conditions than did control participants but not in the AY or BY conditions. Furthermore, patients with schizophrenia showed an increase in AX and BX errors from the short to the long interstimulus interval condition. They observed an increase in AX errors in patients with schizophrenia (but not BX errors) that was greater than that shown by healthy control participants or depressed patient control participants (see Barch & Braver, 2007, for a review of AX-CPT findings in schizophrenia). In the Stroop task, schizophrenia patients showed the predicted increase in interference compared with control participants in the color-naming condition, although the predicted interaction with delay was not found. However, in the lexical disambiguation task, the predicted three-way interaction with condition, delay, and group was found. That is, schizophrenia patients were less likely than were healthy or depressed control participants to produce the subordinate interpretation of the homophone when there was a delay between the context and the response. Although not every prediction was upheld, this work is an example of the ability to use computational models to make novel predictions about psychological and neural-system level mechanisms of cognitive impairment in schizophrenia that can be tested experimentally.

Using models to make predictions about DLPFC activity

As noted, one of the hypotheses embodied in the Cohen et al. (1999) models was that the DLPFC is responsible for the representation and maintenance of context and that schizophrenia patients exhibit deficits in DLPFC function due to reduced DA input. For this reason, the models also make the prediction that schizophrenia patients should show reduced activation of the DLPFC during tasks that require representation and maintenance of context. This prediction is not a particularly novel or a unique hypothesis. Also, numerous studies with a variety of task conditions have shown reduced DLPFC activity in schizophrenia (Minzenberg, Laird, Thelen, Carter, & Glahn, 2009). However, the Cohen et al. models did make specific predictions that individuals with schizophrenia should show reduced DLPFC activity in conditions with a strong demand for context maintenance. Consistent with these predictions, research has shown that schizophrenia patients exhibited reduced activity on long-delay trials in the AX-CPT (Barch et al., 1999), during B versus A cues on the AX-CPT (Edwards, Barch, & Braver, 2010; Holmes et al., 2005; MacDonald et al., 2005; Perlstein, Dixit, Carter, Noll, & Cohen, 2003; Yoon et al., 2008), and during cues that predict the need to overcome a prepotent response (Snitz et al., 2005). Furthermore, schizophrenia patients showed reduced connectivity between frontal and parietal/occipital regions during B cues as compared with control participants, although the models did not make specific predictions about connectivity (Fornito et al., 2011). In addition, research has shown that focused training context maintenance leads to increased DLPFC activity to cues on the AX-CPT task (Edwards et al., 2010) in schizophrenia.

Extension to include a “gating” mechanism

The modeling described herein captured performance of healthy individuals on a range of tasks and simulated effects of reduced DA in DLPFC as a means of capturing the performance in schizophrenia. However, there were key issues not captured by these models. One issue was how humans manage the trade-off between appropriate updating of context information in DLPFC versus protection of already stored information from context/goal-irrelevant information that could disrupt ongoing maintenance. Thus, Braver, Barch, and Cohen (1999) and Braver and Cohen (1999) extended the model to address this issue by postulating that the DA projection to DLPFC serves a possible gating function (also see other models incorporating the basal ganglia into the gating mechanism; Hazy, Frank, & O’Reilly, 2006, 2007). This is accomplished by regulating access of context representations into active memory whereby the system learns what information should be gated into DLPFC via the reinforcement-learning functions of DA (see Fig. 4). In this gating model, DA plays an important control function by enabling flexible updating of active memory in DLPFC while retaining protection against interference. Specifically, this model posited that phasic changes in DA activity mediate both gating and learning effects in the PFC through similar neuromodulatory mechanisms, although possibly through different DA receptor subtypes (Braver & Cohen, 1999; Braver et al., 1999). Similar to the idea that DA potentiates the gain of signals into the DLPFC, the gating effect occurs through transient potentiation of both excitatory afferent and local inhibitory input.

Conversely, learning effects occurs through Hebbian-type modulation of synaptic weights driven by errors between predicted and received rewards. The coincidence of the gating and learning signals produces cortical associations between the information being gated and a triggering of the gating signal in the future. This model also captured the performance of healthy individuals on the AX-CPT task (Braver & Cohen, 1999; Braver et al., 1999). Furthermore, the model captured behavioral effects of presenting interference items (e.g., letters presented in a different color) that occurred between the cue and the probe during the AX-CPT and the impact of such distractors in DLPFC activity (Anticevic, Repovs, Corlett, & Barch, 2011).

The Braver model (Braver & Cohen, 1999; Braver et al., 1999) also embodied a somewhat different hypothesis about the nature of impaired DA function in schizophrenia by positing that schizophrenia may reflect a noisy DA gating signal, which results in increased tonic and decreased phasic DA function, originally proposed by Grace (1991), which may also have relevance for prefrontal function in schizophrenia (Bilder, Volavka, Lachman, & Grace, 2004). The “lesioned” model with the noisy gating function captured AX-CPT performance shown by schizophrenia patients. However, it is not clear whether this hypothesis about the role of DA in schizophrenia matches existing data. A recent meta-analysis of DA function in schizophrenia has suggested evidence of a significant increase in DA availability in schizophrenia (Fusar-Poli et al., 2013; Howes et al., 2012; Samartzis, Dima, Fusar-Poli, & Kyriakopoulos, 2014). There is also evidence for increased occupancy of D2 receptors by DA in schizophrenia (Abi-Dargham et al., 2000). These data are consistent with the hypothesis that tonic DA levels are increased in schizophrenia, which is in line with the proposed deficits in the gating model. However, there is also consistent evidence that schizophrenia exhibits an increase in DA release in response to pharmacological challenge (Abi-Dargham et al., 1998; Abi-Dargham et al., 2004; Abi-Dargham, van de Giessen, Slifstein, Kegeles, & Laruelle, 2009; Laruelle et al., 1996). This is possible evidence for increased phasic release of DA rather than decreased phasic release.

However, positron emission tomography studies of DA function in schizophrenia cannot isolate the type of phasic DA function that the model attempts to capture; thus, more work is needed to understand how alterations in DA function in schizophrenia influence the type of phase-related DA release simulated in the model, which is tightly coupled to ongoing cognitive processing. Moreover, the role of distinct DA receptor subtypes, their alterations in schizophrenia, and their contributions to PFC function remain to be fully incorporated into models that capture the interaction of the basal ganglia and the PFC.

Characterizing Complex Behavioral Disturbances in Schizophrenia via Computational Modeling

We focused on two levels of analysis in which neurobiological deficits in schizophrenia may occur, namely, the level of cells/microcircuits (J. D. Murray et al., 2014) and the level of neural systems (Cohen & Servan-Schreiber, 1992), which can be examined via animal/pharmacological models and neuroimaging experiments, respectively. However, schizophrenia ultimately affects complex behaviors, such as motivation (Barch & Dowd, 2010; Dowd & Barch, 2010), learning (Corlett, Honey, Krystal, & Fletcher, 2011), belief (Corlett, Honey, & Fletcher, 2007), and perception (Kapur, 2003). The ultimate goal of computational neuropsychiatry is to provide a bridge for understanding how synaptic-level disturbances can scale to alterations in neural systems and, ultimately, alter complex behavior. At present, this unifying understanding is out of reach for clinical neuroscience. However, there have been productive efforts to mathematically formalize complex behavioral abnormalities observed in schizophrenia, as well as their relationships to brain activity. Computational models have been applied to characterize observed behavioral alterations and generate experimental predictions about the type of behavioral deficits that may be occurring in patients. Some of these models do not provide strong inferences about cellular- or neural-system-level mechanisms (although some do), but they do provide a highly productive methodological framework for systematically understanding complex behavioral alterations in schizophrenia. It is important to note that this review is not intended to comprehensively review the literature on mathematical modeling of behavior or brain-behavior relationships in schizophrenia (see prior excellent reviews on this topic by Deserno, Boehme, Heinz, & Schlagenhauf, 2013; Maia & Frank, 2011).

Here, we highlight a few focused studies that provide an example for this type of computational approach, which can interface with both behavioral and brain-imaging experiments. We argue that formalizing behavior and brain-behavior relationships in mathematical principles provides a vital tool for understanding specific symptoms in schizophrenia and can also guide experimental studies across levels of analysis. In fact, many of the models described in the following discussion have been used to generate predictions about both behavior and brain-behavior relationships (e.g., see the work of John O’Doherty, Nathaniel Daw, and many other researchers; Daw, Gershman, Seymour, Dayan, & Dolan, 2011; Daw, Niv, & Dayan, 2005; Wunderlich, Rangel, & O’Doherty, 2009; also see Fig. 1). These models can generate predictions about both behavior and brain-behavior relationships in schizophrenia (Gold et al., 2012; Gradin et al., 2011; G. K. Murray et al., 2008; Schlagenhauf et al., 2014).

Modeling of Reward Learning in Schizophrenia

An excellent example for mathematical modeling of behavior applied to schizophrenia is illustrated through studies by James Gold, Michael Frank, and colleagues (Gold et al., 2006; Gold et al., 2008; Gold et al., 2012). Although these studies can be broadly classified as incorporating connectionist models, they have also provided a characterization of complex behavioral abnormalities in schizophrenia. This work collectively focuses on understanding learning disruptions in schizophrenia, which may underpin some more complex abnormalities in belief formation and motivational representations. For instance, Morris, Heerey, Gold, and Holroyd (2008) and Morris, Holroyd, Mann-Wrobel, and Gold (2011) attempted to understand impaired reinforcement learning in schizophrenia. These authors combined both behavioral and electrophysiological recordings to test the hypothesis of a possible reduction in sensitivity to feedback in schizophrenia patients. As noted, the hypothesis that the anterior cingulate cortex (ACC) serves to monitor and detect conflict to modulate cognitive control is not without its critics, and alternative views of the function of the ACC have been put forward and modeled by Holroyd and Coles (2002) and Holroyd and Yeung (2012).

Specifically, Holroyd and Coles (2002) argued that the ACC plays a computational role in response selection by integrating reward-prediction errors generated by the midbrain DA systems over time to determine which motor-control plans should be in charge of the motor system. Holroyd and Coles examined this hypothesis in a computational model based on reinforcement-learning principles. In this model, prediction errors were assumed to be carried by the DA systems, and the basal ganglia was implemented as an adaptive critic that updated the value associated with different response options on each trial via a temporal-difference learning algorithm. This model can simulate both human behavior and activity of the midbrain DA system during reinforcement learning and can also capture the pattern of error-related negativity (ERN) responses during such tasks. The ERN is an event-related-potential component that is greater on error trials than correct trials and is thought to reflect a generator in the ACC.

Morris et al. (2008) and Morris et al. (2011) used this model conceptually and formally to understand reductions in the response ERN (an ERN that occurs when a person makes an error prior to feedback) and the feedback ERN (an ERN in response to feedback). Across different experimental paradigms, they found that schizophrenia patients exhibit consistently reduced response ERNs but not consistently reduced feedback ERNs. They used the model to examine whether changes in prediction error produced by the DA system captures this pattern of impaired response ERN coupled with a relatively intact feedback ERN or whether deficits value computation by the adaptive critic led to this pattern (Gold et al., 2008). This is a good example of where certain types of models can generate inferences across levels of analysis. Their simulations suggested that a deficit in the computation and prediction of value best captured this pattern of data, although the authors acknowledged that other work has suggested that OFC systems may also contribute to the computation of value, not just the basal ganglia (Gold et al., 2012; Wallis, 2007; Waltz & Gold, 2007). This modeling work was relatively unique compared with some of the approaches described earlier because it focused on capturing the pattern of brain activity evoked specifically during task performance. However, in these studies, the researchers did not attempt to capture performance by humans with the model, and it would be important in future work to determine whether the model could capture both behavior and ERN/ACC responses in the same task.

In another study, Waltz and Gold (2007) evaluated reinforcement-learning deficits in schizophrenia. They hypothesized that such abnormalities may be related either to slow inability to learn rewarding contingencies or to inability to evaluate feedback provided on a moment-to-moment basis that can guide behavioral adjustments. Either of these behavioral deficits could play into reinforcement-learning problems in schizophrenia. Waltz and Gold proposed a mechanism for such impairments that was explicitly guided by a computational model of reinforcement learning developed by Frank and Claus (2006). In brief, the model captures aspects of the basal ganglia function and incorporates the specific role of DA in the regulation of positive and negative prediction errors, which, in turn, affect behavioral outcomes. The model further specifies differential involvement of D1 and D2 receptors in driving behavior—specifically, the D1-receptor pathways are thought to be involved in “go” (or appetitive) actions, whereas the D2-receptor pathways are thought to be involved in “no-go” (or withdrawal) actions (Frank, 2005). In this way, the model links system-level physiology (the connectionist modeling approach) to complex learning behavior that can occur in various paradigms (the behavioral modeling approach), which, again, highlights how model and experiment can interact at distinct levels of analysis.

Moreover, this modeling approach can generate predictions regarding specific deficits in schizophrenia depending on the predicted alterations in DA signaling that may, in turn, affect complex learning behavior (which is presently out of reach for microcircuit models reviewed in the first section). Indeed, there is compelling evidence for alterations in DA function in schizophrenia. A series of studies by Abi-Dargham and colleagues (Abi-Dargham et al., 1998; Abi-Dargham et al., 2000; Abi-Dargham et al., 2004; Abi-Dargham et al., 2009) and others (Howes et al., 2012) have shown that schizophrenia may be associated with elevated DA levels in the basal ganglia, which may affect learning outcomes involving the DA system.

On the basis of this evidence, Waltz, Frank, Robinson, and Gold (2007) predicted that patients with schizophrenia might show an increased go propensity during paradigms that involve reinforcement learning. The model generates a parsimonious prediction whereby patients may be more likely to execute a motor action (as opposed to inhibit) when it is actually disadvantageous to do so. In addition, another prediction made by Waltz et al. involves an abnormality in go learning. That is, if there is excessive DA tone, then phasic DA signaling during trials that involve learning may be reduced (i.e., lower signal-to-noise due to increased DA levels). This, in turn, may result in a decreased learning curve that explicitly relies on high phasic/tonic signal-to-noise ratio. With regard to behavior, Waltz et al. formalized this prediction as a specifically lower tendency to execute go responses when appropriate accompanied by an overall elevated likelihood to make go responses in general. The authors found that patients diagnosed with schizophrenia showed a decrease in their learning to respond to those stimuli that signaled reward but not an overall decrease in response rates. It is interesting that Waltz et al. found that patients were no different from matched comparison participants when learning in response to negative feedback. That is, individuals with schizophrenia were able to acquire learning contingencies associated with punishment but not with reward.

Collectively, Waltz et al. (2007) argued that these results are consistent with the notion that patients with SZ have a deficit in procedural go learning. They articulated a link of such a behavioral deficit, as predicted by the computational model, to a possible deficit in DA transmission at D1-type receptors, again supported by the connectionist-level modeling architecture. It is also important to note that this deficit was observed by Waltz et al. even in the context of an overall elevated response rate, which may be related to generally increased tonic DA levels. These deficits were also shown to be correlated with negative symptoms. Overall, the study by Waltz et al. illustrated a link between behavioral and connectionist models, thereby suggesting that intact basal ganglia DA function is critical for appropriate learning. Their study also illustrated how selective DA alterations may affect unique aspects of learning behavior (i.e., reward vs. punishment learning) observed in schizophrenia.

Such deficit in learning may be a key behavioral disturbance that, in turn, contributes to negative symptoms in schizophrenia, which are complex and involve a broad set of behavioral deficits, typically characterized by features such as anhedonia, lack of motivation, and flattened affective expression, among others (Walker, Kestler, Bollini, & Hochman, 2004). To better understand such complex behavioral deficits, Gold et al. (2012) and Gold et al. (2008) have merged mathematical modeling with behavioral experiments. Specifically, these authors postulated that there might be an underlying deficit in some core function that produces the absence of specific behaviors, such as motivation (which fall under the broad rubric of negative symptoms). Gold et al. (2012) and Gold et al. (2008) tested the specific hypothesis that such deficits may in part stem from the patients’ inability to represent the expected value of rewarding outcomes, also suggested by Waltz et al. (2007). However, they also explicitly predicted an intact ability to avoid loss (i.e., intact negative reinforcement learning). This prediction is vital, given that it involves a unique pattern of errors as well as a specific deficit in DA signaling that can be represented within the Frank (2005) model described earlier, which, again, provides a key link between a complex behavioral disturbance and neural-system dysfunction via modeling.

However, a key unanswered question relates to whether specific deficits in learning from positive feedback among individuals with schizophrenia result from a deficit in positive prediction error or possibly a deficit in the ongoing representation of the rewarding outcome (Gold et al., 2008; Gold et al., 2012), with the neurobiological correlate of these deficits in either the basal ganglia system or the orbitofrontal cortex (OFC), respectively. In this framework, the basal ganglia is proposed to mediate slower learning over many trials, whereas the OFC system may be guiding faster explicit learning that involves representing the trial-specific reward outcome temporarily to guide action selection (engaging WM). The two components of this learning system would then make unique contributions to the reward-learning process and may be differentially disrupted in schizophrenia, as predicted by Gold et al. (2012). This is an excellent example of where modeling of complex learning can interface with systems-level neurobiology in schizophrenia, in particular involving alterations in the DA system (Gold et al., 2012).

Gold et al. (2012) attempted to dissociate these two possibilities in an experiment in which patients and matched comparison participants performed a reinforcement-learning task. Specifically, participants were asked to select a picture (complex visual scene) out of a presented pair. There were four pairs of stimuli in total: Two were associated with a high probability of monetary gain and the other two were designed for participants to learn to avoid a loss of money. The probabilities for either gain or loss were 80% and 90% within each pair. This way, the authors parametrically manipulated the probability of a given outcome. The learning phase was followed by a subsequent transfer phase. These results were directly fit to the three different types of computational models. The first model contained only the pure basal ganglia–driven learning system. The second model contained only the putative OFC-driven system that required action selection based on represented reward. The third version was a combination of both systems in which the OFC component is hypothesized to provide feedback onto the basal ganglia system in a trial-dependent fashion on the basis of the expected value. Gold et al. found a striking behavioral dissociation: Compared with healthy comparison participants and patients with low negative symptoms, schizophrenia patients with high negative symptoms were significantly more impaired when they had to learn from rewarding outcomes. Of note, lack of deficits in patients with low negative symptoms could be due to the fact that they were treated patients (in general, reward-learning findings in treated patients with schizophrenia should be interpreted with caution). Conversely, the high-negative-symptom patient group was intact in their ability to acquire loss-avoidance learning. The pattern of behavior exhibited by high-negative-symptom patients was best captured by a computational model mainly driven by striatal stimulus-response learning. In contrast, both control participants and patients with less negative symptoms showed a behavioral pattern that involved the “striatal” slower learning component as well as the “OFC” aspect that involved computing the expected values of their actions.

This Gold et al. (2012) study has collectively provided a highly compelling behavioral finding that offers evidence for a specific disruption in reward learning in those patients with high levels of negative symptoms. In turn, the authors linked these behavioral effects to a learning mechanism that is formalized via a computational model. In that sense, Gold et al. have provided an explicit mechanistic link between complex behavioral disturbances in schizophrenia (i.e., lack of reward learning in the context of intact loss avoidance) with a mathematical formalism of this process that can generate future predictions. This behavioral study indirectly supports the possibility that there may be distinct deficits in the OFC versus the basal ganglia circuits in schizophrenia that affect distinct aspects of learning behavior. We argue that it is precisely this approach that offers an opportunity for translation into a neuroimaging context to formally test OFC/striatal contributions to the pattern of reward-learning deficit in schizophrenia. For instance, even at the simple heuristic level, the model would make the prediction that the pattern of trial-by-trial BOLD signal in the OFC in response to reward-learning trials may be profoundly affected in patients with elevated negative symptoms relative to healthy participants. It is interesting that this framework, although designed by Gold et al. to test a behavioral deficit, could in theory be combined with a pharmacological manipulation of the DA system by making specific predictions regarding the role of elevated DA in disrupting OFC versus striatal circuits. Perhaps another interesting outcome may be that DA would not necessarily play a role in the OFC-mediated computations but that such disruptions may be more related to disrupted tuning in cortical circuits as a result of glutamate/GABA alterations. Testing such competing predictions can inform downstream mechanisms that could guide targeted treatments for complex behavioral defects elegantly characterized by Gold et al. Future studies are needed to continue to refine these normative models to provide explicit links across levels of analyses.

Integration Across Levels of Analysis and Future Directions

As highlighted throughout the article, schizophrenia is a remarkably complex neuropsychiatric illness that affects neural computations and, in turn, results in disruptions of a wide range of adaptive behaviors. Here, we present evidence that computational modeling can serve as a useful method to generate testable predictions across levels of inquiry to help understand and ultimately inform treatment of this complex disorder. In particular, we highlight three conceptual levels of computational modeling that have been applied to experimental work to understand human neurobiology and cognition and, by extension, disruptions in schizophrenia: (a) biophysically based models developed to test cellular-level and synaptic hypotheses, (b) connectionist models that give insight into large-scale neural-system-level disturbances in schizophrenia, and (c) mathematical models that provide a formalism for observations of complex behavioral deficits in individuals with schizophrenia (which may overlap with other of the two aforementioned approaches). It is important to note that we are not attempting to claim that each computational study falls within only one of the three categories, given that a number clearly blend categories. However, we have tried to highlight the importance of matching model type to the best-fitting level of inquiry, with the recognition that many modeling efforts can also interface elegantly across levels of analysis, to maximally guide the interplay between theory and experiment.

Each of these approaches has merits but also limitations, given the level of complexity and analysis that it considers. We provided examples in which different modeling approaches have been successfully applied in experimental and clinical studies of schizophrenia at each level of analysis. Building on this productive interplay, we propose several broad future objectives for the field of computational neuropsychiatry. First, specific research programs should continue to use modeling that is most appropriate to a given level of experimental work. This can be accomplished even by models that scale across analysis levels, given that some microcircuit and connectionist models can generate complex behavioral predictions. We argue that maximal insights can be gained in cases in which modeling is explicitly interwoven with the appropriate level of experiment, even if it cannot inform other levels of analyses. Second, it will be important for the field to continue to merge levels of analysis across both computational and experimental studies. We acknowledge that perhaps no model or experiment can alone address the full level of complexity needed to understand schizophrenia. However, continued efforts to merge computational-modeling methods from cells to neural systems to behavior may ultimately help the field understand how alterations in given neurobiological mechanisms can scale to produce the complex and devastating disturbances observed in patients. An emerging example of precisely this approach is the attempt to scale microcircuit models of neuronal dynamics to generate predictions of large-scale BOLD-signal fluctuations at rest (Deco et al., 2013), which recently has been applied to understand schizophrenia (Yang et al., 2014).

Third, computational modeling should be used to generate predictions about specific therapeutic mechanisms, across both neurobiological and behavioral levels (J. D. Murray et al., 2014), which can, in turn, be tested experimentally. Fourth, computational modeling has the potential to help generate predictions about mechanisms of illness progression from prodromal to chronic illness stages. Such efforts to model the dynamic evolution of schizophrenia can help the field understand illness phase– related mechanisms that may guide appropriate intervention at a given phase of disease progression. Fifth, computational models of schizophrenia can be merged in a more compressive way with neural measurements that can be used for development of biomarkers in a data-driven way. We propose that resting-state neuroimaging approaches offer a promising opportunity, given that they may avoid some performance confounds that exist in cognitive experiments (Yang et al., 2014). Last, it will be vital for clinical psychology and psychiatry-training programs to emphasize the important interplay of neuroscience, behavior, and computation as complementarity tools that can be productively integrated in future studies. Therefore, providing the best possible multidisciplinary training to clinical neuroscience researchers to harness the combination of experimental and computational approaches remains an important objective for the field. By productively combining both theory and experiment, across levels of inquiry, future studies can better inform understanding of mechanisms and, in turn, guide treatment development for schizophrenia in a rational way.