Applications of Statistical Tests in Hand Surgery

Abstract

During the nineteenth century, with the emergence of public health as a goal to improve hygiene and conditions of the poor, statistics established itself as a distinct scientific field important for critically interpreting studies of public health concerns. During the twentieth century, statistics began to evolve mathematically and methodologically with hypothesis testing and experimental design. Today, the design of medical experiments centers around clinical trials and observational studies, and with the use of statistics, the collected data are summarized, weighed, and presented to direct both physicians and the public towards Evidence-Based Medicine. Having a basic understanding of statistics is mandatory in evaluating the validity of published literature and applying it to patient care. In this review, we aim to apply a practical approach in discussing basic statistical tests by providing a guide to choosing the correct statistical test along with examples relevant to hand surgery research.

“Statistics is the grammar of science.”

–Karl Pearson (1857–1936), British mathematician

“The good news is that statistical analysis is becoming easier and cheaper. The bad news is that statistical analysis is becoming easier and cheaper.”¹

C. F. Hofacker, PhD, Professor of Marketing

INTRODUCTION

Statistics is a powerful tool in scientific research. Statistical methods transform ambiguous raw data into meaningful results. Current trends towards Evidence Based Medicine can only flourish in a culture of statistical literacy. Such a culture requires surgeons, who are equipped with the medical knowledge base, to interpret statistical results critically and accurately. Paralleling the exponential increase in medical journals and publications is the use of statistics to make sense of the immense amount of data. However, misuse of statistical analysis leading to misinterpretations has become a prominent theme in many journals.^2–8 The inappropriate use of statistical analysis can lead to incorrect conclusions and is demonstrated by the frequently encountered contradictory results published in the literature. These results create multiple problems. First, from a research perspective, it leads to the wasting of valuable resources as false claims are further investigated. Second, in the clinical setting, patients may be misinformed by the conflicting information. And finally, on a more global level, important health policy decisions that are based on Evidence Based Medicine are delayed. Thus the problem is a serious one and may stem from a poor understanding of statistics followed by the inappropriate use of statistical tests. This problem is relevant to all medical fields, including hand surgery.

Statistical analysis in hand surgery research is unique. It is complicated by the fact that each individual has two hands, each hand has four fingers, and each finger has three joints (metacarpal, proximal and distal interphalangeal joints). The relationship of each of these anatomic structures within an individual makes statistical analysis more complicated. In this review article, we aim to explain the applications and provide examples of the most commonly used statistical tests found in the hand surgery literature. This paper is an extension of the excellent review of the fundamental concepts introduced by Szabo entitled, “Statistical analysis as related to hand surgery.”⁹ In this paper, Dr Szabo defined the common concepts of descriptive statistics (e.g. the difference between mean and mode and between standard deviation and standard error) and inferential statistics (e.g. hypothesis testing, estimation, p-values and power analysis). Szabo concludes his review with some examples of statistical models, including linear and logistic regression models, as well as touching upon a list of non-parametric tests. We recommend the reader use Szabo’s review article as a primer prior to reading this current article. Hand surgeons who stay current with the literature should be familiar with the correct uses of these tests to help them critically read and interpret the research results. In an attempt to lighten this topic, we have judiciously picked “instructions” from the book Life’s Little Instruction Book¹⁰, by the New York Times #1 bestseller author H. Jackson Brown Jr. Analogous to these “instructions” serving as guideposts in life, we aim to illustrate key points in statistics by providing a guideline about how to choose the correct statistical test and discussing various types of commonly used statistical tests with examples from the hand surgery literature.

BEGINNING THE QUEST: CREATING THE QUESTION

#186. Be insatiably curious.

Harold Schoolman, MD, Deputy Director for Research and Education at the National Library of Medicine succinctly states, “Good answers come from good questions, not from esoteric analysis.”¹¹ Formulating testable hypotheses is an important step in clinical investigation when designing the experiment.² Poorly formulated specific aims will impact subsequent stages of the investigation, as this is part of the planning stage.^12–14 Thus the scientific hypotheses under investigation should be explicitly stated from the outset of the study prior to initiating the investigation.¹²

Hypothesis Testing

Two fundamental concepts in statistical analysis are estimation and hypothesis testing. Estimation is the principle of estimating relevant parameters to describe the population from data collected from a sample, or multiple samples. The idea of hypothesis testing originated from Sir Ronald Aylmer Fisher (1890–1962) (Figure 1), an English statistician who revolutionized inferential statistics in the early twentieth century. While studying the effects of different fertilizers on crops, he began to formulate the groundwork of designing experiments. He emphasized the importance of initiating a hypothesis-driven investigation correctly and the importance of succinct specific aims. In hypothesis testing, the null hypothesis (H₀), which states there is no difference or change, and the contrasting alternative hypothesis (H₁) must be stated clearly. These concepts are well defined and explained in Szabo’s review.⁹ We emphasize this point because the selected statistical test depends upon the H₀, which we expand upon below.

Figure 1.

R. A. Fisher at his desk calculator, 1952.

STATISTICAL TESTS

Selection of the correct statistical test depends upon the following criteria: 1) goal of the analysis, reflected in the hypotheses, 2) type of data, 3) whether the observations are independent or dependent, 4) number of groups to be compared, and 5) whether the data are assumed to follow a certain distribution; in other words, should a parametric or non-parametric test be chosen.

Goal of Analysis

#474: Be prepared.

Surgeons know the value of being prepared for the operating theater. It is no different when initiating an investigation. Know what you are looking for. Typically, there are two primary ways of formulating the goal of analysis when hypothesis testing is involved: to test for a difference in a variable between samples or to test for an association between two variables. The goal of analysis is hypothesis driven and should be explicitly stated because it is one criterion that determines which type of statistical test should be performed. The reader is directed towards Dr Szabo’s excellent review on topics related to goals of estimation (e.g. predicting future patients’ probability of having an outcome (i.e. use of multiple regression) and measures of diagnostic test performances (i.e. sensitivity, specificity, and predictive values)).⁹

Type of Data

#254: Keep it simple.

Data are the unprocessed observations from an experiment. The type of data that is being analyzed helps to determine which statistical test to use. Data are broadly classified as categorical (subclassified as ordinal and nominal) or continuous (subclassified as discrete and continuous) (Table 1).¹⁵

Table 1.

Types of Statistical Tests

Goal of Analysis	Is there a difference between the variables in two different groups? (H0: There is no difference between the means, medians, or distributions in the populations.)		Is there an association or relationship between two variables in the population? (H0: There is no association between the variables.)
Type of Data	Continuous			Categorical
Parametric	Unpaired Student’s t-test†	Paired Student’s t-test†	Pearson correlation coefficient	None.
Nonparametric	Wilcoxon rank- sum test*†‡	Wilcoxon signed- rank test†‡	Spearman’s correlation coefficient ‡	Pearson’s Chi Square Test of Independence & Fisher’s exact test

^*The Wilcoxon rank sum test is also known as the Mann-Whitney U test.

^†The unpaired Student’s t-test and the Wilcoxon rank-sum test involve unmatched pairs of data. In contrast, as the name suggests, the paired Student’s t-test and its counterpart, Wilcoxon signed-rank test, involve matched pairs.

^‡These non-parametric tests may involve either ordinal or continuous data.

Categorical Data

Ordinal data suggest an inherent ordering in the classification. The word ordinal has a Latin derivation, ordo, “denoting an order of succession.” However, between each value, the intervals are not equal; examples include rank (medical student, resident, fellow, attending physician), stages of cancer, education level, or salary level. In contrast, nominal data have no inherent order, are non-numerical, and are indicators or types of categories. Examples of nominal data include gender, ethnic groups, or types of job occupations. Generally, categorical data are summarized as percentages or proportions; for example, 60% of the sample population was comprised of males.

Continuous Data

Discrete data can only take certain specified numerical values and can be thought of as counts of events¹⁵; for example, the number of patients in a study, the number of office visits, the number of prior surgeries to an extremity, number of children, or the number of lacerations. Continuous data are measurements that can take on any value within an interval. Examples of continuous data include measurements of range of motion, ulnar variance, age, height, and Disability of the Arm, Shoulder, and Hand (DASH) questionnaire scores. Generally, numerical data are summarized as means; for example, the mean age of the sample population was 56 years of age.

Independent and Dependent Observations

#59: Always accept an outstretched hand.

Close inspection of the eighteenth century French artist Auguste Rodin’s (1840–1917) marble piece, Le Secret, (Figure 2) reveals two right hands embracing each other. Statistically speaking, measurements collected from these two right hands are independent measurements because the observations are measured from two different unrelated individuals. The concept of independent data in hand surgery can be complicated. Hands, wrists, or digits from separate and unrelated individuals are assumed to be independent observations; these are inter-individual observations. In contrast, measurements on the right and left wrists of the same individual are dependent observations; these are intra-individual observations. The commonality is the individual whose baseline individual strength, for example, will influence measurements from both wrists.

Figure 2.

Auguste Rodin’s Le Secret, 1918.

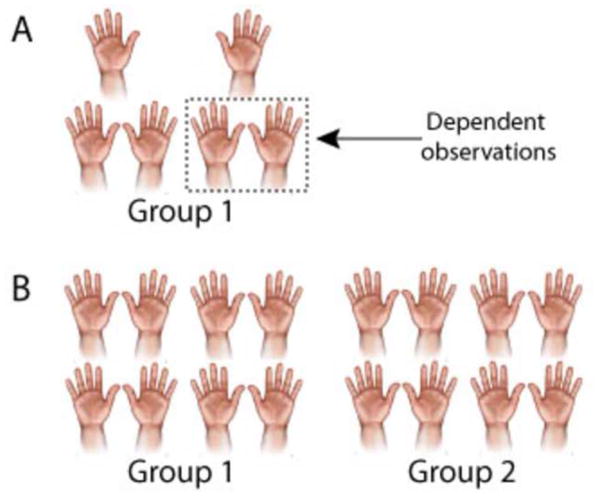
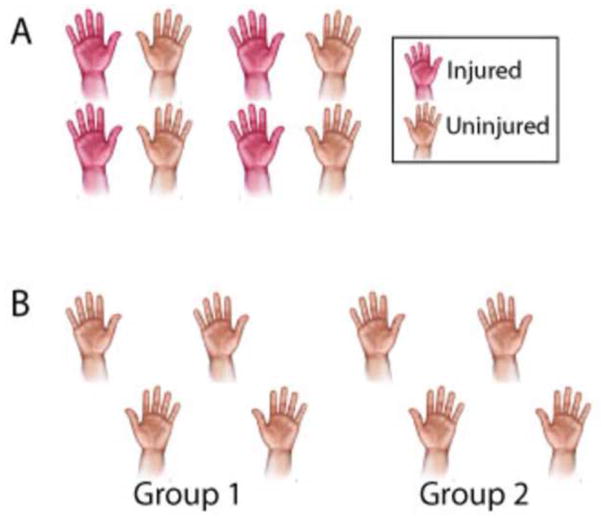
This distinction between independent and dependent variables is important because it also dictates which statistical analysis should be used. If the data include dependent variables, a multilevel analysis may be appropriate, depending on the goal of the analysis. Multilevel analysis is more thoroughly discussed later in this review. Briefly, if the goal of analysis is to compare a single treatment group over time (e.g. several time-points (6 weeks, 3 months, and 6 months) post-operatively) and the data include measurements on bilateral wrists on some individuals (e.g. dependent observations) and one wrist on others (e.g. independent observations) (Figure 3A), a multilevel analysis must be used. Or if data on bilateral wrists in one group of patients are compared with bilateral wrists of a control group (Figure 3B), again a multilevel analysis must be used. In contrast, if the goal of analysis is to compare the injured versus uninjured hands of each individual (e.g. dependent and matched observations) in a single treatment group (Figure 4A), a paired Student’s t-test is appropriate. It is important to understand, however, that the data in a paired Student’s t-test must be reduced to observations that are independent variables, by subtracting one from the other. This will be further discussed in the next section (Student’s t-test section) and clarified as we discuss specific tests and examples later in the review.

Figure 3.

Examples of when multilevel modeling analyses are indicated. A–B. If dependent observations are included, or nested, within a sample group, multilevel modeling analyses are indicated.

Figure 4.

Examples of when the paired Student’s t-test are indicated. A. Injured versus uninjured hands are considered matched pairs. The outcome is comparing observations of the matched pairs, and a paired t-test is indicated. B. If each sample group is comprised of independent observations and sample group 1 is matched to sample group 2 (e.g. twins or pre- and post-operative comparisons of same group), then the groups are matched and the paired Student’s t-test is indicated.

Parametric and Non-parametric tests

“The 50-50-90 Rule: Anytime you have a 50-50 chance of getting something right, there’s a 90% probability you’ll get it wrong.” Andy Rooney, American radio and television personality, humorist and political commentator for CBS News’ program 60 Minutes

#47: Don’t waste time learning the “tricks of the trade.” Instead learn the trade.

This topic is frequently a source of confusion in the surgical literature¹⁶ (…and likely searched through google or Wikipedia by many in an attempt to “learn the tricks” for quick comprehension). In fact, the Polish statistician, Jacob Wolfowitz (1910–1981), defined the term “parametric” in order to introduce and coin the term, “non-parametric.”¹⁷ Wolfowitz stated, “We shall refer to this situation where the knowledge of the parameters, finite in number, would completely determine the distributions involved as the parametric case, and denote the opposite case, where the functional forms of the distributions are unknown, as the non-parametric case.”¹⁷ How confusing!

To simplify, parametric tests commonly assume that a variable in the population follows a normal, or bell-shaped, distribution. In contrast, non-parametric tests make no such assumption. The earliest development of a non-parametric test is attributed to Arbuthnot in 1710 who devised a simple sign test.¹⁸ However, it was not until the 20^th century that non-parametric statistics blossomed. In the 1940s, Frank Wilcoxon, a chemist at American Cyanamid, searched for a statistical method to deal with outliers, extreme and unusual values, in his data set. He observed that these outliers drastically influenced his results when using standard parametric methods. To address such scenarios, he developed non-parametric methods.^19,20 These methods make no assumptions of the distribution population and are frequently called “distribution-free.” Common indications when non-parametric tests should be used are: (1) when the probability distribution of the observations is unknown or does not follow a normal distribution, (2) when the sample size is too small to assess the distributional assumptions made by a parametric test adequately, (3) when the data are ordered with many ties, are rank ordered (ordinal data), or in some instances for categorical data (e.g., for Chi Square tests), (4) when the groups have unequal variances, and finally (5) as Wilcoxon noted, when outliers exist in the dataset.²¹ Because the median, instead of the mean, is typically the measure of center compared by non-parametric tests, the data are not affected by outliers. To test whether the data follow a normal distribution, statistical tests (e.g. Kolmogorov-Smirnov goodness-of-fit test) exist to assess for normality; these tests affirm whether a parametric or non-parametric test is appropriate.¹⁵ Examples of non-parametric tests will be detailed below as we discuss the specific tests. It is important to understand that non-parametric tests are typically less powerful than parametric tests. Many non-parametric tests simplify observations to a “rank” number and much of the actual information is lost.²²

TESTS TO COMPARE DIFFERENCES

#68: Be brave. Even if you’re not, pretend to be. No one can tell the difference.

…until a p-value is calculated! It is important to understand that some tests are used to test a difference between two or more groups and others are used to test for an association. Szabo discusses in his review how to determine a p-value and what it means. We thus continue our review with the various statistical tests and their applications.

Student’s t-test

The unpaired and paired student’s t-tests are parametric tests, often simply referred to as a t-test. The unpaired Student’s t-test compares continuous observations from two different samples to test if the population means, from which the samples are taken from, are equal. The Student’s t-test assumes that the continuous variable has a normal distribution in each sample. Similarly, the paired Student’s t-test involves comparing the means of the differences between two paired or matched samples (e.g. measurements from injured versus uninjured hands of the same individuals (Figure 4A), measurements from one group before and after a treatment intervention, or measurements from twins (Figure 4B), e.g. individually matched). Note that the paired Student’s t-test involves dependent data in the sense that there is a 1:1 corresponding match in each sample. The difference between each set of pairs is calculated, and the mean of the difference of the pairs is analyzed for statistical significance. It is assumed that the paired differences are independent observations.

The “Student” who derived the t-test in the early 1900s was William Sealy Gosset (1876–1937), a chemist working as a brewer at Arthur Guinness, Son and Ltd in Dublin. He applied scientific methods to beer processing; the variability of the raw ingredients of beer such as barley and the vulnerability of the quality of beer to temperature changes led to a series of short experiments with small samples and ultimately to the derivation of the t-test. He published his results under the pseudonym “Student” in Biometrika due to the company’s confidentiality policy.²³

Example

An example of the use of both the unpaired and paired Student’s t-test is in a study by Waitayawinyu and colleagues who retrospectively investigated capitate shortening osteotomy with vascularized bone graft as an effective treatment for ulnar neutral or positive Lichtman stage II (sclerosed lunate) and stage IIIA (collapsed lunate) Kienböck’s disease.²⁴ The authors hypothesized that disease progression would be halted by revascularizing and reducing the mechanical loading on the lunate. Note each patient had one affected wrist. The paired Student’s t-test was thus appropriately used to compare preoperative and postoperative continuous variables (e.g. arc of motion, grip strength, carpal height ratio, and satisfaction scores) using all fourteen patients. The authors also used the unpaired Student’s t-test to compare continuous variables between patients diagnosed with Lichtman stage II (n=6) versus Lichtman stage IIIA (n=8) disease after surgery. The authors concluded that at final average follow-up of 41 months, none of the patients demonstrated progression of the disease. Compared to their preoperative state, the grip strengths and satisfaction scores significantly improved postoperatively (p<0.001), and in comparing patients with stage II versus IIIA Kienböck’s disease, significantly better grip strengths (p=0.008) and satisfaction scores (p=0.006) were observed in stage II disease.²⁴

Wilcoxon rank-sum and Wilcoxon signed-rank tests

These tests are the non-parametric counterparts of the unpaired and paired Student’s t-test, respectively. Frank Wilcoxon (1892–1965) started his career as a chemist but is now best known for his contributions to statistics in the ranking methods.²⁵ In the same publication, he described the rank-sum and signed-rank tests, both of which bear his name.¹⁹ Both tests compare the distribution of continuous or ordinal variables between two groups, without making any assumptions about the distributions.

Example

Augoff and colleagues used non-parametric tests to compare gelatinase A activity, a matrix metalloproteinase (MMP), in Dupuytren’s disease in seventy-one patients.²⁶ Palmar aponeurosis from these seventy-one patients were taken when being treated surgically and compared with sixteen control patients diagnosed with carpal tunnel syndrome. The severity of Dupuytren’s contracture was classified into four clinical stages described by Iselin’s classification scheme. Patients ranging from stage 1 to stage 4 were included in the diseased group. The level of MMP-2 activation, as measured by a ratio of active to latent forms of the enzyme, was compared between these two groups by the Wilcoxon rank-sum test. The median of the MMP-2 ratio of the group with contracture was found to be significantly higher than in control groups (p<0.001). Because the spread of the MMP-2 activation ratios in the diseased group included several outliers, likely due to the inclusion of all four clinical stages, the data were better analyzed by non-parametric methods.²⁶

Example

An example of the Wilcoxon signed-rank test is in an investigation by Kamath and colleagues.²⁷ The authors investigated the functional and radiographic outcomes of low-profile dorsal plating for dorsally angulated distal radius fractures in a study cohort of thirty patients with unilateral fractures. Radiographic outcomes (e.g. continuous measurements: angulation, articular congruity, intra-articular step-off, gap, and radial height) were evaluated pre- and postoperatively in all patients. These continuous variables did not follow a normal distribution, as assessed by the Kolmogorov-Smirnov goodness-of-fit test. Thus, the non-parametric counterpart of the paired Student’s t-test, the Wilcoxon signed-rank test, was appropriately used in the analysis. The authors reported a low complication rate (only 2 of 30 patients underwent hardware revision surgery for screw loosening) and statistically significant improvement post-operatively in radiographic measures with satisfactory radiographic reduction (p<0.001).²⁷

TESTS TO DESCRIBE A RELATIONSHIP OR ASSOCIATION

“A picture may be worth a thousand t tests.”²⁸

–Glinda S. Cooper, PhD and Linda Zangwill, PhD, Epidemiologists

Correlation is used to study the possible association between two variables. The degree of association is indicated by the correlation coefficient, which reveals both the strength and direction of the association between two continuous or ordinal variables. This method of analysis assumes the individuals from whom the observations are measured are independent.

Pearson correlation coefficient

Although the concept of correlations was first introduced by Sir Francis Galton (1822–1911) in the 1880s when he experimented with sweet peas,²⁹ the Pearson correlation coefficient was derived by Karl Pearson (1857–1936) nearly a decade later.³⁰ Pearson correlation coefficient, denoted r, is used to measure a linear relationship, or the degree of association, for two continuous variables. r is a measure of the scatter of points, or observations, plotted on a scatter diagram, underlying a linear trend (Figure 5A–D). Values for correlations can range between −1 and 1. Negative values indicate that one variable tends to decrease as the other increases, whereas positive values indicate that the variables tend to increase together. A correlation of 0 indicates no linear association, and as the value of the correlation moves away from 0, the variables have a stronger association.¹⁵ Generally, correlations from 0 to 0.25 (or −0.25) suggest no association to a weak association; 0.26 to 0.50 (or −0.26 to −0.50) suggest a weak to moderate degree of association; from 0.51 to 0.75 (or −0.51 to −0.75) suggest a moderate to strong association; and correlation coefficients greater than 0.75 (or −0.75) suggest a very strong association.³¹ However, these cut-off values are generally seen as guidelines, and a more concrete measure of the strength of association is the coefficient of determination, denoted as the square of the correlation coefficient (r², 0≤r²≤1). The coefficient of determination measures how much of the variance in one variable is explained by the other variable (Figure 5F–G).²¹ Correlation coefficients are often best understood by visualizing the data distribution on a scatter diagram. If both variables are continuous, a crude test to determine whether the parametric Pearson correlation coefficient is appropriate is to plot the data points on an x-y axis. A linear relationship indicates that the Pearson correlation coefficient is the correct statistical test. If the scatter diagram reveals a nonlinear monotonic relationship, the non-parametric Spearman’s correlation coefficient is appropriate (Figure 5E; discussed below).

Figure 5.

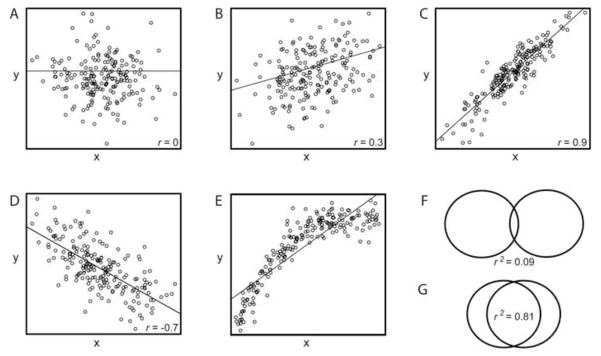
Examples of scatterplots. The overlaying line is from simple linear regression of y on x. The variables x and y are independent. A. Pearson’s correlation coefficient (r) =0. B–D reveal linear relationships. Both B and C reveal positive correlations, whereas D reveals a negative correlation. E. Because the scatterplot reveals a non-linear monotonic relationship, the non-parametric Spearman’s correlation is appropriate in this example. F–G. The coefficient of determination (r²) is illustrated by the overlapping area of the two circles; this illustrates the proportion of variance explained by the other variable. (e.g. Scatterplot B (r=0.3) is to r²=0.09 (F); Scatterplot C (r=0.9) is to G r²=0.81).

Pearson correlation coefficient and p-values

The Pearson correlation coefficient should be interpreted cautiously as it can be misleading.⁷ A p-value does not indicate the strength of the correlation. The strength of the correlation is indicated by the absolute value of r and the coefficient of determination. The p-value reports whether the correlation between two variables exists in the population. The H₀ states there is no linear association in the population between the two variables. It is possible to have a weak correlation coefficient but a significant result, (as in the example that will follow below).

Pearson correlation coefficient and sample size

In addition, caution must be taken with significant testing and the sample size.⁷ With a large sample size, a weak correlation may appear statistically significant. The formula for determining the statistic that gives the p-value is t= r √(n-2/1-r²); for the same value of r, as n increases, so does t, suggesting greater statistical significance. Thus, it is recommended that when correlation coefficients are used, the details of the four parameters relating to the correlation (sample size, r, confidence interval, and p-value) should also be explicitly stated to provide the reader with context of reference.⁷

Example

Gunther and colleagues quantified the relationship between grip strength and various anthropometric measures (i.e. forearm length) by using the Pearson correlation coefficent.³² The correlation between hand width and grip strength of the right hands of adult males was r= 0.306, p<0.001; These two variables are positively associated (e.g. direction of correlation). In other words, grip strength increases as the width of the hand increases. The value of r is 0.306 and coefficient of determination (r²) is 0.09, suggesting a weak association (e.g. magnitude or strength of correlation); in other words the hand width explains about 9% of the variation in grip strength. Despite this weak association, the data are found to be statistically significant denoted by p<0.001, suggesting this association exists in the population from which the sample was selected.

Spearman’s correlation coefficient

Charles Spearman (1863–1945) was an English psychologist better known for his work on the intelligence theory. To support his research on intelligence, he developed mathematical tools, which included Spearman’s correlation coefficient.³³ Spearman’s correlation coefficient uses only the rankings of the observations, or specifically the rank difference. Thus, it can be used if one or both variables are ordinal, and it measures the strength of a monotonic relationship.

Example

Spearman’s correlation test was used to measure test-retest reliability when developing the Michigan Hand Outcomes Questionnaire.³⁴ Each domain contained a number of questions with ordinal response categories, such as strongly agree, agree, neither agree nor disagree, disagree, and strongly disagree, and the questionnaire was completed twice, one week apart, by each participant. Responses in a domain were converted to numbers and ranked to proceed with this statistical test. Five of the six scales in the Michigan Hand Outcomes Questionnaire had correlation scores greater than 0.85, in which a correlation score of 1.0 would indicate a perfect correlation.³⁴

Pearson chi-square test of independence

The non-parametric chi-square test of independence tests for an association between two categorical (e.g. diseased versus not diseased) or nominal (e.g. gender) variables in one population.³⁵ Often the variables are dichotomous, and a contingency (or r × c (row × column)) table is created for analysis; in other words, an association between the variable designated in the row versus column is tested. The chi-square statistic is symbolized by χ², and large values of χ² provide support to reject H₀.²¹ This test was first introduced by Karl Pearson in 1900; his motivation for developing the chi-squared test included testing whether outcomes on a roulette wheel in Monte Carlo were equally probable.³⁶

Example

Martineau and colleagues’ investigated this association of fragment failure in AO C3 distal radius fractures and the use of locking screw versus locking smooth peg fixations in volar plating. The authors used the chi-square test to demonstrate that the order of fragment failure was independent of the type of fixation (e.g. categorical variable) utilized. Their statistical analysis revealed χ² = 0.04155 indicating no significance; for significance at the 0.05 level, the χ² value needed to be greater than or equal to 3.84. The biomechanical result of their investigation demonstrated that regardless of fixation type, the order of fragment failure was independent of type of fixation (locking screw versus peg).³⁷ The chi-square test is the appropriate test because the hypothesis seeks an association between the outcome and the fixation type, both categorical data.

Fisher’s exact test

This non-parametric test is indicated instead of the chi-square test when the sample size is small and the expected count of one of the events, or outcomes, is less than 5.¹⁵ R. A. Fisher derived this test one afternoon during a tea party, when Muriel Bristol claimed she could taste whether tea or milk was added first to a cup of tea.²⁰ Fisher devised a crude experiment, which he later described as a “thought experiment,” to test her claim. This experiment led to Fisher’s exact test.

Example

Naidu and colleagues investigated a rare presentation of pauciarticular Juvenile rheumatoid arthritis (JRA), in which only seven cases of patients with initial manifestations of isolated finger swelling were reviewed. The authors, interested in the disease progression to polyarticular disease, performed a Fisher’s exact test and reported a significantly higher percentage of patients with isolated digital swelling developing polyarticular (≥5 joints) disease (4 of 7 patients, p<0.0307), as opposed to other common manifestations (e.g. having antinuclear antibodies, ≤4 joints affected, and being female) of early onset pauciarticular JRA (5 of 34 patients). In this example, because of the small sample number of events observed for one event (4 patients with initial manifestations of isolated finger swelling having disease progression), the Fisher’s exact test is the appropriate test.³⁸

OTHER TESTS

There are many statistical tests that have not been discussed above. A comprehensive review of these tests is beyond the scope of this brief review paper, and instead we recommend the following texts.^21,39,40 However, we believe it important to highlight a common pitfall encountered in hand surgery literature and present the appropriate statistical methodology that should be used in such scenarios. In many cost-efficient sampling designs in hand surgery, a common error involves assuming independent observations within a dataset without accounting for dependent observations (e.g. bilateral wrists from the same individual; examples illustrated in Figure 3A and B). In such scenarios, a multilevel modeling analysis must be undertaken.

Multilevel modeling analysis

As suggested by the name, this methodology is used for analysis of data with multiple levels of variability. This analysis focuses particularly on nested sources of variability, e.g. two hands on an individual, four fingers on a hand, or three joints on a finger. For example, if one wished to compare groups of surgeons from two different hospitals and their complication rates, several levels of variability must be accounted for; the first level of variability is the hospital (e.g. differing infection rates) and nested within are the two groups of surgeons. Outcomes of patients who had the same surgeon are not independent; for example, the outcomes may be influenced by surgeon skill or training. The analyses should take into account inter-surgeon correlation. Analogous to this, if one wished to compare two groups of patients with each group comprised of both hands from each patient (Figure 3B), the first level of variability is between the two groups of patients and nested within are both hands from each individual. Furthermore, fingers of the same hand are also considered nested. These intra-individual measurements are dependent measures because they come from the same individual. Multilevel analysis must be performed to account for these intra-individual correlations.⁴¹

Example

Brown and colleagues evaluated 169 wrists in 145 patients diagnosed with carpal tunnel syndrome (CTS) and randomized them to either endoscopic (n=84) or open (n=85) carpal tunnel release. As the numbers suggest, 24 patients within the sample suffered bilateral CTS. Each treatment group was comprised of some patients who underwent surgery on bilateral wrists (e.g. dependent observations) whereas others underwent surgery on only one wrist (e.g. independent observations). The authors thus correctly used a type of multilevel analysis, repeated measures analysis of covariance, to compare the two treatment groups. A parametric unpaired Student’s t-test is not appropriate in this scenario because not every observation is paired. The authors evaluated the patients for outcomes of pain relief, paresthesias, two-point discrimination, Semmes-Weinstein monofilament testing and motor strength and ultimately reported no significant difference between the two operations at the end of the follow-up period (84 days postoperatively).⁴²

There are many different types of multilevel analysis (e.g. hierarchical linear models, mixed models, and random-effects models, to name a few). The above example used by Brown and colleagues used repeated measures analysis of covariance.⁴² Many of these tests are extensions of analysis of variance and regression. These statistical tests are typically not taught to most physicians in a biostatistics 101 course and the help of a statistician may be of immense benefit to complete such complicated analysis correctly. Although the details of multilevel analysis are beyond the scope of this review paper, it is important that the reader understands when this type of analysis is indicated.

STATISTICAL LITERACY AND EVIDENCE BASED MEDICINE

#273. Remember that overnight success usually takes about 15 years.

There are only a handful of ways to do a study properly but a thousand ways to do it wrong.⁴³

--David L. Sackett, MD, Founding Director of the Centre for Evidence-Based Medicine at Oxford University

Statistical science plays an important role in medical research. Current medical journals are full of statistical material both relatively simple and increasingly more complex. Recognition of the importance and appreciation of statistics has grown considerably in the recent years, especially with the emergence of Evidence Based Medicine, which on a national level has become a cornerstone for devising health policies.⁴⁴ Moreover, patients with virtually unlimited easily accessible information (e.g. internet), often read the results of investigations literally and rightly express an enormous amount of inquisitiveness. Surgeons are thus not only forced to stay one step ahead of them but should be able to interpret the results themselves and educate the patients. The ultimate reason physicians should seek to improve their statistical reasoning is to ensure their patients are provided with the best available treatment course.