Adaptive coding is constrained to midline locations in a spatial listening task

Abstract

Many neurons adapt their spike output to accommodate the prevailing sensory environment. Although such adaptation is thought to improve coding of relevant stimulus features, the relationship between adaptation at the neural and behavioral levels remains to be established. Here we describe improved discrimination performance for an auditory spatial cue (interaural time differences, ITDs) following adaptation to stimulus statistics. Physiological recordings in the midbrain of anesthetized guinea pigs and measurement of discrimination performance in humans both demonstrate improved coding of the most prevalent ITDs in a distribution, but with highest accuracy maintained for ITDs corresponding to frontal locations, suggesting the existence of a fovea for auditory space. A biologically plausible model accounting for the physiological data suggests that neural tuning is stabilized by inhibition to maintain high discriminability for frontal locations. The data support the notion that adaptive coding in the midbrain is a key element of behaviorally efficient sound localization in dynamic acoustic environments.

most species evolve in complex environments containing diverse sources of sensory information over a very wide range of intensities, frequencies, and locations. Sensory systems must efficiently encode over this wide range of possible stimulus values, given a limited availability of coding resources. One means by which neural systems can overcome this challenge is to adapt on a behavioral timescale in order to represent with particular efficiency the subset of natural stimuli in the current environment. Such adaptive coding is observed across a wide range of species and stimulus modalities and is apparent in the responses of single neurons (Dean et al. 2005; Fairhall et al. 2001; Ohzawa et al. 1982) and across populations of neurons (Dean et al. 2005, 2008; Watkins and Barbour 2008). Fisher information (FI) represents one possible measure of coding quality that can be used to evaluate adaptive coding (Dean et al. 2005).

Nevertheless, despite the apparent advantage adaptive coding would confer on sensory processing, the link between adaptive coding at the neural level and performance in sensory tasks is difficult to establish. Psychophysical assessment of adapted neural systems is often considered with respect to perceptual illusions such as afterimages (McCollough 1965) or changes in perceived orientation of vertical bars [the “tilt” illusion (Solomon et al. 2004)] in vision or misperception in sound-source localization in hearing (Dahmen et al. 2010; Kashino and Nishida 1998). At the cognitive level, the term “cuing” is employed to describe the influence of prior stimulation on sensory performance, for example, in reducing reaction times required to localize a sound source in a given spatial hemifield (Spence and Driver 1994).

However, none of these concepts—aftereffects, mislocalization, or cuing—is easily reconciled with the concept of adaptive coding at the neural level. This normally describes the rapid adjustment of neural tuning properties to better represent the prevailing stimulus environment (Garcia-Lazaro et al. 2007; Maravall et al. 2007; Nagel and Doupe 2006) rather than neural fatigue or higher, perhaps attentional, processes. Here we describe adaptive coding for interaural time differences (ITDs), an auditory spatial cue on which many mammals, birds, and reptiles rely in order to locate the source of a sound. Sensitivity to ITDs depends on detecting instantaneous differences in air pressure generated by the acoustic waveform arriving at each ear and retaining that information until it can be compared in the central nervous system (Goldberg and Brown 1968, 1969; Yin and Chan 1990). We demonstrate that neurons in the inferior colliculus (IC), the major auditory nucleus in the midbrain, represent these differences dependent on their long-term statistical distribution. Despite this dependence, neural discriminability remains highest for frontal locations, even when the stimulus distribution is strongly biased toward one side or the other. We then show evidence of improved spatial discrimination performance by human listeners under closely matched stimulus conditions, but again largely for locations corresponding to frontal space. A model of a biologically plausible, multisynaptic circuit is proposed to explain the neural adaptive coding, through the action of ITD-dependent excitatory and inhibitory cellular conductances. The model suggests that inhibition, via a dedicated anatomical pathway, acts to reduce the distribution dependence of tuning curves in the IC affected by neural adaptation within the excitatory pathway, thus maintaining highest discriminability for frontal locations.

METHODS

Physiological Recordings

Extracellular recordings were made from single neurons in the IC of urethane-anesthetized pigmented guinea pigs. All experiments were approved and carried out under a license issued by the UK Home Office (Project Licence PPL 70/6826) in accordance with the guidelines of the Animals (Scientific Procedures) Act 1986.

Experimental design.

Depth of anesthesia was assessed by means of the pedal withdrawal reflex, and body temperature was maintained at 37°C with a thermostatically controlled heating blanket and rectal probe. Animals were prepared for experimental recordings with previously reported techniques (e.g., Ingham and McAlpine 2004), and, upon transfer to a stereotactic frame (modified from model 1730, David Kopf Instruments, Tujunga, CA) located within a sound-attenuated booth (IAC, Winchester, UK), custom-built earphones were inserted into the hollow ear specula fixating the animal's head to form a sealed pressure-field sound delivery system. Single-unit extracellular recordings were carried out in the right IC with glass-coated microelectrodes of ∼0.9- to 1-MΩ impedance. Electrodes were advanced dorsoventrally from outside the booth by means of a piezoelectric stepper motor. Electrical activity was transmitted from the microelectrode via a head stage to a preamplifier (TDT Medusa RA16PA), amplified, digitized at a sample rate of 25 kHz, and transmitted via fiber-optic cable to an RA16 base station for further amplification and band-pass filtering (variable gain, 600-Hz high-pass filter, 3-kHz low-pass filter). The resulting signals were passed to TDT Brainware, and action potentials exceeding a user-defined trigger level were recorded for analysis.

Sounds were generated, with a 50-kHz sampling rate, with Tucker Davis Technology digital processing hardware (TDT, Alachua, FL; System III), TDT Brainware, Real Time Processor Visual Design Studio (RPvds), and MATLAB software. Stimuli were attenuated (TDT, PA5), amplified (Beyerdynamic A150 Blueprint stereo-amplifier, Burgess Hill, UK), and presented via Beyerdynamic DT-48A loudspeakers fitted and sealed with brass tube attachments to the hollow ear specula. Probe-tube microphones (Knowles Acoustics FG3452, Burgess Hill, UK) inserted in the hollow specula allowed for measurement of the stimuli at a distance of only a few millimeters from the tympanic membrane to ensure that the sounds delivered were well matched between the ears (within ±2 dB for frequencies below 2 kHz). Probe-tube microphones were initially calibrated against a Brüel & Kjær 1/8-in. microphone (type 4136, Stevenage, UK). Diotic pure tones, 50 ms in duration, were presented to assess the characteristic frequency (CF) of isolated single neurons.

High-probability region stimuli.

To assess the ability of IC neurons to represent the underlying statistical distributions of ITDs, broadband noise was presented to both ears simultaneously. The noise waveform at each ear was identical except for an ITD imposed on the ongoing waveform (the ITD at stimulus onset was 0). Every 50 ms, the value of the ITD was selected randomly from a predefined distribution (see Fig. 2A) comprising a high-probability region (HPR) from which 80% of values were selected. The remaining 20% of ITDs were selected with equal probability from values beyond the boundaries of the HPR (the low-probability region, LPR), but limited to the range ±330 μs, the maximum naturally encountered range of ITDs reported for the guinea pig (Sterbing et al. 2003). In total, 7,500 50-ms-epochs were presented for each HPR stimulus. Because of hardware limitations the stimulus could not be presented continuously, and each HPR stimulus was subdivided into 75 segments of 5-s duration (100 epochs), separated by <0.4 s. The noise seeds and the sample of 50-ms epochs were randomly chosen for each segment (i.e., the noise sample and the set of 100 levels differed from segment to segment). No onset ITDs were present at any transition; rather, each frequency component was phase-shifted by the appropriate amount (in opposite directions in either ear) to achieve the required ITD. The use of ongoing-only ITDs in binaural experiments is standard in studies of low-frequency ITD processing and avoids the potentially confounding influence of envelope (i.e., onset) ITDs. Sensitivity to ITDs conveyed in the low-frequency stimulus fine structure is usually dominated by the ongoing component. To assess sensitivity to the mean of a distribution of ITDs, the HPR width was fixed at ±66 μs. To assess sensitivity to the variance, the HPR width was varied between ±6.5 μs and ±330 μs (i.e., a uniform distribution across the animal's ecologically relevant range).

Fig. 2.

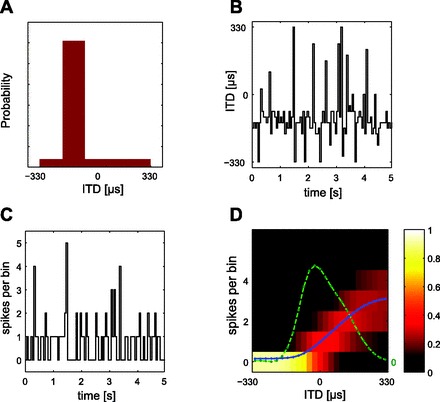
Computation of tuning curves and Fisher information (FI) from neural responses. A: each distribution of ITDs comprises a high-probability region (HPR) from which 80% of values are drawn, the remaining 20% contained within the range encompassed by the guinea pig's physiological range (±330 μs). Here the HPR is centered at −132 μs (i.e., leading in time at the ipsilateral ear) with a width of ± 66 μs. B: identical broadband noise (5 s) was presented to each ear with ITDs selected randomly every 50 ms from the distribution. C: the stimulus modulated the responses of isolated ITD-sensitive neurons (here in the form of a peristimulus time histogram). D: probability density function (pdf) of the response to multiple presentations of the HPR stimulus. The color indicates the probability of a particular spike count (number of spikes over a 50-ms epoch, on the y-axis) occurring in response to the ITD given on the x-axis (or, to be precise, the range of ITDs in an ∼13-μs bin). All presentations of the most negative (ipsilateral-leading) ITD, for example, evoked zero spikes, and therefore all spike counts for this ITD fall into the “0” bin. For increasingly contralateral ITDs, however, the proportion of trials evoking spikes increases, and thus the probability of spike counts occurring in bins other than “0” also increases. Note that as the spike count probability increases the variability of the spike count also increases (indicated by the spread of bins in which spike counts were observed). The spike count vs. ITD function is shown by the blue curve and the calculated FI by the green curve. The FI depends on both the mean of the spike count and its variability.

Sample size.

Responses were recorded from a total of 37 IC neurons, 23 with five HPR stimuli with different mean HPRs and all 37 with responses to three HPR stimuli with different mean HPRs. Twelve neurons were recorded with up to four different HPR stimuli with different HPR variances.

Data analysis.

With TDT Brainware, action potentials were sorted according to waveform characteristics to ensure that data were obtained from a single neuron. Spike times were then exported to MATLAB 7.0 (MathWorks, Natick, MA) for off-line analysis. The response to the first two 5-s segments of the stimulus was discarded. Taking an average latency of 10 ms, the spike count for each 50-ms epoch was calculated, i.e., the spike count 10–60 ms after the start of each new epoch. The ITD and spike count of each epoch were binned into 1 of 50 adjacent bins (∼13 μs wide) evenly spread over the range of ITDs in the stimulus, resulting in an average of ∼36 spike counts for each ITD bin in the LPR and ∼530 spike counts for each ITD bin in the HPR. The rate-vs.-ITD curves (see Figs. 3 and 5) show the average spike count for each ITD bin converted to spike rate (i.e., multiplied by 20).

Fig. 3.

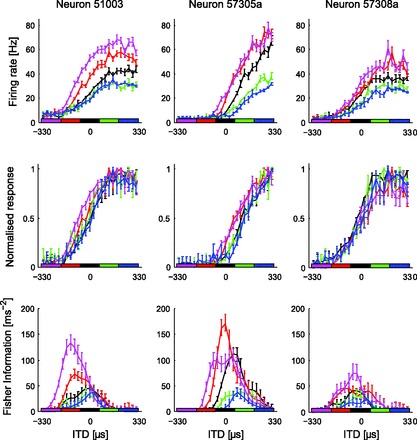
Responses of three IC neurons to HPRs centered at −264, −132, 0, +132, or +264 μs, widths fixed at ±66 μs around the center (horizontal bars along the x-axis). Top: rate-vs.-ITD functions showed highest gain when HPRs were positioned at ipsilateral-leading (negative) ITDs (magenta and red), gain falling as the HPR was shifted to contralateral-leading ITDs. Some neurons (left and center) also showed shifts in their tuning curves along the ITD axis (relative to the zero-centered response) but only for HPRs located at ipsilateral-leading ITDs. Middle: gain and shifts for different HPRs relative to the zero-centered HPR. Bottom: FI indicates information to be highest around zero ITD for the zero-centered HPR, shifting laterally only for HPRs with the longest mean ITDs. In all cases, the bars on the lines are the SE, estimated by bootstrapping for the FI and directly calculated in the figures. Nonoverlapping SEs on 2 different lines are regarded as a significant difference for the single neuron.

Fig. 5.

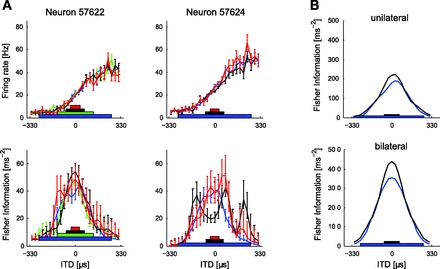
A: responses of 2 neurons where the width of the HPR centered at zero was changed. The width of each HPR ranged from ±6.5 μs to ±264 μs. Since 264 μs is 80% of 330 μs (the full range of ITDs explored) and contains 80% of epochs, the ±264 μs HPR distribution constitutes one in which all ITDs are equally likely (i.e., a uniform distribution across the range ±330 μs). Save for some changes in neural gain, IC neurons were relatively insensitive to changes in the variance of the distribution of ITDs, with little evidence of scaling to accommodate the wider HPRs. The bars on the lines are SE as in Fig. 3. B: the reduction in gain is reflected in reduced FI for ITDs around zero for a wide vs. a narrow distribution (n = 10).

The probability P_a[r|τ] of neuron a giving r spikes in ITD-bin τ was calculated. P_a[r|τ] was smoothed with a two-dimension Gaussian, with standard deviation of 48 μs and 0.8 spikes. Fisher information f_a(τ) for neuron a is given by the equation

$${\text{f}}_a\left(\tau \right)={{\displaystyle \sum _r{\text{P}}_a\left[r|\tau \right]\left(\frac{dIn{P}_a\left[r|\tau \right]}{d\tau }\right)}}^2$$ (1)

Assuming that non-stimulus-dependent variation of each IC spike counts is independent of that of the other neurons (Chechik et al. 2006; Popelar et al. 2003), population Fisher information F(τ) for N neurons is approximated by the equation

$$\text{F}\left(\tau \right)={\displaystyle \sum _{a=1}^N{\text{f}}_a\left(\tau \right)}$$ (2)

Error bars in Figs. 3 and 5A were estimated by a bootstrap method (Efron 1981). The bootstrap was performed by resampling with replacement from the epochs (each epoch having an ITD and spike count) with the number of resampled epochs equal to the original number of epochs. Such random draws were performed 2,000 times, and FI curves were computed for each random draw. Curves shown are the means over all such draws. The estimate of the SE is obtained as the standard deviation around the mean curves over the draws.

In Figs. 4 and 5B, for epochs with ITDs in the HPR of the stimulus, only a random sample of those epochs was used in estimating the FI, such that the average number of epochs per (ITD) bin was the same for the HPR as elsewhere in the function. Owing to the sampling, each neuron's FI function is the median of 20 functions, where each function was obtained using a different sample. Note that this downsampling of the HPRs and the median was not performed for the single-neuron FI plots (and 25 ITD bins of ∼26 μs were used) in Figs. 3 and 5A because of the added time and complication of computing the error bars. However, the FI plots are very similar whether the HPR downsampling is performed or not. For some plots (in Figs. 4B and 5B), each neuron is assumed to have a partner neuron on the opposite side of the brain, with the same response properties, except with the sign of the ITD reversed. This mirroring was performed for visualization only, and all statistical tests were performed on unmirrored data only.

Fig. 4.

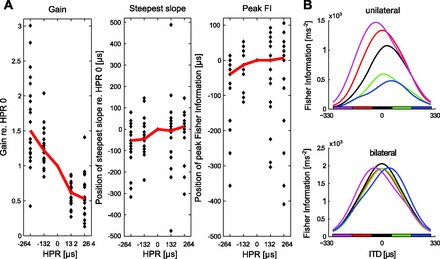
A: plots of neural gain (left), the position of the steepest slope (middle), and the position of peak FI (right) for 23 individual IC neurons for each HPR. Individual values are plotted with respect to the gain, position of steepest slope, and position of peak FI relative to that for the response to the zero-centered HPR. Red lines plot the median values. Some data points are outside the bounds of the plot, so that the median values can be clearly seen. B: summed FI for neurons in response to changes in the center of the HPR. Top: FI for all neurons in one IC. Bottom: mirrored FI, taking account of the contribution of both sides of the brain.

To measure gain changes and changes in the point of steepest slope of rate-vs.-ITD functions, the rate-vs.-ITD functions of neurons were fitted by the function

$$g\left(\tau \right)=R\exp \left(A_1\sin \left(2\pi \left(\theta -{\phi }_1\right)\right)+A_2\sin \left(4\pi \left(\theta -{\phi }_2\right)\right)+A_3\sin \left(6\pi \left(\theta -{\phi }_3\right)\right)\right)+B$$ (3)

where θ is the interaural time difference τ expressed at a proportion of the period Q of the neurons' CF, θ = τ/Q. All other parameters of the equation were varied to fit the data. Fitting was achieved by minimizing the least squared difference between Eq. 3 above and the measured rate-ITD function with the standard MATLAB program fminsearch.m. The function g(τ) is similar to the von Mises distribution function, being modulated and always positive (as are spike rates); however, we have generalized it to account for asymmetries and higher harmonics than the dominant frequency by adding the terms weighted by A₂ and A₃. We found this provided a good fit to the data over the range of ITDs that we used.

The normalized curve fits were constructed from the raw data and the curve fits of Eq. 3 with the formula

$$g_{\text{norm}}\left(\tau \right)=\frac{g_{hist}\left(\tau \right)-g_{\min }}{g_{\max }-g_{\min }}$$ (4)

where g_min is the minimum value of the curve fit over the range of the data and g_max the maximum value of the curve fit over the range of the data and g_hist(τ) is the rate-vs.-ITD function directly constructed from the data as described in the first paragraph of this section.

Modeling

We built a simple mechanistic model of the midbrain ITD pathway comprising medial superior olive (MSO), dorsal nucleus of the lateral lemniscus (DNLL), and IC in order to assess to what extent observed stimulus dependencies of neural tuning characteristics in the IC can be accounted for by established functional and anatomical properties of the ascending auditory system (see Fig. 1). The first stage of the model comprises two homogeneous populations (left and right) of excitatory, ITD-tuned MSO neurons. At the second stage, inhibitory neurons in the left and right DNLL receive inputs from the respective, ipsilateral MSO. Finally, excitatory inputs from the ipsilateral MSO and inhibitory inputs from the contralateral DNLL converge at the final stage of the model: an IC neuron, modeled as a simple leaky integrator, with synaptic depression acting on the MSO inputs. Model parameters were set in accordance with experimentally determined physiological parameters where possible.

Fig. 1.

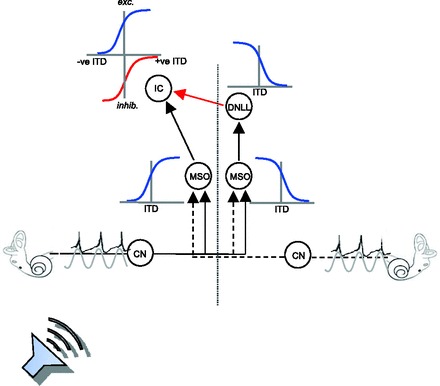
Sound sources (here located closer to one ear than the other) generate phase-locked action potentials in the auditory nerve fibers that are transmitted via the cochlea nucleus (CN) to the 1st stage of binaural integration in the medial superior olive (MSO; 1 in each brain hemisphere). MSO neurons act as binaural cross-correlators, coding the instantaneous value of the interaural time difference (ITD) and responding maximally to sounds leading at the contralateral ear. The output of the MSO—retaining phase-locking capacities—projects ipsilaterally to the major auditory midbrain nucleus, the inferior colliculus (IC). The IC also receives phase-locked inhibitory (GABAergic) input from the dorsal nucleus of lateral lemniscus (DNLL) on the opposite side of the brain, reflecting ITD processing of the MSO in the other brain hemisphere, such that its maximum inhibitory influence (here plotted downward for larger inhibitory influences) is greatest for negative (ipsilateral-leading) ITDs.

The mathematical details of the model were as follows. The rate response of an MSO neuron to a stimulus with instantaneous ITD s(t) was modeled by a Gaussian-shaped ITD-tuning function of width σ, centered at a contralateral-leading ITD Δ_max:

$$r\left(t\right)=r_{\infty }+c·\exp \left(-\frac{{\left(s\left(t\right)-{\Delta }_{\max }\right)}^2}{2{\sigma }^2}\right).$$ (5)

r_∞ and c determine the range of output firing rates. Figure 1 shows the MSO and the slopes of the ITD-tuning functions over the midline (the far slopes of the Gaussian-like tuning curves are not shown).

Assuming a population of identically tuned excitatory MSO neurons with conditionally independent Poisson spiking behavior, we used the following model of synaptic depression (Tsodyks and Markram 1997) to compute the postsynaptic current in a single IC neuron resulting from the ipsilateral MSO input:

$$\frac{\text{d}x}{\text{d}t}=\frac{1-x\left(t\right)}{{\tau }_{\text{rec}}}-U·r\left(t\right)·x\left(t\right)\text{and}\frac{\text{d}y}{\text{d}t}=-\frac{y\left(t\right)}{{\tau }_{\text{in}}}+U·r\left(t\right)·x\left(t\right)$$ (6)

x quantifies the fraction of neurotransmitter available presynaptically, U represents the fraction of available neurotransmitter released per spike and τ_rec determines the rate at which the pool of available neurotransmitter recovers. y denotes the fraction of postsynaptically active neurotransmitter, and τ_in determines its inactivation rate [in this case chosen to mimic fast glutamatergic excitatory postsynaptic currents (EPSCs)]. Finally, the postsynaptic current is assumed to be proportional to y, resulting in the following current-balance equation for the membrane voltage V of a simple integrate-and-fire IC neuron:

$${\tau }_{\text{m}}\frac{\text{d}V}{\text{d}t}=-V\left(t\right)+W·y\left(t\right)+\eta \left(t\right)$$ (7)

where τ_m is the passive membrane time constant, W (in units of voltage) determines the input scale, and η(t) is a zero-mean Gaussian random variable. Upon reaching the threshold voltage V_θ, a spike is generated, after which V is reset to its resting potential (0 mV).

To incorporate inhibition via the contralateral MSO and DNLL (see Fig. 1, red arrow), a neurotransmitter-controlled shunting mechanism was added to the IC current-balance equation that increases the membrane leakage upon activation of postsynaptic GABA receptors, yielding

$${\tau }_{\text{m}}\frac{\text{d}V}{\text{d}t}=-\left(1+\widehat{W}·\widehat{y}\left(t\right)\right)·V\left(t\right)+W·y\left(t\right)+\eta \left(t\right)$$ (8)

Assuming that the contralateral DNLL follows its MSO inputs instantaneously, the number of postsynaptically active GABA_A receptors ŷ(t) is determined by the firing rate r̂(t) of the contralateral MSO, convolved with an exponentially shaped (unit-area) inhibitory postsynaptic potential (IPSP)-like filter with time constant τ̂_in and scaled by a connection weight Ŵ. ITD tuning of the contralateral MSO is exactly opposite to that of the ipsilateral MSO (cf. Eq. 5):

$$\widehat{r}\left(t\right)=r_{\infty }+c·\exp \left(-\frac{{\left(s\left(t\right)+{\Delta }_{\max }\right)}^2}{2{\sigma }^2}\right)$$ (9)

Model parameters throughout all simulations were chosen as follows: r_∞ and c were set such that the MSO neurons had a firing range of 10–85 Hz within the physiological range of ITDs. Tuning width and preferred ITD were σ = 297 μs and Δ_max = 330 μs (i.e., the limit of the physiological range), respectively. Parameters for the synaptic dynamics were U = 0.15, τ_rec = 150 ms, and τ_in = 5 ms. The choice of τ_in reflects the short time course of AMPA-mediated EPSCs, while U and τ_rec were chosen such that the time course of adaptation in the EPSC is in close agreement with the time course of response adaptation of interaural phase difference (IPD)-sensitive IC neurons (52.9 ms for binaural, compared with 38.4 ms for monaural, adaptation) reported by Ingham and McAlpine (2004). Since inhibition in the IC is predominantly GABAergic and believed to be mediated by GABA_A receptors only (see Wu 2005 for an extensive discussion), we set τ̂_in, matching the average of the decay time constants of GABA_A-mediated IPSCs measured in brain slice preparations of rat IC (Wu et al. 2004), even though similar results can be obtained for significantly lower values of τ̂_in. The IC membrane time constant and firing threshold were set to τ_m = 8 ms and V_θ = 12 mV (above resting potential), respectively, based on values reported for IC neurons in rodents, both in brain slices (Reetz and Ehret 1999) and in vivo (Tan et al. 2007). The weight of the excitatory inputs W was fixed to a value of 640 mV throughout, whereas the inhibitory weight Ŵ was chosen as 0 (see Fig. 6A, left), 0.005 (see Fig. 6A, center, and Fig. 6B), or 0.008 (Fig. 6A, right).

Fig. 6.

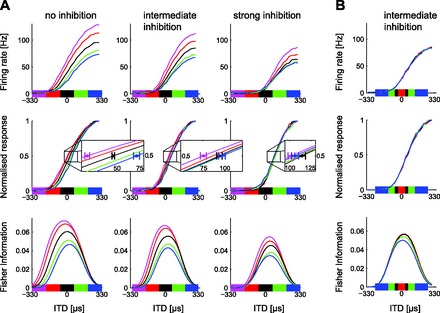
Responses of model IC neurons, showing raw (top) and normalized (middle) discharge rates and FI (bottom). A, left: output of model neuron in which only synaptic depression but no ITD-sensitive GABA_A-mediated inhibition from the DNLL was implemented. Gain changes and shifts for both ipsilaterally and contralaterally centered distributions are evident in response to different HPR centers. These shifts can be observed in the normalized functions and underlie the shifts in FI. Center: ITD-sensitive GABA_A-mediated inhibition from the DNLL is set to an intermediate level such that shifts remain only for ipsilateral-leading HPRs (as observed in some neurons). Right: the inhibition from the DNLL is increased to fully counteract the shift in neural tuning (as observed in other neurons). “Zoomed” insets show the average normalized tuning curves (averaged over many instances of the stimulus and IC integration noise), expanded around the “50% maximum firing” point on the y-axis. Circles indicate average ITD that evoked 50% maximum firing rate, and error bars indicate SD (along the x-axis) around this mean rate for the central and the 2 most lateral distributions. B: widening the HPR around the midline causes a reduction in FI but has little effect on model tuning curves overall, compared with changes in mean (inhibition as in A, center).

Psychophysics

Experimental design.

Ten subjects (7 men and 3 women, aged between 22 and 42 yr) participated in this study. The study was carried out in accordance with the Declaration of Helsinki, with prior approval of the French “Regional Ethics Committee” CPP Ile de France VI. All participants provided informed consent before the experiment. All subjects had self-reported normal hearing. Stimuli were generated for each trial in real time with custom MATLAB programs. Two setups were used for data measurement. Stimuli were played back via a RME Fireface digital-to-analog soundcard in setup 1 and a Creative SB Audigy 2ZS soundcard in setup 2 (both 96-kHz sampling rate), before being passed into a sound-attenuating booth (in both cases IAC 1202-A), where they were presented to the subjects over headphones (Sennheiser HD 250 and Sennheiser HDA 200, respectively). No difference in outcome could be found between the two setups. Adaptor stimuli were 800-Hz-wide bands of Gaussian noise filtered between 100 and 900 Hz (brick-wall FFT filter), presented with a mean overall level of 68 dB SPL, with durations chosen randomly between 1 and 2 s (from a uniform distribution) and ITD randomly chosen from a distribution every 50 ms. Target stimuli were 500-Hz pure tones of 50-ms duration, presented at the same level. Both adaptors and targets included 5-ms onset and offset ramps. Intertrial intervals were of 1.5-s duration. ITDs were computed by delaying stimuli to one ear but without any onset or offset time lag: the signals from both ears were padded to the same length with fresh noise, so that onsets and offsets were synchronous. All subjects completed two sessions of 40-min duration, comprising 450 trials each with various combinations of adaptor position and target position presented in random order (100 repeats per combination, 900 trials per subject overall).

Data analysis.

Sensory sensitivity d′ was computed for each adaptor and target condition by signal-detection theory with the following formula:

$$d\prime =z\left(\text{hits}\right)-z\left(\text{false}\text{alarms}\right)$$ (10)

where z denotes the number of standard deviations from the mean, “hits” the rate of detecting a real difference in ITD between target tones, and “false alarms” the rate of incorrectly classifying a zero-ITD difference as different. A repeated-measures ANOVA was then performed with the d′ values computed for each subject as the dependent variable.

RESULTS

Electrophysiological Recordings

In mammals, ITDs are first processed in the MSO of the brain stem, where coincidence-detector neurons respond maximally to ITDs that compensate for the difference in the time of transmission of a sound from the two ears (Goldberg and Brown 1968, 1969; Jeffress 1948; Yin and Chan 1990). The IC receives ITD-sensitive input from each MSO, a direct excitatory projection from the MSO on the same side of the brain, and a GABAergic inhibitory projection via the DNLL from the opposite side of the brain, itself the target of the ipsilateral MSO (Fig. 1). Thus IC neurons receive maximal excitatory drive for sounds located in one spatial hemisphere (i.e., to one side of the animal's midline) and maximal inhibition for sounds located in the other.

Spike trains of IC neurons were obtained in response to the HPR stimulus—white noise with the ITDs randomly selected every 50 ms, whereby 80% was selected from a predefined HPR (see Fig. 2). This was performed for each neuron with a range of different ITD distributions, systematically varying both the center (mean) and width (variance) of the HPR. For each neuron and stimulus distribution, an ITD tuning curve and a FI (a measure of coding accuracy) curve were computed from the binned, empirical spike count distribution (Fig. 2, see also methods).

Adaptation to the mean of a distribution of ITDs.

Responses of IC neurons were clearly sensitive to changes in the center of the HPR (Fig. 3). The most obvious effect was a progressive reduction in neural response gain, i.e., a divisive reduction in the spiking output for all ITDs, as the HPR center of the distribution was shifted from ipsilateral-leading ITDs to contralateral-leading ITDs (akin to a sound source moving further into contralateral space). Furthermore, the detailed nature of this sensitivity differed depending on the ear at which the sound was leading in time. HPRs in which the sound was leading at the ear contralateral to the recording site (i.e., leading at the left ear; positive ITDs) generated a change in response gain only (green and blue curves, Fig. 3, top). HPRs in which the sound led at the right, ipsilateral ear, however, generated both an increase in gain (relative to the zero-centered HPR) as well as a small, additional shift in the tuning curve of some neurons (magenta and red curves, Fig. 3, top).

To quantify changes in gain, the dynamic response ranges of the rate-vs.-ITD functions were measured as the difference between the maximum and minimum spike rates, acquired by fitting Eq. 3 to the rate-vs.-ITD function. The gain for each HPR was calculated as the response range for that HPR as a proportion of the response range for the HPR centered at 0 μs. The gains for rate-vs.-ITD functions to different HPRs were calculated for 23 neurons, and gain was plotted as function of the HPR (Fig. 4A, left); each symbol indicates the gain for one neuron for the HPR indicated on the x-axis, and the red line plots the median gain over the neural population. Neural gain decreased as the HPR was shifted from ipsilateral- to contralateral-leading ITDs for both of the contralateral-centered HPRs (132 μs and 264 μs), with median gain significantly less than 1.0 (in both cases P < 0.05, n = 23, Wilcoxon signed-rank test) compared with the zero-centered HPR. For both ipsilateral-centered HPRs (−132 μs and −264 μs) gain was significantly greater than 1.0 (in both cases P < 0.05, n = 23, Wilcoxon signed-rank test), compared with responses to the zero-centered HPR.

Rate-vs.-ITD functions were normalized (cf. Fig. 3, middle) to test whether divisive gain changes constituted the only difference between responses to different HPRs. To quantify this, the ITD at which the maximum slope occurred on the fit to the rate-vs.-ITD function was considered a measure of shape; this should remain constant across rate-vs.-ITD functions generated by different HPRs if the only change is a change in neural gain. Normalized rate-vs.-ITD functions showed changes in the shapes of the functions relative to that for the zero-centered HPR, but only for ipsilateral-centered HPRs (Fig. 4A, center); the ITD of the maximum slope of rate-vs.-ITD functions (max-slope-ITD) shifted significantly toward ipsilateral-leading ITDs for the HPR centered at −264 μs (P < 0.05, n = 23, Wilcoxon signed-rank test). That is, the median value (across 23 neurons) of the difference between the max-slope-ITD in the −264 μs HPR adapted case and the max-slope-ITD in the 0 μs case was significantly different than 0. No significant difference from the 0 μs HPR case was seen for the max-slope-ITD in the −132, 132, and 264 μs HPR cases.

For each neuron, FI, a measure of coding accuracy, was assessed to determine whether neurons are more informative about those ITDs most likely to be experienced as part of the HPR. Assuming an optimal decoder, higher FI reflects higher coding accuracy, manifested as a higher capacity to discriminate nearby ITDs based on the neuron's spike count response. A reasonable approximation of FI is the square of the slope of the tuning curves divided by the variance (Dean et al. 2005). Thus FI is high when the variance of the spike count is low and when the spike rate changes steeply with changes in ITD. Since spike count variance of IC neurons tended to be approximately proportional to the spike counts themselves, the peaks of FI functions were typically situated on the lower, rising portion of the slopes of tuning curves (see Fig. 2D).

Although peak FI for individual neurons did indeed follow the HPR to some extent (Fig. 3, bottom), this shift was only significant for HPRs centered at ipsilateral-leading ITDs. Peak FI shifts followed exactly the same pattern as the observed shifts in the slopes of rate-vs.-ITD functions: median peak FI was located at significantly more negative ITDs than for the zero-centered HPR only for responses to the most ipsilateral-leading (−264 μs) HPR (Fig. 4A, right; P < 0.05, n = 23, Wilcoxon signed-rank test). For all other HPRs, the ITD at which the peak FI occurred was not significantly different from that for the zero-centered HPR (P > 0.05, n = 23, Wilcoxon signed-rank test). That is, the median value (across 23 neurons) of the difference between the ITD at which the peak FI occurred for the −264 μs HPR and for the zero-centered HPR case was significantly different, whereas there was no significant difference in the ITD of the peak FI between the zero-centered HPR and the ITD of the peak FI for the other (−132, 132, and 264 μs) HPRs.

The peak FI largely follows the changing position of the slopes of the rate-vs.-ITD functions, as can be seen in Figs. 3 and 4A. The remaining dependence of FI on the HPR, after accounting for the slope shifts, may be due to more subtle changes in the shape of the rate-vs.-ITD function or in the changes in the variability of the spike rate.

Some degree of diversity was evident among the neural population, at least with respect to how neurons responded to changes in the HPR. Most neurons showed shifts in the slopes of their rate-vs.-ITD functions and peak FI in the direction of the HPR for contralateral HPRs, as well as gain changes (Fig. 3, center and left, show examples of such shifting neurons). However, some neurons showed only gain changes, with no shift in the ITD corresponding to the steepest slope or the peak of the FI, or showed no changes in slope but small shifts in the ITD at which the peak of the FI occurred. Summing FI across the population of 23 neurons (Fig. 4B, top) revealed that population FI for stimuli with central HPRs (i.e., 0 μs, black) peaks around 0 μs ITD. For contralateral-leading HPRs (+132 μs, red, and +264 μs, magenta, Fig. 4B, top), the population peak FI is progressively higher in magnitude and shifted contralaterally. For ipsilateral-leading HPRs (−132 μs, green, and −264 μs, blue, Fig. 4B, top), the population peak FI did not shift in a systematic manner and was of substantially lower magnitude, the latter reflecting the relative reduction in gain for ipsilateral-leading HPRs. Similar responses were observed for a larger population of neurons where responses to stimuli with HPRs centered at −132, 0, and +132 μs only were recorded (n = 37; data not shown). Note that identical changes in the gain of rate-vs.-ITD functions will generally only scale the corresponding FI functions; however, gain changes that differ between neurons, or changes in rate-vs.-ITD function shape, allow for other changes in population FI function such as shifts in the ITD at which the peak FI occurs.

Assuming that neurons possess a symmetrical partner in the opposite IC, population FI (n = 23) can be mirrored around zero (midline), taking into account the neural representation of ITD in both brain hemispheres. Mirrored FI revealed that neurons shift their peak coding accuracy with respect to HPRs furthest away from the midline, but again only partially, and not at all for distributions centered at −132 or +132 μs (Fig. 4B, bottom). The shifts observed in the mirrored data reflect the statistically significant difference in the FI functions for the HPR centered at −264 μs, relative to the zero-centered HPR, in the nonmirrored data (all statistics were performed on nonmirrored data, mirrored data being only for visualization). For ITDs within approximately ±50 μs of zero, population FI across both brain hemispheres indicated coding accuracy to be greatest when the population was adapted to an HPR centered at zero (Fig. 4B, bottom, black curve). When the ITD exceeded ±50 μs, FI functions obtained when the neural population was adapted to HPRs centered at −264 or +264 μs provided for the most accurate coding. That is, the magenta FI curves in Fig. 4B, bottom, show the highest FI values, compared with the other FI curves, over most of the ipsilateral range, and the blue curves show the highest FI values over most of the contralateral range. However, it should be noted that the peak FI did not shift sufficiently to align with the HPR center. Thus, at least for the HPRs centered at −264, 0, and +264 μs, the resulting adapted state of the neural population was most suited to code accurately spatial locations close to the most common ITDs of the HPR, among the five different adaptation states tested. Note also that the magnitude of the peak FI is roughly constant across these HPRs.

Adaptation to the variance of a distribution of ITDs.

Fourteen neurons were assessed for their sensitivity to the variance of the HPR, with widths of zero-centered HPRs extending from ±6.5 μs to a uniform distribution (±330 μs; Fig. 5A). There was little evidence of any broadening of rate-vs.-ITD tuning curves to accommodate wider distributions. Population FI, as for the individual tuning curves, did not broaden to take account of the wider variance (Fig. 5B). This means that a widening of the HPR distribution is not reflected in a widening of the neural population's sensitive range for ITD. Comparing population FI at midline (0 μs ITD) for a narrow (±66 μs) versus a wide (±330 μs) stimulus distribution in a group of n = 10 neurons, we found FI to be lower for the high-variance stimulus (P < 0.05, n = 10, Wilcoxon signed-rank test). This change in the population FI would be due to subtle shape, gain, and changes in spike rate variability in the rate-vs.-ITD functions, beyond broadening. This result suggests that the increased variance of the HPR distribution should lead to reduced behavioral discrimination performance specifically for ITDs around the midline.

A Midbrain Macrocircuit for Adaptive Coding of ITD

How can the adaptive tuning of ITD-sensitive neurons be accounted for mechanistically, particularly the significant yet restricted adaptation to strongly lateralized stimulus distributions? Here we present a possible mechanism that is sufficient to explain our data and is consistent with the known anatomy and physiology. Neurons in the MSO, the initial site of ITD processing, encode stimulus ITDs largely independent of their context (Spitzer and Semple 1995). The adaptation we measured in the IC must therefore occur after the somatic MSO response, somewhere along the midbrain ITD pathway comprising a direct excitatory connection to the ipsilateral IC as well as an indirect, inhibitory pathway from the contralateral MSO via the contralateral DNLL (Zhang et al. 1998; see Fig. 1). Such adaptation may, though a context-dependent code, allow more accurate ITD representation in the face of internal noise. In an earlier study, Ingham and McAlpine (2004) demonstrated pronounced spike-rate adaptation (SRA) in IC neurons tuned to the IPD of dichotic pure tones during stimulation at their preferred IPD. This type of SRA is likely to be intrinsic to the excitatory pathway itself, rather than being a consequence of timed inhibition via the DNLL pathway, since the magnitude of inhibition arriving from the contralateral DNLL is minimal for best-IPD stimuli and adaptation constants were relatively slow (∼50 ms).

An exemplary candidate mechanism for SRA is synaptic depression, thought to reflect the depletion of excitatory neurotransmitters during prolonged phases of high presynaptic activity. We investigated the effects of such short-term synaptic plasticity at excitatory MSO-IC synapses through model simulations, and asked whether this simple mechanism alone could account for the stimulus-dependent changes in ITD tuning at the level of the IC. Consistent with previous reports (e.g., Rothman et al. 2009), we find that synaptic depression reduces the gain of ITD tuning curves in the IC in a manner resembling the changes observed in vivo in some important aspects, i.e., the gain of the stimulus-response functions decreases as the center of the stimulus HPR moves from the ipsilateral to the contralateral side (Fig. 6A, left), whereas changes in HPR width have little effect on ITD tuning (data not shown, but similar to Fig. 6B). Nevertheless, this reduced circuit, relying on synaptic depression as the sole source of changes to the ITD-tuning characteristics in the IC, does not account for the specific lateral shift of tuning curves that occurs only for ipsilateral-centered distributions. When IC neurons are modeled as leaky integrators, a pure gain change in the excitatory input currents resulting from synaptic depression translates not only into a change in neural output gain but also into a concomitant lateral shift of the tuning curves (Fig. 6A, left). Inconsistent with our physiological findings, these shifts occur not only for ipsilateral-leading but also for contralateral-leading stimulus distributions. Physiologically plausible ITD tuning can be recovered, however, when the model takes into account the action of known inhibitory inputs originating from the contralateral DNLL.

The DNLL receives its own excitatory input largely from the MSO on the same side of the brain (i.e., contralateral to the IC to which it projects). As a result, the strength of inhibitory input to the IC displays ITD tuning opposite to that of the excitatory input (see Fig. 1). ITD-sensitive inhibition in the IC is therefore strongest for ipsilateral-leading ITDs. This gives rise to varying amounts of contralateral shift due to inhibition alone, as the HPR of the stimulus distribution is shifted across the physiological range of ITDs, acting against the effect of gain changes that arise because of synaptic depression along the excitatory pathway. Depending on synaptic efficacy, these inhibition-evoked, and distribution-specific, shifts can counteract the shifts originating from the excitatory input either partially (Fig. 6A, center) or completely (Fig. 6A, right), allowing this circuit to mimic the behavior of both partially shifting and nonshifting neurons. Inhibition also reduces the difference in neural gain between the ipsilateral and contralateral distributions, thus generally stabilizing the shape of IC tuning curves in the face of varying input statistics compared with a purely excitatory circuit subject to synaptic depression. Importantly, including ITD-sensitive inhibition does not affect the dependence of neuronal tuning on the width of the stimulus HPR, already observed in the reduced model without inhibition: tuning curves are virtually identical for the range of HPR widths employed in the physiological recordings (Fig. 6B). Consistent with our observations in vivo, FI nevertheless decreases around zero ITD as the HPR is widened, despite the neuron's tuning curve remaining relatively unchanged. In the model, spike rate variability around the average response to a particular ITD value (a major determinant of FI) is dominated by the variability in ITD of the inputs themselves. As the stimulus HPR is widened, ITD variability increases, resulting in a reduction in FI. In summary, based on our model, we propose that inhibition via the DNLL reduces the distribution dependence of IC tuning curves originating from the interplay of changing stimulus distributions and neuronal adaptation arising in the excitatory pathway alone. This may serve to maintain an auditory spatial fovea of high ITD discriminability around midline for all but the most strongly lateralized ITD stimulus distributions employed in our electrophysiological experiments.

Discrimination Performance of Human Listeners in a Spatial Listening Task

Discrimination performance following an adapting sound was measured in human listeners with a stimulation paradigm closely matched to the physiological experiments. Over headphones, listeners were presented with trials comprising a relatively long (random duration between 1 and 2 s) adaptor noise burst, followed immediately by a target sequence of two short (50 ms) target pure tones (Fig. 7A). All sounds in the stimulus sequence were lateralized by means of ITD. A localization discrimination task (Same-Different) was performed on the target tones. The target tones could either have the same ITD (correct response “Same”) or ITDs that differed by 200 μs (±100 μs around the nominal target location; correct response “Different”) with equal likelihood. Approximately compensating for the difference in head width between guinea pigs and humans, and consistent with the parameters employed in the electrophysiological recordings, the task was performed at three different mean target locations, corresponding to ITDs of 0 μs (central target), 200 μs (intermediate target), and 500 μs (lateral target). The maximum ITD for humans is ∼690 μs (Moore 2003) compared with ∼330 μs in the guinea pig (Sterbing et al. 2003), i.e., about half of this. To this end, relevant comparable FI values in those figures showing electrophysiological data at approximately 0 μs, 100 μs, and 250 μs would be 0 μs, 200 μs, and 500 μs respectively. For the noise adaptor, a new ITD was randomly selected every 50 ms from a chosen distribution (as in the physiological recordings). Two low-variance distributions were used, containing ITDs within the range of ±100 μs (central adaptor, Fig. 7B, blue) or 400–600 μs (lateral adaptor, Fig. 7B, green). A high-variance distribution was also included, containing ITDs within the range ±600 μs (diffuse adaptor, Fig. 7B, red). Thus, as in the electrophysiological recordings, the range of ITDs encompasses the naturally occurring range of ITDs generated by the (here, human) head. In any given trial, listeners (n = 10) heard one of the three adaptors followed by one of the three target mean positions. The order of presentation of adaptor/target combinations was fully randomized, and all combinations equally likely, and listeners had to indicate whether the two target tones were the same or different. Listeners were instructed that adaptor location was not informative of target location. Results were analyzed in terms of the sensitivity index d′ of signal detection theory (see methods).

Fig. 7.

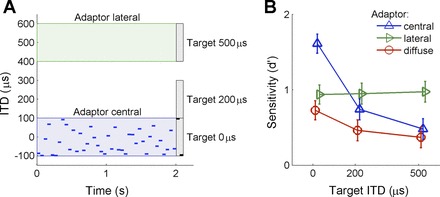
Psychophysical experiment. A: illustration of the behavioral task. A noise adaptor with ITDs randomly drawn each 50 ms was immediately followed by 2 target pure tones, also 50 ms in duration. The uniform distribution for the adaptors covered the ranges −100 to 100 μs for central adaptors, 400 to 600 μs for lateral adaptors, and −600 to 600 μs for diffuse adaptors (not shown). The target tones were centered at ITDs of 0 μs, 200 μs, or 500 μs. Target tones had the same ITDs for “same” trials and ITDs that differed by 200 μs for “different” trials. The example shown here is for a central adaptor, a 0 μs target, and “different” trial. B: discrimination performance (plotted as d′) for each adaptor employed as a function of target location. The mean d′ for the group of listeners (N = 10) is shown, together with the SE. Performance was best for central adaptor and 0 μs target (blue) compared with all other adaptor-target combinations. For lateral adaptors (green), performance remained level independent of the target presented. Discriminating intermediate targets benefited from lateral adaptor presentation. Finally, presentation of the diffuse adaptor (red) resulted in the lowest discrimination performance.

Figure 7 plots discrimination performance at each target location (0, 200, and 500 μs) as a function of the adaptor condition (central, lateral, and diffuse). Overall, discrimination performance was markedly better for central targets preceded by central adaptors. For such central adaptors, shifting the target away from midline resulted in a marked decrease in performance. For lateral adaptors, performance did not change with target location. Following diffuse adaptors (centered at 0 μs but with large variance), performance was better for central than for intermediate and lateral targets, but overall poorer than for all other adaptor conditions. A two-way repeated-measures ANOVA with factors “adaptor” (central, diffuse, lateral) and “target” (central, intermediate, lateral) revealed significant main effects of “adaptor” [F(2,18) = 16.02, P < 0.001] and “target” [F(2,18) = 6.45, P = 0.008]. In addition, a highly significant interaction was observed between adaptor and target conditions [F(4,36) = 8.25, P < 0.001], confirming the joint influence of adaptor and target position on performance.

We also analyzed the data for each target location, employing planned comparisons that contrasted colocated adaptors (adaptor and target from the same location) with the diffuse adaptor condition considered as a baseline. For central targets performance was improved by a central adaptor [t(9) = 4.77, P = 0.001] relative to the diffuse adaptor, and for lateral targets performance was improved by a lateral adaptor [t(9) = 5.50, P < 0.001] compared with the diffuse adaptor. For intermediate targets, as there was no colocated condition, we tested both lateral and central adaptors. Compared with the diffuse baseline, performance was improved for the lateral adaptor [t(9) = 2.65, P = 0.026] but not for the central adaptor [t(9) = 1.51, P = 0.166].

DISCUSSION

We investigated the extent to which adaptation to the distribution of ITDs affects the coding of ITDs in the auditory midbrain of the guinea pig and compared this to the discrimination performance of humans in a spatial listening task. This approach revealed three main findings. First, neural coding of ITDs is sensitive to changes in the mean of a distribution of ITDs. Second, neural sensitivity following adaptation to different mean ITD distributions remains greatest for spatial locations around the midline. Third, human behavioral performance shows a beneficial effect of adaptation on a spatial discrimination task with many similarities to the neural data.

Comparing Neural Adaptive Coding and Human Discrimination Performance in an Adaptive Spatial Listening Task

A critical feature of our study is that we employed a similar paradigm in the electrophysiological experiments and the behavioral task, and strong similarities exist between the two data sets. The main psychophysical finding was that, for central targets, performance was markedly better following a central adaptor than following a diffuse or lateral adaptor, or for other target locations. Consistent with this finding, in the electrophysiology data FI was highest at zero when the HPR was centered at zero. Thus a central tenet of adaptive coding at the neural level—that it should improve performance in the relevant task—was met. In addition, the diffuse adaptor produced poorer behavioral performance overall, but with performance still peaking at the central target location. Consistent with this, the physiological recordings also showed that a high-variance HPR reduced the FI peak value, without shifting its position. Finally, we also included an intermediate target location in the psychophysics (200 μs, corresponding to ∼110 μs in guinea pigs assuming a linear mapping between the respective stimulus ranges used), as the physiological data predicted that discriminability for intermediate targets should be higher after adaptation to a fully lateral HPR on the same side than after central or diffuse adaptor distributions (cf. Figs. 4B and 5B, bottom, respectively). Note that this prediction is counterintuitive: in terms of ITDs, the central adaptor is closer to the intermediate target than the lateral adaptor. Nevertheless, this prediction was verified: performance was better at the intermediate target location for a lateral adaptor compared with a central or diffuse adaptor. We argue that this is a particularly strong indication of a causal relation between adaptive coding in the physiology, at the level of single neurons, and behavioral performance on a spatial task.

Nevertheless, one noticeable difference exists between the physiological and psychophysical data: behavioral performance for lateral targets was markedly better than expected from neural FI curves, which were always very low irrespective of the HPR condition. Consistent with physiology, behavioral performance for lateral targets was better after a lateral adaptor compared with diffuse or central adaptors, but performance for lateral targets after a lateral adaptor was relatively good, contrary to expectations from the low FI curves. Reasons for this mismatch are unclear. They could include as yet unknown species differences in the early auditory pathway between guinea pigs and humans, effects of anesthesia, a different mapping of guinea pig to human ITD space than we assume here, or, inevitably, remaining differences between the passive listening condition and the active task despite our efforts to match them as closely as possible. Related to this latter possibility, Getzmann (2004) and Sach et al. (2000) observed context effects for lateral targets similar to the present data, whereas Maier et al. (2010) did not, and specific differences between paradigms might account for the different outcomes. For instance, Maier et al. (2010) included a silent gap between adaptors and targets and, additionally, employed silence as opposed to diffuse adaptors as a baseline. In both Sach et al. (2000) and Getzmann (2004), the adaptor location was informative about the subsequent target location. It is likely, therefore, that stimulus and procedure details are important for spatial discrimination performance with lateral targets. In all studies, however, a robust context effect was always found for midline target locations. We suggest that this behavioral outcome is consistent with the adaptive coding observed in neural recordings.

How Strongly Adaptive Are Auditory Spatial Cues?

Adaptive coding for ITD, although broadly consistent with that for sound level (Dean et al. 2005), is clearly less pronounced. We observed less of a shift in response functions toward the mean of the prevalent distribution for ITD than Dean et al. (2005) for sound level, where the neural population tended to adapt near fully to the mean of the underlying distribution of sound levels. Instead, ITD functions appear to rise from a relatively fixed location along the ITD axis, and the major change was a reduction in gain as HPRs were positioned progressively more toward contralateral-leading ITDs. FI (mirrored and nonmirrored) was relatively high for ITDs near midline for all HPRs, reflecting greater accuracy for midline spatial positions in sound localization tasks. As Dean et al. (2005) observed, rate-level functions do not shift to accommodate HPRs centered at sound levels below the threshold of baseline response functions. This is likely reflected in our data to the extent that responses would not be evoked by ITDs that lie beyond the range over which binaural coincidence detection in their excitatory (MSO) inputs generates an output. This limits the extent to which response functions adapt to encode ipsilateral-leading HPRs. The adaptive coding seen in the above studies may share some mechanisms with stimulus-specific adaptation in the IC (Lumani and Zhang 2010; Malmierca et al. 2009; Reches and Gutfreund 2008; Zhao et al. 2011). The adaptive coding perspective elucidates a different but related role of adaptation in the auditory system. Rather than rendering oddball stimuli more apparent in the neural response, adaptive coding suggests that adaptation may also shape the neural population response to better represent the whole distribution of possible stimulus values.

A recent study (Dahmen et al. 2010) reported that IC neurons in the ferret adapt their coding capacity to account for the different means and variances of the distribution of interaural level differences (ILDs)—the other binaural cue. Since, in the present study adaptive coding for ITD was found to be mostly restricted to the midline, might this suggest a difference in adaptive coding for the two binaural cues? We argue that the data of Dahmen et al. (2010) do not warrant such a strong conclusion. A viable explanation for apparent adaptation to ILD distributions is that neurons are simply adapting to changes in sound level (as in Dean et al. 2005, 2008) rather than adapting to ILD. There is a remarkable correspondence between the degrees of adaptation to distributions of ILDs (Dahmen et al. 2010) and diotic sound levels (Dean et al. 2005). Consistent with this notion, Tsai et al. (2010) observed ILD sensitivity of neurons in the lateral superior olive (LSO, the presumed primary site of ILD sensitivity) to shift along the ILD axis with increasing overall monaural sound level. Additionally, such monaurally evoked adaptation to sound level combined with an adaptation-unaware decoder would qualitatively predict the psychophysical repulsion effect reported in Dahmen et al. 2010 (see Seriès et al. 2009 regarding the visual tilt aftereffect). Their data could also be accounted for by responses of neurons entirely insensitive to ILD, since an increase in ILD in their stimulus paradigm is always accompanied by a corresponding increase in level at the ipsilateral ear. Finally, in contrast to our study, where distributions confined to the physiological range were employed, Dahmen et al. (2010) employed ILD distributions centered at +15 or −15 dB, which are unlikely to be experienced under natural listening conditions for sounds in the horizontal plane over the range 4–16 kHz (Carlile 1990). In summary, direct comparison between the results of Dahmen et al. (2010) and our own data in terms of their bearing on natural, spatial listening remains tenuous at best.

The limited degree of adaptation observed in encoding of ITDs compared to sound level (Dean et al. 2005) may be rationalized by a simple ethological consideration. Depending on the situation, mean environmental sound intensities can vary over many orders of magnitude. Importantly, despite limited gain control mechanisms in the middle and inner ear, the effective sound level is by and large not under immediate control of the listener, and the task of compensating for such gross differences in scale is thus left to the central nervous system. Conversely, in the context of sound localization, we are able freely to choose the ITD (and ILD) midline simply by turning our heads. Hence, the need for adaptive coding of auditory spatial cues at the neural level may be alleviated by the common behavioral response of a head orientation to sound sources perceived to originate from one side or the other, after which fine discrimination can proceed around the new midline. Our data bear this out, with neural and psychophysical performance dominated by high performance for frontal locations and the biggest benefits of adaptive coding also observed for those frontal locations. It is also unlikely that an unfolding distribution of highly variable binaural cues corresponds to the movement of a single source whose movement is tracked with any precision. Our psychophysical evidence of poor discrimination performance for any target location when a high-variance adaptor was employed is consistent with the view that random and highly variable changes in spatial cues are not treated as originating from a single source in motion but, rather, reflect a complex listening condition in which no one source location dominates. This is also consistent with the reduced performance near zero ITD in the neural data when stimulus variance was high.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.K.M., P.H., N.S.H., G.M.K., D.P., and D.M. conception and design of research; J.K.M. and D.M. performed experiments; J.K.M., P.H., N.S.H., and D.M. analyzed data; J.K.M., P.H., N.S.H., and D.M. interpreted results of experiments; J.K.M., P.H., and N.S.H. prepared figures; J.K.M. drafted manuscript; J.K.M., P.H., N.S.H., D.P., and D.M. edited and revised manuscript; J.K.M., P.H., N.S.H., and D.M. approved final version of manuscript.