A novel mouse running wheel that senses individual limb forces: biomechanical validation and in vivo testing

Abstract

Biomechanical data provide fundamental information about changes in musculoskeletal function during development, adaptation, and disease. To facilitate the study of mouse locomotor biomechanics, we modified a standard mouse running wheel to include a force-sensitive rung capable of measuring the normal and tangential forces applied by individual paws. Force data were collected throughout the night using an automated threshold trigger algorithm that synchronized force data with wheel-angle data and a high-speed infrared video file. During the first night of wheel running, mice reached consistent running speeds within the first 40 force events, indicating a rapid habituation to wheel running, given that mice generated >2,000 force-event files/night. Average running speeds and peak normal and tangential forces were consistent throughout the first four nights of running, indicating that one night of running is sufficient to characterize the locomotor biomechanics of healthy mice. Twelve weeks of wheel running significantly increased spontaneous wheel-running speeds (16 vs. 37 m/min), lowered duty factors (ratio of foot-ground contact time to stride time; 0.71 vs. 0.58), and raised hindlimb peak normal forces (93 vs. 115% body wt) compared with inexperienced mice. Peak normal hindlimb-force magnitudes were the primary force component, which were nearly tenfold greater than peak tangential forces. Peak normal hindlimb forces exceed the vertical forces generated during overground running (50-60% body wt), suggesting that wheel running shifts weight support toward the hindlimbs. This force-instrumented running-wheel system provides a comprehensive, noninvasive screening method for monitoring gait biomechanics in mice during spontaneous locomotion.

biomechanical data reveal critical functional information about how the musculoskeletal system responds to physical stimuli during both adaptive and pathological processes. Mouse models are widely used to study basic mechanisms of musculoskeletal development, adaptation, and disease; however, limited options exist for quantifying locomotor biomechanics in mice. Current methods involve using force platforms (6, 9, 23), but these techniques are challenging due to limitations in force-plate sensitivities and the intermittent locomotor patterns of mice. We believe that running wheels provide a favorable system for high-throughput recording of locomotor biomechanics because of the high level of spontaneous running activity (up to 8 km/night) and the stationary position of running wheels (2, 14). Furthermore, sensitive quantification of locomotor biomechanics with running wheels could benefit a wide set of applications, including studies of the adaptive effects of exercise (10–12, 17) and noninvasive characterization of locomotor pain and musculoskeletal pathology (5, 7, 15, 19).

Recently, we and others (5, 7, 19) have shown that running wheels provide a useful method for detecting functional changes associated with joint pain and musculoskeletal pathology in mice and rats. One reason running wheels are effective for detecting locomotor pathologies is because they stimulate high levels of spontaneous running activity in healthy animals, with nightly wheel-running travel distances exceeding those overground by approximately one order of magnitude (7). Thus wheel-running distances and speeds are a sensitive means of detecting diseases or injuries affecting the musculoskeletal system. Yet, only quantifying basic kinematic information, such as distance and speed, provides limited insight into the mechanism causing the locomotor deficit.

Numerous clinical and animal model studies have shown the benefit of combining gait kinematic and kinetic measurements to better identify underlying gait-related pathologies and musculoskeletal diseases (3, 8, 13, 22). Therefore, we sought to develop a force running-wheel (FRW) system. We modified a standard mouse running wheel to allow for the placement of a strain-gage instrumented rung capable of measuring the normal and tangential reaction forces applied by individual mouse limbs during voluntary locomotion. Force data were combined with high-speed infrared video images and wheel-angle data to create kinetic and kinematic records of force events collected during spontaneous wheel running throughout the night. Here, we report the calibration, sensitivity, and accuracy of this FRW system. We further tested the system by evaluating the locomotor kinematics and hindlimb forces during short-term habituation and chronic adaptation to wheel-running activity in male C57BL/6J mice.

METHODS

We modified a standard stainless-steel mouse running wheel (diameter = 11.5 cm, width = 5.2 cm; Mini Mitter, Bend, OR) to allow for the placement of a force-sensing rung (Fig. 1). This rung was held in place by two strain-sensitive brackets fixed to the main shaft of the FRW. Forces applied to the instrumented rung were measured in the normal and tangential directions through strain gages (EA-06-062AQ-350/E; Vishay, Wendell, NC) applied to both sides of thin spring blades composed of spring steel (Fig. 1). Blade thicknesses for normal and tangential blades were 0.60 mm and 0.85 mm, respectively. A counter-weight was added to the opposite end of the wheel to balance the added weight of the force-rung components (Fig. 1).

Fig. 1.

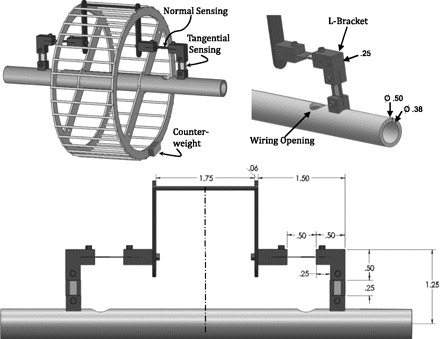
Diagram of the force running wheel (FRW). Foot-rung forces are measured on an isolated rung instrument via strain gages placed on orthogonally oriented spring blades in an L-bracket configuration for force sensing in normal and tangential directions. Strain-gage wiring is passed through an opening in the hollow shaft and connected to a slip ring at the end of the axle (not shown) to allow for strain-gage excitation and data collection. Values are in inches.

We applied strain gages to each spring blade in a chevron bridge configuration, which is similar to a one-half bridge configuration. Details of the chevron bridge configuration are provided in a technical note published by Michigan Scientific (Charlevoix, MI) (16). We completed the chevron bridge circuit on the rotating side of the FRW, which prevented slip-ring electrical noise from interfering significantly with the strain-signal voltage. The bridge output voltages (i.e., strain signals) were transferred from the rotating running wheel to the stationary data acquisition system by passing lead wires through the hollow FRW shaft (Fig. 1) and soldering the leads to a slip ring (low torque S10; Michigan Scientific). Strain-gage voltage changes were recorded from each spring blade through separate channels and used to calculate the force applied to the instrumented rung. The chevron bridge configuration can be susceptible to low amounts of cross talk between channels; however, no appreciable electrical cross talk was observed between strain channels in our measurements due to the high-input impedance of our bridge acquisition module. Strain gages were coated with M-coat D (F006690; Vishay Precision Group, Micro-Measurements Strain Gages and Instrumentation, Wendell, NC) to secure lead wires and protect against incidental moisture. We placed plastic enclosures (1551 TBU Series; Hammond Manufacturing, Cheektowaga, NY) around the spring blade configurations and fixed them to the FRW shaft to protect the strain gages and wiring from animals during testing. These protective fixtures did not affect the mechanical characteristics of the instrumented rung or strain-sensitive brackets. Angular position and speed of the FRW were measured using an optical encoder (HEDS 5640, 500PPR; Avago Technologies, San Jose, CA) fixed to end of the FRW shaft opposite from the slip ring.

We acquired strain output and encoder signals at 10 kHz using National Instruments (NI; Austin, TX) 9237 and NI 9411 modules, respectively, mounted in a NI c-DAQ-9172 chassis. Strain-gage bridge voltages were converted to strain units using the NI 9237 strain measurement module to facilitate comparisons with theoretical values obtained from a finite element model used to optimize the force-rung design, although this conversion step was not necessary for calibrating the force rung. The module was set to record strain values based on a full bridge type I configuration to avoid automatic bridge-completion resistances within the strain acquisition module. We processed and conditioned the strain-signal channels with a custom-written NI LabVIEW program (Version 10.0). We observed that rotating the wheel generated strain signals due to the effects of gravity, vibration, and electromagnetic interference. These sources of signal error were minimized, as discussed in Dynamic evaluation in results.

We collected video data from each event to observe kinematic characteristics, gait patterns, and foot placement. We used a high-speed (200 Hz) infrared camera (IPX-VGA210-LMCN; Imperx, Boca Raton, FL) to record images of running activity during the dark phase when mice are typically most active. The camera was positioned perpendicular to the wheel to acquire sagittal plane images. Ventral plane images were recorded simultaneously in the same field of view using a mirror positioned at a 45° angle beneath the clear acrylic cage bottom. We used an infrared light-emitting diode array (OL66-880; Spectrum Illumination, Montague, MI) mounted perpendicular to the angle of view as the infrared light source. Images were collected and processed using a NI PCI-1426 image acquisition board and NI Vision software in LabVIEW. A complete detailed kinematic analysis of the limb-movement patterns was not possible due to the forward location of the forelimb foot-strikes and a partially obscured field of view in the sagittal plane caused by the plastic strain-gage covering.

We developed a custom-written LabVIEW VI to continuously record and synchronize strain, wheel position, and video image data in a 2.5-s circular buffer to allow for automated data collection. Data were saved to an external hard drive only when strain values exceeded a pre-set strain threshold trigger. This trigger would initiate saving a 2.5-s interval of data, with the foot-strike at the midpoint of the data interval (i.e., 1.25 s pre- and postfoot-strike). This interval was sufficient to include at least two strides before and after the triggering foot-strike for most events. After trigger activation, the system would be reactivated following a delay of 3 s, which was required to allow the previous event to be saved. Although the 3-s delay likely prevented the collection of successful foot-strike events, it had a minimal impact on the time available for force collection. Less than 15% of the total time available during a 12-h running period would be unavailable for force collection if 2,000 force events were collected. To correct for strain-signal drift, strain signals were automatically zeroed to the appropriate angle-dependent strain values using our custom LabVIEW VI data acquisition program. After 30 s of inactivity, the strain output would be recorded and compared with the calibrated strain value for that particular wheel angle. The difference between the two values was considered to be strain-signal drift, and it was subtracted from the recorded strain signal. The 30-s timer was re-set each time the encoder registered a change in wheel angle. This automatic drift correction helped to maintain a consistent baseline strain level for effective use of the strain threshold trigger setting.

Animal experiments.

Male C57BL/6J mice (The Jackson Laboratory, Bar Harbor, ME) were tested on the FRW to validate the FRW and determine the viability of this system to accurately and precisely measure foot-rung forces in running animals. All experiments were conducted in accordance with protocols approved by the Oklahoma Medical Research Foundation's Animal Care and Use Committee. Mice were housed in a temperature-controlled room on 12-h light/dark cycles in the Oklahoma Medical Research Foundation vivarium with ad libitum access to food and water. We assessed the effect of short-term (less than or equal to four nights) and chronic (12 wk) wheel-running activity on locomotor kinematics and kinetics. Chronic wheel running involved unmodified versions of the same wheel used to construct the FRW (diameter = 11.5 cm; Mini Mitter). Mice (16 wk old; n = 5) were tested in the short-term habituation study by evaluating wheel-running performance over the first four nights of housing with the FRW. Minimal differences were observed within the first four nights; thus a single night of running in the FRW system was used to compare the effect of chronic wheel-running experience on locomotor kinematics and kinetics. Mice (25 wk old; n = 5) were housed overnight with the FRW system. These animals had no prior exposure to running wheels. In contrast, experienced running mice (37 wk old; n = 3) had been housed individually with a running wheel for 12 wk prior to testing in the FRW system. Daily running distances were recorded for the chronic running group prior to FRW testing using VitalView software (V4.2; Mini Mitter). During force testing, all animals were provided open access to the FRW from 5 PM until 9 AM the following morning. The light cycle in the testing room matched the standard housing conditions (6 AM–6 PM, light/dark).

Event selection.

On average, animals in the habituation study generated 2,358 ± 674 events (mean ± SD)/night of testing; however, not all events were suitable for further analysis due to nonlocomotor triggering events and inconsistent running speeds (e.g., animals stopping or starting on the wheel during a recorded event). Therefore, we implemented a semiautomated selection process based on speed consistency (SC), gait consistency, and hindlimb foot-strike quality to identify the top 25 events from each night. Only hindlimb strikes from each animal were considered for analysis in this study due to difficulty in observing forelimb foot-strike locations for all events.

We evaluated the SC for each force event using wheel-angular position data from the optical encoder. Events that displayed the most consistent wheel speeds throughout the 2.5-s force-event file were considered to be the most suitable for foot-rung force analysis. A SC score was quantified according to the following equation: SC = R²2^−X, where R² is the linear goodness of fit of the angular position vs. time for the entire force event, and X = ΔV/2V_ave. ΔV is defined as the difference between the maximum and minimum speeds throughout the event file, and V_ave is the average speed of the entire event. Thus both the overall wheel SC and the maximal relative speed change present in the force-event file contribute to the SC score. Both terms in the SC equation vary between zero and one; thus the product of these two terms can yield a maximum value of one (perfectly consistent speed) and a minimum value of zero (extremely inconsistent or no wheel rotation). We used a custom LabVIEW program to batch-process all of the force-event files and rank by SC score. Then, starting with the force event with the highest SC score, we analyzed the event for gait consistency and foot-strike quality. Specifically, we verified that the animal displayed a consistent walking or trotting gait pattern for at least two strides before and after the measured foot-strike. We also confirmed that the paw only contacted the instrumented rung. If the paw contacted multiple rungs or slipped during rung contact, which we observed occasionally, then the event was discarded. Events that displayed satisfactory gait and foot-strike quality were retained for further analysis, and the next event based on the SC score was evaluated. With the use of this approach, we selected 25 events from each night for calculating the individual hindlimb foot-rung forces. By beginning the selection process using an algorithm to calculate and rank the SC scores, we were able to identify 25 events within 20–40 min.

Statistics.

All statistical analyses were conducted using either JMP 8.02 (SAS Institute, Cary, NC) or Prism 5 (GraphPad Software, La Jolla, CA). Values are reported as means ± SD, SE, or 95% confidence intervals (CIs), as indicated in the figure and table legends. To test the effect of short-term exposure to the running wheel on locomotor kinematics and kinetics, values were compared across nights one through four with a repeated-measures ANOVA (Prism software). A post hoc linear trend analysis was conducted to assess trends across the first four nights of wheel running. The effect of a long-term wheel-running experience on locomotor kinematics and kinetics was tested using two-tailed t-tests (JMP software) with a Bonferroni-Holm step-down adjustment for multiple comparisons. Statistical significance was set at P < 0.05.

RESULTS

Static evaluation.

The force sensitivity of the FRW was determined by hanging calibration weights from the instrumented rung in the normal and tangential directions. Weights were varied by magnitude and position along the instrumented rung. Strain output was recorded and used to calculate the calibration constants relating strain values to load magnitude. The sum of the left and right tangential strain channels was linearly related to the applied load and was not affected by the position (Fig. 2A). The sum of the left and right normal channels was also linear; however, it was less sensitive than the tangential component, and it varied linearly with position (Fig. 2A). Thus to account for the position-dependent calibration constant required for normal force measurements, video images were used to identify the position of force application in the running mice (Fig. 2B).

Fig. 2.

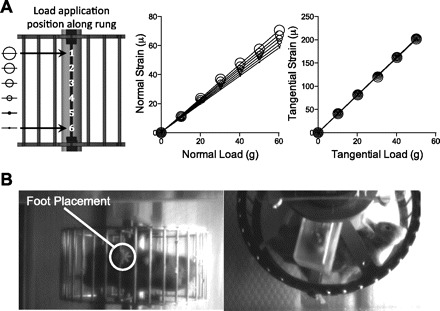
Effect of loading position and magnitude on the force-strain relationship for normal and tangential sensing gages. A: strain magnitude varied linearly (R² > 0.99) with the magnitude of the applied load in both normal and tangential directions for each position. The force-strain relationship for the normal, but not the tangential, gages showed slight position dependence. We accounted for this position dependence when calculating foot-rung reaction forces by identifying the position of force application using synchronized high-speed video. For the purposes of facilitating comparisons to mouse body-mass magnitudes, force calibration units are reported as grams force and can be converted to mN by multiplying by 9.81 m s⁻². B: the position of force application was identified using a ventral image from a high-speed (200 Hz) infrared camera. The ventral view was obtained from a camera positioned perpendicular to the wheel by placing a 45° angled mirror underneath the clear acrylic cage.

We measured normal and tangential force cross talk by applying force in one direction and measuring force readings in the other component. Normal force application caused minor (1.5%) cross talk in the tangential strain components. In contrast, tangential force application produced substantial (38%) cross talk in the normal strain components. The effect of this cross-talk error, however, was minimal in our data set. The small tangential strain magnitudes generated by the hindlimbs of running mice (peak values typically ≤5 g force or 15% body wt) resulted in a <5% error in the normal strain measurements of running mice. Normal and tangential cross-talk components were linear within the range of forces applied by the running animals.

Dynamic evaluation.

Wheel rotation produced periodic strain signals in the normal and tangential directions. We determined that the signals were primarily due to gravitational forces acting on the instrumented rung and not centripetal forces since the magnitude of the signals were primarily dependent on wheel angle and did not substantially change with increasing wheel rotational velocities within a physiologic range. The magnitudes of these gravity-induced signals, especially in the tangential component, were substantial compared with the foot-rung forces. Therefore, we sought to remove the signals by modeling them as sinusoidal waveforms. We calculated the gravitational signals as a function of wheel-angle position using a least-squared curve-fitting approach to compute the constants for the best-fit sinusoidal function based on the noncontact portions of the strain signal. Separate constants were calculated for the normal (Fig. 3A) and tangential (Fig. 3B) components. We then subtracted these best-fit sinusoidal waveforms from the respective strain component to correct for the effect of gravity for each event. We tested whether centripetal force also affected the rung forces by comparing baseline forces at different wheel velocities after gravitational force correction. Baseline forces were similar across a range of physiologic wheel velocities, indicating that centripetal force effects were negligible. Thus the corrected signals resulted in minimal normal and tangential force fluctuations during noncontact periods of wheel running (Fig. 3). Tangential force values were then multiplied by −1 as needed to correct for differences in running direction (i.e., clock-wise vs. counter clock-wise) to allow for a consistent comparison of braking- and propulsive-force patterns.

Fig. 3.

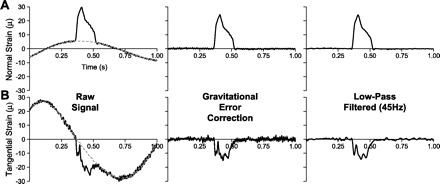
Gravitational error correction and signal conditioning for normal (A) and tangential (B) strain signals. Raw strain signals oscillate with wheel rotation due to the effect of gravity acting on the instrumented rung. This gravitational error was removed by modeling the error as a sinusoidal function of the wheel angle (gray, dashed line) and subtracting it from the raw signal. Additional noise from vibration and electromagnetic interference was removed by a 45-Hz low-pass filter. Tangential strain gages were more sensitive than normal strain gages as seen from Fig. 2A; therefore, tangential strain measurements correspond to lower force magnitudes compared with normal strain values.

Strain readings were also affected by vibration and electromagnetic interference. We determined the force-rung natural frequencies by sharply tapping the rung with a thin metal rod in the normal and tangential directions and analyzing the frequency response. The natural frequency in the normal and tangential directions was 190 Hz and 65 Hz, respectively (Fig. 4, A and B). Additional low-power 60 Hz noise from electromagnetic interference was observed in both strain signals at all times. A fast Fourier transform power spectral analysis of strain signals during wheel rotation with and without a foot-strike event showed that foot-strike frequency components were predominately <35 Hz (Fig. 4). Therefore, we applied a low-pass Butterworth filter at 45 Hz to remove vibration and electromagnetic sources of signal noise. This removed ≥98% of the wheel rotation noise power at frequencies >45 Hz in both the normal and tangential strain signals with minimal effect on the limb-force measurements (Fig. 3).

Fig. 4.

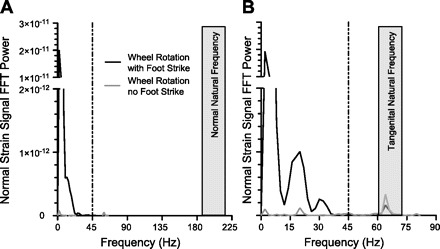
Power spectral density of a typical frequency response for the normal (A) and tangential (B) strain signals during wheel rotation with and without a foot-strike after gravitational signal error correction. The natural frequencies of vibration were >180 Hz and >60 Hz in the normal and tangential directions, respectively. Wheel rotation added strain signals with frequency components below the natural frequencies; however, nearly all signal power from the foot-strike occurred at frequencies <45 Hz for both normal and tangential directions. Therefore, strain signals were conditioned with a low-pass Butterworth filter at 45 Hz. FFT, Fast Fourier transform.

Animal trials.

Animals without any prior exposure to a running wheel habituated quickly to this new locomotor mode. During the first night of exposure to the FRW, the average running speed during each event was tracked in groupings of 10 events for the first 500 events (Fig. 5). These initial speeds were then compared with the overall average speed ± the 95% CI generated throughout the remainder of the night (i.e., >500 events). The results showed that by the 40th event (i.e., fourth grouping), animals were running at speeds within the 95% CI of the average nightly running speed (Fig. 5). Based on an average of 2,358 ± 674 events (mean ± SD) generated/night of testing, these data suggest that mice habituated to the running wheel within the first ∼2% of events collected during the first night. The time taken to generate these first 2% of the force events, however, varied significantly among the animals, suggesting that the habituation period is best approximated by actual running experience rather than access time to the wheel. Average nightly running speeds for the first four nights of wheel running were not significantly different (Table 1), further supporting the observation that wheel habituation occurs quickly within the first night.

Fig. 5.

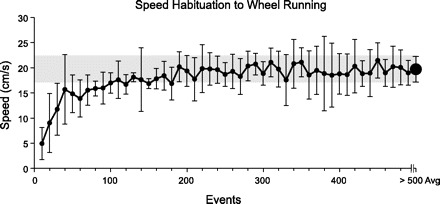
Changes in average wheel-running speed throughout the 1st night of exposure to the FRW. Mice quickly habituated to the FRW, as indicated by the rapid increase in running speed within the 1st 40 events collected during the night. Events were collected automatically when the mouse struck the instrumented force rung. By the 40th event, mice were running at speeds that were within the 95% confidence interval (CI) of speeds generated throughout the remainder of the night. Data represent the mean ± 95% CI of speeds for all mice in 10 sequential event groupings. The running speeds for events >500 were averaged for the final data point, with the gray box indicating the 95% CI. The average running speed shown here is slower than the average speed reported elsewhere, because the speeds associated with the kinetic data were taken from the 25 most consistent speed events, which tended to be faster than the overall average speeds.

Table 1.

Effect of habituation night on kinematic and kinetic variables

	Night				RM-ANOVA
Variable	1	2	3	4	P value
Speed (m/min)	17.4 ± 0.9	16.4 ± 0.6	18.8 ± 0.9	18.7 ± 1.0	0.12
Contact time (ms)	168 ± 1	190 ± 12	173 ± 10	171 ± 9	0.05
Duty factor	0.64 ± 0.01	0.65 ± 0.01	0.63 ± 0.01	0.64 ± 0.01	<0.01*
Peak FN (% BW)	93 ± 4	92 ± 5	95 ± 5	99 ± 5	0.08*
Peak FT,P (% BW)	8.9 ± 0.8	9.2 ± 1.2	7.7 ± 1.1	8.2 ± 1.2	0.68
Peak FT,B (% BW)	−10.2 ± 0.5	−11.4 ± 1.2	−11.0 ± 0.9	−12.6 ± 1.2	0.25

Mean ± SE. Normal force (F_N), tangential propulsive force (F_T,P), and tangential breaking force (F_T,B) are expressed as percentage of body weight (% BW). P values are reported for a repeated-measures ANOVA (RM-ANOVA) test. Significant linear trends across nights were evaluated by post hoc analysis as * P < 0.05.

An analysis of the kinetics of wheel running is generally consistent with there being minor changes over the first four nights of running. There was a statistically significant effect of habituation night on duty factor, measured as the ratio of foot-rung contact time divided by the time between sequential contacts of that foot (Table 1), although the range of average nightly values was small (0.63–0.65). There were significant minor trends for lower duty factors and higher peak normal forces with additional nights of running activity (Table 1). These trends did not correspond to any significant changes in foot-rung contact times or peak-braking or -propulsive tangential forces (Table 1 and Fig. 6C).

Fig. 6.

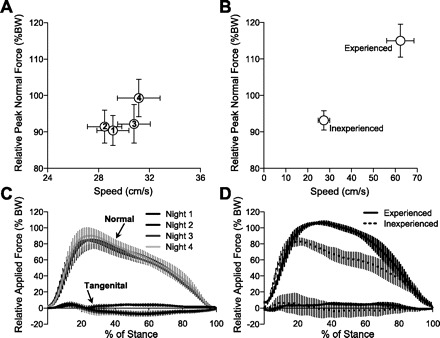
A comparison of foot-rung reaction forces generated by mice with acute vs. chronic exposure to wheel running. A: peak normal forces and running speeds remained similar throughout the 1st 4 consecutive nights of wheel running, indicating that habituation to wheel running occurs quickly within the 1st night. Numbers in circles correspond to the running night. B: 12 wk of wheel-running experience leads to a significant chronic adaptation to wheel running, as indicated by substantially faster running speeds and greater peak normal forces. Foot-rung reaction forces were at least 1 order of magnitude greater in the normal component compared with the tangential component for both acute (C) and chronic (D) running mice. Chronic exposure to wheel running shifted the timing of the peak normal force from ∼20% to 30% of the stance phase. Values are plotted as mean ± SD across animals for each group. % BW, Percent body weight.

The minor trends observed during short-term exposure to a running wheel—faster running speeds, lower duty factors, and higher peak normal forces (Table 1 and Fig. 6A)—were magnified when comparing inexperienced runners with animals with 12 wk of wheel-running experience (Fig. 6B). Experienced wheel runners, which averaged >8 km/day throughout the 12-wk period, ran twice as fast as inexperienced animals and generated significantly shorter contact times, lower duty factors, and higher peak normal forces (Table 2). The loading rate of the normal force component was not significantly higher in the experienced runners despite the higher peak forces, because the peak force occurred at a later percent of the stance phase compared with inexperienced runners (Table 2 and Fig. 6D). This shift contributed to a higher unloading rate in the experienced runners (Table 2 and Fig. 6D). The limb-excursion angle, estimated as the wheel-angular range during hindlimb-force production (Fig. 7), tended to be greater in the experienced runners (69.5 ± 1.8° vs. 55.7 ± 2.7°; mean ± SE), although this difference was not statistically significant following Bonferroni-Holm step-down adjustment for multiple comparisons. The wheel angle at peak normal force production was similar in inexperienced and experienced animals, especially compared with the differences in foot-strike and toe-off angles (Table 2 and Fig. 7).

Table 2.

Effect of wheel-running experience on kinematic and kinetic variables

	Prior Wheel-Running Experience
Variable	None	12 wk
Body Mass (g)	30.8 ± 0.7	29.7 ± 0.5
Speed (m/min)	16.5 ± 0.7	37.0 ± 2.2*
Heel-strike wheel angle (°)	81.9 ± 5.2	77.8 ± 0.6
Toe-off wheel angle (°)	137.6 ± 3.1	147.2 ± 1.3
Peak FN wheel angle (°)	97.2 ± 2.4	100.5 ± 0.2
Contact time (ms)	195 ± 11	108 ± 4*
Duty factor	0.71 ± 0.01	0.58 ± 0.01*
Peak FN (% BW)	93.2 ± 1.2	115.0 ± 2.6*
FN loading rate (g/ms)	0.72 ± 0.09	1.01 ± 0.07
FN unloading rate (g/ms)	−0.24 ± 0.02	−0.49 ± 0.04*
Peak FT,P (% BW)	14.3 ± 4.8	15.4 ± 0.6
Peak FT,B (% BW)	−12.2 ± 2.4	−8.0 ± 0.3

Mean ± SE. Wheel-angle values correspond to the coordinate system (see definition in Fig. 7). F_N, F_T,P, and F_T,B are expressed as a percentage of body weight.

^*P < 0.05 for a two-tailed Student's t-test following Bonferroni-Holm step-down adjustment for multiple comparisons.

Fig. 7.

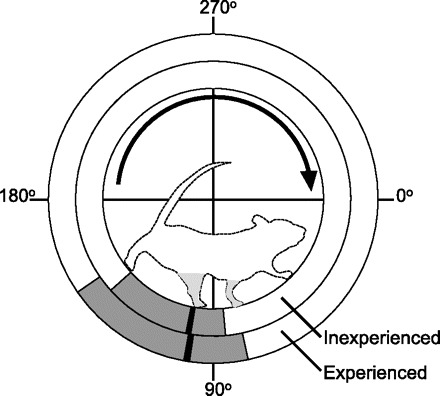
Angular ranges of hindlimb-force production for mice with and without prior wheel-running experience. The faster running speeds of experienced running mice were associated with greater hindlimb anglular excursions during rung contact compared with inexperienced mice, as indicated by the gray bars. Although the peak normal force occurred at a slightly later percent of stance phase in experienced mice, the peak normal force occurred at approximately the same absolute wheel position, as indicated by the black lines. Left limbs are shaded gray.

Significant differences were observed between peak normal and tangential forces. Peak normal forces ranged between 90% and 115% body wt, whereas the magnitude of peak-propulsive and -braking tangential forces ranged between 8% and 15% body wt (Tables 1 and 2). Unlike normal forces, peak tangential forces were not altered with increased running speeds. The pattern of tangential force production was variable, with inexperienced animals tending to produce a brief propulsive impulse during the period of limb loading, as indicated by increasing normal force (the initial ∼25% of the stance phase; Fig. 6C). The propulsive impulse was then followed by a braking impulse. This pattern was reversed in experienced running animals with a brief braking impulse followed by a propulsive impulse, although the high variability and low magnitude of force levels limit the strength of these observations (Fig. 6D).

DISCUSSION

We sought to develop a FRW system for quantifying kinetic and kinematic data from mice during spontaneous running. Such a system may provide a new, comprehensive, and high-throughput approach for noninvasively diagnosing gait pathologies in mouse models of musculoskeletal disease. An important consideration when using running wheels to identify and characterize gait pathologies is to understand how quickly animals habituate to wheel running and generate stable locomotor patterns. Our results indicate that healthy adult male C57BL/6J mice habituate quickly to wheel running, reaching running speeds within the 95% CI of the overall nightly average running speed after ∼40 events (Fig. 5). Given that animals with no prior wheel-running experience generated >2,000 events/night of testing, this corresponds to habituating after <2% of the total night events. Moreover, mice showed minimal changes in kinematic or kinetic variables during the first four nights of wheel running (Table 1 and Fig. 6, A and C). Thus as long as data analysis does not include the very first initial events, our results indicate that the locomotor phenotypes of control, healthy animals may be characterized with a single night of data collection on the FRW system.

Although there are fundamental differences between running on a self-propelled, movable surface vs. overground (20), the biomechanics of wheel running were similar to overground running in many respects. Notably, like overground running, faster wheel-running speeds are associated with lower duty factors and higher peak-reaction forces. Mice with 12 wk of wheel-running experience ran twice as fast as inexperienced mice and generated significantly greater peak normal forces (Table 2). To better understand how the changes in speed, duty factor, and peak normal forces during wheel running compared with overground running, we used a predictive equation first proposed by Alexander and colleagues (1) and more recently evaluated by Witte and co-workers [see Eq. 1 in ref. (21)] that relates peak vertical forces to changes in duty factor. This equation, which is based on the conservation of vertical momentum, predicts an inverse relationship between duty factor and peak vertical force. We used this equation to see if the greater peak normal forces generated by experienced runners could be predicted from the differences in duty factor. With the use of average values for body mass and duty factor from Table 2 and assuming a hindlimb body-mass support constant of 0.84, which was calculated empirically using data for the inexperienced animals, the equation predicts that the lower duty factors of experienced running animals would be associated with a peak normal force of 114% body wt. The accuracy of this prediction—the observed value was 115% body wt—suggests that the hindlimbs are constrained by similar conservation of momentum principles during wheel and overground running and that the hindlimbs support a substantial portion of body weight during wheel running (∼85%). These findings are consistent with the relatively high hindlimb normal forces for wheel running (90–115% body wt for the wheel vs. 50–60% body wt for overground) (6, 23).

Higher hindlimb forces and thus greater hindlimb body-weight support may be due to an inclined body position of mice during wheel running, which would align the gravitational force acting on the center of mass more toward the hindlimbs. The peak hindlimb normal force occurs between 20% and 30% of the stance phase (Fig. 6) and at a wheel angle just past vertical (Fig. 7). Although we have not thoroughly examined the forelimb forces, our preliminary data indicate that the forelimbs generate relatively lower normal forces and greater propulsive tangential forces compared with the hindlimbs. Moreover, the forelimbs also appear to generate approximately equal normal and propulsive tangential peak-force magnitudes. Such a force pattern would allow a propulsive tangential force, which is needed to overcome wheel friction, to also generate a vertically oriented force that would contribute to body-weight support. To conduct an accurate measurement of the forelimb normal forces, additional modifications to the FRW system would be needed to identify the location of the forelimb foot position along the rung.

The most substantial locomotor change that we observed following 12 wk of chronic wheel running was a faster average running speed. This faster speed decreased duty factors and increased peak normal forces. The faster running speed was also associated with an increased angular excursion of the hindlimb during wheel contact. Although we did not quantify limb-phase patterns, no obvious change occurred with the faster running speeds, and gait patterns appear to be best described as a “walking trot”, based on duty factor values >0.5 and diagonal couplet limb-movement patterns. Whereas the tangential forces were small in magnitude, both relative to body weight and relative to the normal forces, chronic wheel running appears to be associated with a shift from a propulsive-to-braking-force pattern to a more continuous propulsive-force pattern throughout the majority of the stance phase. This subtle shift may reflect a more highly adapted running pattern that minimizes negative work. Additional insight into the biomechanical responses to chronic wheel running may be obtained by modifying the frictional resistance of the wheel and thereby altering the mechanical power-output requirements.

The observed characteristics of wheel-running biomechanics in mice are likely dependent on a number of factors, including wheel size, surface, and rotational inertia and resistance. From a behavioral perspective, C57BL/6 mice spontaneously run farther distances on wheels with mesh surfaces compared with rods, and they prefer to run on larger diameter wheels with mesh surfaces when given a choice (4). In this study, the rod surface facilitated collecting individual limb forces, although the video records showed occasional foot-slipping or misplacement on the rung primarily in the inexperienced animals.

In summary, we have described and tested a novel force-instrumented mouse running wheel that is capable of recording hindlimb normal and tangential foot-rung forces during spontaneous locomotion. In healthy mice, the primary hindlimb foot-rung force occurs in the normal component and reaches a peak magnitude approximately equal to body weight. The high levels of spontaneous running-wheel activity, together with an automated method of data collection, provide a unique opportunity to comprehensively sample individual limb forces generated throughout an animal's entire period of nightly activity. Combining these data collection methods with a semiautomated data processing strategy provides a high-throughput and noninvasive approach for characterizing spontaneous mouse locomotor biomechanics. This system provides new insight into the biomechanical and behavioral responses of mice to exercise training. Moreover, we believe that our FRW system overcomes many of the limitations of current approaches used in basic animal pain research, which include brief animal evaluation periods, static rather than dynamic tests, low measurement sensitivity, and tests with low clinical relevance (18). Our findings reported here support further testing of this force-instrumented running-wheel system to provide a rapid, comprehensive database of kinematic and kinetic data to assess alterations in pain-related behavior associated with musculoskeletal injury or disease.

GRANTS

Support for this work was provided by the Oklahoma Medical Research Foundation, an Arthritis Foundation Arthritis Investigator Award, and the Oklahoma Center for the Advancement of Science and Technology.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: G.C.R., M.E., and T.M.G. conception and design of research; G.C.R. and M.E. performed experiments; G.C.R., M.E., and T.M.G. analyzed data; G.C.R. and T.M.G. interpreted results of experiments; G.C.R. and T.M.G. prepared figures; G.C.R. and T.M.G. drafted manuscript; G.C.R., M.E., and T.M.G. edited and revised manuscript; G.C.R., M.E., and T.M.G. approved final version of manuscript.