Abstract
Which is heavier: a pound of lead or a pound of feathers? This classic trick question belies a simple but surprising truth: when lifted, the pound of lead feels heavier—a phenomenon known as the size–weight illusion. To estimate the weight of an object, our CNS combines two imperfect sources of information: a prior expectation, based on the object's appearance, and direct sensory information from lifting it. Bayes' theorem (or Bayes' law) defines the statistically optimal way to combine multiple information sources for maximally accurate estimation. Here we asked whether the mechanisms for combining these information sources produce statistically optimal weight estimates for both perceptions and actions. We first studied the ability of subjects to hold one hand steady when the other removed an object from it, under conditions in which sensory information about the object's weight sometimes conflicted with prior expectations based on its size. Since the ability to steady the supporting hand depends on the generation of a motor command that accounts for lift timing and object weight, hand motion can be used to gauge biases in weight estimation by the motor system. We found that these motor system weight estimates reflected the integration of prior expectations with real-time proprioceptive information in a Bayesian, statistically optimal fashion that discounted unexpected sensory information. This produces a motor size–weight illusion that consistently biases weight estimates toward prior expectations. In contrast, when subjects compared the weights of two objects, their perceptions defied Bayes' law, exaggerating the value of unexpected sensory information. This produces a perceptual size–weight illusion that biases weight perceptions away from prior expectations. We term this effect “anti-Bayesian” because the bias is opposite that seen in Bayesian integration. Our findings suggest that two fundamentally different strategies for the integration of prior expectations with sensory information coexist in the nervous system for weight estimation.
INTRODUCTION
Early work on the classic (perceptual) size–weight illusion (SWI) suggested that this illusion arises from the difference between anticipated and required motor output for lifting two objects of the same mass but different sizes (Charpentier 1891; Müller and Schumann 1889). The argument has traditionally been that, because people expect larger objects to be heavier (Cross and Rotkin 1975; Flanagan and Beltzner 2000), more force is generated when lifting a larger object, resulting in the perception that it is easier to lift (Davis and Roberts 1976; Müller and Schumann 1889). However, the SWI exists in the absence of motor activation. When objects of different heights but identical mass and cross-sectional area are passively placed on subjects' hands, which are supported from below, the shorter object feels heavier (Usnadze 1931). Furthermore, when two objects that elicit the SWI are alternately lifted, the load forces and grip forces applied to the objects become accurate after just 4 to 7 lift pairs (Flanagan and Beltzner 2000; Grandy and Westwood 2006), although the SWI persists unmitigated for ≥20 pairs, indicating that mismatched motor output is not required for the illusion.
There is accumulating evidence that the size–weight illusion instead results from a discrepancy between prior expectations and sensory information about object weight. Similar weight perception illusions are seen when objects are expected to weigh different amounts for reasons other than size. For example, in the material–weight illusion (Ellis and Lederman 1999; Harshfield and DeHardt 1970), people perceive cubes that appear to be made of denser materials such as steel or brass to be lighter than equal-weight, equal-sized cubes that appear to be made of less-dense materials such as wood. Similarly, nongolfers find no difference between the perceived weight of real golf balls and practice balls modified to have the same mass. However, experienced golfers consistently perceive the modified, usually lighter, practice balls to be heavier than the real ones (Ellis and Lederman 1998). These results suggest that experience-dependent expectations about object weight, based on a variety of different object features, drive several weight perception illusions including the SWI (Ellis and Lederman 1998; Jones 1986; Koseleff 1957; Ross 1966). Furthermore, when prior expectations about the relationship between the size and weight of objects are experimentally altered by repeated lifting of unusual small–heavy and large–light objects for thousands of trials over several days, the size–weight illusion reverses (Flanagan et al. 2008). This suggests that, like the weight expectations that guide motor actions, perceptual expectations can also adapt. However, the rate of this adaptation is much slower, suggesting the maintenance of distinct weight expectations for action and perception.
In the context of the SWI, subjects can combine the expectation that the smaller of two objects will be lighter (Cross and Rotkin 1975; Flanagan and Beltzner 2000), with unbiased but imperfect proprioceptive sensory information about the actual weight of each object when forming weight perceptions. Filtering noisy sensory information through prior expectations can yield more accurate estimates than when this information is used alone. Bayes' theorem (or Bayes' law) can be used to determine optimally accurate estimates that minimize errors in judgment, given noisy sensory measurements and prior expectations, and recent studies have suggested that Bayes' law explains several key features of perceptions and motor actions, including certain perceptual illusions (Ernst and Banks 2002; Gregory 2006; Körding and Wolpert 2004; Körding et al. 2004; Norris and Kinoshita 2008; Sato et al. 2007; Stocker and Simoncelli 2006a; Weiss et al. 2002). Therefore Bayes' law may provide a framework for understanding illusory weight perceptions driven by prior expectations.
However, it has been noted that the perceptual biases characterizing the SWI cannot be explained by Bayes' law (Ernst 2009; Flanagan et al. 2006), suggesting that weight estimation, in general, may not be Bayesian. Although previous work has shown that prior expectations about object weight can be processed differently for perception and action (Flanagan and Beltzner 2000), it is unclear whether the mechanisms that govern how these prior expectations can influence the interpretation of sensory information are similar or different. In particular, the dorsal and ventral visual streams may process information separately for actions and perceptions (Goodale and Milner 1992; Milner and Goodale 1993). However, it is not known whether these pathways process visually based prior expectations in fundamentally different ways. Here we contrast the integration of prior expectations with sensory information for weight estimation in perception and involuntary motor action. We show why Bayesian estimation would produce weight and force estimation biases opposite to those seen in a variety of perceptual judgments, including the SWI and the attenuated perception of self-generated tactile sensations and force (Bays et al. 2005; Shergill et al. 2003; Weiskrantz et al. 1971), but consistent with motor output biases in a novel motor analog of the SWI.
METHODS
Participants
Forty healthy human subjects (14 male, 26 female; mean age: 21.4 yrs) with no known neurological deficits participated in this study. All participants gave informed consent and the experimental protocols were approved by the Harvard University Committee on Human Subjects Research (IRB F15817-101).
Tasks
Experiment 1: motor analog of the size–weight illusion.
In the first experimental task, subjects were presented with two cubes of 300-g mass but different sizes (26 and 52 mm). The cubes were covered with duct tape to make them look and feel like they might be made of the same material. Two square pieces (1 × 1 cm) of 120 grit sandpaper were glued to two opposite sides of the cubes, indicating the proper gripping locations and providing increased friction between the subject's fingers and the cubes. Subjects wore a right-handed glove, instrumented for data collection. On the palm side of the glove, we mounted two circular platforms made from acrylic (76.2 mm in diameter) with a 25-N load cell sandwiched between them. The load cell registered the placement and lifting of cubes on and off the acrylic platform. The platform ensured that the weight of both cubes was distributed over the same area to match the proprioceptive response from each one. On the back side of the glove, we mounted a six-axis position sensor and a three-axis accelerometer to measure the position and motion of the subject's hand in space with a resolution of 38 μm and 0.1°.
While seated in a chair, each subject placed his/her right elbow on the table and kept the palm of the gloved right hand horizontal and facing up. Each subject was then asked to grip a cube between the thumb and index finger of the left hand and quickly place it on the platform on the right palm, as shown in Fig. 2A. Subjects maintained a fixed posture with the cube on their palms for 1–2 s and then quickly lifted the cube off using the same thumb–index finger grip. Data were continuously recorded at a sampling frequency of 60 Hz. In experiment 1, 20 subjects performed 50 training lifts of the large cube followed by 8 “novel” lifts of the small cube, whereas the other 20 subjects performed 50 training lifts of the small cube, followed by 8 novel lifts of the large cube. After a 1- to 2-min break, subjects performed two additional blocks of lifting trials (training followed by novel lifts), in which the number of training lifts was reduced from 50 to 25, although the number of novel cube lifts remained at 8.
Fig. 2.
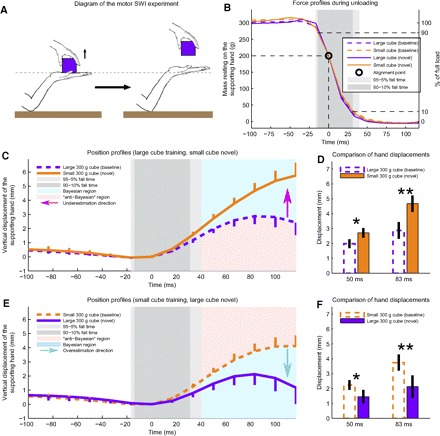
Motor analog of the SWI. A: diagram of the experiment. First, the subject maintains a fixed posture with his right hand while supporting a single cube on his palm. Then he reaches from the top and grabs the cube with his left hand, quickly lifting it up. Without an appropriate anticipatory postural adjustment (APA), the supporting hand would move far up after the lift. Even with a normal compensatory APA, the palm of the supporting hand moves up some amount after the cube has been lifted. An accurate estimate of the weight being unloaded helps reduce hand displacement. B: force profiles during unloading. The dashed lines are the average profiles during the last 10 of the 50 baseline lifts. Solid lines show the corresponding profile during the first novel cube lift. Purple lines are the profiles for the large 300-g cube; orange lines are the profiles for the small 300-g cube. All profiles are aligned to the point in time (zero) when the load is reduced to 200 g. The shaded gray regions represent the 10–90% and 5–95% of the fall time. C and E: position profiles of the supporting hand during the motor analog of the SWI experiment. Line styles and colors are consistent with B. Error bars represent SE across subjects. Bayesian (light blue) and anti-Bayesian (pink) regions are consistent with Fig. 1C. D and F: displacement at 2 instances: 50 and 83 ms after the lift onset.
Experiment 2: anticipatory postural adjustments generated during a controlled misestimation of weight.
In the second experimental task, subjects were presented with a stack of two identically sized, identical-looking cubes, built the same way as the large cubes in the first experiment. We constructed six blocks total, one each of 150, 225, 300, 300, 375, and 450 g mass, and stacked them together to make three stacks of 600 g mass (150 g/450 g, 225 g/375 g, 300 g/300 g) that were indistinguishable from each other.
Subjects placed the stack on the palm of their right hands while maintaining the same fixed arm posture as that in experiment 1 (they transported the cubes by holding only the bottom one so that the individual weights could not be easily determined). Subjects then performed a rapid lift of only the top cube from the stack, as shown in Fig. 4A. After each lifting trial, subjects returned the top cube to the stack on their palm and then picked up the stack by holding the bottom cube and returned it to the table. We then took the stack from them, placed it behind an opaque wall, and then placed another stack in front of them. We repeated these lifting trials 100 times (25 × 4 sets) with five different pair combinations: 150 g/450 g, 225 g/375 g, 300 g/300 g, 375 g/225 g, and 450 g/150 g; 76 lifts were with the “control” pair (300 g/300 g) and 24 “surprise” lifts, 6 with each of the other four pairs, randomly interspersed after the 15th trial. The first 15 trials of the first set were all done with the control pair and served as initial training.
Fig. 4.
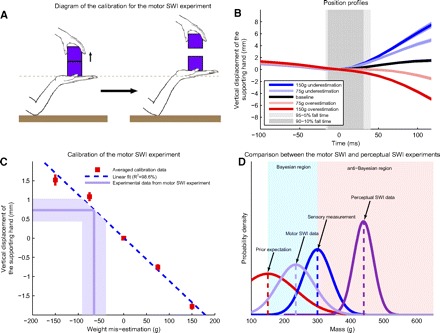
Motor calibration experiment. A: diagram of the experiment used to determine relationship between hand displacement and weight misestimation. The task is the same as before, except the subject places 2 cubes on his hand and then rapidly lifts the top cube of variable and unknown mass. The subject trains with a pair of cubes of equal mass and is then asked to perform the same task with identical looking cube pairs that may differ from one another in mass but average 300 g, the mass of the training cubes. If one underestimates the mass of the object he lifts, his supporting hand goes up, whereas overestimation causes the supporting hand to go down compared with baseline. B: position profiles of the supporting hand during the control experiment. The black curve is the profile generated by the training pair (300 g/300 g); the red curves are generated after lifting lighter weights: 225 g (light red) or 150 g (darker red); and the blue curves are generated after lifting heavier weights: 375 g (light blue) and 450 g (darker blue). C: calibration of the motor SWI. The red squares are experimental data from the calibration experiment at 50 ms, the blue line is a linear fit to these data, the horizontal light purple line indicates the displacement (0.7 mm) associated with weight underestimation for the small cube in the motor analog of the SWI shown in Fig. 2, C and D, and the vertical light purple line shows that the mass of the small cube is underestimated by 65 ± 26 g. The shaded light purple region indicates SE in the data. D: comparison of the classic SWI and motor SWI results to Bayesian integration. Just as in Fig. 1C, we show the sensory estimation, the prior expectations, the Bayesian and anti-Bayesian regions, and the perceptual SWI curve. The light purple Gaussian represents the distribution of weight estimates corresponding to the distribution of hand displacements shown in Fig. 2. Note that the light purple Gaussian represents the mean and SD (not SE) of the motor data, the dark purple Gaussian represents the mean and SD of the perceptual data (as in Fig. 1C). Also note that the widths of the red and blue curves as well as the mean of the red curve are hypothetical.
Experiment 3: replication of the classic size–weight illusion.
In the third experiment we replicated a version of the classic size–weight illusion with the same objects (cubes) as those in experiment 1. Prior to this experiment, subjects removed the data collection glove used in experiments 1 and 2. We used the small cube (26 mm) from experiment 1 and nine large cubes (52 mm), all covered in duct tape to look and feel as if they were made of the same material. The small cube had a mass of 300 g and masses of the large cube spanned the range of 200 to 600 g in increments of 50 g. We prepared three sequences of the large cubes, ordered by their weight: an increasing (I), a decreasing (D), and a pseudorandom (R). Each sequence contained all nine large cubes and no cube appeared twice. For every subject a random arrangement of these three sequences was chosen (e.g., whereas one subject might get I-D-R, another might get D-I-R, etc.) and this determined the order in which the large cubes would be presented. In 27 consecutive trials, subjects were presented with the small cube and a large cube from this arrangement. Subjects were asked whether the small cube felt heavier after lifting both of them off the table, one at a time. Subjects who performed experiment 1 with a small “novel” 300-g cube were asked to lift the large cube first and the small one second before they decided whether the small one felt heavier, whereas the other subjects (who used a large “novel” 300-g cube) were asked to lift the small one first and the large one second.
Data analyses
MOTOR DATA.
Using the data from the load cell, individual lifting trials from the data collected in experiments 1 and 2 were aligned to the time at which the load on the platform decreased by 100 g (about one third of the linear portion of the unloading force profile; see Fig. 2B). For experiment 1 we compared vertical motion of the right hand during the first novel cube lift to the average vertical motion during the previous 10 training cube lifts. We focused our analysis on the first novel cube lift for each subject to avoid the effects of motor adaptation. Significance was computed using paired t-tests. Results from the surprise lifts in experiment 2 were used to estimate the sensitivity of the relationship between weight misestimation and hand displacement using a simple linear regression as shown in Fig. 4C (see following text). We then used this sensitivity estimate to determine the weight estimation bias associated with the hand displacements obtained in experiment 1 for each subject. The mean across subjects of these weight estimates is plotted in Fig. 4D with its associated variance. The measurement-variance apropos to Bayesian estimation (the performance noise experienced by a particular subject) can generally be estimated by finding the within-subject, trial-to-trial variability and averaging this quantity across subjects. However, since we based our analysis (and the mean estimate of the weight bias in the motor task) on the first novel lift, the within-subject variability was not available. We did, however, have an estimate of each subject's trial-to-trial variability for the baseline lifts, which one could reasonably expect to be relatively similar to the novel cube lift trial-to-trial variability. In an attempt to further improve the accuracy of our estimate of the associated variance, we scaled it by the ratio of overall variance in the novel cube lift (across subjects) to the overall variance in a single cube baseline lift (across subjects). Note, however, that this scaling had only a modest effect since this ratio was 1.16. This estimate removes the effect of subject-to-subject variability, but still includes the effects of motor output noise and experimental measurement noise and thus probably slightly overestimates the average variance associated with weight estimation in our sample of subjects.
To estimate the sensitivity of the relationship between weight misestimation and hand displacement in experiment 2, we averaged the vertical hand profiles for each stack configuration—150 g/450 g, 225 g/375g, 300 g/300 g, 375 g/225 g, and 450 g/150 g after excluding the 15 training trials—and performed a simple linear regression.
PERCEPTUAL DATA FROM EXPERIMENT 3.
For each individual large cube, we calculated the probability that each subject would perceive it to be heavier than the small 300-g cube. We then averaged those probabilities across subjects and fit this psychometric data with the standard logistic function shown in Eq. 1 (R2 = 99.6%). The dark purple curve in Fig. 1C was obtained by differentiating this logistic function, fitting a Gaussian pdf to it (R2 = 94.6%) and dividing the associated variance by a factor of 2. Since the variance in these data comes from independent estimates of the weights of the small and the large cube on each trial, we attributed half of the total variance to the weight estimate for the small cube
| (1) |
Fig. 1.
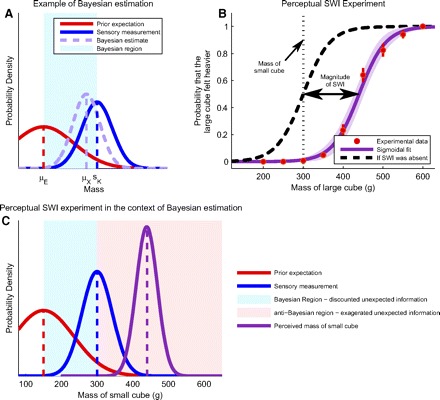
The size–weight illusion (SWI) and Bayesian estimation. A: example of optimal estimation for the weight of a small, heavy object. The red curve represents the likelihood of the prior expectation of weight from seeing the object (μE is the mean of this likelihood), the blue Gaussian represents the distribution of noisy sensory information from feeling it (centered around sK), and the light purple Gaussian is the posterior probability density function (pdf) for the weight, given the prior expectation and sensory information. The mean of this posterior pdf (μX) corresponds to the optimal (Bayesian) weight estimate. The shaded light blue region shows the range of values for which an estimate could be consistent with Bayes' law depending on the variances associated with prior expectations and sensory measurements. B: replication of the SWI. Red dots indicate the probability that a large cube of each mass is perceived to be heavier than a 300-g small cube. Error bars indicate SE. The dark purple sigmoid is a fit through the data. The black curve is a shift of the dark purple sigmoid to a point with no illusion. C: results from the SWI experiment presented as pdfs. The blue Gaussian curve represents the sensory estimates of the mass of the small object; the red Gaussian signifies a hypothetical prior expectation of this mass. The light blue area of the figure indicates the region in which the 2 sources of information would be integrated according to Bayes' law, given that the prior expectation is known to be <300 g. The pink area is the region where the integration would be anti-Bayesian. The dark purple Gaussian-like curve is the derivative of the dark purple sigmoid from B.
RESULTS AND DISCUSSION
A Bayesian perspective on the size–weight illusion
According to Bayes' law (Eq. 2), the likelihood associated with an object's true weight (TW) can be expressed as a normalized product of the prior expectation (based on visual and/or haptic information about the object) and proprioceptive sensory input when holding the object:
| (2) |
To help understand how Bayesian integration applies to the SWI, Bayes' law can be rewritten to explicitly include the effect of object size. We do this by parsing the overall “sensation” of the true weight referenced in Eq. 2 into two components: proprioceptive sensation (PS) of object weight, acquired from holding the object, and the visual sensation of object size (Size), acquired from viewing the object (Eq. 3)
| (3) |
For any given object size, Eq. 3 can be simplified by applying the definition of conditional probability and noting that raw proprioceptive sensation of weight should not depend on object size
| (4) |
In Eqs. 2–4, P(x) refers to the unconditional probability of an event x occurring, whereas P(x|A) signifies the conditional probability of an event x occurring given the occurrence of an event A. Similarly, P(x|A, B) refers to the probability of event x occurring given the simultaneous occurrence of both events A and B.
In the SWI, direct sensory input from proprioceptive force sensors in the arm is unbiased but noisy. We define sK to be the level of this sensory input on trial k and we presume 1) that the distribution of sK can be approximated by a Gaussian probability density function (pdf), N(μs, σs2); and 2) that the prior expectation of the object weight has a pdf that can be approximated by N(μE, σE2). For a small unexpectedly dense object, the distribution of effective sensory input should be centered around its true weight, whereas the distribution of expectations should be biased toward underestimating the true weight of the object (Cross and Rotkin 1975; Flanagan and Beltzner 2000), as shown in red in Fig. 1A.
Application of Bayes' law to a single lift gives the probability distribution for the true weight x, shown in Eq. 5. This distribution is the normalized product of N(μE, σE2) and N(sK, σE2) and will be Gaussian, N(μX, σX2). Note that the peak of this distribution (which in this Gaussian case is the same as its mean) is an optimal estimate, x̂, of the true weight. As shown in Eq. 6, x̂ is a weighted average of μE and sK; therefore based on Bayes' law, it must fall between μE and sK within the light blue colored Bayesian region in Fig. 1A. If independent Bayesian estimates of the true weight are gathered from different subjects, the mean of these estimates would be a weighted average of μE and μS, as shown in Eq. 7
| (5) |
| (6) |
| (7) |
Bayesian estimation viewed as a discount on unexpected information
If we define ε as the unexpected part of the sensory input averaged across samples—the difference between expected and actual sensations (Eq. 8)—it becomes apparent that the average Bayes-optimal weight estimate is simply the sum of the expected weight and a fraction of the unexpected sensory input, as shown in Eq. 9. Note that this fraction (K) is a gain on unexpected sensory input (ε), which must be between zero and one, indicating that Bayes-optimal estimates will always discount unexpected information. Note that this gain (K) is analogous to the gain of a Kalman filter. A gain greater than one would correspond to an exaggeration (rather than a discounting) of unexpected information and would thus reflect an “anti-Bayesian” estimate
| (8) |
| (9) |
Perceptual illusion
We designed experiments to quantify both perceptual and motor estimates of weight in the context of the same SWI, to understand whether the neural systems underlying these estimates integrate prior expectations and unexpected sensory information in similar (or different) ways. Although the perceptual effects of the SWI have been demonstrated in a wide variety of circumstances (Jones 1986; Koseleff 1957), we sought to evaluate the magnitude of perceptual and motor biases associated with the SWI using the same objects. We constructed a set of 14 large cubes (52-mm side) with masses between 200 and 600 g that we tested against a single small cube (26-mm side) with a 300-g mass. Subjects were presented with pairs of cubes (the small one and a randomly chosen large one) and were asked to lift the two cubes one at a time and indicate which felt heavier. The results from this experiment were used to generate the dark purple psychometric curve displayed in Fig. 1B. This curve shows the probability that the small 300-g cube felt lighter than each large cube. These data show that, on average, subjects perceived the small 300-g cube to feel as heavy as a large cube of 440 (47% overestimate) ± 13 g (95% confidence intervals). Differentiating this psychometric curve gives an estimate of the pdf of the perceived weight of the small cube, shown in Fig. 1C. Since the difference between the perceived weight and the expected weight is greater than the difference between the raw sensory information and the expected weight, the gain on unexpected information is greater than one. This means that the perceived weight of the small cube exaggerates the unexpected component of the sensed weight rather than discounting it, indicating that the SWI generates an anti-Bayesian weight estimate.
Interestingly, the SWI is not the only percept that appears to display anti-Bayesian processing of unexpected information. It is well known that predictable self-generated sensations are substantially attenuated compared with sensations arising from unpredictable external stimuli (Bays et al. 2005; Blakemore et al. 2000; Sperry 1950; Weiskrantz et al. 1971). For example, when tapping one finger against another, subjects perceive the taps as weaker than unpredictable externally generated taps of the same force magnitude (Bays et al. 2005). This same effect explains why one cannot tickle oneself (Blakemore et al. 2000; Weiskrantz et al. 1971) and leads to the escalation of force when subjects attempt to match blows with one another (Shergill et al. 2003). It is believed that an attenuation in the sensation of predictable, self-generated forces leads to an increase in the salience of sensations from external stimuli (Bays et al. 2005; Blakemore et al. 2000; Sperry 1950). However, this attenuated perception of self-generated, predictable sensations relative to externally generated, unpredictable sensations is fully equivalent to the exaggeration of unexpected sensation relative to expected sensation. When a fixed-magnitude external stimulus is applied to a stationary target, the raw sensory information generated by it is the same regardless of whether it is expected. This proprioceptive information is primarily from Golgi tendon organs and, as long as the targeted sensory area remains stationary (i.e., the lengths of its muscle fibers remain unchanged), there should be little muscle spindle afferent activity.
If this stimulus is self-generated, the expected sensation should be accurate, especially after repeated exposure. In contrast, if the same stimulus is completely unexpected (i.e., the expected sensation is zero) then the unexpected stimulus will be perceived to be stronger than the expected one, only if the unexpected sensation is exaggerated. As such, it also amounts to an anti-Bayesian estimation, analogous to that displayed in the SWI, because Bayesian estimation always discounts unexpected information by some amount. Therefore the observations about the perceptions of force, pressure, and weight based on proprioceptive and tactile sensory information represent anti-Bayesian integration of sensory information with prior expectations, which exaggerates unexpected sensory information in a variety of circumstances.
However, over the past decade several studies have shown that Bayesian-like processing can underlie both sensory percepts and motor actions when prior expectations are combined with sensory inputs and when different sensory inputs are combined with one another (Ernst and Banks 2002; Körding and Wolpert 2004; Körding et al. 2004; Stocker and Simoncelli 2006a; Weiss et al. 2002; Wolpert et al. 1995) and several perceptual illusions have been explained on the basis of Bayes' law (Gregory 2006; Sato et al. 2007; Stocker and Simoncelli 2006a; Weiss et al. 2002). For example, visual uncertainty biases the perception of speed in a manner consistent with Bayes' law. The prior expectation that most objects are stationary causes subjects to perceive moving objects in a low-visibility situation (characterized by highly uncertain sensory information) as slower than the same objects in a high-visibility situation (Weiss et al. 2002). Furthermore, it has been shown that both visual and haptic sensory data are combined in a statistically optimal fashion that modulates the influence of each in a Bayesian manner when perceiving the length of an object (Ernst and Banks 2002). In the motor system, Bayes' law explains how the magnitudes of responses to visual (Körding and Wolpert 2004) and force pulse (Körding et al. 2004) perturbations are influenced by prior expectations, suggesting that the motor system's estimates of distance and force are formed by Bayesian integration.
Motor illusion
Although the perception of weight and force is apparently anti-Bayesian, the motor system's estimate of force has been shown to be Bayesian on a task that does not involve the SWI (Körding et al. 2004). Therefore we sought to determine whether, in the context of this illusion, the motor system is also fooled by the SWI (anti-Bayesian), unbiased, or Bayesian when estimating weight. To do this, we designed an involuntary motor task sensitive to weight estimation. We studied the generation of anticipatory postural adjustments (APAs) based on the motor system's weight estimate. APAs, which are involuntary muscle actions preceding a voluntary movement, have been shown to assist in minimizing postural changes when subjects raise their arms (Bouisset and Zattara 1981), catch a falling object (Shiratori and Latash 2001), or pull on a fixed handle (Brown and Frank 1987; Cordo and Nashner 1982) by activating muscles not directly involved with the performed action. The magnitude of APAs has been shown to correlate with the size of the expected perturbation (Horak et al. 1989), indicating that they are sensitive to weight estimation (Diedrichsen et al. 2007; Horak et al. 1989; Wing et al. 1997). Furthermore, APAs cannot be voluntarily modulated or initiated (Diedrichsen et al. 2003; Dufossae et al. 1985; Lum et al. 1992), making them unlikely to be directly influenced by perceptual estimates.
A waiter in a restaurant relies on APAs to keep a tray full of drinks steady if he/she holds the tray with one hand while removing a glass with the other. When lifting a glass from the tray, the weight of the tray is reduced by the weight of the glass; consequently, the force used to support the tray must be instantly reduced by this weight if the tray is to be held steady, to prevent the remaining drinks from spilling. If the waiter fails to compensate for the weight change of the tray, it will shift upward. In fact, any mismatch between the required and actual supporting forces would cause a corresponding acceleration of the tray. If the waiter underestimates the weight of the glass he/she picks up—effectively overestimating the weight of the tray remaining in his/her hand—the supporting force the waiter produces after the lift will be greater than that required to support the tray and the tray will be pushed up. If the waiter overestimates the weight of the glass, the tray will move down.
We designed a motor analog of the size–weight illusion based on a version of this waiter task, diagrammed in Fig. 2A. We asked subjects to maintain a fixed arm posture, elbow placed on the table, while supporting the weight of an object placed on the palm of their right hand about 6 in. off the table. For this experiment we used two cubes of 300-g mass: a small one (26-mm side) and a large one (52-mm side). In one group, 20 subjects were first given the large 300-g cube and asked to lift it with their left hand and place it on the palm of their right hand. They were instructed to hold their right arms steady while rapidly lifting the cube using their left hands. After each lift, subjects placed the large cube back on the palm of their right hand. Each subject performed 50 rapid lifting trials (training lifts) of this large 300-g cube, while we recorded the vertical motion of their right hands associated with the left-hand lifts. Subsequently, subjects were given a small 300-g cube, which all subjects judged to be heavier, and were asked to repeat the same lifting task with it 8 times (novel lifts). The cubes were placed on the same circular platform, resting on the palm of the right hand, and were fitted with identical grip surfaces to match the proprioceptive information associated with each one.
Another group of 20 subjects performed the same task in reversed order: 50 training lifts with a small cube followed by 8 lifts of a novel large cube. The results from these experiments are shown in Fig. 2, C and E. Here the dashed traces show the vertical position profile of the supporting (right) hand during the last 10 of the 50 baseline cube lifts, whereas the solid traces show the corresponding position profiles during the first lift of each novel cube. Line colors indicate cube size. Both traces represent the mean across 20 subjects, with error bars indicating SE. We found a 35% increase in postlift displacement for the supporting hand when a novel small cube was lifted, as shown in Fig. 2, C and D (2.7 vs. 2.0 mm, P < 0.01, 50 ms after the lift onset; see Fig. 2D). In contrast, the first novel large cube lift showed a 32% decrease in postlift displacement for the supporting hand compared with baseline, as shown in Fig. 2, E and F (1.5 vs. 2.2 mm, P < 0.01, 50 ms after the lift onset; see Fig. 2F). The increased vertical displacement observed in the novel small cube lifts corresponds to an underestimation of its weight, whereas the decreased displacement observed in the novel large cube lifts corresponds to an overestimation of its weight. Both of these results are consistent with Bayes' law and inconsistent with the anti-Bayesian perceptual weight estimate seen in the classic SWI.
Anticipatory behavior of the motor system
Since we are interested in the anticipatory (feedforward) behavior of the motor system, we studied lifting profiles as close to the lift onset as possible, to avoid contamination of our findings by feedback-driven responses. However, we wanted to examine motion profiles after the load had been fully removed from the supporting hand. Therefore we instructed subjects to lift as rapidly as possible, to minimize the time between lift-force onset and liftoff for the cube. This resulted in the completion of >95% of all the lifts in our task by 50 ms after the lift-force onset (see Fig. 2B), and so we decided to analyze our data at the 50- and 83-ms time points. Because error correction in response to proprioceptive perturbations associated with arm movements typically lags velocity errors by ≥90 ms (Cordo 1990), hand position measured 50–83 ms after lift onset is likely to reflect anticipatory feedforward control of the supporting hand rather than feedback responses to hand displacements. Although electromyographic (EMG) signals from short-latency tendon-jerk reflexes can have latencies as short as 15–20 ms (Jones 1986; Marsden et al. 1976) for human biceps muscle, noticeable changes in position due to these EMG changes can be further delayed by 60–70 ms (Rothwell et al. 1980). However, these short-latency reflexes generally have very small magnitudes, unless high-acceleration perturbations are used, and these responses do not vary across task conditions (Marsden et al. 1976). In contrast, long-latency responses are larger in magnitude and can be modulated by task-specific variables (Rothwell et al. 1980). However, EMG latencies associated with these responses display latencies of 50–60 ms (Marsden et al. 1976; Rothwell et al. 1980), corresponding to position change latencies of ≥110 ms (Rothwell et al. 1980), making it highly unlikely for long-latency reflexes to affect our results 50 or 83 ms after the movement onset. Furthermore, if we repeat the same data analysis at 33 ms after force onset (before liftoff in most trials), we still see significant separation between the baseline and novel profiles in both subject groups (P < 0.05 at 33 ms in both cases).
Another possible explanation for the difference in profiles between the baseline and novel cube lifts might be the existence of increased arm stiffness associated with object novelty. Increased arm stiffness would reduce motor errors in the face of uncertainty about object weight in novel cube lifts. However, increased arm stiffness would predict reduced displacements compared with baseline in both types of novel cube lifts, whereas our data show decreased displacement for the large novel cube but increased displacement for the small novel cube, consistent with a discounting of unexpected sensory information when the motor action is planned. Moreover, these opposite displacements are nearly symmetric (0.7 mm in both cases), suggesting that the effects of any stiffness changes are much smaller than the effects associated with changes in anticipatory motor output that reflect the discounting of unexpected sensory information.
Note that in the former data analysis, we used only the first lifting trial of the novel object to avoid any effects of motor adaptation. In fact, subjects performed 8 consecutive lifting trials with each novel object after the initial 50-trial training period with the familiar object. Following this 8-trial block, subjects were administered two 25-trial retraining periods with the familiar object, each followed by an additional 8-trial novel cube lifting block. We show that the motor adaptation over the course of the first 8 novel cube lifts can be approximated by a decaying exponential having a time constant of 2 trials [r = 0.65, F(2,13) = 4.65, P < 0.03; Fig. 3, A and C] or a line with a slope of −0.056 mm/trial [r = 0.55, F(1,14) = 5.99, P < 0.03]. Furthermore, when we compare the first novel lifts from each of the 3 consecutive lifting blocks (those lifts are separated by 25 lifting trials with the baseline object and 7 trials with the novel object) as shown in Fig. 3, B and D, we see that the novelty effect is reduced to practically 0 by the end of the experiment at a rate of −0.35 mm/block [r = 0.92, F(1,4) = 21.7, P < 0.01]. These results indicate rapid adaptation of the motor system's prior expectation about object weight both within and across blocks, despite the persistence of a perceptual bias caused by the size–weight illusion, consistent with previous work (Flanagan and Beltzner 2000; Grandy and Westwood 2006).
Fig. 3.
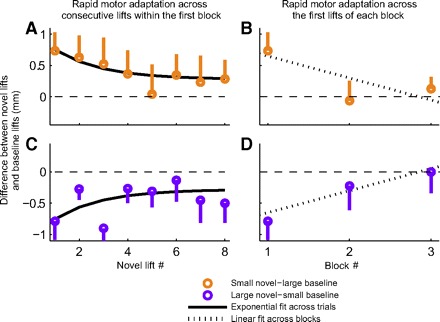
Rapid adaptation in the motor analog of the SWI. Whereas the data in Fig. 2 show the biases in motor output displayed in the very first novel cube lift, here we show how these biases change within a block of 8 repeated lifts of the novel cube and across 3 such blocks of novel cube lifts. Differences in position profiles of the supporting hand between the novel and baseline lifts 50 ms after the lift onset are shown. Each point represents an average difference across subjects and error bars represent SE. For each subject we computed the difference between a particular “novel” lift and the mean of the last 10 baseline trials. The orange points (A and B) are the differences between small cube novel and large cube baseline lifts and the purple points (C and D) are the differences between large cube novel and small cube baseline lifts. A and C: the data for the 8 novel cube lifts in the first block. The fit is a decaying exponential with a time constant of just 2 trials [r = 0.65, F(2,13) = 4.65, P < 0.03]. These data could also be fitted by a line with a slope of −0.056 mm/trial [r = 0.55, F(1,14) = 5.99, P < 0.03]. B and D: the first novel cube lift in each of the 3 blocks. The data show a decay at a rate of −0.35 mm/block [r = 0.92, F(1,4) = 21.7, P < 0.01].
Quantifying weight estimates in the motor illusion
To assess the amount of weight estimation bias in the motor system responsible for the changes in hand displacement we observed, we designed a control experiment in which we asked each subject to place a stack of two identically sized, identical-looking cubes on the palm of his/her right hand while maintaining the same fixed arm posture as that in the previous experiment (subjects transported the cubes by holding only the bottom one so that the individual weights could not be easily determined). Subjects then performed a rapid lift of only the top cube from the stack, as shown in Fig. 4A. We repeated these trials 100 times with five pairs of identical-looking objects, all with a total mass of 600 g: 150–450, 225–375, 300–300, 375–225, and 450–150; 76 of 100 lifts were with the “control” pair (300–300) and 24 “surprise” lifts were randomly interspersed, 6 with each of the other pairs. We used the results from these surprise lifts to determine the relationship between the amount of weight estimation bias and postlift displacement of the right hand. We found a simple linear relationship between the amount of weight misestimation and the postlift displacement of the right hand (R2 = 98.6%, P < 0.001) at 50 ms postlift, which we used as a calibration function. This calibration reveals that the 0.7-mm increase in displacement we found in the motor analog of the SWI experiments at 50 ms postlift corresponds to a 65-g (22%) underestimation, as shown in Fig. 4C, indicating that the motor system estimates the small cube mass to be 235 rather than 300 g on the first novel-object lift.
Bayesian versus anti-Bayesian integration
If the APAs in our task were scaled solely based on the prior expectation of the weight of the small cube, we should see an APA corresponding to an 87.5% underestimate, since the volume of the small cube is one eighth that of the large one. Alternatively, if these APAs were based on proprioceptive sensory input alone, there should be no difference in the lifting profiles for the two cubes. The 22% underestimation we see for the small cube is consistent with a gain on unexpected information of 0.75 as defined in Eq. 9, corresponding to a 25% discount on unexpected sensory information. Although our results suggest that the gain on unexpected information is <1.0, consistent with Bayesian estimation, we lack the data necessary to show that this gain corresponds to the ratio of variances shown in Eq. 9 because the certainty of the prior is difficult to estimate. Thus we demonstrate opposite biases for the motor and perceptual weight estimates and show that perceptual biases are oppositely directed from the biases that would be generated by Bayesian integration. However, although the direction of the motor illusion is consistent with Bayesian integration, we cannot assess whether its magnitude matches that predicted by Bayes' law. Overall, our findings indicate that whereas the perceptual system estimates the small cube to be 47% heavier than a comparable large cube, the motor system estimates this small cube to be 22% lighter, as shown in Fig. 4D.
These results suggest that the motor system combines prior expectation and real-time sensory information to generate a Bayesian-like weight estimate, discounting the value of unexpected sensory information, whereas the perceptual system combines these information sources in an anti-Bayesian manner, exaggerating the value of unexpected sensory information. This gives rise to oppositely biased weight estimates for perception and action. We believe that this is the first demonstration of opposite illusions (i.e., opposite biases) for perception and action in the context of the same task. These results suggest that the nervous system uses two entirely different mechanisms to integrate prior expectations with current sensory information about object weight.
Different priors for action and perception
Previous studies of lifting dynamics during the SWI have suggested that the motor system and the perceptual system may form prior expectations independently (Flanagan and Beltzner 2000; Grandy and Westwood 2006). Because these studies focused on forces applied to objects suddenly lifted from a table top, direct sensory information was not available during the planning of these lifts and thus could not be integrated with prior expectations. Therefore the initial pattern of grip force applied when a person lifts an object from a table top reflects the motor system's expectation of that object's weight, rather than the integration of sensory information about object weight (Flanagan et al. 2003). Studies of initial grip force show that the motor system adapts this expectation about object weight in just three to five trials in the context of the SWI (Flanagan and Beltzner 2000; Grandy and Westwood 2006), whereas the perceptual system requires hundreds or thousands of trials to adapt its expectations (Flanagan et al. 2008). The striking difference between adaptation rates for these expectations suggests that the neural bases for the weight expectations levied by the motor system and the perceptual system are indeed separate. Thus these studies provide clear evidence for the maintenance of separate expectations of object weight for perception and action; however, they do not provide an opportunity to assess how prior expectations are combined with direct sensory information when both are available. In the current work, we studied how the nervous system processes the integration of prior expectations and sensory information for action and perception and found oppositely biased weight estimates for perception and action, reflecting divergent mechanisms for the processing of unexpected information.
Perception versus action in the CNS
The idea that the nervous system may process sensory information differently for perceptual and motor tasks is not new. For example, visual information is processed in two pathways: the dorsal and ventral streams (Mishkin and Ungerleider 1982; Ungerleider and Mishkin 1982). It has been hypothesized that the dorsal stream primarily carries spatial information for action and the ventral stream primarily carries information about object identity for perception (Goodale and Milner 1992; Milner and Goodale 1993). However, although there is clear physiologic evidence for separate streams in the neural processing of visual information, the evidence that a particular visual quality, such as the size of an object, is processed differently for perception and action is still highly controversial. (de Grave et al. 2005; Franz 2001; Smeets and Brenner 2006). Much of this controversy stems from a series of studies (Aglioti et al. 1995; Haffenden et al. 2001) that contend that the effects of visual illusions on the perception of object size do not carry over to motor actions. However, the data from these studies and several others (de Grave et al. 2005; Franz 2001) show that motor actions can also be substantially affected by perceptual illusions, often to similar extents, leading several authors (de Grave et al. 2005; Franz 2001; Smeets and Brenner 2006) to suggest that these visual illusions have similar effects on perception and action. In addition, several aspects of the methodology used in these studies have been called into question, in particular the specificity of the measures used to assess the effect of the illusion on perception and action (Franz 2001; Smeets and Brenner 2006). For example, grip aperture has been widely used to assess the effects of visual size illusions on action (Aglioti et al. 1995; Franz 2001; Haffenden et al. 2001). However, it has been shown that grip aperture is planned based on the position of each grasp point rather that the distance between them (Brenner and Smeets 1996; Jackson and Shaw 2000; Smeets and Brenner 2008, 1999). Because visual size illusions generally have little effect on the perceived position of individual points within the illusory figure, the finding that grip aperture is somewhat resistant to a size illusion may reflect a dichotomy between the processing of visual information for size and position, rather than between perception and action (Brenner and Smeets 1996; Jackson and Shaw 2000; Smeets and Brenner 2008).
Information streams for action
Anticipatory postural adjustments, which are believed to be resistant to voluntary modulation (Diedrichsen et al. 2003; Dufossae et al. 1985; Lum et al. 1992), are modulated by the primary motor cortex (M1) (Chouinard et al. 2005; Gahery and Nieoullon 1978; Massion 1992), the cerebellum (Diedrichsen et al. 2005; Massion 1992; Rabe et al. 2009; Rispal-Padel et al. 1982), the supplementary motor area (SMA) (Massion 1992; Sakreida et al. 2005), and the dorsal premotor area (PMd) (Byblow et al. 2007; Chouinard et al. 2005; Massion 1992; Sakreida et al. 2005). Transcranial magnetic stimulation (TMS) of M1 disrupts the trial-to-trial adaptation of APAs, whereas the same stimulation applied over PMd disrupts the ability to use visual cues to form prior expectations about object weight (Chouinard et al. 2005). Interestingly, TMS stimulation over PMd has been shown to enhance the ability of motion of one limb to facilitate activation of another limb, which is required for APA formation, whereas ventral premotor area (PMv) stimulation does not (Byblow et al. 2007). Patients with cerebellar damage can produce appropriate APAs in common tasks (Diedrichsen et al. 2005; Massion 1992); however, degeneration of the cerebellum, which is strongly connected to structures in the dorsal visual stream, interferes with the formation of novel APAs and the adaptation of preexisting ones (Diedrichsen et al. 2005; Horak and Diener 1994) but not the adaptation of grip forces (Rabe et al. 2009).
These findings suggest a dissociation between the control of APAs and grasping. Two areas of premotor cortex, PMd and PMv, which receive largely distinct inputs, may mediate this dissociation. The motor commands associated with APAs may be primarily driven by sensory input from the dorsal stream, whereas sensory input from the ventral visual stream may be most important for the control of grasping. Correspondingly, the inputs to PMd are from structures generally associated with the dorsal stream of visual processing (Hoshi and Tanji 2007; Kaas 2004; Rizzolatti and Luppino 2001), whereas PMv is substantially connected to ventral stream structures (Lu et al. 1994; Rizzolatti and Luppino 2001; Webster et al. 1994). In general, PMv is believed to exert more control over distal movements, such as the shaping of fingers during precision grip (Davare et al. 2006; Fogassi et al. 2001; Hoshi and Tanji 2007), whereas PMd is closely associated with movement of more proximal joints including the shoulder and the elbow (Cisek et al. 2003; Davare et al. 2006; Hoshi and Tanji 2006), which are generally associated with APAs. Correspondingly, PMv and PMd activities are specifically activated by biological motion associated with proximal and distal joints, respectively (Sakreida et al. 2005). This is in line with previous ideas about the control of the fingers during grasping (Hoshi and Tanji 2007; Rizzolatti and Luppino 2001), including studies that have shown that PMd-sparing inactivation of PMv knocks out grasping movements while leaving reaching movements intact (Davare et al. 2006; Fogassi et al. 2001).
These findings are compatible with the idea that PMd is more involved with complex sensorimotor integration like that involved in the formation of APAs, whereas PMv supports the coding of actions in a way that is more directly based on sensory information about object properties (Hoshi and Tanji 2007; Rizzolatti and Luppino 2001), such as the control of grasp aperture. The idea that ventral stream information feeds PMv, which controls grasp, may explain why previous work focused on grasp aperture has generally found somewhat incomplete dissociations between perception and action (Aglioti et al. 1995; Haffenden et al. 2001), and were often difficult to reproduce (de Grave et al. 2005; Franz 2001), whereas the current study, which focused on the control of arm posture, demonstrates diametrically opposed illusions for perception and action.
A recent imaging study (Chouinard et al. 2009) supports the idea of a close relationship between the control of grasping actions by PMv and the illusory perception of weight. The authors found no changes in neural activity in PMd, M1, or cerebellum that correlated with the illusory perception of weight while gripping and lifting an object. Instead, the only illusion-related activity observed was registered in an area of PMv, which displayed density-related, but not size-related, activity. Combined with the idea that PMv activity controls grasping behavior when reaching for objects (Hoshi and Tanji 2007; Rizzolatti and Luppino 2001), whereas PMd activity correlates with the mismatch between expected and actual grip forces (Schmitz et al. 2005), these findings suggest both a close connection between the control of grasp and the (illusory) perception of weight and also a dissociation between the production of force and the perception of weight.
Rapid adaptation of the motor system can obscure illusory effects
A key issue for the identification for motor illusions is the effect of motor adaptation. If feedback about motor performance is available, errors that occur on one trial can be used to correct future actions. Because the error-dependent adaptation of motor expectations can be exceedingly rapid, motor output can go from clearly biased to nearly unbiased in just 3–5 trials (Chang et al. 2008; Flanagan and Beltzner 2000; Grandy and Westwood 2006). Therefore studies that average the results of many (5–18) trials (Aglioti et al. 1995; Chang et al. 2008; Haffenden et al. 2001) may fail to detect motor illusions, even if they are initially present. For this reason we focused on the first instance in which subjects interacted with a novel cube (irrespective of whether it was the small or large one) to minimize the possible effects of motor adaptation. This allowed us to show that the initial weight estimate of the motor system is not only immune to the perceptual illusion, but is instead biased in the opposite direction to the perceptual estimate. Examination of the data from subsequent lifts in our study reveals that errors associated with the motor illusion we demonstrate are rapidly attenuated over the course of just 2–4 trials (see Fig. 3), consistent with previous work on motor adaptation (Krakauer 2009; Krakauer et al. 2000; Scheidt et al. 2000, 2001; Smith et al. 2006; Thoroughman and Shadmehr 2000).
In a recent study, the grip force and load force profiles associated with using one hand to lift objects from the other showed that the lifting hand produced more appropriate motor output when lifting an object from the other hand than that from a table top (Chang et al. 2008), indicating that sensory information from one hand can be used to modulate the actions of the other. In both the table-top and bimanual conditions, rapid motor adaptation led to the application of appropriate lift and grip forces after just a few trials. However, examination of the force profiles from the initial trial on which an object was lifted from the other hand reveals two interesting features. First, the required grip force is overestimated for both objects compared with subsequent trials, although the load force is not; and second, both lift and grip forces were generally greater for the large object than for the small one. Although the first of these effects was not specifically analyzed and the second was not statistically significant (P > 0.1 for all relevant statistical tests), the first suggests that grip force but not load force is substantially modulated not only by the expected weight of an object but also by the uncertainty about this weight and the second would be predicted by Bayesian integration, consistent with our current findings.
Opposite illusions versus opposite behavior
A few previous studies have documented oppositely directed perceptions and actions that do not arise from opposite illusions, but rather from the experimental conditions chosen for comparison (Ganel et al. 2008; Grandy and Westwood 2006). In one such study (Grandy and Westwood 2006), grip forces associated with alternate rapid lifting of a small, lighter object (2.7 N) and a large, heavier one (3.2 N) from a table were measured. After several trials, motor adaptation led to the application of appropriate grip forces for both objects, although the SWI persisted—consistent with previous results (Flanagan and Beltzner 2000). Because the large object was chosen by the experimenter to be heavier than the small object and the SWI was sufficiently powerful to overcome the weight difference between them, the larger object was perceived as lighter (i.e., illusory underestimation), whereas grip forces associated with it were appropriately greater (i.e., accurate estimation). This resulted in oppositely directed perceptions and actions without the presence of opposite illusions; i.e., the motor system's behavior was accurate, whereas the perceptual estimate was biased by the SWI. In contrast, our findings show illusions that oppose one another and generate opposite biases in the motor and perceptual systems. The current illusions depend on the integration of prior expectations with sensory information, unlike the grip force patterns previously studied that reflect only prior expectations about object weight (Flanagan and Beltzner 2000; Flanagan et al. 2001), rather than the integration of sensory information with these expectations.
Contrast enhancement and efficient coding
Because the integration of prior expectation and raw sensory information by the perceptual system exaggerates unexpected sensory information (rather than discounting it) in the SWI, it cannot be optimal (i.e., minimize the variance) for producing accurate weight estimates in the presence of sensory noise. However, the exaggeration of unexpected sensory information in this anti-Bayesian weight estimation can be viewed as a type of contrast enhancement, an information-processing mechanism that is pervasive throughout early sensorineural processing of auditory, somatosensory, and visual information (Barlow 2001). Contrast enhancement can be especially useful for the detection of object features to aid in classification. For example, in the visual system, contrast enhancement can improve the ability to detect the edges of objects and thus identify their shapes at the cost of reduced ability to identify raw luminance levels or to accurately compare luminance in two different regions of the same visual scene (Albers 1975). A light object placed on a dark background appears lighter than it is. If we apply a simplistic Bayesian framework to this example, where the background color represents the prior expectation and the light object is the raw sensory information, we see that contrast enhancement produces a posterior in which the difference between the prior and the sensory information is exaggerated, thus forming an anti-Bayesian estimate.
Another apparently anti-Bayesian phenomenon that has been extensively studied is the tilt aftereffect (Campbell and Maffei 1971; Gibson 1937). After staring at a vertical grating for a period of time (30 s to a few minutes), a grating with similar orientation appears to be tilted further away from vertical than it is. Looking at this phenomenon from a Bayesian perspective, we would expect that prolonged exposure to a vertical grating will help form a prior expectation that the grating is most likely to be vertical (at 90°). Subsequent presentation of a rotated grating (e.g., 80°) would be combined with this prior expectation and we would expect the net estimate of the tilt to be between 80 and 90°, consistent with a discount on unexpected information. Note that the tilt aftereffect instead shows a repulsive, contrast-enhancing bias such that the perceived angle in this case is close to 75° (Campbell and Maffei 1971). This corresponds to an exaggeration of unexpected sensory information and an anti-Bayesian estimate.
It has been suggested that the repulsive bias seen in the tilt aftereffect might be compatible with Bayesian estimation if the adaptation was interpreted to affect the likelihood function rather than the prior (Simoncelli 2009; Stocker and Simoncelli 2006b). However, this explanation is somewhat difficult to defend because prior expectations must be derived from previous experience (Ellis and Lederman 1998; Flanagan et al. 2008; Körding and Wolpert 2004). Additionally, the tilt illusion, which has essentially the same sensory consequences as those of the tilt aftereffect (Campbell and Maffei 1971; Gibson 1937; Wainwright 1999), is believed to arise from the same mechanisms (Schwartz et al. 2007) but cannot reasonably be explained by an adapted likelihood function because no adaptation occurs. Furthermore, the classic SWI in which two equal-mass but different-sized objects are compared cannot be explained by differences in adapted likelihood functions because 1) the SWI is present on the first lift, before adaptation could occur; and 2) these likelihood functions would apply to raw sensory information about weight, which is the same for both objects.
Repulsive, contrast-enhancing biases are thought to be compatible with the efficient coding hypothesis. This hypothesis suggests that neural representations of information maximize the efficiency of information transmission. A key mechanism for accomplishing this is the reduction of redundancy in information transmission (Barlow 1990). Consequently, efficient coding schemes remove correlations between transmitted perceptual variables because correlations between these variables would lead to redundant information transmission with suboptimal efficiency (Barlow 2001; Wainwright 1999). In these schemes, correlations between variables are generally removed by increasing mutual inhibition (Barlow 1990). Because prior expectations generally represent correlations between variables (e.g., the expectation driving the SWI is that object size and weight are positively correlated) and Bayesian integration biases sensory estimates toward these expectations, inhibitory decorrelation—which increases the independence between variables—produces biases that are opposite to Bayesian integration biases.
On the face of it, it would seem that optimal estimation (via Bayesian integration) and efficient coding for optimal transmission of information should produce similar, if not the same, effects. However, as discussed earlier, the biases produced are generally opposite of one another. How can this be? The answer is that these information-processing schemes are optimal for different things. In particular, efficient coding schemes dictate how sensory signals should be encoded to maximize the information carried during transmission (Wainwright 1999). This produces an adaptive encoding that must be decoded after transmission for the original sensory signals to be recovered without distortion. However, these efficient coding schemes do not specify how the original sensory signal should be decoded. The theories of efficient coding generally attempt to explain perceptual biases as a result of a “coding catastrophe” (Schwartz et al. 2007)—i.e., downstream decoding mechanisms do not provide any compensation for upstream adaptive encoding. Thus according to this theory, the encoding is adaptive but the decoding is not, resulting in a mismatch between the two that accounts for perceptual biases. This mismatch occurs because efficient coding schemes are not concerned with how information from these sensory signals should be used after transmission. On the other hand, optimal estimation is concerned only with how sensory signals are decoded; here the computational goal is to provide decoded estimates, based on sensory information, that are maximally accurate.
This suggests that although certain perceptions might not be optimally accurate (consistent with Bayesian integration), they might reflect optimal information encoding, transmission, or storage. Alternatively, contrast enhancement in the perception of weight may help to identify or classify objects that are lighter or heavier than expected so that appropriate behavioral strategies might be triggered, such as altering the posture used to grasp an object. In fact, even though our motor actions generally benefit from maximally accurate estimates, the cognitive decisions informed by our perceptions may be better served by the ability to determine and remember when objects are different from expected even at the expense of accurate estimation. Further study is required to determine whether the perceptual biases observed in the classical SWI reflect efficient coding or task-dependent contrast enhancement or an entirely different mechanism for sensory integration.
Although we may not fully understand why anti-Bayesian perceptual estimates occur, it is clear that these estimates are oppositely biased from Bayesian estimates, suggesting the existence of multiple mechanisms for integration of prior expectations with raw sensory information. Widespread experimental evidence of Bayesian integration has accumulated over the last few decades (Ernst and Banks 2002; Körding and Wolpert 2004; Körding et al. 2004; Sato et al. 2007; Stocker and Simoncelli 2006a; Weiss et al. 2002). However, the current work makes it clear that Bayesian integration is not universal because it does not always occur—even under conditions in which it could apply—when prior expectations and raw sensory information are known to influence final estimates.
GRANTS
This work was supported by a Sloan Research Fellowship from the Alfred P. Sloan Foundation and a Scholar Award from the McKnight Endowment for Neuroscience to M. A. Smith.
ACKNOWLEDGMENTS
We thank R. Chen for help with the scientific illustrations; S. Orozco and B. Shields for help with the experiments; and G. Sing, H. Wu, and N. Gonzalez Castro for helpful discussions.
REFERENCES
- Aglioti S, DeSouza JFX, Goodale MA. Size-contrast illusions deceive the eye but not the hand. Curr Biol 5: 679–685, 1995. [DOI] [PubMed] [Google Scholar]
- Albers J. Interaction of Color. New Haven, CT: Yale Univ. Press, 1975, p. 86. [Google Scholar]
- Barlow H. The exploitation of regularities in the environment by the brain.Behav Brain Sci 24: 602–607, 2001. [DOI] [PubMed] [Google Scholar]
- Barlow HB. A theory about the functional role and synaptic mechanism of visual after-effects. In: Vision: Coding and Efficiency, edited by Blakemore CB. Cambridge, UK: Cambridge Univ. Press, 1990, p. 363–375. [Google Scholar]
- Bays PM, Wolpert DM, Flanagan JR. Perception of the consequences of self-action is temporally tuned and event driven. Curr Biol 15: 1125–1128, 2005. [DOI] [PubMed] [Google Scholar]
- Blakemore SJ, Wolpert D, Frith C. Why can't you tickle yourself? Neuroreport 11: R11–R16, 2000. [DOI] [PubMed] [Google Scholar]
- Bouisset S, Zattara M. A sequence of postural movements precedes voluntary movement. Neurosci Lett 22: 263–270, 1981. [Google Scholar]
- Brenner E, Smeets JBJ. Size illusion influences how we lift but not how we grasp an object. Exp Brain Res 111: 473–476, 1996. [DOI] [PubMed] [Google Scholar]
- Brown JE, Frank JS. Influence of event anticipation on postural actions accompanying voluntary movement. Exp Brain Res 67: 645–650, 1987. [DOI] [PubMed] [Google Scholar]
- Byblow WD, Coxon JP, Stinear CM, Fleming MK, Williams G, Muller JFM, Ziemann U. Functional connectivity between secondary and primary motor areas underlying hand–foot coordination. J Neurophysiol 98: 414–422, 2007. [DOI] [PubMed] [Google Scholar]
- Campbell FW, Maffei L. Tilt after-effect: fresh look. Vision Res 11: 833–840, 1971. [DOI] [PubMed] [Google Scholar]
- Chang EC, Flanagan JR, Goodale MA. The intermanual transfer of anticipatory force control in precision grip lifting is not influenced by the perception of weight. Exp Brain Res 185: 319–329, 2008. [DOI] [PubMed] [Google Scholar]
- Charpentier A. Analyse experimentale quelques de la sensation de poids [Experimental study of some aspects of weight perception]. Arch Physiol Norm Pathol 3: 122–135, 1891. [Google Scholar]
- Chouinard PA, Large ME, Chang EC, Goodale MA. Dissociable neural mechanisms for determining the perceived heaviness of objects and the predicted weight of objects during lifting: an fMRI investigation of the size-weight illusion. NeuroImage 44: 200–212, 2009. [DOI] [PubMed] [Google Scholar]
- Chouinard PA, Leonard G, Paus T. Role of the primary motor and dorsal premotor cortices in the anticipation of forces during object lifting. J Neurosci 25: 2277–2284, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Crammond DJ, Kalaska JF. Neural activity in primary motor and dorsal premotor cortex in reaching tasks with the contralateral versus ipsilateral arm. J Neurophysiol 89: 922–942, 2003. [DOI] [PubMed] [Google Scholar]
- Cordo PJ. Kinesthetic control of a multijoint movement sequence. J Neurophysiol 63: 161–172, 1990. [DOI] [PubMed] [Google Scholar]
- Cordo PJ, Nashner LM. Properties of postural adjustments associated with rapid arm movements. J Neurophysiol 47: 287–382, 1982. [DOI] [PubMed] [Google Scholar]
- Cross DV, Rotkin L. The relation between size and apparent heaviness. Percept Psychophys 18: 79–87, 1975. [Google Scholar]
- Davare M, Andres M, Cosnard G, Thonnard JL, Olivier E. Dissociating the role of ventral and dorsal premotor cortex in precision grasping. J Neurosci 26: 2260–2268, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis CM, Roberts W. Lifting movements in the size-weight illusion. Percept Psychophys 20: 33–36, 1976. [Google Scholar]
- de Grave DDJ, Biegstraaten M, Smeets JBJ, Brenner E. Effects of the Ebbinghaus figure on grasping are not only due to misjudged size. Exp Brain Res 163: 58–64, 2005. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Verstynen T, Hon A, Lehman SL, Ivry RB. Anticipatory adjustments in the unloading task: is an efference copy necessary for learning? Exp Brain Res 148: 272–276, 2003. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Verstynen T, Hon A, Zhang Y, Ivry RB. Illusions of force perception: the role of sensori-motor predictions, visual information, motor errors. J Neurophysiol 97: 3305–3313, 2007. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Verstynen T, Lehman SL, Ivry RB. Cerebellar involvement in anticipating the consequences of self-produced actions during bimanual movements. J Neurophysiol 93: 801–812, 2005. [DOI] [PubMed] [Google Scholar]
- Dufossae M, Hugon M, Massion J. Postural forearm changes induced by predictable in time or voluntary triggered unloading in man. Exp Brain Res 60: 330–334, 1985. [DOI] [PubMed] [Google Scholar]
- Ellis RR, Lederman SJ. The golf-ball illusion: evidence for top-down processing in weight perception. Perception 27: 193–201, 1998. [DOI] [PubMed] [Google Scholar]
- Ellis RR, Lederman SJ. The material–weight illusion revisited. Percept Psychophys 61: 1564–1576, 1999. [DOI] [PubMed] [Google Scholar]
- Ernst MO. Perceptual learning: inverting the size-weight illusion. Curr Biol 19: R23–R25, 2009. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415: 439–443, 2002. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Beltzner MA. Independence of perceptual and sensorimotor predictions in the size-weight illusion. Nat Neurosci 3: 737–741, 2000. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Bittner JP, Johansson RS. Experience can change distinct size-weight priors engaged in lifting objects and judging their weights. Curr Biol 18: 1742–1747, 2008. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Bowman MC, Johansson RS. Control strategies in object manipulation tasks. Curr Opin Neurobiol 16: 650–659, 2006. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, King S, Wolpert DM, Johansson RS. Sensorimotor prediction and memory in object manipulation. Can J Exp Psychol 55: 87–95, 2001. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Vetter P, Johansson RS, Wolpert DM. Prediction precedes control in motor learning. Curr Biol 13: 146–150, 2003. [DOI] [PubMed] [Google Scholar]
- Fogassi L, Gallese V, Buccino G, Craighero L, Fadiga L, Rizzolatti G. Cortical mechanism for the visual guidance of hand grasping movements in the monkey: a reversible inactivation study. Brain 124: 571–586, 2001. [DOI] [PubMed] [Google Scholar]
- Franz VH. Action does not resist visual illusions. Trends Cogn Sci 5: 457–459, 2001. [DOI] [PubMed] [Google Scholar]
- Gahery Y, Nieoullon A. Postural and kinetic coordination following cortical stimuli which induce flexion movements in cats limbs. Brain Res 149: 25–37, 1978. [DOI] [PubMed] [Google Scholar]
- Ganel T, Tanzer M, Goodale MA. A double dissociation between action and perception in the context of visual illusions: opposite effects of real and illusory size. Psychol Sci 19: 221–225, 2008. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. Adaptation, after-effect, and contrast in the perception of tilted lines. II. Simultaneous contrast and the areal restriction of the after-effect. J Exp Psychol 20: 553–569, 1937. [Google Scholar]
- Goodale MA, Milner DA. Separate visual pathways for perception and action. Trends Neurosci 15: 20–25, 1992. [DOI] [PubMed] [Google Scholar]
- Grandy MS, Westwood DA. Opposite perceptual and sensorimotor responses to a size–weight illusion. J Neurophysiol 95: 3887–3892, 2006. [DOI] [PubMed] [Google Scholar]
- Gregory RL. Editorial essay. Perception 35: 431–432, 2006. [DOI] [PubMed] [Google Scholar]
- Haffenden AM, Schiff KC, Goodale MA. The dissociation between perception and action in the Ebbinghaus illusion: nonillusory effects of pictorial cues on grasp. Curr Biol 11: 177–181, 2001. [DOI] [PubMed] [Google Scholar]
- Harshfield SP, DeHardt DC. Weight judgment as a function of apparent density of objects. Psychon Sci 20: 365–366, 1970. [Google Scholar]
- Horak FB, Diener HC. Cerebellar control of postural scaling and central set in stance. J Neurophysiol 72: 479–493, 1994. [DOI] [PubMed] [Google Scholar]
- Horak FB, Diener HC, Nashner LM. Influence of central set on human postural responses. J Neurophysiol 62: 841–853, 1989. [DOI] [PubMed] [Google Scholar]
- Hoshi E, Tanji J. Differential involvement of neurons in the dorsal and ventral premotor cortex during processing of visual signals for action planning. J Neurophysiol 95: 3596–3616, 2006. [DOI] [PubMed] [Google Scholar]
- Hoshi E, Tanji J. Distinctions between dorsal and ventral premotor areas: anatomical connectivity and functional properties. Curr Opin Neurobiol 17: 234–242, 2007. [DOI] [PubMed] [Google Scholar]
- Jackson SR, Shaw A. The Ponzo illusion affects grip-force but not grip-aperture scaling during prehension movements. J Exp Psychol Hum Percept Perform 26: 418–423, 2000. [DOI] [PubMed] [Google Scholar]
- Jones LA. Perception of force and weight: theory and research. Psychol Bull 100: 29–42, 1986. [PubMed] [Google Scholar]
- Kaas JH. Evolution of somatosensory and motor cortex in primates. Anat Rec Part A Discov Mol Cell Evol Biol 281A: 1148–1156, 2004. [DOI] [PubMed] [Google Scholar]
- Körding KP, Ku S-p, Wolpert DM. Bayesian integration in force estimation. J Neurophysiol 92: 3161–3165, 2004. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature 427: 244–247, 2004. [DOI] [PubMed] [Google Scholar]
- Koseleff P. Studies in the perception of heaviness. Acta Psychol 13: 242–252, 1957. [Google Scholar]
- Krakauer JW. Motor learning and consolidation: the case of visuomotor rotation. Adv Exp Med Biol 629: 405–421, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci 20: 8916–8924, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu MT, Preston JB, Strick PL. Interconnections between the prefrontal cortex and the premotor areas in the frontal-lobe. J Comp Neurol 341: 375–392, 1994. [DOI] [PubMed] [Google Scholar]
- Lum PS, Reinkensmeyer DJ, Lehman SL, Li PY, Stark LW. Feedforward stabilization in a bimanual unloading task. Exp Brain Res 89: 172–180, 1992. [DOI] [PubMed] [Google Scholar]
- Marsden CD, Merton PA, Morton HB. Stretch reflex and servo action in a variety of human muscles. J Physiol 259: 531–560, 1976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massion J. Movement, posture and equilibrium: interaction and coordination. Prog Neurobiol 38: 35–56, 1992. [DOI] [PubMed] [Google Scholar]
- Milner AD, Goodale MA. Visual pathways to perception and action. Prog Brain Res 95: 317–337, 1993. [DOI] [PubMed] [Google Scholar]
- Mishkin M, Ungerleider LG. Contribution of striate inputs to the visuospatial functions of parieto-preoccipital cortex in monkeys. Behav Brain Res 6: 57–77, 1982. [DOI] [PubMed] [Google Scholar]
- Müller GE, Schumann F. Über die psychologischen Grundlagen der Vergleichung gehobener Gewichte. Pflügers Arch XLV: 37–112, 1889. [Google Scholar]
- Norris D, Kinoshita S. Perception as evidence accumulation and bayesian inference: insights from masked priming. J Exp Psychol Gen 137: 434–455, 2008. [DOI] [PubMed] [Google Scholar]
- Rabe K, Brandauer B, Li Y, Gizewski ER, Timmann D, Hermsdorfer J. Size–weight illusion, anticipation, and adaptation of fingertip forces in patients with cerebellar degeneration. J Neurophysiol 101: 569–579, 2009. [DOI] [PubMed] [Google Scholar]
- Rispal-Padel L, Cicirata F, Pons C. Cerebellar nuclear topography of simple and synergistic movements in the alert baboon (Papio papio). Exp Brain Res 47: 365–380, 1982. [DOI] [PubMed] [Google Scholar]
- Rizzolatti G, Luppino G. The cortical motor system. Neuron 31: 889–901, 2001. [DOI] [PubMed] [Google Scholar]
- Ross HE. Sensory information necessary for the size-weight illusion. Nature 212: 650–650, 1966. [DOI] [PubMed] [Google Scholar]
- Rothwell JC, Traub MM, Marsden CD. Influence of voluntary intent on the human long-latency stretch reflex. Nature 286: 496–498, 1980. [DOI] [PubMed] [Google Scholar]
- Sakreida K, Schubotz RI, Wolfensteller U, von Cramon DY. Motion class dependency in observers' motor areas revealed by functional magnetic resonance imaging. J Neurosci 25: 1335–1342, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato Y, Toyoizumi T, Aihara K. Bayesian inference explains perception of unity and ventriloquism aftereffect: identification of common sources of audiovisual stimuli. Neural Comput 19: 3335–3355, 2007. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Dingwell JB, Mussa-Ivaldi FA. Learning to move amid uncertainty. J Neurophysiol 86: 971–985, 2001. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol 84: 853–862, 2000. [DOI] [PubMed] [Google Scholar]
- Schmitz C, Jenmalm P, Ehrsson HH, Forssberg H. Brain activity during predictable and unpredictable weight changes when lifting objects. J Neurophysiol 93: 1498–1509, 2005. [DOI] [PubMed] [Google Scholar]
- Schwartz O, Hsu A, Dayan P. Space and time in visual context. Nat Rev Neurosci 8: 522–535, 2007. [DOI] [PubMed] [Google Scholar]
- Shergill SS, Bays PM, Frith CD, Wolpert DM. Two eyes for an eye: the neuroscience of force escalation. Science 30: 187–187, 2003. [DOI] [PubMed] [Google Scholar]
- Shiratori T, Latash ML. Anticipatory postural adjustments during load catching by standing subjects. Clin Neurophysiol 112: 1250–1265, 2001. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP. Optimal estimation in sensory systems. In: The New Cognitive Neurosciences IV, edited by Gazzaniga MS. Cambridge, MA: MIT Press, 2009, p. 525–535. [Google Scholar]
- Smeets JBJ, Brenner E. A new view on grasping. Motor Control 3: 237–271, 1999. [DOI] [PubMed] [Google Scholar]
- Smeets JBJ, Brenner E. Ten years of illusions. J Exp Psychol Hum Percept Perform 32: 1501–1506, 2006. [DOI] [PubMed] [Google Scholar]
- Smeets JBJ, Brenner E. Grasping Weber's law. Curr Biol 18: R1089–R1090, 2008. [DOI] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: 1035–1043, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperry RW. Neural basis of the spontaneous optokinetic response produced by visual inversion. J Comp Physiol Psychol 43: 482–489, 1950. [DOI] [PubMed] [Google Scholar]
- Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci 9: 578–585, 2006a. [DOI] [PubMed] [Google Scholar]
- Stocker AA, Simoncelli EP. Sensory adaptation within a Bayesian framework for perception. Adv Neural Inform Process Syst 18: 1291–1298, 2006b. [Google Scholar]
- Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature 407: 742–747, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ungerleider LG, Mishkin M. Two cortical visual systems. In: Analysis of Visual Behavior, edited by Ingle DJ, Goodale MA, Mansfield RJW. Cambridge, MA: MIT Press, 1982, p. 549–585. [Google Scholar]
- Usnadze D. Über die Gewichtstauschung und ihre Analoga [Aspects of weight illusions]. Psychol Forsch 14: 366–379, 1931. [Google Scholar]
- Wainwright MJ. Visual adaptation as optimal information transmission. Vision Res 39: 3960–3974, 1999. [DOI] [PubMed] [Google Scholar]
- Webster MJ, Bachevalier J, Ungerleider LG. Connections of inferior temporal areas teo and te with parietal and frontal-cortex in macaque monkeys. Cereb Cortex 4: 470–483, 1994. [DOI] [PubMed] [Google Scholar]
- Weiskrantz L, Elliott J, Darlington C. Preliminary observations on tickling oneself. Nature 230: 598–599, 1971. [DOI] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci 5: 598–604, 2002. [DOI] [PubMed] [Google Scholar]
- Wing AM, Flanagan JR, Richardson J. Anticipatory postural adjustments in stance and grip. Exp Brain Res 116: 122–130, 1997. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science 269: 1880–1882, 1995. [DOI] [PubMed] [Google Scholar]


