Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
letter
. 2015 May 1;593(Pt 9):2241–2242. doi: 10.1113/JP270123

From a basic principle of evolution to the heart rate of mammals

Yuh-Ying Lin Wang 1,✉, Wei-Kung Wang 2
PMCID: PMC4422577  PMID: 25931409

Danchin et al. (2014) proposed that physiology and evolutionary biology need to be better integrated; Paterson et al. (2014) stated that cardiovascular biology and the integration of evolutionary biology with physiological science are two major subjects for The Journal of Physiology. In response to these important views, we first proposed that power saving is one basic principle for the evolution of a biological system, then correlated the principle with the structures and the operating mechanism of the ventricular aortic (VA) system and discussed the proper heart rates for mammals.

The blood input from the left ventricle to the aorta is not a continuous constant flow but bursts in a pulsatile manner with period, TH, or heart rate, fH. This enables the power generated from the heart to be transmitted to the whole arterial system, not by direct blood flow but via waves. Delivering power by wave is a more efficient mechanism just as an EM wave is of higher efficiency as compared with a DC current in transmitting electric power.

When meeting the arch of the aorta, the blood changes its momentum and gives rise to a force that causes a periodic damped forced oscillatory motion of the elastic aortic walls in the radial direction (Lin Wang & Wang, 2014). The 180 deg bending of the aortic arch is a power saving structure which converts most of the high dissipated blood kinetic energy to the low dissipated elastic potential energy of the aortic wall.

All large arteries in vivo are subjected to large longitudinal tension; this special physical character is a clue that the wave propagation in large arteries has the same mechanism as a transverse string wave. As the pressure forces are being balanced by the elastic restoring forces of circumferential stress, the force for the radial oscillation of a segment of aorta is contributed mainly by the radial components of the longitudinal tension and the shearing stress provided by the two neighbouring wall segments. Based on this concept, a PR wave equation which factors in the arterial wall as the major wave medium (Lin Wang et al. 2004, Lin Wang & Wang, 2014) has been derived. Thus, sparing blood from the major wave medium enhances the power saving ability of the VA system during wave propagation. As the heart keeps giving the aortic system impulsive blood input with period TH, it offers harmonic forces of discrete frequencies fn = nfH, with n = 1, 2, 3, …. Since the PR wave equation is a linear equation, we may analyse the effect of one particular harmonic force of frequency fn, and the overall response will be a linear superposition of those caused by all the existing frequencies.

Supplying a continuous sinusoidal force of frequency f to one end of a low damped string at position z = 0, a continuous harmonic transverse oscillation of the same frequency and wave velocity C will be responded along the whole string, and the amplitude of oscillation for the small segment at a distance z from the force source is proportional to the absolute value of 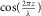Inline graphic, with 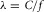Inline graphic as the associated wavelength. Similarly, a sinusoidal force source of frequency 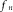Inline graphic acting on the arch of the aorta at z = 0, will cause any segment of the aortic wall to conduct a radial harmonic oscillation and initiate the associated harmonic pressure wave with the same frequency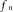Inline graphic. 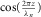The amplitude of the harmonic pressure wave at a distance z from the arch of the aorta is then proportional to the absolute value of Inline graphic.

In our description of the VA system as a distributed-cyclic-hydraulic press (DCHP) of multiple ranks (Lin Wang & Wang, 2013), every branching site along the aorta can be treated as a lower-rank distribution depot to initiate the oscillatory motion of the connecting arteries by supplying them the hydraulic pressure force source. For example, branches from the aortic arch (near z = 0) supply the arteries of head, neck and arms; branches from the aorta ends (at z = L) supply the common iliac arteries and then the arteries of the lower limbs; and the side branches near z = L/2 supply the renal arteries.

Pressure is a continuous physical parameter, the design that branch arteries to the head are connected near the arch of the aorta ensures the maximum amplitude pressure sources at these distribution depots so long as the heart is beating. This design reveals that providing hydraulic pressure force to transmit blood to the head is of the first priority since it is essential under any circumstance.

The amplitude of the nth harmonic pressure wave near z = L is proportional to 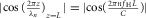Inline graphic. If the amplitudes also have their maximum values for all n, the distribution depots near the entrances of the iliac arteries will also be able to supply maximum harmonic hydraulic pressure forces for all n to initiate the radial oscillation of the connected arteries. This condition can be fulfilled if the heart beats at a frequency to be

graphic file with name tjp0593-2241-m7.jpg 1

with M as an arbitrary integer.

Equation 1 shows that for integer M = 1, Inline graphic (or the fundamental wavelength is equal to 2L) is the lowest efficient heart rate that can be maintained by a mammal of aortic length L and wave velocity C. Milnor (1979) has proposed that pulse wavelength and arterial length are matched in a way that minimizes cardiac work. For the evolutionary rule that encourages power saving we provide an exact physical model to explain the inverse correlation between heart rate and body size.

As the wave velocity C varies in different situations, a healthy heart may adjust to a different heart rate. In response to a long term strenuous exercise, a heart may even double its rate (Barnard et al. 1973) which corresponds to M = 2 in eqn 1 and is the second lowest efficient heart beat that can be maintained by a mammal.

If the heart beats at its lowest efficient heart rate at the midpoint of the aorta, z = L/2, the pressure will have the maximum amplitude for the harmonic components, with n = 2, 4, 6,…, while at z = L/3, the harmonic pressure will have maximum amplitude for n = 3, 6, 9,…. Stacy & Giles (1959) assumed that arteries of an organ can be lumped together as an oscillatory system with inertia and elasticity, and under this model approximation, every individual organ may be treated as a harmonic oscillator with its characteristic natural frequency forg. Hence to initiate the highest radial oscillation of the organ artery by fulfilling the frequency matching or resonance condition, and thus to reach the highest power saving, the position z = L/2 is suitable to connect an organ with natural frequency forg to be of the magnitude 2fH, 4fH, or 6fH…, while the position z = L/3 is suitable to connect an organ with natural frequency forg to be 3fH, 6fH,…. In our previous study on rats, we found that the natural frequency of a kidney is associated with 2fH (Lin Wang et al. 1991). This might offer an evolutionary reason why most kidneys of mammals are connected near the midpoints of the aorta. However, many further in vivo studies are needed to analyse the similarity of organ positions in mammals.

Additional information

Competing interests

None declared.

References

  1. Barnard RJ, Gardner GW, Diaco NV, MacAlpin RN. Kattus AA. Cardiovascular responses to sudden strenuous exercise – heart rate, blood pressure, and ECG. J Appl Physiol. 1973;34:833–837. doi: 10.1152/jappl.1973.34.6.833. [DOI] [PubMed] [Google Scholar]
  2. Danchin É. Pocheville A. Inheritance is where physiology meets evolution. J Physiol. 2014;592:2307–2317. doi: 10.1113/jphysiol.2014.272096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Lin Wang YY, Chang SL, Wu YE, Hsu TL. Wang WK. Resonance. The missing phenomenon in hemodynamics. Circ Res. 1991;69:246–249. doi: 10.1161/01.res.69.1.246. [DOI] [PubMed] [Google Scholar]
  4. Lin Wang YY, Jan MY, Wang GC, Bau JG. Wang WK. Pressure pulse velocity is related to the longitudinal elastic properties of the artery. Physiol Meas. 2004;25:1397–1403. doi: 10.1088/0967-3334/25/6/005. [DOI] [PubMed] [Google Scholar]
  5. Lin Wang YY. Wang WK. A hemodynamics model to study the collective behavior of the ventricular-arterial system. J Appl Phys. 2013;113:024702. [Google Scholar]
  6. Lin Wang YY. Wang WK. Anatomy of arterial systems reveals that the major function of the heart is not to emit waves associated with the axial blood motion. J Physiol. 2014a;592:409. doi: 10.1113/jphysiol.2013.267344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lin Wang YY. Wang WK. The PR wave equation – a primary and realistic arterial pressure wave equation for the quantitative and collective study of the cardiovascular system. Chin J Phys. 2014b;52:916–926. [Google Scholar]
  8. Milnor WR. Aortic wavelength as a determinant of the relation between heart rate and body size in mammals. Am J Physiol. 1979;237:R3–R6. doi: 10.1152/ajpregu.1979.237.1.R3. [DOI] [PubMed] [Google Scholar]
  9. Paterson DJ. Howells S. The Journal of Physiology annual report 2013–14: Another year of progress. J Physiol. 2014;592:811–821. [Google Scholar]
  10. Stacy RW. Giles FM. Computer analysis of arterial properties. Circ Res. 1959;7:1031–1038. [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES