The mechanochemical cycle of mammalian kinesin-2 KIF3A/B under load

Summary

The response of motor proteins to external loads underlies their ability to work in teams and determines the net speed and directionality of cargo transport. The mammalian kinesin-2, KIF3A/B, is a heterotrimeric motor involved in intraflagellar transport and vesicle motility in neurons. Bidirectional cargo transport is known to result from the opposing activities of KIF3A/B and dynein bound to the same cargo, but the load-dependent properties of kinesin-2 are poorly understood. We used a feedback-controlled optical trap to probe the velocity, run length and unbinding kinetics of mouse KIF3A/B under various loads and nucleotide conditions. The kinesin-2 motor velocity is less sensitive than kinesin-1 to external forces, but its processivity diminishes steeply with load, and the motor was observed occasionally to slip and reattach. Each motor domain was characterized by studying homodimeric constructs, and a global fit to the data resulted in a comprehensive pathway that quantifies the principal force-dependent kinetic transitions. The properties of the KIF3A/B heterodimer are intermediate between the two homodimers, and the distinct load-dependent behavior is attributable to the properties of the motor domains, and not to the neck-linkers or the coiled-coil stalk. We conclude that the force-dependent movement of KIF3A/B differs significantly from conventional kinesin-1. Against opposing dynein forces, KIF3A/B motors are predicted to rapidly unbind and rebind, resulting in qualitatively different transport behavior from kinesin-1.

Introduction

The kinesin-2 motor KIF3A/B is an essential protein in mice that is involved in organelle transport and mitosis [1]. The two different motor domains, KIF3A and KIF3B, and a light chain, KAP3, form a heterotrimeric protein complex that is expressed ubiquitously in mammals. KIF3A/B is one of the most abundant kinesin family motors [2], and is particularly enriched in neuronal tissue, where it plays a role in fast axonal transport and axonogenesis [3]. Heterotrimeric kinesin-2 motors are present in diverse organisms, including algae and protozoa, where their functions are often linked to ciliogenesis and intraflagellar transport (IFT) [4]. In higher organisms, ciliopathies resulting from the disruption of IFT are linked to developmental defects and polycystic kidney disease [3, 5].

The effect of mechanical load on kinesin mechanochemistry is best understood for kinesin-1 (conventional kinesin). Optical trapping experiments have shown that kinesin-1 steps processively against hindering loads approaching stall force [6–8], and have provided insights into both the force-dependent kinetic transitions [9] and gating mechanisms by which the ATP hydrolysis cycles of the two motor domains are maintained out of phase to ensure efficient stepping with high processivity [10, 11]. Despite recent investigations into the kinetics [12] and load-dependent performance of different kinesin-2 motors [13, 14], the details of their force-dependent mechanochemistry are lacking. Under loads from a stationary optical trap, the time that Xenopus kinesin-2 motors stall before detaching from the microtubule was found to be less than half that of kinesin-1 [14], and C. elegans kinesin-2 was found to have shorter run lengths than kinesin-1 at comparable forces [8, 15]. The unloaded processivity of mammalian kinesin-2 was also found to be considerably less than that of kinesin-1, and this reduced processivity could be explained by the longer neck linker domain of kinesin-2 [16]. Another unresolved question is whether the heterodimeric structure of kinesin-2 plays any role in its load-dependent processivity [15, 17].

Because several kinesin-2 motors are often attached to a single cargo, and can interact with kinesin-1, opposing dynein motors, or even myosin [18], understanding their force-dependent behavior is critical for describing their function in living cells. Experiments have been conducted in vitro on teams of identical [19] and opposing motors [20], and models describing cargo transport by multiple motors have been advanced [21–23]. While such models can capture aspects of the observed transport dynamics, their phase-space is large, and the predicted behavior can vary extensively depending upon the choice of input parameters. Single-molecule investigations have not resolved the question of whether kinesin-1 and kinesin-2 motors respond differently to external loads.

Developing a quantitative understanding of bidirectional transport requires a detailed characterization of the load-dependent stepping dynamics of KIF3A/B, and the contribution from each subunit to the function of the holoenzyme. Using optical tweezers equipped with a force clamp applied to mammalian KIF3A/B, we set about addressing the following questions: (1) How do kinesin-2 motors behave under external loads? (2) Are the two heads of kinesin-2 functionally equivalent? (3) What influences do the dimerization domains and neck linkers of kinesin-2 have on the load-dependent properties of the motor? Answering these questions is important for describing the fundamental mechanism by which N-terminal kinesin motors generate force, and for understanding how different kinesin family members may be fine-tuned for specific cellular functions.

Results

Load-dependent KIF3A/B stepping differs from kinesin-1

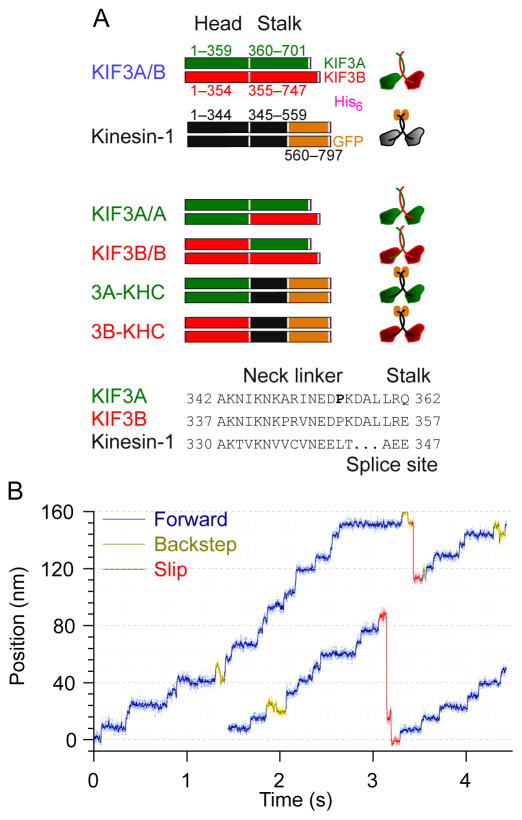
To explore the influence of external load on the stepping kinetics of kinesin-2, we used a bead assay and optical trap to study heterodimeric mouse KIF3A/B and homodimeric mutants, comparing their behavior to the well-characterized Drosophila kinesin-1 wild type [17, 24] (Figure 1A). Hereafter, we refer to the motor domains and associated neck-linkers of the KIF3A and KIF3B gene products as “A heads” and “B heads,” respectively. KIF3A/B refers to the full-length, his-tagged wild-type dimer with both A and B heads. The KIF3A/A and KIF3B/B constructs have the B head substituted with an A head and vice versa, generating motors with identical heads, while retaining the wild-type heterodimeric coiled-coil stalk, as described previously [17].

Figure 1. KIF3A/B stepping against hindering load in an optical force clamp.

(A) Recombinant kinesin constructs used in the study. KIF3A/B (blue label) consists of the full-length KIF3A (green) and KIF3B (red) sequences fused to a C-terminal His₆ tag (pink). Kinesin-1 (black label) is a truncated DmKHC construct (black) fused to the GFP sequence (orange) and a His₆ tag. Homodimeric mutants were generated by joining the KIF3A or KIF3B motor domains to the stalks of KIF3A/B or Kinesin-1. The splice site was the junction between the neck linker and stalk for the respective motors. Two additional mutants of 3A-KHC were also created: 3A-KHC_P>A replaces the KIF3A NL proline (P, bold) by alanine, and 3A-KHC_P>A,ΔDAL, which carries the identical mutation, together with a deletion of the three C-terminal neck-linker residues (DAL, underscored).

(B) Representative records of single-molecule movement for KIF 3A/B (4 pN hindering load, 5 μM ATP) displaying forward steps of 8 nm (blue), backsteps of 8 nm (olive) and slips of variable distance (red).

All three KIF3 constructs gave robust, processive movement at ATP concentrations as low as 100 nM (Figures 1B and S1D). Single-motor conditions were confirmed based on Poisson statistical behavior [25]. Steps measuring 8 nm, the microtubule lattice spacing, were observed under a variety of forces and ATP concentrations (Figures 1B, S1A–C, and S1E–F), suggesting that kinesin-2 moves in a similar hand-over-hand fashion to kinesin-1.

Kinesin-2 runs were infrequent, but consistent from run to run for all constructs. This intermittent activity was not observed in chimeras where KIF3 motor domains were fused to kinesin-1 coiled-coil domains (see below). Both kinesin-1 and KIF17, a homodimeric kinesin-2 motor, as well as the KIF3A/B ortholog KLP11/20, are known to be autoinhibited by their stalks [15, 26, 27]. Our observations are therefore consistent with a mechanism by which the native KIF3A/B stalk or tail, but not the stalk of kinesin-1, weakly inhibits the KIF3A/B motor domains in a similar manner.

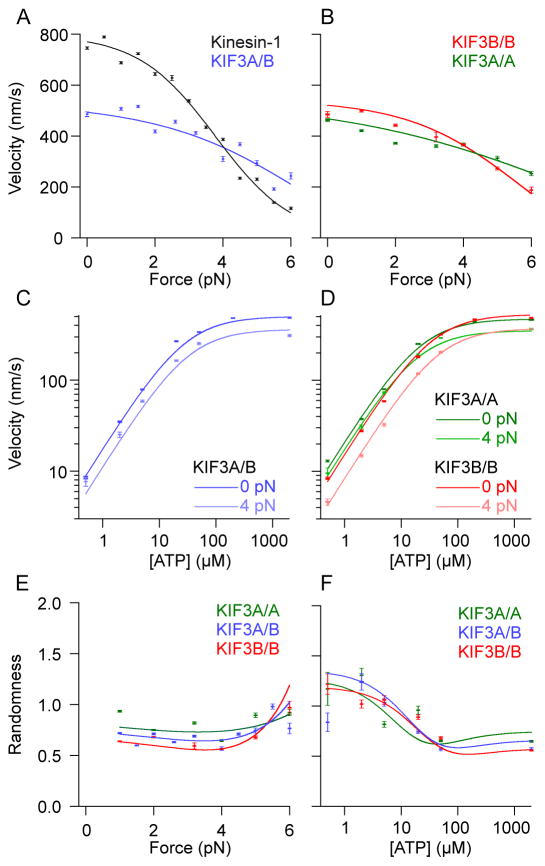
Using force-clamp conditions, the properties of kinesin-2 and kinesin-1 were compared across a wide range of forces and ATP concentrations. The first observation was that the velocity of KIF3A/B was much less affected by hindering loads than kinesin-1 (Figure 2A). This contrast indicates that there are differences in the force-dependent rate constants between the two motor families, which result in a crossover in velocities around 4 pN. To detect any differences in the mechanochemical properties of the two KIF3A/B heads, the force-velocity relationships of KIF3A/A and KIF3B/B homodimers were characterized (Figure 2B). KIF3B/B was slightly faster than KIF3A/A at low load, but was slowed to a greater extent by hindering loads. The ATP dependence of velocity at different loads was also assessed (Figures 2C and 2D). Interestingly, for all conditions, the KIF3A/B velocity was close to the average of the corresponding KIF3A/A and KIF3B/B velocities (Figure 2), indicating that the wild-type heterodimeric KIF3A/B motor may, from a simple kinetic perspective, be considered to be largely the sum of its parts (the A and B heads). This conclusion gained additional support from measurements of the KIF3A/B randomness parameter versus load [28], which was intermediate between that of KIF3A/A and KIF3B/B (Figures 2E and 2F).

Figure 2. Motor velocity and randomness as a function of load and ATP.

(A, B) Force-velocity curves from force-clamp optical trapping experiments.

(C, D) Velocity at varying ATP concentrations under zero load and 4 pN hindering load.

(E) The randomness parameter, r, as a function of force at 2 mM ATP.

(F) The randomness parameter, r, as a function of ATP at 4 pN hindering load.

Data points and error bars (s.e.m.) indicate experimental velocities or randomness values. Solid curves were derived from a global fit to the data. (see Figure 3, Tables S1, S2, and Supplemental Experimental Procedures). Velocity and randomness results for KIF3A/A in 5 μM ATP are shown in Figures S2A, S2B. Comparisons between KIF3A/B and kinesin-1 randomness vs. force or ATP concentration are shown in Figures S2E and S2F.

Model accounts for processive stepping of KIF3A/B under load

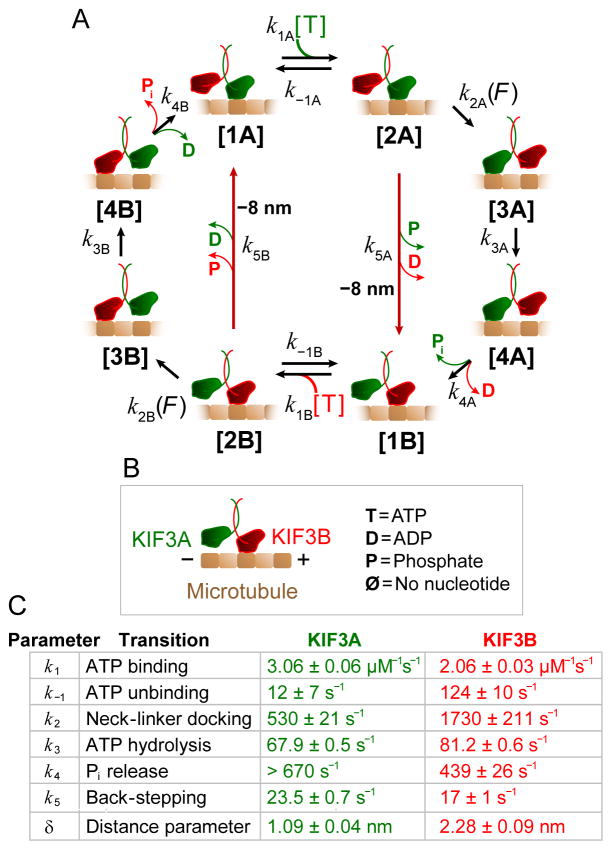
To explore kinetic and mechanical differences between the A and B heads in greater detail, we constructed a combined minimal kinetic pathway for KIF3A/B, and used this model to fit the load-dependent velocity and randomness results of Figures 2, S2A, and S2B. Figure 3 shows the mechanochemical cycle for KIF3A/B, which encompasses two 8-nm steps. The corresponding cycle for the KIF3A/A motor was obtained by replacing the states involving the B head cycle ([1B]–[4B]) with those of the A head ([1A]–[4A]), and vice versa for KIF3B/B. All 13 free kinetic parameters (assuming a large fixed value for k_4A) were globally fit to the 17 velocity and randomness curves, using the analytical expressions supplied in Supplemental Experimental Procedures. Parameter values are given in Figure 3C, and fits of the model to the data are displayed as solid lines in Figures 2, S2A, and S2B.

Figure 3. Modeling the KIF3A/B mechanochemical cycle.

(A) Processive stepping pathway for KIF3A/B. Transitions k_5A and k_5B (dark red arrows) are associated with backsteps.

(B)Legend for the cycle in (A). KIF3A (green) and KIF3B (red) form the KIF3A/B dimer that moves on MTs (brown).

(C) Table of fit parameters and standard errors of fit for the global fit of the kinetic model to the data of Figures 2, S2A and S2B. Assignments of the mechanochemical transitions that correspond to each rate constant in the pathway are indicated. A three state model (combining states 3 and 4) was sufficient to model most of the data; however, fitting the model to the randomness data required four states for head B.

The data for head A were not sufficient to constrain parameter k_4A, so in the actual fit, states 3A and 4A were lumped, equivalent to assuming a very rapid transition [3A] → [4A]. The lower bound for this transition was estimated using FitSpace. Similar model fits were carried out for kinesin-1 and kinesin-2 mutants (Tables S1, S3).

As a starting point for the processive stepping cycle, we used the A head in its microtubule-attached, nucleotide-free state ([1A]; this choice is arbitrary). At a given force, the ATP-dependence for each construct exhibited Michaelis-Menten-type kinetics. To account for changes in the apparent Michaelis-Menten constant, K_M, with force, we introduce reversible ATP binding, [1A]↔[2A], directly followed by a load-dependent transition [2A]→[3A] [8]. The forward step of the motor occurs during this transition, and its rate is slowed exponentially under hindering load, according to k_2A(F)=k_2A,0 exp(−F·δ/k_BT), where k_2A,0 is the unloaded rate, δ is a characteristic distance parameter, and k_BT is Boltzmann’s constant times the absolute temperature. The next step in the pathway, [3A]→[4A], is ATP hydrolysis, and the final step, [4A]→[1B], consists of attachment and ADP release by the tethered head, followed by phosphate release and detachment by the trailing head, to complete one step [29]. A similar cycle is then repeated by head B.

Occasional backstepping, where the kinesin motor moves 8 nm toward the microtubule minus-end, occurs infrequently for kinesin-1, but its frequency can increase significantly when gating (head-head communication) is reduced, for example, by lengthening the neck-linker [30]. Backstepping generally exerts only a small effect on velocity (except near the stall force), but it can have a large effect on second-order statistics, such as the randomness parameter [28]. Under 4 pN of hindering load and 5 μM ATP, we observed a 3% probability of backstepping for kinesin-1, consistent with previous observations, and a 6 % backstepping probability (N = 1504) for KIF3A/B (Figure 1B). Backstepping probabilities for the other kinesin-2 constructs were 8% for KIF3A/A (N = 1206) and 3% for KIF3B/B (N = 1107).

The high observed randomness values for kinesin-2 (Figures 2E and 2F) could not be modeled using simple kinetic schemes. We therefore introduced backstepping explicitly into the kinetic model, as transitions that connect the ATP-bound state to the initial state for the opposite head (red arrows for [2A] → [1B] and [2B] → [1A] in Figure 3A). These transitions, with rates k_5A and k_5B, correspond to 8.2-nm backsteps towards the microtubule minus (−) end. For simplicity, all necessary events in the backstepping sub-pathway, such as rebinding of the rear head and possible premature ATP hydrolysis that lead to front-head detachment [30], have been lumped into a single rate constant. With the two backstepping transitions incorporated, the global fit of the model to the KIF3A/B data generated backstepping rates that varied with force and ATP, and were comparable to the experimental values (e.g., 9% predicted at 4 pN hindering load and 5 μM ATP, vs. 6% measured).

Using the experimental data as constraints, the kinetic model of Figure 3 was able to generate satisfactory fits to the force- and ATP-dependent velocity and randomness data of Figure 2. The FitSpace Explorer algorithm [31] was used to confirm that the system was constrained (that is, not underdetermined, and with no fitting parameters subject to large uncertainties); confidence contours and parameters are supplied in Figure S3 and Table S2 and a detailed explanation is given in the Supplemental Experimental Procedures. The lower bound for k_4A was also estimated using FitSpace. The model represents a reasonable minimal kinetic scheme for KIF3A/B, and highlights salient differences between the hydrolysis cycles of heads A and B.

Kinesin-2 processivity is strongly force-dependent

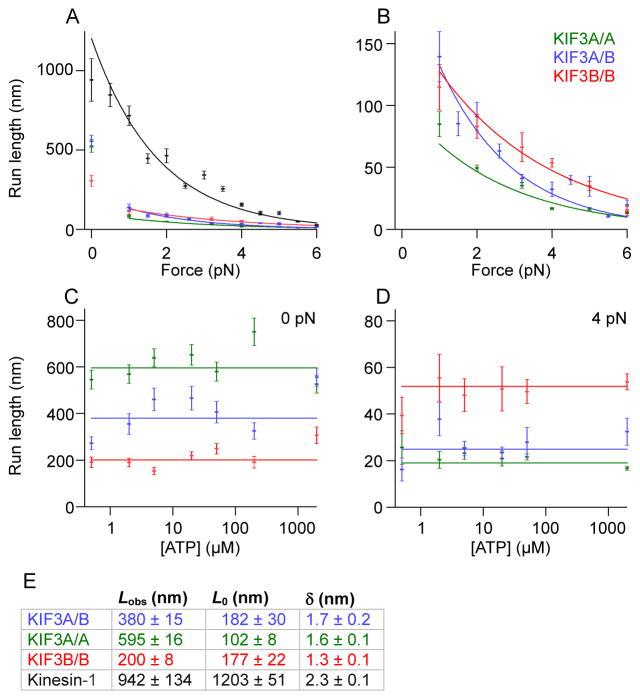
The force-dependence of processivity is critical to how kinesin-driven intracellular transport will be affected by the actions of opposing motors, or by obstacles within the cell. To determine whether kinesin-2 processivity was maintained against significant opposing forces, we analyzed the load dependence of its run length in a force-clamp assay. Unexpectedly, we found that the processivity of kinesin-2 dropped sharply when a hindering force was applied, such that runs consisted of a mere handful of steps under modest loads (Figures 4, S2C and S2D). Unlike kinesin-1, where run lengths depend only moderately upon load, there were two regimes of processivity for kinesin-2: unloaded and loaded. Unloaded run lengths were fairly long for kinesin-2, approaching those of kinesin-1, but against any appreciable external load applied by the force clamp (down to a lower limit of ~1 pN), stepping was disrupted and motors lost processivity. To quantify the dependence on force, F, the mean run lengths under hindering load, L, were fit to the exponential expression, L=L₀ exp (−F·δ/k_BT), where L_o is the unloaded run length and δ is the distance parameter. Distance parameters were similar for kinesin-1 and kinesin-2, but their run lengths extrapolated to zero load (based on hindering load data) differed by nearly an order of magnitude (Figure 4E). Furthermore, the L₀ values derived from fits for kinesin-2 constructs with a KIF3A head were significantly lower than the measured unloaded run length, L_obs. This difference reinforces the distinction between the unloaded and loaded regimes, because L₀ and L_obs would be expected to be equal if the run length varied continuously across all loads. Under assisting forces, kinesin-2 run lengths were too short to be reliably measured, indicating a significant asymmetry in motor properties with respect to the direction of the applied load.

Figure 4. Dependence of processivity on load and ATP.

(A) Run length for KIF3 constructs as a function of force, together with kinesin-1 (in dark grey). Mean run lengths (± s.e. of fit) at each force were calculated from exponential fits to the run-length distribution. Solid curves represent fits to the expression L = L₀ exp (−F·δ/k_BT), where L_o is the run length extrapolated to zero load from hindering-load data and δ is the distance parameter.

(B) KIF3 data from panel (A) rescaled, showing the differences among motor constructs.

(C, D) ATP dependence of KIF3 run lengths under zero load and 4 pN hindering load. Values are mean ± s.e. of fit. Solid lines show fits over all ATP levels.

(E) Table of parameters for fits to data in (A) and (B). L_obs is the unloaded run length obtained by video tracking, averaged for all ATP concentrations. Run length results for KIF3A/A in 5 μM ATP and for 6 pN load are displayed in Figures S2C and S2D.

As with velocity and randomness results, the KIF3A/B run lengths were intermediate between those of KIF3A/A and KIF3B/B under nearly all ATP and load conditions (Figure 4), suggesting that the detachment rate for the heterodimer reflects the additive behavior of its two different motor domains. Unlike a previous report [17], there was no evident ATP dependence to the run length, measured under zero load or 4 pN hindering load (Figures 4C and 4D). The difference is attributable to the improved assay conditions. We also observed transient detachments, followed by reattachments, under hindering loads, hereafter referred to as “slips” (Figures 1B and S1D–E). Slips were observed at the end of 28% of runs by KIF3A/B (2 mM ATP, 4 pN hindering load, N =109). The slipping frequency was similar for KIF3B/B (27%, N = 780), and even higher for KIF3A/A (41%, N = 742). The observed frequency depends upon the run length, because short runs offer a smaller distance over which motors can rebind before the attached bead exits the detection region. The reported difference between KIF3A/A (which has short run lengths under load) and KIF3B/B therefore represents a lower bound. At 5 μM ATP, the slipping frequency was similar for all three constructs (25–31%, N = 145–305). Slips were also observed for a chimera with KIF3A heads but a kinesin-1 neck and stalk (3A-KHC, 42%, N = 842, described below) but almost no slipping was found with the corresponding KIF3B chimera (3B-KHC, 7%, N = 651), nor for wild-type kinesin-1 (3%, N = 577).

How can one understand the strong load dependence of kinesin-2 processivity in terms of the underlying mechanochemistry? As kinesin takes a forward step, the probability of the motor detaching from the microtubule is determined by a competition between the forward attachment of the unbound tethered head and the dissociation of the bound partner head. The sensitive load dependence of kinesin-2 processivity could therefore be caused by (1) faster dissociation from the one-head-bound state or (2) slower binding of the tethered head under load (or both). To examine the first possibility, we measured the unbinding kinetics of kinesin-1 and kinesin-2 motors subjected to rapid increases in load, as described in the following section. To examine the second possibility, we modified the neck linker domain, which is predicted to alter the binding kinetics of the tethered head.

Force-dependent unbinding dynamics

By measuring unbinding forces, that is, the forces at which kinesin motors mechanically detach from microtubules, it is possible to probe the load dependence of dissociation in various nucleotide states [32]. To avoid potential artifacts from dimerization domains, and to collect sufficient statistics for model fitting, experiments were carried out using the homodimeric chimeras 3A-KHC and 3B-KHC, which consist of KIF3 motor domains and neck linkers fused to a truncated kinesin-1 dimerization domain and stalk (Figure 1A). These motors were previously characterized in single-molecule assays [33]: like full-length KIF3A/B, they step processively along microtubules under load (Figures S1G and S1H). However, their binding efficiency in assays was considerably greater than that of full-length KIF3 constructs, and their kinesin-1-derived stalks removed any concerns about possible differences in elastic compliance when comparing kinesin-2 results with kinesin-1.

The force-dependent unbinding rate, k_off(F), can be characterized by the unloaded off-rate, k₀, and a distance parameter, δ, according to k_off(F) = k₀ exp(F·δ/k_BT) [34]. In our experiments, the external load was ramped linearly with time, i.e., F = αt, where α is the loading rate, in pN s⁻¹. The corresponding unbinding force distribution was modeled by:

$$N(F)=Cexp\left\{\frac{\mid F\mid \delta }{k_{\mathrm{B}}T}+\frac{[1-exp(\mid F\mid \delta /k_{B}T)]k_{\mathrm{B}}T}{\delta \alpha \tau }\right\}$$ (1)

where τ = 1/k₀ and C is a constant (adapted from [32]). Parameters k₀ and δ were obtained by fitting the data of Figure 5A.

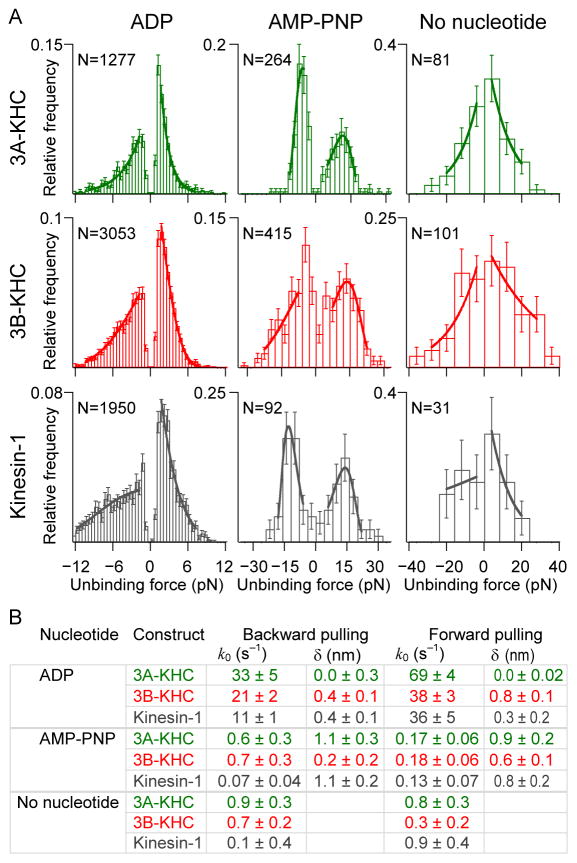
Figure 5. Unbinding force measurements.

(A) Unbinding force histograms for 3A-KHC, 3B-KHC and kinesin-1 (rows) in 1 mM ADP, 0.5 mM AMP-PNP, or no nucleotide (columns). Negative unbinding forces correspond to pulling kinesin toward the microtubule minus-end (the hindering load direction); positive forces are toward the plus-end (assisting load direction). Loading rates: 100 pN s⁻¹ for ADP; 10 pN s⁻¹ for AMP-PNP and no nucleotide (apyrase). Solid lines represent fits to the data under each curve for each pulling direction. Bins with few counts were excluded as well as data at low forces due to the possibility of missed events.

(B) Fit parameters (± s.e. of fit), are shown for each construct and experimental condition, using the parameters indicated in Eq. (1). k₀ is the unloaded off-rate and δ is the characteristic distance parameter. For microtubule dissociation rates during processive stepping, see also Figure S4.

Unbinding forces were measured in different nucleotide states and for different pulling directions. AMP-PNP (0.5 mM) was used to mimic the ATP state, apyrase (10 U/ml) with no added nucleotide was used to assess the nucleotide-free (apo) state, and ADP (1 mM) was used to assess the ADP state. The apo and ATP states were assayed with a loading rate α = 10 pN s⁻¹, but the fast unbinding in ADP required a much higher loading rate, α = 100 pN s⁻¹.

Some general conclusions can be drawn from the data of Figure 5. First, all kinesin constructs bound quite tightly to the microtubule in the presence of AMP-PNP or no nucleotide. The unbinding rates from these states were significantly lower than the detachment rates determined under similar loads during processive runs (Figure S4), so detachment from these states during processive movement is considered highly unlikely. Second, the unbinding rates in ADP were higher for KIF3A or KIF3B than for kinesin-1, consistent with the shorter run lengths of kinesin-2 motors (Figure 4). Third, the detachment rates in the forward direction in ADP were higher than corresponding rates in the rearward direction. Finally, the load dependence of all detachment rates was very weak (maximum δ = 1.1 nm). Because this load dependence was smaller than the load dependence of the run lengths (Figure 4), the unbinding event itself is unlikely to be the main force-dependent quantity that determines processivity. Put another way, the unbinding rates are correlated with run lengths under load, but these cannot explain the precipitous drop in run length that is observed between unloaded and loaded runs.

The unbinding rates for kinesin-1 in ADP were considerably higher than those previously reported for kinesin-1, which were estimated using a 20-fold lower loading rate [32]. From fits to the backward pulling data (Figure 5B), it can be seen that k₀ is 2–3 fold higher for KIF3A and KIF3B than for kinesin-1. Significant asymmetry in the detachment rate between forward and backward pulling has been reported previously for kinesin-1 [32] and it is found here to be a feature of kinesin-2, as well. Using separate unloaded detachment rates for each direction resulted in significantly better fits to the measured distributions (reduced χ² = 1.0; kinesin-1 in ADP) compared with a single variable (reduced χ² = 3.3).

Unbinding rates in AMP-PNP for kinesin-2 and kinesin-1 were similar in the assisting direction, but hindering loads generated much higher unbinding rates for kinesin-2. The corresponding distributions for AMP-PNP displayed clear maxima, indicating relatively strong force-dependencies, with distance parameters around 1 nm. In the absence of nucleotides, the average unbinding force ranged between 9 and 16 pN for all constructs. Unlike in the presence of AMP-PNP or ADP, where motors repeatedly reattached to the microtubule following mechanical unbinding, only a single measurement could be performed per bead under nucleotide-free conditions. The failure of reversible binding may have been due to the mechanical denaturation of motors lacking bound nucleotide, or their detachment from the bead surface. Regardless, the absence of rebinding rendered it unfeasible to collect statistics for the accurate determination of the force sensitivity for detachment (δ). From the limited data available, however, it is clear that detachment rates were low (k<1 s⁻¹) for all constructs.

Differences in neck-linker and neck-coil domains do not explain load-dependent processivity

Besides differing in their core catalytic domains, kinesin-1 and kinesin-2 also differ in their neck linker domains. The kinesin-1 head neck linker consists of 14 residues, whereas the A and B heads of kinesin-2 both have 17-residue neck linkers [16]. Previous work has established that the differences in unloaded processivity between kinesin-1 and -2 likely result from differences associated with their neck linkers, and not their core motor domains [16, 33]. Here, we tested whether the contrasting load-dependent properties of kinesin-1 and -2 result from differences in neck linker length or amino acid sequence.

Experiments were conducted to compare the load dependence of the velocity and run length for construct 3A-KHC with construct 3A-KHC_P>A, which has an effectively longer neck linker, due to swapping out a kinked proline residue [16], and with 3A-KHC_P>A,ΔDAL, which has a 14-residue neck linker, similar to kinesin-1 (Figure 1A). The unloaded run lengths depended strongly upon the neck linkers, with 3A-KHC_P>A being less, and 3A-KHC_P>A,ΔDAL being considerably more, processive than 3A-KHC (Figure 6A). Quantitatively, these effects were even larger than differences scored previously [16], possibly attributable to using a bead assay for the present experiments, rather than fluorescently-tagged motors (beads are less prone to diffuse away from the microtubule than single proteins). Remarkably, any effects of neck-linker length vanished when force was applied, with all three motors displaying similar run lengths (Figure 6A; Table S4). This finding suggests that even a small external force can disrupt any enhanced gating effects that may result from shortening the neck linker.

Figure 6. Effect of neck-linker length on force-dependent properties of KIF3.

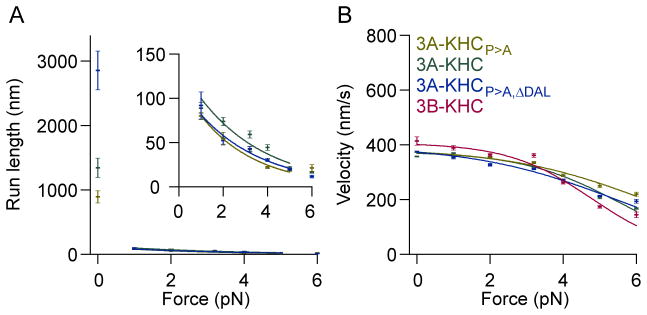
Data from chimeric constructs consisting of kinesin-2 heads fused to the kinesin-1 stalk (2 mM ATP).

(A) Load dependence of run length for 3A-KHC constructs with different neck-linker domains, along with 3B-KHC, color-coded as in panel B. Values at each force are mean ± s.e. of fit to exponential run length distributions. Run lengths as a function of force were fit to exponential functions; parameters are given in Table S4.(B). Inset: Expanded view of run lengths at non-zero loads.

(B) Load dependence of velocity, colored as shown (legend). Velocity data were fit using a 3-state model with a single force-dependent transition. Parameters are given in Table S3. A comparison between velocities and run lengths for homodimers with the native KIF3A/B stalk (KIF3A/A and KIF3B/B) and the kinesin-1 stalk (3A-KHC and 3B-KHC) is shown in Figure S5. The corresponding data for kinesin-1 with an extended neck linker are displayed in Figure S6 and Table S1

Changing the neck linker length also had no major effect on the velocities of the different 3A-KHC constructs, when subjected to either low or high loads (Figure 6B; Table S3). The force-velocity relationship for 3B-KHC was similar to that of 3A-KHC, and the load dependence was slightly weaker than for 3A and 3B homodimers that included the normal kinesin-2 coiled-coil domain (Tables S3, S4 and Figures 3 and S5). The run lengths of 3B-KHC were very short for all forces: only a few steps, on average (Figure S5).

We also compared the behavior of kinesin-1 to kinesin-1_DAL, which includes the last three residues of the kinesin-2 neck linker inserted between the kinesin-1 neck-linker and neck-coil domains. Extending the kinesin-1 neck linker significantly reduced the unloaded run length, and moderately reduced the unloaded velocity, as noted previously [16], but the load dependence was not influenced significantly (Figure S6, Table S1). Hence, the contrasting behavior of kinesin-1 and kinesin-2 under load is not explained by differences in the lengths of their neck linkers.

As a final test, we swapped the neck linker domains between kinesin-1 and kinesin-2. 3A-KHC with a kinesin-1 neck linker behaved similarly to 3A-KHC (data not shown), whereas kinesin-1 with a KIF3A neck-linker was not-functional. Because neck linker docking involves interactions with complementary residues in the core motor domain [35], it is not surprising that the linkers are not fully interchangeable. Why the kinesin-2 motor retained function is not clear, but it is possible that specific docking of the neck-linker to the core motor domain is necessary for kinesin-1, but not for kinesin-2.

Discussion

The goal of this study was to examine the performance of kinesin-2 family motors under load, and to assess the relative contributions of its two different motor domains, along with the neck-linker and stalk domains, to motility. By performing force-clamped measurements using an optical trap, we found unique features that set this family apart from conventional kinesin motors. Under load, the run length of mouse KIF3A/B is sharply reduced, compared to its unloaded run length, or to that of kinesin-1 under load. It is also less than half the run length of KLP11/20, the C. elegans ortholog [15]. Despite this reduced processivity, however, the velocity of KIF3A/B is much less affected by loads than kinesin-1. The key rate constants that set the stepping rate and processivity therefore have strikingly different load dependencies for kinesin-2 and kinesin-1. By studying homodimeric mutants, we were able to derive a two-head stepping model that fit all the available force-clamp data. The force-velocity and force-run-length curves for KIF3A/B were intermediate between those of KIF3A/A and KIF3B/B, demonstrating that the heterodimer properties could be modeled as an admixture of the behavior of the two motor domains. Furthermore, when fused to a kinesin-1 coiled-coil, both KIF3A and KIF3B homodimers were functional, suggesting that the heterodimeric aspect of the kinesin-2 stalk does not play a dominant role in motor mechanics.

By fitting a kinetic scheme of the KIF3A/B mechanochemical cycle to the data, we find that the canonical model for kinesin-1 stepping can be adapted to describe kinesin-2. Kinesin-2 binds strongly to microtubules in its nucleotide-free, ATP-waiting state, and the lack of ATP dependence for the run length indicates that microtubule release takes place from another (distinct) point in the kinetic cycle. When moving against an opposing load, the velocity of KIF3B/B was slowed to a greater extent than KIF3A/A, and the run length of KIF3B/B was reduced to a lesser extent than KIF3A/A. In that sense, the behavior of KIF3B/B was more similar to kinesin-1 than KIF3A/A. In the cycle of Figure 3, the data were best fit by a model in which the load dependence of neck-linker docking for KIF3B (δ for step k₂) is twice that for KIF3A. The structural basis for this difference is not clear, since the neck linker domains only differ by two residues, neither of which is implicated in key docking interactions with the core catalytic domain and neck cover strand [35].

One hypothesis is that the unconventional load-sensitivity of kinesin-2 might be attributable to its longer neck linker domain. The kinesin step is believed to consist of a concerted conformational change (neck linker docking) followed by a diffusive component, where the tethered head searches for its next binding site. Thus, a plausible expectation might be that extending the neck linker would bias the ability of the tethered head to find its next microtubule binding site when stepping, particularly under loaded conditions. However, the available data (Figures 6 and S5) show that this is not the case: alterations to the neck-linker length and neck-coil domains had negligible effects. Hence, differences in the mechanical properties of kinesin-1 and kinesin-2 reside in the properties of their core motor domains.

No obvious advantage for cellular function emerged from combining two different motor domains, based on comparisons of the velocity and run length of heterodimeric. KIF3A/B and the engineered homodimeric constructs, KIF3A/A and KIF3B/B, which all displayed similar behavior. In this respect, mouse kinesin-2 KIF3A/B differs substantially from C. elegans kinesin-2 KLP11/20, where the engineered homodimer KLP11/11 (equivalent to KIF3B/B) was reported in a previous study to be twofold slower in multiple-motor gliding assays, and non-processive in single-molecule bead assays [15].

The diminished processivity of kinesin-2 under load could, in principle, result from a greater load dependence of the microtubule affinity, or from a load-dependent increase in the time spent in the low microtubule-affinity state. To determine whether microtubule affinity was a determining factor, we performed unbinding-force experiments. Consistent with the robust processivity observed at low ATP concentrations, kinesin-2 motor domains were strongly bound in the nucleotide-free state. Slow unbinding was also found for heads carrying AMP-PNP, which mimics the ATP-bound state. The off-rates under rearward forces in these high-affinity states were greater for kinesin-2 than kinesin-1 but they were significantly lower than the detachment rates when motors stepped against hindering loads at saturating ATP (Figures 5 and S4), and therefore cannot account for the observed processivity differences. In the ADP state, the unbinding rates for KIF3A and KIF3B heads were higher than for kinesin-1, which is broadly consistent with their contrasting run length behavior. However, the force dependencies for detachment in ADP did not differ significantly between motor families, and were significantly weaker than the force dependence of the run lengths (e.g., δ = 0.4 nm for kinesin-1 unbinding force in ADP vs. δ = 1.8 nm for kinesin-1 run length). The load dependence of kinesin-2 processivity cannot therefore be explained simply by differences in the microtubule affinities of various nucleotide states. Instead, the data suggest that the loss of kinesin-2 processivity under load results from the motor spending a greater portion of its hydrolysis cycle in a low-affinity state.

Run-length measurements revealed two distinct regimes of kinesin-2 processivity: loaded and unloaded. Unloaded run lengths were relatively long and strongly influenced by the neck linker length. By contrast, even at a 1 pN (the lowest force explored with the force clamp), run lengths were an order of magnitude shorter and apparently independent of the neck linker length (Figure 6). This disparity contrasts sharply with kinesin-1, where extensions of the neck linker reduced run lengths to a similar degree from zero load out to loads approaching the stall force (Figure S6). A further distinguishing characteristic of kinesin-2 was its occasional tendency to slip backwards, then rapidly reattach to the microtubule and continue stepping (Figures 1B and S1D). Together, these behaviors point toward a mechanism in which motors may spend a portion of the hydrolysis cycle in a weakly-bound state that is readily dissociated by external load. Such a weak binding state may share similarities to diffusive mechanisms proposed for processive KIF1A monomers [36]. Alternatively, motors may periodically detach during processive runs, but the presence of an external load may block reattachment in a way not experienced by conventional kinesin. Slipping was observed for the KIF3B/B homodimer and to an even greater degree for the KIF3A/A homodimer and KIF3A motor domains fused to kinesin-1 coiled-coils. Because kinesin-1 does not slip, this finding argues against electrostatic tethering by the neck-coil domain as the dominant cause of slipping [37]. Instead, the slipping behavior is more likely attributable to an inherent property of the KIF3A/B motor domains, in particular to KIF3A.

Processive kinesin-2 behavior under load has important implications for understanding bidirectional transport in cells. IFT particles, neuronal vesicles, melanosomes, and other cargoes transported by kinesin-2 also carry dynein, and their overall direction of movement is thought to result from competition between plus- and minus-end directed motors [4, 18, 38], which may additionally be subject to regulation. Conventional kinesin-1 slows and eventually stalls under increasing hindering loads. Kinesin-2 motors, as we show here, rapidly dissociate under hindering loads, and are able to rebind quickly after slipping backward. Kinesin-2 behavior is therefore more dynamic than kinesin-1. Computational models have shown that the net direction of bidirectional transport and the directional switching rate depend sensitively upon the parameters that describe the load-dependent properties of motors, and particularly upon their detachment rates [22, 39]. The present work supplies a set of quantitative measurements for constraining such models. We note that kinesin-2 run lengths vary nearly exponentially with external load. However, the effective rate of motor dissociation from the microtubule is not similarly exponential, as assumed by at least one model [22]. Instead, the effective dissociation rate is supplied by the motor velocity divided by the run length, and both of these quantities display different load dependence. The kinesin-2 dissociation rate increases steeply with load (Figure S4), making this motor particularly amenable to dynamic switching during bidirectional transport. The residence time of kinesin-1 on the microtubule, by contrast, is predicted to vary minimally under the influence of opposing loads.

Experimental procedures

Kinesin constructs

Kinesin constructs were prepared as described [17]. KIF3A/B, KIF3A/A and KIF3B/B constructs with native stalks terminated by a His₆ tag were expressed in Sf9 cells.

All other constructs were all expressed in E. coli. [16, 33]. The construct described as “kinesin-1” was generated from the D. melanogaster kinesin heavy chain (KHC) with a stalk truncated at residue 559, fused to a his-tagged GFP sequence. The remaining constructs all had stalks (residues 345–559) identical to kinesin-1, above. The motor domains and neck-linkers for 3A-KHC and 3B-KHC were those from KIF3A and KIF3B respectively. 3A-KHC_P>A and 3A-KHC_{P>A, ΔDAL} were identical to 3A-KHC, with the exception of a proline-to-alanine substitution in the neck linker (AA 355) and, for 3A-KHC_{P>A, ΔDAL}, the deletion of the three last amino acids (DAL) of the neck-linker.

Optical trapping assay

Optical trapping was carried out as described [30]. For all experiments, the motility buffer was 80 mM PIPES, 1 mM EGTA, 4 mM MgCl₂, 2 mg ml⁻¹ BSA, 2 mM dithiothreitol, 10 μM Taxol (Paclitaxel), and nucleotides at the desired concentration. An oxygen scavenging system (1 mg ml⁻¹ glucose, 50 μg ml⁻¹ glucose oxidase and 12 μg ml⁻¹ catalase) was added immediately before use. For high-force unbinding experiments in the presence of AMP-PNP or apyrase, higher concentrations of scavenging system were used (5 mg ml⁻¹ glucose, 250 μg ml⁻¹ glucose oxidase and 60 μg ml⁻¹ catalase). The kinesin molecule was linked to 440-nm-diameter streptavidin-coated polystyrene beads (Spherotech) via a biotinylated Penta-his anti-body (Qiagen). Beads and protein were incubating on a rotator at 4°C for 2 h or more.

Instrumentation

All data were collected with the instrument described in [40]. For force-clamp experiments, the data were recorded at 20 kHz, decimated to 2 kHz, and the position signal was low-pass filtered at 1 kHz. The force-clamp was updated at 500 Hz to maintain a constant offset distance between the trap and bead centers of roughly 80 nm. The laser power was adjusted for each clamp force, and each bead used was calibrated as described [40].

For unbinding force experiments, the trap was maintained at a fixed position, and force was ramped by moving the stage at a constant velocity through the linear region of the trap. Trap stiffness was adjusted appropriately to assure that the bead stayed within this linear region (~120 nm).

Data analysis

The data were analyzed using IGOR Pro 6.0 (WaveMetrics) to obtain velocities, run lengths and randomness values for each experimental condition. Velocity distributions were obtained from individual linear fits to kinesin runs (N = 50–700). Each run length distribution was fit to an exponential distribution, excluding the first bins to account for missing events. The randomness parameter, r, is defined as:

$$r=\underset{t\to \infty }{\text{Lim}}\frac{\langle x{(t)}^2\rangle -{\langle x(t)\rangle }^2}{d\langle x(t)\rangle }$$

where x(t) is motor position, d is the step size, and the angle brackets denote the ensemble average [28]. In all, over 25,000 events were scored in the analysis.

The resulting curves for velocity and randomness, as functions of ATP and force, were fit globally using IGOR Pro: 17 curves for KIF3A/A, KIF3A/B and KIF3B/B were fit simultaneously to constrain 13 free parameters. The analytical expressions used in the curve fitting were generated in Mathematica 8.0 (Wolfram Research) using methods previously described [30, 41]. The full expressions can be found in the Supplemental Experimental Procedures.

The force-dependences of run lengths under hindering loads were fit by exponentials. Because no ATP-dependence of run lengths was observed, these data were fit by a constant. For unbinding-force measurements, separate fits were performed for the distributions obtained for forward and backward pulling directions (see Results section). The characteristic distance, δ, was constrained to be positive.