Delayed Feedback Model of Axonal Length Sensing

Abstract

A fundamental question in cell biology is how the sizes of cells and organelles are regulated at various stages of development. Size homeostasis is particularly challenging for neurons, whose axons can extend from hundreds of microns to meters (in humans). Recently, a molecular-motor-based mechanism for axonal length sensing has been proposed, in which axonal length is encoded by the frequency of an oscillating retrograde signal. In this article, we develop a mathematical model of this length-sensing mechanism in which advection-diffusion equations for bidirectional motor transport are coupled to a chemical signaling network. We show that chemical oscillations emerge due to delayed negative feedback via a Hopf bifurcation, resulting in a frequency that is a monotonically decreasing function of axonal length. Knockdown of either kinesin or dynein causes an increase in the oscillation frequency, suggesting that the length-sensing mechanism would produce longer axons, which is consistent with experimental findings. One major prediction of the model is that fluctuations in the transport of molecular motors lead to a reduction in the reliability of the frequency-encoding mechanism for long axons.

Introduction

A fundamental question in cell biology is how the sizes of subcellular stuctures are determined to scale with the size of the cell and with physiological requirements. It appears that self-organizing processes, together with physical constraints, play a major role in controlling organelle size (1). At least three distinct control mechanisms have been identified (2).

• 1.Molecular rulers. In the case of linear structures such as filaments, size control can be achieved by a molecular ruler protein whose length is equal to the desired length of the growing structure. One classical example is the length of the λ-phage tail, which is determined by the size of the gene product H (gpH) (3). During assembly of the tail, gpH is attached to the growing end in a folded state and protects the growing end from the terminator gene product U (gpU). As the tail elongates, gpH stretches such that when it is fully extended, further growth exposes the tail to the action of gpU.
• 2.Quantal synthesis. Size could be controlled by synthesizing exactly enough material to build a structure of the appropriate size—a process known as quantal synthesis. For example, precursor protein levels are known to affect the length of flagella in the unicellular green alga Chlamydomonas reinhardtii (4), and the length of sea urchin cilia is correlated with the concentration of the protein tektin (5). One prediction of the quantal synthesis model is that doubling the number of flagella should halve their length. However, studies of Chlamydomonas mutants indicate a much weaker dependence of length on the number of flagella, suggesting that there is an additional length-controlling mechanism involving dynamic balance (6) (see below).
• 3.Dynamic balance. Dynamic structures are constantly turning over, so for them to maintain a fixed size, there must be a balance between the rates of assembly and disassembly. If these rates depend on the size in an appropriate way, then there will be a unique balance point that stabilizes the size of the organelle. For example, eukaryotic flagellar microtubules undergo continuous assembly and disassembly at their tips, in which a constant rate of disassembly is balanced by a length-dependent rate of assembly due to a fixed number of molecular motors transporting from the cell body, leading to a fixed flagellar length (6–8). An analogous dynamic balance mechanism is thought to control the length of actin-based structures, such as the stereocilia of the inner ear (9,10). Here, actin filaments constantly treadmill back toward the cell body, with disassembly at the base balanced by assembly at the tip. The latter depends on the diffusion of actin monomers to the tip, which results in a length-dependent rate of assembly. It has also been suggested that a diffusion-induced length dependence of the assembly rate plays a role in the control of the hook length in bacterial flagella (11). A different balance mechanism appears to control the length of microtubules in yeast, where kinesin motors move processively to the microtubule tips where they catalyze disassembly. Longer microtubules recruit more kinesin motors from the cytoplasm, which results in a length-dependent rate of disassembly. When this is combined with a length-independent rate of assembly, a unique steady-state microtubule length is obtained (12–17). A related mechanism involves the modulation of microtubular dynamic instabilities, that is, the catastrophe frequency (18,19).

The problem of length control is particularly acute for the axons of neurons, which exhibit the most significant size differences of any cell type, ranging from several microns to a meter in humans. It is likely that different growth mechanisms operate at different stages of development (20). For example, the initial growth of an axon is determined by preprogrammed transcription factor levels (quantal synthesis) (21), whereas the interstitial growth rates of axons that have connected to their targets is driven by stretching of the organism (22). A major question is whether or not there is an intrinsic length sensor that can coordinate between the transcriptional and metabolic processes controlled by the nucleus and the differential axonal growth and length maintenance. In vitro experimental studies of axonal growth in a variety of neuronal types support the existence of intrinsic length sensors (23–26), but the underlying mechanisms are still largely unknown. Given the lengths involved, it is unlikely that a diffusion-based mechanism or a molecular ruler such as a microtubule can be involved.

Recently, Rishal et al (27,28) have proposed a bidirectional motor transport mechanism for cellular-length sensing in axons, which would form the front end of a length control mechanism that is distinct from those described in the above list. A schematic illustration of the motor-based model is shown in Fig. 1. An anterograde signal is transported by kinesin motors from the cell body to the tip of the growing axon, where it activates the dynein-mediated transport of a retrograde signal back to the cell body. The retrograde signal then represses the anterograde signal via negative feedback, resulting in an oscillating retrograde signal whose frequency decreases with axon length. If axonal growth rates are correlated with this frequency, then spatial information regarding the length of the axon can be communicated to the cell body, where the frequency-dependent activation of transcription factors (29) could regulate axonal growth. One major prediction of the model based upon computer simulations is that reducing either anterograde or retrograde signals (by the partial knockdown of kinesin or dynein motor activity) should increase axonal length. This prediction has been confirmed experimentally in peripheral sensory neurons (27). We note that a previous model presented by Kam et al. (26) is inconsistent with the experimental data. The earlier model assumes that the unidirectional transport of a retrograde signal by dynein motors maintains axonal growth until the signal at the cell body becomes too weak due to a constant rate of signal loss en route. In this case, the partial knockdown of motor activity would lead to shorter axons.

Figure 1.

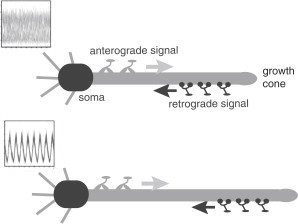
Schematic diagram of the bidirectional motor-transport mechanism for axonal length sensing hypothesized by Rishal et al. (27). A kinesin-based anterograde signal activates a dynein-based retrograde signal that itself represses the anterograde signal via negative feedback. The frequency of the resulting oscillatory retrograde signal decreases with axonal growth.

In this article, we develop a mathematical model of the biophysical mechanism proposed by Rishal et al. (27) to carry out a more systematic investigation of the dynamical process that generates oscillations, and how the oscillation frequency depends on various biophysical parameters. We first consider a simple delay-differential equation with negative feedback that models the chemical signals at the somatic and distal ends of the axon. The molecular motors are not modeled explicitly; rather, their active transport is assumed to introduce a discrete delay that varies linearly with axonal length. We show how oscillations arise at a critical axonal length via a Hopf bifurcation, and we obtain a length-dependent frequency consistent with the previous computational model. We then construct a system of advection-diffusion equations that couple the chemical signaling with the active transport of kinesin and dynein motors. Each advection-diffusion equation is an effective mean-field equation for the transport of a population of motors of a given type, which randomly switch between a motile state (bound to a microtubule) and a diffusive state (unbound). We show how this model supports a similar length-dependent frequency to the delayed-feedback model. We also show how knockdown of either motor type increases the frequency, thus leading to longer axons, as found experimentally. One prediction of our model is that the critical axonal length at which oscillations first occur increases with diffusivity D, but the frequency of oscillations beyond criticality is relatively insensitive to D. Although the diffusion term partially captures the stochastic nature of motor transport, there are additional levels of stochasticity that are not captured by the mean-field model. By carrying out numerical simulations of 1) the computational model of Rishal et al. (27) and 2) a stochastic version of our advection-diffusion model, we show that there are fluctuations in the frequency of the oscillatory signal whose coefficient of variation (standard deviation/mean) increases monotonically with length. This suggests that the proposed mechanism for axonal length sensing could break down for long axons.

Model formulation

Delayed-feedback model

Consider an axon of length L with x = 0 corresponding to the proximal end (adjacent to the cell body or soma) and x = L corresponding to the distal end (axonal tip). In this article, we ignore the dynamics of L by exploiting the fact that axonal growth occurs much more slowly than the timescales of motor transport. Under this adiabatic approximation, we can treat L as fixed and investigate the occurrence of oscillations in chemical signaling for fixed length. This is then used to determine how the frequency of oscillations varies as a function of length. Let u_E(t) denote the anterograde chemical signal at x = L at time t, which is transported by kinesin motors from the proximal end at x = 0. In a similar way, let u_I(t) denote the retrograde signal at x = 0 at time t, which is transported by dynein motors from the distal end, x = L. For the moment, we will assume the simplest possible model of active transport, in which both types of motor travel at a constant speed, v, along the axon (via binding to polarized microtubules). This means that for given length L, there is delay, τ = L/v, between the production of a signal at one end and its arrival at the opposite end. This motivates the following delayed-feedback model (see Fig. 2):

$$\frac{d{u}_{\text{E}}}{dt}=I_0-\gamma u_{\text{E}}-W_{\text{I}}f\left(u_{\text{I}}\left(t-\tau \right)\right),$$ (1a)

$$\frac{d{u}_{\text{I}}}{dt}=-\gamma u_{\text{I}}+W_{\text{E}}f\left(u_{\text{E}}\left(t-\tau \right)\right),$$ (1b)

where γ is a decay rate. For simplicity, we take the decay rate to be the same for both chemical signals. The weights W_E and W_I determine the strength of the positive and negative feedback terms based on some form of Michaelis-Menten kinetics, so that f is given by the Hill function

$$f\left(u\right)=\frac{u^n}{K^n+u^n}$$ (2)

for dissociation constant K and Hill coefficient n. We take n = 4 and fix the scale of the weights W_E and W_I and the input I₀ by setting K = 2. The constant input, I₀, determines the rate at which kinesin packets are released at x = 0 in the absence of negative feedback (W_I = 0).To match with the results of Rishal et al. (27), we take γ⁻¹ = 100 s. Since kinesin and dynein motor velocities, v, are of order 1 μm/s, it follows that τγ = 1 corresponds to an axonal length of 100 μm. In the following, we fix the units of time by setting γ = 1.

Figure 2.

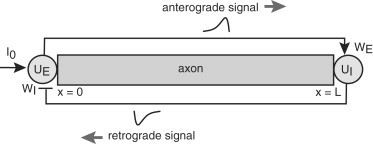
Schematic diagram of the feedback model. See text for details.

Linear stability analysis

To relate our model to the length-sensing mechanism hypothesized by Rishal et al. (27), we look for a periodic solution of the coupled system given by Eq. 1 and determine how the effective frequency, ω, of the solution (if it exists) depends on the delay, τ, and thus on the axonal length, L. First, setting time derivatives to zero in Eq. 1 yields the steady-state solutions $u_E^{\ast }$ and $u_I^{\ast }$:

$$u_{\text{E}}^{\ast }=I_0-W_{\text{I}}f\left(u_{\text{I}}^{\ast }\right),u_{\text{I}}^{\ast }=W_{\text{E}}f\left(u_{\text{E}}^{\ast }\right).$$ (3)

Linearizing Eq. 1 about the steady state yields the linear system

$${\dot{y}}_{\text{E}}=-y_{\text{E}}-{\alpha }_{\text{I}}{y}_{\text{I}}\left(t-\tau \right)$$ (4a)

$${\dot{y}}_{\text{I}}=-y_{\text{I}}+{\alpha }_{\text{E}}{y}_{\text{E}}\left(t-\tau \right),$$ (4b)

where, for P = E,I, $y_{\text{P}}\left(t\right)\equiv u_{\text{P}}\left(t\right)-u_{\text{P}}^{\ast }$, ${\dot{y}}_{\text{P}}\equiv d{y}_{\text{P}}/dt$, and ${\alpha }_{\text{P}}\equiv W_{\text{P}}{f}^{\prime }\left(u_{\text{P}}^{\ast }\right)$. This has the solution y_P(t) = e^λtY_P, with λ determined from the eigenvalue equation set

$$\left(\lambda +1\right)e^{\lambda t}{Y}_{\text{E}}=-{\alpha }_{\text{I}}{Y}_{\text{I}}{e}^{\lambda \left(t-\tau \right)}$$ (5a)

$$\left(\lambda +1\right)e^{\lambda t}{Y}_{\text{I}}={\alpha }_{\text{E}}{Y}_{\text{E}}{e}^{\lambda \left(t-\tau \right)}.$$ (5b)

In accordance with standard analysis of delay differential equations, we determine the necessary conditions for the emergence of a time-periodic solution via a Hopf bifurcation, setting λ = iω and Y_P = U_P + iV_P in Eqs. 5a and 5b. Equating real and imaginary parts in the resulting system yields a matrix equation A(U_E,V_E,U_I,V_I)^⊤ = 0 with

$$\mathbf{A}=\left(\begin{array}{cccc}1& -\omega & {\alpha }_{\text{I}}\text{cos}\left(\omega \tau \right)& {\alpha }_{\text{I}}\text{sin}\left(\omega \tau \right)\\ \omega & 1& -{\alpha }_{\text{I}}\text{sin}\left(\omega \tau \right)& {\alpha }_{\text{I}}\text{cos}\left(\omega \tau \right)\\ -{\alpha }_{\text{E}}\text{cos}\left(\omega \tau \right)& -{\alpha }_{\text{E}}\text{sin}\left(\omega \tau \right)& 1& -\omega \\ {\alpha }_{\text{E}}\text{sin}\left(\omega \tau \right)& -{\alpha }_{\text{E}}\text{cos}\left(\omega \tau \right)& \omega & 1\end{array}\right)$$

For (U_E,V_E,U_I,V_I)^⊤ to be nontrivial, we require the matrix A to have a zero determinant. It turns out that this holds if U_I = V_E = 0 and $V_{\text{I}}=\pm \sqrt{{\alpha }_{\text{E}}/{\alpha }_{\text{I}}}{U}_{\text{E}}$. We thus obtain the following conditions for a Hopf bifurcation:

$$\omega =\text{cot}\left(\omega \tau \right),\sqrt{{\alpha }_{\text{E}}{\alpha }_{\text{I}}}\text{sin}\left(\omega \tau \right)=1.$$ (6)

It is clear that these conditions cannot be satisfied in the absence of a delay (τ = 0). Indeed, setting τ = 0 in Eqs. 5a and 5b shows that there exists a pair of eigenvalues given by ${\lambda }_{\pm }=-1\pm \sqrt{-{\alpha }_{\text{I}}{\alpha }_{\text{E}}}$. Since the real part of λ_± is always negative, it follows that the steady-state $\left(u_{\text{E}}^{\ast },u_{\text{I}}^{\ast }\right)$ is stable, and periodic solutions cannot exist in the absence of a delay. On the other hand, if $\sqrt{{\alpha }_{\text{E}}{\alpha }_{\text{I}}}>1$, then a pair of complex conjugate eigenvalues crosses the imaginary axis at a critical positive delay, τ_c, which depends on $\sqrt{{\alpha }_{\text{E}}{\alpha }_{\text{I}}}$ (see Fig. 4 a). Although this is not sufficient to guarantee the emergence of a stable periodic solution via a supercritical Hopf bifurcation for τ > τ_c, the existence of stable oscillations beyond the Hopf bifurcation point can be verified numerically as illustrated in Fig. 3. Moreover, the frequency of the oscillation decreases monotonically with τ such that there is an approximately fivefold decrease in frequency when axonal length reaches ∼ 1000 μm (see Fig. 4 b). This is in agreement with the computational model of Rishal et al. (27).

Figure 4.

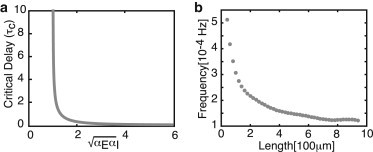
(a) Plot of critical delay τ_c as a function of the effective coupling parameter $\sqrt{{\alpha }_{\text{E}}{\alpha }_{\text{I}}}$. Both are in units of 100 s. (b) Frequency of periodic solutions plotted against axonal delay. Parameter values are as in Fig. 3.

Figure 3.

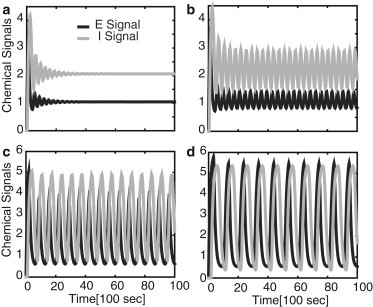
Chemical signal oscillations in the delayed-feedback model given by Eq. 1 for various values of the delay (in units of 100 s): τ = 0.2 (a); τ = 0.29 (b); τ = 0.75 (c); and τ = 1.5 (d). Other parameter values are n = 4, I₀ = 6, W_E = W_I = 5.5 such that τ_c ≈ 0.25.

The Hopf bifurcation condition given by Eq. 6 can only be satisfied if $\sqrt{{\alpha }_{\text{E}}{\alpha }_{\text{I}}}>1$. Since ${\alpha }_{\text{P}}\equiv W_{\text{P}}{f}^{\prime }\left(u_{\text{P}}^{\ast }\right)$, it follows that the strengths, W_P, of the chemical signals carried by kinesin and dynein, respectively, must be sufficiently strong and/or the Hill function must be sufficiently steep. The latter suggests that oscillations are facilitated if the interactions between the chemical signals and the opposing molecular motors are cooperative in nature, as determined by the value of the Hill coefficient n in Eq. 2. In conclusion, our simple mathematical model makes explicit the crucial role of negative feedback in the proposed frequency-encoding mechanism for axonal length sensing, and it provides an analytical framework for studying such a mechanism. However, as it stands, the model is too phenomenological. In particular, it does not explicitly take into account the motion of the molecular motors. To incorporate the latter, we now consider a spatially extended version of our model that takes the form of an advection-diffusion equation.

Advection-diffusion model

Let c_± (x,t) denote the density of kinesin (+) and dynein (−) motors at position x along the track. A simple model of active motor transport is to assume that the motor densities evolve according to an advection-diffusion equation (30–32):

$$\frac{\partial c_{+}}{\partial t}=-v\frac{\partial c_{+}}{\partial x}+D\frac{{\partial }^2{c}_{+}}{\partial x^2}$$ (7a)

$$\frac{\partial c_{-}}{\partial t}=v\frac{\partial c_{-}}{\partial x}+D\frac{{\partial }^2{c}_{-}}{\partial x^2}.$$ (7b)

These are supplemented by the following boundary conditions at the ends, x = 0,L:

$$D{\partial }_x{c}_{+}\left(L,t\right)=0,D{\partial }_x{c}_{-}\left(0,t\right)=0$$ (8)

and

$$J_{+}\left(0,t\right)=J_{\text{E}}\left(t\right),J_{-}\left(L,t\right)=J_{\text{I}}\left(t\right),$$ (9)

where we have introduced the fluxes

$$J_{\pm }\left(x,t\right)=\pm v{c}_{\pm }\left(x,t\right)-D\frac{\partial c_{\pm }}{\partial x}.$$ (10)

The boundary conditions given by Eq. 8 impose the condition that the Fickian contribution to the flux of motors exiting the axon is zero. We are also assuming that at end x = 0, kinesin motors are injected in the anterograde direction at a rate J_E(t), whereas at end x = L, dynein motors are injected at a rate J_I(t) in the retrograde direction. For simplicity, we take the mean speed and diffusivity of both motor species to be the same. Although dynein motors tend to move more slowly than kinesin motors, they are of the same order of magnitude. Moreover, we obtain similar results if the differences between the motors are taken into account.

Suppose that each kinesin motor complex carries an amount κ_E of excitatory chemical signaling molecules, X_E, and each dynein motor carries an amount κ_I of inhibitory chemical signaling molecules, X_I. When kinesin motors reach x = L they release the molecules X_E, which then enhance the injection rate of mobile dynein motors, whereas when dynein motors reach x = 0, they release the molecules X_I, which then reduce the injection rate of mobile kinesin motors. We thus take

$$J_{\text{E}}\left(t\right)=v\left(I_{\text{E}}-w_{\text{I}}f\left[u_{\text{I}}\left(t\right)\right]\right)$$ (11a)

$$J_{\text{I}}\left(t\right)=-v{w}_{\text{E}}f\left[u_{\text{E}}\left(t\right)\right],$$ (11b)

where u_E(t) is the concentration of X_E at x = L, u_I(t) is the concentration of X_I at x = 0, and I_E is the flux of kinesin motors injected at the proximal end. The latter evolve according to the pair of equations

$$\frac{d{u}_{\text{E}}}{dt}=-\gamma u_{\text{E}}+{\kappa }_{\text{E}}{c}_{+}\left(L,t\right)$$ (12a)

$$\frac{d{u}_{\text{I}}}{dt}=-\gamma u_{\text{I}}+{\kappa }_{\text{I}}{c}_{-}\left(0,t\right).$$ (12b)

In the case of pure ballistic motor transport at a fixed speed, v, and D = 0, the above model reduces to our delayed-feedback model. First, note that the solutions to Eqs. 7a and 7b have the simple form

$$c_{+}\left(x,t\right)=F_{+}\left(t-x/v\right),c_{-}\left(x,t\right)=F_{-}\left(t+x/v\right),$$ (13)

with functions F₊ and F₋ determined by the boundary conditions in Eq. 9—the boundary conditions in Eq. 8 are not needed for these quasilinear differential equations. Thus,

$$F_{+}\left(t\right)=I_{\text{E}}-w_{\text{I}}f\left[u_{\text{I}}\left(t\right)\right],F_{-}\left(t+L/v\right)=w_{\text{E}}f\left[u_{\text{E}}\left(t\right)\right].$$ (14)

Substituting this into Eqs. 12a and 12b, we recover our previous model given by Eq. 1 with I₀ = κ_EI_E, and W_p = k_pw_p for P = E,I. The spatially extended model can be analyzed along similar lines to the simpler model using Green’s functions (see Materials and Methods), and it also supports chemical oscillations with a length-dependent frequency (see Results).

Materials and Methods

Analysis in terms of Green’s functions

In the case where the diffusion coefficient is nonzero, the solution to Eqs. 7a and 7b subject to the boundary conditions of Eqs. 8 and 9 is given by:

$$c_{+}\left(x,t\right)={\int }_0^{\text{L}}{G}_{+}\left(\xi ,0;x,t\right){\psi }_{+}\left(\xi \right)d\xi +v{\int }_0^t{G}_{+}\left(0,\sigma ;x,t\right)\left[I_{\text{E}}-w_{\text{I}}f\left(u_{\text{I}}\left(\sigma \right)\right)\right]d\sigma$$ (15)

and

$$c_{-}\left(x,t\right)={\int }_0^{\text{L}}{G}_{-}\left(\xi ,0;x,t\right){\psi }_{-}\left(\xi \right)d\xi +v{\int }_0^t{G}_{-}\left(L,\sigma ;x,t\right)w_{\text{E}}f\left(u_{\text{E}}\left(\sigma \right)\right)d\sigma ,$$ (16)

where ψ₊ and ψ₋ are the initial conditions for c_± and G_± are the Green’s functions for the respective advection-diffusion operators (see appendix):

$$G_{+}\left(\xi ,\sigma ,x,t\right)=\sum _{n=1}^{\infty }{e}^{\left(-\left(D{\lambda }_n+\frac{v^2}{4D}\right)\left(t-\sigma \right)\right)}{e}^{\left(-\frac{v}{2D}\left(\xi -x\right)\right)}\times \left(\text{sin}\left(\sqrt{{\lambda }_n}x\right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_{n}x}\right)\right)\left(\text{sin}\left(\sqrt{{\lambda }_n}\xi \right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n\xi }\right)\right)$$ (17a)

$$G_{-}\left(\xi ,\sigma ,x,t\right)=\sum _{n=1}^{\infty }{e}^{-\left(D{\lambda }_n+\frac{v^2}{4D}\right)\left(t-\sigma \right)}{e}^{\frac{v}{2D}\left(\xi -x\right)}\times \left(\text{sin}\left(\sqrt{{\lambda }_n}x\right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_{n}x}\right)\right)\left(\text{sin}\left(\sqrt{{\lambda }_n}\xi \right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n\xi }\right)\right),$$ (17b)

where λ_n is an eigenvalue of the advection-diffusion operator satisfying $4Dv\sqrt{{\lambda }_n}\text{cot}\left(\sqrt{{\lambda }_n}L\right)=4D^2{\lambda }_n-v^2$. Substituting Eqs. 15 and 16 into Eqs. 12a and 12b, respectively, yields

$$\frac{d{u}_{\text{E}}}{dt}=-u_{\text{E}}+v{\kappa }_{\text{E}}\left({\int }_{-\infty }^t{G}_{+}\left(0,\sigma ;L,t\right)\left(I_{\text{E}}-w_{\text{I}}f\left[u_{\text{I}}\left(\sigma \right)\right]\right)d\sigma \right)$$ (18a)

and

$$\frac{d{u}_{\text{I}}}{dt}=-u_{\text{I}}+v{\kappa }_{\text{I}}\left({\int }_{-\infty }^t{G}_{-}\left(L,\sigma ;0,t\right)w_{\text{E}}f\left[u_{\text{E}}\left(\sigma \right)\right]d\sigma \right).$$ (18b)

We have taken the lower time limit to be t = −∞ to eliminate the transient terms.

Equation 18a and 18b have the steady-state solution

$$u_{\text{E}}^{\ast }=v{\kappa }_{\text{E}}{\overline{G}}_{+}\left(L\right)\left(I_{\text{E}}-w_{\text{I}}f\left[u_I^{\ast }\right]\right)$$ (19a)

$$u_{\text{I}}^{\ast }=v{\kappa }_{\text{I}}{\overline{G}}_{-}\left(L\right)w_{\text{E}}f\left[u_{\text{E}}^{\ast }\right],$$ (19b)

with

$${\overline{G}}_{+}\left(L\right)={\int }_{-\infty }^{\infty }{G}_{+}\left(0,0;L,t\right)dt,{\overline{G}}_{-}\left(L\right)={\int }_{-\infty }^{\infty }{G}_{-}\left(L,0;0,t\right)dt.$$

Linearizing Eqs. 18a and 18b about the steady states gives

$${\dot{y}}_{\text{E}}=-y_{\text{E}}-v{\alpha }_{\text{I}}{\int }_{-\infty }^t{G}_{+}\left(0,\sigma ;L,t\right)y_{\text{I}}d\sigma$$ (20a)

$${\dot{y}}_{\text{I}}=-y_{\text{I}}+v{\alpha }_{\text{E}}{\int }_{-\infty }^t{G}_{-}\left(L,\sigma ;0,t\right)y_{\text{E}}d\sigma .$$ (20b)

Introducing the causal Green’s function ${\mathcal{G}}_{\pm }\left(t\right)=G_{\pm }\left(t\right)H\left(t\right)$, where H(t) is the Heaviside function, we can take the upper time limit in the convolution integrals to be t = ∞. Fourier transforming the resulting linearized system using the convolution theorem then yields

$$\left(i\omega +1\right)Y_{\text{E}}=-v{\alpha }_{\text{I}}{\hat{\mathcal{G}}}_{+}\left(\omega \right)Y_{\text{I}}$$ (21a)

$$\left(i\omega +1\right)Y_{\text{I}}=v{\alpha }_{\text{E}}{\hat{\mathcal{G}}}_{-}\left(\omega \right)Y_{\text{E}},$$ (21b)

where

$${\hat{\mathcal{G}}}_{\pm }\left(\omega \right)={\int }_{-\infty }^{\infty }{\mathcal{G}}_{\pm }\left(t\right){\text{e}}^{-i\omega t}dt,Y_{\text{P}}\left(\omega \right)={\int }_{-\infty }^{\infty }{y}_{\text{P}}\left(t\right){\text{e}}^{-i\omega t}dt.$$

Equations 21a and 21b are identical in form to Eqs. 5a and 5b for λ = iω under the replacement ${\text{e}}^{-i\omega \tau }\to v{\hat{\mathcal{G}}}_{+}\left(\omega \right)$. Thus, we can derive conditions for the occurrence of a Hopf bifurcation much as they are derived in the delay differential equation model. That is, we take ω to be real and set Y_P = U_P + iV_P for P = E,I:

$$\left(i\omega +1\right)\left(U_{\text{E}}+i{V}_{\text{E}}\right)=-v{\alpha }_{\text{I}}\left(U_{\text{I}}+i{V}_{\text{I}}\right){\hat{\mathcal{G}}}_{+}\left(\omega \right)$$ (22a)

$$\left(i\omega +1\right)\left(U_{\text{I}}+i{V}_{\text{I}}\right)=v{\alpha }_{\text{E}}\left(U_{\text{E}}+i{V}_{\text{E}}\right){\hat{\mathcal{G}}}_{-}\left(\omega \right),$$ (22b)

with

$${\hat{\mathcal{G}}}_{+}\left(\omega \right)=\sum _{n=0}^{\infty }\frac{1}{i\omega +D{\lambda }_n+\frac{v^2}{4D}}{e}^{\left(\left(D{\lambda }_n+\frac{v^2}{4D}\right)\sigma \right)}{e}^{\left(-\frac{v}{2D}\left(\xi -x\right)\right)}\times \left(\text{sin}\left(\sqrt{{\lambda }_n}x\right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n}x\right)\right)(\text{sin}\left(\sqrt{{\lambda }_n}\xi \right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n}\xi \right))$$ (23a)

$${\hat{\mathcal{G}}}_{+}\left(\omega \right)=\sum _{n=0}^{\infty }\frac{1}{i\omega +D{\lambda }_n+\frac{v^2}{4D}}{e}^{\left(\left(D{\lambda }_n+\frac{v^2}{4D}\right)\sigma \right)}{e}^{\frac{v}{2D}\left(\xi -x\right)}\times \left(\text{sin}\left(\sqrt{{\lambda }_n}x\right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n}x\right)\right)\left(\text{sin}\left(\sqrt{{\lambda }_n}\xi \right)+\frac{2D\sqrt{{\lambda }_n}}{v}\text{cos}\left(\sqrt{{\lambda }_n}\xi \right)\right).$$ (23b)

We then equate real and imaginary parts and solve the resulting 4 × 4 matrix equation for the vector (U_E,V_E,U_I,V_I)^T.

Numerical methods and parameter values

We simulated the advection-diffusion model given by Eq. 7 using a backward Euler time discretization. We used an upwind scheme for the spatial discretization associated with the advection term and a central difference scheme for the spatial discretization of the diffusion term. Let $U_j^n$ be the numerical approximation to the true solution of c₊ in Eq. 7 at the jth spatial lattice point and the nth time step, let $V_j^n$ be the numerical approximation to the true solution of c₋ in Eq. 7 at the jth spatial lattice point and the nth time step, let k be the time step, and let h be the spatial step. Then, the finite difference scheme used was

$$\frac{U_j^{n+1}-U_j^n}{k}=-v\frac{U_j^{n+1}-U_{j-1}^{n+1}}{h}+D\frac{U_{j+1}^{n+1}-2U_j^{n+1}+U_{j-1}^{n+1}}{h^2}$$ (24a)

$$\frac{V_j^{n+1}-V_j^n}{k}=v\frac{V_{j+1}^{n+1}-V_j^{n+1}}{h}+D\frac{V_{j+1}^{n+1}-2V_j^{n+1}+V_{j-1}^{n+1}}{h^2},$$ (24b)

where v and D are the motor velocities and diffusion coefficients, respectively. For Eqs. 18a and 18b, we used an explicit scheme. To account for the Neumann and Robin boundary conditions, which are given by Eqs. 8 and 9, respectively, we used ghost points. That is, if there are N spatial lattice points with Nh = L, we introduced points at the lattice point N + 1 and −1 to account for the boundary conditions:

$$\begin{array}{l}\frac{U_{N+1}^n-U_{N-1}^n}{2h}=0,\frac{V_1^n-V_{-1}^n}{2h}=0\hfill \\ v{U}_0^n-D\frac{U_1-U_{-1}}{2h}=v\left(I_{\text{E}}-w_{\text{I}}f\left[u_{\text{I}}\left(t\right)\right]\right)\hfill \\ -v{V}_N^n-D\frac{V_{N+1}^n-V_{N-1}^n}{2h}=-v{w}_{\text{E}}f\left[u_{\text{E}}\left(t\right)\right].\hfill \end{array}$$

We solve for the ghost lattice points in the schemes for the boundary conditions and substitute them into Eqs. 24a and 24b.

The motor velocity, v, was chosen to be 1 μm/s based on generally known distributions of velocities for kinesin and dynein motors. Other parameters were chosen for suitable computation of Eq. 7. The one thing we made sure of was to keep I_E > w_I to allow for the continued propagation of the solutions to Eq. 7. This corresponds to ensuring that the background flux of kinesin motors at the proximal end is sufficient to overcome the suppressive effects of the retrograde signal from the dynein motors. Choosing w_I > I_E causes an abrupt end to the solutions and is not realistic for our biological mechanism to function. Unless otherwise noted, parameter values were taken as follows: I₀ = 10, w_E = w_I = 9, γ_E = γ_I = 1, κ_E = κ_I = 1, v = 1 μm s⁻¹, D = 0.1 μm² s⁻¹, L = 100 μm, h = 0.1 μm, k = 1 s.

Results

As shown in Materials and Methods, the advection-diffusion model is structurally similar to the simple delayed-feedback model, except that the discrete delay τ = L/v is replaced by a distribution of delays given by a corresponding Green’s function that depends on the axonal length, L. This suggests that the advection-diffusion model will also exhibit oscillations beyond a critical length, L_c, whose frequency decreases monotonically beyond L_c. This is indeed found to be the case, as illustrated in Fig. 5. In contrast to the previous model, we can now also keep track of the density profile of the kinesin and dynein motors during a single cycle of the chemical oscillations. The variation in the density profiles at different points in the cycle are shown in Fig. 6. Fig. 6 a shows a growing distribution of kinesin motors due to injection at the proximal end and negligible dynein. Subsequent excitation of the dynein motors by the chemical signal transported by the kinesin motors results in a growing dynein distribution (Fig. 6 b). This leads to inhibition of the kinesin motors (Fig. 6 c). The reduction in the kinesin motor density causes the density of dynein motors to diminish throughout the axon, which then allows the kinesin density to grow again (Fig. 6 d).

Figure 5.

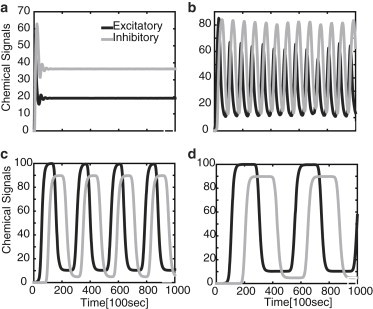
Chemical signal oscillations in the advection-diffusion model described by Eq. 7 for various axonal lengths: L = 100 μm (a); L = 500 μm (b); L = 1000 μm (c); and L = 2000 μm (d). Other parameter values are I₀ = 10, w_E = w_I = 9, γ = 1, κ_E = κ_I = 1, v = 1 μm s⁻¹, and D = 0.1 μm² s⁻¹.

Figure 6.

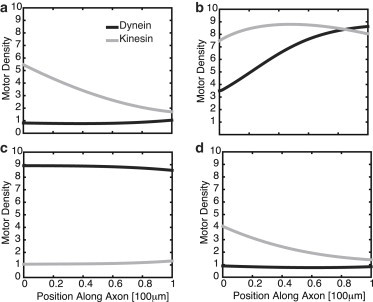
Spatial profiles for kinesin and dynein motors at different times during one cycle of period T = 2π/ω after transients have disappeared. (a) t = 0. (b) t = T/4. (c) t = T/2. (d) t = 3T/4. The initial condition for the kinesin motors is a hyperbolic secant function, whereas the initial condition for the dynein motors is zero. Here, L = 100 μm and other parameters are as in Fig. 5.

One immediate issue that arises is how the emergence of oscillations and the length-dependent frequency depend on the diffusivity D. We find that for sufficiently long axons, the frequency ω is approximately independent of D. On the other hand, the critical length, L_c, for the emergence of oscillations does depend on D. This is illustrated in Fig. 7, which shows the variation in frequency as a function of length for different diffusivities. In each case, the frequency is a monotonically decreasing function of L, consistent with the delayed-feedback model. Increasing diffusion coefficient D also increases L_c so that it can result in the disappearance of the oscillations, as shown in Fig. 8.

Figure 7.

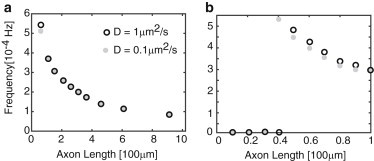
Variation in frequency as a function of length for different diffusivities in the advection-diffusion model. Other parameters are the same as in Fig. 5. (a) Plot showing that the frequency is insensitive to D except at small axonal lengths. (b) Plot showing that the main effect of diffusivity is to modify the critical length at which a Hopf bifurcation occurs. (A zero frequency indicates that the system is operating below the Hopf bifurcation point, so there are no oscillations.)

Figure 8.

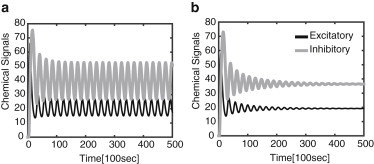
Chemical signals in the advection-diffusion model for D = 0.1 μm² s⁻¹ (a) and D = 100 μm² s⁻¹ (b). Here, L = 500 μm and other parameter values are as in Fig. 5.

Knockdown of molecular motor activity

One of the key predictions of the mechanism proposed by Rishal et al. (27) is that when the number of motors in a given axon are inhibited or knocked down, the axon’s length should grow due to a resulting increase in the frequency of the retrograde signal. We can model the partial knockdown of kinesin motors in an axon by decreasing the background rate of kinesin flux I₀. In a similar way, we can model dynein knockdown by decreasing w_E, the strength of the kinesin-mediated excitation of dynein activity at the distal end. In both cases, we find that the required axon length for the normalized frequency to decay to a particular value is greater than when kinesin or dynein motors are knocked down to a lesser extent (see Fig. 9).

Figure 9.

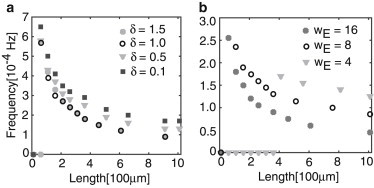
Variation in frequency as a function of length for decreasing flux δ ≡ I₀ − w_I (a) (representing knockdown of kinesin) and decreasing excitatory coupling, w_E (b) (representing knockdown of dynein). Other parameters are the same as Fig. 5.

Effects of noise

Modeling active motor transport in terms of an advection-diffusion equation is a mean-field treatment of the underlying stochastic transport mechanism, in which motors randomly switch between a motile state (bound to a microtubule) and a stationary or slowly diffusing state (unbound to a microtubule). Although the advection-diffusion equation partially captures the stochastic nature of motor transport at the population level, there are additional sources of stochasticity not taken into account by the mean-field model. First, the stochastic transport of an individual molecular motor is more accurately described by a differential Chapman-Kolmogorov equation, which determines the probability density that the motor is at a particular location and in a particular internal state (mobile or stationary) at time t (32). If the transition rates between the internal states are sufficiently fast compared to the hopping rate of motors along the filament, then a quasi-steady-state reduction of the Chapman-Kolmogorov equation to a Fokker-Planck equation can be carried out (33). Furthermore, if the number of motors is sufficiently large, and they move independently (i.e., no exclusion effects), then the concentration of motors can be represented by an advection-diffusion equation, which is obtained by multiplying the Fokker-Planck equation by the number of motors. It follows that additional stochastic effects arise in the case of a finite number of motors and slow transition rates. Yet another possible source of noise is the random loss of chemical signals carried by the motors, or the failure of a motor to rebind to the track; these would also lead to additional decay terms in the mean-field model.

The presence of various sources of noise suggests that the encoding of axonal length in terms of the frequency of a retrograde chemical signal could break down for long axons due to the accumulation of fluctuations. We will demonstrate this by presenting results of simulations of 1) a slightly modified version of the computational model of Rishal et al. (27) and 2) a stochastic version of our advection-diffusion model. The former explicitly takes into account finite-size effects by tracking the motion of individual motors. However, rather than explicitly modeling the stochastic stop-and-go motion of molecular motors, Rishal et al. (27) assume that each motor undergoes ballistic motion with a constant velocity that is generated from an experimentally determined velocity distribution, one for kinesin and the other for dynein. We implemented the computational model from that study using the same velocity distributions, but with a modified scheme for injecting motors at each end. That is, rather than injecting motors as packets of fixed size, we injected individual motors at an instantaneous rate given by J_E(t) and J_I(t), respectively (see Eqs. 11a and 11b). The background flux of kinesin motors at x = 0, J_E, was taken to be 100 motors/min, each motor was assumed to carry one unit of chemical signal, and it was assumed that w_E = w_I = 9. The results of computer simulations are shown in Fig. 10 averaged over 100 trials (see below). The mean oscillation frequency decreases monotonically with axonal length L, as in our advection-diffusion model, but the relative size of fluctuations increases with L. This is established by plotting the coefficient of variation (CV), which is the standard deviation over the mean, as a function of length L. It can be seen that axons of length L = 1000 μm have CV ≈ 0.12, indicating nontrivial noise levels.

Figure 10.

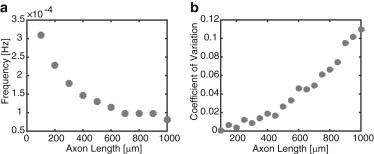
Effects of noise on the frequency-encoding mechanism for axonal length sensing in the computational model of Rishal et al. (27) with modified end conditions (see text for details). (a) Average frequency versus axonal length. (b) Coefficient of variation versus axonal length. The plots were obtained by running the simulations over 100 trials.

It is important to note that our advection-diffusion model is not a mean-field version of the above computational model but is based on a more realistic model of the stop-and-go transport of molecular motors. (The random switching between motile and nonmotile states would generate the velocity distributions used in the Rishal et al. model.) Inclusion of finite-size effects is expected to generate some form of multiplicative noise terms in the underlying advection-diffusion model. We hope to explore this issue in more detail elsewhere. Here, we take a more brute-force approach by adding a constant white-noise term to the righthand side of Eqs. 7a and 7b:

$$\frac{\partial c_{+}}{\partial t}=-v\frac{\partial c_{+}}{\partial x}+D\frac{{\partial }^2{c}_{+}}{\partial x^2}+\mu {\xi }_{+}\left(x,t\right)$$ (25a)

$$\frac{\partial c_{-}}{\partial t}=v\frac{\partial c_{-}}{\partial x}+D\frac{{\partial }^2{c}_{-}}{\partial x^2}+\mu {\xi }_{-}\left(x,t\right),$$ (25b)

with μ the noise strength, $\langle {\xi }_{\pm }\left(x,t\right)\rangle =0$, and

$$\langle {\xi }_{\pm }\left(x,t\right){\xi }_{\pm }\left(x^{\prime },t^{\prime }\right)\rangle =\delta \left(t-t^{\prime }\right)\delta \left(x-x^{\prime }\right),\langle {\xi }_{\pm }\left(x,t\right){\xi }_{\mp }\left(x^{\prime },t^{\prime }\right)\rangle =0.$$

The boundary conditions for this model are the same as in the deterministic advection-diffusion model. It is important to note that the above stochastic advection-diffusion model does not exactly conserve the number of molecular motors. However, conservation is approximately satisfied, since ${\int }_0^L{\xi }_{\pm }\left(x,t\right)dx\approx 0$. The units of μ are $1/\sqrt{\text{length}\times \text{time}}$. We find that the variance in the frequency of oscillations is approximately independent of length—the variance for different values of the noise strength, μ, are plotted in Fig. 11 a. Since the mean frequency is a monotonically decreasing function of length, it follows that the relative size of frequency fluctuations increases with length. This is illustrated in Fig. 11 b, where we plot the CV as a function of length for μ = 1. As in the computational model, the size of fluctuations increases monotonically with axonal length. Note that for μ = 1, the CV for L = 1000 μm is about 10 times larger than that obtained in the computational model (see Fig. 10 b). The two different models yield comparable-sized fluctuations for μ = 0.1. Irrespective of this, a major prediction of both stochastic models is that the variance in the frequency of oscillations grows with axonal length, indicating a significant degradation in the reliability of frequency coding as a length-sensing mechanism for very long axons.

Figure 11.

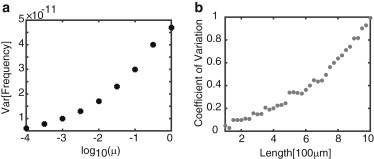
Effects of noise on the frequency-encoding mechanism for axonal length sensing in the stochastic advection-diffusion model. (a) Variance in oscillation frequency (determined by the peak of the power spectrum) versus noise strength μ. (b) Variance in frequency versus axonal length. The plots were obtained by solving the stochastic partial differential equations over 1000 trials with μ = 1.

Note that we use a heuristic method for measuring the size of frequency fluctuations in Figs. 10 and 11. That is, we consider N trials for a fixed axonal length, and for each run we look at the power spectrum of the retrograde signal. The frequency is assumed to be encoded by the peak of the power spectrum for ω > 0. The mean and variance of the set of peak frequencies across the N trials are then calculated for each axonal length. One limitation of this method is that identification of the peak of the spectrum is difficult at large axonal lengths. Nevertheless, a high CV is consistent with a broad power spectrum, as illustrated in Fig. 12 in the case of the stochastic advection-diffusion equation. For short axons (L = 100 μm), the spectrum is characterized by a sharp peak around the mean frequency of oscillations. On the other hand, the spectrum is much broader for long axons (L = 1000 μm), so that it is difficult to extract the mean frequency. Of course, the lengthscale at which noise becomes significant will depend on the value of the noise strength, μ. However, the general trend is clear: any stochasticity in the motion of the molecular motors will lead to the accumulation of errors in the length-sensing mechanism as the length of the axon increases.

Figure 12.

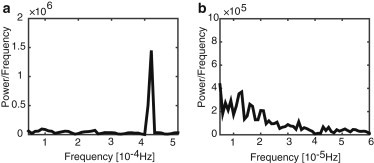
Power spectra of the retrograde chemical signal generated by the stochastic advection-diffusion model of Eq. 25 for (a) L = 100 μm and (b) L = 1000 μm. Other parameters are as in Fig. 5.

Discussion

In this article, we developed a mathematical model for axonal length sensing based on a biophysical mechanism recently proposed by Rishal et al. (27). We showed that the underlying dynamical mechanism involves delayed negative feedback due to the finite propagation speeds of molecular motors. This can be incorporated into the kinetic equations for retrograde chemical signaling using a discrete delay, τ = L/v, or by convolving the chemical signals with the Green’s function of an advection-diffusion equation for motor transport. Both versions of the model support chemical oscillations that emerge via a Hopf bifurcation, resulting in a frequency that is inversely related to the axonal length. Furthermore, the advection-diffusion version of the model suggests that knockdown of either kinesin or dynein motors results in a longer axon (see Fig. 9). These results are consistent with the experimental and computational studies carried out by Rishal et al. (27). The advantage of our mathematical model is that it provides a compact dynamical framework for understanding the origin of the oscillations and exploring how the length-sensing mechanism depends on various biophysical parameters.

One prediction of our model is that the effective diffusivity, D, of motor transport only has a weak effect on the retrograde signal frequency’s dependence on axonal length. That is, increasing D increases the critical length, L_c, for the onset of oscillations in the retrograde signal, but once oscillations have formed, the frequency is approximately D-independent. A second prediction is that fluctuations in the transport of molecular motors result in a reduction in the reliability of the frequency-encoding mechanism as the length increases (see Fig. 11). This could have significant implications for the viability of such a mechanism within the context of axonal injury, where accurate information regarding the location of the injury is needed to target regeneration at the correct location (26).

There are a number of issues that we hope to explore in future work. First, it would be interesting to derive an effective stochastic advection-diffusion equation with multiplicative noise, starting from a full stochastic model of stop-and-go motor transport. Such a model would need to keep track of the total number of kinesin and dynein motors. In our simplified model, we assumed a sufficient supply of kinesin motors at the proximal end and of dynein motors at the distal end. The model was self-regulating due to the feedback signals. Another crucial issue is how the oscillatory retrograde signal could be decoded at the cell body to control axonal length. One possibility is that the oscillation drives a regulatory gene network (29). Interestingly, it has been shown that such networks are more robust in the face of a noisy environment when frequency-modulated rather than amplitude-modulated (34). The effects of extrinsic noise due to the stochastic nature of motor transport and intrinsic noise within a gene network can be investigated by using our mathematical model for generating chemical oscillations as the front end of a frequency-modulated gene network.

Author Contributions

P.C.B. designed the research, P.C.B. and B.K. developed the analysis, B.K. performed the numerical simulations, and P.C.B. and B.K. wrote the article.

Appendix: Derivation of the Green’s Functions

In this appendix, we derive the explicit formulae of Eqs. 17a and 17b for the Green’s functions, $G_{-}\left(\xi ,\sigma ;x,t\right)$, of the advection-diffusion model. For concreteness, we will focus on the Green’s function G₊, since the derivation of G₋ is very similar. The Green’s function G₊ is defined according to the equation

$$-\frac{\partial G_{+}}{\partial \sigma }-v\frac{\partial G_{+}}{\partial \xi }-D\frac{{\partial }^2{G}_{+}}{\partial {\xi }^2}=\delta \left(x-\xi \right)\delta \left(t-\sigma \right),$$

where δ(x) is the Dirac-Delta function, supplemented by the boundary conditions

$$v{G}_{+}\left(\xi ,\sigma ;x,t\right)+D\frac{\partial G_{+}\left(\xi ,\sigma ;x,t\right)}{\partial \xi }=0,\xi =0,L.$$

Introducing the linear differential operator L acting on functions $u=u\left(\xi ,\sigma \right)$ yields

$$Lu\equiv \frac{\partial u}{\partial \sigma }+v\frac{\partial u}{\partial \xi }-D\frac{{\partial }^{2}u}{\partial {\xi }^2},$$

and we define the inner product as

$$\langle f,g\rangle \equiv {\int }_0^L{\int }_0^{\infty }fgdtdx.$$

We can then rewrite the equation for G in the more compact form

$$L^{†}{G}_{+}\left(\xi ,\sigma ;x,t\right)=\delta \left(x-\xi \right)\delta \left(t-\sigma \right),$$ (26)

where L^† is the adjoint operator:

$$L^{†}u\equiv -\frac{\partial u}{\partial \sigma }-v\frac{\partial u}{\partial \xi }-D\frac{{\partial }^{2}u}{\partial {\xi }^2}.$$

Using integration by parts and the boundary conditions on G and the kinesin concentration, c₊, one can show that

$$\langle G_{+},L{c}_{+}\rangle =\langle c_{+},L^{†}{G}_{+}\rangle -{\int }_0^L{G}_{+}\left(\xi ,0;x,t\right)c_{+}\left(\xi ,0\right)d\xi -{\int }_0^{\infty }{G}_{+}\left(0,\sigma ;x,t\right)v\left(I_E-w_{I}f\left[u_I\left(\sigma \right)\right]\right)d\sigma ,$$

which reduces to Eq. 15, since $\langle G_{+},L{c}_{+}\rangle =0$, $\langle c_{+},L^{†}{G}_{+}\rangle =c_{+}\left(x,t\right)$, and G₊(0,σ;x,t) = 0 for σ > t (causality).

It remains to solve the adjoint problem given by Eq. 26. Introduce the change of variables, $\overline{\sigma }=t-\sigma$, and set $G_{+}\left(\xi ,\sigma ;x,t\right)=G\left(\xi ;x,\overline{\sigma }\right)$. We then have

$$\frac{\partial G}{\partial \overline{\sigma }}-v\frac{\partial G}{\partial \xi }-D\frac{{\partial }^{2}G}{\partial {\xi }^2}=\delta \left(\xi -x\right)\delta \left(\overline{\sigma }\right),$$ (27)

with $G\left(\xi ;x,\overline{\sigma }\right)=0$ for $\overline{\sigma }<0$. Applying the Laplace transform to Eq. 27 with

$$\tilde{G}\left(\xi ;x,s\right)={\int }_0^{\infty }{\text{e}}^{-st}G\left(\xi ;x,t\right)dt,$$

we obtain

$$s\tilde{G}-v{\tilde{G}}^{\prime }-D{\tilde{G}}^{″}=\delta \left(\xi -x\right)$$

where the prime symbol denotes differentiation with respect to ξ for fixed s,x. It is convenient to eliminate the first derivative term by setting $\tilde{G}\left(\xi ;x,s\right)=g\left(\xi ;x,s\right)\varphi \left(\xi \right)$ for an appropriately chosen function ϕ. Substituting into the equation for $\tilde{G}$ gives

$$-D\varphi g^{″}-\left(v\varphi +2D{\varphi }^{\prime }\right)g^{\prime }+\left(s\varphi -v{\varphi }^{\prime }-D{\varphi }^{″}\right)g=\delta \left(\xi -x\right).$$

Hence, imposing ${\varphi }^{\prime }=-\frac{v}{2D}\varphi \Rightarrow \varphi =e^{\left(-\frac{v}{2D}\xi \right)}$, we see that g satisfies the self-adjoint (Sturm-Liouville) equation

$$g^{″}+\left(-\frac{v^2+4Ds}{4D^2}\right)g=-\frac{1}{D}{e}^{\left(\frac{v}{2D}x\right)}\delta \left(\xi -x\right)$$ (28)

We can then solve this equation in terms of the eigenfunctions ${\zeta }_n$ and eigenvalues λ_n of the second-order equation

$${\zeta }_n^{″}+{\lambda }_n{\zeta }_n=0,$$

supplemented by the homogeneous boundary conditions

$$-\frac{v}{2}{\zeta }_n\left(0\right)+D\frac{d{\zeta }_n}{d\xi }\left(0\right)=0$$

$$\frac{v}{2}{\zeta }_n\left(L\right)+D\frac{d{\zeta }_n}{d\xi }\left(L\right)=0.$$

The latter follow from the boundary condition for G₊. Using the fact that the eigenfunctions form a complete orthonormal set, we have the expansions

$$\delta \left(\xi -x\right)=\sum _{n=1}^{\infty }{\zeta }_n\left(x\right){\zeta }_n\left(\xi \right)$$

and

$$g\left(\xi ;x,s\right)=\sum _{n=1}^{\infty }{a}_n\left(x,s\right){\zeta }_n\left(\xi \right)$$

Substituting these into Eq. 28, we can solve for a_n(x,s) to obtain

$$g\left(\xi ;x,s\right)=\sum _{n=1}^{\infty }\frac{1}{s+D{\lambda }_n+\frac{v^2}{4D}}{e}^{\left(\frac{v}{2D}x\right)}{\zeta }_n\left(x\right){\zeta }_n\left(\xi \right).$$

Substituting g and ϕ back into the formula for $\tilde{G}$, inverting the Laplace transform, and reverting back to original time coordinates, we finally obtain

$$G_{+}\left(\xi ,\sigma ;x,t\right)=\sum _{n=1}^{\infty }{e}^{\left(-\left(D{\lambda }_n+\frac{v^2}{4D}\right)\left(t-\sigma \right)\right)}{e}^{\left(-\frac{v}{2D}\left(\xi -x\right)\right)}{\zeta }_n\left(\xi \right){\zeta }_n\left(x\right).$$ (29)

Using standard methods to solve boundary value problems, we find that

$${\zeta }_n=\text{sin}\sqrt{{\lambda }_n}x+\frac{2D\sqrt{\lambda }}{v}\text{cos}\left(\sqrt{{\lambda }_n}x\right),$$

where λ_n solves

$$4Dv\sqrt{{\lambda }_n}\text{cot}\left(\sqrt{{\lambda }_n}L\right)=4D^2{\lambda }_n-v^2.$$

We thus obtain Eq. 17a.