Surfing along Filopodia: A Particle Transport Revealed by Molecular-Scale Fluctuation Analyses

Abstract

Filopodia perform cellular functions such as environmental sensing or cell motility, but they also grab for particles and withdraw them leading to an increased efficiency of phagocytic uptake. Remarkably, withdrawal of micron-sized particles is also possible without noticeable movements of the filopodia. Here, we demonstrate that polystyrene beads connected by optical tweezers to the ends of adherent filopodia of J774 macrophages, are transported discontinuously toward the cell body. After a typical resting time of 1–2 min, the cargo is moved with alternating velocities, force constants, and friction constants along the surface of the filopodia. This surfing-like behavior along the filopodium is recorded by feedback-controlled interferometric three-dimensional tracking of the bead motions at 10–100 kHz. We measured transport velocities of up to 120 nm/s and transport forces of ∼70 pN. Small changes in position, fluctuation width, and temporal correlation, which are invisible in conventional microscopy, indicate molecular reorganization of transport-relevant proteins in different phases of the entire transport process. A detailed analysis implicates a controlled particle transport with fingerprints of a nanoscale unbinding/binding behavior. The manipulation and analysis methods presented in our study may also be helpful in other fields of cellular biophysics.

Introduction

Filopodia are actin-filled, thin, rodlike cell protrusions with a thickness of a few tenths of a micrometer (1) and a length that is in most cases in the range of a few micrometers (2,3). Filopodia emerge in different kinds of cells. In addition to the functions of filopodia in growth-cone pathfinding, cell motility, cell spreading, and wound healing, filopodia are known to play an important role in phagocytosis (4,5). Filopodia have been shown to retract and pull particles bound to the filopodial tips toward the cell body (5–8). This constitutes an additional mechanism, which enhances the efficiency of particle uptake during cell invasion. Whereas active movements of dorsal filopodia, such as filopodial retraction, are controlled by a reorganization of the underlying cytoskeleton through polymerization processes and work of molecular motors, the so-called surfing mechanism does not require dynamics of filopodia, such as displacements or length variations. Using epithelial cells, it was shown that viruses can surf along adherent filopodia toward the cell body before cell entry as a variant of a viral trafficking process (9,10). Filopodia surfing enables pathogens to approach the cell without activating the retraction mechanisms of filopodia. In a similar context, the transport of microbeads along the surface of growth cones has been studied to measure retrograde actin flow (11,12).

It is unclear whether linking processes between target and cell surface and the subsequent cargo transport are based on the same mechanisms for viruses and filopodia as for beads and growth cones. Further insight is needed into the stochastic binding processes controlling a directed transport of local probes such as beads. Analysis of the motion of the bead is useful for uncovering molecular processes inside the filopodium, when the bead is connected to the membrane or the cytoskeleton. These mechanisms are related to processes that regulate force generation and sensing via the extracellular matrix (13,14). In this study, we demonstrate that phagocytosis of 1-μm-radius latex beads can also be initiated by a surfer-like transport process along a filopodium, which we investigate using optical-tweezers-based measurements. In our experiments, the transport processes are induced by placing beads on adherent filopodia of J774 mouse macrophages. Bead fluctuations are analyzed using statistical mechanics methods.

We show that the position and orientation fluctuations of the bead, which is in contact with a filopodium, can be analyzed to reveal the fingerprints of a molecular interaction between the uncoated bead and the connecting interface (15). The interaction can be studied by analyzing the temporal changes in effective binding stiffness and friction parameters, which we are able to measure in all three dimensions (16). These multimodal analyses indicate the occurrence of specific molecular processes that can explain the observed phenomena. To our knowledge, the reported transport of micrometer-sized beads along filopodial protrusions toward the cell body constitutes a novel mechanism to initiate phagocytosis and should be considered with respect to the various means of mammalian immune response.

Optical tweezers-based investigation of bead transport

The J774 macrophages examined in this work form protrusions that are in strong conjunction with the coverslip on which they grow. Once linked to the glass surface, the protrusions usually do not unbind again.

To study the cellular response upon particle binding, the bead is placed by the optical trap onto the upper surface of an adherent filopodium. This is illustrated by the scheme in Fig. 1 A and the differential interference contrast (DIC) images of Fig. 1 C (see also video in the Supporting Material).

Figure 1.

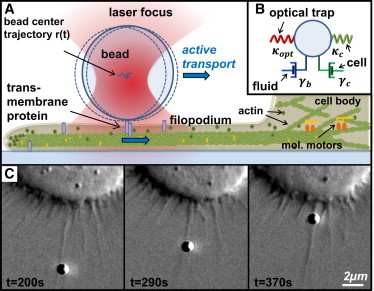
Transport of beads along adherent filopodia initiated and analyzed by optical tweezers. (A) Sketch of the mechanistic model describing the transport process along an adherent filopodium toward the cell body. The transported bead is tracked interferometrically in 3D. (B) Kelvin-Voigt model for the bead interacting with the surrounding fluid (friction (γ_b)), the optical trap (trap stiffness (κ_opt)), and the cellular protrusion (with elements γ_c and κ_c). (C) DIC image series of J774 macrophage transporting a bead along a filopodium toward its cell body. The bead is captured and tracked inside the focused laser beam during the entire retraction process. To see this figure in color, go online.

Materials and Methods

Cell culture and handling

The cells used for the experiments are J774.1 murine mouse macrophages (17). The cells were cultivated according to the protocol provided by the distributor (DSMZ, Braunschweig, Germany). Before the experiments, the cells have to be seeded on coverslips. To assure access for the optical tweezers, an appropriate confluency is important. A cell coverage between 10% and 30% of the coverslip surface at the day of the experiments turned out to be reasonable. Since the cells need some time to adhere to the coverslip, cell preparation is usually done 1 day before the experiments. To provide physiological conditions during the experiment, the coverslip carrying the cells is mounted together with 1 mL cell culture medium on a removable, temperature-controlled insert (Bioscience Tools, San Diego, CA) (see also Fig. S2 in the Supporting Material).

Optical trapping and interferometric tracking

The experiments were performed on a self-developed optical tweezers setup, which is based on a standard inverted microscope frame (AxioObserver, Zeiss, Germany). The microscope is equipped with a three-dimensional (3D) piezo stage and is extended by standard units for optical trapping and tracking (18), such as a 1064 nm laser (SLS, Barsbüttel, Germany) stabilized by a noise eater (TEM, Hamburg, Germany), and feedback control via an acoustooptic modulator (AOM) (AA Opto-Electronic, Orsay, France).

The transport process is studied by tracking the 3D position of the bead using back-focal-plane (BFP) interferometry at frequencies of 10 to 100 kHz. Before every experiment, the optical trap and the QPD detection system were calibrated according to the methods described by Gittes and Schmidt (19) and by Rohrbach and colleagues (18,20). To keep the trapped bead within the linear range of the detection system, a software-controlled feedback mechanism was used to move the 3D piezo stage. Compared to the 1-μm polystyrene bead, the filopodia are thin and weakly scattering structures that only marginally affect the interference intensity of the trapping laser in the BFP of the detection objective lens and thus the 3D tracking accuracy.

Data recording and preparation

The bead displacements from the trap center are tracked with nanometer precision using BFP interferometry. In combination with the feedback-controlled movements of the piezo stage, the position of the bead center relative to the coverslip and thus relative to the adherent cell body can be obtained during the entire transport process. Since the transport takes place in an arbitrary direction, a coordinate rotation is applied to the trace. The new coordinate system is selected in such a manner that the x axis is in the direction of filopodial extension. We obtain thereby the final trace r(t) and thus the mean bead movements and fluctuations in the directions parallel and perpendicular to the direction of filopodial extension.

The DIC video data, which were recorded simultaneously with the bead-position data, were analyzed to identify different processes, such as binding of other filopodia or objects to the bead, obstacles obstructing bead movement, or the approach of the cell body.

Mathematical description of the transport

The bead stochastical motion affected by an adherent filopodium can be described by the Langevin equation

$${\mathbf{F}}_{\gamma \text{b}}\left(\dot{\mathbf{r}}\right)+{\mathbf{F}}_{\text{opt}}\left(\mathbf{r},t\right)+{\mathbf{F}}_{\text{c}}\left(\mathbf{r},\dot{\mathbf{r}},t\right)+{\mathbf{F}}_{\text{th}}\left(t\right)=0,$$ (1)

which will be used to analyze and identify the transport characteristics. Here, r describes the bead-center position, ${\mathbf{F}}_{\gamma b}$ is the frictional force of the bead in the surrounding fluid, F_opt is the optical force, and F_c is the force exerted on the bead by the cell. Since the motion is, even on short timescales, highly overdamped, the inertial force can be neglected. The system is driven by a random thermal force, F_th, which accounts for the Brownian motion of the particle. The optical force can be expressed by ${\mathbf{F}}_{\text{opt}}\left(\mathbf{r},t\right)=-{\hat{\kappa }}_{\text{opt}}\left(\mathbf{r}-{\mathbf{r}}_{\text{trap}}\left(t\right)\right)$, where ${\mathbf{r}}_{\text{trap}}\left(t\right)$ denotes the position of the center of the optical trap and ${\hat{\kappa }}_{\text{opt}}$ a tensor containing the direction-variant force constant of the optical trap in its linear approximation. The linear frictional force can be expressed by ${\mathbf{F}}_{\gamma b}=-{\gamma }_b\dot{\mathbf{r}}$, where ${\gamma }_{\text{b}}$ is the friction coefficient of the bead in the surrounding fluid. In first-order approximation, the binding of the bead to the filopodium is assumed to be harmonic. The transmembrane protein, which is assumed to constitute the bond between the bead and the filopodium, is displaced along the filopodium (see Fig. 1 A). This displacement leads to the transport of the bead toward the cell body. The bond is described by a time-varying harmonic potential and thus a force ${\mathbf{F}}_{\kappa \text{c}}=-{\hat{\kappa }}_{\text{c}}\left(t\right)\left(\mathbf{r}\left(t\right)-{\mathbf{r}}_{\text{c}}\left(t\right)\right)$, where ${\hat{\kappa }}_{\text{c}}\left(t\right)$ denotes the tensor containing the linearized stiffness parameters and ${\mathbf{r}}_{\text{c}}\left(t\right)$ is the equilibrium bead position corresponding to this bond. In addition to this elastic term, the cell exerts frictional forces on the bead, expressed by the linearized force ${\mathbf{F}}_{\gamma \text{c}}=-{\hat{\gamma }}_{\text{c}}\left(t\right)\left(\dot{\mathbf{r}}\left(t\right)-{\dot{\mathbf{r}}}_{\text{c}}\left(t\right)\right)$, where ${\hat{\gamma }}_{\text{c}}\left(t\right)$ is a tensor containing the friction parameters in the respective directions. Considering the interacting force between the bead and the cell, ${\mathbf{F}}_{\text{c}}={\mathbf{F}}_{\kappa \text{c}}+{\mathbf{F}}_{\gamma \text{c}}$, the Langevin equation (Eq. 1) for the bead position can be expressed by

$$\underset{\text{friction}\text{in}\text{solution}}{\underbrace{{\gamma }_{\text{b}}\dot{\mathbf{r}}\left(t\right)}}+\underset{\text{friction}\text{exerted}\text{by}\text{cell}}{\underbrace{{\hat{\gamma }}_{\text{c}}\left(t\right)\left(\dot{\mathbf{r}}\left(t\right)-{\dot{\mathbf{r}}}_{\text{c}}\left(t\right)\right)}}+\underset{\text{optical}\text{force}}{\underbrace{{\hat{\kappa }}_{\text{opt}}\left(\mathbf{r}\left(t\right)-{\mathbf{r}}_{\text{trap}}\left(t\right)\right)}}+\underset{\text{binding}\text{to}\text{the}\text{cell}}{\underbrace{{\hat{\kappa }}_{\text{c}}\left(t\right)\left(\mathbf{r}\left(t\right)-{\mathbf{r}}_{\text{c}}\left(t\right)\right)}}={\mathbf{F}}_{\text{th}}\left(t\right).$$ (2)

This expression describes the bead mean transport and fluctuations in the presence of the cell and is used in the next two sections to analyze the bead's transport and its fluctuations.

Mean movement of the bead

Considering only the slowly varying part of Eq. 2 corresponds to averaging over the fluctuations (F_th(t) = 0). This leads to a set of coupled first-order ordinary differential equations for the bead position, ${\mathbf{r}}_{\text{lp}}\left(t\right)$, the filopodial position, ${\mathbf{r}}_{\text{c,lp}}\left(t\right)$, and the position of the optical trap, ${\mathbf{r}}_{\text{trap,lp}}\left(t\right)$, in all three dimensions (lp refers to lowpass)

$${\dot{\mathbf{r}}}_{\text{lp}}\left(t\right)\left({\gamma }_{\text{b}}+{\hat{\gamma }}_{\text{c}}\left(t\right)\right)+{\mathbf{r}}_{lp}\left(t\right)\left({\hat{\kappa }}_{\text{opt}}+{\hat{\kappa }}_{\text{c}}\left(t\right)\right)-{\dot{\mathbf{r}}}_{\text{c,lp}}\left(t\right){\hat{\gamma }}_{\text{c}}\left(t\right)-{\mathbf{r}}_{\text{trap,lp}}\left(t\right){\hat{\kappa }}_{\text{opt}}-{\mathbf{r}}_{\text{c,lp}}\left(t\right){\hat{\kappa }}_{\text{c}}\left(t\right)=0.$$ (3)

Assuming that transport distances are negligibly small during the bead relaxation time (${\dot{\mathbf{r}}}_{\text{lp}}\left(t\right)$ →0 and ${\dot{\mathbf{r}}}_{\text{c,lp}}\left(t\right)$ →0), the lowpass-filtered bead position, ${\mathbf{r}}_{\text{lp}}\left(t\right)=\left({\hat{\kappa }}_{\text{opt}}{\mathbf{r}}_{\text{trap,lp}}\left(t\right)+{\hat{\kappa }}_{\text{c}}{\mathbf{r}}_{\text{c,lp}}\left(t\right)\right)/\left({\hat{\kappa }}_{\text{opt}}+{\hat{\kappa }}_{\text{c}}\right)$, reflects the potential minimum resulting from the current forces of the filopodium and the optical trap. In many cases, the effect of the optical forces can be neglected, which leads to ${\mathbf{r}}_{\text{lp}}\left(t\right)\approx {\mathbf{r}}_{\text{c,lp}}\left(t\right)$. In this case, ${\mathbf{r}}_{\text{lp}}\left(t\right)$ approximately describes the movement of the bond between bead and filopodium.

Particle fluctuations

The fluctuations of the bead are influenced by the acting forces and by the properties of the local environment. In particular, when the bead is in contact with the cell, the bead fluctuations change significantly. To analyze these fluctuations, only the high-frequency part of the Langevin equation (Eq. 2) is considered. In this case, the slowly varying bond can assumed to be constant in time, which leads to ${\mathbf{r}}_{\text{c,hp}}\left(t\right)={\mathbf{r}}_{\text{c}}$ and ${\dot{\mathbf{r}}}_{\text{c,hp}}\left(t\right)=0$. Here, the bond should be regarded as the actual minimum of the potential corresponding to the force ${\mathbf{F}}_{\kappa c}$ and not as a diffusing binding molecule. For the high frequencies, the Langevin equation (Eq. 2) reduces to

$$\left({\gamma }_{\text{b}}+{\hat{\gamma }}_{\text{c}}\left(t\right)\right){\dot{\mathbf{r}}}_{\text{hp}}\left(t\right)+\left({\hat{\kappa }}_{\text{opt}}+{\hat{\kappa }}_{\text{c}}\left(t\right)\right)\left({\mathbf{r}}_{\text{hp}}\left(t\right)-\frac{{\hat{\kappa }}_{\text{opt}}{\mathbf{r}}_{\text{trap,hp}}+{\hat{\kappa }}_{\text{c}}{\mathbf{r}}_{\text{c,hp}}}{{\hat{\kappa }}_{\text{opt}}+{\hat{\kappa }}_{\text{c}}}\right)={\mathbf{F}}_{\text{th,hp}}\left(t\right).$$ (4)

This is equivalent to the assumption that the influence of the filopodium on the bead can be described by a Kelvin-Voigt model and thus can be represented by a purely viscous damper, ${\hat{\gamma }}_{\text{c}}$, and a purely elastic spring, ${\hat{\kappa }}_{\text{c}}$, connected in parallel (see Fig. 1 B). Since the optical trap also acts as a spring, and the interaction with the fluid surrounding the bead can be described as a viscous damper, the influence of the filopodium in the Kelvin-Voigt assumption leads to an additive change in friction, $\gamma ={\gamma }_{\text{b}}+{\gamma }_{\text{c}}$, and stiffness, $\kappa ={\kappa }_{\text{opt}}+{\kappa }_{\text{c}}$, in all spatial dimensions (see Fig. 1 B).

Analysis methods

Velocity

The velocity is obtained by differentiation of the lowpass-filtered (Hamming window, corner frequency 1 Hz) component of the position trace pointing along the filopodial extension. In this time regime, the frictional components of the equation of motion (Eq. 2) can be neglected. The bead-center velocity, ${\dot{\mathbf{r}}}_{\text{lp}}\left(t\right)$, can be approximated to be the velocity of the molecular bond to the filopodium, ${\dot{\mathbf{r}}}_{\text{c,lp}}\left(t\right)$.

Friction and coupling strength

A suitable and common method to determine the quantities κ and γ from the fluctuation data is correlation analysis. The autocorrelation function $AC({\mathbf{r}}_i\left(t\right),\tau )=\langle {\mathbf{r}}_i\left(t\right)\times {\mathbf{r}}_i(t+\tau )\rangle$ of the positions of a fluctuating object in a harmonic potential experiencing linear friction is given by

$$AC({\mathbf{r}}_i\left(t\right),\tau )=\langle {\mathbf{r}}_i{\left(0\right)}^2\rangle e^{-\tau /{\tau }_{0,i}}=\frac{k_{\text{B}}T}{{\kappa }_i}\text{exp}\left(-\tau {\kappa }_i\text{/}{\gamma }_i\right),$$ (5)

where $i=x,y,z$ refers to the spatial dimension and k_BT is the thermal energy. For time differences much shorter than the autocorrelation (relaxation) time, τ << ${\tau }_{\text{ac,i}}$, the exponential can be approximated as linear, resulting in

$$A{C}_i({\mathbf{r}}_i\left(t\right),\tau <<{\tau }_{0,i})\approx \frac{k_{\text{B}}T}{{\kappa }_i}\left(1-\tau {\kappa }_i\text{/}{\gamma }_i\right).$$ (6)

The static part (τ = 0) of the bead-position autocorrelation yields the stiffness parameter, κ. The dynamic part of the autocorrelation, the drag parameter, γ, can be extracted from a linear fit to the slope of the autocorrelation for short time delays, τ. Alternatively, the stiffness, κ, of a harmonic potential can be extracted from the standard deviation $\sqrt{\langle {\mathbf{r}}^2\rangle }$ of the bead fluctuations

$${\kappa }_i=\frac{k_{\text{B}}T}{\langle {\mathbf{r}}_{\mathbf{i}}^2\rangle }.$$ (7)

To separate the mean bead movement from the fluctuations, and to get rid of disturbing vibrations of the piezo stage (mainly below a frequency of 250 Hz), a highpass filter (Hamming window; corner frequency, f_cor = 400 Hz) was applied to the data before further analysis. The relative changes in κ(r_lp) and γ(r_lp) according to Eq. 6 do not depend critically on f_cor (data not shown). On a timescale of Δt = 10–100 ms, the obtained highpass-filtered position data approximately represent thermal equilibrium, since the maximal transport distance during Δt is much smaller than the bead fluctuation width.

We approximate the connection of the bead to the cell using Kelvin-Voigt models to extract the relative changes of ${\gamma }_{\text{c}}$ and ${\kappa }_{\text{c}}$, which reveal important quantitative information about the binding strength of the bead to the filopodium and about properties of the filopodium itself. Therefore, the stiffness of the optical trap, ${\kappa }_{\text{opt}}$, has to be subtracted from the measured total stiffness, $\kappa$, to obtain the binding stiffness of the bead to the cell, ${\kappa }_{\text{c}}=\kappa -{\kappa }_{\text{opt}}$. Likewise, the friction parameter ${\gamma }_{\text{c}}=\gamma -{\gamma }_{\text{b}}$ has to be rectified from the viscous friction, ${\gamma }_{\text{b}}$, of the bead in the medium.

Results

After the bead has been brought, with the optical trap, into the vicinity of an adherent filopodium, it usually tethers very fast. Typically, the linkage of the bead to the filopodium is stronger than the forces that can be applied by the optical tweezers (F_opt ≤ 50 pN). In particular, it is impossible to wrest the bead away from the filopodium by means of the optical forces. Nevertheless, it is often possible to move the bead along the filopodium over distances of several micrometers. This movement along the filopodium is hindered when the bead suddenly gets stuck at a point where the optical forces are not strong enough to move the bead any further. After the immobilization of the bead, the binding to the filopodium is usually much stiffer (see Section S5 in the Supporting Material).

Transport lengths and velocities

Several transports of beads along filopodia have been analyzed. Usually, the adherent bead did not show a directed movement for a certain rest time period, t_rest, at the beginning. On average, this rest time was ∼83 s. At t = t_rest, the bead suddenly starts to move along the filopodium toward the cell body. The bead transport distances vary from 3.6 μm to >12 μm (see Table 1). The mean transport velocity during the actual transport between t = t_rest and the approach of the cell body could be determined to be 60 nm/s.

Table 1.

Transport characteristics of filopodia surfing

Data	Length (μm)	Transport Duration(s)	Velocity (nm/s)	Rest Time (s)	Stiffness Rest Time (pN/μm)	Stiffness Transport (pN/μm)	Lateral Trap Stiffness (pN/μm)
1	12.2	285	43	112	876	229	51.5
2	7.5	107	71	—	106	149	44.5
3	8.5	112	76	70	724	967	43
4	3.7	51	74	110	505	479	51.5
5	3.6	89	41	—	56	93	51.5
6	7.2	113	63	41	82	240	32.5
7	7.1	129	55	85	322	1025	4.15
Mean	7.1	126	60	83, 60	381	454
SD	2.9	74	15	29, 60	329	389

Total distance, duration, velocity, rest time, and mean stiffness during rest time and bead transport of seven different transport processes. The stiffnesses are rectified by the trap stiffness. The lateral trap stiffnesses are also shown. The axial trap stiffnesses are five times weaker. Dashes indicate unrecorded measurements.

The results presented here are a representative detailed analysis of one of these transport events. This event corresponds to data set 1 in Table 1, the images shown in Fig. 1 C, and the video in the Supporting Material.

Temporal change of binding during transport

The continuous tracking of the bead-position fluctuations, ${\mathbf{r}}_{\text{hp}}\left(t\right)$, relative to the mean transport trace, ${\mathbf{r}}_{\text{lp}}\left(t\right)$, of the bead center allows extraction of the time-varying binding constants and the friction constants in all three dimensions, as explained by Eqs. 5 and 6.

In Fig. 2, the lowpass-filtered trace, ${\mathbf{r}}_{\text{lp}}\left(t\right)$, of the bead center is shown together with the stiffness parameters, ${\kappa }_i\left(t\right)$, the friction parameters, ${\gamma }_i\left(t\right)$, and the lowpass-filtered velocity, $v_{\text{lp}}\left(t\right)$. An increase in κ_i corresponds to a tighter binding to the filopodium, whereas an increase in γ_i, corresponds to an increased viscosity of the medium to which the bead bound to the filopodium is subjected.

Figure 2.

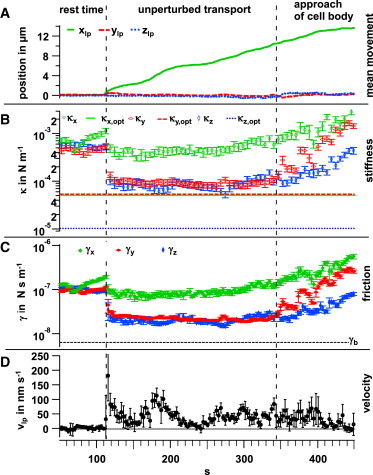
Temporal variation of binding strength and friction during transport. The transport process can be divided into intervals of resting (t < 111 s), pure transport (111–340 s), and approach to the cell body (t > 340 s), as indicated by the vertical dashed lines. (A) The mean bead movement, ${\mathbf{r}}_{lp}\left(t\right)=\left(x_{lp}\left(t\right),y_{lp}\left(t\right),z_{lp}\left(t\right)\right)$, is shown in the rotated coordinate system, with x denoting the direction of transport, y the perpendicular horizontal component, and z the approximate vertical component. (B and C) The stiffness, ${\kappa }_i(\mathbf{r},t)$ (B), and friction parameters, ${\gamma }_i(\mathbf{r},t)$, change with space and time and are determined within time intervals of 100 ms of the highpass-filtered trace. Each data point represents the mean values in a time window of 3 s. Error bars correspond to the standard deviation within the 3 s intervals. (D) The 1 Hz lowpass-filtered velocity, $v_{lp}(\mathbf{r},t)$, in the direction of filopodial extension changes significantly during the pure-transport phase. To see this figure in color, go online.

Typical bead transport can be divided into three functional phases: the rest time, without directed bead movement; the actual transport along the filopodium; and a third phase that includes the approach to the cell body and the uptake of the bead. These phases, which can also be identified in most other data sets listed in Table 1, can be discriminated by the different bead fluctuation parameters, separated by vertical dashed lines in Fig. 2. All phases, i.e., the rest time, the transport itself, and the approach of the cell body, as well as the start of the transport, which constitutes the transition between rest time and the actual transport phase, are analyzed in further detail in the next paragraphs.

Rest time before transport

After the bead is attached to a filopodium, no significant directed movement or transport of the bead is visible over the rest time, t_rest, which was determined to be 84 ± 30 s in five experiments (see Table 1). As illustrated in Fig. 3 A, several abrupt displacements are visible, which are possibly due to binding events or rupture of molecular bonds.

Figure 3.

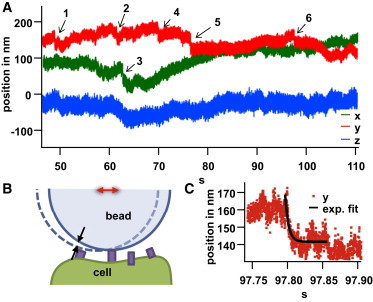
Changes in the bead-center fluctuations during rest. (A) Bead-center trajectory during the rest time, t_rest, showing abrupt jumps in different directions, indicated by arrows 1–6. (B) Sketch of a mechanistic model explaining jumps in the bead-center fluctuations (red double arrow) as a result of molecular unbinding/binding events at the surface. (C) Magnification of jump number 6, indicating a temporal relaxation with exponential fit. The fits provide the decay times τ₁ = 25 ± 1 ms, τ₂ = 16 ± 1 ms, τ₃ = 6.7 ± 0.5 ms, τ₄ = 2.5 ± 0.5 ms, τ₅ = 3,4 ± 0.2 ms, and τ₆ = 4.8 ± 0.4 ms at the respective points in time, as indicated in (A). To see this figure in color, go online.

The displacement events were fitted by exponential decays leading to decay times between 2.5 ms and 25 ms, with a mean value of 10 ms. The reattachment relaxations, τ₁,… τ₆, are significantly longer than the autocorrelation times, ${\tau }_i={\gamma }_i/{\kappa }_i$ ≈ 0.3–0.5 ms, which represent a measure of the strength of binding to the cell within the period t < t_rest. The equilibrium values, τ_I, are obtained by Eq. 5 or from the ratio γ/κ, extracted from Fig. 2. As indicated in Fig. 3 B, a vertical binding or unbinding/release event between the bead surface and a membrane surface can be translated to a lateral displacement of the bead center. This possible effect, called mechanical amplification (21), translates a small movement in one direction into a larger movement in a perpendicular direction defined by the bead radius and the bond-to-bond distance on the surface. However, the decay times, in the order of some milliseconds, are not affected by the mechanical amplification.

Bond release and start of transport

After 1–2 min of rest time, the bead suddenly starts to move. The event that triggers the start of the transport is not necessarily the same in the different experiments. Whereas the bead slowly starts to move in the transport cases shown in Section S4 of the Supporting Material, in the exemplary experiment treated here, the bead transport started with an abrupt displacement at t_rest = 112 s. The jump of the bead-center position by Δx = 119 nm, Δy = 64 nm, and Δz = 196 nm corresponds to an exponential relaxation into a new potential minimum (Fig. 4 A). This relaxation is accompanied by a significant drop-off in stiffness and friction, as shown in Figs. 4 B and Fig. 2, B and C.

Figure 4.

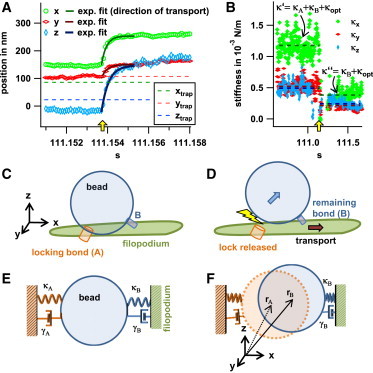
Trace at the starting point of the actual transport. (A) The position-versus-time plots were fitted by exponential functions resulting in the stated decay times (see Fig. 3 legend). The distances of the abrupt movement can be determined to be 119 nm, 64 nm, and 196 nm for x, y, and z directions, respectively, resulting in a total distance of 238 nm. (B) Stiffness parameters resulting from thermal fluctuations. Mean values before and after t = t_rest are indicated by the dashed lines in the corresponding color. (C and D) Mechanistic model for the release of a locking bond, A (C), and the start of transport through a second bond, B (D), at t > t_rest. (E and F) Sketch of a corresponding Kelvin-Voigt model with stiffness parameters κ_A and κ_B, friction parameters γ_A and γ_B, and equilibrium positions r_A and r_B. To see this figure in color, go online.

A mechanistic model for the release of a bond and the start of transport is sketched in Fig. 4, C and D, with the corresponding Kelvin-Voigt models depicted in Fig. 4, E and F. In this model, the interaction between the cell and the bead corresponds to two bonds, which are described by the Kelvin-Voigt elements. The release of a locking bond (or group of bonds) (bond A in Fig. 4 C) at t = t_rest leads to a relaxation of the bead into a new potential minimum, which is determined by the remaining bond(s), B. According to this model, the measured total stiffness is given by the sum of the stiffness of the involved bonds and the stiffness of the optical trap. From the known stiffness of the optical trap, ${\kappa }_{\text{opt},i}$, and the measured total stiffnesses before, ${\kappa }_i^{\prime }$, and after, ${\kappa }_i^{″}$, bond rupture, the stiffnesses of the locking bond, ${\kappa }_{A,i}={\kappa }_i^{\prime }-{\kappa }_i^{″}$, and the remaining bond, ${\kappa }_{B,i}={\kappa }_i^{″}-{\kappa }_{\text{opt},i}$, can be obtained in their harmonic approximations. As illustrated by Fig. 4 F, the force-balanced (zero-load) condition for the bead leads to

$$-{\hat{\kappa }}_{\text{opt}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{trap}}\right)-{\hat{\kappa }}_{\text{A}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{A}}\right)-{\hat{\kappa }}_{\text{B}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{B}}\right)=0$$ (8)

before the release and

$$-{\hat{\kappa }}_{\text{opt}}\left({\mathbf{r}}^{″}-{\mathbf{r}}_{\text{trap}}\right)-{\hat{\kappa }}_{\text{B}}\left({\mathbf{r}}^{″}-{\mathbf{r}}_{\text{B}}\right)=0$$ (9)

after the release of bond A. Here, the single-prime coordinate, ${\mathbf{r}}^{\prime }={\langle \mathbf{r}\rangle }_{[\mathit{t}<t_{\text{rest}}]}$, corresponds to the mean position before release and the double-prime coordinate, ${\mathbf{r}}^{″}={\langle \mathbf{r}\rangle }_{[t>t_{\text{rest}}+\tau ]}$, to the mean position after release. The values for ${\mathbf{r}}^{\prime }$ and ${\mathbf{r}}^{″}$ were obtained from the averages over 0.5 s before and after the release, respectively. The zero-load bead positions, ${\mathbf{r}}_{\text{A}}$ and ${\mathbf{r}}_{\text{B}}$, represent the equilibrium positions of the bead influenced by the respective bond only. These positions can be obtained according to Eqs. 8 and 9 and as illustrated in Fig. 4 F,

$${\mathbf{r}}_{\text{B}}={\mathbf{r}}^{″}+\frac{{\kappa }_{\text{opt}}}{{\kappa }_{\text{B}}}\left({\mathbf{r}}^{″}-{\mathbf{r}}_{\text{trap}}\right)$$ (10)

$${\mathbf{r}}_{\text{A}}={\mathbf{r}}^{\prime }+\frac{1}{{\kappa }_{\text{A}}}\left({\kappa }_{\text{opt}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{trap}\right)+{\kappa }_{\text{B}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{B}}\right)\right).$$ (11)

The prerelease forces on the bead resulting from bond(s) A/B, ${\mathbf{F}}_{\text{A/B}}^{\prime }=-{\hat{\kappa }}_{\text{A/B}}\left({\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{A/B}}\right)$, can be calculated from the deflections, ${\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{A/B}}$, from these equilibrium positions. The postrelease force, ${\mathbf{F}}_B^{″}=-{\hat{\kappa }}_B\left({\mathbf{r}}^{″}-{\mathbf{r}}_B\right)$, can be obtained from the deflection ${\mathbf{r}}^{″}-{\mathbf{r}}_{\text{B}}$.

For the breakup of the bond at t = t_rest, forces of about $\left|{\mathbf{F}}_{\text{B}}^{\prime }\right|$ = 70 pN were summoned by the transport machinery. The corresponding energies, $\Delta G_{\text{A/B}}\approx \left(1/2\right){\sum }_{i=x,y,z}{\kappa }_{\text{A/B},i}{\left(r_i^{\prime }-r_{\text{A/B},i}\right)}^2$, stored in the bonds can be estimated to be ΔG_A = 1505 k_BT and ΔG_B = 2134 k_BT. The sudden displacement of the bead center starting at t = t_rest by (|Δr| = 0.24 μm) can be well fitted by exponential functions,

$$r_i\left(t\right)=\Delta r_i\left(1-e^{-t/{\tau }_{off,i}}\right)=\frac{{\mathbf{F}}_{A,i}^{\prime }}{{\kappa }_i^{″}}\left(1-e^{-t{\kappa }_i^{″}/{\gamma }_i^{″}}\right),$$ (12)

with a mean relaxation constant of τ_off = 221 ms. This equation describes the stretching of the viscoelastic component by Δr_i upon a force step of height ${\mathbf{F}}_{\text{A},i}^{\prime }$ acting in direction i = x,y,z. The relaxation time, τ_off, is of the same size as the autocorrelation time at the beginning of the transport process, ${\tau }_{\text{ac}}^{″}={\gamma }_i^{″}/k_i^{″}=206\text{ms}$. Here, the double-prime quantities directly correspond to the time after the release. Table S1 in the Supporting Material provides a summary of all the parameters characterizing the change in molecular binding extracted from the equations above.

Although we could also observe a transition between the resting and moving of beads in the other experiments, we could not identify any abrupt displacements or decays in the stiffness there.

Change in transport velocity and connection orientation

Once the transport starts, the bead moves with variable velocity along the filopodium. The transport velocity varies between slow speeds, v_lp = 0–10 nm/s, and high speeds, v_lp = 100–120 nm/s. However, in none of the experiments, a complete transport stop could be detected. The mean velocity of all our transport experiments is 60 ± 15 nm (see Table 1), whereas the average transport velocity in this exemplary experiment is 43 nm/s.

However, bead transport is not purely translational but involves orientational changes as well. Analysis of the 3D bead fluctuations provides additional information about the transport process, as well as the formation and release of bonds between bead and filopodium. For quantitative analysis, it is helpful to divide the bead displacements into a movement along the filopodial extension (x axis), a radial movement, r = (y² + z²)^1/2, and an angular movement, φ = atan(z/y), perpendicular to the filopodium. To analyze the radial and angular movement, the fluctuations in the yz-plane were analyzed in each direction φ (varied in steps of Δφ = 1°) to obtain the connection stiffness, ${\kappa }_{\text{c}}\left(\phi \right)=\kappa \left(\phi \right)-{\kappa }_{\text{opt}}\left(\phi \right)$, rectified from the stiffness of the optical trap, ${\kappa }_{\text{opt}}\left(\phi \right)$.

Fig. 5 A shows a mechanistic model of the bead fluctuations around the cross section of the filopodium, where the angle φ of maximal stiffness is interpreted as the tilt angle of the bead relative to the filopodium (see Discussion). As illustrated in Fig. 5 B, the two-dimensional (2D) position histogram of the bead-center fluctuations has an elliptical shape, where the short half-axis defines the maximal radial connection stiffness, κ_max, and the long half-axis the minimal stiffness, κ_min. Fig. 5 C shows the variation of the radial stiffness as a function of the azimuthal angle φ, revealing the direction of maximal and minimal stiffness. Thus, the orientation of the elliptical histogram is defined, and it changes with time, as indicated by the three curves in Fig. 5 C.

Figure 5.

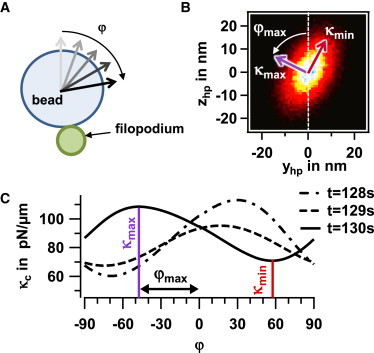
Analysis of orientational changes. (A) Mechanistic sketch of bead attached to filopodium illustrating the angle φ. (B) 2D elliptical-position histogram perpendicular to the filopodium axis with minimal and maximal connection stiffness, κ_min and κ_max. The angle φ indicates the tilt of the fluctuation volume. (C) Change in connection stiffness, κ_c(ϕ), for different angles of analysis and at three different times during transport. To see this figure in color, go online.

During the transport of the bead along the filopodium, the connection stiffness in the x direction, κ_c,x(t), changes on a timescale of seconds (Fig. 6 A). Of greater interest, the ratio between κ_max(t) and κ_min(t) changes, as indicated by the gray shaded area between the two courses. The greater the ratio κ_max/κ_min, which varies between 1.2 and 3.5, the larger is the ellipticity of the fluctuation volume. An increase in κ_max(t) is generally accompanied by a decrease in κ_min(t). The angular orientation ${\phi }_{\text{max}}\left(t\right)$, i.e., the stiffest binding radial to the filopodium, varies as ${\phi }_{\text{max}}$ = −60° … +60° during the directed transport (Fig. 6 B). It can be seen that the ellipticity of the fluctuation volume, or, respectively, the strongest κ_max(t), occurs for larger angles up to 60°. Remarkably, the transport velocity increases and decreases in a manner similar to the fluctuations of ${\phi }_{\text{max}}$ (Fig. 6 C).

Figure 6.

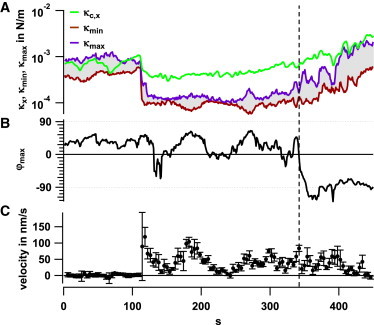
Change in transport velocity and binding configuration. (A) Temporal change of the longitudinal connection stiffness, κ_c,x, and the maximal and minimal stiffnesses, κ_max and κ_min. (B) Temporal change of the angle ϕ_max, at which the connection stiffness is maximal. (C) Temporal change of the transport velocity, v_tp(t). Dashed line indicates the end of directed transport. To see this figure in color, go online.

Stepwise transport

All recorded bead-center trajectories, $\mathbf{r}\left(t\right)=\left(x\left(t\right),y\left(t\right),z\left(t\right)\right)$, were either lowpass-filtered, to extract the mean movements of the bead, or highpass-filtered, to analyze κ and γ through the bead fluctuations. Using lowpass filtering, we could detect several discontinuous trajectories, which can be best illustrated by 2D position histograms, as shown in Fig. 7 A. Here, six accumulations of bead positions are shown in gray, with a 100 Hz lowpass-filtered trajectory overlaid in red. Steps are usually hardly visible in unfiltered time traces, as shown in Fig. 7 B. However, by applying a step-finding algorithm (22), steps can be estimated by size and dwell time. An output parameter from this algorithm is the steppedness, S, which constitutes a measure for the clarity of appearance of steps of mean length 〈s〉 in a trace. The resulting S(〈s〉) of the mean step sizes 〈s〉 is indicated in Fig. 7 C. By selecting the maximum steppedness, which corresponds to a mean step size of 〈s〉 = 10 nm, we obtain a step size distribution as shown in Fig. 7 D.

Figure 7.

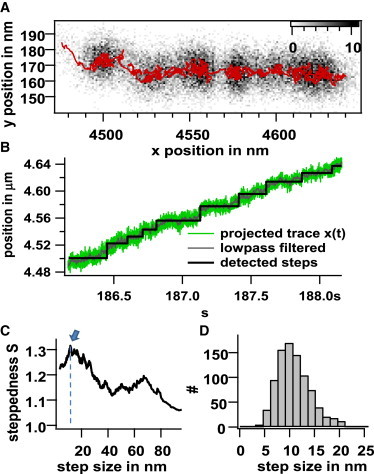
Detection of steps during transport. (A) 2D bead center position histogram in the xy plane in a time window of 2 s. The overlaid dark red trace is from a lowpass-filtered trajectory (100 Hz, Hamming window). (B) Unfiltered bead-position x(t) (green), lowpass-filtered bead-position (gray), and stepped traces evaluated by the step-finding algorithm (black). The mean slope of the trace corresponds to a velocity of 〈v〉 = 60 nm/s. (C) Steppedness, S, as a function of corresponding mean step size 〈s〉. (D) Histogram of ∼800 detected steps with step sizes obtained by the fit, which corresponds to the maximum value of the steppedness in (C). To see this figure in color, go online.

Approach to the cell body

As displayed in Fig. 2, both the stiffness and friction parameters increase strongly during the approach to the cell body. An increase in these parameters could be observed in all measurements. Despite the high quality of the DIC images, the connection of the bead to the filopodia cannot be extracted. However, as described above, the analysis of the bead-center fluctuations reveals significant changes in the fluctuation width and thereby in the connection stiffness to the filopodium, as shown in Fig. 8 A. Here, the two dashed arrows indicate two points in time where the cell connection stiffness changes strongly. These events likely correspond to the approach of a second filopodium, which hinders bead fluctuations (see Discussion). The possible geometrical configurations are illustrated by two sketches and DIC images (Fig. 8, B and C). In the end phase of the experiment (t ≥ 440 s), the connection stiffness close to the cell membrane was on average 2.2 times higher than the average stiffness during the transport, making it more difficult for the bead to escape from the cell.

Figure 8.

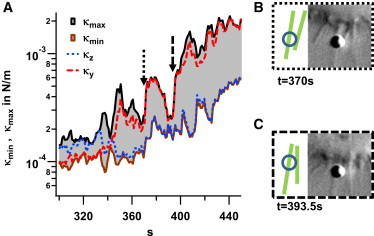
Change in 3D binding strength upon binding to other filopodia. (A) Lateral components of stiffness parameter κ(t) during the approach to the cell body. The parameters for minimal, κ_min(t), and maximal, κ_max(t), lateral stiffness are shown by the brown and black curves, respectively. (B and C) DIC microscopy images illustrate the bead position (blue circle) relative to the cell body and other filopodia (green lines) at time points indicated by arrows in (A), revealing strong changes in the maximal stiffness, κ_max. To see this figure in color, go online.

Discussion

In several studies, filopodia extension and retraction have been shown to be controlled by retrograde actin flow (23,24). It is widely accepted that retrograde flow is driven by myosin motors transporting the actin backbone toward the interior of the cell. This flow is sustained by polymerization at the plus end of the actin backbone in the tip of the filopodium, whereas depolymerization of the actin backbone takes place in the inner part of the cell cortex. The polymerization process alone would lead to an elongation of the filopodium, but it is (over)compensated to a variable degree by the myosin transport. The interplay of these two processes determines the total velocity and force of the filopodial elongation and retraction. Both processes are used to explain the transport process for a bead along a filopodium. It has been hypothesized that cortical myosin II, a nonprocessive plus-end motor with Δx_myo ≈ 5–10 nm working-stroke length (25–28), is mainly responsible for the retrograde transport of the actin backbone (9,23).

Transport lengths and velocities

In this study, the mean transport velocity of the bead, ${\overline{v}}_{\text{b}}$ = 60 nm/s, is the average of seven experiments, with a standard deviation of 15 nm/s (Table 1). Given that the transport velocity varies along each filopodium over transport lengths between 3.6 μm and 12 μm, the deviation of ±15 nm/s is relatively small, thereby indicating that the underlying transport process is the same. In none of the experiments, a complete transport stop could be detected. Similar variations of slow and fast transport, with velocities of 100–170 nm/s, were measured in a previous study for viruses surfing along filopodia of epithelial cells (9), giving further evidence for this transport mechanism. Those authors showed that transport is blocked by adding blebbistatin, which inhibits myosin II.

Equal velocities for polymerization and retrograde flow

Assuming that myosin II, with its very small duty ratio, is responsible for the retrograde transport of the actin backbone, and that our 1-μm-sized bead is connected via transmembrane linkers to the backbone, the measured mean transport speed of 60 nm/s would result in a mean step rate of $f_{\text{step}}={\overline{v}}_{\text{b}}/\Delta x_{\text{myo}}$ = 6 Hz for the retrograde backbone movement. This motion is assumed to be organized by myosin II motors, which have a very small duty ratio. A simple estimate of the minimum number of motors operating at this mean frequency is given below. However, the degree of intermotor coupling (29) cannot be estimated.

Since the adherent filopodium is neither retracting nor elongating, the mean polymerization speed at the filopodial tip must be ${\overline{v}}_{\text{poly}}={\overline{v}}_{\text{b}}$ = 60 nm/s, provided that the backbone is in contact with the membrane (see also Section S6 of the Supporting Material). For a filopodium consisting of N actin filaments (each with two protofilaments), the rate of monomers with length a = 5.4 nm attaching at N filaments is $N\times f_{\text{poly}}=N\times 2{\overline{v}}_{\text{b}}\text{/}a$ = N × 22 Hz. For a filopodium of, e.g., N = 10 filaments, >200 monomers/s on average must be transported to the tip of the backbone and polymerize (30). On longer timescales, other affecting proteins inside the filopodium, such as Cdc42, ENA/VASP, and FMNL2, also regulate actin polymerization. However this diffusion-based regulation process takes significantly longer than a direct mechanical connection via the actin backbone.

Reorganization of molecular linkers before transport

We measured rest times before the start of transport along the filopodium, t_rest, between 41 s and 112 s in five of seven experiments. Lehmann et al. (9) have hypothesized that for murine leukemia virus (MLV), this time is required to recruit transmembrane proteins that link the virus to the backbone. Whereas Lehmann et al. measured resting times of only ∼10 s for the recruitment of mCAT-1 receptors and establishment of the oligomerized receptor to the actin filaments, the times we measured for link recruitment and establishment were significantly longer. There may be several reasons for this discrepancy between the results of our study and those of Lehmann and colleagues in addition to their use of a different cell type: 1) the mobility of the linker protein in our study is smaller; 2) its local concentration is lower; 3) the establishment of the linker takes longer; 4) it requires more linking proteins to start the transport; and 5) a molecular clutch (31) has to be released to start the transport. Whereas the much smaller virus in the Lehmann study (9) can recruit specific receptors, the uncoated 1-μm-sized polystyrene bead in our study may need a more complicated sequence of receptor activation to trigger the uptake by filopodia surfing.

It is known that the cell membrane and embedded proteins have an impact on the function and mechanics of filopodia. Among the membrane-associated proteins that are relevant for filopodial dynamics are the I-BAR protein IRSp53, which deforms the membrane, the integral membrane protein LPR1, and the protein N-WASP, which links actin filaments to the membrane.

As illustrated by Fig. 3, the bead center undergoes abrupt jumps during the rest time, suggesting a molecular reorganization of linkers binding to the bead. From the width of the thermal fluctuations, we determined (autocorrelation) relaxation times of 0.3–0.5 ms, indicating a tight binding of the bead to the filopodium. These times are much shorter than the (reattachment) relaxation times of 2.5–25 ms, which might be needed to establish new bonds (see Fig. 3 C). This might be an indication for the release and lock of a molecular clutch, which has to counteract against the transport forces of the retrograde flow. Further investigations, using, e.g., specific fluorescence labeling or FRET measurements need to be performed to identify these multistep processes of transmembrane linkage that enable transport.

Bond release and start of transport with at least 70 pN pulling force

In the example analyzed here, the bead transport starts with an abrupt movement. Fig. 4 A shows an exponential relaxation into a new short-time equilibrium position in all three dimensions, with a mean decay time of τ_off = 220 ms and a total displacement of Δr = 0.24 μm. According to the measured connection stiffnesses of 500–1170 pN/μm before the release (see Fig. 4 B), the force applied by the transport system to release the bond was F′ ≈ 70 pN, corresponding to an energy of ΔG ≈ 2000 kT stored in the bonds. Since this is much more than the energy for ATP hydrolysis, ΔG_ATP ≈ 22.5 kT, required for a single motor step (32), it is likely that the stress is established over time.

The hypothesis of a released bond is supported by the strong drop in connection stiffness displayed in Fig. 4 B at time point t_rest (yellow arrow). Such a behavior may correspond to the release of a molecular clutch, e.g., integrin (31), which held the bead before its directed transport. Alternatively, the bead may have been attached to the coverslip beside the filopodium by coincidence, hindering transport during the resting time and thus giving the linker molecules enough time to recruit or assemble.

The relatively high transport force provides further hints about the mechanism of the transport. A locally organized bead transport, for example, by myosin VI motors stepping toward the minus end of the backbone with a stall force of ∼3 pN, would require the work of at least 70/3 pN ≈ 23 myosin VI motors connected to the bead, which would need to have been recruited during the rest time of the bead. This seems to be an unlikely constellation, especially in regard to the intermotor coupling and the organized stepping along a limited number of binding sites, all of which must bind on a small area on the surface of the actin filaments. In a similar way, such high forces cannot result from membrane forces (F_mem) alone, which have been estimated to be in the range of 10–20 pN (1). As discussed further above, it is more likely that the transport is driven by the work of myosin II motors binding to the actin backbone in the cortex of the cell. By a simplified addition of forces similar to that described above, this would require at least (70 pN − F_mem)/2 pN = 25–30 myosin II motors pulling at the same time on the actin backbone, assuming a maximum motor pulling force of 2 pN each (33).

Stepwise transport along the filopodium

The hypothesis of collective work of myosin II motors (9) is further supported by the stepwise transport of the bead, as illustrated in Fig. 7. A first indication for a discontinuous retraction process, which may result from coordinated motor stepping, is given by the accumulations in the 2D bead-position histograms (see Fig. 7 A), which can be detected frequently (see also the dark red lowpass-filtered trajectory). The origin of these histograms can be thought of as a distribution of well-separated sharp points convolved with the fluctuation distribution of the 1-μm large bead. Therefore, deconvolution approaches might be helpful to retrieve steps of molecular motors. However, here we analyzed long traces more thoroughly using an established iteratively working step-finding algorithm (22). This algorithm reveals the most probable mean step size (see Fig. 7, C and D) among the many different steps detected. The most likely step size of 〈s〉 = 10 nm is roughly the power-stroke distance of myosin II, and the occurrence of steps during transport is an indication of discontinuous and coordinated work, a typical behavior of molecular motors (5). Several coordinated motors must be involved in the retraction process due to the high transport forces. However, provided that no artifacts are produced by generation of the histogram, a completely uncoordinated stepping behavior of the motors would not allow the observation of steps during retraction, as shown by Brownian dynamics simulations (F.K., unpublished data).

Temporal change of binding during transport

As shown in Fig. 5, the binding stiffness of the bead to the filopodium changes with time. Here, the lateral stiffness component is analyzed in further detail. Assuming that the stretching of any connection of the bead to the filopodia is stiffer than the bending of this connection, the angle of maximal lateral stiffness corresponds to an elongation of the connection consisting of, for example, a molecular bond. From geometrical considerations, as illustrated by the mechanistic model of the bead fluctuations around the filopodium cross section in Fig. 5 A, the angle of maximal stiffness can be interpreted as the tilt angle of the bead relative to the filopodium. The analysis of the fluctuations thus provides a quantitative measure of the geometry, nature, and strength of the molecular link of the bead to the filopodial backbone, which can hardly be revealed from the microscopy images. As illustrated in the example of Fig. 6, the temporal variation in connection stiffness, κ_c, is correlated to the orientation of the bead center relative to the filopodium, as well as to the transport velocity. At high transport velocities between 50 and 100 nm/s, the bond between bead and membrane seems to be at the side of the filopodium. One possible explanation for the variation of angle φ is a rotation of the actin backbone inside the shaft of the filopodium (34–36). The displayed change in bead orientation relative to the filopodium requires forces that can also be exerted by the transmembrane linkers. If we disregard the possibility that other filopodia act on the bead at this position and that the actin backbone is rotated, it appears to be likely that the transmembrane molecules bind to and unbind from the bead, forcing it to orientate in a preferable position (in this case not directly above the filopodium) and transporting it at high velocities when the transmembrane linkers are active.

As discussed above, it seems to be plausible, and also a very attractive focus for future experiments, that the stepping rate of the myosin motors and the corresponding polymerization rate in the filopodium tip can be altered externally. This is possible when the bead is linked to the backbone and external forces act on the bead (e.g., by the optical trap). An intermediate disconnection of transmembrane linkers to the bead will possibly not influence the retrograde transport of the actin backbone.

Approach to the cell body

Although the high-contrast DIC images shown in Fig. 8, B and C, indicate that more filopodia are acting on the bead close to the cell body, the change in the bead transport and binding characteristics cannot be revealed by microscopy images alone. As mentioned above, tracking of the change in bead fluctuation behavior allows an estimation of the connection strengths during the approach to the cell body. As shown in Fig. 8 A, there is an overall increase in the connection stiffnesses κ_max and κ_min, which, however, reveal some significant modulations in connection strength over some seconds, as indicated by the dashed arrows. A comparison with the synchronized video recordings indicates that this might be affected by a second filopodium, which further hinders the bead fluctuations. In the cases shown in Fig. 8, B and C (t = 370 s and 393 s, respectively), the maximal stiffness increases, whereas the minimal stiffness is affected only in the first case (Fig. 8 B) to a minor degree. In this period of time, the maximal stiffness corresponds in good approximation to the horizontal axis (see Figs. 6 and 8). It is likely that initially the second filopodium decreases the fluctuation width by sterical interaction only before an additional binding process happens. The second decrease of the stiffness components around t = 385 s indicates that no persistent linkage to the additional filopodium via transmembrane molecules has been established. For t > 400 s, the cell builds up more and stronger filopodia connections to engulf the particle, as observed in Fig. 8 A.

The analysis shown in Figs. 6 and 8 emphasizes the potential of combining thermal noise tracking with high-resolution microscopy. The analysis of fluctuating particle motions provides much more information about the interaction with the local cellular environment than can be revealed by standard microscopy techniques or by tracking the mean position values without fluctuations.

Conclusions

We have shown that, similar to viruses, large particles such as 1-μm-sized beads surf along adherent filopodia toward the cell body. This constitutes to our knowledge a hitherto unknown mechanism by which phagocytes can increase the uptake probability of particles by means of filopodia. Since the bead was not coated with any ligands, the connection to the transport machinery via transmembrane proteins happened spontaneously upon bead contact enabled by the optical tweezers. In several experiments, we could observe resting periods of 1–2 min before the transport starts and periods of directed transport. Sudden changes in the fluctuation width of the bead-center positions, which we tracked interferometrically in 3D, indicate molecular binding and unbinding, likely due to trans-transmembrane proteins. Based on the measured strength of the bead connection to the membrane, a sudden start of the transport and displacement of the bead center revealed the release of a yet undefined lock, which required a pulling force of the transport system of ∼70 pN. We argued that this high force must have been exerted mainly by myosin II motors pulling the actin backbone of the filopodium toward the cell center. Since the length of the adherent filopodium does not change, the backbone retraction velocity must be compensated by the actin polymerization rate at the tip of the filopodium. Observed variations in the bead transport velocity of between 10 and 100 nm/s are likely controlled by cooperative work of myosin motors, which also must control the polymerization rate in the tip of the filopodium by the mechanical connection via the actin backbone. By applying a step-detection algorithm to the position traces, we determined a step size of 10 nm, typical for myosin II, as the most probable step size while the bead was connected to the actin backbone.

Transporting an object along an adherent filopodium seems to constitute an additional approach of phagocytes to initiate uptake of particles. The particle transport presented in this study can be ascribed to a retrograde translation of the actin backbone supported by myosin motors, similar to the processes leading to retraction of dorsal filopodia (5,37). Particle surfing along filopodia represents another cellular mechanism, which the efficiency of the mammalian immune response system can be increased.

The different techniques for measuring and analyzing particle fluctuations presented in this study should be helpful to other scientists working in the area of cell biology. The changes in particle connection strengths and friction coefficients, extracted from the fluctuations, provide much deeper insights into transport processes on the molecular scale than can be achieved with standard microscopies.

Author Contributions

F.K. performed experiments, analyzed data, and prepared all graphs. A.R. initiated and supervised the project. A.R. and F.K. wrote the article.

Supporting Citations

References (38,39) appear in the Supporting Material.