Three-dimensional human facial morphologies as robust aging markers

Abstract

Aging is associated with many complex diseases. Reliable prediction of the aging process is important for assessing the risks of aging-associated diseases. However, despite intense research, so far there is no reliable aging marker. Here we addressed this problem by examining whether human 3D facial imaging features could be used as reliable aging markers. We collected > 300 3D human facial images and blood profiles well-distributed across ages of 17 to 77 years. By analyzing the morphological profiles, we generated the first comprehensive map of the aging human facial phenome. We identified quantitative facial features, such as eye slopes, highly associated with age. We constructed a robust age predictor and found that on average people of the same chronological age differ by ± 6 years in facial age, with the deviations increasing after age 40. Using this predictor, we identified slow and fast agers that are significantly supported by levels of health indicators. Despite a close relationship between facial morphological features and health indicators in the blood, facial features are more reliable aging biomarkers than blood profiles and can better reflect the general health status than chronological age.

Introduction

Aging is a major risk factor for many complex diseases¹. Reliable prediction of the aging process is not only important for quantitatively assessing the degree of the aging process and its reversal^2,3, but also important for assessing the risks of aging-associated diseases and for designing individualized treatment schemes⁴. However, despite intense research, so far there is no reliable aging marker to measure the biological age of an individual⁴. With the recent development of three-dimensional (3D) imaging technology, such as the widely used stereo photogrammetric camera system 3dMDface System (www.3dmd.com), and methods to reconstruct 3D images with single-pixel detectors⁵, 3D facial data are now used in many fields, such as disease diagnosis and facial morphology comparison between ethnic populations^6,7,8. For example, it has been extensively used to recognize many dysmorphic syndromes, such as Noonan syndrome, Velocardiofacial syndrome, Williams syndrome, Smith-Magenis syndrome, 22q11 deletion syndrome, Fabry disease, autism spectrum disorders and Wolf-Hirschhorn syndrome⁹.

Facial aging is one of the most prominent and readily accessible phenotypes of human aging. However, very few studies have characterized changes associated with the aging face. Initial reports suggested that skin and soft tissues play important roles in showing signs of facial aging^10,11,12. Other studies have revealed that the loss of facial bone volume also contributes greatly to age-dependent facial alterations. Using computed tomography scans, researchers observed larger eye sockets, reduced angle of brow and significant angle changes of the lower jaw as people age¹³, indicating that facial bone morphology is strongly associated with aging. As facial aging is a complex process involving soft tissues and skeleton structures, it is influenced by many factors, such as exposure to sunlight and body weight¹². Thus, large variations exist in facial aging across individuals and ethnic populations. In the field of face recognition, the main differences in exterior facial structure that make individuals distinguishable from each other allow recognition analysis to achieve relatively high accuracy¹⁴. One caveat of facial aging analysis is the difficulty in collecting facial images of the same individual from young to old stages during the whole lifetime. As such longitudinal morphology data are unavailable, the most feasible strategy is to collect images of different people from different age groups for facial aging analysis.

Previous studies have tried to estimate human age using 2D facial images^15,16,17. To date, few studies have used 3D images to analyze human facial aging. One study used 400 subjects between 0 and 50 years old to train a face growth model, which showed that the main component associated with face size changed greatly from 0 to 18 years of age with no significant changes in subjects older than 18 years¹⁸. Therefore, this component mainly describes face growth before adulthood. More importantly, to study facial aging and to quantify related phenotypes, adult subjects from a wider range of ages are particularly required.

All published studies using 2D or 3D face-based age prediction aim to minimize the variations among different samples to generate the best predictor for chronological age from human faces by focusing on developmental ages. Their major goal was to distinguish whether a face belongs to a baby, an adolescent, a young adult or an elderly person. None of these studies focused on aging, where facial changes are relatively subtle compared with changes during development, nor did they address why some people look older or younger than their peers. Additionally, no assessment was made as to whether the differences between appearance and actual age are physiologically relevant, which can only be validated by an independent set of physiological parameters, such as blood health indicators. Here we acknowledge that there are large variations among people of the same age and tried to identify such variations and examine whether they reflect the physiological age differences among people. This is a more important question than simply predicting chronological age, or predicting age over large developmental changes, because aging is a special phase of the human lifespan where an aging biomarker, or the difference in biological age and chronological age during aging, is important for clinicians to design personalized medical treatment and for individuals to improve their life styles and health.

To uncover facial features indicative of overall health and chronological age, we collected 3D human facial images and blood profiles of > 300 subjects well-distributed across ages ranging from 17 to 77 years old, and generated the first comprehensive map of the aging human facial phenome by quantifying specific aging-related facial phenotypes from the image data.

To compare 2D facial images of different individuals, Turaga et al.¹⁹ used landmarks and geometric relationships to describe face shapes and the relative differences. As our 3D facial data are spatial coordinates, we can use a precise transformation to first align all the facial images together using our previously developed 3D facial image registration tool^20,21. After alignment, each vertex can be directly used as a scaled landmark to be compared for facial morphological or geometric changes during aging where any changes between different images are already relative position changes. We also quantified 10 intuitive facial features based on the 17 salient landmarks to present a subset of the most obvious facial indexes among the > 30 000 vertices we examined. By aligning and transforming all vertices' values, the information for all 3D geometric vertices is used to extract aging-related facial changes. This allows us to not only examine predefined shapes and metrics, but also to de novo discover any patterns arising from differentially positioned vertices.

We identified several facial features such as the eye slope and mouth-nose distance to be significantly correlated with aging. Strikingly, although we found that facial morphology features are significantly correlated with health indicators in the blood, facial features are more reliable aging biomarkers than blood profiles and can better reflect general health status than chronological age.

Results

Overview of facial morphological changes

To track the general aging patterns exhibited on the face, we acquired 332 human faces of Chinese origin and reconstructed the average face profiles within each age group at 10-year intervals.

We applied our previously developed high-density point-wise registration algorithm to align different faces across all 3D facial images^20,21, which consists of three major steps: (1) Landmark recognition: starting with the collected raw 3D face images, the nose tip is first automatically recognized on each face by the sphere pattern fitting approach, and then pose normalization is performed to render all faces to a uniform frontal view. Other facial landmarks are then automatically annotated by a principle component analysis (PCA)-based feature recognition approach. Our landmark recognition method is highly accurate, with an average root mean square error of ∼1.7 mm from manually annotated results²⁰. (2) Registration: a reference facial image, in which its mesh is re-sampled for an even point distribution with a density of about 1 pixel/mm², is warped to register every sample facial image by matching the already recognized landmarks via the non-rigid thin-plate spline transformation. Therefore, the mesh points of the reference face are projected to the sample facial image to find their one-to-one correspondences. We then use the projection points to re-define the sample facial surface mesh. As the same reference facial image is used, the re-defined sample faces (3D point sets) are point-wisely corresponded across all samples. We also use non-rigid registration under the guidance of landmarks to ensure that the point-wise correspondence is approximately anatomically homologous. Now, each sample facial image is represented by a set of 32 251 corresponding 3D points. (3) Alignment: the generalized procrustes analysis is then used to align all the registered facial images into a common coordinate system. Finally, complete geometric data of the 32 251 marker points are obtained. Each sample can be represented by a shape vector of concatenated coordinates for all vertices. We then used the high-density geometric data to obtain coordinate changes and de novo extract shape changes associated with aging.

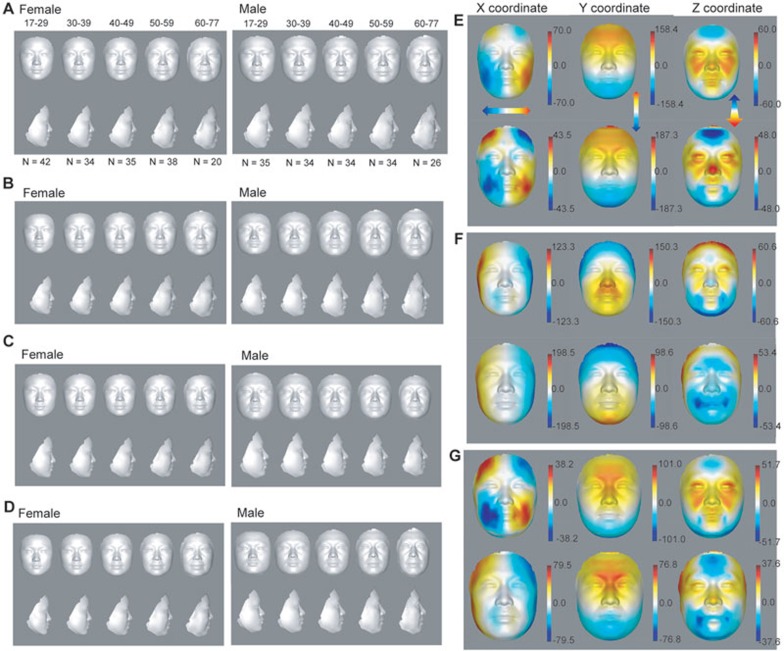
We first computed the average facial shape based on all the sample shape vectors in each age group. These average profiles of females and males visually revealed major signatures of facial morphological changes during aging (Figure 1A and Supplementary information, Table S1).

Figure 1.

Visualization of facial aging. (A) The female and male average profiles of five age groups from 17 to 77 years old. N indicates the number of subjects in each age group. (B-D) Synthesized female and male average profiles between −2 and +2 SD of loading values of age-correlated PLS component 1 (B), component 2 (C) and combined components 1 and 2 (D). (E-G) Heat map of 3D effects displaying loading values of age-correlated PLS component 1 (E), component 2 (F) and combined components 1 and 2 (G) shown on female and male faces. The loading values were multiplied by 10 000. Red and blue denote, respectively, higher and lower values along x-, y- and z-axes.

There are many changes exhibited in these average faces, especially in the mouth, nose and eye regions. From young adulthood to old age, the mouth elongates, the nose becomes wider, the mouth-nose distance increases and eye corners droop. Young faces are smoother and thinner than old faces; old faces have more face sagging, subcutaneous fat accumulation and fuller cheeks than young faces (Figure 1A and Supplementary information, Table S1). Overall, our reconstructed average face profiles reflect the general patterns of facial aging.

Principle components underlying facial aging patterns

To detect age-associated principle components on 3D facial images, we performed partial least squares regression (PLSR) analysis, which upon regressing to age is able to maximize the variance of observations caused by aging²². The cumulative variance in the facial morphology data explained by the first three components are 57.97% and 62.14% in females and males, respectively, and among them the first component explains 33.76% and 28.23% of the variance in females and males, respectively. We visualized each of the first two principle components by synthesizing 3D faces with a different SD, from −2 to +2 SD, along the first or second component starting from the average of all male or female faces from our sample collection (Figure 1B and 1C). Synthesis of different scaling models can display component-related signatures¹⁸. With the increase in PLS component 1, which is highly correlated with age (Pearson Correlation Coefficient (PCC) = 0.49 and 0.54 for males and females, respectively, see below), both female and male faces look older, with increased nasolabial folds and drooping eyelids. Even eye pouches could be easily seen from the side view of the male face when component 1 reached mean + 2 SD (Figure 1B). Although PLS component 1 displayed a positive correlation with face size, component 2, which is also positively correlated with age, showed a negative correlation with face size. To determine the combined effect of these two components, we synthesized a face based on both PLS components 1 and 2 (Figure 1D). By combining these two components, their influence on face size was reduced, although there is a trend for the mean − 2 SD face to be broader and the mean + 2 SD face to be longer, in particular for the male face (Figure 1D). Other local aging features, however, are reinforced. For example, despite the narrowing of the face by PLS component 2, mouth width is not reduced by component 2. Particularly for the female PLS component 2 (Figure 1C), the mouth width also extends as in component 1. This is further confirmed by the synthesized face from the combined effect of PLS components 1 and 2 (Figure 1D).

We examined which specific regions were represented by the first two PLS components by visualizing their loading values in each of the three dimensions on the average male or female face from our sample collection. One of the effects of PLS component 1 is to widen the lower jaw including the mouth region and to narrow the forehead (Figure 1E). Another effect is to elongate the vertical axis of the face, increasing the distance between the upper and lower sides of the face. These effects were observed in both females and males. The z-axis of PLS component 1 also protrudes both upper and lower eyelids. For females, it also influences cheeks resulting in a fleshy face, which might be caused by sagging skin and accumulating fat. However, for males, protruding nose and reducing height of forehead are the most obvious changes in z-axis as PLS component 1 loading increases. Males and females shared significantly high similarity of morphological changes across the three dimensions of component 1 (PCC = 0.85, 0.99 and 0.78 for x-, y- and z-axes, respectively, P < 2.2e − 16). Component 2 tends to narrow the face and reduces the distance between the upper and lower sides of the face (Figure 1F), which has an opposite effect to component 1 both in females (PCC = −0.63, −0.36 and 0.4 for x-, y- and z-axes, respectively, P < 2.2e − 16) and in males (PCC = −0.4, −0.79 and 0.11 for x-, y- and z-axes, respectively, P < 2.2e − 16). Each axis of component 2 is also highly similar between females and males (PCC = 0.95, 0.83 and 0.45 for x-, y- and z-axes, respectively, P < 2.2e − 16). The combined effect of the loading of components 1 and 2 on the x-, y- or z-axis shows a slight increase in face length and a slight decrease in face width over age (Figure 1D and 1G).

Aging-associated facial morphological phenotypes

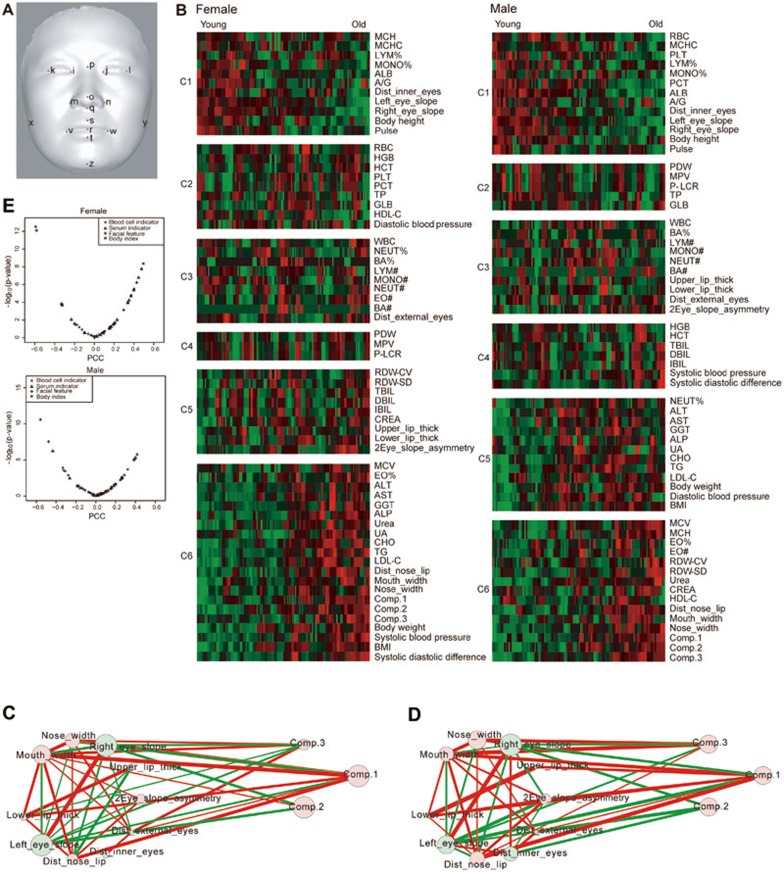
Next, we quantified morphological phenotypes of facial aging to confirm the visual observations described above. We quantified 10 facial morphological phenotypes (Figure 2A and Supplementary information, Data S1): the distance between the nose and mouth, mouth width, nose width, interocular distance, upper lip thickness, lower lip thickness, external canthi width, left eye corner slope, right eye corner slope and the asymmetry of two eye corner slopes.

Figure 2.

Aging-related facial morphological phenotypes. (A) The 17 landmarks used to align all faces. (B) Clustering of all quantified facial features, blood serum indicators, blood cell indicators, body indexes and PLS components in females and males. (C) The correlation network of female facial features and PLS components. (D) The network of male facial features and PLS components. Node size is proportional to the correlation between the feature or component and age. (E) Distribution of correlations between chronological age and each quantitative feature in females and males.

To visualize relationships between the various components and features and age, we clustered all of them across different individuals and ages (Figure 2B) using the BIC-SK algorithm²³. Two major clusters, clusters 1 and 6 show negative and positive correlations, respectively, with age (Figure 2B). In Cluster 1, the average interocular distance decreases with age (Figure 2B) for both females and males. In Cluster 6, the average nose-to-mouth distance, mouth width and nose width are clustered together and increase during aging (Figure 2B). By both ANOVA and Kruskal-Wallis rank sum test, these differences among age groups are highly significant (Figure 2B and Table 1). These trends are similar to those reported by manually measuring these parameters in 13 940 Han Chinese²⁴, and the changes are all consistent with the age-related PLS components, which both broaden the width of the lower jaw and the mouth (Figure 1E). Moreover, the effects of component 1 on two sides of the nose and on the canthus (Figure 1E) are also in accordance with alterations in measurements of nose width and interocular distance (Figure 2B and Table 1). The y-axis effect of component 1 showed a strong correlation with the quantitative measurement of the mouth-nose distance. For example, component 1 elongates the distance between the upper and lower sides of the face (Figure 1E), which was indeed confirmed by the increase in distance between mouth and nose during aging (Figure 2B and Table 1).

Table 1. The significances of the differences in quantitative facial phenotypes across age groups determined by ANOVA or Kruskal-Wallis rank sum test.

Facial phenotype	Female		Male
	ANOVA	Kruskal-Wallis rank sum test	ANOVA	Kruskal-Wallis rank sum test
Distance between the nose and mouth	2.19E – 03	3.82E – 04	1.46E – 05	1.34E – 05
Mouth width	4.57E – 06	7.34E – 05	1.39E – 03	1.80E – 03
Nose width	9.75E – 04	6.63E – 04	3.42E – 02	2.14E – 02
Interocular distance	2.40E – 03	1.72E – 03	4.24E – 04	6.35E – 04
Left eye corner slope	4.78E – 10	5.52E – 08	4.22E – 07	2.00E – 06
Right eye corner slope	5.85E – 11	1.13E – 08	3.59E – 09	1.72E – 08
Asymmetry of two eye corner slopes	8.01E – 02	7.43E – 02	8.92E – 02	8.52E – 02
Upper lip thickness	2.71E – 01	6.55E – 01	7.72E – 01	6.60E – 01
Lower lip thickness	1.14E – 01	2.22E – 01	5.04E – 01	4.88E – 01
External canthi width	4.55E – 03	2.13E – 03	3.75E – 01	2.95E – 01

We also quantified the slope between inner and outer eye corners for each subject. We found that while the outer eye corners of most young Han Chinese are upturned, they drop over age, displaying an overall downturn in the old individuals (i.e., the average slope is negative for subjects older than 60 years). The median slope in different age groups steadily and significantly decreases with age in both females (Kruskal-Wallis rank sum test, P = 5.52E − 08 and 1.13E − 08 for left and right eyes, respectively; Figure 2B and Table 1) and males (Kruskal-Wallis rank sum test, P = 2.0E − 6 and 1.72E − 08 for left and right eyes, respectively; Figure 2B and Table 1). The PLSR analysis also showed that one of the vertical effects of component 2 was to drop eye corners (Figure 1F).

The quantification of the asymmetry of slopes between the left and right eyes indicates that although the slopes are asymmetric (unpaired two-sided Student's t-test, P = 0.035 and 0.039 for female and male, respectively), the change of asymmetry during aging is not significant (Figure 2B and Table 1).

We also visualized the significant correlations among quantified facial features (P < 0.05) in a network (Figure 2C and 2D), where the width of edges are proportional to the PCC between two features across all individuals of the same sex. In both females and males, high correlations exist between upper and lower lip thickness, right and left eye slope, and nose and mouth width. This indicates that these binate facial features have similar changes during aging. In females, there is a very negative correlation between mouth-nose distance and upper lip thickness. It is consistent with the possibility that the increased distance between nose and upper lip with aging is to some extent caused by the decrease in the upper lip thickness. The network also shows that PLS component 1 is highly positively correlated with mouth width, nose width and mouth-nose distance and so on. PLS component 2 is highly negatively correlated with left and right eye slope, especially in females (Figure 2C and 2D). These are all consistent with the visual effects of PLS components 1 and 2.

Comparison to health indicators in the blood

For the same individuals in our cohort, we also performed routine blood tests and obtained general blood biochemical profiles. This allowed us to examine the correlations between chronological age and the blood profiles that evaluate general health status. Compared with the age-related blood profiles, facial features have more significant correlations with chronological age (Figure 2E and Supplementary information, Table S2) and are therefore more reliable aging biomarkers. For females, the left eye slope (PCC = −0.58, P = 7.78E − 13) and right eye slope (PCC = −0.59, P = 2.96E − 13) have higher and more significant correlations with chronological age than the total cholesterol (CHO) level, which has the highest and most significant correlation with chronological age among blood indicators (PCC = 0.48, P = 1.75E − 8) in females. For males, the left eye slope (PCC = −0.48, P = 2.87E − 8) and right eye slope (PCC = −0.56, P = 2.56E − 11) have higher and more significant correlations with chronological age than the albumin (ALB) level, which has the highest and most significant correlation with chronological age among blood indicators (PCC = −0.43, P = 6.04E − 7) in males.

There are obvious differences in blood indicators between female and male subjects. For females, the CHO (PCC = 0.48, P = 1.75E − 8) and low-density lipoprotein cholesterol (LDL-C: PCC = 0.45, P = 1.67E − 7) levels are significantly correlated with age. In contrast, for males, the correlations between these two blood serum indicators and age are less significant (CHO: PCC = 0.26, P = 4.03E − 3; LDL-C: PCC = 0.12, P = 0.18); however, the ALB level (PCC = −0.43, P = 6.04E − 7) has a significant correlation with age. The disparity between female and male CHO/LDL-C correlations with age is concurrent with the very significant differences between female and male ALB levels (unpaired two-sided Student's t-test, P = 1.76E − 4). Male ALB levels stably decrease with aging. However, for females, the average ALB level is lower than male except in the oldest age group (in their 70s), where the ALB level becomes similar in females and males. As serum ALB can interact with CHO²⁵ and enhance CHO efflux by acting as shuttles^26,27, high ALB levels might reduce intracellular CHO levels and make them less associated with age in males.

In general, while blood indicators are associated with age in a sex-dependent manner, aging-related facial changes did not differ between males and females. This indicates that aging-related facial changes are more general and stable markers for human aging.

3D facial image-based age predictor

To see whether we can use the age-related facial features to predict physiological age and identify slow and fast agers within the same age group, we first tried to predict the chronological age of each individual using a regression model composed of age-associated PLS components using a leave-one-out (LOO) method. For both female and male samples, 34 components are required to account for 95% of the total variation (Supplementary information, Table S3 and Figure S1).

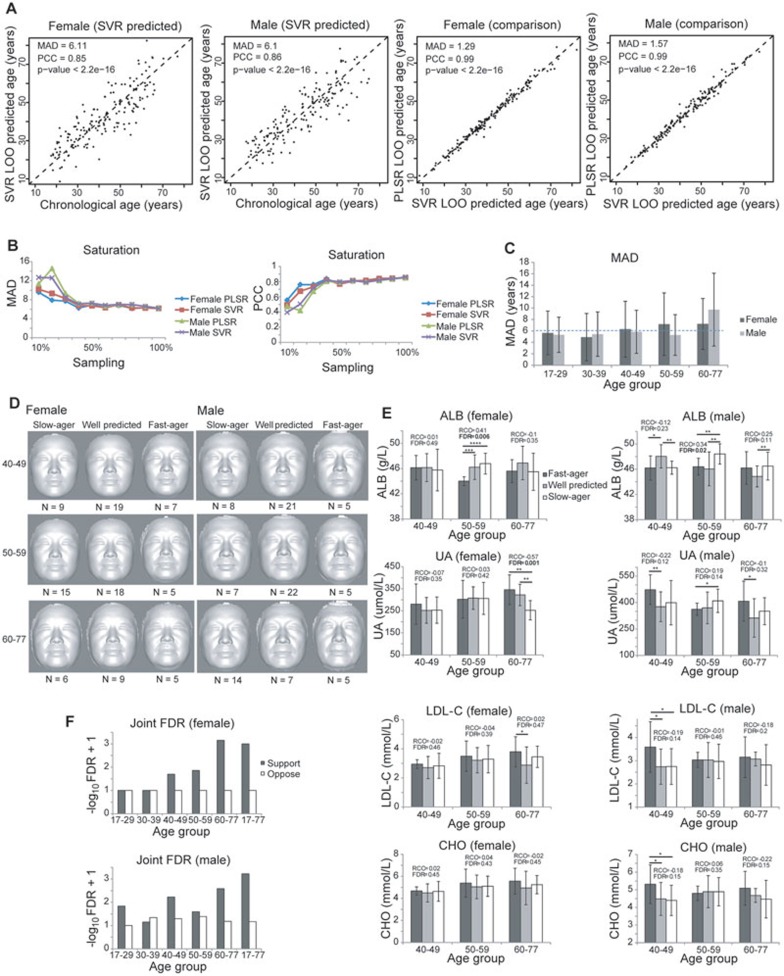
To verify that it indeed entails such a large number of independent components to generate an accurate age predictor from the images, we also trained a support vector regression (SVR) model (linear kernel) using our 3D facial morphological data and compared the prediction results produced by the two methods (PLSR LOO vs SVR LOO; Figure 3A and Table 2). This SVR model used three coordinates of the evenly distributed 32 251 vertices. The predicted ages by the two predictors are very similar (PCC = 0.99 between the predicted ages given by the two methods for both female and male samples; Figure 3A), with SVR showing a slightly better performance in predicting chronological age for both females and males with a mean absolute deviation (MAD) of 6.11 and 6.10 years for independent female and male samples, respectively (Table 2). Sorted by prediction weights in the SVR model, only a small fraction of the vertices, the top 200-300 vertices, are essential for age prediction (Supplementary information, Figure S2A and S2B). These are mainly concentrated on the regions of eyes and nasolabial folds (Supplementary information, Figure S2A and S2B). The SVR regularization algorithm, which is intended to reduce the risk of over-fitting when processing high-dimensional data, revealed a similar level of performance of the SVR predictors based on all vertices or the top 300 vertices (Supplementary information, Figure S2C and S2D).

Figure 3.

Prediction of physiological age, slow and fast agers based on 3D facial images. (A) Correlation of age predicted by facial vertices-based SVR predictors with the actual age of the subjects, and the correlation between SVR- and PLSR-predicted ages. Predictors are trained separately in females and males using all but one sample to predict the age of the left-out sample. The predictors are generated based on ages accurate to the day. (B) The deviations and correlations between predicted and real ages reach saturation levels with > ∼40% of the samples. Curves of each predictor show MAD and PCC between predicted age and chronological age when 10%, 20%,..., or 100% of the data was used to build the predictors. (C) MAD between the chronological ages and predicted ages in each age group. Error bars denote SD. (D) The average profiles of the predicted fast agers, slow agers and well-predicted female and male subjects in age groups older than 40 years. The classification is based on the age difference > 6 years between predicted age and chronological age. N indicates the number of subjects in each class of each age group. (E) Levels of the most age-correlated health indicators in predicted fast agers, slow agers and well-predicted subjects. The classification is the same as in D. ^*, ^**, ^*** and ^**** denote unpaired one-sided Student's t-test P < 0.1, 0.05, 0.001 and 0.0001, respectively. RCC stands for Spearman's rank correlation coefficient between each sample class (rank 1, 2 and 3 for predicted fast agers, well-predicted subjects and slow-agers, respectively) and indicator level. FDR stands for false discovery rate, which is the fraction of times among 1 000 sample label permutations that give RCC ≥ the real RCC. Error bars denote SD. (F) The joint FDR for all age-associated blood indicators' RCC to slow- and fast-ager classification in females and males in each age group. FDR is calculated as the fraction of times among 1 000 sample label permutations that have larger than or equal to the real number of indicators whose absolute RCC are greater than the defined cut-off (female 0.4 and male 0.2). Support denotes the cases of positive RCCs for Cluster 1 indicators and negative RCCs in Cluster 6 indicators; oppose denotes the opposite.

Table 2. The performance of different methods to predict age based on 3D facial images. The predictors are generated based on ages accurate to the day.

	PLSR		SVR
	Female	Male	Female	Male
Correlation	0.85	0.85	0.85	0.86
Mean absolute deviation (year)	6.18	6.21	6.11	6.10

We have also tried cross-validation by non-overlapping 90%/10% splits (that is using 90% of the samples to build the predictor and using the rest 10% of the samples to test and calculate the MAD). The results (female MAD = 6.13 and 6.1 for PLSR and SVR, respectively; male MAD = 6.38 and 6.03 for PLSR and SVR, respectively) are very similar to the above LOO cross-validation results. This indicates that the performance of our predictor is not dependent on the cross-validation strategies.

In order to test the sufficiency of sample size, we performed saturation analysis, by using 10%, 20%,..., or 100% of the data to do the LOO cross-validation (predictors are trained using all but one sample to predict the age of the left-out sample for randomly sampled 10%, 20%,..., or 100% of the data), and examined the MAD and PCC between predicted age and chronological age. As shown by both parameters, the results reach saturation levels at ∼40% of our current sample size (Figure 3B). In other words, adding more samples will not generate any results different from what we have seen now, and the current sample size is more than enough to represent the stable statistics in even larger sample sizes.

The high consistency across these different models and different subsets of the data suggests not only that our models do not over-fit the data, but also that the average 6-year deviation of the predicted ages (by either model) from the chronological age truly reflects the aging differences across samples, and hence characterizes/separates the fast and slow agers from the average population. Based on the SVR predictor, within each age group we defined three classes of samples, fast agers, which are predicted older than their chronological ages, slow agers, which are predicted younger than their chronological ages, and well-predicted samples by the small age difference between an individual's predicted age and chronological age. Fast and slow agers are those whose predicted ages are > 6 years older and younger than their chronological ages, respectively. We found that both the MAD and the variation of absolute deviation in older age groups (> 40) are relatively larger compared with younger age groups (< 40) and increase with age (Figure 3C), suggesting that slow and fast agers in older groups are more common than in younger groups.

Therefore, we further focused on the slow and fast agers predicted in the older age groups to see whether they are indeed fast and slow agers.

We first examined whether the predictions can be visually validated using the average faces of the three classes in each age group older than 40 years old. As shown in Figure 3D, the slow- or fast-ager classes indeed look younger or older than other average faces. In addition, the quantitative facial features also show significant differences among the three classes within each age group older than 40 years old (Supplementary information, Figure S3A). In contrast, consistent with the smaller variations predicted by our age predictor, the average faces in the two younger age groups do not show obvious age differences among the three classes (Supplementary information, Figure S3B).

Slow and fast agers identified by 3D facial image-based age predictor deviate in health status

We then examined whether the slow and fast agers also deviate in their health status as reflected by levels of the blood health indicators. Despite the unexpected significant differences in the ALB level of the male 40-49 age group and the UA level of the male 50-59 age group (Figure 3E), the health status, especially the aging-associated blood health indicators (ALB, UA, CHO and LDL-C levels), did support our facial imaging-based fast, normal and slow-ager classifications. In older female samples (50-59 years old), the ALB level showed an increasing gradient from fast to normal and slow-ager samples, with the well-predicted and slow-ager classes each having significantly higher ALB levels than fast agers (Spearman Rank Correlation Coefficient (RCC) = 0.41, false discovery rate (FDR) = 0.006 based on 1 000 sample label permutations; Figure 3E). For the female samples from 60 to 77 years old, the UA level in the slow-ager class is significantly lower than that in normal and fast-ager classes (RCC = −0.57, FDR = 0.001; Figure 3E). For the male samples from 50 to 59 years old, the ALB level in the slow-ager class is significantly higher than that in normal and fast-ager classes (RCC = 0.34, FDR = 0.02; Figure 3E). For the male samples from 60 to 77 years old, the UA level in the fast-ager class is higher than that in normal and slow-ager classes (Figure 3E). In both females and males, the LDL-C and CHO levels lack such significant patterns but still tend to be higher in the fast-ager class than in normal or slow-ager class for 40-49 and 60-77 age groups (Figure 3E).

Other health indicators that are positively or negatively correlated with age, (in the positively and negatively age-correlated clusters 1 and 6, respectively in Figure 2B) also generally support our facial imaging-based fast, normal and slow ager classifications (Supplementary information, Figure S4). For example, ALB and A/G levels decrease with age in females (female Cluster 1 in Figure 2B), and the slow-ager class shows a slower decrease in ALB and A/G levels and tends to have higher levels of these two blood indicators than other classes in females; MCV and MCH levels in males are positively correlated with age (male Cluster 6 in Figure 2B), and the fast-ager class also shows higher levels of these two blood cell indicators/measurements than other classes (Supplementary information, Figure S4). The FDR based on 1 000 sample label permutations showed that the gradient patterns from fast to slow agers are very significant, especially the gradient increase in the levels of Cluster 1 blood health indicators (that decrease with age; Figure 2B) from fast to slow agers, and the gradient decrease in the levels of Cluster 6 blood health indicators (that increase with age) from fast to slow agers (Supplementary information, Figure S4). The absolute RCCs that are consistent with the direction of our classifications are significantly higher than random expectations (unpaired one-sided Student's t-test, P = 0.09 and 0.03 for females and males, respectively; Supplementary information, Figure S5), while those that are inconsistent with our classifications are not significantly different from random expectations (unpaired one-sided Student's t-test, P = 0.80 and 0.20 for females and males, respectively; Supplementary information, Figure S5). The joint FDRs of all blood health indicators in clusters 1 and 6 supporting our slow- and fast-ager predictions are 0.01 and 0.006 for females and males, respectively, and there is an increase in the level of significance with age (Figure 3F). In contrast, the joint FDRs of all blood health indicators in clusters 1 and 6 opposing our slow- and fast-ager predictions are not significant (1.0 and 0.68 for females and males, respectively). Therefore, we observed a general pattern that if the level of an indicator decreases with age, the slow-ager subjects tend to have a higher level of the indicator than other subjects, whereas if the level of an indicator increases with age, the fast-ager subjects will have a higher level of the indicator than other subjects.

Similar patterns were also observed when the slow- and fast-ager deviation was set to 7 instead of 6 years (Supplementary information, Figure S6). Overall, these results suggest that, based on our SVR model, facial images can be utilized to accurately predict physiological age and can well reflect the levels of health indicators in the blood.

We further examined whether our prediction, compared with using the chronological age, can better reflect the biological ages of the outliers. Using the level of blood indicators as a surrogate for biological age in the slow and fast agers (|predicted age − chronological age| > 6), we computed the correlation between the blood indicator levels and predicted/chronological ages in these outliers. These results showed that the predicted ages indeed have higher correlations with these individuals' blood profiles than their chronological ages (Supplementary information, Figure S7).

The good performance of the age predictor is not due to other aging-associated factors

Next, we asked whether the good performance of the age predictor is due to other factors that are strongly correlated with age. This is unlikely the case given the much higher correlation between our PLS/SVR model-predicted age and chronological age (PCC = 0.85/0.85 and 0.85/0.86 for females and males, respectively) than that between a single age-associated feature and chronological age (e.g., for BMI, PCC = 0.37 and 0.25 for females and males, respectively). Still, we built a new PLS regression model for age, adjusting for BMI, or for the levels of LDL-C, CHO and ALB, which are age-associated features. We found that the PCC between ages predicted by our original PLS model and a new PLS model adjusted for each of these two features (BMI and LDL-C/CHO/ALB levels) are all above 0.99 for either female or male (Supplementary information, Table S4). This suggests that the good performance of our predictor is not due to any single one of these age-associated features.

We also examined the loading values of the model after adjusting for BMI (Supplementary information, Figure S8A), or for CHO, LDL-C and ALB levels (Supplementary information, Figure S8B). Based on the loading values of PLS component 1, there is almost no difference between the new PLS models (Supplementary information, Figure S8) and our original model (Figure 1E).

Furthermore, when we rejected all the image features/vertices that show association with BMI (PCC ≥ 0.3) or with CHO, LDL-C and ALB levels (PCC ≥ 0.3) from our PLS models, we still obtained very similar power for age prediction and aging outlier prediction (Supplementary information, Table S5). The PCCs between ages predicted by our original PLS model and a new PLS model that rejected all BMI-associated features are 0.987 and 0.99 for females and males, respectively. Ages predicted by a new PLS model that rejected all CHO-, LDL-C- and ALB-associated features are also similar to those predicted by our original PLS model (PCC = 0.995 and 0.992 for females and males, respectively).

Facial features associated with age-associated health indicators

We also inferred PLS models for the levels of the age-associated health indicators CHO, LDL-C, HDL-C and ALB. From the visualization of the effect of the first component on the average face (Figure 4), the first component of PLS correlated with CHO and LDL-C levels and showed similar patterns, which is expected by the high correlation between CHO and LDL-C levels (for female, PCC = 0.91, P < 2.2e − 16; for male, PCC = 0.89, P < 2.2e − 16). Their patterns show clear region-specific subcutaneous fullness, which might be due to the accumulation of subcutaneous fat. The effects of these first components are mainly on the fullness of cheeks in the x-axis and the height of the below-eye regions (eye pouches), nasolabial folds and eyelids in the z-axis. HDL-C and ALB show contrary patterns to CHO and LDL-C, as they are associated with reduced fullness of the cheeks and regions below the eyes (Figure 4). Interestingly, ALB displayed unique additional effects, such as the enlargement of the forehead (x- and z-axes), and the decrease of height of the nose tip (z-axis; Figure 4). Besides the above four blood serum indicators, visualization of PLS component 1 linear to the other 14 blood serum indicators and 24 blood cell-related indicators is provided in Supplementary information, Figure S9.

Figure 4.

Heat map of 3D effects showing loading values of PLS component 1 correlated with CHO, LDL-C, HDL-C or ALB level on female and male faces. Loading values were multiplied by 10 000. Red and blue denote, respectively, higher and lower values along x-, y- and z-axes.

Discussion

Various changes occur on human faces during aging. We intended to capture the signatures of these alterations in order to understand more about the human aging process. In this study, we provided a comprehensive and systematic analysis on 3D facial morphology for more than 300 individuals of a wide age range from 17 to 77 years old. Scherbaum et al.²⁸ used 3D facial scans from 95-month-old children to 360-month-old young adults to learn how children faces grow based on a nonlinear model. Facial changes during early development and aging are very different. We noticed that their linear model is more stable than the nonlinear model. Although the nonlinear model has a potential to capture all the mutual dependencies between parameters, our focus is to stably capture only aging-related variations among samples. Furthermore, through our 3D facial image alignment step, the images are transformed and normalized so that any nonlinear changes related to the offset in the alignment have been already removed.

We found that our predictor's MAD increases with age, which can be also observed in many other studies. Several published 2D facial image studies all showed increases in MAD in older groups. Geng et al.¹⁵ observed much larger MADs in adults compared with babies or youngsters using 2D facial images. We also noted that the MAD in their predictor is much larger than ours for the same age group (8 vs 6 years). In the study by Turaga et al., there is also an increase in MAD in samples with older ages. For example, their predictor's MAD is ∼8.84 years for a data set with ages ranging from 20 to 90 years, and the MAD is ∼5.89 years for another dataset with ages ranging from 0 to 69 years, where 70% of the samples are under 20 years of age¹⁹. The MAD also has an increasing trend with age in the study by Weidner et al.²⁹, in which they predicted age based on the level of methylation at three DNA methylation loci with a very similar MAD as our facial image-based predictors.

Our study exemplified the application of 3D imaging techniques to aging research. Although this study is cross-sectional in nature, it is the first to show that 3D facial imaging technology is capable of acquiring high-density facial morphology profiles with high accuracy and utilize them to infer age-related features and predict the process of aging.

Using these data, we developed quantification methods for human facial aging features. We found that mouth width, nose width and mouth-nose distance increase with aging, while eye corners droop with age. These aging trends of the quantitative facial features are visually supported by the synthesized faces derived from PLSR-identified major age-associated components. Across different age groups, the PLS components are highly correlated with the age-associated quantitative facial features. Here by looking at only the Chinese population, we do not know whether similar trends are present in other ethnic groups.

Unlike facial features, the correlations between blood indicators and age are different in males and females. For females, the CHO and LDL-C levels are significantly positively correlated with age, whereas for males, these two blood serum indicators do not show very significant correlation with age. In contrast, the ALB level in males showed a significant negative correlation with age. Thus, facial features have more consistent aging-related changes between female and male than blood indicators. This indicates that aging-related facial changes are more general and stable markers for human aging than blood features. This is potentially important because removing sex as a confounding factor will get us one step closer to monitoring the aging process itself. Using facial features, we trained a SVR predictor to identify fast and slow agers. These predicted slow and fast agers are well supported not only by their facial appearances, but also by blood profiles for health status, indicating that the predicted physiological age based on 3D facial images can better reflect general health status than chronological age, and that 3D facial images can be a good predictor or biomarker for human aging and probably other aging-associated functional decline. It should be noted that we performed two types of independent analyses here: age prediction and facial feature quantification. We used the latter as independent evidence to validate the former, but did not include these quantified features into the age predictor. Therefore, feature quantifications do not influence the performance of the age predictor. Instead, it provides additional support to our findings, especially because it is the most expected result by human intuition.

The results of this study uncovered a reliable and convenient aging marker. By utilizing a non-invasive procedure on the face only, the overall state of aging can be accurately assessed, much more accurately than routine physical examinations. This suggests not only that youth is “skin deep”, but also that health is “written” on the face. People of the same chronological age have different physiological ages that can differ on average by ± 6 years. Our reliable 3D facial image-based predictor of the physiological age is potentially useful for quantitatively assessing the degree of the aging process and its reversal, and for assessing the risks of aging-associated diseases to design individualized treatments.

Materials and Methods

Data acquisition

The study was approved by the ethics committee of the Shanghai Institutes for Biological Sciences. 3D facial images and routine physical indicators (routine blood indexes, general blood biochemical parameters and body indexes) were collected at Beijing Centers for Diseases Control and Prevention (CDC) and Centers for Preventive Medical Research. All participants provided written informed consent prior to this study. All subjects (169 Chinese females and 163 Chinese males) for this study have no history of facial surgery or facial abnormalities. As described in previous study³⁰, we used the 3dMDface system to capture 3D facial images of about 40 000 vertices per face.

The detailed procedure of our photo capture is: first, we adjusted the height of the chair for each subject; second, we asked the subject to not move while taking the photo, the actual photo capture time is ∼1.5 ms and only during this brief moment the subject needs to remain static; and third, after the photo is captured, the operators needed several seconds to wait for the 3dMD software to synthetize the 3D visualization and the operators confirmed that there was no non-neutral expressions, otherwise the photo would be retaken. For all female participants, the operators made sure that there were no obvious cosmetics. All male participants needed to be clean-shaven.

Detailed description of the 18 blood serum indicators, 24 blood cell indicators and 7 body indexes can be found in Supplementary information, Data S1.

Image processing

High-density surface registration for all the 3D facial images was done by our previously developed software for automatic landmark annotation and point-wise registration across all 3D facial images²⁰, where it automatically recognizes 17 landmarks on 3D facial images and makes dense point correspondence in a very efficient and accurate way. In this way, all samples were well mapped to a standard frame and ready to be analyzed.

The design of PLSR analysis

PLS analysis^16,31 was applied to the 3D facial morphology data of female and male samples and regressed to age and each blood indicator, respectively. It is different from PCA, which maximizes the variance of the scores. PLS maximizes the covariance between the scores and the response, and it identifies components that are more relevant for the response. PLS can obtain more age-related components than PCA. The PLS regression is performed as follows (for each sample, X_i is represented by a shape vector involving x, y and z coordinates for all m vertices).

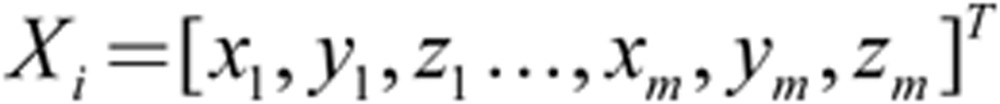The PLS models were built by using the R package 'pls'³², and by using age, or each blood indicator as the observation vector.

Given P = [p₁|p₂| ..., |p_n] as the output loading matrix and b = [b₁, b₂,..., b_n] as a vector of SD of projection scores of n components to be used in different scales between −2 and +2 that controls the shape variation, the computed loading values p_i can be treated as decomposition of the whole face most strongly associated with the observations and can be directly added to the coordinates of the vertices of the average face to synthesize new faces²¹.

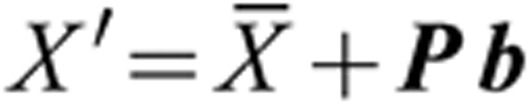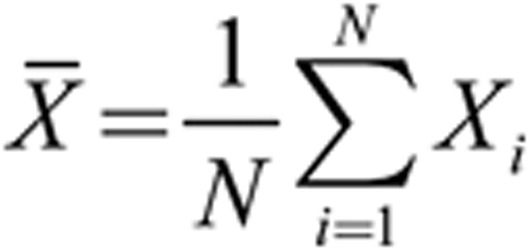When combining the first two components to examine their synthesized effect on the face, we used their loading values p_i (i = 1, 2) multiplied by each component's SDs b_i (i = 1, 2) and then added the two results together to the average profile as shown by the above formula (N denotes the number of samples).

Age prediction analysis

R packages were used for PLS¹⁶ and SVR analyses^17,33. The input data are the same as described above for the PLSR analysis. For both analyses, the LOO method was used (predictors are trained using all but one sample and then used to predict the age of the left-out sample).

Supplementary Information

Supplementary information, Figure S1

Correlation of age predicted by facial vertices-based PLSR predictors with the actual age of the subjects.

Supplementary information, Figure S2

Age predicted by 3D facial image vertices-based SVR predictors.

Supplementary information, Figure S3

Differences between predicted and actual ages in each age group and the mean 3D facial images in well predicted, slow- and fast-ager classes of younger age groups.

Supplementary information, Figure S4

Levels of other age-correlated blood health indicators in predicted fast-agers, slow-agers and well predicted subjects when the classification is based on the age difference > 6 years between predicted age and chronological age.

Supplementary information, Figure S5

The distribution of RCCs between each Cluster 1/6 blood health indicator and the predicted slow- and fast-ager classifications or that between each health indicator and permuted classifications within each age group.

Supplementary information, Figure S6

Levels of the blood health indicators (showed in Fig. 3E) in predicted fast-agers, slow-agers and well-predicted subjects when the classification is based on the age difference > 7 years between predicted age and chronological age.

Supplementary information, Figure S7

Correlation between blood indicators and predicted/chronological age in slow- and fast-agers (|predicted age — chronological age| > 6).

Supplementary information, Figure S8

The loading values of PLS component 1 of the new PLS model adjusted for BMI (A) or for cholesterol, LDLC and albumin (B) in three dimensions.

Supplementary information, Figure S9

The heat map of 3D-effects showing loading values of PLS component 1 correlated with other indicators from 18 blood serum indicators and 24 blood-cell related indicators (except CHO, LDL-C, HDL-C and ALB in Fig. 4) on female and male faces.

Supplementary information, Table S1

Age distribution of subjects.

Supplementary information, Table S2

Pearson Correlation Coefficients (PCCs) of each feature or component with chronological age.

Supplementary information, Table S3

The distribution of cumulative explained variance.

Supplementary information, Table S4

Correlations between ages predicted by the PLS model with or without adjusting for the age associated features, BMI, or LDLC, cholesterol and albumin.

Supplementary information, Table S5

Correlations between age predicted by the PLS model with or without removing image features/vertices that are highly correlated (PCC>=0.3) to the age associated features, BMI, or LDLC, cholesterol and albumin.

Supplementary information, Data S1

Supplementary Notes