Efficient Multiple-Trait Association and Estimation of Genetic Correlation Using the Matrix-Variate Linear Mixed Model

Abstract

Multiple-trait association mapping, in which multiple traits are used simultaneously in the identification of genetic variants affecting those traits, has recently attracted interest. One class of approaches for this problem builds on classical variance component methodology, utilizing a multitrait version of a linear mixed model. These approaches both increase power and provide insights into the genetic architecture of multiple traits. In particular, it is possible to estimate the genetic correlation, which is a measure of the portion of the total correlation between traits that is due to additive genetic effects. Unfortunately, the practical utility of these methods is limited since they are computationally intractable for large sample sizes. In this article, we introduce a reformulation of the multiple-trait association mapping approach by defining the matrix-variate linear mixed model. Our approach reduces the computational time necessary to perform maximum-likelihood inference in a multiple-trait model by utilizing a data transformation. By utilizing a well-studied human cohort, we show that our approach provides more than a 10-fold speedup, making multiple-trait association feasible in a large population cohort on the genome-wide scale. We take advantage of the efficiency of our approach to analyze gene expression data. By decomposing gene coexpression into a genetic and environmental component, we show that our method provides fundamental insights into the nature of coexpressed genes. An implementation of this method is available at http://genetics.cs.ucla.edu/mvLMM.

CLASSICALLY, genome-wide association studies have been carried out using single traits. However, it is well known that genes often affect multiple traits, a phenomenon known as pleiotropy, and more recently it has been shown that performing association mapping with multiple traits simultaneously may increase statistical power (Korol et al. 2001; Ferreira and Purcell 2009; Liu et al. 2009; Avery et al. 2011; Korte et al. 2012). Analysis of multiple traits increases power because intuitively, multiple-trait measurements increase sample size relative to a single-trait measurement. However, utilizing the additional data is not straightforward as measurements from the same individual are not independent. This issue is analogous to that of association analysis in cohorts of related individuals, where trait measurements between related individuals are not independent. Variance component methods model this correlation structure by assuming that the covariance due to genetics between related individuals is proportional to their kinship coefficient (Kang et al. 2008). This constant of proportionality normalized by the total trait variance is related to narrow-sense heritability of the trait (the variance accounted for by additive genetic effects) (Yang et al. 2010).

When the same genetic variants affect multiple traits, trait values for an individual will tend to be correlated. Similarly, shared environmental effects also introduce some level of correlation between traits. A fundamental problem in understanding the relationship between the traits is determining the proportion of the total correlation due to genetics and the proportion due to environment. Classical approaches originating from animal breeding and agricultural research solve this problem by modeling the statistical relationship between traits, using a linear mixed model (LMM) (Falconer 1981; Mrode and Thompson 2005). These approaches decompose the between-trait correlation into both a genetic component and an environmental component and then use the LMM framework to obtain estimates for these quantities. The LMMs used in these classical approaches can be adapted for use in genome-wide association studies (GWAS) by utilizing them to test the association between genetic variants and multiple traits. Multiple-trait variance component methods closely follow the approach utilizing kinship values to model the covariance between different traits among different individuals, such that the genetic covariance between two individuals’ traits is proportional to their kinship coefficient (Henderson and Quaas 1976). In this case, the constant of proportionality is a function of the two trait heritabilities as well as the genetic correlation. These types of models are widely utilized in the plant breeding (Malosetti et al. 2008; Kelly et al. 2009; Verbyla and Cullis 2012) and animal breeding communities (Ducrocq and Besbes 1993). Similarly, multiple-trait models represent the covariance between traits within an individual as a function of both genetics and shared environment.

To utilize LMMs for association analysis, an iterative procedure must be employed to identify the maximum-likelihood estimates of the parameters of the statistical model used for association. The use of LMMs for single traits has been limited by the computational complexity of traditional maximum-likelihood procedures: $O\left(n^3\cdot t\right)$, where n is the number of individuals in the study and t is the number of iterations necessary for the maximum-likelihood algorithm to converge. However, recently developed estimation algorithms have made LMMs computationally efficient and feasible for large population cohorts (Kang et al. 2008, 2010; Lippert et al. 2011; Zhou and Stephens 2012), reducing the computational complexity of from $O\left(n^3\cdot t\right)$ to $O\left(n^3+n\cdot t\right)$, enabling genome-wide association mapping for single traits using LMMs. Unfortunately, the previous approaches (Kang et al. 2008, 2010; Lippert et al. 2011; Zhou and Stephens 2012) cannot be directly applied to multiple-trait LMMs, meaning that the same computational inefficiencies that limited the widespread use of LMMs for single-trait GWAS now hinder the scale at which researchers can perform multiple-trait GWAS. More specifically, with p traits measured over n individuals the covariance matrix relating the p traits measured over the n individuals will be of size $np\times np$ and the running time for classical multivariate LMMs is $O\left(n^3{p}^3\cdot t\right)$. In other words, even when p is small (e.g., $p=2$), the running time scales as the cube of the number of individuals in the sample, meaning that the use of multiple-trait LMMs is not feasible for large sample sizes.

A widely utilized approximation to using the $np\times np$ covariance matrix is to assume that the genetic and environmental effects are independent, which allows the decomposition of the $np\times np$ matrix into the Kronecker product of an $n\times n$ matrix and a $p\times p$ matrix. This type of approach is widely utilized in the plant breeding literature (Malosetti et al. 2008; Kelly et al. 2009; Verbyla and Cullis 2012). In our work we reformulate this decomposition, using the matrix-variate normal distribution (Gupta and Nagar 2000). Using this formulation, we show how a simple data transformation leads to a model equivalent to the abovementioned model while allowing maximum-likelihood inference to be performed in computational time essentially linear in the size of the data set, given a one-time cost of $O\left(n^3\right)$ and $O\left(n^2\right)$. In a simple case, let us assume that p << n (e.g., 2 vs. $10,000$) and that we have only a global mean for each trait; this leads to a total computational complexity of $O\left(n^3+n^{2}p+\left(p^3\left(n+1\right)\right)\cdot t\right)$. The iterative part of the algorithm is then essentially linear in the size of the data set. We call our method the matrix-variate linear mixed model (mvLMM). Our approach differs from previous approaches in the plant and animal breeding communities in that our inference approach is more closely related to the EMMA algorithm (Kang et al. 2008) while previous inference methods are more closely related to the average information restricted maximum-likelihood (REML) algorithm as implemented in ASReml (Gilmour et al. 1995). The reason why algorithms such as EMMA (Kang et al. 2008), EMMAX (Kang et al. 2010), FaST-LMM (Lippert et al. 2011), and GEMMA (Zhou and Stephens 2012) and related methods have become popular in human GWAS is that they take advantage of the specific formulation of the variance components to allow for efficient estimation compared to methods such as ASReml that can be applied to a more general set of models.

We demonstrate the efficacy of our method by analyzing correlated traits in the Northern Finland Birth Cohort (Sabatti et al. 2008). Comparing it to a standard approach (Lee et al. 2012), we show that our method results in a >10-fold time reduction for a pair of correlated traits, taking the analysis time from ∼35 min to ∼2.5 min for the cubic operations plus another 12 sec for the iterative part of the algorithm. In addition, the cubic operation can be saved so that it does not have to be recalculated when analyzing other traits in the same cohort. Finally, we demonstrate how this method can be used to analyze gene expression data. Using a well-studied yeast data set (Smith and Kruglyak 2008), we show how estimation of the genetic and environmental components of correlation between pairs of genes allows us to understand the relative contribution of genetics and environment to coexpression.

Methods

Modeling multiple traits with the matrix-variate linear mixed model

Given a set of p traits for n individuals, a standard statistical model for the ith trait vector, denoted by $y_i$, is given by the following LMM, the model relating phenotypes to genotypes, which is

$$y_i=X{\beta }_i+g_i+e_i,$$

where $X{\beta }_i$ represents the mean term for the ith trait such that X is an $n\times q$ matrix encoding q covariates including the SNP being tested, $g_i$ represents the population structure or genetic background component, and $e_i$ represents the effect due to environment and error. We use $y_{ij}$ to represent the value of the ith trait for the jth individual. We have assumed that the covariates determining the mean will be shared among traits, but this is not a requirement. The variance of $y_i$ is given by the following, assuming that $\text{cov}\left(g_i,e_i\right)=0$,

$$\begin{array}{c}\text{var}\left(y_i\right)=\text{var}\left(g_i\right)+\text{var}\left(e_i\right)\\ ={\sigma }_{g\left(i\right)}^{2}K+{\sigma }_{e\left(i\right)}^{2}I,\end{array}$$

where ${\sigma }_{g\left(i\right)}^2$ represents the genetic variance component for trait i, K represents the $n\times n$ kinship matrix calculated using a set of m known variants, and ${\sigma }_{e\left(i\right)}^2$ represents the environmental and error variance. We note this model asumes i.i.d. environmental errors for a given trait, which is maybe unrealistic for some applications (Bello et al. 2012). We use $K_{jk}$ to represent the entry of the kinship matrix corresponding to the relation between the jth and kth individuals. From these models (Henderson and Quaas 1976; Mrode and Thompson 2005), it follows that the covariance between measurements for individuals j and k for trait i is given by

$$\text{cov}\left(y_{ij},y_{ik}\right)={\sigma }_{g\left(i\right)}^2{K}_{jk}.$$ (1)

We now consider models with multiple traits. By letting ${\rho }_{im}$ represent the correlation between traits i and m due to genetic effect and letting ${\lambda }_{im}$ represent the correlation due to an individual’s environment, the covariance between the trait measurements i and m for individual j is

$$\begin{array}{c}\text{cov}\left(y_{ij},y_{mj}\right)=\text{cov}\left(g_{ij},g_{mj}\right)+\text{cov}\left(e_{ij},e_{mj}\right)\\ ={\rho }_{im}{\sigma }_{g\left(i\right)}{\sigma }_{g\left(m\right)}+{\lambda }_{im}{\sigma }_{e\left(i\right)}{\sigma }_{e\left(m\right)}.\end{array}$$ (2)

Assuming that environmental effects are independent between individuals, let the covariance between traits i and m for individuals j and k be

$$\text{cov}\left(y_{ij},y_{mk}\right)=K_{jk}{\rho }_{im}{\sigma }_{g\left(i\right)}{\sigma }_{g\left(m\right)}.$$ (3)

In fact, these models are standard models utilized in the animal and plant breeding communities.

A straightforward approach to represent this model is to stack all of the traits for each trait into one long vector of length $np$ and then represent their covariances in a $np\times np$ matrix populated using Equations 1–3. However, this matrix will have $n^2{p}^2$ elements and fitting this model to estimate the parameters for even a small number of phenotypes is computationally intractable.

Matrix-variate normal distribution

We note that the $np\times np$ covariance matrix above has a significant amount of structure as evident in Equations 1–3. In fact, this matrix can be represented by the sum of two matrices, each of which is a Kronecker product of an n × n and p × p matrix. This decomposition is widely utilized in the plant breeding literature (Malosetti et al. 2008; Kelly et al. 2009; Verbyla and Cullis 2012). In our work, the main contribution is that we provide an efficient method for performing inference in these models efficiently by modeling the full set of trait measurements, using a matrix-variate normal distribution. The matrix-variate normal distribution is a generalization of the multivariate normal distribution to matrices (Gupta and Nagar 2000). The matrix-variate normal distribution is a very natural way to represent these types of factored models. Unlike in a multivariate normal model where the data are concatenated into a single vector of length np, in a matrix-variate model, the data $\left(Y\right)$ are an $n\times p$ matrix where each column is a trait. Instead of representing a covariance structure using a single $np\times np$ matrix, the matrix variate normal distribution represents the covariance using two matrices: a $p\times p$ matrix A that represents the covariance between columns of the data and an $n\times n$ matrix B that represents the covariance between rows of the data. In a matrix-variate normal distribution, the mean $\left(M\right)$ is now an $n\times p$ matrix. We denote a matrix-variate normal model, using the notation $N_{n\times p}\left(M,A,B\right)$.

Using the matrix-variate normal distribution, our model can be represented as

$$Y=Z+R,$$

where Y is the $n\times p$ matrix of traits; Z follows a matrix-variate normal distribution with mean $X\beta =X\left[{\beta }_1\dots {\beta }_p\right]$ and covariance matrices Ψ and K, where Ψ is a $p\times p$ matrix representing the correlation between traits due to genetics; and K is the kinship matrix. R follows a matrix-variate normal distribution with mean zero and covariance matrices Φ and $I_n$, where Φ is a $p\times p$ matrix representing the covariance between traits due to environment and error. The ith diagonal component of Ψ is given by ${\sigma }_{g\left(i\right)}^2$ and the $i,j$ th component by ${\rho }_{ij}{\sigma }_{g\left(i\right)}{\sigma }_{g\left(j\right)}$, and similarly ${\mathrm{\Phi }}_{ij}={\lambda }_{ij}{\sigma }_{e\left(i\right)}{\sigma }_{e\left(j\right)}$. The distribution for Y is then summarized as follows, where $N_{n\times p}\left(M,A,B\right)$ denotes the matrix-variate normal distribution with mean matrix M and columns and row covariance matrices A and $B:$

$$Y\sim N_{n\times p}\left(X\beta ,\mathbf{\Psi },K\right)+N_{n\times p}\left(0,\mathbf{\Phi },I_n\right).$$ (4)

Efficient maximum-likelihood computation

Likelihood evaluation for the matrix-variate distribution given by Equation 4 is accomplished by evaluating the equivalent multivariate normal distribution. By using the $\text{vec}\left(\right)$ operator, which creates a vector from a matrix input by concatenating the columns of the matrix, we are able to represent the distribution given in Equation 4 in the following way, where ⊗ represents the Kronecker product of two matrices:

$$\text{vec}\left(Y\right)\sim N_{np}\left(\text{vec}\left(X\beta \right),\mathbf{\Psi }\otimes K+\mathbf{\Phi }\otimes I_n\right).$$

The likelihood computation for this model takes time on the order of ${\left(np\right)}^3$. This computational time becomes prohibitive when maximizing the likelihood function while considering a large cohort with multiple traits. Previous work has shown how similar multivariate models with Kronecker product matrices can be utilized efficiently when residual errors are independent (Stegle et al. 2011). However, it is not known how these models may be used efficiently when residual errors are correlated, which is the case for our model. To remedy this problem, we introduce a transformation that results in a reduced computational time.

Let the eigendecomposition of $K=H_K{S}_K{H}_k^{\prime }$. This decomposition is calculated with a computational complexity of $O\left(n^3\right)$. Let L be a $p\times p$ matrix that diagonalizes both Ψ and Φ, such that $L\mathbf{\Psi }{L}^{\prime }=I$ and $L\mathbf{\Phi }{L}^{\prime }=D$, a diagonal matrix. This bidiagonalization can be accomplished in $O\left(p^3\right)$ (details are in the Diagonalizing two matrices section below). We then define the matrix $M=\left(L\otimes H_k^{\prime }\right)$. The transformed data vector $Y_T$ is defined as $Y_T=M\text{vec}\left(Y\right)$. This transformed vector has the following distribution:

$$Y_T\sim N\left(M\text{vec}\left(X\beta \right),I\otimes S_k+D\otimes I\right).$$

The log likelihood of $Y_T$ is then given as follows:

$$\begin{array}{l}L\left(Y_T|X\beta ,\mathbf{\Psi },K,\mathbf{\Phi }\right)\\ =-\frac{np}{2}ln\left(2\pi \right)-\frac{1}{2}ln\left|I\otimes S_k+D\otimes I\right|\\ -\frac{1}{2}{\left(M\text{vec}\left(Y_T-X\beta \right)\right)}^{\prime }{\left(I\otimes S_k+D\otimes I\right)}^{-1}\\ \times \left(M\text{vec}\left(Y_T-X\beta \right)\right)+\text{log}\left(\left|M\right|\right).\end{array}$$

To calculate the likelihood given Ψ and Φ, we first obtain the transformation matrix M, which is accomplished in $O\left(n^3+p^3\right)$. Next, we compute the transformed data vector $Y_T$ in $O\left(n^{2}p+p^{2}n\right)$. Given $Y_T$, we obtain an estimate of β, denoted by $\widehat{\beta }$, which we show may be accomplished in $O\left(n{p}^3{q}^2+p^3{q}^3+n{p}^{2}q\right)$, and given this we calculate the residual vector $Y_T-M\text{vec}\left(X\widehat{\beta }\right)$ in $O\left(n{p}^{2}q+np\right)$. Finally, the likelihood is computed in $O\left(np\right)$. Part of the reason that our approach is efficient is that much of the computations can be reused for many analyses. For example, the matrix M that is computed in $O\left(n^3+p^3\right)$ requires diagonalizing the K matrix, which requires $O\left(n^3\right)$ time and needs to be performed only once for the complete analysis of the data set. Similarly, the transformed data vector $Y_T$ can be computed in $O\left(n^{2}p+p^{2}n\right)$, does not depend on which variant is actually being tested, and can be computed only once for each set of traits that is being considered. Thus the likelihood computation for each variant is dominated by $O\left(n{p}^3{q}^2\right)$, utilizing the quantities that were computed once. In addition, in many scenarios we can assume that the effect sizes are small as in human studies. Under this assumption, we can fit the variance parameters just once, assuming that $\beta =0$, and then use this estimate to test each variant. In this case, computing the maximum likelihood reduces to $O\left(np\right)$. This transformation is similar to the approaches in the plant breeding literature to speed up computations, using two eigendecompositions (Piepho et al. 2012).

This assumption is the same assumption that differentiates EMMAX (Kang et al. 2010) from EMMA (Kang et al. 2008). While this assumption is appropriate for human studies where most identified genetic variants have very small effects, this assumption may not be appropriate for plant and animal models where there are often several loci with very strong effects. An approach to handle this case while avoiding refitting the variance parameters for each variant is to first identify the variants with strong effects, using the above assumption, and then refit the variance parameters after including these strongly associated variants as fixed effects in the model.

Restricted Maximum-Likelihood Computation

The REML and the maximum-likelihood (ML) solutions should be similar when the model contains no covariates or only a bias term. However, when this is not the case, parameter estimates obtained in REML analysis may deviate significantly from those of ML. We obtain the REML version of the mvLMM by extending the ML solution (Welham and Thompson 1997). By denoting the log-likelihood obtained by ML as $L_{\text{ML}}$ and similarly for REML, we define the following log-likelihood function. For a standard multivariate normal vector y with distribution $N\left(T\alpha ,\mathbf{\Theta }\right)$,, where T is $n\times q$, the REML is ${\text{LL}}_{\text{REML}}={\text{LL}}_{\text{ML}}+(1/2)\left[qln\left(2\pi \right)+ln\left(|T^{\prime }\mathbf{T}|\right)-ln\left(|T^{\prime }{\mathbf{\Theta }}^{-1}T|\right)\right]$ (Kang et al. 2008). Given this standard result, we define the REML log-likelihood for the mvLMM in the following:

$$\begin{array}{c}{\text{LL}}_{\text{REML}}={\text{LL}}_{\text{ML}}\\ +\frac{1}{2}[qln\left(2\pi \right)+ln\left(\left|\left(L^{\prime }\otimes {\left(H_k^{\prime }X\right)}^{\prime }\right)\left(L\otimes H_k^{\prime }X\right)\right|\right)\\ -ln\left(\left|\left(L^{\prime }\otimes {\left(H_k^{\prime }X\right)}^{\prime }\right){\left(I\otimes S_k+D\otimes I\right)}^{-1}\left(L\otimes H_k^{\prime }X\right)\right|\right)].\end{array}$$

The computational cost of the operations required to define ${\text{LL}}_{\text{REML}}$ does not change the order of the computational complexity.

Estimating genetic correlation

To evaluate the likelihood function in Equation 5, we obtain estimates for the parameters Ψ and Φ We estimate these parameters under the null model, where SNPs are not included as covariates. This assumption has been used previously and is valid for cases when the effect due to each SNP is small (Kang et al. 2010; Lippert et al. 2011). First, for each trait i, we fit the basic LMM from Equation 1, to identify the optimal values of the variance parameters ${\sigma }_{g\left(i\right)}^2$ and ${\sigma }_{e\left(i\right)}^2$. Holding these parameters constant, we perform a two-dimensional global grid search to identify the optimal genetic and environmental correlation parameters. With caching, the likelihood calculation takes time on the order of $O\left(p^3+n{p}^3\right)$. This time will be multiplied by a constant $k^2$ when searching over a grid of size k for each correlation parameter. That is, if we evaluate the likelihood for each genetic and environmental correlation combination for a grid size of k, then we need to evaluate the likelihood $k^2$ times.

To expand this approach to more than two traits, we propose a straightforward pairwise approach to identify the maximum-likelihood parameters. Instead of performing a full grid search over the correlation parameters, we identify the ML estimates of the parameters in each pair of traits. This procedure will be much faster than a full grid search over all pairs of traits and we discuss in Supporting Information, File S1, Figure S1, Figure S2, and Table S1 why this procedure is also more robust.

Calculating sampling variance for parameter estimates

We calculate the sampling variance of the variance parameters and the correlation parameters, using standard multivariate theory. Generally, the sampling variance of a ML parameter is given by the inverse of Fisher’s information (or average information) matrix evaluated at the ML parameters (Searle et al. 1992). Using the search technique we describe, we identify the ML parameters for a given set of traits and then use these parameters to estimate the sampling variance, using Fisher’s information matrix.

Association analysis

To identify genetic variations that have an effect on our traits of interest, we employ a hypothesis-testing framework. We first estimate the effect that a particular SNP x has on each of the traits, using the mvLMM model, and then we jointly test m hypotheses, each testing the effect of the SNP on a given trait. Our null hypothesis for this test is that the SNP has no effect on any of our traits and the alternative hypothesis is that it has an effect on one or more of the traits.

To obtain estimates for the SNP effect sizes, we include one SNP in the model at a time and estimate β from Equation 5. First, we obtain the maximum-likelihood parameters for Ψ and Φ under the null model in which the SNP has no effect, as described in the previous section. Then, given these two parameters, we compute an estimate of the coefficient matrix $\widehat{\beta }$, using the following result.

In the previous section, we defined a transformation $M=\left(L\otimes H_k^{\prime }\right)$ and used it to define a transformed data vector $Y_T$. The mean of the transformed data is given by $M\text{vec}\left(X\beta \right)=\left(L\otimes {H^{\prime }}_k^{\text{}}\right)\text{vec}\left(X\beta \right)$, which can be reduced as follows:

$$\begin{array}{l}\left(L\otimes H_k^{\prime }\right)\text{vec}\left(X\beta \right)\\ =\text{vec}\left(H_k^{\prime }X\beta L^{\prime }\right)\\ =\text{vec}\left(X*\beta L^{\prime }\right)\\ =\left(L\otimes X*\right)\text{vec}\left(\beta \right).\end{array}$$

Here we have let $X*=H_k^{\prime }X$. By denoting $\text{vec}\left(\beta \right)$ as ${\beta }_T$, we obtain an estimate $\widehat{\beta }$, using the following result, where $\text{unvec}\left(\right)$ represents the reversal of the $\text{vec}\left(\right)$ operation and we have let $P=\left(I\otimes S_k+D\otimes I\right)$, the transformed data covariance matrix:

$$\begin{array}{c}{\widehat{\beta }}_T={\left[\left(L^{\prime }\otimes X^{*\prime }\right)P^{-1}\left(L\otimes X^{*}\right)\right]}^{-1}\left(L^{\prime }\otimes X^{*\prime }\right)P^{-1}M\text{vec}\left(Y\right)\\ \widehat{\beta }=\text{unvec}\left({\widehat{\beta }}_T\right).\end{array}$$

Since P is a diagonal matrix, ${\widehat{\beta }}_T$ can be computed in $O\left(n{p}^3{q}^2+p^3{q}^3+n{p}^{2}q\right)$ given the one-time cost of $O\left(n^{2}q\right)$ for computing $X*$.

The statistic for testing the proposed hypothesis is obtained by defining a transformation matrix R so that $R{\widehat{\beta }}_T=\left[{\widehat{\beta }}_{1,x},{\widehat{\beta }}_{2x},\dots ,{\widehat{\beta }}_{px}\right]\prime$, where ${\widehat{\beta }}_{ix}$ is the coefficient estimate for the effect of SNP x on trait i. Therefore, given this matrix, we define the F-statistic for testing association in Equation 5, which under the null follows an F-distribution with p numerator degrees of freedom and $np-pq$ denominator degrees of freedom, where ${\widehat{\sigma }}^2=\widehat{\text{var}}\left(P^{-1/2}{Y}_T\right)$ and $\widehat{\text{var}}(\dots )$ represents the sample variance. Details of this test can be found in McCulloch and Neuhaus (1999):

$$f=\left(R{\widehat{\beta }}_T\right)\prime {\left(R{\left[\left(L^{\prime }\otimes X^{*\prime }\right)P^{-1}\left(L\otimes X^{*}\right)\right]}^{-1}{R}^{\prime }\right)}^{-1}\left(R{\widehat{\beta }}_T\right)\cdot \frac{1}{p{\widehat{\sigma }}^2}.$$

Diagonalizing two matrices

We are given two positive semidefinite matrices Φ and Ψ and we wish to identify a matrix L that diagonalizes both of these matrices. This is accomplished in the following way. First, we obtain the eigendecomposition of $\mathbf{\Psi }=H_{\mathbf{\Psi }}{S}_{\mathbf{\Psi }}{H}_{\mathbf{\Psi }}^{\prime }$ and then define a matrix $R=S_{\mathbf{\Psi }}^{-1/2}{H}_{\mathbf{\Psi }}^{\prime }$, so that $R^{\prime }\mathbf{R}={\mathbf{\Psi }}^{-1}$. Next, we obtain an eigendecomposition $R\mathbf{\Phi }{R}^{\prime }={QDQ}^{\prime }$ and then define a matrix $L=Q^{\prime }R$. With this we see that $L\mathbf{\Psi }{L}^{\prime }=I$ and that $L\mathbf{\Phi }{L}^{\prime }=D$. The entire procedure has complexity $O\left(p^3\right)$.

Genotype and phenotype data

We apply our method to the Northern Finland Birth Cohort data (Sabatti et al. 2008), which were used in Kang et al. (2010) and Korte et al. (2012). This data set consisted of 5326 individuals that had been filtered to reduce the presence of family structure. The data set contains 331,450 autosomal SNPs after application of the exclusion criteria of Hardy–Weinberg equilibrium $\left(p<{10}^4\right)$, genotyping completeness $\left(<95\text{\%}\right)$, and minor allele frequency $\left(<1\text{\%}\right)$. Missing genotypes are replaced with the minor allele frequency. Missing phenotypes are replaced with the phenotypic mean.

We use a well-studied yeast data set (Smith and Kruglyak 2008) consisting of 109 yeast strains each with 5793 gene expression measurements. Bivariate association mapping is performed on all 2956 available SNPs. Gene expression values were normalized and subjected to quality control by Smith and Kruglyak (2008) and we utilized the same data as they.

Results

Association and genetic correlation in the Northern Finland Birth Cohort

Association:

We apply our method to the Northern Finland Birth Cohort, a founder cohort consisting of 5043 individuals, each of which has multiple-trait measurements for four different metabolic traits. We analyze a total of six pairs of traits or all combinations of four traits: HDL and LDL cholesterol, C-reactive protein (CRP), and triglycerides (TG). Association between each SNP and each pair of traits is evaluated by assuming that under the null hypothesis the SNP does not affect either trait.

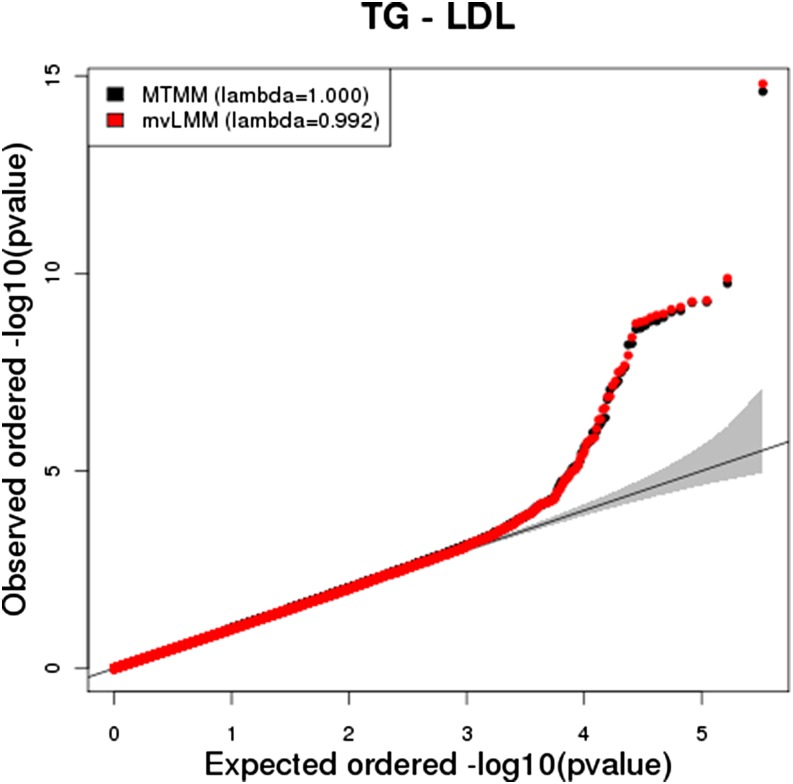
We compare our results to the analysis of Korte et al. (2012), which analyzed the same data using a classically based multiple-trait LMM, which they refer to as the multitrait mixed-model (MTMM) method. Our results are highly concordant ($r=$0.96–0.99), indicating that our method is consistent with classical approaches. For example, Figure 1 compares the QQ plots of the mvLMM and MTMM for the joint analysis of TG and LDL.

Figure 1.

QQ Plot comparing MTMM and mvLMM P-values obtained when performing analysis with LDL and TG.

Over 99% of associations identified in marginal analysis are also identified when respective pairs of traits are mapped (significance threshold of 1.5e-7). However, the joint mapping uncovers more significant associations; 19 new associations are identified across all trait pairs. For example, in the analysis of TG with CRP, we identify a SNP (rs2000571) with a P-value of 8.58e-7 and with the MTMM a P-value of 1.7e-6. This SNP was not significant in the marginal analysis of TG (1.7e-5) or CRP (0.03), but belongs to a region on chromosome 11 that has been shown to harbor variants contributing to triglycerides (Braun et al. 2012). Many of the identified associated SNPs were more significant in the mvLMM compared to the MTMM, which we suspect is because the mvLMM finds the actual parameters that maximize the likelihood. We also apply our method to analyze all four traits simultaneously and the results are shown in Table 2. For all variants, at least one of the pair of trait P-values is more significant than the all-trait P-value. Thus it appears that in this scenario, it is best to follow a single-trait analysis with the all-pairs analysis. This raises the more general issue of how one should apply a method such as this and we provide some guidance in the Discussion.

Table 2. Joint analysis of all traits compared to all pairwise combinations.

rs ID	All	HDL_CRP	HDL_LDL	HDL_TG	LDL_CRP	TG_CRP	TG_LDL
rs3764261	3.115800e-01	2.610400e-31	6.167100e-31	7.179700e-33	3.857500e-01	2.301000e-01	2.475900e-01
rs1532624	5.934000e-01	7.134300e-24	1.286400e-23	1.477200e-24	4.096300e-01	1.467800e-01	1.844000e-01
rs2794520	2.936500e-13	4.404900e-22	3.241900e-01	2.812900e-01	2.030400e-22	5.021100e-23	8.300500e-01
rs7499892	3.460300e-02	3.303200e-16	1.553200e-16	1.935800e-20	6.642000e-01	3.166200e-01	6.211500e-01
rs2592887	3.707500e-10	6.883400e-17	9.482500e-02	1.104900e-01	5.918400e-17	8.024200e-17	7.710100e-01
rs646776	5.625600e-02	6.116800e-02	2.055800e-14	2.914200e-01	2.389500e-15	2.819600e-01	1.587700e-15
rs1532085	9.795800e-01	2.046400e-11	2.626800e-11	2.063700e-15	8.229500e-01	2.304300e-01	2.445000e-01
rs1811472	6.488000e-10	1.028000e-14	1.075200e-01	1.334100e-01	7.085600e-15	8.336700e-15	7.862900e-01
rs12093699	3.487700e-08	2.803100e-14	8.704700e-01	9.775600e-01	1.324500e-13	5.136100e-14	8.555500e-01
rs2650000	2.150800e-06	3.117800e-11	4.840500e-01	5.395800e-01	1.412700e-11	1.175100e-11	7.312200e-01
rs6728178	1.348000e-02	3.726700e-06	3.718900e-11	8.567700e-09	1.192200e-07	1.192900e-06	5.170100e-10
rs6754295	1.244400e-02	4.028300e-06	3.838300e-11	1.715000e-08	9.608700e-08	2.323300e-06	8.179200e-10
rs693	5.549800e-02	3.253100e-02	4.795900e-11	3.963400e-03	1.410000e-10	1.015900e-02	1.324700e-10
rs7953249	6.533200e-06	2.201500e-10	4.063400e-01	4.969100e-01	1.016400e-10	8.025500e-11	7.893600e-01
rs1169300	1.736100e-05	9.062700e-10	5.325500e-01	7.450100e-01	3.118100e-10	1.515200e-10	6.399000e-01
rs2464196	1.619700e-05	9.053200e-10	6.220200e-01	7.569200e-01	4.075100e-10	1.744700e-10	7.528400e-01
rs673548	4.967500e-02	4.309800e-06	2.014500e-10	3.655500e-09	1.150800e-06	5.222900e-07	1.055400e-09
rs415799	2.000800e-01	2.320400e-07	1.493100e-07	2.216300e-10	7.457500e-01	2.088500e-01	3.640400e-01
rs676210	5.072700e-02	5.251900e-06	2.883700e-10	5.535600e-09	1.364200e-06	7.256100e-07	1.583900e-09
rs174546	1.379500e-01	1.590200e-01	8.556400e-07	9.688800e-03	1.623200e-05	1.427300e-02	4.819700e-10
rs102275	1.678600e-01	1.112900e-01	5.655100e-07	9.205100e-03	1.723700e-05	1.722200e-02	7.111600e-10
rs1260326	4.928500e-01	1.036300e-01	2.940800e-01	7.494900e-10	8.537200e-02	1.110700e-09	1.140400e-09
rs261336	6.096900e-01	1.066600e-04	1.045000e-03	9.195300e-10	7.777300e-02	2.454000e-04	5.129400e-04
rs174537	1.410500e-01	1.549200e-01	1.474200e-06	1.113400e-02	3.039100e-05	1.637500e-02	1.306000e-09
rs1535	1.565800e-01	1.949600e-01	1.776900e-06	1.539500e-02	2.517300e-05	2.155300e-02	1.698300e-09
rs174556	6.854800e-02	3.880900e-01	1.614800e-06	5.138000e-02	5.632100e-06	5.600000e-02	1.846800e-09
rs10096633	7.343600e-01	1.076800e-05	1.327200e-05	2.542900e-09	6.869700e-01	7.121200e-08	2.132500e-08
rs735396	4.019400e-04	3.576200e-08	4.346600e-01	4.457100e-01	1.036900e-08	2.650500e-09	4.197800e-01
rs3923037	1.198500e-03	2.762800e-03	3.162700e-08	1.440400e-06	9.422300e-07	6.535200e-06	4.137700e-09
rs2126259	1.323700e-02	4.359000e-09	9.557500e-08	1.423400e-04	5.889200e-06	2.068100e-04	6.961300e-04
rs9989419	9.182800e-01	1.922700e-08	1.983700e-08	4.919800e-09	9.527800e-01	8.393700e-01	8.597400e-01
rs780094	6.157600e-01	2.610900e-01	6.568900e-01	7.159300e-09	2.491000e-01	2.042200e-08	1.189700e-08
rs11668477	4.263400e-01	4.826000e-02	8.350000e-09	1.810800e-02	2.422300e-08	4.300100e-02	3.161500e-08
rs11265260	7.116800e-06	4.158100e-08	2.523900e-02	2.956100e-02	1.047600e-08	9.316100e-09	3.308700e-01
rs1800961	6.390900e-01	1.094000e-08	1.636900e-07	1.074400e-07	1.981400e-01	1.465700e-03	1.085900e-02
rs754524	4.032900e-02	1.337000e-01	1.529600e-08	1.141300e-01	3.017000e-08	3.648500e-01	2.833300e-08
rs2075650	7.106400e-03	3.324200e-04	5.500700e-04	3.998700e-04	2.922700e-07	2.092800e-08	1.028800e-05
rs255049	8.151200e-01	2.079900e-07	2.294600e-08	1.371900e-07	3.933200e-01	4.514200e-01	8.102700e-02
rs166358	5.721200e-01	7.791800e-07	8.254800e-07	3.621500e-08	4.471400e-02	5.396600e-01	1.480400e-02

We compare the P-values of the analysis of all four traits to the six possible pairwise trait analyses. In all cases, the pairwise analyses are more significant. ID, identification number.

Genetic correlations:

In multiple-trait models, the total trait correlation is partitioned into a genetic and an environmental component. The genetic component of the correlation (the genetic correlation) represents the part of the total trait covariance that is attributed to genetics normalized by the genetic variances. This quantity provides insight into the genetic architecture of the relationships between traits. We estimate the genetic correlations for each pair of traits analyzed in the Finland Birth Cohort and compare these estimates with those obtained using a standard implementation of a bivariate LMM as implemented in genome-wide complex trait analysis (GCTA) (Lee et al. 2012). Table 1 compares estimates of genetic correlation obtained with GCTA and the mvLMM. When we compare our results to those of GCTA, we find that the two methods yield similar results, with genetic correlation estimates falling <1 standard deviation from one another. In addition, the running time for the classical approach was ∼35 min, while the running time for the mvLMM was on average ∼12 sec, given a one-time cost of 2.5 min shared across pairs of traits.

Table 1. Genetic correlation estimates in the Finland Birth Cohort.

Trait pair	Phenotypic correlation	mvLMM genetic correlation	GCTA genetic correlation
HDL/CRP	−0.19	0.28 ± 0.19	0.26 ± 0.22
HDL/LDL	−0.13	−0.16 ± 0.11	−0.18 ± 0.11
HDL/TG	−0.37	−0.37 ± 0.17	−0.32 ± 0.16
LDL/CRP	0.09	0.03 ± 0.17	−0.02 ± 0.17
TG/CRP	0.21	−0.62 ± 0.26	−0.75 ± 0.41
TG/LDL	0.32	0.33 ± 0.16	0.29 ± 0.14

We compare the maximum-likelihood estimates obtained with the mvLMM with those obtained with GCTA and find that the results are very similar.

Bivariate analysis in yeast data

Gene coexpression, defined as the correlation between expression levels of a pair of genes estimated in a set of individuals, is a fundamental quantity that has been utilized for a variety of applications (Stuart et al. 2003; Subramanian et al. 2005; Ghanzalpour et al. 2006; Lee et al. 2006). There are two prevalent views about the meaning of significant coexpression. The first is that coexpression stems from similar environmental conditions such as disease status (Heller et al. 1997). The second comes from the systems genetics literature where it is thought that coexpressed genes have a similar genetic regulatory program and that specific genetic variants drive modules of coexpressed genes (Ghanzalpour et al. 2006; Lee et al. 2006). However, correlation estimates from gene expression levels measure the combined effect of both the genetic and the environmental components. Our methodology allows us for the first time to decompose the coexpression into a genetic and environmental component.

We utilize the major gain in efficiency of our approach to perform an analysis that is not feasible with current methods. Using a well-studied yeast data set (Smith and Kruglyak 2008) consisting of 109 yeast strains each with 5793 gene expression measurements, we perform a bivariate analysis, estimating genetic correlations for all 5793 chose 2 gene expression pairs. Within this data set several regions of the genome have been implicated to harbor genetic variation that affects many gene expression levels.

Using a set of hotspot locations derived from Smith and Kruglyak (2008), we define a set of 13,508 hotspot gene pairs by extracting all pairs of genes that lie in each known hotspot. We then compare the phenotypic correlation to the total proportion of covariation accounted for by genetics for each of these pairs. Assuming that hotspot pairs are under the same genetic regulation, we expect that the phenotypic correlation for any given pair should reflect this by having a high value. However, this might not be the case if the environmental correlation between the pair contributes in such a way to lower the overall phenotypic correlation. Therefore, an estimation of the total phenotypic covariation attributed to genetics may better reflect the fact that the two genes are under the same genetic program.

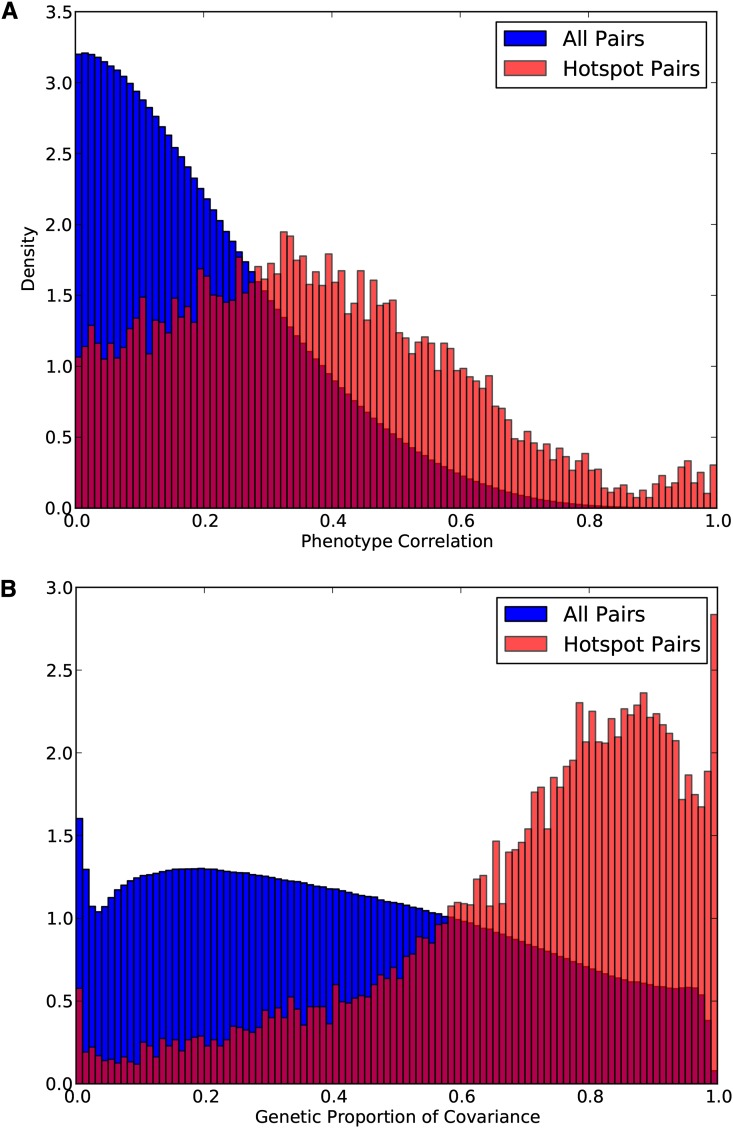
In Figure 2A, we plot the histogram of the absolute value of the total phenotypic correlation for all gene pairs and for hotspot gene pairs. We see that the distribution of phenotypic correlations for hotspot pairs is shifted toward higher correlations with respect to all pairs, giving an indication of coregulation. However, most of the pairs have correlation <0.5. Figure 2B shows the same plot generated using the total proportion of the phenotypic covariation attributed to genetics. In Figure 2B, we observe that the estimated genetic correlation for hotspot pairs is dramatically skewed toward 1. In fact, most of the pairs have a genetic covariance >0.7. This result suggests that the estimated genetic correlations on average give a stronger indication of coregulation compared to the phenotypic correlation.

Figure 2.

Comparison of the phenotypic correlation with the total proportion of the correlation accounted for by genetics for all gene pairs and for gene pairs from regulatory hotspots. We compare the phenotypic correlation with the total proportion of correlation accounted for by genetics to assess the ability of the genetic correlation to differentiate gene pairs that are coregulated. Utilizing a set of known hotspots, we derive a set of hotspot gene pairs, where a hotspot pair is defined as a gene pair in which both genes lie in a given hotspot. We find that the genetic correlation differentiates these coregulated pairs better than the overall trait correlation.

Discussion

In this article, we introduced a method for performing multitrait genome-wide association analysis and for the estimation of the genetic correlation. Our method is based on classical theory, but introduces a computational advance that makes it much faster, reducing running time >10-fold when compared with the classic approach. We have shown that our method achieves similar results to those of the classical approach. In addition, we have shown that the ability to quickly estimate genetic correlation may be of great benefit to researchers, leading to fundamental insights into the architecture of complex traits.

The ability to quickly optimize multiple-trait linear mixed models will have a large impact on the ability to dissect complex traits. For example, multiple-expression quantitative trait loci (multi-eQTL) may be discovered by mapping multiple traits to genetic variants across the genome. The ability to perform this type of research is infeasible with current methodologies. In addition, we have shown that the genetic correlation between gene expression measurements may be a better indicator of coregulation. It stands to reason that these genetic correlations may be used in coexpression analysis and lead to the discovery of gene modules that are truly coregulated and not in part due to environmental correlations.

We note that in our model, the genetic background component is assumed to have a covariance structure, defined by the matrix K, which is computed using all of the marker genotypes. This model inherently assumes that the effect size of each genetic variant is drawn from a normal distribution with equal variance. This may be inaccurate for several reasons. First, not all of the markers are causal variants and even among the variants that are causal, their effect sizes may vary widely. Second, many of the causal variants themselves may not be genotyped in the study and the markers are merely proxies for these causal variants. This difference between the estimated covariance structure from the markers and the true covariance structure has been shown to lead to inaccurate heritability estimates (de Los Campos et al. 2013) and may lead to inaccuracies in estimates of genetic correlations. A more appropriate term from the quantities we estimate maybe “genomic heritabilities” and “genomic correlations.”

Our method presents an approach for jointly performing association analysis for multiple traits. However, the question remains of what is the best way to analyze a data set with multiple traits. Unfortunately, there is no clear answer. If a variant affects only a single trait, then an individual trait-by-trait analysis is the most powerful to identify such a trait because analyzing more than one trait increases the degrees of freedom of the statistical test. On the other hand, if a variant affects multiple traits, then analyzing all traits together will be more powerful. From a practical perspective, we advocate first analyzing each trait independently and then applying this method to groups of traits where there are suspected shared genetic components and increasing the number of traits analyzed until the P-values become less significant. Our estimates of genetic correlation can guide identification of potential groups of traits. Any such sequential strategy complicates issues of controlling type I errors. Exactly how to control type I errors in this context is an important avenue of future work.