A Moderated Nonlinear Factor Model for the Development of Commensurate Measures in Integrative Data Analysis

Abstract

Integrative data analysis (IDA) is a methodological framework that allows for the fitting of models to data that have been pooled across two or more independent sources. IDA offers many potential advantages including increased statistical power, greater subject heterogeneity, higher observed frequencies of low base-rate behaviors, and longer developmental periods of study. However, a core challenge is the estimation of valid and reliable psychometric scores that are based on potentially different items with different response options drawn from different studies. In Bauer and Hussong (2009) we proposed a method for obtaining scores within an IDA called moderated nonlinear factor analysis (MNLFA). Here we move significantly beyond this work in the development of a general framework for estimating MNLFA models and obtaining scale scores across a variety of settings. We propose a five step procedure and demonstrate this approach using data drawn from n=1972 individuals ranging in age from 11 to 34 years pooled across three independent studies to examine the factor structure of 17 binary items assessing depressive symptomatology. We offer substantive conclusions about the factor structure of depression, use this structure to compute individual-specific scale scores, and make recommendations for the use of these methods in practice.

Integrative data analysis (IDA) is a methodological framework that allows for the fitting of models to data that have been pooled across two or more independent sources (Curran, 2009; Curran & Hussong, 2009; Hofer & Piccinin, 2009; Hussong, Curran & Bauer, 2013; McArdle, Grimm, Hamagami, Bowles & Meredith, 2009). Like other tools for research synthesis such as qualitative literature reviews and meta-analysis, IDA responds to the strong need for a cumulative approach to scientific inquiry (Curran, 2009; Gans, 1992; Hunter & Schmidt, 1996; Meehl, 1978). However, unlike other existing methods, IDA provides a means for directly comparing results both within and across multiple studies through the direct analysis of primary data. Although not appropriate in every context, IDA has the potential benefits of internal replication of findings across independent studies; increased statistical power; greater sample heterogeneity to facilitate subgroup comparisons; higher frequencies of low baserate behavior; more rigorous psychometric assessments of constructs; and longer periods of developmental study (Hussong et al. 2013). IDA is a particularly powerful tool for efficiently using existing resources to address novel research questions by taking advantage of the rich datasets currently available within the scientific community.

Despite the many potential advantages of this approach, there remain a number of distinct challenges to conducting IDA in practice (Cooper & Patall, 2009; Bauer & Hussong, 2009; Curran & Hussong, 2009). Chief among them is the development of commensurate measures in which scale scores for a given theoretical construct are anchored to a common metric as a function of potentially different items with potentially different response options drawn from multiple independent studies. The simplest approach aims to obtain identical measurement by reducing the item set to only the same set of shared items both in terms of item stems and response options that appear in all studies. However, the restrictive requirement of identical measurement across datasets is not necessary to create commensurate measures and may not be the most desirable approach (Bauer & Hussong, 2009; Curran et al., 2008; Hussong et al., 2013). When items vary over studies (e.g., by item stem, response option, or assessment across studies), IDA techniques can be used to create comparable measures across datasets that contain at least some common items in addition to unique items that appear in only one or in a subset of datasets. Only when reliable and valid commensurate measures have been obtained is it possible to then use these in joint, pooled analyses across the multiple data sets. Thus the creation of commensurate scale scores is a fundamental prerequisite for conducting rigorous tests of substantive hypotheses using an IDA framework. It is the creation of these scores that is our focus here.

We have implemented two techniques for developing commensurate measures in the context of IDA. The first draws on the standard two-parameter logistic item response theory (2PL IRT; e.g., Thissen & Wainer, 2001) model to create scale scores that account for differences in the magnitude of the relations between the items and the underlying factor as a function of study membership as well as potential sources of between-person heterogeneity within study such as respondent age, ethnicity, or gender (Curran et al., 2008; Flora, Curran, Hussong & Edwards, 2008). An advantage of this IRT-based approach is that the estimation of the scale scores is based on which items were endorsed rather than simply how many items were endorsed while taking into account differences in item functioning due to study membership and respondent characteristics.

However, these IRT procedures are not without limitations (Bauer & Hussong, 2009). Most notably, potential differences in item functioning must be tested one characteristic at a time, making it difficult to determine the unique source of differences in item functioning (e.g., young vs. old are compared, then males vs. females, then study 1 vs. study 2, etc.). Moreover, only discrete factors predicting differences in item functioning can be included in this model (e.g., gender, study membership). Yet important covariates such chronological age may be continuously distributed and nonlinearly related to the parameters that define the underlying measurement model. These challenges can combine to introduce significant limitations when using standard IRT models to achieve commensurate measurement within IDA.

In response to these limitations, we developed a second method that draws upon recent developments in generalized linear and nonlinear item-level factor analysis (e.g., Bartholomew & Knott, 1999; De Boeck & Wilson, 2004; Moustaki, 1996; Skrondal & Rabe-Hesketh, 2004). More specifically, we proposed the moderated nonlinear factor analysis (MNLFA) model that allows for the creation of scale scores based on all available items for a given participant while accounting for potential differences in both the latent factor and the individual items as a function of observed covariates (Bauer & Hussong, 2009). This approach simultaneously tests whether a measure is invariant across important factors such as age, gender, and study membership with respect to factor means and variances as well as item intercepts and factor loadings. For example, we can directly test whether a continuously distributed covariate such as age is systematically associated with higher levels of depression (the factor mean) and greater variability of depression (the factor variance) while avoiding the need to create discrete groups based on age (e.g., old vs. young). In addition, we can test whether specific items on a depression scale are differentially endorsed (the item intercepts) or more strongly indicative (the factor loadings) of underlying depression when age is measured on a continuum. Tests such as these are not possible using standard IRT or CFA approaches and are particularly important in IDA applications in which individual characteristics such as gender, age and ethnicity must be considered simultaneously to avoid potential confounding of individual effects with study group membership (e.g., one study has a higher proportion of boys and another a higher proportion of adolescents).

In our prior work we have described the core elements of the MNLFA and have briefly demonstrated this method as applied to the scoring of five indicators of alcohol involvement across two studies (Bauer & Hussong, 2009). However, many IDA applications of MNLFA are far more complex, involving more data sets, more items, greater sample heterogeneity, and more complex measurement models. In these more realistic settings, a number of preliminary analyses are required to assess the items in the analysis, their dimensionality, and the appropriate specification of MNLFA models. In this paper we move significantly beyond our prior work through the development and demonstration of a general testing strategy for these more complex cross-study measurement designs that might be applied in many different types of IDA settings. We begin by reviewing the parameterization and estimation of the MNLFA model. We then describe the experimental design and measurement of the data to which we will apply our models. Next, we propose a principled strategy for the development of commensurate measures and we demonstrate this using real data assessing internalizing symptomatology over time. We conclude with a discussion of limitations, recommendations, and directions for future research.

Moderated Nonlinear Factor Analysis

Bauer and Hussong (2009) proposed the moderated nonlinear factor model, or MNLFA. It is nonlinear because it allows for a variety of nonlinear link functions to be used to relate the observed items to the underlying latent factor that in turn provides for the simultaneous inclusion of any combination of continuous, binary, ordinal, or discrete items. It is moderated because one or more covariates can be included to simultaneous influence factor means and variances as well as the item intercepts and loadings. In other words, the moments of the latent factor and the parameters that relate the items to the factor can all vary in magnitude as a function of one or more covariates. Because specific link functions can be defined for each individual item, the traditional linear confirmatory factor analysis (CFA) model, the nonlinear CFA, and the 2PL IRT model can be considered special cases of the MNLFA model. In what follows we explicate the unidimensional MNLFA model, assuming that all items represent a single common factor. We later note how this assumption can be evaluated empirically.

The generalized linear factor analysis model

We begin by defining the generalized linear factor analysis (GLFA) model for a set of observed items. The factor model may be written as

$$g_i\left({\mu }_{ij}\right)={\nu }_i+{\lambda }_i{\eta }_j$$ (1)

where g_i represents the appropriate link function for item i, μ_ij represents the expected value for item i for person j, ν_i and λ_i represent the intercept and factor loading for item i, respectively, and η_j represents the latent factor score for individual j. Just as in traditional linear CFA models, the latent factor scores are assumed to be normally distributed as η_j ~ N(α, Ψ); unlike CFA models, the item-specific residual terms are not explicitly defined but are implied by the conditional response distributions. It is often useful to express Equation (1) in terms of the inverse of the link function such that

$${\mu }_{ij}=g_i^{-1}\left({\nu }_i+{\lambda }_i{\eta }_j\right)$$ (2)

where all is defined as before.

To see the relation between the GLFA and more traditional factor models, we can first consider the GLFA when applied to a set of continuously distributed indicators. Here the link function is simply the identity function and the response distribution is normal. This leaves

$${\mu }_{ij}={\nu }_i+{\lambda }_i{\eta }_j$$ (3)

which is the usual linear CFA expressed in GLFA terms. Similarly, we can consider the GLFA applied to a set of binary indicators. Here the appropriate link function is the logit and the response distribution is Bernoulli. This leaves

$${\mu }_{ij}=\frac{1}{1+exp\left[-\left({\nu }_i+{\lambda }_i{\eta }_j\right)\right]}$$ (4)

which is an alternative yet equivalent expression of the standard 2PL IRT model (e.g., Takane & de Leeuw, 1987). Other link functions can be defined for ordinal or count distributions depending upon the scaling of each individual item (e.g., Bauer & Hussong, 2009, p.107).

Model invariance

A key characteristic of the GLFA described above is that the parameters that define the model (e.g., α, ψ, ν_i, λ_i) are assumed to be invariant over all between-person covariates. In other words, the latent variable mean and variance and the item intercepts and slopes are all assumed equal for males and females, for young and old, for individuals drawn from Study 1 or Study 2, and so on. However, we can extend the GLFA to allow the parameters to vary as a function of one or more explanatory covariates, and we can even consider higher-order interactions among the covariates themselves.

We begin by allowing the mean and variance of the latent factor to vary as a function of one or more exogenous moderators. That is, we now assume that η_j ~ N(α_j,ψ_j) where

$${\alpha }_j={\alpha }_0+\sum _{q=1}^Q{\alpha }_q{x}_{qj}$$ (5)

and

$${\psi }_j={\psi }_{0}exp\left(\sum _{q=1}^Q{\omega }_q{x}_{qj}\right)$$ (6)

respectively. Conceptually, these are nothing more than regression equations in which the latent mean and variance for individual j is expressed as a function of an optimally weighted linear combination of the predictors (i.e., x_qj where q =1, 2, …, Q predictors). The mean equation is a standard linear expression, and the variance is log-linear given that it is bounded at zero.

Thus far we are assuming that the factor loadings and item intercepts are invariant across the covariates; this too can be relaxed to allow for the possibility that some items function differently for different individuals (e.g., respondents originating from different studies, or of different genders or ages). We begin by extending Equation (1) such that

$$g_i\left({\mu }_{ij}\right)={\nu }_{ij}+{\lambda }_{ij}{\eta }_j$$ (7)

where the addition of the subscript j on the intercept and factor loading reflects that these can now deterministically vary across individuals as a function of one or more covariates. More specifically,

$${\nu }_{ij}={\nu }_{0i}+\sum _{q=1}^Q{\nu }_{qi}{x}_{qj}$$ (8)

and

$${\lambda }_{ij}={\lambda }_{0j}+\sum _{q=1}^Q{\lambda }_{qi}{x}_{qj}$$ (9)

where all is defined as before. Similar expressions can be given for the thresholds of ordinal items or the zero-inflation parameters of count outcomes, and different predictor sets can be used for the structural and measurement components of the model; see Bauer and Hussong (2009, p.109) for further details.

Importantly, these expressions reduce to more traditional multiple group CFA or IRT models given specific characteristics of the predictors. For example, if we chose an identity link function, a normal response distribution, and a single binary predictor x_j, then Equations (5), (6), (8), and (9) would correspond to a two-group CFA with continuous indicators. Similarly, if we chose a logit link function, a Bernoulli response distribution, and a single binary predictor x_j, then these same equations would correspond to a two-group 2PL IRT model for binary indicators (net standard parameterization differences; Takane & de Leeuw, 1987). The advantage of the MNLFA is that any combination of link functions and response distributions can be chosen for the set of items, each parameter of which can vary as a function of one or more covariates.

Traditional approaches to measurement invariance

It is important to consider the relation between the MNLFA framework and that of more traditional approaches to evaluating measurement invariance within the factor analysis tradition. The collected work on measurement invariance is vast, a comprehensive review of which is well beyond the scope of our work here. Briefly, the classic definition of measurement invariance is the extent to which the same measurements conducted under different conditions yield the same measures of the attributes under study (e.g., Meredith, 1964, 1993; Meredith & Horn, 2001; Widaman, Ferrer & Conger, 2010; Widaman, Grimm, Early, Robins & Conger, 2013; Widaman & Reise, 1997). Varying types of invariance can be met across group or over time including configural, weak (or metric), strong (or scalar), and strict (Meredith, 1993); partial forms of invariance can also be considered (e.g., Byrne, Shavelson & Muthén, 1989; Cheung & Rensvold, 1999; Yoon & Millsap, 2007). The motivating goal is to place the factor scores on a comparable metric so that between-group or over-time comparisons can be validly made.

Almost without exception, the traditional approach to factorial invariance is focused on either discrete group membership (e.g., males vs. females, treatment vs. control) or discrete time assessment (wave 1 vs. wave 2; age 12 vs. age 13). Typically only one grouping factor is considered at a time, although it is more common to consider multiple measures of time in longitudinal settings (e.g., Ferrer, Balluerka, & Widaman, 2008; Meredith & Horn, 2001; Widaman et al., 2010). As we noted above, the MNLFA can be parameterized in a way to correspond to these existing methods of testing factorial invariance; however, the MNLFA can be extended to include not only indicators with mixed (and discrete) response scales, but also to simultaneously express differences in the factor mean and variance (impact), as well as factor loadings and intercepts (differential item functioning, DIF), that may exist across the values of multiple exogenous covariates.

The ability to incorporate impact and DIF as a function of multiple covariates is a key strength of the MNLFA approach. Whereas some items may function equivalently across groups and/or over time (i.e., be invariant), other items may show DIF as a function of one or more covariates. These latter items then uniquely relate to the underlying factor for individuals with each specific combination of values for the relevant covariates. There is thus a subset of common, invariant items that link the measurement of the latent factor over groups or time and a subset of items expressing DIF that are uniquely related to the latent factor as defined by each combination of the set of covariates. The common and unique items are then optimally combined in the process of scoring to maximize the available information.

Controversy exists regarding whether and when factor means, variances and covariances, or score estimates can be validly compared across segments of the population when DIF occurs (Byrne et al., 1989). Widaman and Reise (1997) argued that the comparison of factor means, variances and covariances is most valid when the results are invariant under appropriate rescaling factors (or ARF-invariant), a condition which requires full invariance. When DIF exists, however, comparisons made at the level of the factor are less certain, because the differences that are observed depend on which indicators are selected to be invariant in the fitted model. One must therefore assume that the empirical procedures used to identify DIF arrive at the correct invariant and non-invariant item sets. As shown by Yoon and Millsap (2007), the likelihood of correctly identifying the items with and without DIF increases with the proportion of invariant items. Reise, Widaman & Pugh (1993) suggested that a majority of indicators should be invariant. However, it is not always clear how best to interpret these findings and recommendations within the MNLFA approach, given that DIF may arise as a function of multiple covariates. For instance, suppose for 10 items, two displayed DIF as a function of gender, two displayed DIF as a function of age, and two displayed DIF as a function of study. With respect to any one of the covariates, eight out of 10 items are invariant, but with respect to all of the covariates only four out of 10 items are invariant. The question of how much DIF is permissible when making comparisons between factor means, variances and covariances, or factor score estimates based on a MNLFA thus remains open to further research.

Estimation

The MNLFA can be conceptualized as a nonlinear latent factor model with a set of linear and nonlinear constraints imposed on the parameter space. Estimation is computationally intensive and can often take hours or even days to complete given current CPU speeds. Bauer and Hussong (2009, pp.124–125) provide details about the definition of the marginal likelihood of the MNLFA and alternative methods available for minimization. In our own work we have primarily used adaptive Gaussian quadrature as provided in SAS PROC NLMIXED (SAS Institute, 2008, Chapter 61), although other methods of numerical integration and software packages are available.

Scoring

Given that the ultimate goal of our use of the MNLFA here is to provide maximally valid and reliable scale scores that can then be taken to ancillary analysis (e.g., growth models, multilevel models), we require a method of scoring. By scoring, we mean the model-based estimation of person-specific factor scores. To do this, we capitalize on a version of Bayes’ theorem to estimate the mode of the posterior distribution of η_j; see Equation A2 in Bauer and Hussong (2009) for details. The mode of the posterior distribution is often referred to as the modal a posteriori (or MAP) estimate of η_j (e.g., Bock & Aitken, 1981). We can estimate MAPs for each person in the sample based on the final parameterization of the MNLFA model, and these scores then become the unit of analysis for subsequent modeling.

Application of MNLFA to repeated measures data

The models that we have described up to this point have invoked the standard assumptions of independence; that is, it is assumed that no two residuals are any more or less related than any other two residuals (e.g., Raudenbush & Bryk, 2002). However, in many applications of IDA, particularly those involving repeated measures data, this assumption is directly violated. This is easy to see in that two assessments randomly drawn from a single individual are likely to be positively correlated whereas one assessment randomly drawn from each of two separate individuals are not. To address this issue, we recommend using a calibration sample strategy. We define a calibration sample to consist of a single observation randomly drawn from the set of available repeated measures for each individual. For example, if one individual contributed three repeated observations and a second individual contributed six observations, a single time-specific observation would be randomly drawn from the set of three and six available observations for each individual, respectively. This ensures that the assumption of independence is maintained.

Next, all of the MNLFA procedures described above are applied to the calibration sample. Once a final measurement model is developed, the entire set of model parameter estimates are retained and used to compute time-specific MAP scores for the full set of repeated measures available for each subject. Continuing with our prior example, although a single observation would be randomly selected for the cases with three and six available repeated measures, the parameter estimates from the final measurement model would be used to obtain scores for all three and six repeated measures, respectively. In this way, the measurement model may be fully developed and optimal scores can be obtained while preserving the assumption of independence. We discuss other options for drawing calibration samples later in the paper.

Summary

Thus far we have described a general moderated nonlinear factor analysis model that is designed to obtain person- and time-specific scores within an IDA framework. However, the complexity of the MNLFA results in many possible strategies for model building and testing, particularly when considering many items drawn from multiple studies in which some are shared across study and others are not. We next propose a principled model building strategy that could be used in complex applications of IDA in practice and demonstrate this using a detailed example from our own IDA project.

The Longitudinal Measurement of Depression Across Three Independent Studies

Our motivating example focuses on the creation of commensurate measures of depression based on items drawn from three independent longitudinal studies of children of alcoholic parents and matched controls. These three studies are strong candidates for IDA because they sample overlapping populations, they have some common and some unique items assessing depression, they have overlap in the age periods sampled across studies, and each boasts a strong methodology in its own right (e.g., community recruitments, high retention, rich assessment batteries). The three studies include the Michigan Longitudinal Study (MLS; Zucker et al., 2000) that contributes assessments from ages 11 to 30; the Adolescent/Young Adult and Family Development Project (AFDP; Chassin, Barrera, Bech, Kossak-Fuller, 1992) that contributes assessments from ages 11 to 34; and the Alcohol and Health Behavior project (AHBP; Sher, Walitzer, Wood & Brent, 1991) that contributes assessments from ages 17 to 34. Collectively, the three studies administered multiple items assessing depression over ages 11 to 34 for 1,972 individuals through 9,322 total individual assessments.

Item selection

The first step is to identify the pool of potential items to be considered for inclusion in the computation of the commensurate measure of the theoretical construct under study. When selecting items it is important to consider specific item and scale characteristics. First, the common item pool should contain at least a core set of identical or harmonized¹ items that we can assume similarly reflect the theoretical construct across studies. These items will be used to define the factor of interest and thus allow tests of differences in the functioning of other items in the total item pool (i.e., common plus all unique items assessed within a subset of studies). Second, at least some of these common items should be theoretically central to assessing the construct of interest. Given that these common items are used to define the factor of interest, internal validity of the construct is assumed to be enhanced with greater theoretical centrality of these core items. Third, the common items, along with the unique items within study, should form a single dominant factor. We used these guidelines to identify items from two well established instruments for assessing depression across the three studies for the computation of our commensurate measure to be used for subsequent analysis.

Specifically, these items came from two versions of the Child Behavior Checklist (CBCL; Achenbach & Edelbrock, 1981) and the Brief Symptom Inventory (BSI; Derogatis & Spencer, 1982). Both the CBCL and BSI are widely used instruments, particularly in long-term longitudinal studies. Two studies used one instrument: AHBP participants aged 17 to 34 completed only the BSI and AFDP participants aged 11 to 34 completed the CBCL. However, MLS participants completed both the CBCL from ages 11 to 18 and the BSI from ages 11 to 30. This assessment design permits strong comparisons of instrument performance within the same study (MLS) as well as study differences within the same instrument with age-matched participants.

Defining a testing strategy for complex IDA measurement designs

Our proposed measurement and scoring strategy is composed of five specific steps. First, we perform graphical and descriptive analyses of individual items assessed over time both within and across studies; the goal of these analyses is to identify potential age and study trends in the item set as well as aberrant item patterns that may suggest challenges in establishing unidimensionality of the underlying factor. Second, we formally test the dimensionality of our item pool using factor analysis; in this step we use both exploratory and confirmatory nonlinear factor analysis to refine our item pool to meet the assumption of unidimensionality for the MNLFA and the goal of extracting scale scores to assess this construct. Third, we evaluate factor (mean and variance) and item (intercept and factor loading) differences as a function of key covariates using MNLFA. We identify candidate covariates based on substantive theory and empirical necessity. In many IDA applications, multiple longitudinal studies might be combined to result in a broad developmental period under study; for example, in our own work we examine trajectories of depression in participants moving from early adolescence into late adolescence and into mid-adulthood. Care must be taken to incorporate any developmental differences in the manifestation of the underlying construct in both the measurement and scoring procedures. Fourth, we create individual- and age-specific scale scores in the integrated longitudinal dataset for each repeated assessment of depression.

Finally, we systematically examine the quality of our estimated scores using a variety of graphical and inferential techniques. Given that the ultimate goal of IDA is to obtain scale scores for subsequent analyses, this fifth step is particularly important and can involve sensitivity analyses testing the stability of our results over the calibration sample used to generate scale scores; graphical analysis of item characteristic curves and test information plots; and analyses testing the predictive validity of our scores against extant measures. Through these five steps, we articulate our proposed testing strategy for developing commensurate measures in IDA that addresses the complexities likely to be encountered when applying these techniques in practice.

Method

Samples and Procedures of Contributing Studies

To demonstrate our proposed analytical strategy, we conduct a comprehensive MNLFA of data drawn from three independent studies that each sampled children of alcoholic (COA) parents and matched controls. The Michigan Longitudinal Study (MLS) used a rolling, community-based recruitment to sample (target) sons aged 3–5 from 338 families (n=262 COAs and 72 controls) as well as 258 similarly-aged siblings of these target children recruited later in time (Zucker et al., 2000), yielding a total sample of 596 children from 338 families. COA families were identified through court-arrest records for male drunk drivers and through community canvassing. Fathers in COA families had to meet criteria for alcoholism during adulthood based on self-reports (Feighner et al., 1972) as well as reside with target sons and be in intact marriages with the biological mothers of these sons at baseline. Contrast families were recruited through community canvassing in the neighborhoods in which COA families resided and were matched to COA families on the basis of age and sex of the target child and parallelism of community characteristics; both parents of controls had to be free of lifetime alcohol and drug disorders. As part of a larger data collection effort, all children assessed in this study completed brief annual interviews between the ages of 11 and 18 as well as longer wave assessments every 4 years between ages 11 and 30. These data from ages 11 to 30 were the focus here.

In the Adolescent/Adult Family Development Project (AFDP; Chassin, Flora, & King, 2004; Chassin, Rogosch, & Barrera, 1991), 454 families (246 COAs and 208 match controls) completed three annual interviews beginning when the target child was aged 10–15. In two young adult follow-ups occurring at 5 year intervals, 363 full biological siblings were included who were similarly-aged to the targets. The combined sample of targets and siblings was 846 from 454 families. COA families were recruited via court records, wellness questionnaires from a health maintenance organization, and community telephone surveys (for details see Chassin et al., 1992). Inclusion criteria for COA families were: living with a biological child aged 11–15, non-Hispanic Caucasian or Hispanic ethnicity, English speaking, and a biological and custodial parent who met DSM-III lifetime criteria for alcohol abuse or dependence. Matched control families were recruited by phone screens of families identified through reverse directory searches based on identified COAs. Control families matched COA families on the basis of ethnicity, family composition, target child’s sex and age and socioeconomic status. Direct interview data confirmed that neither biological nor custodial parents met criteria for a lifetime alcoholism diagnosis. Data were collected with computer-assisted interviews either at families’ homes or on campus, or by telephone for out-of-state, young adult participants.

In the AHBP (Sher et al., 1991), 489 college freshmen (250 COAs and 237 controls) completed four annual assessments as well as two additional post-college follow-ups (at 3 and 4 year intervals). Participants were recruited based on screening an incoming class of college freshmen (Crews & Sher, 1992; Sher & Descutner, 1986) as well as subsequent interviews to confirm reports of parent alcoholism in the COAs. COAs were included in the study if they indicated that their biological father met criteria for alcoholism. Diagnostic interviews and questionnaires were primarily completed in person, but telephone interviews (and mailed questionnaires) were used more commonly as increasing numbers of participants relocated over time.

We pooled these three samples to form an integrated data analysis sample; see Table 1 for a summary of demographic characteristics of the individual and pooled samples. Because analyses used the accelerated longitudinal structure of these aggregate data (e.g., Mehta & West, 2000), we describe the IDA sample with respect to the underlying age distribution of participants rather than wave of assessment. All observations from ages 11 to 34 were included in this sample, resulting in a total of 1,972 participants from 1,227 families contributing a total of 9,322 observations. The sample was 57% male, 15% minority (primarily Hispanic), 58% COA, and had a mean parent education level of 3.05 (measured as the maximum of either parent’s educational attainment assessed on a 6 point scale ranging from [0] less than 12 years or not a high school graduate to [5] graduate or professional school training; see Table 1).

Table 1.

Integrative data analysis sample description by study

	MLS (n=641)	AFDP (n=846)	AHBP (n=485)	Pooled Repeated Measures Sample (n=1972)
Age	15.24 (3.12)	21.17 (7.05)	22.79 (4.77)	19.81 (6.21)
% Male	71.0	52.4	47.2	57.2
% COA	76.0	50.4	48.7	58.3
% Minority	2.3	30.3	6.2	15.3
% Parent ASP	14.8	9.6	7.8	11.0
% Parent Depression	24.6	16.8	36.3	25.0
Parent Education	2.59 (1.18)	3.09 (1.13)	3.62 (1.14)	3.05 (1.21)

Note: Tabled values are means and percentages with relevant standard deviations are in parenthesis. There were participants missing data on Parent ASP (n =217), Parent Depression (n =211), and Parent Education (n =3). Percentages were calculated based on non-missing data.

Measures

Demographic variables

The demographic variables included child gender (0=girl, 1=boy) and chronological age assessed by self-report when available and otherwise by parent-report.

Parent alcoholism

Parental alcoholism diagnosis was assessed using a dichotomous indicator of whether or not either parent met DSM criteria for a lifetime diagnosis of alcohol abuse or dependence as assessed at baseline by parent-report in the MLS and AFDP studies and by target-report in AHBP (0=non-alcoholic parents only, 1=parental alcoholism). In the MLS, a lifetime diagnosis was made by a trained clinician using DSM-III criteria based on reports across three instruments (Diagnostic Interview Schedule-III: Robins & Helzer, 1982; Robins, Helzer, Croughan, & Ratcliff, 1981; Short Michigan Alcohol Screening Test: Selzer, Vinokur & Van Rooijen, 1975; Drinking and Drug History Questionnaire: Zucker, Noll, & Fitzgerald, 1988). In AFDP, a lifetime diagnosis was made based on DIS-III parent self-reports or Family History-Research Diagnostic Criteria spousal-reports (Andreasen, Endicott, Spitzer & Winokur, 1977). In AHBP, targets confirmed parental alcoholism status by completing the Family History Research Diagnostic Criteria interview (Endicott, Andreasen, & Spitzer, 1978).

Internalizing symptoms

Multiple self-report items assessed internalizing symptomatology within each study. Because our goal was to use the MNLFA-derived scores in subsequent analysis, we wanted items that assessed symptomatology with respect to a specific time-period; that captured internalizing symptoms as they might be differentially expressed over development; and that had response scales that could be made comparable across studies. Two instruments contributed items across the three studies that met these criteria: the Brief Symptom Inventory (BSI; Derogatis & Spencer, 1982) and the Youth Self-Report version of the Child Behavior Checklist (CBCL; Achenbach & Edelbrock, 1981). Participants completed the BSI in both MLS and AHBP, the CBCL in the MLS, and an adapted form of the CBCL (Achenbach & Edelbrock, 1978) in the AFDP. Across instruments, those assessing internalizing symptoms (other than somatization) included 33 items. Response scales ranged from 0 to 2 for CBCL items in MLS, 0 to 4 for CBCL items in AFDP, and 0 to 4 for BSI items in MLS and AHBP. To create harmonized response scales across studies (that is, where all items scores are based on the same response options) and to reduce sparseness in upper category responses, all symptoms were scored as absent (symptom=0) versus present (symptom=1 when item greater than or equal to 1 across studies).²

Results

Step One: Graphical and Descriptive Analyses of Individual Items

To identify age trends in the individual items as well as potentially aberrant items, we examined item frequency plots as a function of each covariate (age, study membership, gender and parent alcoholism). For example, Figure 1 displays items plots reflecting the log odds of endorsement by age stratified by study. These plots indicate that most items show moderate stability through adolescence and with decreased endorsement in adulthood. However, one curious exception is noted. An item assessing the symptom of being “overtired” showed a sharp increase as a function of age only in the AFDP sample that contrasts with other items in the scale. This aberration raises question about whether the “overtired” item is part of the construct of depression in this item set, or is operating differently within the AFDP study. With some exceptions, we expect that endorsement rates for items that measure the same construct will generally move together across age and other covariates of interest.³ Given this single aberration, we dropped this item from our item pool before moving to step two. Overall, marginal item endorsement rates ranged from 3% to 55%, with only two items having pooled endorsement rates of less than or equal to 5% across time and study; see the first column of Table 2 for all endorsement rates.

Figure 1.

Endorsement rates for each of the 33 individual internalizing items as a function of subject age.

Note: Endorsement rates are shown as logits computed at each discrete age, and smoothed lines are fitted to show continuous trends across age. These are non-parametric and intended for graphical representation only. The aberrant item in AFDP was not assessed after age 17.

Table 2.

Results of unidimensional nonlinear exploratory factor analysis for 17 depression items.

Item Description	Proportion Endorsed	Standardized Loading (se)
1. Lonely	.46	.83 (.02)
2. Cries a lot	.25	.65 (.03)
3. Fears will behave badly	.17	.55 (.05)
4. Have to be perfect	.50	.56 (.03)
5. No one loves me	.15	.82 (.03)
6. Worthless/inferior	.19	.86 (.02)
7. Prefers being alone	.34	.45 (.05)
8. Feels guilty	.24	.70 (.02)
9. Is secretive	.48	.62 (.04)
10. Is underactive	.29	.49 (.05)
11. Unhappy/sad/depressed	.43	.82 (.02)
12. Worried	.55	.71 (.02)
13. Hopeless about future	.18	.76 (.03)
14. Acts to harm self	.03	.64 (.07)
15. Thinks about killing self	.05	.69 (.05)
16. Blue	.37	.81 (.03)
17. No interest in things	.28	.67 (.03)

Note: parameter estimates and standard errors based on weighted least squares estimation with mean and variance correction.

Step Two: Dimensionality Testing through Nonlinear Exploratory Factor Analysis

To extract a unidimensional factor assessing internalizing symptomatology from our item pool, we estimated a nonlinear exploratory factor analysis (EFA) using Mplus version 6.11 (Muthén & Muthén, 2010). Like the MNLFA defined earlier, the nonlinear EFA model assumes that participants are independent, so we first selected a calibration sample in which each individual contributed a single randomly selected observation from their available set of repeated assessments within the pooled dataset. Table 1 shows the demographic characteristics for the fully integrated sample; these summary statistics also hold for the calibration sample given that all but one reported demographic are time-invariant characteristics. The one logical exception is that in the calibration sample the age distribution is based on a single observation instead of the complete set of repeated measures as is presented in Table 1; the mean and standard deviation of age in the calibration sample was 16.01 (3.96) in MLS, 22.77 (6.98) in AFDP, 22.60 (4.82) in AHBP, and 20.53 (6.44) in the pooled sample.

To evaluate the consistency of our results, we fitted EFA models both to the calibration sample pooled across datasets (i.e., the pooled calibration sample) and within each dataset separately (i.e., the within-study calibration samples). Because all of our items were binary, we used a probit link function with weighted least squares with mean and variance adjusted chi-square fit statistics (WLSMV); this is a limited- information procedure that involves computation and analysis of the tetrachoric correlation matrix for the items (see Wirth and Edwards, 2007, for a review). The advantage here is that WLS provides both eigenvalues (to help assess dimensionality) and chi-square difference tests and fit indices (to aid in the evaluation of omnibus and nested model fit). We do not present detailed results for all models given space constraints; we do present fit criteria for our final EFA.

First, we determined dimensionality within each of four datasets: the three contributing samples and the fully pooled sample. For the MLS, AHBP, and pooled datasets, the internalizing items were optimally characterized by a two factor solution, primarily indicated by the existence of two large eigenvalues. Closer evaluation of the item content showed these factors to clearly represent depression (17 items) and anxiety (15 items). Within the AFDP sample one dominant factor emerged. A two-factor solution consistent with the other contributing studies was likely occluded in AFDP due to existence of just two items assessing symptoms of anxiety; the remaining items clearly defined a depression factor.

We then compared the entire set of factor solutions to determine which items to retain for a depression factor. Our criteria for item inclusion were that an item had to uniquely load on the depression factor within the pooled calibration sample (i.e., loading is greater than .40 on the primary depression factor and less than .35 on the secondary factor) and the item must uniquely load on the depression factor for at least half of the within-study nonlinear EFAs.⁴ Based on these criteria, we retained 17 items from the broadband internalizing construct that focused exclusively on depressive symptomatology. We re-estimated the nonlinear EFA in the pooled calibration sample with the 17 retained items and a one factor solution was clearly supported with all items significantly loading on the factor. This final model fit the data well: χ²(119)=349.75, p<.01, RMSEA=.03, CFI=.98, TLI=.97. The factor loadings indicated that our items differed in their relatedness to the underlying depression factor but all contributed significantly to defining the factor (see the second column of Table 2).

Step Three: Testing for Factor and Item Differences through MNLFA

We next fitted MNLFA models to the calibration sample to test for differences in the factor means, factor variances, item intercepts, and item factor loadings as a function of study membership AFDP, MLS, or AHBP), continuous age centered at 18 (including linear, quadratic and cubic trends),⁵ parent alcoholism, and gender. To define the scale of the latent factor we fixed the conditional mean and variance of the factor to 0 and 1, respectively, when all covariates are equal to zero (indicating non-COA girls drawn from the AFDP study at age 18). In other words, we fixed α₀ = 0 and ψ₀ = 1 in Equations (5) and (6) freely estimated all item loadings and intercepts.

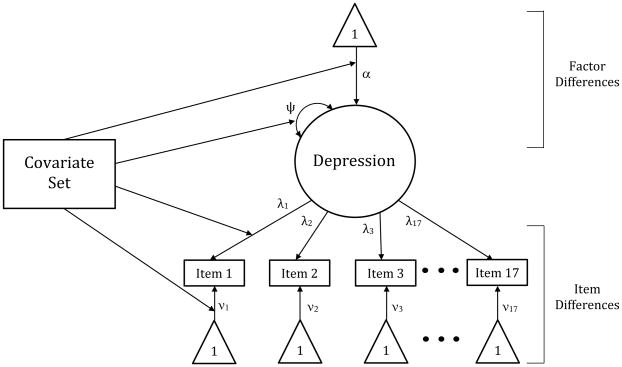
Our testing strategy for this step involved estimating two sets of models using the pooled calibration sample. The first set tested whether covariates predicted mean and variance differences in the latent factor of depression consistent with Equations (5) and (6) from above. The second set tested whether covariates predicted intercept and factor loading differences in the specific items after accounting for factor differences, which is consistent with Equations (8) and (9) from above. We tested for item intercept and loading differences on an item-by-item basis in the presence of the factor mean differences.⁶ That is, we examined the moderating effects of the covariates on the factor loading and intercept for the first item, then moved to the second item, and so on; resulting in 17 independent sets of item analyses.⁷ This highly conservative sequential strategy was used to account for potential differences in item functioning that might inform subsequent scoring. We ordered these two sets of models (factor-level and item-level) in this way to remain consistent with the traditional methods of testing differential item functioning in DIF (e.g., Flora et al., 2008). However, this strategy then allows us to substantially extend the traditional methods typically used for evaluating invariance to test hypotheses in ways not currently possible. After identifying the optimal combination of the set of predictors for each individual item and factor parameter, we estimated a full model that included all of the covariate effects for all 17 items simultaneously as well as the final effects from our conditional factor mean and variance models; all contributing effects remained significant in this full model. Figure 2 depicts a path diagram for the final complete MNLFA model.

Figure 2.

Path diagram for final MNLFA model for 17 binary items assessing depressive symptomatology.

Note: the metric of the latent factor was set by fixing the conditional intercept and variance of the factor to 0 and 1, respectively.

Our proposed strategy incorporates a model building approach in which we first tested the main effects of the covariates; we then added all two-way interactions between age and the three other covariates (study membership, parent alcoholism and gender) as well as study and the other covariates (parental alcoholism and gender); finally, we added three-way and related two-way interactions of substantive interest between age, study and gender and between age, study and parent alcoholism. We used this model building strategy for substantive reasons; namely, we viewed age effects as substantively fundamental for estimating the functional form of the depression factor and item characteristics over age that will inform later analysis when we return to the repeated measures in the pooled calibration sample. It is also critical to include the effects of study to account for the complex nature of the IDA design, permitting us to test questions about study comparability directly. After estimating each set of models within the series, we eliminated non-significant interaction terms using an alpha of .01 to approximately account for multiple comparisons.⁸

The results from the final model incorporating both factor and item differences are presented in Table 3 (factor mean and variance) and Table 4 (item intercepts and factor loadings). As predicted by theory, the significant effects of parent alcoholism on the factor mean of depression indicated that children of alcoholic parents reported higher rates of depression than did their peers (α̂ = .23, t=4.07). Moreover, linear (α̂ =−.70, t=−5.04), quadratic (α̂ =−.63, t=−2.58) and cubic (α̂ =.56, t=3.12) effects of age on the depression factor mean indicated that, on average, rates of depressive symptoms were stable through adolescence, decreasing in young adulthood and increasing again after the late 20’s. The effects of age across the continuum were moderated by both study membership and gender; the point estimates and standard errors for these effects are presented on lines 8 through 14 in Table 3. To help with interpretation, Figure 3 displays model-implied conditional mean plots across age and stratified by covariates for the depression factor.

Table 3.

Results from final scoring MNLFA model testing covariate effects on factor mean and variance.

Covariate Effect	Estimate (se)	t	p
Factor Mean
1. Age	−0.70 (.14)	−5.04	<.0001
2. Age2	−0.63 (.25)	−2.58	0.0098
3. Age3	0.56 (.18)	3.12	0.0018
4. MLS	−0.86 (.08)	−10.87	<.0001
5. AHBP	−0.28 (.12)	−2.28	0.0227
6. Gender	−0.48 (.08)	−5.82	<.0001
7. COA	0.23 (.06)	4.07	<.0001
8. Age by MLS	0.85 (.15)	5.81	<.0001
9. Age by AHBP	−3.77 (.91)	−4.13	<.0001
10. Age2 by AHBP	4.84 (1.64)	2.95	0.0033
11. Age3 by AHBP	−1.73 (.76)	−2.29	0.0222
12. Age by Gender	0.25 (.16)	1.58	0.1140
13. Age2 by Gender	1.03 (.31)	3.29	0.0010
14. Age3 by Gender	−0.74 (.23)	−3.18	0.0015
Factor Variance
15. Age	0.02 (.10)	0.21	0.8372
16. AHBP	−0.13 (.19)	−0.66	0.5106
17. Age by AHBP	0.80 (.27)	2.90	0.0038

Note: Age, Age² and Age³ refer to the linear, quadratic and cubic age trends respectively. Age is centered at 18 years old and divided by 10 to control the magnitude of the polynomial terms. The parameter estimates for the factor mean effects are on a standard normal scale when all covariates are equal to zero.

Table 4.

Results from final scoring MNLFA model testing covariate effects on item intercepts and factor loadings.

Item Covariate Effect	Intercept (se)	Loading (se)
1. Lonely	0.79 (.20)	2.36 (.16)
AHBP	1.05 (.22)	-
2. Cries a lot	0.45 (.15)	1.45 (.12)
Age	−0.34 (.12)	-
Gender	−2.09 (.17)	-
3. Fears behave badly	−0.68 (.17)	1.22 (.16)
4. Have to be perfect	0.70 (.11)	1.06 (.08)
5. No one loves me	−2.00 (.25)	2.55 (.23)
Age	−0.64 (.20)	-
MLS	0.88 (.27)	-
6. Worthless/inferior	−1.23 (.20)	2.49 (.19)
MLS	0.55 (.21)	-
7. Prefers to be alone	0.18 (.15)	0.91 (.12)
8. Feel guilty	−0.46 (.13)	1.11 (.15)
Age	−0.63 (.21)	−0.12 (.32)
Age2	0.52 (.18)	2.05 (.69)
Age3	-	−1.31 (.42)
MLS	−0.83 (.19)	-
9. Is secretive	1.34 (.21)	1.38 (.15)
10. Is underactive	0.14 (.16)	1.02 (.13)
Age	0.71 (.24)	-
11. Unhappy/sad/depressed	0.98 (.19)	1.93 (.19)
MLS	-	0.95 (.29)
12. Worried	1.51 (.18)	1.66 (.13)
Age	0.59 (.15)	-
MLS	−0.70 (.18)	-
Age by MLS	−0.91 (.31)	-
13. Hopeless about future	−0.49 (.24)	2.07 (.21)
Age	1.04 (.36)	-
Age2	−1.41 (.37)	-
Gender	0.89 (.24)	-
14. Acts to harm self	−3.06 (.31)	1.66 (.35)
15. Thinks about killing self	−2.38 (.20)	1.67 (.23)
16. Blue	2.02 (.38)	2.83 (.36)
Age	3.33 (.78)	2.96 (.77)
17. No interest in things	−0.37 (.25)	1.69 (.21)
Gender	0.56 (.21)	-
COA	0.68 (.21)	-
Age	-	2.97 (.88)
Age2	-	3.02 (.99)
Age3	-	−2.96 (.93)

Note: Each tabled value corresponds to the regression parameters defined in Equations (8) and (9). All tests of item intercepts and loadings were estimated in the presence of factor mean and variance effects presented in Table 3. Age, Age² and Age³ refer to the linear, quadratic and cubic age trends respectively. Age is centered at 18 years old and divided by 10 to control the magnitude of the polynomial terms.

Figure 3.

Conditional model-implied age trends as defined by the final MNLFA model.

The top panel of Figure 3 presents the model-implied mean depression across age conditioned on gender; girls maintained their depressive symptom levels over adolescence, decreased with early adulthood but then show a later increase again as they enter their 30’s. For boys, depression decreased throughout the observation period, though more steeply in adolescence than in adulthood. The middle panel presents the model-implied mean depression across age conditioned on study membership; younger AFDP participants had higher levels of depression than those in MLS, though these differences disappeared for those in their late 20’s as depression increased for MLS and decreased for AFDP over age. AHBP participants showed sharp decreases in depression in the early adult years, leveling out with lower depressive symptoms for those in their mid-20’s at rates lower than in either AFDP or MLS. Finally, the bottom panel presents the model-implied expected level of depression across age conditioned on parental alcoholism status; the shape of the age trends is quite similar, although children with an alcoholic parent report greater levels of depression across all ages. The only effects of covariates found to predict variance in the depression factor showed that AHBP participants had greater variability in their levels of depression with increasing age than did participants in the AFDP and MLS (ω̂ =.80, t=2.90); we do not highlight this effect graphically.

The complete set of estimated effects for item intercepts and factor loadings are reported in Table 4. Results indicated that six of the 17 items showed no differences in functioning across age, gender, COA status and study membership (i.e., fears behave badly, have to be perfect, prefers being alone, is secretive, acts to harm self, and thinks about killing self). Six additional items showed differential item functioning only in item intercepts reflecting differences in probability of endorsing these items at equivalent levels of underlying depression. For example, on average, higher levels of underlying depression were required for boys to endorse item 2 (cries a lot) compared to girls, whereas this gender difference was reversed for item 13 (hopeless about the future). Younger participants endorsed item 10 (underactive) at higher levels of depression than did older participants though the opposite trend was found for item 2 (cries a lot). Controlling for these effects, AHBP study members endorsed item 1 (lonely) at lower levels of depression than those in other studies and those in MLS endorsed item 6 (worthless) at lower levels of depression than did participants in other studies.

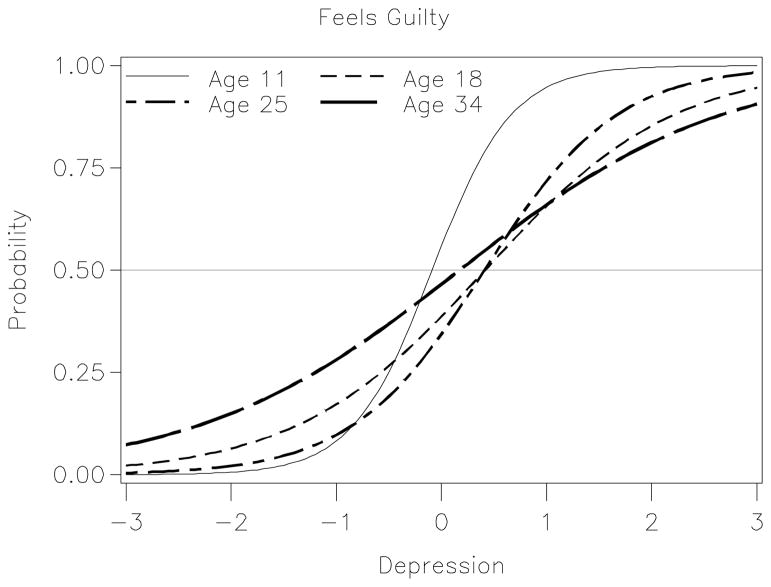
Other items showed more complex patterns of differential item functioning, particularly those involving age trends. We again plotted these complex findings to guide interpretation. For example, as shown in Figure 4, for item 12 (worried) the strength of the relation between the item and the factor is equal for AFDP and MLS at age 11, but higher levels of depression are needed to endorse the item for MLS as age increases. Findings for item 8 (feels guilty) were even more complex involving differential item functioning on both item intercepts and factor loadings for multiple covariates. Figure 5 shows that both the factor loading and item intercept vary continuously across age; these differences are seen in changes in both the intercept and slope of the trace lines as a function of age.

Figure 4.

Item #12 “worried” showing intercept impacted by study and age.

Note: three candidate ages were selected from all possible ages to highlight the continuous effects of age on the item intercept.

Figure 5.

Item #8 “feels guilty” showing both intercept and loading varying as a continuous function of age for AFDP study

Step Four: Estimating scale scores in the integrated longitudinal dataset

To derive scale scores, we used the complete set of parameter estimates from our final MNLFA model fitted to the calibration sample to score the full, integrated dataset with all repeated assessments using PROC NLMIXED in SAS (SAS Institute, 2008). This procedure allowed us to produce maximum a posteriori (MAP) scores for depression symptoms that could then be used in subsequent hypothesis testing. Because these analyses incorporate the effects identified in our MNLFA testing strategy, the scale scores also simultaneously account for differences in the factor mean, factor variance, item intercepts, and factor loadings due to the respondent’s age, study membership, gender, and parent alcoholism.

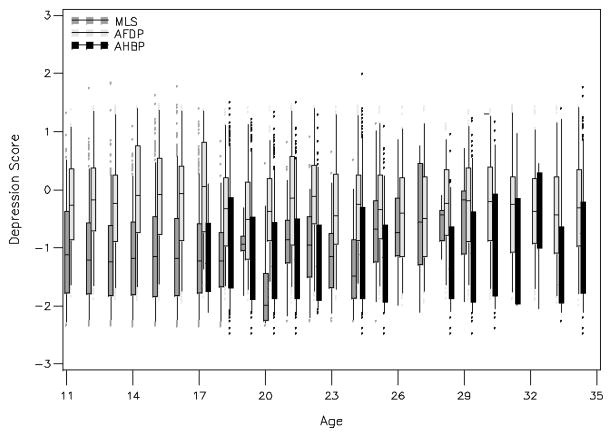
We estimated MAPs for the entire sample to obtain a subject-specific score at all available ages (i.e., 1,972 participants contributing a total of 9,322 person-time observations) and these scores are graphically presented in Figure 6. There are many ways in which these scores can be plotted, and here we simply show these as a function of age and study membership. The box plots reflect mean changes in depression over time that are accompanied by substantial individual variability both within- and across-age. The scores are now available to be used to fit any of a variety of statistical models to study the course, causes, or consequences of depression across adolescence and young adulthood.

Figure 6.

Final factor score estimates for the complete sample plotted over age and stratified by study.

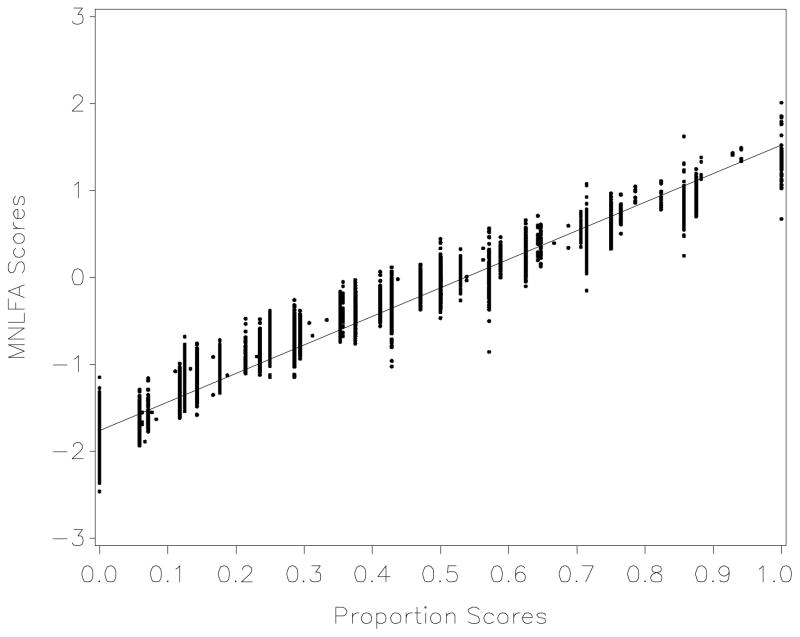
To better understand the potential advantages of the factor scores we compare the depression scale scores to an alternate, commonly used scoring method based on a simple computation of the proportion of items endorsed at any given assessment (see Figure 7). Although the two scoring methods produce highly correlated scores (r=.97), this reflects the high correspondence in relative ranking of scores between the two methods. In contrast, the MNLFA testing strategy produced much greater variability in scores that is unavoidably lost through proportion scoring. This is most evident by noting that for each discrete value of a proportion score (i.e., a single value on the x-axis) there is an entire distribution of MAP scores produced through the MNLFA procedure (i.e., the corresponding range of values on the y-axis). This is more clearly seen in Figure 8 in which the complete distribution of MNLFA scores is shown for a single proportion score value of .24 (corresponding to the positive endorsement of any four of the 17 items). Greater variability in the MAP scores occurs because the scoring procedure takes into account which items were endorsed in a given assessment period and by whom and not simply how many items were endorsed. The results of the MNLFA showed that some items are more indicative of depression than are others, and this illustrates how this model can be used to incorporate unique information on individual differences that is not captured using standard scoring methods.

Figure 7.

Scatterplot of MNLFA scores against corresponding proportion scores.

Note: the x-axis represents the discrete values of simple proportion scores computed as the mean of binary items endorsed; the y-axis represents the range of MNLFA scores that are associated with each discrete proportion score.

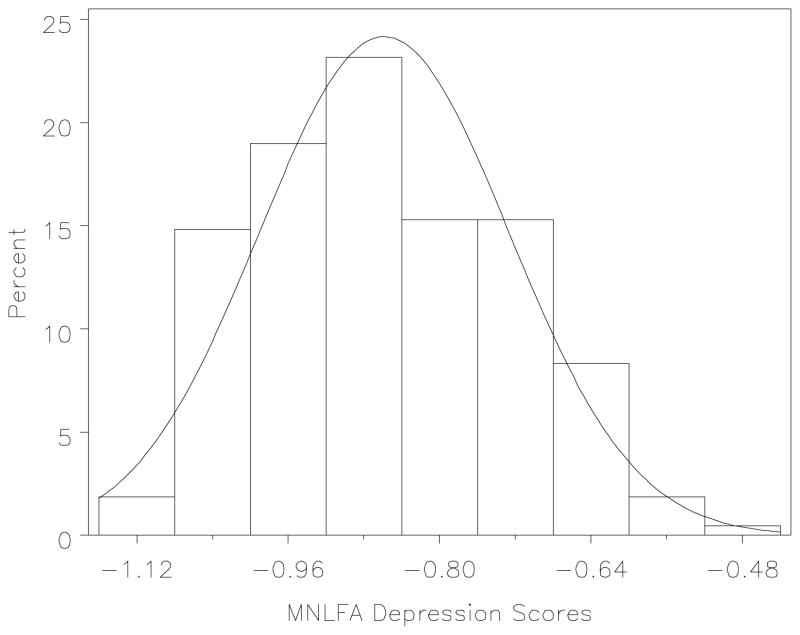
Figure 8.

The complete distribution of MNLFA scores associated with a specific proportion score of .24 (4 out of 17 items endorsed).

Step Five: Evaluating the quality of the final depression scale scores

The final step in our proposed framework is to evaluate the quality of the final scores. This step is often subjective, the specifics of which are informed by the goals of the application and the characteristics of the available data. Here we demonstrate three components: cross-validation of scoring with a new calibration sample; examination of information curves; and graphical examination for outliers. However, additional strategies such as empirical tests of convergent and divergent validity and sensitivity analysis relative to alternative model parameterizations are also possible.

Recall that the scoring model was based on a calibration sample in which a single age-linked observation was randomly selected for each individual. To empirically evaluate the stability of solutions across samples, we drew a new random calibration sample; the sample demographics were identical to those presented in Table 1 (because these are time-invariant characteristics) but the mean and standard deviation for age was 20.33 (6.39). We rescored the data using this new calibration sample and these scores correlated r=.997 with those obtained from the initial calibration sample. This result suggests that our scoring method was not unduly determined by the characteristics of the calibration sample.

Next, we computed the total information curve for the final set of obtained scores. There are a variety of ways to compute information for the MNLFA model, and in Figure 9 we present plots of information calculated at four candidate ages (11, 18, 25, and 32) where all other covariates are held at their respective means. The curves highlight several interesting characteristics about the obtained scores. For example, at the younger ages the curves are symmetric and centered around zero indicating optimal measurement is obtained at the grand mean of depression. Further, these distributions systematically shift to the left as individuals advance in age indicating that precision increases at values falling approximately one standard deviation below the mean of depression. Taken together, these plots indicate that not only do the calculated scores reflect adequate precision across a range of underlying depressive symptomatology, but this precision varies as a function of age.

Figure 9.

Total information curves computed at four specific ages.

Note: The horizontal reference lines represent a reliability of .85.

Finally, we conducted a series of outlier detection analysis using extensive graphical representations of the scores as a function of a large set of person-specific covariates. For example, we plotted the obtained scores as a function of study membership, gender, alcoholism diagnosis, age, ethnicity, and a number of other person-specific measures. None of these graphical analyses indicated any potentially aberrant or outlying observations. These diagnostics would need to be further considered when fitting specific models to these data, but we do not pursue this further here.

Taken together, it appears that the obtained scores are not sensitive to the initial calibration sample, are reliable across a large set of values of the underlying latent factor, and are not characterized by a subset of aberrant or outlying observations. These scores could now be used as the unit of analysis in second-stage modeling to test specific substantive hypotheses of interest.

Discussion

In this paper we have proposed a structured and principled strategy for developing commensurate measures in IDA that addresses complexities likely to be encountered in applying these techniques in practice. Through five steps, we evaluated trends in the raw data that inform our modeling strategies, established dimensionality of the measured construct, evaluated differential item functioning on the basis of key theoretically meaningful covariates, created scale scores, and examined the quality of these scale scores. These steps provide a means for cross-validation of our findings through the comparison of potential trends found in graphical analysis and tested within inferential analysis. These steps also evaluate specific assumptions in the modeling approach, such as unidimensionality of the item set and specification of nonlinear and interactive covariate effects on differential item functioning. Importantly, the strategy also builds on the strengths of the structural equation modeling approach to psychometric evaluation. The methods can be applied through existing, commercially available software and extend psychometric models to the context of measurement for integrative data analysis. This testing strategy is flexible and may be directly extended to account for IDA contexts that include more studies, less item overlap across studies, and even more complex patterns of differential item functioning.

Although our exemplar demonstrates an instance in which obtaining commensurate measures is successfully achieved, the same testing strategy may uncover contexts in which valid scores cannot be obtained. For example, by pruning items to establish the assumption of unidimensionality, adequate item coverage may be found deficient in some studies. In the current analyses, a secondary factor assessing anxiety was identified in the exploratory factor analysis, but only two items contributed to this construct in one of our studies and these were not theoretically central to the construct of anxiety. If we were to pursue a commensurate measure of anxiety in the current context, we would clearly have inadequate scale scores based on two items in a single study and thus we would likely have no choice but to exclude that study from the measurement procedures and subsequent IDA involving the measure of anxiety.

A core feature of our proposed testing strategy is the ability to examine differential item functioning due to study membership providing a direct test of the extent to which items can be allowed to differ in precisely how they contribute to the computation of the final scale scores derived for future analysis. In our example, 11 of our 17 items showed differential item functioning across study, and the pattern was not consistent across items. By taking into account differences in item intercepts, factor loadings as well as factor means and variance due to study membership, our estimated scores account for study differences in these indices. This differential tuning of scores as a function of study membership and other covariates thus has advantages beyond anchoring scores to a common metric across studies.

One issue that arises in nearly any IDA application is the need to make sometimes subjective decisions about various aspects of the analysis. For example, we chose to use a single calibration sample to which we fitted both the EFA and MNLFA models; we then randomly extracted a second calibration sample to cross-validate the scoring model as a test of sensitivity of our obtained scores to possible idiosyncrasies related to the initial calibration sample. We found no evidence of sensitivity as reflected in the correlation between the two sets of scores exceeding r=.997. However, we could have instead extracted one calibration sample for our EFA model, a second for our MNLFA model, and a third to obtain our final scoring parameters. Given the stability of our two calibration samples (in large part due to the high quality data and large sample sizes), we strongly expect this alternative strategy would make little or difference in our final analyses. However, in other IDA applications there may exist a greater risk for sample-to-sample heterogeneity in the calibration sample and drawing a new calibration sample for each stage in the analysis could be beneficial.

Another decision point is the extent to which response scales are harmonized prior to fitting the EFAs or MNLFAs. For the items we considered here, some were originally defined by three response options and some by five depending on the scale and the study from which it was drawn. We collapsed these three- and five-option responses to a binary scale for two reasons. First, there was extreme sparseness in the higher values of the five-level response options with a number of items literally having no endorsement of some values on the scale at some ages; the five-by-five bivariate contingency tables often had more empty cells than not. We thus collapsed across these values because the models were not analytically tractable with this degree of non-responses across the entire set of times. Second, we did not want to potentially confound the number of response options with study membership. That is, if one study were to have only three options and one study to have only five options, then between-study differences might arise solely from the differential options presented to the participants. However, it is important to stress that any response harmonization be done carefully with the motivating goal of preserving as much data integrity as possible, particularly given that collapsing across multiple values naturally leads to a loss of precision, among other issues (e.g., MacCallum, Zhang, Preacher & Rucker, 2002).

Conclusion

By proposing a general framework for developing commensurate measures across broader and more complex empirical contexts, we hope to expand the potential use of integrative data analyses to a wider array of substantive applications than is currently possible. Although a variety of approaches to integrative data analyses are making an appearance in the empirical literature, the pooling of item-level data across multiple independent studies presents opportunities not available through other study integration approaches (Curran & Hussong, 2009; Hofer & Piccinin, 2009; Hussong et al., 2013; McArdle et al., 2009). To the extent that commensurate measures may be validly and reliably derived across multiple studies, item-level integrative data analysis permits us to address novel research questions, to directly test the replication of effects across studies, to examine factors that may account for study differences in predicted effects, and to efficiently use the large pool of high quality databases currently available in the behavioral and social sciences.