Natural and orthogonal model for estimating gene–gene interactions applied to cutaneous melanoma

Abstract

Epistasis, or gene–gene interaction, results from joint effects of genes on a trait; thus, the same alleles of one gene may display different genetic effects in different genetic backgrounds. In this study, we generalized the coding technique of a natural and orthogonal interaction (NOIA) model for association studies along with gene–gene interactions for dichotomous traits and human complex diseases. The NOIA model which has non-correlated estimators for genetic effects is important for estimating influencing from multiple loci. We conducted simulations and data analyses to evaluate the performance of the NOIA model. Both simulation and real data analyses revealed that the NOIA statistical model had higher power for detecting main genetic effects and usually had higher power for some interaction effects than the usual model. Although associated genes have been identified for predisposing people to melanoma risk: HERC2 at 15q13.1, MC1R at 16q24.3 and CDKN2A at 9p21.3, no gene–gene interaction study has been fully explored for melanoma. By applying the NOIA statistical model to a genome-wide melanoma dataset, we confirmed the previously identified significantly associated genes and found potential regions at chromosomes 5 and 4 that may interact with the HERC2 and MC1R genes, respectively. Our study not only generalized the orthogonal NOIA model but also provided useful insights for understanding the influencing of interactions on melanoma risk.

Introduction

In the past several years, searching for genetic factors that cause various human complex traits and diseases has become one of the most important and challenging goals for modern geneticists. Genome-wide association studies (GWASs), in which every locus is usually analyzed separately, have identified a large number of causal variants for human genetic diseases and traits, such as cancer, diabetes and heart disease (Craddock et al. 2010; Ehret et al. 2011; Amos et al. 2011). However, one of the limitations of this single-locus analytical strategy is that interactions between loci or between genes and environmental exposures are usually ignored (Culverhouse et al. 2002; Moore 2003). For this reason, more efforts are being made to characterize the complex network between multiple genes that contribute to disease outcome.

Epistasis means that a genetic effect is modulated by effects from other loci or the genetic background. Gene–gene (G × G) interaction most commonly refers to a departure from additive genetic effects of several genes on a trait; thus, the same alleles of one gene could display different genetic effects in different genetic backgrounds. Epistasis was initially characterized in an animal model in the early 1900's as playing an important role in determining some phenotypes (Wilson 1902). For common human diseases and disorders, such as anemia, cystic fibrosis and complex autoimmune diseases, the relevance of gene–gene interactions is still being studied but became a more prominent explanation for the failure of GWAS to explain much of the variation in risk among individuals in the last decade (Nagel 2001, 2005; Wandstrat A 2001). Moreover, epistasis was recently revealed to be the main force in long-term molecular evolution (Breen et al. 2012). Several methods have been developed for searching for the interactions when performing genetic association studies (Ritchie et al. 2001; Hahn et al. 2003; Chung et al. 2007; Gayan et al. 2008; Rajapakse et al. 2012). The major motivation of developing these approaches is to improve the power of detecting effects and to provide a more comprehensive assessment of genetic architecture influencing a trait (Kraft et al. 2007).

The natural and orthogonal interaction (NOIA) framework was initially developed for association studies of quantitative traits allowing gene–gene interactions (Alvarez-Castro and Carlborg 2007). Its statistical formulation provides an approach in which the estimates of the genetic effects remain orthogonal; that is, they are consistent in reduced models. This holds true even if Hardy–Weinberg Equilibrium (HWE) is violated. One of the advantages of the NOIA framework relies on its convenience for model selection to find the complex genetic architecture underlying the outcome trait. By enabling the modeling of multiple loci along with their interactions, the NOIA statistical model provides meaningful estimates of genetic effects as it leads to orthogonal decomposition of genetic variance (Alvarez-Castro et al. 2008). Therefore, the NOIA statistical model renders a more meaningful calculation of the heritability of a trait when compared with traditional models. Ma et al. (2012) recently extended the NOIA model for modeling joint influencing from genetic factors and environmental exposure for quantitative traits. Treating the genotypic values at a log odds scale, they applied the NOIA statistical model for the analysis of case–control data as well and identified a few potential gene–environment interactions contributing to the lung cancer risk.

Cutaneous melanoma (CM) is a highly aggressive malignant tumor of melanocytes and accounts for the majority of deaths from skin cancer. CM is a common cancer and about 55,560 new cases of melanoma in situ were diagnosed in 2012 (Siegel et al. 2012). GWAS and family-based approaches have revealed several loci that influencing CM risk. Studies of the data from The University of Texas MD Anderson Cancer Center found most significant associations between melanoma risk and the melanocortin 1 receptor (MC1R) located at chromosome region 16q24.3, the HECT and RLD domain containing E3 ubiquitin protein ligase 2 (HERC2)/oculocutaneous albinism II (OCA2) at region 15q13.1 and cyclin-dependent kinase inhibitor 2A (CDKN2A or p16) at 9p21.3 (Bishop et al. 2009; Sturm et al. 2008). HERC2 and MC1R have been found to be associated with pigmentary phenotypes such as skin, hair and eye (Ghilardi et al. 2002; visser et al. 2012). CDKN2A (or p16) is a putative tumor suppressor gene which is involved in multiple human cancer types (Nobori et al. 1994). Although one-locus association studies have been applied widely to investigate melanoma risk, the gene–gene interactions underlying this disease have not been fully exploited. Exploring how these genetic loci jointly influencing the development of melanoma can provide important clues in the pathogenesis and treatment of melanoma.

In this study, we mainly focus on the applicability of the NOIA framework in genetic association studies and extended it to the case of a qualitative trait. For testing the gene–gene interactions in the association modeling, adding the interaction effect into the modeling always results in lost power to detect the main genetic effects, that is, the additive and dominant effects. The usual functional one-locus model uses natural substitution for the parameter estimations which renders a non-orthogonal model whenever a dominance component is modeled, which means that the hypothesis tests lose power when the interaction terms are incorporated into the modeling. The NOIA statistical model overcomes this disadvantage because of its orthogonality. That is, even we add several additional parameters (for interaction) to NOIA modeling, estimation of the parameters for main effects will not be influenced.

In this study, we evaluated the behavior of the NOIA statistical model over the usual functional model for detecting the genetic effects, through both simulation analyses and application on melanoma dataset. Specifically, we evaluated the performance of these two models for detecting genetic effects while allowing for interaction for both quantitative traits and case–control traits when the interaction coefficients were positive, negative or zero values. In most scenarios we simulated, the NOIA orthogonal model presented higher power and yielded more precise estimators than the usual functional model. In addition, we also extended the NOIA statistical model to reduced models including the additive, dominant and recessive models. Application to the melanoma dataset showed that the full NOIA statistical model had higher power than the full usual functional model in the one-locus analysis. The NOIA statistical model also had higher power in the two-locus analysis allowing interaction effects. We validated the main genetic effects of previously identified associated variants influencing melanoma risk using the NOIA statistical model. For the first time, significant interaction effects between SNP rs6871296 and HERC2 gene, SNP rs10009093 and MC1R gene contributing to the melanoma risk were indicated by application of our models.

Methods

Two-locus gene–gene interaction models

The statistical formulation of the NOIA model for quantitative traits was first described by Alvarez-Castro and Carlborg (2007). As shown in Ma et al. (2012), the genotypic vector G can be expressed as, in the one-locus statistical model,

$$\left(\begin{array}{c}{G}_{11}\\ G_{12}\\ G_{22}\end{array}\right)=S_s{\overline{E}}_s=\left(\begin{array}{ccc}1& -\overline{N}& -\frac{2p_{12}{p}_{22}}{V}\\ 1& 1-\overline{N}& \frac{4p_{11}{p}_{22}}{V}\\ 1& 2-\overline{N}& -\frac{2p_{12}{p}_{22}}{V}\end{array}\right)\left(\begin{array}{c}\mu \\ \alpha \\ \delta \end{array}\right),$$ (1)

Which ensures orthogonality of the estimates of the three parameters. Further details about these notations can be found in Ma et al. (2012). Alvarez-Castro et al. (2008) noted that the statistical model was an orthogonal model that had uncorrelated estimates of the parameters, which is also reflected by variance components decomposition (Ma et al. 2012). The test statistics for main effects of orthogonal (or statistical) model and functional model for a univariate analysis has been derived recently (Xiao et al. 2013). They showed loss of power for detecting main effects for the functional model due to confounding between dominance and main effects in most cases. The interaction functional Wald test with dominance components will also suffer from dependence among the parameters. In the current study, we mainly focus on applying the NOIA statistical model for testing association along with gene–gene interactions. We also evaluated some of the statistical benefits of using this novel model and particularly the effect of the dependence in the parameters on test statistics for the functional model which we will introduce later in this section and of orthogonality for the NOIA model.

To extend the model to a two-locus model allowing gene–gene interaction, we assumed that a quantitative trait is influenced by two diallelic loci, A and B. We use p_ij and q_ij to denote the genotype frequencies of genotype A_ij and B_ij, respectively. N_A is the number of variant allele A₂ and N_B is the number of variant allele B₂. N̄_A and N̄_B denote the means of N _A and N_B, respectively, whereas V_A and V_B denote the variance of N_A and N_B, respectively. Therefore, N̄_A = p₁₂ + 2p₂₂, V_A = p₁₂ + 4p₂₂ − (p₁₂ + 2p₂₂)², Correspondingly, N̄_B = q₁₂ + 2q₂₂, V_B = q₁₂ + 4q₂₂− (q₁₂ + 2q₂₂)².

For two-locus gene–gene interaction models, as described by Alvarez-Castro and Carlborg (2007), the vector of two-locus genotypic values, G_AB, can be built as follows:

$$G_{AB}=S_{AB}·E_{AB}=(S_B\otimes S_A)·E_{AB},$$ (2)

if the two loci, A and B, are in linkage equilibrium. E_AB is the two-locus vector of genetic effects; S_AB is the two-locus genetic effect design matrix which is the Kronecker product of the design matrix of loci B and A. From NOIA one-locus statistical model (Eq. (1)), the two-locus modeling vectors G_AB, E_AB and design matrix S_AB can be obtained by the Kronecker product of one-locus modeling as follows:

$$G_{AB}=\left(\begin{array}{c}{G}_{B_{11}}\\ G_{B_{12}}\\ G_{B_{22}}\end{array}\right)\otimes \left(\begin{array}{c}{G}_{A_{11}}\\ G_{A_{12}}\\ G_{A_{22}}\end{array}\right),$$ (3)

$$S_{AB}^S=S_B^S\otimes S_A^S=\left(\begin{array}{ccc}1& -{\overline{N}}_B& -\frac{2q_{12}{q}_{22}}{V_B}\\ 1& 1-{\overline{N}}_B& \frac{4q_{11}{q}_{22}}{V_B}\\ 1& 2-{\overline{N}}_B& -\frac{2q_{11}{q}_{12}}{V_B}\end{array}\right)\otimes \left(\begin{array}{ccc}1& -{\overline{N}}_A& -\frac{2P_{12}{P}_{22}}{V_A}\\ 1& 1-{\overline{N}}_A& \frac{4P_{11}{P}_{22}}{V_A}\\ 1& 2-{\overline{N}}_A& -\frac{2P_{11}{P}_{12}}{V_A}\end{array}\right),$$ (4)

$$E_{AB}^S=E_B^S\otimes E_A^S=\left(\begin{array}{c}1\\ {\alpha }_A\\ {\delta }_A\end{array}\right)\otimes \left(\begin{array}{c}1\\ {\alpha }_B\\ {\delta }_B\end{array}\right)=\left(\begin{array}{c}\mu \\ {\alpha }_A\\ {\delta }_A\\ {\alpha }_B\\ \alpha \alpha \\ \delta \alpha \\ {\delta }_B\\ \alpha \delta \\ \delta \delta \end{array}\right).$$ (5)

The coding matrix, $S_{AB}^S$, can be used in a two-locus association test along with gene–gene interactions. For this model, there are nine parameters to be inferred, including one baseline term (μ), two additive terms (α_A and α_B), two dominant terms (δ_A and δ_B), and four interaction terms (αα, δα, αδ and δδ). This is a full model with both additive and dominant effects. We extended this statistical model to the reduced genetic models, including additive, dominant and recessive models (supplementary text).

Traditionally, the one-locus genotypic values are usually coded as (−1, 0, 1) or (0, 1, 2) for the additive effect. Dominant effect is sometimes added for full modeling coded as (0, 1, 0). Both of these two models are referred to as a natural or functional model in the NOIA framework, as it uses natural scale of allele counts for estimating the genetic effects and reflects the functionality of the alleles at the locus. Unlike the statistical model, the genetic effects in this functional model are using natural substitutions rather than based on the population effects which depend upon genotype frequencies. Similarly, using the (0, 1, 2) functional coding approach, the two-locus genetic effect design matrix can be obtained as the Kronecker product of the two design matrices,

$$S_{AB}^F=S_B^F\otimes S_A^F=\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 2& 0\end{array}\right)\otimes \left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 2& 0\end{array}\right)=\left(\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 1& 2& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 1& 0& 0& 1& 0& 0\\ 1& 1& 1& 1& 1& 1& 1& 1& 1\\ 1& 2& 0& 1& 2& 0& 1& 2& 0\\ 1& 0& 0& 2& 0& 0& 0& 0& 0\\ 1& 1& 1& 2& 2& 2& 0& 0& 0\\ 1& 2& 0& 2& 4& 0& 0& 0& 0\end{array}\right).$$ (6)

Therefore, the genotypic values can be expressed as

$$\left(\begin{array}{c}{G}_{1111}\\ G_{1211}\\ G_{2211}\\ G_{1112}\\ G_{1212}\\ G_{2212}\\ G_{1122}\\ G_{1222}\\ G_{2222}\end{array}\right)=s_{AB}^F\cdot \left(\begin{array}{c}R\\ a_A\\ d_A\\ a_B\\ aa\\ da\\ d_B\\ ad\\ dd\end{array}\right).$$ (7)

Herein, we use Greek letters for the genetic effects to distinguish with those from the statistical model. Reduced models, including additive, dominant and recessive models, were also extended for the usual functional model (Supplementary text). As in the one-locus functional model, the estimation of the parameters was not based on the genotype frequencies and therefore reflects the main and interaction effects in a different way when compared with the statistical model. This model is not orthogonal. The relationship between the NOIA statistical model and usual functional model can be derived straightforwardly through $S_{AB}^F{E}_{AB}^F=S_{AB}^S{E}_{AB}^S$ (Alvarez-Castro and Carlborg 2007).

Simulation methods

We performed simulation analyses for both quantitative and case–control traits by applying the NOIA statistical G×G interaction model (Eq. (4)) and the usual functional G×G interaction model (Eq. (6)).

To simulate samples of independent individuals with a quantitative trait controlled by two diallelic loci, we assumed that there was no linkage disequilibrium (LD) between the two markers. For locus A, a value of the minor allelic frequency (p) was given in the simulated population. Genotypes A₁₁, A₁₂ and A₂₂ were assigned to an individual with probabilities (1 − p)², 2p(1 − p) and p² respectively. Similarly, the minor allelic frequency (p) was given to locus B. Genotypes B₁₁, B₁₂ and B₂₂ were assigned to an individual with probabilities (1 − q)², 2q(1 − q) and q² respectively. From a pre-specified vector of parameters, ${\overrightarrow{E}}_F^{\mathrm{T}}=[R,a_A,d_A,a_A,d_A,aa,ad,da,dd]$, we assigned each individual a genotypic value according to his/her assigned two-locus genotypes. Then, by randomly generating a value from a normal distribution with pre-specified mean and variance (0 and ${\sigma }_e^2$), we generated an observed phenotype/trait by adding this residual to the previously assigned genotypic value. We used data from 2,000 individuals as a replicate and simulated 1,000 replicates for each genetic model.

In this part of our investigation of quantitative traits, three scenarios were simulated with different interaction terms (Table 1). The minor allele frequencies for both loci were set to 0.3, and the residual variance ${\sigma }_e^2$ was 144.0. The true values of the nine parameters in these three scenarios are shown in Table 1.

Table 1. Simulation parameter values of genetic effects for quantitative and case–control traits dataset.

	R	aA	dA	aB	dB	aa	ad	da	dd
Quantitative trait
Scenario 1	100.00	1.50	0.40	1.10	0.50	0.80	0.23	0.32	0.12
Scenario 2	100.00	1.50	0.40	1.10	0.50	−0.80	−0.23	−0.32	−0.12
Scenario 3	100.0	1.50	0.40	1.10	0.50	0	0	0	0
Case–control trait
Scenario 1	−2.0	0.50	0.30	0.40	0.37	0.15	0.08	0.10	0.04
Scenario 2	−2.0	0.50	0.30	0.40	0.37	−0.15	−0.08	−0.10	−0.04
Scenario 3	−2.0	0.50	0.30	0.40	0.37	0	0	0	0

R is the intercept term; a_A and d_A are the additive and dominant effects of locus A; a_B and d_B are the additive and dominant effects of locus B; aa, ad, da and dd are the interaction effects between locus A and locus B. Interaction coefficients are positive values for scenario 1, negative for scenario 2, and zero for scenario 3 which means no interaction. Main additive effect and dominant effect all exist in every scenario for both traits

To investigate whether the setting of allele frequency influencing the testing of the effects, we also simulated a quantitative trait with minor allele frequency 0.49. The pre-specified value for the genetic effect terms remained the same as in previous simulations for quantitative traits.

Ma et al. (2012) thoroughly derived the formulation of the statistical model in quantitative traits and demonstrated that a similar statistical model could also be defined for a qualitative trait by handling the genetic effects as the logit scale of the outcome. Similarly, we performed a case–control simulation analysis in our study. We used logistic model and Bayes theorem to determine the genotypes of each individual according to the pre-specified genetic effect terms, ${\overrightarrow{E}}_F^{\mathrm{T}}$. For each replicate, 1,000 cases and 1,000 controls were simulated, and a total of 1,000 replicates were simulated. The minor allele frequency was set to 0.30. Three scenarios were simulated with different interaction terms. The generated values of the parameters in the three different scenarios for qualitative traits are shown in Table 1.

Analysis of G × G interactions influencing melanoma risk

We applied the NOIA statistical model and the usual functional model to the CM data, samples from a genome-wide case–control study including 1,804 cases and 1,026 controls. Single-nucleotide polymorphisms (SNPs) were genotyped from Illumina Omni 1-Quad_v1-0_B array and 783,945 SNPs remained after the quality control and other filtering procedures were applied (Amos et al. 2011). The CM samples were collected from patients treated at The University of Texas MD Anderson Cancer Center between 1998 and 2008, and the controls were collected from the friends of the patients with matched sex and age during the same period. All the participants were non-Hispanic whites. The details of the genome-wide case–control study have been described previously (Amos et al. 2011). The initial goal of that study was to detect novel loci that predisposed whites to CM. The objective of the current study was to apply the newly developed methods to validate the already identified potential causal SNPs and gene–gene interactions that contribute to melanoma risk. We also attempted to compare the performance of the NOIA statistical model with that of the usual functional model on genetic effects detection. Logistic regression was used for the genetic effects estimation, and the P values were obtained using the Wald test statistic with the null hypothesis that the coefficient was zero. The Manhattan plots for the P values tested for the additive, dominant and interaction effects were graphed by Haploview software.

Results

simulation study

For quantitative traits and case–control traits, analyses of three scenarios were performed when there were positive, negative or zero values for the interaction coefficients respectively (Table 1).

First, we performed simulation studies on a quantitative trait under three scenarios. Our first simulation exhibited both main effects of two genes and their interactions with the true effect values

$${\overrightarrow{E}}_F^{\mathrm{T}}=[R,a_A,d_A,a_B,d_B,aa,ad,da,dd]=[100.00,1.50,0.40,1.10,0.50,0.80,0.50,0.32,0.12].$$

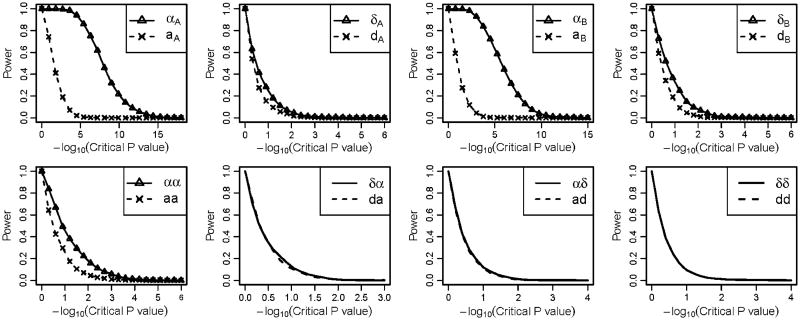
Figure 1 illustrates the power of the NOIA statistical model and usual functional model on detecting the four main genetic effects including the additive effects and the dominant effects of locus A and locus B, and four interaction effects between locus A and locus B For detecting the main genetic effects, the NOIA statistical model clearly had higher power than the usual functional model, especially for additive effects (Fig. 1, upper panel). The NOIA statistical model also exhibited slightly higher or equal power than the usual functional model for detecting the interaction effects except for the dominance-by-dominance term (Fig. 1, bottom panel). The density distribution of the parameters estimated from these replicates is shown in Figure S1. Clearly, the variance of all the main genetic effects (a_A, d_A, a_B and d_B) and most of the interaction effects (aa, ad and da) estimated from the NOIA statistical model was much smaller than those from the usual functional model (Fig. S1). Furthermore, the estimations of the genetic effects were both accurate for the two models, as the peaks were all located around the simulated true values (Fig. S1).

Fig. 1.

Power under different critical values of the P values obtained using the Wald test for the quantitative simulation dataset under scenario 1 when the interaction terms were positive. For each graph, Greek symbols and solid lines correspond to the NOIA method, and the broken line corresponds to the functional method. The upper panel is for the additive effects and dominant effects of locus A and locus B, respectively. The bottom panel is for the interaction effect between locus A and locus B. The simulating values of the genetic effects were ${\overrightarrow{E}}_{\mathrm{F}}^{\mathrm{T}}=[R,a_A,d_A,a_B,d_B,aa,ad,da,dd]=[100.00,1.50,0.40,1.10,0.50,0.80,0.50,0.32,0.12]$. Corresponding values of the statistical genetic effects were ${\overrightarrow{E}}_{\mathrm{S}}^{\mathrm{T}}=[102.39,2.35,0.59,1.97,0.74,1.04,0.28,0.37,0.12]$

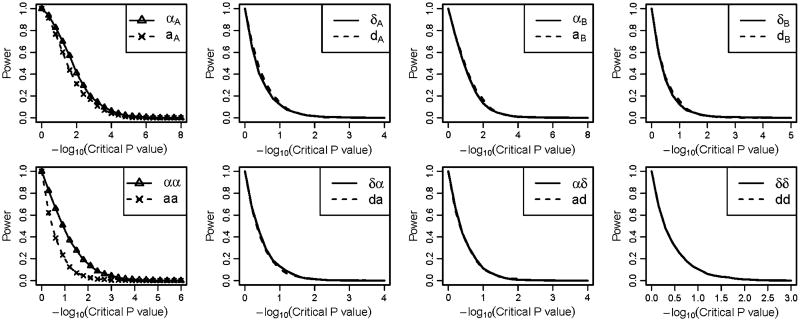
To explore whether the values of the interaction terms influencing the estimations of the parameters, we simulated a second scenario in which the interaction effect coefficients were set to be negative values and ${\overrightarrow{E}}_F^{\mathrm{T}}=[100.00,1.50,0.40,1.10,0.50,-0.80,-0.23,-0.32,-0.12]$. A similar pattern with the first scenario was observed for the power of detecting the genetic effects; however, in this scenario the preference of the statistical NOIA model over the usual functional model on detecting the main effect of locus A and locus B was not obvious (Fig. 2). For some of the main genetic effect parameters, the usual functional model showed slightly higher power than the NOIA statistical model.

Fig. 2.

Power under different critical values of the P values obtained using the Wald test for the quantitative simulation dataset under scenario 2 when the interaction coefficients were negative. For each graph, Greek symbols and solid lines correspond to the NOIA method, and the broken line corresponds to the functional method. The upper panel is for the additive effects and dominant effects of locus A and locus B, respectively. The bottom panel is for the interaction effect between locus A and locus B. The simulating values of the genetic effects were ${\overrightarrow{E}}_{\mathrm{F}}^{\mathrm{T}}=[R,a_A,d_A,a_B,d_B,aa,ad,da,dd]=[100.00,1.50,0.40,1.10,0.50,-0.80,-0.23,-0.32,-0.12]$. Corresponding values of the statistical genetic effects were ${\overrightarrow{E}}_{\mathrm{S}}^{\mathrm{T}}=[101.49,0.97,0.21,0.63,0.26,-1.04,-0.28,-0.37,-0.12]$

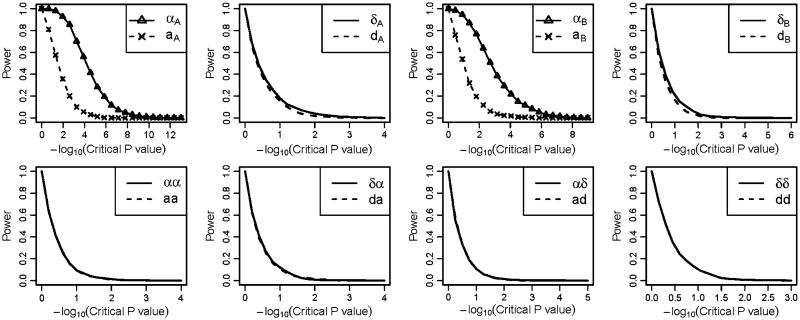
We also analyzed a third scenario, in which there were no interaction effect and only the main genetic effects from the two loci influencing the trait (Fig. 3). For this scenario, the NOIA statistical model still had higher power for detecting the main genetic effects (Fig. 3, upper panel). The NOIA statistical and usual functional model yielded similar false-positive rates for detecting the interaction effects, both of which were close to the nominal value (Fig. 3, bottom panel). The density distributions of the parameters estimated from these replicates in scenario 2 and scenario 3 of quantitative traits simulations were shown in Figure S2–S3.

Fig. 3.

Power under different critical values of the P values obtained using the Wald test for the quantitative simulation dataset under scenario 3 when no interaction effects present. For each graph, Greek symbols and solid lines correspond to the NOIA method, and the broken line corresponds to the functional method. The upper panel is for the additive effects and dominant effects of locus A and locus B, respectively. The bottom panel is for the interaction effect between locus A and locus B. The simulating values of the genetic effects were ${\overrightarrow{E}}_{\mathrm{F}}^{\mathrm{T}}[R,a_A,d_A,a_B,d_B,aa,ad,da,dd]=[100.00,1.50,0.40,1.10,0.50,0.0,0.0,0.0,0.0]$. Corresponding values of the statistical genetic effects were ${\overrightarrow{E}}_{\mathrm{S}}^{\mathrm{T}}=[101.94,1.66,0.40,1.30,0.50,0.0,0.0,0.0,0.0]$

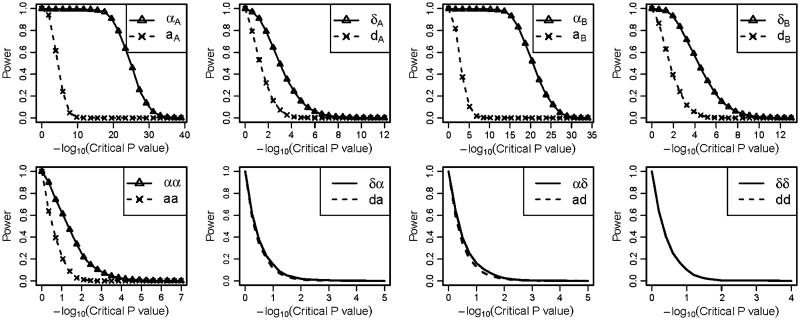
Figures 4 and S4–S5 show the results obtained from the case–control trait simulations. In Fig. 4, the simulating values of the genetic effects were ${\overrightarrow{E}}_F^{\mathrm{T}}=[-2.00,0.50,0.30,0.40,0.37,0.15,0.08,0.10,0.04]$, in which main genetic effects and interaction effects influencing the outcome trait and the interaction coefficients were positive values. Similar to the simulation studies of the quantitative traits, the NOIA statistical model had higher power than the usual functional model for detecting most of the genetic effect terms. The parameter of the dominant-by-dominant interaction effect was exactly the same between these two models, which is expected from the equation of the models $S_{AB}^F{E}_{AB}^F=S_{AB}^S{E}_{AB}^S$. Interestingly, when we set the interaction terms to be negative values, where ${\overrightarrow{E}}_F^{\mathrm{T}}=[-2.00,0.50,0.30,0.40,0.37,-0.15,-0.08,-0.10,-0.04]$, the power of both models for detecting additive effects of locus A or locus B was similar to that of these two models when the interaction terms were positive (Fig. S4).

Fig. 4.

Power under different critical values of the P values obtained using the Wald test for the case–control simulation data-set under scenario 1 when positive interaction effects present. For each graph, Greek symbols and solid lines correspond to the NOIA method, and the broken line corresponds to the functional method. The upper panel is for the additive effects and dominant effects of locus A and locus B, respectively. The bottom panel is for the interaction effect between locus A and locus B. The simulating values of the genetic effects were ${\overrightarrow{E}}_{\mathrm{F}}^{\mathrm{T}}[R,a_A,d_A,a_B,d_B,aa,ad,da,dd]=[-2.00,0.50,0.30,0.40,0.37,0.15,0.08,0.10,0.04]$. Corresponding values of the statistical genetic effects were ${\overrightarrow{E}}_{\mathrm{S}}^{\mathrm{T}}=[-1.07,0.78,0.36,0.70,0.45,0.23,0.10,0.12,0.04]$

For the third scenario, in which no interaction effects were present for the case–control trait, the power of the NOIA statistical model was still higher than that of the usual functional model to detect the main effects, while the false discovery rates for detecting the interaction effects remained the same (Fig. S5). For all the scenarios we simulated, the density distributions of the eight parameters are shown in supplementary Figures (Figs. S6–8). The estimation of the genetic effects was accurate, and the variance of the effects from the NOIA statistical modeling was less than that from the usual functional model for most parameters.

We also studied a setting with MAF 0.49 (Figs. S9–10). The NOIA statistical model still had higher power than the usual functional model for detecting the main genetic effects. To evaluate the false positive rates of the two models, we also simulated a null scenario where no any effect existed. The false-positive rates of the NOIA statistical model at the 0.05 significance level for detecting the eight genetic effects are 0.051, 0.044, 0.054, 0.048, 0.061, 0.044, 0.055 and 0.058. The false-positive rates of the usual functional model for detecting the eight genetic effects are 0.042, 0.04, 0.04, 0.037, 0.051, 0.058, 0.052 and 0.058.

Application to melanoma susceptibility

To evaluate the performance of the NOIA statistical model and usual functional model, we carried out GWAS of 2,831 white participants, including 1,805 cases and 1,026 controls for 799,671 SNP genotypes. To identify novel and verify the previously identified causal SNPs, we performed initial analyses using the one-locus NOIA statistical model without dominance component included. The Q–Q plot for the sample is shown in Figure S11. No obvious inflation of the test (λ= 1.011) was observed for the test statistic. Next, we applied the one-locus NOIA model with dominance component included to the melanoma dataset. SNPs with rare homozygotes (genotype cut-off value was 0.005, 123,902 SNPs removed) were filtered and the Q–Q plot is shown in Figure s12 (λ = 1.014). λ = 0.93 was obtained if the SNPs without all three genotypes were not filtered, reflecting the conservative nature of genotype-based tests (compared to allele based tests) if any of the genotypes is not present in the data. The one-locus association results showed that nine SNPs were significant reaching the genome-wide association level (5.0 × 10⁻⁸) and 140 SNPs were significant at the 1.0 × 10⁻⁴ level (Table 2, Table S1). Among the most significant SNPs that contribute to melanoma risk, two regions were found to be genome-wide significant (Table 2). They are located on 15q13.1 (centered at the HERC2/OCA2 region) and 16q24.3 (around MC1R gene). These two most significant SNPs located in these two regions are rs1129038 (P = 3.73 × 10⁻⁸, odds ratio [OR] 0.70, 95 % confidence interval [CI] 0.61–0.79) and rs4785751 (P = 1.13 × 10⁻¹⁰, Or 1.43, 95 % CI 1.29–1.60), respectively. The risk variants of these two SNPs were A and G, respectively. The SNPs located around MTAP were shown to be the third highly significant regions which are located at 9p21.3. The most significant SNP, SNP9-21789598 (P = 4.15 × 10⁻⁷), is located at the 5′-UTR of the MTAP gene, close to the CDKN2A gene.

Table 2. Top SNPs result from genome-wide association analysis of melanoma by NOIA statistical one-locus model using logistic regression (P < 1.0 × 10⁻⁶).

CHR	SNP	A1	A2	A2 freq	Position	OR (95 %CI)	P value	Gene symbol
16	rs4785751	A	G	0.53	88556918	1.43 (1.29–1.60)	1.13 × 10−10	DEF8
16	rs4408545	A	G	0.54	88571529	1.43 (1.28–1.59)	3.81 × 10−10	AFG3l1
16	rs11076650	A	G	0.46	88595442	1.40 (1.26–1.56)	1.65 × 10−9	DBNDD1
16	rs8051733	A	G	0.36	88551707	1.42 (1.27–1.59)	2.66 × 10−9	DEF8
16	rs7195043	A	G	0.50	88548362	0.72 (0.64.0.80)	5.73 × 10−9	DEF8
16	rs11648898	A	G	0.18	88573487	1.57 (1.35–1.84)	1.46 × 10−8	AFG3L1
15	rs1129038	A	G	0.22	26030454	0.70 (0.61–0.79)	3.73 × 10−8	HERC2
16	rs4785752	A	G	0.53	88562642	0.73 (0.66–0.82)	4.14 × 10−8	DEF8
16	rs4785759	A	C	0.53	88578381	0.73 (0.66–0.82)	4.26 × 10−8	AFG3L1
15	rs12913832	A	G	0.78	26039213	1.43 (1.25–1.62)	6.15 × 10−8	HERC2
16	rs10852628	A	G	0.31	88607428	1.40 (1.24–1.58)	6.94 × 10−8	DBNDD1
9	rs6475552	A	G	0.50	21691674	1.32 (1.19–1.48)	3.71 × 10−7	LOC402359
9	SNP9-21789598	A	G	0.49	21789598	0.75 (0.68–0.84)	4.15 × 10−7	MTAP
9	rs7848524	A	G	0.50	21691432	0.76 (0.68–0.84)	4.28 × 10−7	LOC402359
16	rs4238833	A	C	0.40	88578190	1.34 (1.20–1.50)	4.56 × 10−7	AFG3l1
9	rs2383202	A	G	0.49	21700215	1.32 (1.19–1.47)	5.24 × 10−7	LOC402359
9	rs12380505	A	G	0.50	21685893	0.76 (0.68–0.85)	6.02 × 10−7	LOC402359
9	rs1335500	A	G	0.49	21701675	1.32 (1.18–1.47)	6.24 × 10−7	LOC402359
9	rs1452658	A	G	0.50	21690795	1.32 (1.18–1.47)	7.22 × 10−7	LOC402359

The odds ratio (Or), confidence interval (CI) and P value are shown for the additive effect testing

To compare the performance of the NOIA statistical model with that of the usual functional model on one-locus association study, we compared the top SNPs identified by these two models in a Manhattan plot (Fig. 5). The NOIA statistical model showed a highly significant main additive effect signal in the HERC2 regions (Fig. 5a) at 15q13.1 whereas the usual functional model did not (Fig. 5b). The identification of the other two regions at 9p21.3 and 16q24.3 was similar for the two models. No obvious signal for the dominance effects was identified by either model (data not shown).

Fig. 5.

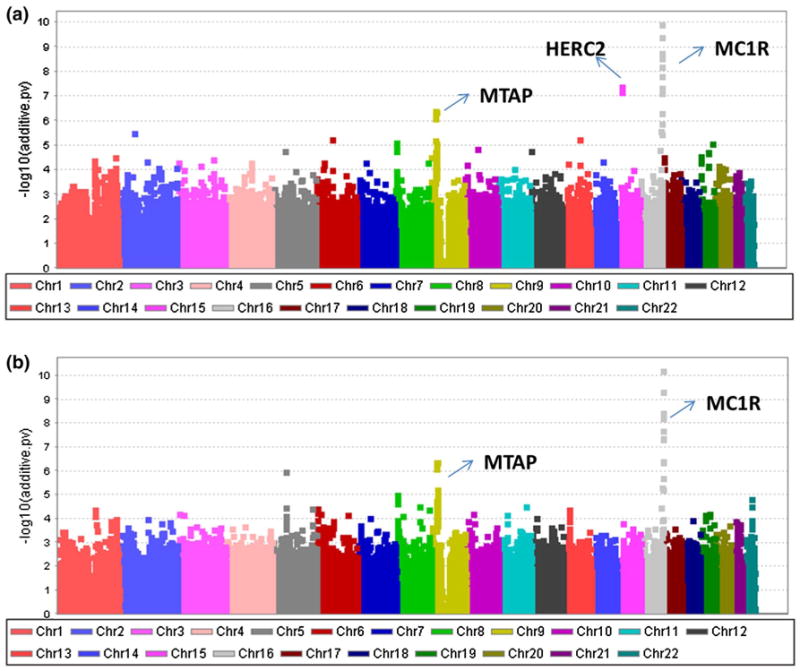
Manhattan plot for the genome-wide association studies of the CM susceptibility by one-locus scan. Detection of the additive effect through a the NOIA statistical model and b the usual functional model

We further applied the NOIA statistical model (Eq. 4) and the usual functional model (Eq. 6) on the two-locus association study in which gene–gene interactions testing were incorporated. Attempting to identify potential SNPs that interacted with the two significant genes (HERC2 and MC1R) while contributing to the association with melanoma risk, we selected rs1129038 and rs4785751, the two most significant SNPs, as the reference SNPs for the two-locus scan, respectively. We then performed a genome-wide, two-locus scan by treating these two SNPs as reference SNPs separately and compared the performance of the NOIA statistical model with that of the usual functional model for detecting the main genetic and interaction effects.

First, for SNP rs1129038 in HERC2 region, the NOIA statistical model still showed a strongly significant signal with P value in the 1 × 10⁻¹⁰ significance level on the two significant regions adjacent to the MTAP and around MC1R genes for the additive effects, whereas the functional model had no obvious signal (Fig. 6a, b). Compared to the one-locus scan (Fig. 5a), the overall power for detecting the additive effect did not decrease in the NOIA two-locus model when additional parameters were included in the model (Figs. 5a, 6a). This is not the case for the functional model (Figs. 5b, 6b). Moreover, no significant signal was observed for the dominant effects by either model (data not shown). For the four interaction terms, except the dominant-by-additive (da) interaction term, no obvious signal was identified by either model. A series of significant SNPs around gene IL31RA (interleukin-31 receptor A) and DDX4 on chromosome 5 were identified by the NOIA statistical model for interacting with rs1129038 at the da interaction term (Fig. 6c), where the da term means the interaction between the additive component of the rs1129038 and the dominant component of the candidate interacting SNP. These signals were not identified by the usual functional model (Fig. 6d). We then checked the LD status between the significant SNPs around the IL31RA gene and the significant SNPs around the DDX4 gene, showing that the two genes are in strong LD.

Fig. 6.

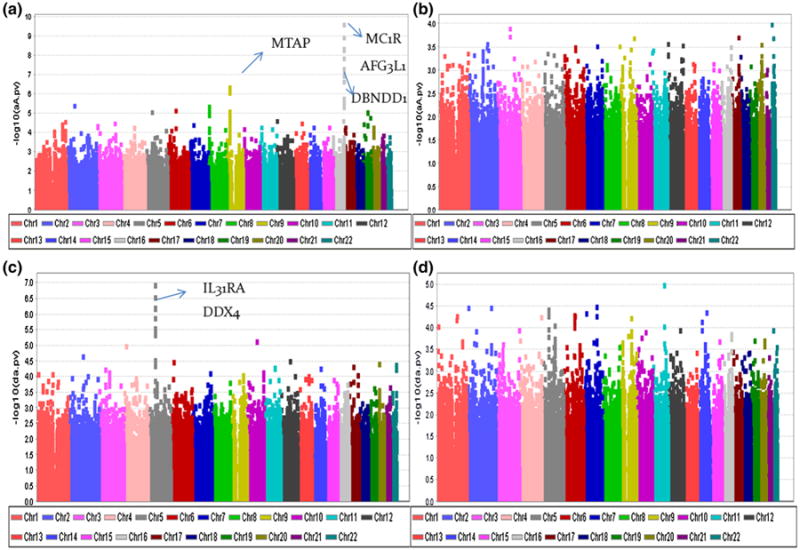
Manhattan plot for the genome–wide association studies of the CM susceptibility by two-locus scan for rs1129038. Detection of the additive effect (α_A and a_A) through a the NOIA statistical model and b the usual functional model; detection of the dominant–additive interaction effect (δα and da) through c the NOIA statistical model and d the usual functional model

Table 3 presents the top SNPs interacted with rs1129038 at the da interaction term analyzed by the NOIA statistical two-locus interaction model. Four SNPs near gene IL31RA and three SNPs near gene DDX4 were showing significant interaction with rs1129038 reaching the 1.0 × 10⁻⁶ significance level. However, other than the da interaction effect and the main additive effect from rs1129038, no main effects from the candidate interacted SNPs were identified.

Table 3. P values for the main effects and interaction effects when rs1129038 are used for reference SNP in the two-locus association analysis by NOIA statistical model (P < 10⁻⁶).

CHR	SNP	Coordinate	Gene symbol	P value
				Add_A	Dom_A	Add_B	Dom_B	Add-Add	Dom-Add	Add-Dom	Dom-Dom
5	rs6871296	55175024	LOC402216	0.07	0.02	5.78E–08	0.46	0.45	1.06 × 10−7	0.90	0.91
5	rs3857290	55182187	Il31RA	0.08	0.03	6.26e–08	0.45	0.45	2.57 × 10−7	0.87	0.83
5	rs6876491	55181692	Il31RA	0.04	0.02	4.19e–08	0.33	0.47	5.73 × 10−7	0.86	0.92
5	rs10042075	55178483	Il31RA	0.03	0.01	3.01e–08	0.35	0.51	6.03 × 10−7	0.86	0.73
5	rs327240	55216666	Il31RA	0.02	0.25	2.61e–08	0.34	0.61	1.20 × 10−6	0.75	0.27
5	rs3843458	55090435	DDX4	0.03	0.12	6.69e–08	0.26	0.46	2.60 × 10−6	0.70	0.60
5	rs957459	55118231	DDX4	0.07	0.05	6.65e–08	0.28	0.46	2.92 × 10−6	1.00	0.36
5	rs10035707	55098280	DDX4	0.06	0.05	6.43e–08	0.28	0.46	4.07 × 10−6	0.99	0.33
10	rs12775320	78584174	KCNMA1	0.61	0.42	1.95e–07	0.00	0.50	6.58 × 10−6	0.78	0.51
4	rs6825100	17305532	KIAA1276	0.27	0.10	7.30e–08	0.15	0.49	9.49 × 10−6	0.04	0.28

Locus B is the reference SNP, rs1129038; locus A is the candidate interacted SNP that scanned from the whole genome

Add additive effect, Dom dominant effect, Add-Add additive–additive interaction effect, Dom-Add dominant–additive interaction effect, Add-Dom additive–dominant interaction effect, Dom-Dom dominant–dominant interaction effect

Similarly, we compared the performance of the gene–gene interaction models for detecting genes that interacted with rs4785751 around MC1R gene. Comparing the performance of the NOIA statistical model and that of the usual functional model on detection of the main additive effects, the former still remained the signal for those identified strongly associated regions while the latter did not (Fig. 7). No interaction effects were identified by either model for rs4785751.

Fig. 7.

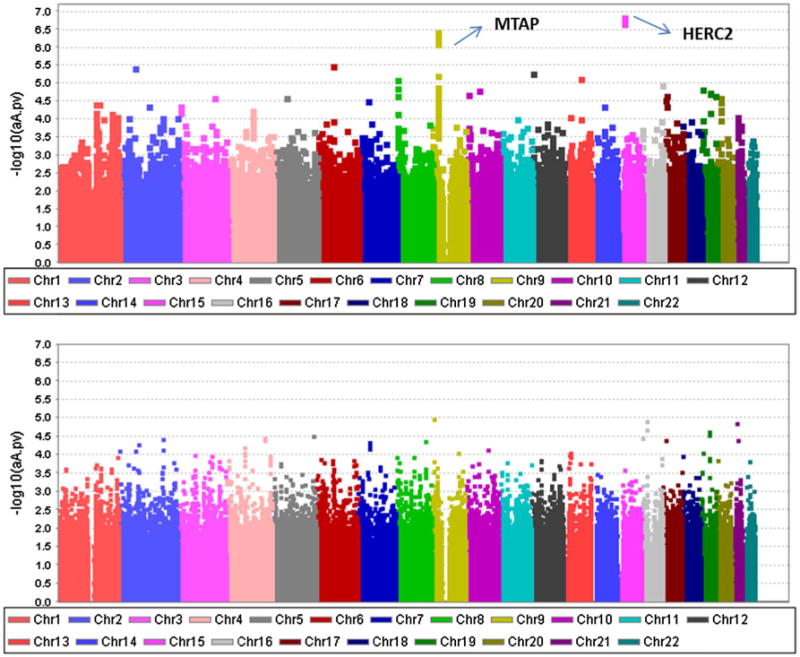
Manhattan plot for the genome-wide association studies of the CM susceptibility by two-locus scan for rs4785751. Detection of the additive effect (α_A and a_A) through a the NOIA statistical model and b the usual functional model

Finally, we also applied the reduced NOIA statistical model, the additive models (details shown in supplementary text), for detecting the gene–gene interactions that contribute to melanoma risk. For the second reference SNP, rs4785751, significant SNPs were identified for the additive-by-additive interaction effect (P = 7.07 × 10⁻⁶) (Table 4). These SNPs are located in chromosome 4 close to gene PGRMC2.

Table 4. P values and estimates for the main effects and interaction effects when rs4785751 was used for reference SNP in the two-locus association analysis by NOIA additive statistical model (P < 10⁻⁵).

CHR	SNP	Coordinate	Gene symbol	Estimates			P value
				Add_A	Add_B	Add-Add	Add_A	Add_B	Add-Add
4	rs 10009093	143849384	FLJ44477	0.08	0.37	−0.55	0.32	5.29 × 10−11	7.07 × 10−6
4	rsl0019366	129459033	PGRMC2	0.02	0.36	−0.44	0.76	1.09 × 10−10	9.23 × 10−6
4	rs4975181	129466845	PGRMC2	0.10	0.37	−0.35	0.09	8.91 × 10−11	9.71 × 10−6
4	rsl 1723210	129500895	PGRMC2	0.06	0.36	−0.45	0.44	1.24 × 10−10	9.84 × 10−6

Locus B is the reference SNP, rs4785751; locus A is the candidate interacted SNP that scanned from the whole genome

Add additive effect, Add-Add additive-additive interaction effect

Discussion

In most scenarios we simulated, the NOIA statistical model presented higher power for detecting additive effects and some interaction effects compared with the usual functional model. In other words, the functional model more likely to estimate the non-zero parameters as not different from zero for the main genetic effect and some interaction effect parameters than the statistical model. The NOIA model also yielded more precise estimators. Moreover, the investigation of type I error showed no significant difference of these two models. Analyses of the melanoma dataset also showed higher power of the NOIA statistical model by one-locus and two-locus genome-wide scan. The interaction analyses of the melanoma dataset showed that the NOIA statistical model preserved power for detecting the main genetic effects. The functional model lost power when multiple loci were jointly modeled. The NOIA statistical model identified potential epistasis between the rs1129038 (located around HERC2 gene) and IL31RA gene at chromosome 5 while the functional model did not. Another significant region interacting with rs4785751 around MC1R gene was also identified, PGRMC2 located at 4q26, by the NOIA statistical additive G × G model.

For the analyses of melanoma data, the NOIA one-locus statistical model provided confirmatory evidence of the association of three previously identified causal regions with melanoma risk, HERC2 at 15q13.1, MC1R at 16q24.3 and CDKN2A at 9p21.3. Compared to the NOIA statistical model, the usual functional one-locus model including a dominance component did not detect the most significant region, the HERC2 gene, which has been well characterized in the previous studies (Amos et al. 2011). When we compare our analyzed results from the full usual functional model to those from the additive model (Fig. 5), we found that the HERC2 signal was detected very clearly by the usual additive model but not by the usual full model. Thus, we conclude the NOIA model has higher power than the usual functional model in one-locus genome-wide scans when a full genetic model is used. The increase in power from Wald-type tests also reflects the change in the standard errors of the tests if we look at the test statistics of the usual functional model and the NOIA model with dominance component testing incorporated (Xiao et al. 2013).

The interaction analyses showed that the power of the NOIA statistical model was higher than that of the usual functional model for detecting main genetic effects when interactions are included. When main and interaction effects between the two loci were modeled, the usual functional model presented lower power while the statistical model maintained its power for detecting the main genetic effects (Fig. 6a). This result reflects one of the important properties of the NOIA model, orthogonality. Using orthogonal models for quantitative traits analysis or binary diseases yields consistent estimation for genetic effect in reduced models. Here, we clearly see that the functional model had no consistent estimation when multiple loci were modeled together.

Moreover, the NOIA statistical model identified potential interaction between the rs1129038 (located around HERC2) and a region at chromosome 5, whereas the functional model did not. This region is located in the 5′-UTR of IL31RA gene at 5q11.2 and the intron of the gene DDX4 at 5p15.2-p13.1. The expression of IL31RA is induced in activated monocytes and constitutively expressed in epithelial cells and may function in skin immunity (Ghilardi et al. 2002). It was also recently found that IL31RA was associated with neuroblastoma risk by GWAS (Capasso et al. 2013). The interesting aspect of this interaction is that no main genetic effect was found for these SNPs. The interaction is based on the dominant-by-additive interaction term. Although it is hard to interpret the dominant-by-additive interaction term here, it is possible that only the reference locus (rs1129038) has a main effect while a significant interaction effect exists for gene–gene interaction. Another significant region, PGRMC2 located at 4q26, interacting with rs4785751, was also identified, by the NOIA additive model. This is the first report of the implication of potential genes and regions that were shown to interact with SNPs associated with melanoma risk. These interactions need to be confirmed by future validation studies which suggest that the NOIA statistical model is preferable on epistasis detection to the usual functional model. Although the sample size in this study was sizeable, there are a very large number of SNPs that were tested in this study, so that the very significant results we obtained could still reflect a false-positive result.

We also found another important characteristic of the NOIA one-locus framework. Both the full NOIA and functional models with dominance components are ill-conditioned if the SNP has only two or less genotypes in the population. This arises because of the value of the determinant of X^TX (X is the design matrix) was equal to zero when the dominance component is included in the testing. For the additive models without the dominance component testing, the determinant value of X^TX is not equal to zero. When the design matrix is noninvertible, one needs to use generalized inverses as alternative in setting up the tests rather than the inverse procedure that in R programming software. Therefore, in our Q–Q plots, the λ values were less than 1.0 (0.86–0.92) when performing NOIA or usual functional one-locus models with dominance component testing on melanoma dataset. After we removed the SNPs with minor genotype frequency <0.005, the λ values changed to 1.014 and 1.023 for the NOIA and usual model, respectively (Fig. S12). According to our analyses, we suggest to apply the NOIA full model in two stratifications for one-locus scan of real data. For SNPs with all three types of genotypes, NOIA full model is preferred to identify potential dominant effects while maintaining the power to detect additive effects. Additive model would be better for those SNPs to get right distributions if they do not have all three genotypes.

In this study, we compared the NOIA statistical model and usual functional model for analyzing epistasis, or gene–gene interactions, for quantitative traits and dichotomous diseases. These two models can be transformed to each other but they have different meanings for their parameters and the test statistics varies reflecting non-orthogonality for many functional models. The NOIA statistical model utilizes the population properties estimated from the sample, whereas the usual functional model focuses on the biological properties. It should be noted that the genotype frequencies used in the NOIA model should only be estimated from the genotype data of the sample, according to the NOIA theory derived in Alvarez-Castro and Carlborg (2007), to have orthogonal estimates of the parameters. Depending on how the sample is selected from the population, the estimated genotype frequencies and thus the parameters generated from the NOIA statistical model may be significantly different from their population counterparts. Nevertheless, as far as power of detecting the main and interaction effects are concerned, using the estimated frequencies should provide an accurate test statistic. One might be tempted to use better estimated genotype frequencies from other source that are closer to the true population parameters than what can be estimated from the data set of interest. However, using those “better” estimates of genotype frequencies would reduce the orthogonality of the NOIA statistical model. The usually used functional approach is based on the observed genotype instead of the population frequencies that were used in the NOIA statistical model. The advantage is that the results are easier to interpret. However, the disadvantage of the functional model is that the estimated regression coefficients are not orthogonal, when dominance components are modeled (Xiao et al. 2013). Parameters from application of the NOIA model describe the variance components, rather than allele substitution effects, so may be seen as having a less clear interpretation. This is the first time the performance of the NOIA statistical model in detecting gene–gene interactions and main effects are evaluated since they were developed in 2007 (Alvarez-Castro and Carlborg 2007).

Whether there are factors that influencing interaction effects without playing marginal effects has been a critical issue in genetic association studies (Cordell 2009). In single-locus analysis, each locus is considered separately. Therefore, factors that influencing interaction effects without displaying marginal effects will be missed, as they do not lead to marginal correlation between the genotype and outcome phenotype. Our results demonstrated that the NOIA interaction models is capable of detecting interaction effects without influencing the estimation of the main effects, which could explain more missing heritability of human complex diseases. The usual traditional models do not have this advantage since it loses power when more parameters are added to the modeling.

Beyond the two-locus interactions, we may also expect interaction among multiple loci, for instance, three-locus interactions. One may simply extend the full and additive NOIA statistical models to the case of three-locus interactions by straightforwardly applying Kronecker products. We applied the NOIA three-locus interaction models to the melanoma data on the significant SNPs contributing to the melanoma risk but did not find signal for three-locus interactions. We also applied the three-locus interaction models on the significant SNPs contributing to lung cancer risk that was investigated in Ma et al. (2012), but again no three-way interactions were identified. This may be because even less power is available to detect high-order models for the given sample size. Large datasets will be required to estimate these parameters accurately. Interpreting the interactions is also complicated even for two-locus interactions. Validation from replication analysis and experiments to explain how they interact with each other is a challenging task. The underlying mechanism of the interactions is also difficult to explain.

The difference between the NOIA statistical model and the usual functional model lies largely in their focus. The former is characterized by orthogonal parameters that denote average effects of allele substitutions over population, whereas the latter focuses on the natural allele substitutions for parameter estimation. Estimating contributions to overall variance as performed in an NOIA analysis has the advantage of allowing orthogonal estimates of components that directly contribute to heritability. Use of NOIA derived approaches has a more direct application in characterizing genetic architecture for population-based studies than is provided by functional models. They are different viewpoints of a similar analysis. Nonetheless, when investigating the epistasis or gene–environment interactions, choosing the most appropriate framework is still important. For hypothesis testing using Wald or scores tests, as we showed in this study, power can be higher for the NOIA models. We thus recommend that the NOIA statistical model be used for one-and two-locus association tests if dominant effects and/or interaction effects are of interest because of its higher power and its desired statistical properties.

In summary, we have for the first time demonstrated using simulated and real data that the NOIA statistical model can be applied to association studies of gene–gene interaction for both quantitative and binary traits. We evaluated the performance of NOIA model for logistic regression applied to binary data. We showed by simulated and real data that the functional models have lost power for detecting main effects due to confounding between the dominance and main effects in most cases, which is consistent with the previous declaration from the theoretical derivation of the test statistics in Xiao et al. (2013). The main advantages of the NOIA statistical model, compared to the usual functional model, include (a) it can show greater power in detecting interaction effects between genes, and (b) it is more powerful when detecting the main effects in the presence of interaction effects. Application of the NOIA statistical model to the melanoma data resulted in discovery of some potential interaction effects between Il31RA and HERC2 genes, 4q26 and MC1R genes.

Finally, it should be noted that the hypothesis we test when comparing the functional and the statistical models should be understood in terms of the overall effects of a gene and the interaction effect between two genes, instead of the concrete values of the parameters. The additive, dominant and interaction parameters have different definitions in these two models and thus cannot be directly compared. In this sense, the NOIA approach we advocate is more suitable to detect for genetic factors in the presence of G × G interaction than to exactly characterize an interaction effect between two genes.