Estimation and Reduction of Target Registration Error

Abstract

Fiducial-based registration is often utilized in image guided surgery because of its simplicity and speed. The assessment of target registration error when using this technique, however, is difficult. Although the distribution of the target registration error can be estimated given the fiducial configuration and an estimation of the fiducial localization error, the target registration error for a specific registration is uncorrelated with the fiducial registration error. Fiducial registration error is thus an unreliable predictor of the target registration error in a particular case. In this work, we present a new method to estimate the quality of a fiducial-based registration and show that our measure is correlated to the target registration error. We also show that our method can be used to reduce registration errors caused by fiducial localization error. This has direct implication on the attainable accuracy of fiducial-based registration methods.

1 Introduction

Fiducial-based registration is an important technique in Image Guided Surgery (IGS). It is often utilized to align image information to the surgical space in an operating room. In this context, fiducial markers are attached to the patient and an image is acquired. The physical location of the fiducial markers in the operating room is obtained as well as the location of the markers in the image and the two point sets are registered to each other. Error in identifying the correct location of the fiducials, called Fiducial Localization Error (FLE) [1] can occur which causes error in the registration between the image and surgical space. An analytical solution for the distribution of errors in fiducial registration has been proposed [1, 2, 3], but this solution does not permit the assessment of the target registration error in a particular case. Fiducial Registration Error (FRE) is often used as a surrogate for the Target Registration Error (TRE) that is the quantity of clinical interest [4]. Unfortunately, it has been shown [5] that TRE and FRE are uncorrelated. FRE is thus an unreliable predictor of registration accuracy.

In this work, we propose a method to estimate the quality of a registration that correlates with TRE and therefore produces a value that correlates with the true registration accuracy at a target location. The next section describes our technique, which we call AQUIRC for Assessing Quality Using Image Registration Circuits. In the results section, simulation results we have obtained to demonstrate the correlation between our measure and TRE are presented and future work and applications are discussed.

2 General Algorithm

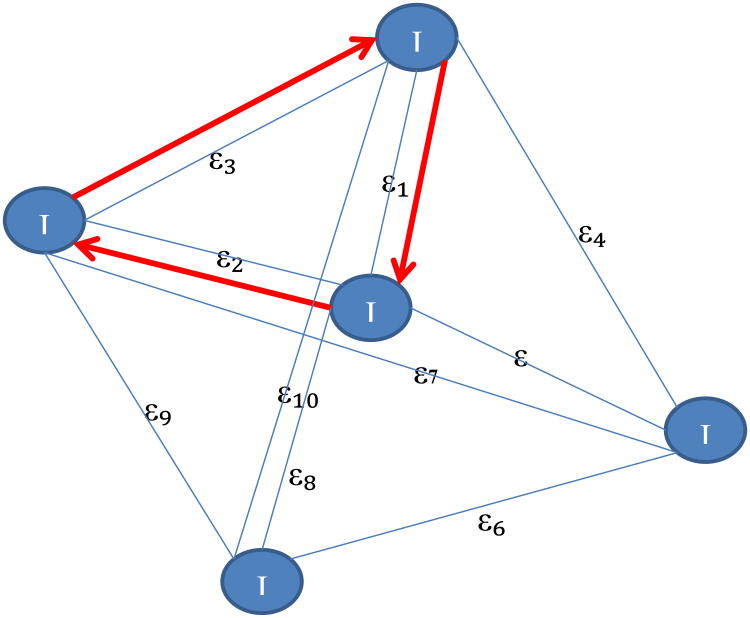
This work was first proposed in [6] for global atlas selection and was utilized to estimate the quality of intensity-based rigid image registration in [7]. AQUIRC builds on the idea of registration circuits which was proposed as a consistency measure by Woods et al. [8] and Holden et al. [9]. Here, a registration circuit involves three fiducial configurations A, B, and C and three transformations T_AB, T_BC, and T_CA. As discussed by Fitzpatrick [10], using only one registration circuit can lead to an underestimation of registration error because the error made along one edge in the circuit may correct error introduced from a separate edge in the circuit. It was observed that using the registration circuit T_CA(T_BC(T_AB(X))) does not correlate with error, but that if you consider a registration circuit computed out of order, e.g. T_AB(T_BC(T_CA(X))), this then is able to correlate with error. For example, we calculate the registration circuit in Figure 1 shown in red arrows as the transformation from I₁ to I₃, I₂ to I₁, and finally I₃ to I₂.

Figure 1. Example complete graph with one circuit shown in red arrows.

In this work, we expand upon the idea of a registration circuit to multiple circuits. We start with a set of fiducial configurations and compute pair-wise registrations between all elements in the set, creating a complete graph as shown in Figure 1. The complete graph of registrations is similar to what is done by Christensen [11]. In [11], however, they used the complete graph of registrations of images as an overall measure of the quality of a registration algorithm, rather than as a method to determine the quality of individual registrations as we have done here. If our initial set contains N fiducial configurations, where each fiducial configuration is a set of fiducial markers, the graph contains $\left(\begin{array}{c}\mathrm{N}\\ 2\end{array}\right)$ edges. With each edge in this graph, we associate an initially unknown measure of registration quality called ε that we wish to solve for. There are $\left(\begin{array}{c}\mathrm{N}\\ 3\end{array}\right)$ unique registration circuits that can be formed from a complete graph (here we have used registration circuits of size 3; the circuit size can be increased to form more registration circuits but this was not yet explored).

Next, we define a measure of registration error that can be computed across a circuit. To compute this error, we select a target point or set of points in A, say X. We then compute the transformed point(s) X′ as X′ = T_AB(T_BC(T_CA(X))). The quality of registrations across circuit A, B, C, is then defined as E_C = dissimilarity(X, X′). The dissimilarity measure can be defined for specific applications. The value, E_C, is affected by the error of three registrations, i.e., the registration error between A and B, the registration error between B and C, and the registration error between C and A. With only one circuit the contribution of each component cannot be computed. It can, however, be estimated with more than one circuit. To achieve this we make the assumption that each registration affects the quality measure multiplicatively, i.e., ε_ABC= ε_A*ε_B*ε_C or, log(ε_ABC) = log(ε_A)+log(ε_B)+log(ε_C). An additive model is also applicable and was tested, yet the multiplicative model performed better, and for brevity, we do not include the additive results in the paper. Computing this expression for all possible circuits and rearranging them in matrix form, we obtain

$$\left[\begin{array}{c}1110\dots 0\\ 1011\dots 0\\ 1101\dots 0\\ 0111\dots 0\\ .\\ .\\ .\end{array}\right]\left[\begin{array}{c}log({\mathrm{\varepsilon }}_1)\\ log({\mathrm{\varepsilon }}_2)\\ log({\mathrm{\varepsilon }}_3)\\ .\\ .\\ .\\ log({\mathrm{\varepsilon }}_{\left(\begin{array}{c}\mathrm{N}\\ 2\end{array}\right)})\end{array}\right]=\left[\begin{array}{c}log({\mathrm{E}}_{{\mathrm{c}}_1})\\ log({\mathrm{E}}_{{\mathrm{c}}_2})\\ log({\mathrm{E}}_{{\mathrm{c}}_3})\\ .\\ .\\ .\\ log({\mathrm{E}}_{{\mathrm{c}}_{\left(\begin{array}{c}\mathrm{N}\\ 3\end{array}\right)}})\end{array}\right]$$ (1)

in which E_Ci is defined as the (X, X′) value around circuit i. This expression can be rewritten as P̿ε̄ = log(Ē_c). As a result of the multiplicative assumption, log(ε̄) can be solved for using a linear least squares solution

$$log(\overline{\mathrm{\varepsilon }})={\left({\overline{\overline{\mathrm{P}}}}^{\mathrm{T}}\overline{\overline{\mathrm{P}}}\right)}^{-1}{\overline{\overline{\mathrm{P}}}}^{\mathrm{T}}log(\overline{{\mathrm{E}}_{\mathrm{c}}})$$ (2)

and finally solving for ε̄

$$\overline{\mathrm{\varepsilon }}={\mathrm{e}}^{log(\overline{\mathrm{\varepsilon }})}$$ (3)

We are currently working on a proof of conditions on the registration circuits for when P̿ is full rank and therefore (P̿^T P̿) is invertible. Experimentally P̿ has been observed to be full rank when N ≥ 5. We define P̿ to be all unique circuits in the graph of size 3.

2.1 AQUIRC Applied to Fiducial-Based Registration

For this work, we utilize the fiducial registration method that minimizes the FRE between two sets of points. The fiducial registration method uses singular-value decomposition as was done in Algorithm 8.1 in [12]. We also define the function dissimilarity(X, X′) to be the TRE(X, X′) where TRE(X, X′) is defined as the Euclidean distance between X and X′ because, as explained below, our set X contains a single element.

3 Experiments and Results

To test our algorithm we repeat an experiment that was performed by Fitzpatrick which showed analytically and experimentally that FRE and TRE are uncorrelated [5]. Using the same experiment, we show that our quality measure is correlated to the TRE.

3.1 Experiments

In Experiment 1 in [5], Fitzpatrick simulates an actual Deep Brain Stimulation case with 4 fiducials and a target location in the deep brain. The fiducials serve as anchors for the microTargetingTM Platform, FHC, Inc. also referred to as STarFixTM that guides the electrodes used in the procedure to the target location in the deep brain. The location of the four fiducials x₁, x₂ x₃, and x₄ as well as the target position x_t are:

$$x_1=\left[\begin{array}{c}197\\ 217\\ 115\end{array}\right],x_2=\left[\begin{array}{c}109\\ 225\\ 121\end{array}\right],x_3=\left[\begin{array}{c}83\\ 139\\ 127\end{array}\right],x_4=\left[\begin{array}{c}202\\ 132\\ 130\end{array}\right],x_t=\left[\begin{array}{c}144\\ 155\\ 57\end{array}\right]$$

Following the same simulation model as in [5], we first apply a rotation R and translation t to the location of the fiducials x₁, x₂, x₃, and x₄ as well as to the target position x_t, which results in the corresponding positions y₁, y₂, y₃, y₄, and y_t. We consider the fiducials x₁, x₂, x₃, and x₄ and x_t to be in the surgical space while the rotated and translated fiducials y₁, y₂, y₃, y₄, and y_t are considered to be in the image space. Again, as in [5], we set the rotation R to be 10, 20, and -30 degrees about the x, y, and z axes and we set the translation t to be (7, -10, 100) mm (which was chosen as an arbitrary mis-registrationin [5]).

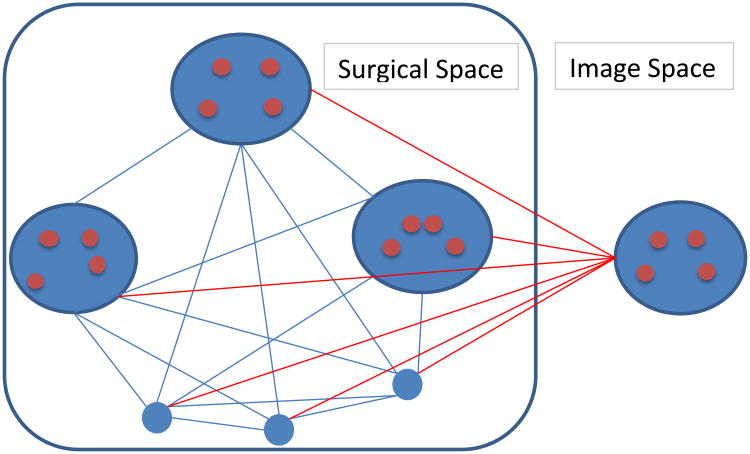
We perturb the location of the fiducials in surgical space using a fiducial localization error drawn from a random distribution with zero mean and variance of FLE/3, where FLE is set to 1mm. This is done N times to create a set of N perturbed fiducial configurations (as seen in the left of Figure 2). We then compute all pair-wise fiducial registrations between each of the N fiducial configurations in the surgical space as well as between these and the unperturbed fiducial configuration in the image space, creating the complete graph of registrations necessary to compute our algorithm. We then apply our algorithm and calculate the ε value for each of the registrations. In this work, we consider the TRE, FRE, and ε values for the registrations between the fiducial configurations in the surgical space and the fiducial configuration in the image space, which results in N values for TRE, FRE, and ε (this is represented as the red links in Figure 2). FRE is defined as the root mean square distance between the fiducial points in image space and the points transformed from image space to surgical space using the computed transformations. For each run, we thus produce N FRE values. Similarly, TRE is defined as the Euclidean distance between the target position in image space and the position of the target transformed from image space to surgical space. We repeat this process in a Monte Carlo simulation; creating thousands of N sets of fiducials.

Figure 2.

Diagram of the experiment methodology. The surgical space contains N fiducial configurations that are created by adding FLE to the original fiducial locations. The image space contains the rotated and translated fiducials. Each set of fiducial configurations are registered to every other configuration, both in image space and in surgical space. The red links represent the registrations for which we calculate the TRE, FRE and ε values.

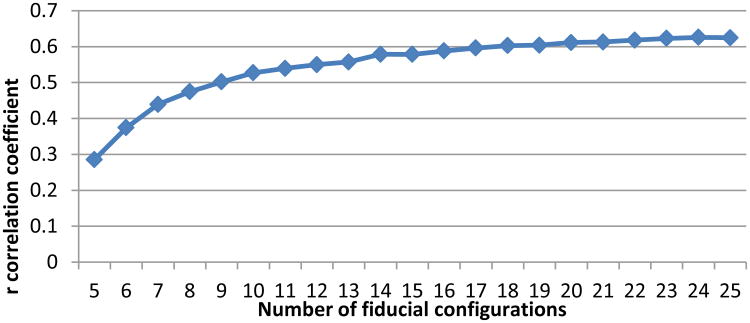
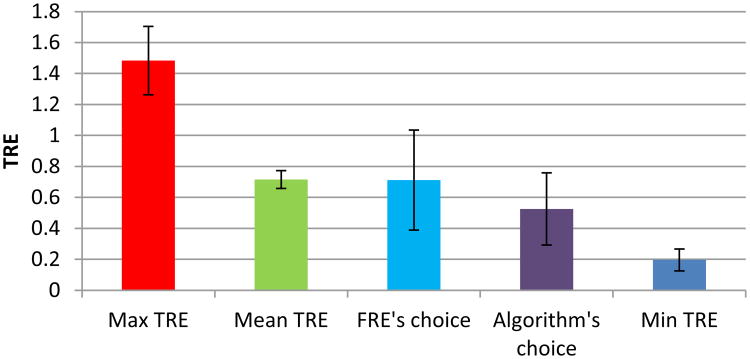
In the first experiment we utilize an N of size 30 over 1000 simulations. We calculate the correlation between the TRE values and that of the FRE and ε values. In the second experiment we test the effect N has on our results by varying the size of N from 5 to 25, using 5000 simulations for each N. Again, we calculate the correlation between TRE and the ε values for each N. Finally, in the third experiment, we test the ability of our algorithm to improve the TRE in a fiducial-based registration scenario. To do this we utilize an N of 30 over 1000 simulations. For each simulation we calculate the mean TRE of all 30 fiducial configurations, the min TRE of all 30 fiducial configurations, the max TRE of all 30 fiducial configurations, the TRE of the fiducial configuration that AQUIRC identifies as being of the highest quality, and the TRE of the fiducial configuration with the minimum FRE.

3.2 Results

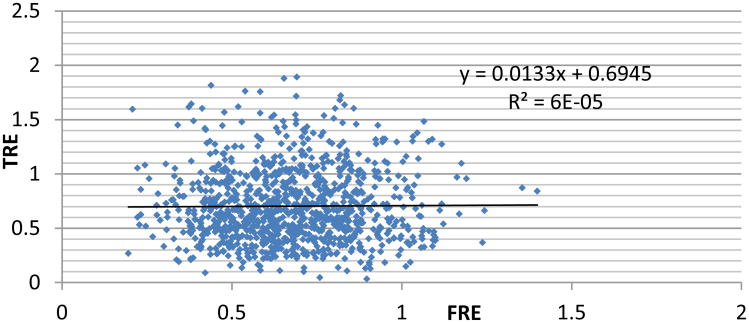
The results of experiment 1 are shown in Figures 3 and 4. In Figure 3 we show a scatter plot of the FRE and TRE values (the points in both scatter plots were reduced to a random sampling of 1000 data points for better visualization).

Figure 3.

Scatter plot of the TRE and FRE values.

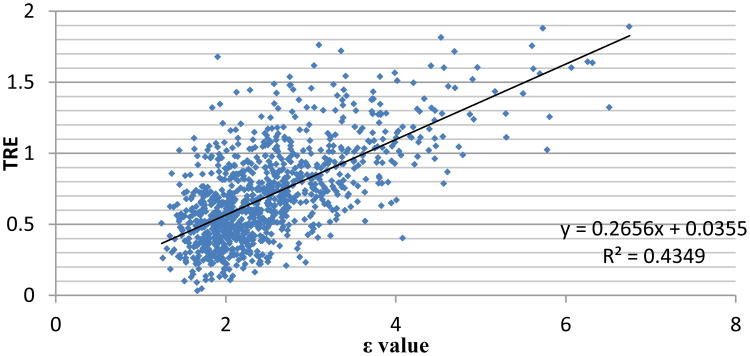
Figure 4.

Scatter plot of the TRE and ε values.

As can be seen, we produce a correlation that is very similar to the one found in [5], with an r = -0.0012, which is not statistically significant (p = 0.8351). In Figure 4 we show the correlation between our algorithm's ε value and TRE. In this case there is a statistically significant correlation of r = 0.6414 and a p < 0.001. The results of experiment 2 are shown in Figure 5. By increasing the number of fiducial configurations that we utilize in the surgical space we can increase the correlation between TRE and ε, producing better estimations of the quality of error in fiducial registrations. The results of experiment 3 are shown in Figure 6; it shows the practical utility of our algorithm. If, for every simulation, we choose the configuration with the lowest ε value, the TRE is reduced by a statistically significant 0.191 mm when compared to the mean TRE value and is reduced by a statistically significant 0.1861 when compared to the TRE of the fiducial configuration with the minimum FRE. The figure also shows the mean and standard deviation of the TRE values when the configurations with the max and min TRE values are selected at every run, respectively.

Figure 5.

Correlation between TRE and ε as a function of the number of fiducial configurations utilized in the surgical space.

Figure 6.

Bar graph of the mean value and standard deviation of the TRE value across 1000 simulations. For each simulation we calculate the mean TRE of all 30 fiducial configurations, the min TRE of all 30 fiducial configurations, the max TRE of all 30 fiducial configurations, the TRE of the fiducial configuration that AQUIRC identifies as being of the highest quality, and TRE of the fiducial configuration with the minimum FRE.

4 Discussions/Future Work

In this work we have introduced a method that produces a measure of registration quality that is correlated to the target registration error. We are unaware of any other published work that describes a technique that is able to do so. We have shown that the number of fiducial configurations that are utilized in the complete graph of registrations affects the quality of our algorithm's estimation and that by increasing the number of configurations the correlation between our measure and TRE increases. A practical limitation on the number of configurations is computation time. Indeed as the number of configurations increases so does the size of the graph that needs to be constructed. Most importantly for practical applications, we also show that by choosing the configuration that our algorithm identifies as producing the best registration, we can reduce the average TRE.

To use our algorithm in practice, all that is needed is to acquire the location of the fiducial markers in the image space as well as in surgical space. The location of the markers in surgical space can then be randomly perturbed by an FLE that is representative of the error that naturally occurs when attempting to identify the coordinates of the markers in the operating room (alternatively, the position of the markers in physical space could be perturbed). These sets of markers can then be registered together to form a complete graph of registrations and AQUIRC is applied. The ε value of the unperturbed configuration, i.e., the position of the fiducials selected by the end user, can then be compared to the distribution of ε values produced by our algorithm. If the unperturbed ε value is large compared to the perturbed ε values, the end user could be warned of a potential registration problem.

In the future, we will investigate various types of models that could better represent the combination of error that occurs when combining multiple transformations than the multiplicative model we have used in this work. We will also explore further the distribution of ε values and attempt to define statistical tests that would permit to quantify the quality of a particular registration. If successful, this would provide end users with quantitative measures of accuracy for a particular registration. This would represent a major advance in the field of fiducial-based registration.