GLYCAM06: A Generalizable Biomolecular Force Field. Carbohydrates

Abstract

A new derivation of the GLYCAM06 force field, which removes its previous specificity for carbohydrates, and its dependency on the AMBER force field and parameters, is presented. All pertinent force field terms have been explicitly specified and so no default or generic parameters are employed. The new GLYCAM is no longer limited to any particular class of biomolecules, but is extendible to all molecular classes in the spirit of a small-molecule force field. The torsion terms in the present work were all derived from quantum mechanical data from a collection of minimal molecular fragments and related small molecules. For carbohydrates, there is now a single parameter set applicable to both α- and β-anomers and to all monosaccharide ring sizes and conformations. We demonstrate that deriving dihedral parameters by fitting to QM data for internal rotational energy curves for representative small molecules generally leads to correct rotamer populations in molecular dynamics simulations, and that this approach removes the need for phase corrections in the dihedral terms. However, we note that there are cases where this approach is inadequate. Reported here are the basic components of the new force field as well as an illustration of its extension to carbohydrates. In addition to reproducing the gas-phase properties of an array of small test molecules, condensed-phase simulations employing GLYCAM06 are shown to reproduce rotamer populations for key small molecules and representative biopolymer building blocks in explicit water, as well as crystalline lattice properties, such as unit cell dimensions, and vibrational frequencies.

Introduction

Carbohydrates are involved in numerous biological functions, such as recognition in axonal growth or path-finding,¹ blood anticoagulation,² cell-cell recognition,³ antibody–antigen inter-actions,⁴ structure factors in extra-cellular matrices,⁵ and post- or cotranslational modifications of polypeptides.⁶ Correct glycosylation patterns are essential for normal cell and organism function, and aberrant glycosylation is associated with numerous human diseases.^7,8 To provide a structural basis for the multitude of biological roles played by carbohydrates, it is imperative that their spatial and dynamic properties be accurately determined. Experimental structure determination methods such as X-ray crystallography,^9–11 NMR spectroscopy,^12–15 and fluorescence energy-transfer spectroscopy¹⁶ have been applied in studies of carbohydrate conformation, either free or complexed with proteins. While NMR spectroscopy has been extensively used to characterize the dynamics of glycans in solution,¹⁷ interglycosidic linkage conformations are notoriously difficult to determine by NMR spectroscopy because of the paucity of nuclear Overhauser effects (nOes),¹⁸ the uncertainties in the Karplus-type equations employed to interpret scalar J-coupling constants¹⁹ and the potential for the linkage to populate multiple rotamer states.²⁰ Moreover, NMR techniques employed to determine the structural properties of polysaccharides or protein–carbohydrate complexes are limited by molecular weight constraints. Alternatively, X-ray crystallography can be a powerful source of structural information. However, the presence of multiple glycoforms often prevents crystallization of glycoproteins, and the inherent flexibility of oligosaccharides is the presumed reason for the notable absence of X-ray structures for any but the smallest systems.

Theoretical methods, such as Monte Carlo and molecular dynamics (MD) simulations, are employed increasingly to augment the experimental approaches in determining the conformational properties of carbohydrates, and biomolecules in general. The level of interest in applying classical simulations to oligosaccharides arises from experimental limitations and is demonstrated by the numerous force fields and parameter sets that have been derived for carbohydrates (See ref. 17 for a review). The performance of several parameter sets, which included the first version of GLYCAM (GLYCAM_93²¹), has been quantitatively evaluated against data from quantum mechanical calculations²² as well as on a relative basis, using a chemometric analysis from 20 second-generation carbohydrate force fields.²³ The conclusion from those comparisons was that no single parameter set or force field consistently out-performed the others. In a study that focused on the abilities of three prominent biomolecular force fields to reproduce experimental solution data for two related disaccharides, the second version of GLYCAM (GLYCAM2000²⁴) with AMBER performed well in terms of conformational predictions.²⁵ Although the GLYCAM_93²¹ and 2000²⁴ parameter sets, augmented by terms from the AMBER parameters,²⁶ have been employed frequently in the study of oligosaccharides^{5,22–25,27–32} and oligosaccharide–protein complexes,^{10,14,33–39} they have some serious limitations. Earlier GLYCAM versions performed poorly at reproducing diffusion rates in explicit solvent MD simulations, and differed substantially from other carbohydrate parameter sets in the prediction of putative radial pair distribution functions (RPD) between hydroxyl groups and TIP3P⁴⁰ water.²⁵ For example, the RPD for the O3-atom in methyl α-D-isomaltoside computed with GLYCAM2000a resulted in a less structured secondary hydration shell, and a first hydration shell at 3.0 Å, which was higher than the average distance between O_carbohydrate…O_water atoms found in carbohydrate crystals (2.77 Å).⁴¹ The first hydration shell of the O₃…O_water RPD had a peak density value of 1.0, which compared unfavorably with the experimental value of about 3.0 for the RPD of O_water…O_water.²⁵ The computed O₃…O_water RPD employing the present version of GLYCAM (GLYCAM06) resulted in a first hydration shell at 2.75 Å with a peak density of 1.6 and a well-defined secondary hydration layer at about 5.0–5.5 Å. This improvement in GLYCAM06 was due to the utilization of AMBER-consistent van der Waals parameters for the hydroxyl oxygen. In the case of self-diffusion rates of α-D-isomaltose GLYCAM2000a gave a value that was about twice the experimental value.²⁵ The self-diffusion rate computed with GLYCAM06 was 3.6 × 10⁻²⁶ cm²/s, which is in agreement with the experimental value of 4.2 × 10⁻²⁶ cm²/s.²⁵

The previous versions of GLYCAM were designed with the intention that they would introduce the minimal parameters necessary to add carbohydrate functionality to AMBER, and otherwise to maintain consistency with the AMBER force field development philosophy.²¹ Regarding transferability, GLYCAM development followed the general approach employed in biomolecular force fields of defining a single dihedral angle term for each molecular-class-specific linkage. Analogous to the treatment of peptide backbone dihedral angles, the rotational properties associated with glycosidic linkages were characterized by a single dihedral angle term specific to a unique atomic sequence, present only in carbohydrates. All other potentially contributing terms associated with that linkage were explicitly eliminated.²¹ That approach facilitated precise fitting to QM rotational data, but was specific to six-membered ring forms (pyranosides) and to the anomeric configuration. This limited the ability to readily introduce new chemical functionality into GLYCAM, to study ring conformational interconversions, and to apply it to other ring sizes (furanosides, in particular).⁴²

The derivation of a highly consistent and transferable parameter set for modeling carbohydrates and glycoconjugates (GLYCAM06) is the focus of the present work. In light of accumulated applications of GLYCAM_93,^{10,22–25,27–31,43–48} several areas were targeted for improvement. In particular, the parameter set should (1) be transferable to all carbohydrate ring conformations and sizes, (2) be self-contained and therefore readily transferable to many quadratic force fields, (3) not require specific atom types for α- and β-anomers, (4) be readily extendible to carbohydrate derivatives and other biomolecules, (5) be applicable to monosaccharides and complex oligosaccharides, (6) be rigorously assessed in terms of the relative accuracy of its component terms, and (7) avoid the use of 1–4 electrostatic or non-bonded scaling factors.²⁴ In a study of the ω-angle rotation (O₅—C₅—C₆—O₆) in monosaccharides, we observed that O₆ may interact with either O₄ (in a 1–5 relationship) or O₅ (in a 1–4 relationship) and the use of 1–4 scaling therefore unbalanced these interactions leading to an inability to correctly predict rotamer populations.²⁴

Parameterization of GLYCAM06 employed training and test sets of ~100 molecules from the chemical families of hydrocarbons, alcohols, ethers, amides, esters, carboxylates, molecules of mixed functional groups as well as simple ring systems related to cyclic carbohydrates, as outlined in Table 1. If a molecule had the potential of forming an internal hydrogen bond during a torsion rotation, two rotational energy curves were examined, one in which a hydrogen bond was allowed, and a second in which the hydrogen bond was disallowed.

Table 1.

Model Compounds Employed in the Development of GLYCAM06.

Molecular class	Parameter	Training set	Test set
Hydrocarbons	HC–CG–CG–HC	Ethane
	CG–CG–CG–CG	Butane	2,3-dimethylbutane, 2-methylbutane, and ethylcyclohexane
	HC–CG–CG–CG	Propane	2-methylpropane, 2,2-dimethylpropane, and methyl cyclohexane (axial and equatorial)
Alcohols	HO–OH–CG–H1	Methanol	Propan-2-ol
	HO–OH–CG–CG	Ethanol and propan-2-ol
	OH–CG–CG–HC	Ethanol and 2-methylpropan-2-ol
	CG–CG–CG–OH	Propanol	1,1,2,2-tetramethylpropanol, 2,2-dimethylpropanol, hydroxymethylcyclohexane (equatorial) and butanol
	OH–CG–CG–OH	1,2-ethanediol and 1,2-propanediol	2-methyl-1,2-propanediol, 2,3-butanediol, 2-methyl-2,3-butanediol, and 2,3-dimethyl-2,3-butanediol
Ethers	H1–CG–OS–CG	Methoxymethane	Methoxyethane, 2-methoxypropane, and 2-methoxy-2-methylpropane
	CG–CG–OS–CG	Methoxyethane and 2-methoxypropane	2-methoxy-2-methylpropane, 2-methoxypropane, 2-tert-butoxy-2-methylpropane, methoxycyclohexane (axial and equatorial), and 2-isopropoxypropane
	CG–CG–CG–OS	Methoxypropane and 1-methoxy-2-methylpropane	1-methoxy-2,2-dimethylpropane
	OS–CG–CG–OS	1,2-dimethoxyethane	1,2-dimethoxypropane, 1,2-dimethoxy-2-methylpropane, 2,3-dimethoxybutane, 2,3-dimethoxy-2-methylbutane, and 2,3-dimethoxy-2,3-dimethylbutane
	OS–CG–OS–CG	1,1-dimethoxyethane, 2,2-dimethoxypropane and Tetrahydro-2-methoxy-2H-pyran (axial and equatorial)	Tetrahydro-2-methoxy-2H-pyran-3-ol (axial and equatorial) and Tetrahydro-2-(tetrahydro-2H-pyran-2-yloxy)-2H-pyran
Amides	N–CG–CG–CG	N-(2,33-trimethylbutan-2-yl) acetamide and N-propylacetamide	N-tert-pentylacetamide and N-sec-butylacetamide
	H–N–C–O,	Acetamide
	HC–CG–C–N
	H1–CG–N–C/CG	N,N-dimethylacetamide, and N-isopropylacetamide
	HC–CG–CG–N	N-tert-butylacetamide
	CG–N–C–O,	N,N-dimethylacetamide	N-methylacetamide, N-ethylacetamide,
	CG–N–C–CG		N-isopropylacetamide and N-tert-butylacetamide
	CG–CG–N–C	N-tert-butylacetamide and N-isopropylacetamide, N-(tetrahydro-2H-pyran-3-yl) acetamide	N-ethylacetamide and N-(tetrahydro-2-methoxy-2H-pyran-3-yl) acetamide
Esters	H1–CG–OS–C	Methyl acetate
	OS–C–CG–HC	Methyl acetate
	CG–OS–C–O,	Methyl acetate
	CG–C–OS–CG
	CG–CG–OS–C	Ethyl acetate and tetrahydro-2H-pyran-3-yl acetate	tetrahydro-2-methoxy-2H-pyran-3-yl acetate and (tetrahydro-2H-pyran-2-yl)methyl acetate
Carboxylates	O2–C–CG–CG	2-methyl propanoate
	OH–CG–CG–C	3-hydroxy propanoate	2-methyl-3-hydroxy propanoate
	HC–CG–C–O2	Acetate
Ether alcohols	OH–CG–CG–OS	Methoxyethanol and 2-methoxypropanol	2-methoxybutan-3-ol, 2-methoxy-2-methylpropanol, 2-methoxy-2-methylbutan-3-ol and 2-methoxy-2,3-dimethylbutan-3-ol
Ether amides	OS–CG–CG–N	N-(1,1-dimethyl-2-methoxyethyl) acetamide and N-(1-methoxypropan-2-yl)acetamide	N-(1-methoxy-2-methylpropan-2-yl)acetamide and N-(1-methoxypropan-2-yl)acetamide
	CG–OS–CG–N	N-(2-methoxyethyl)acetamide and N-(2-methoxypropyl)acetamide
Molecular class	Parameter	Training set	Test set
Alcohol amides	OH–CG–CG–N	N-ethanolacetamide	N-(2-hydroxypropyl)acetamide, N-(2-hydroxy-2-methylpropyl)acetamide and N-(3-hydroxy-2,3-dimethylbutan-2-yl)acetamide
Ether carboxylates	O2–C–CG–OS	2-methoxyacetate, 2-methoxypropanoate, 2,2-dimethoxyacetate, 2-methoxy-2-methylpropanoate and (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid (ionized)
	OS–CG–CG–C	3-methoxypropanoate	2-methyl-3-methoxypropanoate
	C–CG–OS–CG	2-methoxyacetate, 2-methoxypropanoate, 2-methoxy-2-methylpropanoate, (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid (ionized) and (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid (neutral)	α-5-N-acetylneuraminic acid

To maintain consistency with the current AMBER protein parameters, the B3LYP/6-31++G(2d,2p)//HF/6-31G* level of theory was selected as the reference for all valence quantum calculations.⁴⁹ Energies at this level may be expected to display minimal basis set superposition error (BSSE),⁵⁰ which is not only important for determining accurate interaction energies, but also for locating minima and establishing barrier heights along the valence reaction coordinates. It has been shown that the B3LYP functional performs well in carbohydrates and related molecules,^50–52 and was therefore selected for our force field development. Of particular importance for dynamics, this level of theory leads frequently to a reduction of barrier heights for internal rotations relative to those obtained with the HF/6-31G* method, resulting in increased conformational sampling for oligosaccharides.

Methods

Quantum Mechanical Calculations

Quantum mechanical calculations were performed using the Gaussian98 software package.⁵³ Geometries were optimized using the Gaussian98 default optimization criteria, unless otherwise noted. The HF/6-31G* level of theory was employed for neutral fragments, whereas for anionic molecules diffuse functions were added. Rotational energy curves were generated by varying the relevant torsion angle from 0–360° in 30° increments while optimizing all other variables. Single point energies were computed at the B3LYP/6-31++G(2d,2p) level of theory.

Molecular Mechanics Calculations

All molecular mechanics (MM) calculations were performed using either the AMBER7⁵⁴ or AMBER8⁵⁵ software packages, with nonbonded and electrostatic scaling factors (SCEE, SCNB) set to unity. The valence parameters were determined by minimizing the error between the energies obtained from the ab initio and molecular mechanics calculations in the traditional manner.

Molecular Dynamics

Molecular dynamics (MD) simulations were carried out with the explicit inclusion of solvent (TIP3P)⁴⁰ under isothermal–isobaric (nPT) conditions. Charged systems were neutralized by adding the appropriate number of counter ions. In general, the initial solvent configurations were optimized through 50 cycles of steepest descent and 950 cycles of conjugate gradient energy minimization with the SANDER module, followed by minimization of the entire system through the same protocol. The entire system was then annealed by heating from 5 to 300 K in 50 ps, followed by cooling to 5 K in another 50 ps. Initial velocities were assigned from a Boltzmann distribution at 5 K. Prior to the production dynamics stage the entire system was thermally equilibrated by heating again from 5 to 300 K in 150 ps. A 2-fs time step was used to integrate the equations of motion, using the Verlet Algorithm.⁵⁶ Long-range electrostatic interactions were treated using the particle mesh Ewald summation. A dielectric constant of unity was employed in all MD and MM calculations. Bonds containing hydrogen were constrained to their equilibrium lengths using the SHAKE algorithm.⁵⁷

Potential of Mean Force Calculations

The weighted histogram analysis method (WHAM)⁵⁸ was used to calculate potentials of mean force (PMF).⁵⁹ To ensure maximum sampling along the reaction coordinate, harmonic force constants of 10 and 5 kcal/mol were used for regions of high (maxima) and low (local and global minima) potential energies, respectively. Prior to the PMF calculations, the system was equilibrated following the protocol outlined in the MD section. Umbrella sampling was performed for 140 ps under nPT conditions with a time-step of 2 fs.

Single Molecule and Ensemble-Averaged Charge Calculations

The atomic partial charges of all molecules employed in the gas phase for the development of valence bond, angle, and torsional parameters were derived from the HF/cc-pVTZ//HF/6-31G* molecular electrostatic potential (MEP), employing the restrained electrostatic potential (RESP)⁶⁰ charge fitting methodology, with a hyperbolic charge restraint weight of 0.0005, as indicated by Bayly et al.⁶⁰ However, partial charge sets destined for condensed-phase simulations were generated from the HF/6-31G*//HF/6-31G* MEP, appropriate for TIP3P⁴⁰ water simulations. For the condensed-phase charge sets, a RESP charge restraint weight of 0.01 was employed, based on earlier MD simulations of experimental crystal lattices of α-D-glucopyranose,³¹ wherein this value led to optimal reproduction of unit-cell dimensions of the crystal.

In GLYCAM06, the issue of charge-conformation coupling was addressed by employing ensemble-averaged (EA) charge sets.⁶¹ For any given monosaccharide, an MD simulation, typically 50–100 ns was performed in TIP3P water, with 100–200 structures being selected from the trajectory for individual charge calculations. For each of these snapshots partial charges were calculated by fitting to the HF/6-31G* MEP. Prior to the charge calculations, each structure was optimized at the HF/6-31G* level, with the rotatable exocyclic bonds constrained to their MD conformations.⁶¹ The charges were then averaged for each monosaccharide to afford a final EA charge set, as exemplified in Table 2. These sets of charges were thus weighted by the actual occurrence of a particular solution conformation in an MD simulation. For these terminal monosaccharides, the average RESP-derived charge on the aglycon was −0.194 au, with the total charge on the glycoside equal to +0.194 au (Q_term), for overall charge neutrality. To generate charges on nonterminal residues, the charge on the linking hydroxyl proton is added to that of the linking oxygen atom to give a new charge, Q_ol. Next, Q_term is subtracted from Q_ol to afford the final charge on the linking oxygen atom. This results in an overall charge of zero for nonterminal residues.

Table 2.

Ensemble-Averaged Partial Charge^a Sets for the Methyl Glycosides of D-Glcp, D-Manp, and D-Galp.

	D-GlcpOMe		D-ManpOMe		D-GalpOMe
Atom	α	β	α	β	α	β
CMe	0.259 ± 0.01	0.267 ± 0.01	0.275 ± 0.01	0.262 ± 0.01	0.262 ± 0.01	0.264 ± 0.01
OMe	−0.470 ± 0.03	−0.454 ± 0.02	−0.532 ± 0.03	−0.406 ± 0.03	−0.478 ± 0.03	−0.455 ± 0.03
C1	0.527 ± 0.08	0.378 ± 0.08	0.496 ± 0.07	0.262 ± 0.05	0.488 ± 0.09	0.372 ± 0.08
C2	0.246 ± 0.09	0.310 ± 0.10	0.245 ± 0.07	0.241 ± 0.09	0.339 ± 0.10	0.357 ± 0.10
O2	−0.713 ± 0.03	−0.718 ± 0.02	−0.716 ± 0.03	−0.664 ± 0.03	−0.724 ± 0.02	−0.727 ± 0.03
H2O	0.437 ± 0.03	0.437 ± 0.02	0.446 ± 0.02	0.431 ± 0.02	0.431 ± 0.02	0.432 ± 0.02
C3	0.286 ± 0.10	0.284 ± 0.11	0.251 ± 0.11	0.263 ± 0.13	0.253 ± 0.09	0.259 ± 0.11
O3	−0.699 ± 0.03	−0.709 ± 0.03	−0.696 ± 0.03	−0.692 ± 0.04	−0.701 ± 0.02	−0.695 ± 0.02
H3O	0.427 ± 0.02	0.432 ± 0.01	0.431 ± 0.02	0.430 ± 0.02	0.433 ± 0.02	0.433 ± 0.02
C4	0.254 ± 0.12	0.276 ± 0.13	0.326 ± 0.16	0.349 ± 0.15	0.204 ± 0.08	0.203 ± 0.10
O4	−0.710 ± 0.03	−0.714 ± 0.03	−0.732 ± 0.04	−0.746 ± 0.03	−0.673 ± 0.04	−0.664 ± 0.04
H4O	0.436 ± 0.02	0.440 ± 0.02	0.438 ± 0.02	0.443 ± 0.02	0.436 ± 0.03	0.436 ± 0.02
C5	0.283 ± 0.11	0.225 ± 0.12	0.276 ± 0.15	0.206 ± 0.13	0.216 ± 0.09	0.140 ± 0.09
O5	−0.574 ± 0.07	−0.470 ± 0.06	−0.507 ± 0.07	−0.393 ± 0.06	−0.527 ± 0.07	−0.402 ± 0.07
C6	0.276 ± 0.04	0.282 ± 0.044	0.266 ± 0.05	0.273 ± 0.05	0.308 ± 0.05	0.319 ± 0.05
O6	−0.682 ± 0.02	−0.688 ± 0.02	−0.688 ± 0.02	−0.680 ± 0.02	−0.684 ± 0.03	−0.692 ± 0.02
H6O	0.418 ± 0.02	0.424 ± 0.02	0.422 ± 0.02	0.419 ± 0.02	0.418 ± 0.02	0.419 ± 0.02

^aFrom 200 snapshots evenly extracted from a 50-ns MD simulation.

Nonbonded van der Waals parameters were taken directly from the PARM94 parameter set, which are also employed in the current distribution of AMBER parameter sets AMBER9.⁶²

Vibrational Analysis

Vibrational frequencies were computed for α-D-glucopyranose using the NMODE facility in AMBER9 with the GLYCAM parameter set. The calculation was performed on a monomer and on a 64-unit crystal. In both calculations, the initial structure was adapted from neutron scattering crystallographic data (PDB ID: GLUCSA10).⁶³ The NMODE calculations were performed with default settings except for the values of the 1–4 nonbonded and 1–4 electrostatic scale factors, which were each set equal to unit as suggested by earlier work.³¹ Both monomer and crystal were minimized to ΔRMS = 1 × 10⁻⁵. Since periodic boundary conditions are not implemented in NMODE, the 64-mer was minimized as if it were a discrete nanoparticle. Frequency analyses were also performed on the monomer at the HF/6-31G*//6-31G* and B3LYP/6-31++G(2d,2p)//6-31++ G(2d,2p) levels of theory.

Because of the complexity of the molecular structures, particularly in the 64-mer, a program (DMODES, for “describe modes”) was written to automatically detect and assign vibrational modes. Although assignments for glucopyranose have often^64–68 been made based on the potential energy distribution (PED) within each vibrational mode, NMODE facilitates use of the eigenvectors (collection of atomic motion vectors). Primarily for this reason, DMODES bases its assignments on the motions and relative kinetic energies of the atoms. However, there are other reasons to make assignments based on motion rather than PED’s. While PED assignments are limited to bonded and near-neighbor nonbonded interactions, motion analysis can easily consider concerted motions of atoms far removed from each other. For example, motion analysis can assign ring expansions and deformations, assignments that are far more difficult to make using PED analysis. In addition, motion analysis yields assignments that are intuitive and that use language familiar to spectroscopists. The use of a computer program in general is, of course, also preferred to visual inspection of the eigenvector data because of increases in speed, objectivity, and reliability. At present, DMODES is in the prototype stage and is of limited general usefulness, but a copy of the code can be obtained by contacting the authors.

In brief, DMODES employs the relationships of individual atomic motions with respect to each other and to the molecular geometry to determine an appropriate description of the vibrational motion for a mode. For example, the dot product of a unit motion vector for atom i, ${\stackrel{⌢}{\mathbf{v}}}_i$, with a corresponding unit bond vector, $\stackrel{⌢}{{\mathbf{B}}_{\mathit{ij}}}$, indicates the extent to which the motion is a stretch along that bond. Since the dot product of two unit vectors yields the cosine of the angle between them, the result of this calculation will be nearly ±1 if the motion is parallel to the bond (stretching) and ~0 if the motion is perpendicular (bending or torsioning). Similarly, bending and torsional motions of a system i—j—k can be determined using eq. (1):

$${\stackrel{⌢}{\mathbf{v}}}_i•\left({\stackrel{⌢}{\mathbf{B}}}_{\mathit{ij}}\times {\stackrel{⌢}{\mathbf{B}}}_{\mathit{jk}}\right)$$ (1)

If this relationship is nearly zero, the motion lies within the plane formed by i, j, and k and is therefore a bend (if also determined not to be a stretch). If the magnitude of the relationship is nearly one, the motion is nearly perpendicular to the plane and is torsional. Intermediate values, of course, correspond to mixtures of torsion and bending. DMODES employs a set of cutoff values to distinguish between motions.

The significance of an individual atom’s motion was determined using the relative kinetic energy of the atom. Each atom’s motion vector represents its relative velocity at its vibrational potential energy minimum. The vector magnitudes can therefore be converted into relative kinetic energies, which correspond to the significances of the individual atomic motions within the vibrational mode. Although DMODES considered each atomic motion, the primary vibrational modes, which are presented here, were assigned on the basis of the most significant motion within each motion class. The implications of this choice are discussed in more detail in the results and conclusions section.

Assignments for the 64-mer required additional considerations. Since NMODE does not employ crystal-based symmetry arguments when calculating frequencies, 4608 normal modes (3N, where N = 64 units × 24 atoms per unit) were generated. Also, since an accurate frequency calculation requires a minimization, the positions of the atoms were necessarily displaced somewhat from their perfect-crystal locations. Because of this, the assignments for the 64 units, while generally similar, were each unique. To reduce the 294,912 different motion assignments, the data were treated in the following manner. First, the motions of all 64 units were assigned as usual for each vibrational frequency. During the assignment, the overall importance of each unit’s motion to each mode was scored by summing the magnitudes of the motion vectors for each of the atoms in the unit. The motion vectors used for this score had previously been altered to remove any overall translational component (due to lattice-wide motions). The maximum magnitude sum for each frequency was then determined. If, within any frequency, a unit’s magnitude was at least 50% of the largest magnitude, the results of its motion analysis were included in the results presented here. This procedure removes from our immediate attention those motions that occur with low intensity, being primarily due to resonance with more energetic motions of nearby neighbors. However, it does not discount resonances that result in motions that are more energetic, if somewhat unexpected. An example of the latter appears in the data and is discussed below.

Modern characterizations of the infrared and Raman spectra of carbohydrates typically employ some form of calculation of the PED when making assignments,^64–71 though they occasionally use more traditional methods.^69,71 Those that rely significantly⁷¹ or exclusively⁷² on traditional methods, as well as the occasional computation,⁷⁰ will often employ more descriptive terminology in their assignments. While the assignment method employed here was designed to translate more readily into standard spectroscopic descriptions, it is important, also, to compare with the less-intuitive PED-based systems. To present a balanced comparison with experimental data, we have chosen to compare with four experimental studies.^67,68,70,71 Since the various assignment naming methodologies do not always translate in a one-to-one correspondence (for an illustration, see Fig. 20 in Wells and Atalla⁷¹), we have chosen categories that are sufficiently broad that they facilitate comparisons, but are also narrow enough that the comparisons remain useful.

Of the four experimental studies considered here, two^70,71 employed traditional assignment nomenclature and two^67,68 assigned based on PEDs. All four used one or more computational method to make assignments, though one⁷¹ also used traditional methods, e.g., isotopic substitution, to guide their assignments. Three^67,68,70 compared their calculations with spectra from earlier studies,^{64–66,69,72} but their results are being used here instead of the earlier work because of the detailed assignments they provided. Since our interest is comparison with experiment, only the experimentally observed frequencies from these studies are considered here. Additionally, we have only considered those experimental frequencies for which assignments were offered.

Since our assignments are based on the most energetic motion class within a given mode, we compared with only the most significant (first on the list) potential energy contribution within any PED assignment.^67,68 With no hierarchy of significance apparent in the work of Gregurick and Kafafi,⁷⁰ each assignment within a frequency was counted. The ranges from Wells and Atalla⁷¹ come mostly from their Figure 20, with occasional modifications based on the accompanying text, the latter being necessary for proper correlation to the set of motion classes being considered here.

Since IR and Raman intensities are not calculated natively by NMODE, and since the focus of the present study is the extent to which the force field reproduces vibrational frequencies we will not consider them here. In our comparisons with experimental data below, where both IR and Raman frequencies are available, we have compared with only the former, since the frequencies usually differ by only a few wavenumbers, which is not significant in this work. For modes that are not IR active, we have compared with the Raman frequency.

Results and Discussion

Atomic Partial Charges

The accurate reproduction of the electrostatic properties of a molecule is essential in a classical force field that seeks to quantitatively model intermolecular interactions of polar molecules, such as carbohydrates, proteins, and nucleic acids in water. The complexity of this requirement is reflected by the number of partial atomic charge derivation schemes reported in the literature. These include empirical methods, in which charges are fit to reproduce liquid densities and heats of vaporization,⁷³ or a popular alternative, and that used in AMBER, in which the charges are fit to reproduce quantum mechanical MEPs.²⁶ It should be noted that the concept of a partial charge is artificial but convenient, thus there is no definitive approach to their assignment.

A common drawback of several empirical methods is that they rely on reproducing bulk liquid properties and cannot be applied readily to solutes. In all MEP partial charge-based models, there are limitations that arise from the omission of a mechanism for incorporating the dependence of partial charge on molecular conformation.^74,75 In addition, it is not necessarily ideal to locate the partial charges at the nuclear positions,^40,76 nor do all atoms require partial charges.⁷⁷ Close examination of ESP-charges computed for biomolecular fragments⁷⁴ revealed that aliphatic hydrogen atoms tend to have small magnitude charges, as expected from the low bond polarity of most C—H bonds. Further, charges on all hydrogen atoms showed wide fluctuations coupled to the central carbon atom. However, the net charge of the methyl or methylene groups displayed minimal fluctuations. In GLYCAM_93,²¹ the effects of basis set and ESP-fitting algorithm on partial charges in carbohydrates were examined and again indicated the same behavior for aliphatic groups.

A second problematic area is that of charge partitioning. While MEP-fitting has the advantage of reproducing intermolecular interaction energies, caution must be exercised in the selection of atoms that will be included in the fitting procedure. Francl et al.⁷⁷ performed singular value decomposition analyses on the least-squares matrices used to assign partial charges in a series of compounds, which frequently showed that an optimal fit to the ESP was achievable with fewer charges than the total number of atoms, suggesting that consistent reproduction of the MEP can be obtained by assigning zero net charges to some atoms. Consequently, in GLYCAM06, restraints were employed in the ESP fitting to ensure that the charges on all aliphatic hydrogen atoms were zero, leading to consistent charge sets with minimal degradation in the accuracy of the fit. For example, the omission of partial atomic charges on aliphatic hydrogens in methyl α-D-mannopyranoside had essentially no effect on the molecular dipole moment (4.589 D) relative to the all atom charge model (4.581 D), and resulted in only an approximate 2.5% increase in the relative error in the fit to the potential.

In contrast to intermolecular interactions, which are well reproduced by MEP-derived partial charges, intramolecular interactions or solution properties are often poorly reproduced, unless conformationally averaged charges are employed. This issue becomes particularly significant when considering the relative energies of conformational isomers. For example, in the case of cyclohexanol, slightly different partial charge sets result from MEP fitting for both the equatorial and axial forms. When separate charge sets are utilized, incorrect relative energies of the ring conformations were obtained. However, accurate prediction of the relative energies between the chair forms, ⁴C₁↔ C₄ (<1 kcal/mol)⁷⁸ necessitated employing a common charge set for both the equatorial and axial species.

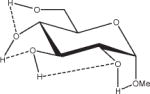
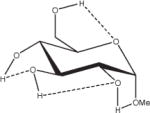
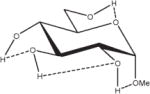
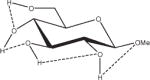
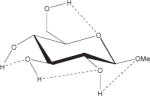
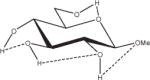
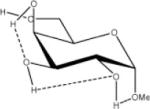
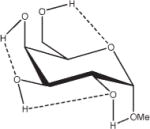
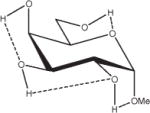
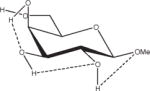
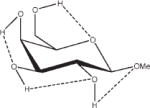
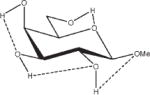
Extension of this logic to monosaccharides is challenged by notable variations among partial charge sets as a function of both anomeric and ring-carbon configuration. From the data in Table 2, both changes in anomericity (α, β) and hydroxyl group configuration (methyl α,β-D-glucopyranoside, α,β-D-GlcpOMe; methyl α,β-D-mannopyranoside, α,β-D-ManpOMe; and methyl α,β-D-galacotopyranoside, α,β-D-GalpOMe) resulted in partial charge sets that were statistically indistinguishable. Therefore, it is reasonable to generate a single charge set that can be used for either anomer of a given monosaccharide. However, a limitation in employing anomer-averaged charge sets is the loss of precision in the calculated intermolecular properties. Nevertheless, with a single charge set for a given monosaccharide, the relative intramolecular energies of ring conformations in which the anomeric configuration becomes inverted (⁴C₁↔¹C₄) can now be effectively computed. For an example of the effect of charge protocol on internal energies, consider the relative energies of the α- and β-anomers of GlcpOMe. At the HF/6-31G*//HF/6-31G* level of theory the α-anomer is predicted to be 1.46 kcal/mol more stable than the β-anomer, while at the B3LYP/6-31++G(2d,2p)//HF/6-31G* level, this value is 0.77 kcal/mol, which is in good agreement with other recently reported theoretical results.⁷⁹ Using GLYCAM06 and the α,β EA (RESP<α,β>) charge set derived from Table 2, the α-anomer was predicted to be 1.15 kcal/mol more stable, a value between the HF/6-31G* and B3LYP/6-31++G(2d,2p) results. When the same calculations were performed using the individual EA charge sets, (RESP<α>) for α-D- and (RESP<β>) β-D-GlcpOMe, the relative energy was reversed, with the β-anomer predicted to be the more stable by 4.19 kcal/mol. Illustrating further the concept of a common charge set, the relative energies of 12 low-energy conformers of D-GlcpOMe and D-GalpOMe, computed using GLYCAM06 were compared with their respective HF/6-31G*//HF/6-31G* values, Table 3. In the case of D-GlcpOMe, when anomer-specific charges were used, the predicted relative energies were once more reversed relative to the QM-predicted values, with the most stable α-conformer being 4.45 kcal/mol less stable than the most stable β-conformer. When <α,β> EA charge sets were employed, the resulting relative energies were comparable once more with the QM values; the α-anomer being preferred by 1.29 kcal/mol. It can be inferred that this energy difference has an electrostatic origin, since a common parameter set was employed for both anomers. Among the β-D-GlcpOMe conformers, the trend in the GLYCAM06 predicted relative energies (β1 < β3 < β2) did not reproduce that determined by QM (β2 < β1 < β3). This variance, however, is insignificant given that the higher energy conformers in both the QM and MM calculations are all within 0.6 kcal/mol of the global minima. In the case of D-GalpOMe, the GLYCAM06-computed relative energies employing anomer-specific charge sets resulted in both large energy differences (11.71 kcal/mol) and incorrect anomer preferences (β < α). Once more, the correct trends were predicted when the RESP<α,β> charge set was used, with the most stable α-anomer being 1.58 kcal/mol more stable than the lowest energy β-anomer, which compared favorably with the QM value of 1.88 kcal/mol. This strategy of averaging anomer- specific charges could be extrapolated to obtain a common set of charges for all the glycosides (RESP<overall>). Employing this charge set in D-GlcpOMe and D-GalpOMe, the α-anomer was correctly predicted to be more stable by 1.12 and 1.79 kcal/mol, respectively.

Table 3.

Influence of Charge Protocol on Conformational Relative Energies (E_rel) Computed with GLYCAM06 for the α- and β-Anomers of D-GlcpOMe and D-GalpOMe.

		Erel
			Charge protocol
Glycoside conformation (D-GlcpOMe)		(HF/6-31G*//HF/6-31G*)a	EA-RESPb <overall>	EA-RESPc <α, β>	EA-RESPd <α>, <β>
α1		0.00e	0.00e	0.00e	4.45e
α2		0.11	0.69	0.58	4.97
α3		0.00	0.22	0.26	4.56
β1		1.30	1.12	1.29	0.00
β2		1.23	1.67	1.75	0.5z
β3		1.46	1.24	1.44	0.29
α1		1.62	1.76	1.89	13.65
α2		1.18	0.94	0.82	12.86
α3		0.00	0.00	0.00	11.71
β1		3.24	3.18	3.42	1.93
β2		2.90	2.99	2.65	0.77
β3		1.88	1.79	1.58	0.00

^aRelative energies taken from Ref. 61. Dotted lines indicate hydrogen bonds.

^bCharges computed by averaging the EA charges of: the α- and β-anomers of all glycosides.

^cCharges computed by averaging the EA charges of: the α- and β-anomers of each glycoside.

^dCharges computed by averaging the EA charges of: each anomer on each glycan.

^eRelative to the lowest energy conformation for each glycoside. Units are kcal/mol.

Bond Lengths and Angles Parameters

The stereoelectronic effects that give rise to valence bond and angle variations at the anomeric carbon atom in pyranoses are well known.^80,81 These variations are not only dependent on anomericity, but also influenced by the size of the aglycon.⁸² The stereoelectronic effects may be incorporated into Type II classical force-fields through stretch-bend and stretch-torsion cross terms.⁸³ However, these cross terms do not exist in well-established macromolecular force fields, such as AMBER,²⁶ CHARMM,⁸⁴ and GROMOS.⁸⁵ In GLYCAM_93, these geometrical variations were incorporated by defining anomer-specific atom types, each with unique values for the bond (K_r) and angle force constants (K_θ), and the equilibrium bond lengths (r_eq) and angles (θ_eq). While the use of unique atom types for the different anomeric carbon atoms facilitated the inclusion of these stereoelectronic effects, it inhibited the ability of the force field to model processes involving ring inversions, which are equivalent to anomer interconversions. In addition, maintaining nongeneralizable anomer-dependent parameters prevented facile extension of the force field to nonstandard glycosyl residues. In the present parameterization, a common set of parameters has been derived for both α- and β-anomers employing a single sp³ atom type (CG). For example, in the previous scheme, a 2-deoxymonosaccharide would require new parameters to be derived, whereas in the current approach all such derivatives are implicitly allowed.

In principle harmonic stretching and bending force constants may be derived from spectroscopic data. However, such data are not available for all molecules of interest to this work. In addition, to be consistent with the use of QM data in the derivation of rotational barriers, we wished to employ only gas-phase force constants. Thus all force constants were derived by fitting a classical harmonic function to a distortion energy curve, computed at the B3LYP/6-31++G(2d,2p) level.

The accurate determination of the bending force constants for atomic sequences involved in glycosidic angles ensures that the flexing and rotational dynamics of the molecule will be correctly reproduced. Values of K_θ for the C—O—C and O—C—O angles were estimated from distortion analyses of the applicable angles in methoxymethane and 1,1-dimethoxyethane, respectively. Fitting to the QM energy curves, computed over the range θ_eq ± 10°, gave K_θ values of 50 kcal/rad² and 100 kcal/rad² for the C—O—C and O—C—O angles, respectively. The average relative errors in these curve fits were 0.73 and 0.16 kcal/mol, respectively. These angle-bending constants are slightly softer than those employed in GLYCAM_93 C—O—C (60.0 kcal/rad²) and O—C—O (110.0 kcal/rad²).²¹

It should be noted that the experimentally observed bond lengths and valence angles in molecules such as carbohydrates and amino acids should not be employed as equilibrium values. These complex molecules contain internal strain forces that perturb the bond lengths and angles away from their theoretical equilibrium values. Equilibrium values, however, may be estimated from small carefully selected molecular fragments. These equilibrium values may differ significantly from the observed valence angles in larger molecules. In addition, effects associated with intermolecular interactions can lead to considerable differences between the QM values for bonds and angles, and those observed experimentally. For example, in the case of peptide bonds, the average experimental C—N bond length (1.33 Å) from a survey of crystal structures from the Cambridge Crystallographic Data Bank differs markedly from both the gas-phase electron diffraction, and MP2/6-31G* values of 1.386 and 1.365 Å, respectively, computed for N-methylacetamide.^86,87 Similarly, the θ_eq value for the C—O—C angle in GLYCAM06 (111.6°) is smaller than the average values observed in α-(2→8) trisialoside (117°),⁸⁸ and generally in saccharides (116.5°).^89,90 Nonetheless, using tetrahydro-2-methoxy-5-(tetrahydro-2H-pyran-2-yloxy)-2H-pyran, Figure 1, the GLYCAM06 minimized structure gave a glycosidic valence angle of 116.8°, comparable with that found in experimental structures of glycosides.⁹⁰ When methyl α-D-Glcp(1→4)α-D-Glcp and methyl β-D-Glcp-(1→4)β-D-Glcp, Figure 1, were employed the glycosidic angles were 117.3° and 116.9°, respectively, which compared favorably with experimental observations.⁹⁰

Figure 1.

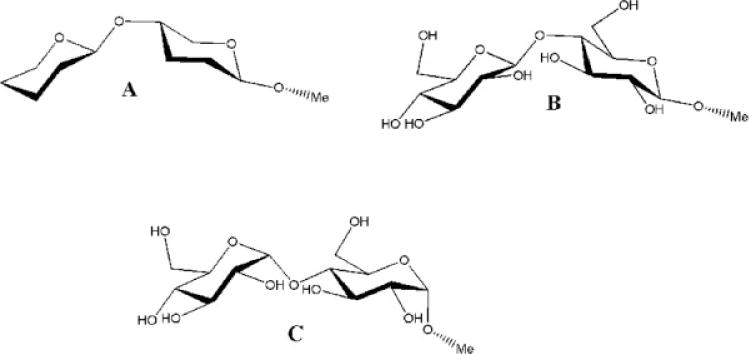
Tetrahydro-2-methoxy-5-(tetrahydro-2H-pyran-2-yloxy)-2H-pyran (A), methyl β-D-glucopyra-nosyl-(1→4)-β-D-glucopyranoside (B), and methyl α-D-glucopyranosyl-(1→4)-α-D-glucopyranoside (C).

The bond and angle parameters developed in this work are presented in Table 4. Only six out of 35 bond, and 20 out of 91 angle parameters were eventually transferred from the existing GLYCAM_93 parameter set.

Table 4.

Force Field Parameters in GLYCAM06.

Bond	Krb	reqc	Bond	Kr	req
C–OSa	450.0	1.323	C–HCa	331.0	1.090
CG–CG	310.0	1.520	C–H1	410.0	1.092
CG–HCa	340.0	1.090	OH–HOa	553.0	0.960
CG–H1a	340.0	1.090	N–Ha	434.0	1.010
CG–H2a	340.0	1.090	CY–OHa	320.0	1.410
CG–OH	320.0	1.430	CG–OS	285.0	1.460
CG–C	220.0	1.530	CG–OY	320.0	1.410
CG–N	337.0	1.450	CY–CG	310.0	1.520
C–Oa	570.0	1.229	CY–OSa	320.0	1.410
C–Na	490.0	1.335	CY–OYa	320.0	1.410
C–O2a	656.0	1.250	CY–C	220.0	1.530
Angle	Kθd	θeqe	Angle	Kθ	θeq
CG–OS–C	60.0	117.0	OS–CG–N	106.9	107.9
OS–C–Oa	80.0	125.0	CG–CG–Na	80.0	109.7
OS–C–CG	95.0	110.8	H1–CG–Na	50.0	109.5
HC–CG–HC	40.0	109.5	H2–CG–Na	50.0	109.5
H1–CG–H1	45.0	109.5	C–CG–CGa	63.0	111.1
H2–CG–H2	45.0	109.5	C–CG–HCa	50.0	109.5
CG–CG–HC	45.0	112.0	C–CG–H1a	50.0	109.5
CG–CG–H1	45.0	111.0	C–CG–H2a	50.0	109.5
CG–CG–H2	45.0	111.0	C–N–CGa	50.0	120.0
CG–CG–CG	45.0	113.5	CG–N–CGa	50.0	118.0
OH–CG–CG	70.0	107.5	H–N–CGa	30.0	118.0
H1–CG–OH	60.0	110.0	C–N–Ha	30.0	122.0
H2–CG–OH	60.0	110.0	H–N–Ha	35.0	120.0
CG–OH–HO	55.0	109.5	H2–C–N	55.0	112.4
CY–OH–HO	55.0	109.5	H2–C–O	55.0	112.2
CG–OS–CG	50.0	111.6	OS–CG–C	63.0	112.36
CT–OS–CG	50.0	111.6	O2–C–OHa	80.0	126.0
OS–CG–CG	70.0	108.5	OS–CY–CG	70.0	108.5
OY–CG–CG	70.0	108.5	OH–CY–CG	70.0	108.5
H1–CG–OS	60.0	110.0	OY–CG–CG	70.0	108.5
H1–CG–OY	60.0	110.0	OH–CY–C	63.0	112.4
H2–CG–OS	60.0	110.0	OS–CY–C	63.0	112.4
H1–C–O	60.0	110.0	OY–CY–C	63.0	112.4
H1–C–N	55.0	112.4	OY–CY–OH	100.0	112.0
OS–CG–OS	100.0	112.0	OY–CY–OS	100.0	112.0
OH–CG–OS	100.0	112.0	CG–CY–Ca	63.0	111.1
O2–C–O2	80.0	126.0	CG–OS–CY	50.0	111.6
O2–C–CG	70.0	115.0	CG–OY–CY	50.0	111.6
CG–C–Na	70.0	116.6	O2–C–CY	70.0	115.0
CG–C–Oa	80.0	120.4	HC–CG–CY	45.0	112.6
N–C–Oa	80.0	122.9	CG–CG–CY	45.0	113.5
N–CG–HCa	50.0	109.5
Torsion	Vnf/2	γg,nh	Torsion	Vn/2	γ,n
OS–CG–CG–C	−0.10	0.0, 3	OS–CG–OS–CT	0.37	0.0, 3
	0.10	0.0, 2		1.27	0.0, 2
	−1.00	0.0, 1		0.30	0.0, 1
OH–CG–CG–C	0.10	0.0, 3	OH–CG–OS–CG	0.37	0.0, 3
	0.20	0.0, 2		1.27	0.0, 2
	−2.50	0.0, 1		0.30	0.0, 1
CG–CG–OS–C	−0.04	0.0, 3	H2–CG–OS–CG	0.10	0.0, 3
	0.47	0.0, 1		0.60	0.0, 2
CG–OS–C–O	−3.20	0.0, 2	H2–CG–OS–CT	0.10	0.0, 3
CG–C–OS–CG	3.00	0.0, 2		0.60	0.0, 2
H1–CG–OS–C	0.00	0.0, 3	HC–CG–CG–OS	0.05	0.0, 3
OS–C–CG–HC	0.00	0.0, 3	HC–CG–CG–OY	0.05	0.0, 3
HC–CG–CG–HC	0.13	0.0, 3	H1–CG–CG–OS	0.05	0.0, 3
H1–CG–CG–HC	0.17	0.0, 3	H2–CG–CG–OS	0.05	0.0, 3
H2–CG–CG–HC	0.17	0.0, 3	H–N–C–O	−2.50	0.0, 2
H1–CG–CG–H1	0.17	0.0, 3		2.00	0.0, 1
H1–CG–CG–H2	0.17	0.0, 3	H–N–C–H1	−2.50	0.0, 2
HC–CG–CG–CG	0.10	0.0, 3	H–N–C–CG	0.0	0.0, 1
H1–CG–CG–CG	0.15	0.0, 3	HC–CG–C–O	0.0	0.0, 3
H2–CG–CG–CG	0.15	0.0, 3	HC–CG–C–N	0.0	0.0, 3
HO–OH–CG–H1	0.18	0.0, 3	CG–OS–CG–N	−0.90	0.0, 1
HO–OH–CG–H2	0.18	0.0, 3	OS–CG–CG–N	−1.30	0.0, 1
HO–OH–CY–OY	0.18	0.0, 3	OY–CG–CG–N	−1.30	0.0, 1
HO–OH–CY–C	0.18	0.0, 3	OH–CG–CG–N	−1.50	0.0, 1
HO–OH–CY–CG	0.18	0.0, 3	CG–CG–CG–N	0.40	0.0, 1
HO–OH–CG–CG	0.18	0.0, 3	HC–CG–CG–N	0.10	0.0, 3
CG–CG–CG–CG	0.45	0.0, 1	H1–CG–CG-N	0.10	0.0, 3
OH–CG–CG–HC	0.05	0.0, 3	H2–CG–CG–N	0.10	0.0, 3
OH–CG–CG–H1	0.05	0.0, 3	N–CG–CG–N	0.00	0.0, 1
OH–CG–CG–H2	0.05	0.0, 3	HC–CG–CG–C	0.10	0.0, 3
OH–CG–CG–CG	0.10	0.0, 3	H1–CG–CG–C	0.10	0.0, 3
OS–CG–CG–CG	−0.27	0.0, 1	CG–CG–CG–C	0.45	0.0, 1
OS–CG–CG–CY	−0.27	0.0, 1	CG–CG–N–C	0.00	0.0, 1
OY–CG–CG–CG	−0.27	0.0, 1	OS–CG–N–C	2.03	0.0, 2
H1–CG–OS–CG	0.27	0.0, 3		1.00	0.0, 1
CG–OS–CG–CG	0.16	0.0, 3	OS-CG-N-H	−0.43	0.0, 2
CT–OS–CG–CG	0.16	0.0, 3		1.52	0.0, 1
OH–CG–CG–OH	0.55	0.0, 3	CG–CG–N–H	0.10	0.0, 3
	0.95	0.0, 2	H1–CG–N–CG	0.00	0.0, 3
	−0.10	0.0, 1	H2–CG–N–CG	0.00	0.0, 3
OH–CG–CG–OS	0.25	0.0, 2	H1–CG–N–H	1.00	0.0, 1
	−1.10	0.0, 1	H2-CG-N-H	1.00	0.0, 1
OH–CG–CG–OY	0.25	0.0, 2	H1–CG–N–C	−1.00	0.0, 1
	−1.10	0.0, 1	H2-CG-N-C	−1.00	0.0, 1
H1–CG–CG–OY	0.05	0.0, 3	CG–N–C–O	−2.80	0.0, 2
OS–CG–CG–OS	0.82	0.0, 2	CG–N–C–CG	−2.70	0.0, 2
OS–CG–CG–OY	0.82	0.0, 2	HC–CG–C–O2	0.00	0.0, 1
OS–CG–OH–HO	0.18	0.0, 3	CG–CG–C–O2	−1.50	0.0, 2
OS–CG–OS–CG	0.37	0.0, 3	H1–CG–C–O2	0.00	0.0, 1
	1.27	0.0, 2	H2–CG–C–O2	0.00	0.0, 1
	0.30	0.0, 1	OS–CG–C–O2	−2.25	0.0, 2
			CG–OS–CG–C	0.00	0.0, 2
Torsion	Vn/2	γ, n	Torsion	Vn/2	γ,n
H1–CT–OS–CG	0.27	0.0, 3	OS–CY–CG–HC	0.05	0.0, 3
CG–OS–CT–CT	0.16	0.0, 3	OY–CY–CG–HC	0.05	0.0, 3
CT–OS–CG–CG	0.16	0.0, 3	CG–OS–CY–CG	0.16	0.0, 3
OS–CG–OS–CT	0.37	0.0, 3	CG–OY–CY–CG	0.16	0.0, 3
	1.27	0.0, 2	OH–CY–C–O2	−2.25	0.0, 2
	0.30	0.0, 1	OS–CY–C–O2	−2.25	0.0, 2
CG–N–C–CT	0.00	0.0, 2	OY–CY–C–O2	−2.25	0.0, 2
OY–CY–OS–CG	0.37	0.0, 3	CG–CY–C–O2	−1.50	0.0, 2
	1.27	0.0, 2	CG–OS–CY–C	3.50	0.0, 1
	0.30	0.0, 1	CG–OY–CY–C	0.00	0.0, 1
OH–CY–OY–CG	0.37	0.0, 3	HC–CG–CY–C	0.10	0.0, 3
	1.27	0.0, 2	CG–CG–CY–C	0.45	0.0, 3
	0.30	0.0, 1	CY–OS–CG–CG	0.16	0.0, 3
OS–CY–OY–CG	0.37	0.0, 3	CY–OY–CG–CG	0.16	0.0, 3
	1.27	0.0, 2	CY–OS–CG–H1	0.27	0.0, 3
	0.30	0.0, 1	CY–OY–CG–H1	0.27	0.0, 3
OH–CY–CG–CG	−0.27	0.0, 1	CY–CG–CG–CG	0.45	0.0, 1
OS–CY–CG–CG	−0.27	0.0, 1	CY–CG–CG–HC	0.10	0.0, 3
OY–CY–CG–CG	−0.27	0.0, 1	CY–CG–CG–H1	0.15	0.0, 3
OH–CY–CG–HC	0.05	0.0, 3	CY–CG–CG–OH	0.10	0.0, 3
Improper torsions
X–X–N–H	1.0	180.0, 2
X–X–C–O	10.5	180.0, 2
X–X–N–CG	1.5	180.0, 2
X–O2–C–O2	10.5	180.0, 2
X–O2–C–OH	10.5	180.0, 2
van der Waals
	R*i	εj
H	0.6000	0.0157
HO	0.0000	0.0000
HC	1.4870	0.0157
H1	1.3870	0.0157
H2	1.2870	0.0157
O	1.6612	0.2100
O2	1.6612	0.2100
OH	1.7210	0.2104
OS	1.6837	0.1700
OY	1.6837	0.1700
CG	1.9080	0.1094
CY	1.9080	0.1094
C	1.9080	0.0860

^aValence terms incorporated from the AMBER PARM94 parameter sets (CG corresponds to CT).

^bBond stretching force constant (kcal/mol Ų).

^cBond length (Å).

^dAngle-bending force constant (kcal/mol rad²).

^eAngle (degrees).

^fIndicates relative barrier to rotation (kcal/mol).

^gPhase factor (degrees).

^hPeriodicity or n-fold term in Fourier series expansion.

ⁱvan der Waals radius (Å).

^jMinimum energy in the Lennard-Jones 6–12 potential (kcal/mol).

Torsion Parameters

The GLYCAM_93 force field, as well as other current biomolecular force fields, such as the PARM99⁹¹ parameterization in AMBER, frequently employ a single atomic sequence to define the torsion properties for a given bond. For example, in GLYCAM_93, the rotation associated with the φ-angle was defined by the terms for the O₅—C₁—O_X—C_X sequence only; with a specific torsion term required for each α- and β-anomer. The related terms C₂—C₁—O_X—C_X and H1—C₁—O_X—C_X were explicitly set to zero. While this approach may lead to accurate reproduction of the QM rotational energy curves, it suffers from a lack of transferability. In view of making the parameters in GLYCAM06 fully transferable we adopted a more general approach wherein all atomic sequences had an explicitly defined set of torsion terms. Each term was derived by fitting to rotational energy curves for a molecular training set composed of relevant small molecules. Because of the symmetry of these small molecules, no phase angles were required. The omission of phase angles further facilitates parameter transferability. However, as each rotational energy is now the result of the sum of the contributions from the constituent atomic sequences, the overall accuracy is limited by the sum of errors in each term. The benefits in terms of applying to novel molecular classes is particularly important for carbohydrates as they frequently exist in highly derivatized forms in vivo.

Together with the nonbonded terms, torsion terms are crucially important for force fields to correctly model the conformational and particularly, the dynamic properties of macromolecules. As opposed to bond and angle parameters, in which only small excursions from equilibrium values are observed, torsional rotations may cover the entire range between 0 and 360°, and frequently exhibit more than one energy minimum. To achieve correct thermodynamic and kinetic behavior during MD simulations, it is important that both the relative energies of the minima and the barrier heights between them be reproduced. Thus, we not only sought to locate the minima and maxima, but also to reproduce all barrier heights. To assess the extent to which this had been achieved for each molecular class, the errors between the QM and MM rotational energies were computed over the entire range of the curves, <Error>_curve, and the minima, <Error>_minima, are presented in Table 5.

Table 5.

Average^a Overall Errors in the GLYCAM06 Torsional Energies Relative to B3LYP/6-31++ G(2d,2p)//HF/6-31G* Values for the Molecules and Specific Atomic Sequences in the Training Set.

			Relative error
Atomic sequence	A	B	<Errorb>curve	% of maximum barrierc	<Errord>minima
Hydrocarbons (Overall)			0.15	2.0	0.11
A–CG–CG–B	HC, CG	HC, CG	0.15	2.0
Alcohols (Overall)			0.45	5.0	0.28
A–CG–CG–B	OH, H1	OH, H1, HC, CG	0.50	6.0
A–OH–CG–B	HO	H1, CG	0.09	6.0
Ethers (Overall)			0.56	4.0	0.35
A–CG–CG–B	OS, H1	OS, H1, HC, CG	0.30	2.0
A–OS/OY–CG/CY–B	CG	OS, H1, H2	0.65	6.0
Amides (Overall)			0.64	4.0	0.38
A–N–C–B	H, CG	CG, O	1.14	7.0
A–CG–N–B	H1, CG	H, C	0.18	4.0
A–CG–C–B	HC, CG	O, N	0.63	7.0
A–CG–CG–B	N, H1	HC, H1, CG, N	0.41	4.0
Esters (Overall)			0.44	3.0	0.23
A–CG–C–B	HC	OS	0.02	8.0
A–CG–OS–B	H1,CG	C	0.46	4.0
A–OS–C–B	CG	CG, O	0.40	3.0
Carboxylates (Overall)			0.72	38.0	0.60
A–CG/CYe–C–B	HC, CG	O2	0.14	7.0
Ether alcohols (Overall)			0.61	6.0	0.59
A–CG–CG–B	OS, H1	OH, H1	0.61	6.0
Ether amides (Overall)			1.12	9.0	1.10
A–CG–N–B	OS, H2	H, C	1.93	15.0
A–OS–CG–B	CG	N, H2	0.64	9.0
A–CG–CG–B	N, H1	OS, H1	0.37	6.0
Alcohol amides (Overall)			0.49	5.0	0.41
A–CG–CG–B	OH, H1	N, H1	0.49	5.0
Ether carboxylates (Overall)			0.80	29.0	0.80
A–CG–C–B	OS, H1	O2	0.55	31.0
A–OS–CG–B	CG	C	1.18	42.0

^aThe polar moieties show the largest overall errors, which may not be surprising because the classical force field employed does not include atomic polarizabilities.

^bAverage relative error over entire curve.

^c(<Error>_curve/Maximum barrier height) × 100.

^dAverage relative error of mimima.

^eCY = CG and OY = OS in sialic acids only.

Hydrocarbons

Hydrocarbons provide the foundation for any biomolecular force field. As can be seen from the data in Table 5, the force field reproduced the gas-phase relative energies for these simple molecules very well, with an average error in the energies over the entire rotational energy curve of 0.15 kcal/mol and an error in the <Error>_minima of 0.11 kcal/mol.

Rotating about the central C_sp3—C_sp3 (CG—CG) bond in butane allowed us to examine how several torsion parameters performed collectively, namely those associated with the CG—CG—CG—CG, CG—CG—CG—HC, and HC—CG—CG—HC sequences. GLYCAM06 predicted the stabilization of the trans conformation, relative to the gauche conformation, of 1.16 kcal/mol, in reasonable agreement with both the B3LYP/6-3111G(2d,2p) value computed here of 0.95 kcal/mol and the experimental range of 0.74–0.90 kcal/mol.^92–94 For this molecule, the GLYCAM06 rotational barriers were determined to be 5.51 kcal/mol at 0° and 3.15 kcal/mol at 120°, which may be compared with the B3LYP/6-31++G(2d,2p) values of 5.80 and 3.33 kcal/mol, respectively, and with the experimental values⁹² of 4.56 and 3.62 kcal/mol, respectively.

Alcohols

The hydroxyl groups of alcohols make this class of compounds particularly relevant in the development of force fields for nucleic acids and carbohydrates. The overall errors in the fits for alcohols were <Error>_curve 5 0.45 kcal/mol and <Error>_minima = 0.28 kcal/mol. The alcohols with a single hydroxyl group were easier to fit and resulted in <Error>_curve = 0.20 kcal/mol, while the fit was slightly degraded for the diols with <Error>_curve = 0.73 kcal/mol.

Mono-Alcohols

Mono-alcohols were used for the derivation of parameters that involved hydroxyl groups without the inclusion of other electronegative groups. As relates to the rotational behavior of the hydroxyl protons, the H1—CG—OH—HO rotational barrier in methanol was determined at the B3LYP/6-31++G(2d,2p) level and with GLYCAM06 to be 1.03 and 1.08 kcal/mol, respectively, both in excellent agreement with the experimental value⁹⁵ of 1.07 kcal/mol. For ethanol, GLYCAM06 determined the trans conformation about the CG—CG—OH—HO torsion to be 0.34 kcal/mol more stable than the gauche conformation, which may be compared with the experimental value^95–97 of 0.40 kcal/mol, while the B3LYP/6-31++G(2d,2p) level overestimated the stability of the gauche conformer by 0.30 kcal/mol. The barrier to rotation between the gauche conformations was determined to be 1.11 kcal/mol, which compared well with the B3LYP/6-31++G(2d,2p) value and experimental range⁹⁸ of 1.01 kcal/mol and 0.8–1.2 kcal/mol, respectively. Similarly, for propan-2-ol, GLYCAM06 determined the gauche (defined by H1—CG—OH—HO) conformer to be more stable than the trans by 0.11 kcal/mol, which may be compared with the experimental^96,97 and QM values of 0.45 ± 0.21 and 0.24 kcal/mol, respectively. The GLYCAM06 value for the HC—CG—CG—OH rotational barrier in ethanol was found to be 3.09 kcal/mol, compared with the B3LYP/6-31++G(2d,2p) value of 3.07 kcal/mol, which both slightly underestimated the experimental range^95,99 of 3.32–3.55 kcal/mol.

Developing parameters for the CG—CG—CG—OH sequence was challenging due primarily to the different conformational preferences of this torsion in open-chain and cyclic systems. In open-chain systems, using n-propanol as an example, the gauche conformation computed here at the MP2/6-31++G(2d,2p)//MP2/6-31G** level, was favored over the trans by 0.21 kcal/mol. In contrast, the equatorial conformer of cyclohexanol¹⁰⁰ in which the sequence CG—CG—CG—OH is trans, is more stable than the axial conformation (CG—CG—CG—OH is gauche) by 0.56 kcal/mol. The differences between the open-chain and the cyclic preferences appear to reside in induction effects, which are difficult to account for in a classical mechanical treatment lacking polarizability.¹⁰¹ Therefore, GLYCAM06 was derived to slightly overestimate the trans conformation in n-propanol (0.77 kcal/mol) over the gauche to optimize the performance of this parameter in glycan rings. As a result, optimal agreement was achieved for the rotational energy profile of the equatorial conformation of hydroxymethylcyclohexane Figure 2, as well as in highly substituted open-chain alcohols, such as 2,2-dimethylpropanol and 1,1,2,2-tetramethylpropanol.

Figure 2.

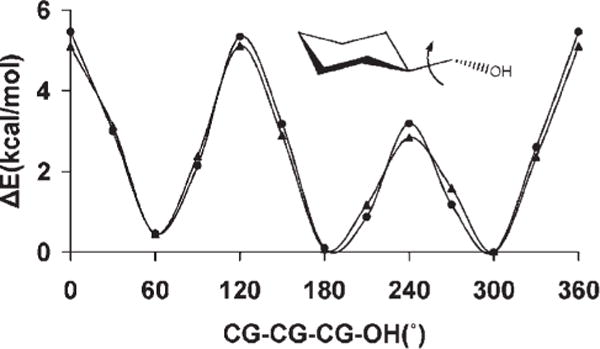
B3LYP/6-31++ G(2d,2p) (▲) and GLYCAM06 (●) rotational energy curves about the exocyclic CG-CG bond in hydroxymethylcyclohexane.

Diols

Diols mimic the atomic sequence, O—C—C—O prevalent in the vicinal hydroxyl fragments on the rings of common glycosyl residues. The torsional preferences for this linkage affect ring conformations as well as the rotamer preferences of exocyclic side chains, such as in sialic acid. This torsion term is most strongly influenced by the OH—CG—CG—OH parameters as well as by internal hydrogen bonding. To establish the relative contributions from each of these effects, rotational energy curves for the O—C—C—O linkage were computed both allowing and prohibiting the formation of internal H-bonds.²⁴ The ability of GLYCAM06 to reproduce these relative energies and trends was illustrated by the average error values <Error>_curve and <Error>_minima, in the rotational energy profiles. For example, in 2,3-butanediol <Error>_curve = 0.40 kcal/mol and <Error>_minima = 0.35 kcal/mol when internal H-bonding was allowed, while <Error>_curve = 0.34 kcal/mol and <Error>_minima = 0.21 kcal/mol when internal H-bonding was disallowed.

The presence of the OH—CG—CG—OH dihedral angle in the exocyclic glyceryl side chains of sialic acids such as 5-N-acetyl-neuraminic acid (Neu5Ac) is significant in determining the conformational properties of the side chain, Figure 3. The side chain features two dihedral angles, which bear the OH—CG—CG—OH sequence: ω₈ (O₇C₇C₈O₈) and ω₉ (O₈C₈C₉O₉). The tendency for the OH—CG—CG—OH angle to adopt the gauche conformation in simple diols has been referred to as the gauche effect.²⁴ However, in Neu5Ac, while ω₉ populates all three staggered rotamers, ω₈ predominantly exists in the trans conformation, as ascertained from both solution NMR^88,102–104 and X-ray crystallography^105,106 studies. A pair of intramolecular hydrogen bonds, between H8O and the oxygen atoms of the carboxylate group, and H7O and the carbonyl group of the amido moiety, appears to stabilize this rotamer. However, the magnitude of this stabilization is unclear, as the same trans preference for ω₈ is also observed in the β-anomer,¹⁰⁶ in which the intramolecular H8O-carboxylate H-bond is not possible. Application of the initial parameters for the OH—CG—CG—OH torsion term, generated by fitting to the QM rotational energy curves for compounds in the initial training set of diols, in solvated MD simulations, did not quantitatively reproduce the rotamer populations for the glyceryl side chain in Neu5Ac. In contrast to experimental data, the initial parameters led to a strong predilection for the gauche rotamer. Consequently a new approach was adopted in developing torsional parameters for the OH—CG—CG—OH atomic sequence.

Figure 3.

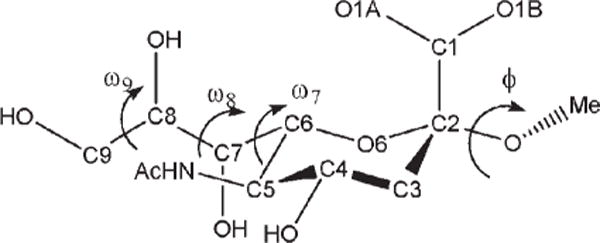
Key exocyclic torsion angles in α-neuraminic acid.

The initial values for the OH—CG—CG—OH torsion term were modified by systematically adjusting the V₁ coefficient until explicitly solvated MD simulations of Neu5Ac were able to reproduce the solution populations for ω₈. Because our goal was to increase the sampling of the trans rotamer of ω₈, and only the energy function of the V₁ coefficient has a single minimum at 180°, only this term was modified. Next, the effect of the different V₁ values on the stability of the ring conformations in selected monosaccharides was evaluated, because the OH—CG—CG—OH atomic sequence is also present in ring systems. Because the entire range of V₁ values were consistent with predicting the ring conformational preferences, and a series of MD simulations of Neu5Ac indicated that different V₁ values resulted in a predominant occurrence of the ω₈ trans rotamer, the most consistent value was finally determined by performing explicitly solvated MD simulations of 1,2-ethanediol, and selecting the value that best reproduced its experimentally determined rotamer populations.

The rotamer sampling of ω₈ in the glyceryl side chain, employing different V₁ values are presented in Table 6. Traversing these values from −1.0 to 1.0 kcal/mol resulted in an overall increase in the occurrence of the trans rotamer, indicating that an adjustment of this coefficient was necessary to reproduce the solution conformational properties of ω₈.

Table 6.

ω₈ (O7–C7–C8–O8) Trans and Gauche Rotamer Populations From a 10-ns Explicit Solvent MD Simulation of α-Neu5Ac as a Function of the V₁ Coefficient.

V1 (kcal/mol)	Trans	Gauche
−1.0	30	70
−0.8	59	41
−0.6	32	68
−0.4	41	59
−0.2	88	12
0.0	84	16
0.2	67	33
0.4	83	17
0.6	86	14
0.8	88	12
1.0	98	2

As mentioned earlier, the OH—CG—CG—OH term is also present in monosaccharide rings, most commonly existing in gauche relationships, Figure 4. Increasing the V₁ coefficient could induce a preference for the trans relationships of OH—CG—CG—OH dihedral angles present in ring systems, subsequently introducing artifactual ring flips during MD simulations. To determine whether the different V₁ coefficients had any influence on the stabilities of pyranose chair conformations when the parameters were employed in MD simulations, the MM generalized Born surface area (MMGBSA) implicit solvation model was used to compute the average MM energies of α-D-Manp and α-D-idopyranose (α-D-Idop) in both ⁴C₁ and ¹C₄ conformations. In the experimental solution conformations, α-D-Manp displays a single trans and two gauche O—C—C—O conformations in both the ⁴C₁ and ¹C₄ chair forms. In contrast, α-D-Idop displays three trans and three gauche O—C—C—O conformations in the ⁴C₁ and ¹C₄ chair forms, respectively.

Figure 4.

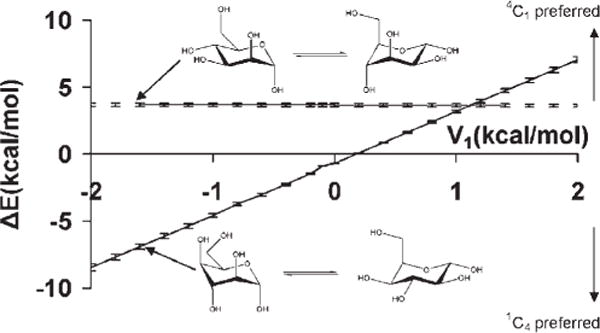
Differences in average molecular mechanical energies from MD simulation data (1 ns) for the ⁴C₁ and ¹C₄ chair forms as a function of the V₁ coefficient for the OH—CG—CG—OH atomic sequence in α-D-mannopyranose (upper), and α-D-idopyranose (lower).

For each monosaccharide, 1-ns explicit solvent MD simulations were performed in which the ring was either in the ⁴C₁ or ¹C₄ conformation. Snapshots were selected from the last 500 ps at 1 ps intervals from each simulation, and water molecules were removed. Using different V₁ coefficients the average MM energies of the individual chair conformers of each monosaccharide were determined by averaging the MMGBSA computed energies of the 500 selected snapshots. Over the entire range of V₁ values, the calculations predicted a consistent preference for the ⁴C₁ over the ¹C₄ conformations in α-D-Manp, Figure 3. This insensitivity of the α-D-Manp ring conformation relative to the V₁ coefficient can be attributed to the similar distribution of the trans and gauche O—C—C—O conformations in both chair forms. The preference for the ⁴C₁ over the ¹C₄ conformer is also expected due to the unfavorable axial configuration of the hydroxymethy1 group at C5, in addition to the energetically disallowed 1–3 interaction between the axial hydroxyl group at C3 and the C5 hydroxymethyl group. On the other hand, traversing the range of the V₁ coefficients in the α-D-Idop system, there was a preference for the ¹C₄ conformation at the negative extreme (−2.0 kcal/mol) with a progressive increase in the stabilization of the ⁴C₁ conformation toward the positive extreme (2.0 kcal/mol). This trend is expected because for negative V₁ coefficients, the V₁ energy profile as a function of dihedral angle has a maximum barrier at 180°, the reverse being true for positive coefficients. Thus the exclusive presence of the O—C—C—O trans conformations in the ⁴C₁ structure leads to a destabilization for negative V₁ values, but becomes a stabilizing factor for positive values of V₁.

From MD simulations of methyl α-Neu5Ac, observation of the ω₈ trans and gauche rotamer populations as a function of V₁, Table 6, indicated that the following values: −0.2, 0.0, 0.4, 0.6, 0.8, and 1.0 kcal/mol, would lead to rotamer preferences that were consistent with experimental data. In addition, the MMGBSA calculations showed that these coefficients would not cause spurious ring flips during MD simulations. Therefore, the most consistent coefficient was determined by performing explicit solvent MD simulations of 1,2-ethanediol, with V₁ ranging from −0.5 to 0.5 kcal/mol, in increments of 0.1 kcal/mol. The conformational properties of 1,2-ethanediol have been extensively investigated by both experimental and theoretical studies,^107,118 which predict a predominance of the gauche conformation, albeit to different extents, ranging from gauche:trans 99:1¹¹⁶ to 67:33.¹¹⁵ Experimental NMR data¹¹⁷ indicate a mixture of 80:20% gauche:trans populations in solvents with low dielectric constants. Chidichimo et al.¹¹⁰ reported the existence of only the gauche conformation. However, their studies were done using nematic-lyotropic crystalline solutions. A V₁ value of −0.1 kcal/mol best reproduced the experimental populations obtained in conditions most similar to those of the simulation, with a gauche:trans ratio of 81:19%. Using this value of −0.1 kcal/mol a PMF-WHAM analysis of methyl α-Neu5Ac with ω₈ as the reaction coordinate was carried out. This analysis produced an energy profile with the trans rotamer being more stable by ~1.0 kcal/mol relative to the + gauche conformer, and 1.2 kcal/mol with respect to the −gauche conformer, Figure 5. The rotational barriers to transition between +gauche and −gauche conformers were ~2.4 and 3.4 kcal/mol, respectively, indicating some transition to the +gauche rotamer. The MD simulations correctly predicted the solution behavior of the glyceryl ω₈ torsion, Figure 5. To assess further the extent to which these new parameters were able reproduce the B3LYP/6-31++G(2d,2p) rotational energies, the rotational energy curves for the O—C—C—O torsions for 2,3-butanediol were determined for comparison, Figure 6. As expected, when intramolecular hydrogen bonds are allowed, there is a stabilization of the gauche conformers over the trans conformer. When intramolecular hydrogen bonds are excluded, by constraining the hydroxyl proton to a trans orientation (HO—OH—CG—CG = 180°), or by substituting the hydroxyl protons with methyl groups, electrostatic repulsions between the oxygen atoms reverse the relative stabilities of the rotamers, resulting in the trans rotamer being the most stable. The <Error>_curve = 0.87 kcal/mol and <Error>_minima = 0.35 kcal/mol when internal H-bonding was allowed, and <Error>_curve = 1.04 and <Error>_minima = 0.61 kcal/mol when internal H-bonding was disallowed. Comparing these error values to those determined using the initial OH—CG—CG—OH parameters, indicated that the present parameters resulted in fits that were slightly less accurate. However, this slight degradation was necessary for the correct prediction of the solution conformational properties of the glyceryl side chain of sialic acid.

Figure 5.

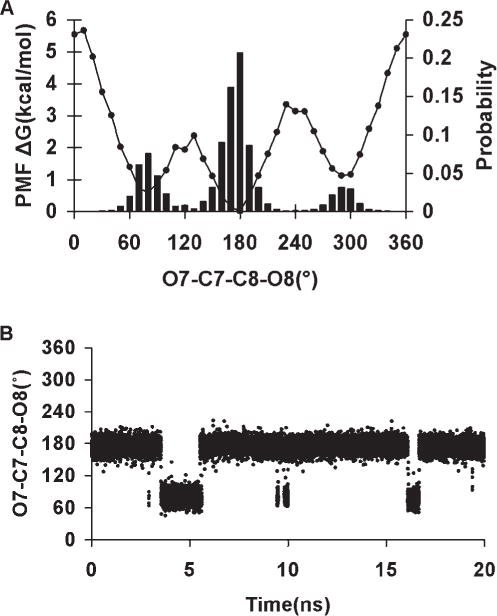
PMF-WHAM analysis for the ω₈ (O7—C7—C8—O8) torsion in α-5-N-acetyl-neuraminic acid (A). ω₈ population sampling over a 20-ns MD trajectory (86% trans and 14%-gauche) V₁ = −0.1 kcal/mol (B).

Figure 6.

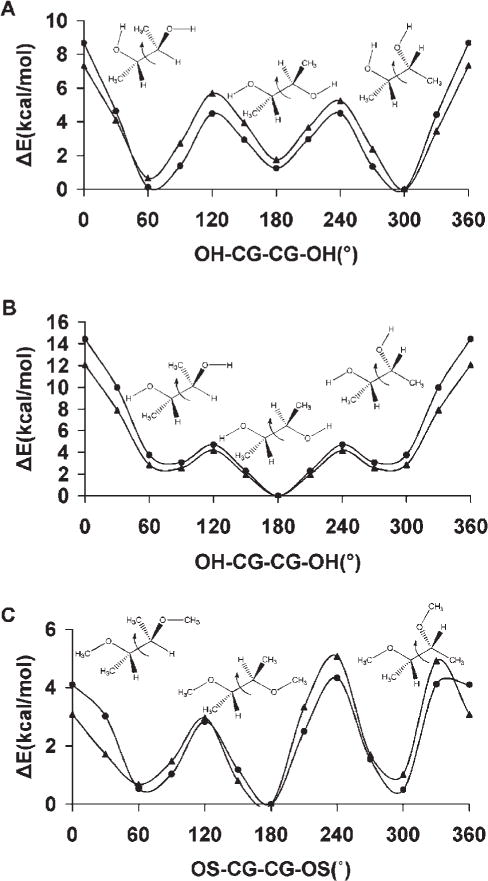
Rotational energy curves for 2,3-butanediol, with internal H-bonds (A), without internal H-bonds (B) and (C) 2,3-dimethoxybutane in which internal H-bonds are prohibited by the substitution of hydroxyl protons with methyl groups. B3LYP/6-31++ G(2d,2p) (▲); GLYCAM06 (●).

Ethers

The parameters derived from ethers are important to the accurate description of carbohydrate ring conformational properties as well as the rotational properties of glycosidic linkages. The overall accuracy of the derived torsion terms is indicated in the <Error>_curve and <Error>_minima of 0.56 and 0.35 kcal/mol, respectively. In methoxymethane, GLYCAM06 yielded a rotational barrier for the H1—CG—OS—CG torsion of 2.31 kcal/mol, in reasonable agreement with the B3LYP/6-31++G(2d,2p) and experimental values¹¹⁹ of 2.43 and 2.62 kcal/mol, respectively.

The OS—CG—CG—OS torsion term is particularly important for glycans having a 1→6 linkage. The simplest molecule exhibiting this torsion term is 1,2-dimethoxyethane (DME). A single V₂ coefficient of 0.82 kcal/mol for this term leds to good overall reproduction of the gas-phase data for the entire set of diethers, with a value of <Error>_curve = 0.30 kcal/mol (Table 5) for the OS—CG—CG—OS and associated parameters. This term is also significant in branched glycans, which may exhibit glycosidic linkages between vicinal hydroxyl groups within the glycan ring. Incorrect parameters for this term may alter the conformational stability of the glycan ring. To quantify the behavior of the parameters for this linkage, we examined the rotational properties of the central C_sp3—C_sp3 (CG—CG) bond in 2,3-dimethoxybutane. As can be seen from the data in Figure 6, the parameters well reproduced the QM data for 2,3-dimethoxybutane.

To assess further the applicability of the parameters for the OS—CG—CG—OS sequence to solution phase studies, the conformer populations of DME from a 20-ns explicit solvent MD simulation were compared with those determined from solution phase experimental data. The conformers were characterized by the rotational preferences of the dihedral angles composed of the C_sp3—O_sp3 (CG—OS) bonds, and the central CG—CG bond; with T and G denoting the trans and gauche conformations, respectively. Theoretical^120–122 and experimental^123–125 techniques have been employed to elucidate these conformational properties in aqueous solutions at different DME concentrations, and in the gas phase. There was a general preference for the G rotamer around the CG—CG bond, and for the T rotamer around the CG—OS bonds, with the major conformers identified as the TTT, TGT, TGG′, TGG, and TTG.¹²⁴ Notable, were the observations that the populations of the various conformers differed in aqueous solutions relative to those present in neat liquid or in the gas phase. The populations also displayed a dependence on temperature. In the gas phase, the TTT, TGT, and TGG′ were the major rotamers, while in neat liquid and aqueous solutions, the TGT and TGG were predominant,^123,124 indicating that DME-DME and DME-H₂O interactions influenced rotamer populations. Thus, our 20-ns MD-derived conformer populations were compared with those observed experimentally at low DME concentrations. The populations determined from the MD simulations could be ranked as: TGT (56%), TGG (13%), TTT (11%), TGG′ (10%), TTG (6%), and others (4%), which concurred qualitatively with experimental observations that the TGT and TGG predominate.^123,124

Anomeric Linkages

Anomeric linkages, represented by the C—O—C—O torsion angle common to all carbohydrates, are often modeled in pyranosides by tetrahydro-2-methoxy-2H-pyran (axial) and tetrahy-dro-2-methoxy-2H-pyran (equatorial), corresponding to α- and β-pyranosides, respectively.^21,126 In GLYCAM_93, reproduction of the C—O—C—O rotational energies for the α- and β-link-ages was accomplished by using unique torsion parameters for each anomer, which were distinguished by different atom types for the anomeric carbon atom. Here, we use a single parameter for both anomeric configurations. Both GLYCAM06 and GLYCAM_93 correctly reproduced the B3LYP/6-31++G(2d,2p) rotational energy profiles, with <Error>_curve values of 0.45 kcal/mol (GLYCAM06) and 0.3 kcal/mol (GLYCAM_93), for the α-glycosides, while for the β-glycosides the <Error>_curve values were 0.36 kcal/mol (GLYCAM06) and 0.57 kcal/mol (GLYCAM_93). Therefore, employing a torsion term common to both α- and β-glycosides did not lead to degradation in the fit to the relevant rotational energy curves. As depicted in Figure 7, GLYCAM06 reproduced the rotational topologies for both α- and β-anomers, showing good quantitative agreement with the B3LYP/6-31++G(2d,2p) energies. The HF/6-31G* rotational energy curve for tetrahydro-2-methoxy-2H-pyran (axial) displayed a global minimum at 60°, and a less stable local minimum at 300°, while for tetrahydro-2-methoxy-2H-pyran (equatorial), the global minimum was at 300° with a local minimum 5 kcal/mol higher at ~60°. Three of these minima are consistent with the minima based on expectations due to the stabilizing exo-anomeric effect,¹²⁷ and the repulsive steric interactions. However, the minimum of tetrahydro-2-methoxy-2H-pyran (axial) located at 300° has not been observed experimentally, even though it displays a stabilizing exo-anomeric effect, presumably due to large steric repulsions between the hydrogen atoms of the aglycon and that of C2. This structure was subjected to a subsequent optimization at the MP2/6-311++G(2d,2p) level of theory, during which it collapsed to the global minimum energy structure with the C—O—C—O torsion of ~60°.

Figure 7.

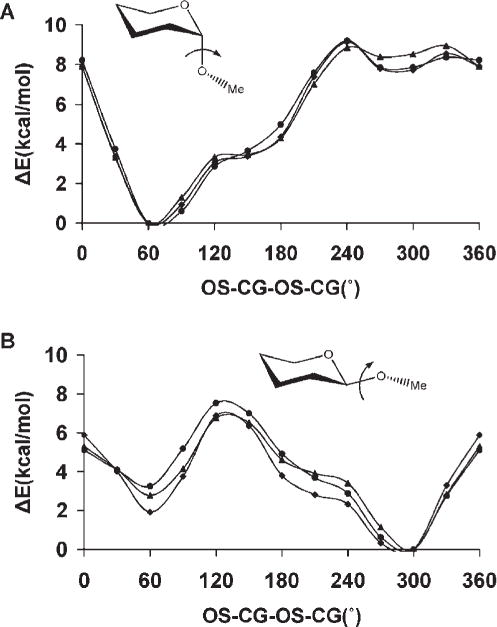
B3LYP/6-31++ G(2d,2p) (▲), GLYCAM06 (●) and GLYCAM_93 (◆) rotational energy curves about the CG-OS bond in tetrahydro-2-methoxy-2H-pyran (axial), (A), and tetrahydro-2-methoxy-2H-pyran (equatorial), (B), for the united-atom (GLYCAM06) and all-atom (GLYCAM_93) charge models.

Amides and Esters

Amide and ester parameters are relevant to a carbohydrate force field since many monosaccharides contain N- and O-acetyl moieties. In addition, N-linked glycans are attached via an amide bond to asparagine side chains in glycoproteins.

The exact extent of deviation from planarity in the ground-state amido groups, and the origin of the large barrier to rotations about the N_sp2—C_sp2 (N—C) bond in amides have been the subject of an extensive study.¹²⁸ From their highest level calculation (CCSD(T)/PVTZ) Fogarasi and Szalay found that the optimized structure of methanamide was exactly planar. It is accepted that the large barrier to rotation is associated with the breaking of π-delocalization at 90°. Langley and Allinger.¹²⁹ observed that the rotational barrier is sensitive to which proton is rotated and the out-of-plane distortion of the proton not constrained by the torsional rotation. When either H—N—C—O torsion angle for one proton is driven above 90°, the unconstrained proton lags behind and follows an out-of-plane, rather than a purely torsional, energetic pathway.¹²⁹ Consequently, in acetamide the two different H—N—C—O dihedral angles were both varied counterclockwise from 0 to 90°, and from 180° to 90°, resulting in two transition states at the 90° angle having rotational barriers of 13.96 and 10.87 kcal/mol, corresponding to the 0→90° and 180→90° paths, respectively. In both transition states the nitrogen atom is pyramidal. In the lower energy state the unconstrained proton is closer to the carbonyl oxygen (H_unconst—N—C—O = 22°), while in the higher energy state this proton is farther from the oxygen atom (H_unconst—N—C—O = −154°). The rotational energies in GLYCAM06 were in line with the B3LYP/6-31++G(2d,2p) values, although GLYCAM06 underestimated the barrier heights by ~2.0 kcal/mol in each case, Figure 8. In general, the amide parameters performed well, giving <Error>_curve = 0.64 kcal/mol and <Error>_minima = 0.38 kcal/mol.

Figure 8.

B3LYP/6-31++G(2d,2p) (▲) and GLYCAM06 (●) rotational energy curves about the N—C bond in (A) acetamide, (B) N,N-dimethylacetamide, and (C) N-methylacetamide.

To determine the torsion terms relevant to substituted amides, the rotational energy curves of N-methylacetamide and N,N-dimethylacetamide were utilized. The latter molecule enabled the derivation of a rotational profile consisting solely of the two coupled torsion terms (CG—N—C—O/CG—N—C—CG), while N-methylacetamide allowed us to examine the transferability of the CG—N—C—O/CG—N—C—CG and the H—N—C—O/H—N—C—CG coupled torsion pairs. As it is impossible to separate these terms, coupled through a 180° phase-shift, the energy contributions were derived by simultaneously fitting to the QM-derived rotational energy curve, employing torsional angles of θ° (CG—N—C—O) and θ + 180° (CG—N—C—CG), in a nonlinear least-squares approach. For N,N-dimethylaceta-mide GLYCAM06 gave the rotational barrier about the N_sp2—C_sp2 bond to be 14.6 kcal/mol, which is lower than the B3LYP/6-31++G(2d,2p) value of 16.9 kcal/mol. However, GLYCAM06 is in better agreement with the NMR determined¹³⁰ effective barrier of 15.3 kcal/mol, Figure 8. The transferability of the GLYCAM06 parameters was illustrated by the reproduction of the B3LYP/6-31++G(2d,2p) rotational energy curve for the N_sp2—C_sp2 bond in N-methylacetamide, in which the trans rotamer was correctly predicted to be less stable than the cis rotamer, Figure 8. N,N-dimethylacetamide was also used to parameterize the CG—N—CG—H1/C—N—CG—H1 coupled torsion pair. The C—N—CG—H1 torsion is present in N-acetylated carbohydrates, and its parameters are relevant to the C—N—CG—H2 linkage present in N-linked sugars. GLYCAM06 gave a rotational barrier of 0.64 kcal/mol for the N—CG bond, which may be compared with the B3LYP/6-31++G(2d,2p) value of 0.59 kcal/mol.

Esters were employed for generating parameters necessary for extending the force field to model the properties of O-acetylated carbohydrates such as those common in certain bacterial capsular polysaccharides, and in the sialic acid residues of higher animals.¹³¹ The overall <Error>_curve computed for the parameters of the following atomic sequences H1—CG—OS—C, HC CG C—OS, CG—OS—C—O, CG—OS—C—CG and CG—CG—OS—C were 0.03, 0.02, 0.18, 0.62, and 0.45 kcal/mol, respectively.

The GLYCAM06 rotational energy barrier for the O-methyl group (H1—CG—OS—C) in methyl acetate was 0.91 kcal/mol which can be compared with the B3LYP/6-31++G(2d,2p) and microwave¹³² values of 0.87 and 1.22 kcal/mol, respectively. The negligible rotational energy barrier for the acetyl-methyl group (HC—CG—C—OS) of 0.25 kcal/mol was also in good agreement with both B3LYP/6-31++G(2d,2p) (0.23 kcal/mol) and experimental (0.29 kcal/mol) values.¹³² In esters, the CG—OS—C—O and CG—OS—C—CG dihedral angles are coupled through a 180° phase-shift. The parameters for these atomic sequences were derived by following the same simultaneous fitting approach employed in developing the coupled parameters (CG—N—C—O/CG—N—C—CG) in amides, with torsional angles of θ° (CG—OS—C—O) and θ + 180° (CG—OS—C—CG). This simultaneous fit resulted in V₂ values of −3.20 and 3.0 kcal/mol for CG—OS—C—O and CG—OS—C—CG atomic sequence, respectively. The GLYCAM06 rotational energy curve for the CG—OS—C—O sequence resulted in a local minimum at 180°, which was 7.52 kcal/mol less stable than the global minimum at 0°. This relative energy underestimated the IR spectroscopy¹³³ value of 8.5 ± 1.0 kcal/mol, but was comparable to the B3LYP/6-31++G(2d,2p) value of 7.48 kcal/mol.

Lastly, N-tert-butylacetamide and N-(tetrahydro-2H-pyran-3-yl) acetamide were utilized to determine the coupled torsion parameters (CG—CG—N—H/CG—CG—N—C) and (H1—CG— N—H/CG—CG—N—C), while ethyl acetate and tetrahydro-2H-pyran-3-yl acetate were employed in deriving the C—OS— CG—CG parameters, Figure 9. The B3LYP/6-31++G(2d,2p) rotational energy curve for the CG—CG—N—C sequence in N-tert-butylacetamide resulted in a threefold 120° periodic profile, which GLYCAM06 reproduced with <Error>_curve = 0.05 kcal/mol. For this rotation in tetrahydro-2H-pyran-3-yl acetate, however, both GLYCAM06 and the B3LYP/6-31++G(2d,2p) energies resulted in asymmetric profiles with a broad low energy global minimum at 90°, which was ~1.75 kcal/mol more stable than a local minimum at 300°. The minimum energy structure at 90° is consistent with the conformational properties of the acetamido moiety in the solid-phase structures of Neu5Ac methyl ester and its monohydrate,^106,134 as well as the solution-phase NMR structure of β-D-2-deoxy-2-N-acetylglucopyranoside,¹³⁵ in which the carbonyl group almost eclipses the ring C—H bond. This spatial orientation results in an approximate trans dihedral angle between the amide proton and the ring aliphatic hydrogen atom in the H1—CG—N—H sequence. It should be noted that at the global minimum of the CG—CG—N—C sequence being driven, the H1—CG—N—H dihedral angle is approximately at the trans conformation. The ability of these parameters to model their corresponding rotational energy curves was reflected in the <Error>_curve and <Error>_minima values of 0.52 and 0.08 kcal/mol, respectively, Figure 9. However, during a 10-ns MD simulation of N-acetyl 2-deoxy-N-acetyl-β-D-glucopyranoside employing the QM-derived parameters, rotation about the C_sp3—N_sp2 (CG—N) bond to the local minimum (τ_C-N-C2-H2 ≈ 180°) occurred after ~1 ns. This rotamer remained stable throughout the remainder of the simulation. A very recent experimental and QM-NMR study of the conformational properties of this group in GlcNAc indicated that the H—C_sp3—N_sp2—H atomic sequence exists only in the trans low energy con-formation(τ_{C–N–C2–H2} ≈ 0°), but displays broad librations around that minimum.¹³⁶ Therefore, to increase the stability of the H1—CG—N—H trans rotamer, and ultimately prevent this conformational transitions from occurring, V₁ terms were introduced for the H1—CG—N—H and H1—CG—N—C parameters to determine a reasonable value. The V₁ coefficients were varied from 0.0 to 2.0 kcal/mol in increments of 0.5 kcal/mol, and PMF calculations were performed for each value, employing N-(tetrahydro-2H-pyran-3-yl) acetamide with the C1—C2—N—C dihedral angle as the reaction coordinate. Based on the ~2 kcal/mol increase in the relative energy of the local minimum, Figure 9, the pair of values 1.0 and −1.0 kcal/mol was selected for the H1—CG—N—H and H1—CG—N—C torsion parameters, respectively. Employing these values, a 50-ns MD simulation performed with N-acetyl 2-deoxy-N-acetyl-β-D-glucopyranoside did not display any conformational transitions of the acetamido moiety. The origin of the observed solution-phase transitions, when employing the purely QM-derived torsion terms, remains undetermined.

Figure 9.

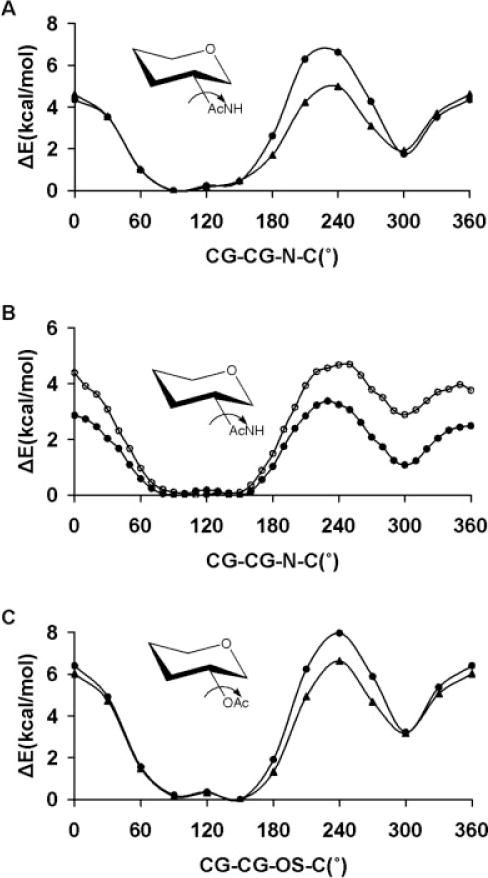
Rotational energy curves about the N—CG bond in N-(tetrahydro-2H-pyran-3-yl) acetamide (A), B3LYP/6-31++G(2d,2p) (▲), GLYCAM06 (●), H1—CG—N—H (V₁ = 0.0 kcal/mol) and H1—CG—N—C (V₁ = −0.17 kcal/mol), in vacuum. PMF-WHAM analysis for the CG—CG—N—C sequence in N-(tetrahydro-2H-py-ran-3-yl) acetamide, H1—CG—N—H (V₁ = 1.0 kcal/mol) and H1—CG—N—C (V₁ = −1.0 kcal/mol) (O) and H1—CG—N—H (V₁ = 0.0 kcal/mol) and H1—CG—N—C (V₁ = −0.17 kcal/mol) (●), (B), in explicit solvent. Rotational energy curves about the OS—CG bond in tetrahydro-2H-pyran-3-yl acetate, B3LYP/6-31++G(2d,2p) (▲), GLYCAM06 (●), (C).

In the case of ethyl acetate, rotating the about the C_sp3—O_sp3 bond in the atomic sequence (CG—CG—OS—C) resulted in a symmetric B3LYP/6-31++G(2d,2p) energy curve, which produced a large barrier (7.45 kcal/mol) at 0°, with minima at the trans configuration as well as at 90° and 270°. A negligible QM-determined rotational energy barrier (0.83 kcal/mol) separated the global trans minimum from the local minima at 90° and 270°. These results were consistent with previous theoretical studies of ethyl acetate.¹³⁷ GLYCAM06 reproduced the B3LYP/6-31++G(2d,2p) relative energies over the entire curve with <Error>_curve = 0.45 kcal/mol. As for the CG—CG—OS—C rotation in tetrahydro-2H-pyran-3-yl acetate, both B3LYP/6-31++G(2d,2p) and GLYCAM06 produced similar asymmetric energy profiles, Figure 9. The <Error>_curve for this atomic sequence was 0.54 kcal/mol. To assess the extent to which GLYCAM06 could model other O-acetylated pyranosyl moieties, rotations were performed around the C_sp3—O_sp3 bond in both tetrahydro-2-methoxy-2H-pyran-3-yl acetate and (tetra-hydro-2H-pyran-2-yl)methyl acetate, Figure 10. Unlike the rotational energy profile of tetrahydro-2H-pyran-3-yl acetate, the energy profile of tetrahydro-2-methoxy-2H-pyran-3-yl acetate resulted in a barrier to rotation at ~30°, which could arise from Coulombic repulsions between the carbonyl oxygen and the oxygen atom of the methoxy group. Compared to the QM-value, GLYCAM06 underestimated this repulsion by about 2.31 kcal/mol. Overall, there was a good reproduction of the B3LYP/6-31++G(2d,2p) data (<Error>_curve values of 0.89, and 0.50, kcal/mol, respectively).

Figure 10.

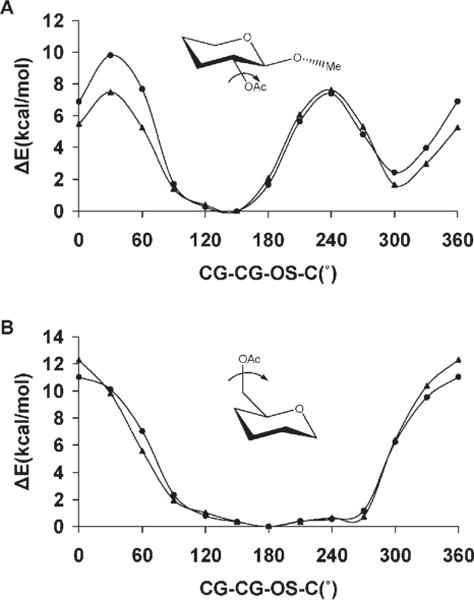
B3LYP/6-31++ G(2d,2p) (▲), and GLYCAM06 (●) rotational energy curves in (A) tetrahydro-2-methoxy-2H-pyran-3-yl acetate and (B) (tetrahydro-2H-pyran-2-yl)methyl acetate.

Carboxylates

Under physiological conditions, the extent to which carboxylate groups are ionized depends on their pKa. In the case of the ionic state it should be noted that it will never exist in the absence of a counter ion, such as sodium. It is generally presumed that uronic and ulosonic acids exist in the ionized form, and parameters were derived accordingly, with exceptions noted below. The B3LYP/6-3111G(2d,2p) rotational energy curve about the C_sp2—C_sp3 (C—CG) bond in 2-methylpropanoate displayed minima at 120° and 300°. For this rotation, GLYCAM06 was fit to the MP2/cc-pVDZ rotational energies, Figure 11, with <Error>_curve and <Error>_minima values of 0.72 and 0.60 kcal/mol, respectively. The QM-determined rotational energy barrier of the carboxyl group was 0.8 kcal/mol. This is a very low rotational barrier, which is less than the room temperature equipartition energy of a molecule (kT). Thus during an MD simulations, free rotations of the carboxylic group about the C—CG bond are expected. To this extent, it was more important to ensure reasonable barriers to rotation, than to identify the minima.

Figure 11.

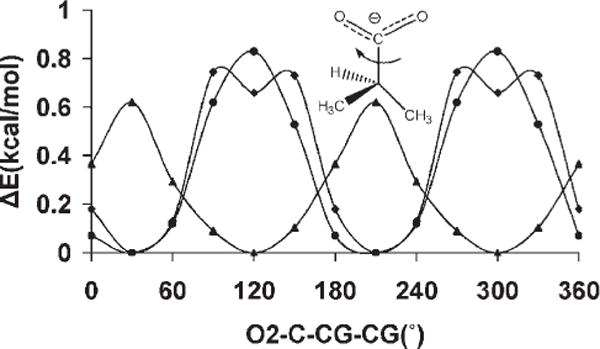
QM and GLYCAM06 rotational energy curves about the C—CG bond in 2-methylpropanoate MP2/cc-pVDZ (◆), B3LYP/6-3111G(2d,2p) (▲),GLYCAM06 (●).

In addition to the O2—C—CG—CG torsion term, modeling uronic acids also required the development of parameters for the OH—CG—CG—C and OS—CG—CG—C sequences. The OH—CG—CG—C parameters were derived using 2-hydroxy-proponoate as the model compound, by simultaneously fitting to two sets of curves: with and without the presence of an internal hydrogen bond between the hydroxyl and carboxyl groups. For the OH—CG—CG—C rotations, the <Error>_curve was 0.79 kcal/mol and <Error>_minima was 0.31 kcal/mol (with the inclu sion of intramolecular H-bond), while <Error>_curve and <Error>_minima were 0.96 mol⁻¹ and 0.16 kcal/mol, respectively (when the H-bond was disallowed). The <Error>_curve and <Error>_minima for the OS—CG—CG—C rotations were 1.15 and 0.09 kcal/mol, respectively.

Mixed Functional Groups

Mixed functional groups that are present in carbohydrates include the alcohol–ethers, alcohol–amides, and ether-amides. alcohol–ethers are required in the derivation of torsion terms that model the torsion angles involving the ring oxygen and the C2 hydroxyl group as well as the glycosidic ether oxygen and other ring hydroxyl groups. These molecules with mixed functionalities can form intramolecular H-bonds, hence rotational energy curves were derived in the presence and absence of internal H-bonds, as appropriate. The B3LYP/6-31++G(2d,2p) and GLYCAM06 OH—CG—CG—OS rotational energy curves for 2-methoxybutan-3-ol are shown in Figure 12. Overall for ether-alcohols, the <Error>_curve was 0.61 kcal/mol with a value of 0.59 kcal/mol for the <Error>_minima.

Figure 12.

B3LYP/6-31++G(2d,2p) (▲) and GLYCAM06 (●) rotational energy curves about the CG—CG bond in 2-methoxybutan-3-ol with internal hydrogen bonds (A) and without internal hydrogen bonds (B).

The highly polar mixed functionality of ether–amides was challenging to parameterize (Fig. S1, supplementary materials), as indicated in the overall values of <Error>_curve = 1.12 kcal/mol and <Error>_minima = 1.10 kcal/mol. In terms of carbohydrates, the OS—CG—N—C parameter is relevant to the modeling carbohydrate–protein linkages. In this set of parameters, the OS—CG—N—C parameter was the least accurate with <Error>_curve = 1.93 kcal/mol. The other ether amide parameters performed better as can be seen in Table 5.

To determine the torsion parameters associated with the OH—CG—CG—N rotation, molecules having both alcohol and amide functionality were employed. The overall values for <Error>_curve and <Error>_minima were 0.49 and 0.41 kcal/mol, respectively. The performance of these parameters is exemplified by N-ethanolacetamide as shown in Figure 13.

Figure 13.

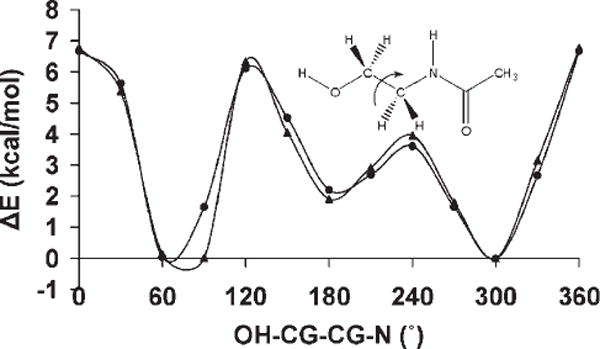
B3LYP/6-31++G(2d,2p) (▲) and GLYCAM06 (●) rotational energy curves about the CG—CG bond in N-ethanolacetamide.

Special Cases

Ulosonic Acids

For GLYCAM06 to correctly model the glycosidic conformational properties of ulosonic acids such as 5-N-acetylneuraminic acid (Neu5Ac), a class of sugars frequently present at the termini of eukaryotic cell surface glycans, accurate parameterization of the anomeric angle φ (C_xC_xO_x−1C_x−1) is required, Figure 3. Unlike most glycosyl residues, ulosonic acids contain a carboxyl functional group attached to the anomeric carbon atom, which alters the rotational preferences for the φ-angle in this class of compounds. In solution, the φ-angle predominantly exists in two conformations, −gauche and trans, in an ~1:1 ratio.^104,138 The torsion term (C—CY—OS—CG) associated with the carboxylate group for Neu5Ac contributes significantly to the φ-angle conformation in these carbohydrates. Generating parameters for this torsion term proved challenging; exhibiting ether–carboxylate mixed functionality. Initial MD simulations of the glycoside of methyl α-Neu5Ac employing parameters generated by fitting to gas-phase QM rotational energy profiles of either ionized or protonated 2-methoxypropanoate resulted in the sampling of only the −gauche rotamer about the φ-angle of methyl α-Neu5Ac. The inability of the initial parameters to reproduce experimental φ populations may originate from the omission of charge polarizabilities in the force field. Thus, we took the approach of empirically varying the V₁ coefficient of this term until we obtained the proper rotamer distribution for φ from explicitly solvated simulations of methyl α-Neu5Ac. By changing the V₁ value from 1.0 to 8.0 kcal/mol it was possible to shift the preference of the sampling from predominantly —gauche to exclusively trans. An intermediate value of 3.5 kcal/mol reproduced the experimental rotamer distribution, Figure 14. Employing this V₁ term, a PMF analysis was carried out to determine the energy profile of the φ-angle in methyl α-Neu5Ac in solution, Figure 14. The PMF results indicated that the −gauche and trans conformers now displayed similar relative energies in solution, with a stabilization energy of ~2.3 kcal/mol over the +gauche. The rotational energy barrier between the −gauche and trans conformers was ~1.4 kcal/mol. The small barrier to rotation results in the frequent transitions between the two rotamers, as observed in the MD simulation trajectory, Figure 14. To assess whether this new torsional coefficient could model a mixed system of ionized and neutral carboxylic acid groups, the GLYCAM06 rotational energy curve for the rotation around the exocyclic C_sp3—O_sp3 (C₁—O₁) bond was compared with the B3LYP/6-31++G(2d,2p) curves for both ionized and neutral (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid, Figure 15. Notably, the GLYCAM06 rotational behavior appeared to be a compromise between each of the QM curves in ionized and neutral (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid.

Figure 14.

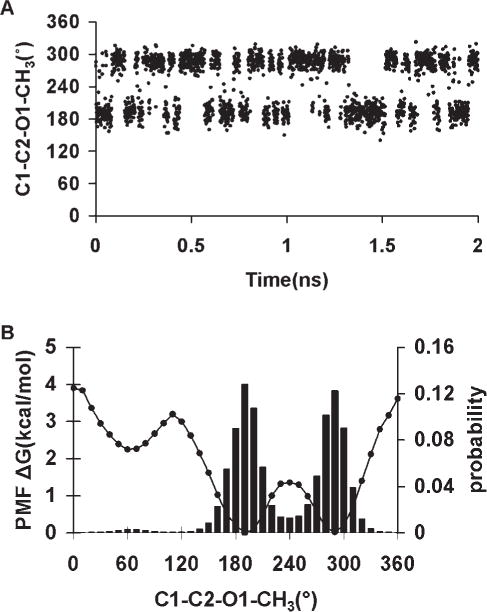
Population distributions from a 2-ns MD simulation trajectory V₁ = 3.5 kcal/mol, (A). Potential of mean force (PMF) and statistical weighted-histogram analysis method (WHAM) for φ (C_x—C_x—O_x−1—C_x−1) in methyl α-5-N-acetylneuraminic acid, (B).

Figure 15.

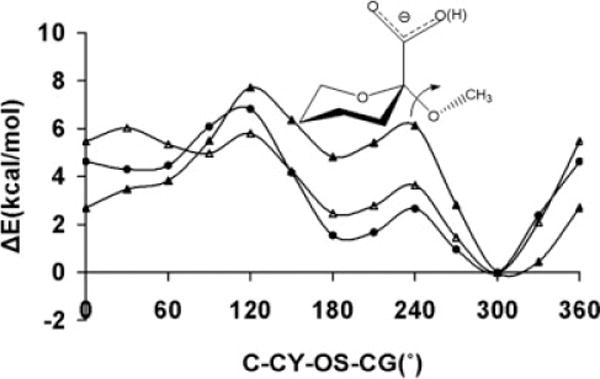
The rotational energy curves about the CG—OS bond in (R)-tetrahydro-2-methoxy-2H-pyran-2-carboxylic acid computed with GLYCAM06 (●) employing the ionized species, and at the B3LYP/6-31++G(2d,2p) level for both the ionized (▲) and neutral (△) species.

Force Field Validation

In the course of developing torsion parameters for molecules in the training set, most of the parameters were validated concurrently by determining how well GLYCAM06 was able to reproduce the B3LYP/6-31++G(2d,2p) rotational energy curves for test molecules, or by performing MD simulations and comparing MD-computed rotamer populations to those observed experimentally. In this section, we extend the validation by examining how the parameters collectively perform in selected glycans.

Unlike the earlier parameterization of GLYCAM,²¹ which was based on carbohydrate-specific analogues, only small representative molecules of a broad diversity were employed in the derivation of GLYCAM06. Therefore, validation of the force field by comparison with carbohydrate molecules provides an independent assessment of the ability of this small-molecule-based approach to model carbohydrate properties. Explicit solvent MD simulations (50 ns) were performed for α-D-GlcpOMe, α-D-GalpOMe and α-D-ManpOMe, and compared with NMR experimental data, such as rotamer populations and scalar ³J-couplings. While scalar ³J-couplings can rarely provide a complete picture of the structural properties of carbohydrates, when combined with nOe distances both datasets can provide valuable insights about oligosaccharide conformational properties. Average ring puckering parameters were also computed from the MD simulation data and compared with solid phase neutron diffraction data. The comparison of ring puckering parameters between gas-phase and crystallographic data is not ideal. However, Momany and Willet¹³⁹ have shown that the geometrical properties of pyranosyl rings from gas-phase B3LYP/6-31G* calculations were remarkably close to those determined in the solid-phase, suggesting that the packing environment may not have a significant effect on the geometry of the ring.

In solution, the rotamer preferences of the ω-angle (O₅—C₅—C₆—O₆) involving the exocyclic hydroxymethyl group are greatly influenced by the stereochemistry at the C4 position and the polarity of the solvent.²⁸ The three accessible staggered rotamers about the C₅—C₆ bond are generally designated gauche–gauche (gg), gauche–trans (gt), and trans–gauche (tg) with respect to the dihedral angles O₅—C₅—C₆—O₆ and C₄—C₅—C₆—O₆, respectively. A significant test of a carbohydrate force field is its ability to reproduce the rotamer populations about the C₅—C₆ exocyclic bonds because the populations are sensitive to the energetic balance between the formation of intramolecular and solute–solvent hydrogen bonds.¹⁴⁰ The ability of GLYCAM06 to reproduce the NMR J-couplings for the C₅—C₆ bond is reflective of the performance of its dihedral, nonbonded, and electrostatic components.

Homonuclear scalar ³J-couplings between the H₅—C₅— C₆—H_6R/H_6S hydrogen atoms from a 50-ns explicit solvent MD simulation of α-D-GlcpOMe were computed, employing an experimentally parameterized Karplus equation.¹⁴¹ Values computed over the entire trajectory resulted in coupling constants of 5.4 ± 1.7 Hz and 2.9 ± 2.0 Hz for ³J_H5H6R and ³J_H5H6S, respectively, which compared favorably with experimental values,^142–144 Table 7. In the course of the MD simulation, rotations about the exocyclic C₅—C₆ bond resulted in each of the rotational states of the ω-angle being populated. The MD gg:gt:tg populations, 62:36:2, were in good agreement with the experimentally observed populations of 57:38:5¹⁴⁴ and 53:47:0.¹⁴²

Table 7.

Scalar ³J-Couplings (Hz) and Exocyclic Hydroxymethyl Rotamer Populations Computed from MD Simulation (50 ns) Versus Experimental Data for Methyl α-D-Glcp and α-D-Galp.

	3JH5,H6R	3JH5,H6S	gg (%)	gt (%)	tg (%)
Methyl α-D-Glcp
Experimenta	5.49	2.39	53	47	0
Experimentb	5.4	2.3	57	38	5
GLYCAM06	5.4 ± 1.7	2.9 ± 2.0	62	36	2
Methyl α-D-Galp
Experimenta	7.8	6.0	14	47	39
Experimentb	8.6	3.7	16	75	9
Experimentc	8.3	4.0	21	61	18d
			13	70	17e
			15	69	16f
GLYCAM06	7.9 ± 1.6	3.7 ± 1.8	8	75	18

^aRef. 142.

^bRef. 144.

^cRef. 143.

^dEmploying equations A (Table 3), with the ³J_HH values derived from a Karplus equation that includes the effects of the electronegativities, and orientations of α-substituents).

^eEmploying equations B1 (Table 3), with the ³J_HH values derived from a Karplus equation that includes the effects of the electronegativities, and orientations of α-substituents).

^fEmploying equations G (Table 3), with the ³J_HH values derived from a Karplus equation that includes the effects of the electronegativities, and orientations of α-substituents).

Similar J-calculations were performed for α-D-GalpOMe, the C-4 epimer of Glcp. From the MD data, the ³J_H5H6R and ³J_H5H6s coupling constants were 7.9 ± 1.6 and 3.7 ± 1.8 Hz, respectively. Several experimental values have been reported for the ³J_H5H6R/S coupling constants and the gg:gt:tg populations of α-D-GalpOMe, Table 7. The MD-computed values for ³J_H5H6R and ³J_H5H6S fell within the experimental ranges of 7.8–8.6 Hz and 3.7–6.0 Hz, respectively.^142–144 With respect to the gg:gt:tg populations, the MD values of 6:76:18 showed good agreement with the more recent data.

In addition to bond rotational properties, pyranose ring puckering parameters, ring interproton torsion angles and distances provide another means of assessing the accuracy of the ring geometry. Analyses of the Cremer and Pople¹⁴⁵ ring puckering parameters over the 50-ns MD simulations of α-D-GlcpOMe, α-D-GalpOMe and α-D-ManpOMe indicated stable ⁴C₁ ring chair forms, with (Q,θ) values of (0.55 ± 0.04, 6 ± 10), (0.57 ± 0.04, 24 ± 8) and (0.55 ± 0.04, 1 ± 10), respectively, which were in good agreement with the values determined from solid state neutron diffraction experiments of (0.57, 2.3),¹⁴⁶ (0.57, 4.9),¹⁴⁷ and (0.56, 0), respectively.¹⁴⁶

Ring interproton distances and dihedral angles are a source of NMR-restraints employed in determining the ring geometries of glycans. In addition, the distances provide internal calibration references employed in the elucidation of glycan conformational properties from nOe data. Thus, the feasibility of employing GLYCAM06 to predict glycan ring conformational properties was determined by its ability to reproduce experimental interproton distances and dihedral angles. A comparison of interproton distances and dihedral angles computed using GLYCAM06, and those determined from neutron diffraction data^146,147 for α-D-GlcpOMe, α-D-GalpOMe and α-D-ManpOMe is presented in Table 8. To make a direct comparison between experimental and theoretical data, the coupling constants between vicinal ring-hydrogen atoms were computed from solvated MD simulations of α/β-D-GlcpOMe, α/β-D-GalpOMe, and α/β-D-ManpOMe, and compared with available solution-phase NMR experimental data, Table 9. The overall agreement between the GLYCAM06-derived and experimental data are quite good. However, theoretical and experimental values for the ³J_H4H5 and ³J_H1H2 constants in α/β-D-GalpOMe and β-D-ManpOMe, respectively, were in weaker agreement. Superimpositions of the crystal structures with energy-minimized and average ring geometries of these pyranosides, computed from the MD simulations did not reveal any structural distortions (Fig. S2, supplementary materials). This error may be arising from electronic hyperconjugative effects between the lone pair of electrons on the ring oxygen atom and the antibonding orbital of the C5—H5 or the C1—H1 bonds when the anomeric center is in the β-configuration, which are not included in classical force fields. Using the B3LYP functional with the cc-pV5ZT and 5s2p1d basis sets for hydrogen and heavy atoms, respectively, QM NMR predictions from the B3LYP/aug-cc-pVTZ optimized neutron diffraction structures of α- and β-D-GalpOMe resulted in ³J_H4H5 values of 1.9 and 1.2Hz, respectively.

Table 8.

Distances and Dihedral Angles Between the Ring Hydrogen Atoms Computed From MD Simulation (50 ns) Versus Experimental Data for Methyl α-D-Galp, α-D-Glcp and α-D-Manp.

	α-D-GalpOMe		α- D-GlcpOMe		α- D-ManpOMe
	Experimenta	GLYCAM06	Experimentb	GLYCAM06	Experimentb	GLYCAM06
H1–H2	2.396	2.40 ± 0.1	2.473	2.41 ± 0.1	2.562	2.52 ± 0.1
H1–H3	3.827	3.83 ± 0.1	3.795	3.86 ± 0.1	3.817	3.79 ± 0.1
H1–H4	4.874	4.95 ± 0.1	4.065	4.23 ± 0.1	4.109	4.21 ± 0.1
H1–H5	3.605	3.75 ± 0.1	3.634	3.74 ± 0.1	3.639	3.78 ± 0.1
H2–H3	3.053	3.05 ± 0.1	3.046	3.05 ± 0.1	2.440	2.42 ± 0.1
H2–H4	3.792	3.83 ± 0.1	2.500	2.78 ± 0.2	3.829	3.86 ± 0.1
H2–H5	3.907	3.99 ± 0.1	3.919	4.00 6 0.1	4.057	4.17 6 0.1
H3-H4	2.436	2.45 6 0.1	3.033	3.05 ± 0.1	3.053	3.05 ± 0.1
H3–H5	2.485	2.53 ± 0.2	2.607	2.76 ± 0.2	2.592	2.66 ± 0.2
H4–H5	2.457	2.45 ± 0.1	3.050	3.04 ± 0.1	3.070	3.05 ± 0.1
H1C1C2H2	50.49	51.07 ± 7.5	56.86	54.02 ± 7.7	−69.03	−67.21 ± 6.9
H2C2C3H3	−176.08	−175.74 ± 7.3	−178.44	−171.18 ± 7.9	−53.69	−54.98 ± 6.9
H3C3C4H4	53.97	55.99 ± 6.9	174.53	166.95 ± 8.4	172.41	172.99 ± 7.7
H4C4C5H5	−59.23	−58.12 ± 6.8	−175.73	−171.72 ± 8.4	−173.52	−171.59 ± 8.3

^aRef. 147.

^bRef. 146

Table 9.

Ring ³J_HH Computed From a 50-ns MD Simulation Using GLYCAM06 Compared with Experimental Values. (Experiment/GLYCAM06).

Spins	α-D-GlcpOMe	β-D-GlcpOMe	α-D-GalpOMe	β-D-GalpOMe	α-D-ManpOMe	β-D-ManpOMe
3JH1H2	3.8/3.5 ± 0.8	8.0/9.9 ± 0.5	4.0/3.8 ± 0.8	7.9/9.8 ± 0.9	1.8/2.2 ± 0.5	0.9/3.0 ± 0.7
3JH1H2	9.8/9.9 ± 0.4	9.4/9.7 ± 0.6	10.3/10.1 ± 0.2	9.9/10.0 ± 0.4	3.5/3.4 ± 0.8	3.2/3.2 ± 0.8
33JH1H2	9.1/9.7 ± 0.6	9.2/9.7 ± 0.6	3.4/3.3 ± 0.7	3.4/3.2 ± 0.8	9.5/10.0 ± 0.3	9.6/10.0 ± 0.4
3JH1H2	10.1/9.9 ± 0.4	9.7/10.0 ± 0.4	1.0/3.0 ± 0.7	1.1/2.9 ± 0.7	–	9.7/9.9 ± 0.6

Another indication of the performance of a biomolecular force field is its ability to reproduce experimentally determined unit cell geometries. In general, unit cell dimensions are influenced by internal torsional rotations as well as by van der Waals and electrostatic intermolecular interactions. However, it is recognized that in polar molecules such as carbohydrates, the treatment of electrostatics is crucial in reproducing experimental crystal geometries.³¹ The suitably of the present treatment of electrostatics in GLYCAM06 was assessed by comparing the average difference between the unit cell geometries of a methyl α-D-Glcp crystal computed from a 1-ns MD simulation to those determined experimentally.⁶³ The average difference computed with GLYCAM06 was 1.2 Å, which showed better performance when compared with the average differences computed with GLYCAM_93,²¹ CHARMM HGFB,¹⁴⁸ and GROMOS (93)¹⁴⁹ of 1.7, 1.8, and 1.6 Å, respectively.

The results of the frequency calculations, assignments, and comparisons to the various experimental results are summarized in Figure 16. The character of the assignments generated by our program is illustrated in Table 10, where we have listed the primary motion assigned by DMODES to each vibrational frequency for the monomer calculated by NMODE. The notations are described in the caption. The assignments for the monomer were also checked by visually inspecting corresponding plots of the atom positions with energy-weighted motion vectors. For the comparisons with experiment, the DMODES-generated assignments were grouped into the broader classes used in Figure 16, Figure 17 and Table 11.

Figure 16.

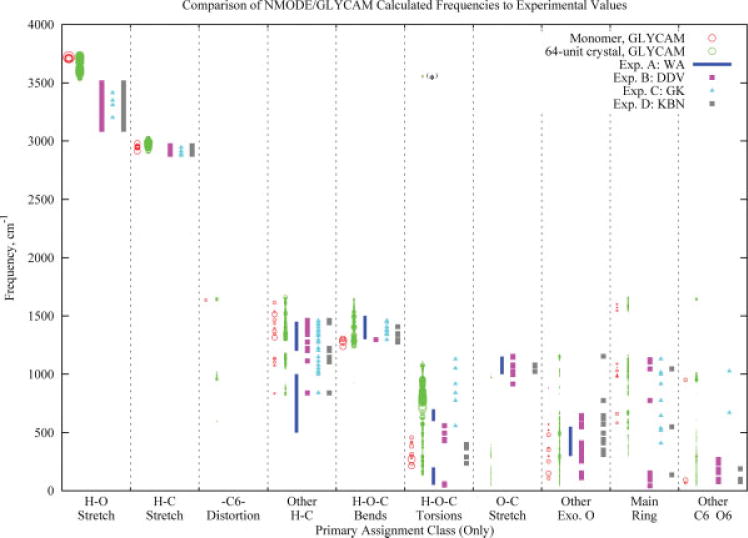
Comparison with experimental results of frequencies calculated by NMODE/GLYCAM for a monomer and a 64-unit crystal. The diameter of the circles for the calculated values corresponds to the relative kinetic energy associated with the motion used to determine the assignment, and not to photoabsorption intensity. For the monomer, the kinetic energy is relative to only the one molecule; for the crystal, it corresponds to a motion in a particular molecule, but relative to all 64 molecules. Some frequencies included here might not be observable by IR and/or Raman spectroscopy. Calculated crystal frequencies lower than 40 cm⁻¹ are not included in the figure. In the list of assignment classes, “Exo. O” refers to exocyclic oxygens, oxygen atoms connected to the main ring but that are not part of the ring. (*) These frequencies occurred in a single molecule at the face of the crystal and are not expected to occur frequently in nature. Citations: (A) Wells and Atalla⁷¹; (B) Dauchez et al.⁶⁷ (C), Gregurick and Kafafi⁷⁰; (D) Kuttel et al.⁶⁸ Please see the text for further discussion of the figure. The details of the individual assignments, as well as the frequencies, eigenvectors, etc., can be obtained by contacting the authors.

Table 10.

Primary Assignments for Monomer Frequencies Calculated by NMODE/GLYCAM.

Frequency, cm−1	Primary assignment
66	T[O6-C6-H61(1.000)]
91	T[O6-C6-C5(1.000)]
107	U(ETO)[O3(1.064),O4(0.904),O2(0.568),[&B,O3-C3-H3(1.000)]]
149	U(ETO)[O1(0.976),[&T,O1-C1-C2(1.000)]]
214	T[H4O-O4-C4(1.000)]
231	T[H4O-O4-C4(1.000),H6O-O6-C6(0.498),C6-O6-H6O(0.427), C6-C5-C4(0.422)]
253	U(ECO)[O1(1.027),[&S,O1-HO1(1.000)][&B,O1-C1-C2(1.000)]]
272	T[H6O-O6-C6(1.000)]
282	T[H2O-O2-C2(1.000)]
298	U(ECO)[O3(0.950),O4(0.907),O2(0.377),[&B,O4-C4-C3(1.000)]]
303	T[HO1-O1-C1(1.000)]
313	T[HO1-O1-C1(1.000)]
353	U(ERBO)[O3(1.076),[&S,O3-C3(1.000)]]
369	U(ERBO)[O2(0.982),[&B,O1-C1-H1(1.000)]]
382	T[H2O-O2-C2(1.000)]
410	T[H3O-O3-C3(1.000)]
422	T[H3O-O3-C3(1.000),HO1-O1-C1(0.742)]
458	T[H3O-O3-C3(1.000)]
481	U(RB)[O5(0.833),[&B,O5-C1-C2(1.000)]]
521	U(ROPD)[O5(0.735),C4(0.668),[&T,O5-C5-C4(1.000)]]
570	U(RC)[O5(0.657),C3(0.505),[&S,O5-C1(1.000)]]
584	U(RC)[C4(0.974),C5(0.734),[&B,C4-C3-O3(1.000)]]
661	U(RB)[C1(0.929),O5(0.386),[&T,C1-O1-HO1(1.000)]]
835	ST[H61(1.000),H62(0.620)]
881	U(RB)[O5(0.335),[&S,C1-H1(1.000)]]
951	T[C6-C5-O5(1.000)]
977	U(ROPD)[C4(0.870),[&T,C4-C3-O3(1.000)]]
983	U(RB)[C1(0.616),C4(0.356),[&T,C3-C4-O4(1.000)]]
995	U(RC)[C1(0.770),O5(0.755),[&S,C1-O5(1.000)]]
1028	U(ROPD)[C5(1.005),C2(0.388),[&S,C5-H5(1.000)]]
1054	U(RC)[C5(0.316),[&T,C3-C4-H4(1.000)]]
1073	U(ECH)[H3(0.989),[&T,H3-C3-O3(1.000)]]
1088	U(RB)[C2(0.768),C4(0.667),[&S,C2-O2(1.000)]]
1103	U(ECH)[H4(0.953),H5(0.877),[&T,H4-C4-O4(1.000)]]
1130	U(ETH)[H5(0.837),H4(0.529),[&T,H5-C5-C4(1.000)]]
1135	U(ECH)[H2(0.964),[&T,H2-C2-O2(1.000)]]
1236	B[HO1-O1-C1(1.000)]
1274	B[H3O-O3-C3(1.000)]
1285	B[H2O-O2-C2(1.000)]
1302	B[H6O-O6-C6(1.000)]
1303	B[H4O-O4-C4(1.000),H6O-O6-C6(0.588)]
1315	ST[H61(1.000),H62(0.900)]
1344	U(ECH)[H5(0.821),H4(0.802),[&T,H5-C5-O5(1.000)]]
1367	U(ECH)[H2(0.985),[&T,H2-C2-O2(1.000)]]
1393	U(ETH)[H4(1.005),H2(0.725),[&B,H3-C3-C4(1.000)]]
1433	U(ETH)[H2(0.984),H3(0.896),[&T,H2-C2-C1(1.000)]]
1466	U(ETH)[H5(0.923),H4(0.630),[&T,H5-C5-C4(1.000)]]
1513	U(ETH)[H1(0.999),[&T,H1-C1-C2(1.000)]]
1537	U(ECH)[H5(0.857),[&T,H5-C5-C6(1.000)]]
1545	U(RC)[C4(0.921),C1(0.456),[&T,C3-C2-H2(1.000)]]
1571	U(RB)[C3(0.580),[&S,C2-C1(1.000)]]
1599	U(RB)[C2(0.799),C4(0.558),[&T,C2-C1-O1(1.000)]]
1613	AT[H62(1.000),H61(0.999)]
1635	S[C6-O6(1.000),C6-C5(0.868)]
2912	SS[H61(1.000),H62(0.975)]
2944	U(EOPSH)[H3(0.993),H4(0.873),H2(0.434),[&S,H3-C3(1.000)]]
2947	U(ERBH)[H1(0.894),[&S,H1-C1(1.000)]]
2947	U(ERBH)[H1(0.893),[&S,H1-C1(1.000)]]
2951	U(EOPSH)[H5(1.000),H2(0.947),H3(0.422),[&S,H5-C5(1.000)]]
2956	U(EOPSH)[H4(0.997),H3(0.980),[&S,H4-C4(1.000)]]
2980	AS[H62(1.000),H61(0.954)]
3709	S[H2O-O2(1.000)]
3711	S[H6O-O6(1.000)]
3711	S[H4O-O4(1.000),H6O-O6(0.518)]
3714	S[H3O-O3(1.000),H4O-O4(0.420)]
3720	S[HO1-O1(1.000)]

Assignment notation details: Assignments begin with a class abbreviation (e.g., S, AT, ETH, etc.) and are followed by a list of atom sets significantly involved in that sort of motion. In any atom set, the first atom is the one whose motion is being considered. Stretches and bends are referenced to 1 and 2 other valence-connected atoms, respectively. Torsions are referenced to only two other atoms (and not three) because torsional motion is considered as being about a given bond. For toroidal and circumferential (ring) motions, each set includes only the atom(s) moving most significantly with respect to the ring. The weights in parentheses are a general indication of the significance of the motion. Weights for simple (non-ring) motions are all scaled so that the maximum significance is 1. Weights for ring-related motions are scaled accordingly, but after the simple motions are scaled, so their significances might be greater than one. Assignment abbreviations: Simple motions are noted without prefix or suffix. They are: S = stretch; B = bend; T = torsion. Complex motions typically have a prefix, a suffix, or both, in addition to an indication of motion type. The motion types, in addition to those employed in simple modes are: OPS = out of plane stretch (axial atoms); OPD = out of plane distortion; RB = ring “breathing” (expansion/contraction) motion; RC = ring circumferential motion; RT = ring toroidal motion. The prefix E indicates that the motion is of exocyclic atoms (O or H). In the combinations ET and EC, the T stands for toroidal and the C, for circumferential. The prefix S or A represents “symmetric” or “asymmetric.” For example, SS indicates symmetric stretch of two equivalent atoms. An “O” or “H” suffix indicates oxygen or hydrogen. A lack of a suffix indicates motion of the main ring. Concerted ring-related motions that do not fall easily into one of the above classes are prefixed with “U.”

Figure 17.

Range of frequencies associated with C—O and C—C stretches as calculated by NMODE/GLYCAM for the 64-unit monomer. The figure includes all C—O and C—C stretches in each molecule, regardless of relative importance to the mode. Circle diameters correspond to the relative kinetic energy associated with the stretching motion within the mode (see also discussion of Fig. 16). The experimental range is taken from Wells and Atalla,⁷¹ and corresponds to “heavy atom stretches.”

Table 11.

Comparison of Vibrational Analyses for the α-D-Glucopyranose Monomer Using Geometries Computed at the Molecular Mechanics and Quantum Mechanics Levels.

NMODE GLYCAM	B3LYP /6-31++g(2d,2p)//6-31++g(2d,2p)		HF/6-31G*//6-31G*
Frequency cm−1	Frequency cm−1	IR Intensity (kmmol−1)	Frequency cm−1	IR Intensity (kmmol−1)
		H—O Stretches
3720	3857	39.1	4132	63.8
3714	3851	40.3	4119	56.3
3711	3826	45.9	4099	59
3711	3825	52	4095	95.4
3709	3811	49.4	4089	56.1
		H—C Stretches
2980	3063	43.3	3283	78.6
2956	3057	15.7	3270	32.8
2951	3040	19.7	3266	34.3
2947	3031	17	3224	56.9
2947	3012	42.4	3207	58.6
2944	2992	17.9	3195	2.8
2912	2988	58.4	3189	49.8
		—C6— Distortions
1635	1458	12.2	1635	0.6
	1065	52.3	1206	37.4
	421	3.2	463	42.7
	Other H—C (Bends, Distortions, Toroidal and Circumferential Motions)
1613	1498	6.9	1667	7
1537	1441	19.1	1620	11
1513	1416	13.3	1593	6
1466	1410	3.8	1583	25.1
1433	1387	1.9	1567	27.5
1393	1382	12.6	1552	47.9
1367	1366	8.1	1536	30.5
1344	1357	4.8	1515	23.2
1315	1351	38.3	1502	17.7
1135	1290	7	1486	26
1130	1281	13.5	1416	6.4
1103	1265	14.7	1402	42.4
1073	1232	20.9	1368	91.3
835	1222	22.1	1300	102.5
	1194	25.7	944	24.5
	850	12.8
		H–O—C Bends
1303	1276	62.3	1437	72.5
1302			1339	51.6
1285			1321	57.5
1274
1236
		H–O—C Torsions
458	384	65.1	444	84.8
422	366	58.7	424	51.9
410	360	44.9	419	105.2
382	332	93	386	98.9
313	226	79.7	306	20.1
303	221	50.8	262	123.2
282	171	94	252	55.4
272			207	90.3
231
214
		Other Exocyclic (Non-Ring) O Motions
881	1102	72.2	1298	69.2
570	1042	287.4	1274	190.4
521	637	28	696	25.6
481	555	23.7	602	18.3
369	534	18.9	581	51.4
353	436	25.7	486	65.9
298	400	38.5	399	17.2
253	269	13.6	293	2.8
149	251	8.6	274	2.9
107	247	9.9	155	1.8
	143	3.9
	113	3
		Motions of the Ring
1599	1464	12	1258	142.8
1571	1148	53.8	1255	29.1
1545	1129	13.3	1228	25.6
1088	1117	95.9	1215	207.9
1054	1082	71.9	1152	16.6
1028	1075	42.2	1126	32
995	1049	112.1	1099	16.5
983	1012	43	979	20.5
977	995	14.3	851	49.3
661	908	12.2	653	43.7
584	770	38.4
	595	22.1
		Other Motions of C6 and O6
951	306	14.3	1193	60.8
91	94	6.4	334	9.3
66	65	0.9	123	2.4
			106	4.7
			75	2.9

In general, the agreement between the calculated frequencies and the experimental results is good, with the only notable exceptions being the H—O stretches, which are about 5% blue-shifted. This deviation is likely due to the use of the gas-phase H—O stretching frequency for methanol in the initial derivation of the AMBER HO—OH stretching constant.¹⁵⁰ Since the gas-phase H—O stretching frequency of methanol is about 360 cm⁻¹ higher than the liquid phase value, it is reasonable to expect that a smaller force constant would produce better results in the condensed phases.

We have chosen to use the standard AMBER values for the H—O stretches, and also the H—C, for two reasons. First, we wish to minimize the introduction of new atom types, and associated complications, into the AMBER force field. Second, fitting force constants to quantum-derived separation energies for these bond stretches does not improve the function of the force field. Instead, the quantum derived force constants increase the normal mode frequency disagreement to 10–20%. However, although the current values work well, the AMBER force field is used primarily for condensed-phase simulations, so it may be valuable to reevaluate the use of the current HO—OH stretching constant.

Although the O—C stretches seem in Figure 16 to differ by ~50%, the issue is more complex, and is partly one of assignment. As with the experimental work, we also see O—C stretches in the region ~ 1000–1200 cm⁻¹, as is illustrated for the 64-mer in Figure 17. However, according to our molecular mechanics analysis of the monomer and the 64-mer, as well as the quantum analyses of the monomer (Tables 10 and 11 for the monomer data), the O—C stretches do not account for the major portion of the vibrational kinetic energy at these frequencies. In Figure 17, we present all frequencies calculated for the crystal that corresponded to a C—C or O—C stretch. The figure shows that the calculation yields many C—C and O—C stretches in the range of “heavy atom stretches” given by Wells and Atalla.⁷¹ The more intense stretches at the lower frequencies are all parts of larger, more complex motions that would not typically be assigned as stretches, so frequencies in these ranges are not expected to correspond to experiment. On the other hand, the presence of the cluster of high-frequency C—C stretches, about 1400–1600, is puzzling. The cause of the discrepancy is not known. Kuttel et al.,⁶⁸ reported similar calculated frequencies, although theirs also included O—C stretches. They attributed the high frequencies to the influence of ring-atom bond and angle force constants that are not mitigated by the presence of cross terms in the force field. Although our outlying frequencies might have a similar cause, further investigation is needed to determine the precise cause of the discrepancy.

The agreement with experimental results for bending, distortion, and torsion modes, on the other hand, is very good (Figure 16). Our calculated ranges significantly overlap experimental ranges for these motion classes, though the experimental ranges do not always agree with each other. For example, consider the data for the H—O—C torsions. These show the least consensus among the other studies. This may in part be due to difficulties translating between assignment conventions, but it may more likely represent a wide variability in those torsional frequencies, as is found for the 64-unit calculation. Similar arguments might be made for the “other C6 & O6” class. It should be noted that the Gregurick and Kafafi⁷⁰ study used a different assignment method than what was used in the other studies to which we compare our results, which might account for the difference between their results and those of the others within these classes.

Two features in Figure 16 that are specific to the results of this study require further discussion. The first is the presence of the highest frequency —C6— distortion modes. There were no assignments offered by the other studies that satisfactorily correlated with this motion, which is essentially the movement of the C6 atom along a line between the C5 and O6 atoms. There is accompanying motion in C5 and in the two hydrogens attached to C6, but the primary energy is in the motion of the C6. Note that this discussion only applies to the —C6— distortion modes above 1500 cm⁻¹ (the lower frequency modes are other stretching motions of the C6 atom, for example, along the bond to one of the aliphatic hydrogens). Considering the strong stretching character of the motion, it is likely that the frequency reported here is only approximate. Normal mode analysis of the HF/6-31G* data for the monomer revealed a similar mode at 1635 cm⁻¹ (Table 11). The density functional calculation generated a similar mode at 1458 cm⁻¹. This mode is likely to be real, but may be difficult to observe since the motion is highly symmetric. In all of the quantum calculations in which the vibrational kinetic energy was primarily coupled to the motion of C6 between C5 and O6, the IR intensity calculated for that mode was small.

The other feature of note is the small cluster of very high frequency H—O—C torsions noted with (*) in Figure 10. Note that the relative energy associated with the motion is small, but it was not small enough to be filtered out by the procedures described earlier. The motions responsible for these anomalous assignments make physical sense, and are likely to occur in nature, but may be too weak to be observed. The cluster of torsions arises due to an accidental resonance. In the 64-unit crystal used for the calculation, the minimization resulted in a configuration such that a stretch of the O2—HO2 of a single molecule would necessarily excite torsion of the hydroxyl HO6 of another neighboring molecule. Since one of the molecules was situated at one a face of the crystal, and since NMODE does not employ periodic boundaries, the isolated behavior was not representative of the bulk properties.

Conclusions

This work describes the derivation of a parameter set for classical quadratic force fields that accurately models carbohydrates, but which can also be generalized to more diverse molecules by virtue of the noncarbohydrate specific nature of the parameters. QM calculations were employed to compute properties that are difficult or impossible to access experimentally, such as, bond and valence angle deformation force constants, dihedral angle rotational barriers, and electrostatic properties. The structures of the biomolecular building blocks (monosaccharides in the present case) were taken from experimental neutron diffraction data. Consistent with the AMBER force field, the PARM94 parameter set for van der Waals terms was employed. Particular attention was given to those properties that most impact the overall 3D structure and dynamics of biopolymers; namely, internal electrostatic interactions, solute–solvent interactions, and internal rotational barriers. While we derived partial atomic charges by fitting to the QM molecular electrostatic potentials (so called ESP-fitting), we departed from the general practice of assigning partial atomic charges to every atom in the molecule adopted in our earlier work (GLYCAM_93, GLYCAM2000) by not fitting partial charges to aliphatic hydrogen atoms. In addition, the current parameterization removes the need to treat 1–4 non-bonded interactions as a special case; that is, 1–4 scaling has been removed.

Although the parameter set is complete for carbohydrates, the methodology and the force field may be readily extended to lipids, proteins, and nucleic acids. The generality of the parameters is exemplified by the utilization of a common set of terms for α-and β-carbohydrate anomers. When combined with appropriate charge sets, these common terms provide a means of predicting the relative energies of interconverting ring forms. Not surprisingly, for nonpolar molecules the parameters derived by fitting to gas-phase B3LYP/6-31++G(2d,2p) data successfully reproduced the QM rotational energies. In addition, the force field was able to reproduce solid state ring puckering parameters, ring inter-proton torsion angles and distances, solution phase populations of the ω-angle, and scalar ³J-coupling constants for the H₅—C₅—C₆—H_6R/S atoms in representative carbohydrates. In highly polar molecules, however, the percentage errors in the torsional energies were occasionally high, and in the case of carboxylate ions the gas-phase QM-derived parameters failed to reproduce solution phase conformational properties. The expectation that condensed phase simulations, employing dihedral terms fit to gas-phase QM data, can reproduce solution rotamer populations is founded on the assumption that internal electrostatic polarization is relatively independent of internal rotation, either in the gas or condensed phases. This is frequently a reasonable assumption for relatively nonpolar molecules, but we found that as molecular polarity increased the observed condensed phase rotamer populations began to deviate from experimental expectations. This is clearly the case for ionic systems, for which it was necessary, in the absence of an explicit treatment of polarizability, to adjust the dihedral terms empirically to achieve accurate behavior in the aqueous solution. However, the empirically-corrected rotational energy curves were shown to differ only modestly from the gas-phase QM data. For such systems an iterative procedure, which involved explicit solvent MD simulations, was adopted to generate the torsion parameters. The inadequacy of the gas-phase QM-derived torsion terms when applied to highly polar molecules may be attributed to the absence of charge polarizability in the classical force field. The development of a polarizable version of GLYCAM is underway.