Accounting for Shared and Unshared Dosimetric Uncertainties in the Dose Response for Ultrasound-Detected Thyroid Nodules after Exposure to Radioactive Fallout

Abstract

Dosimetic uncertainties, particularly those that are shared among subgroups of a study population, can bias, distort or reduce the slope or significance of a dose response. Exposure estimates in studies of health risks from environmental radiation exposures are generally highly uncertain and thus, susceptible to these methodological limitations. An analysis was published in 2008 concerning radiation-related thyroid nodule prevalence in a study population of 2,994 villagers under the age of 21 years old between August 1949 and September 1962 and who lived downwind from the Semi-palatinsk Nuclear Test Site in Kazakhstan. This dose-response analysis identified a statistically significant association between thyroid nodule prevalence and reconstructed doses of fallout-related internal and external radiation to the thyroid gland; however, the effects of dosimetric uncertainty were not evaluated since the doses were simple point “best estimates”. In this work, we revised the 2008 study by a comprehensive treatment of dosimetric uncertainties. Our present analysis improves upon the previous study, specifically by accounting for shared and unshared uncertainties in dose estimation and risk analysis, and differs from the 2008 analysis in the following ways: 1. The study population size was reduced from 2,994 to 2,376 subjects, removing 618 persons with uncertain residence histories; 2. Simulation of multiple population dose sets (vectors) was performed using a two-dimensional Monte Carlo dose estimation method; and 3. A Bayesian model averaging approach was employed for evaluating the dose response, explicitly accounting for large and complex uncertainty in dose estimation. The results were compared against conventional regression techniques. The Bayesian approach utilizes 5,000 independent realizations of population dose vectors, each of which corresponds to a set of conditional individual median internal and external doses for the 2,376 subjects. These 5,000 population dose vectors reflect uncertainties in dosimetric parameters, partly shared and partly independent, among individual members of the study population. Risk estimates for thyroid nodules from internal irradiation were higher than those published in 2008, which results, to the best of our knowledge, from explicitly accounting for dose uncertainty. In contrast to earlier findings, the use of Bayesian methods led to the conclusion that the biological effectiveness for internal and external dose was similar. Estimates of excess relative risk per unit dose (ERR/Gy) for males (177 thyroid nodule cases) were almost 30 times those for females (571 cases) and were similar to those reported for thyroid cancers related to childhood exposures to external and internal sources in other studies. For confirmed cases of papillary thyroid cancers (3 in males, 18 in females), the ERR/Gy was also comparable to risk estimates from other studies, but not significantly different from zero. These findings represent the first reported dose response for a radiation epidemiologic study considering all known sources of shared and unshared errors in dose estimation and using a Bayesian model averaging (BMA) method for analysis of the dose response.

BACKGROUND

Increased incidence of thyroid cancer is a well established dose-related late effect of exposure to ionizing radiation at young ages demonstrated in epidemiological studies of populations exposed to the 1945 atomic bombings of Hiroshima and Nagasaki, Japan (1), the 1986 Chornobyl reactor accident (2, 3) as well as a number of other exposed populations (4). However, because thyroid cancer is a rare disease, it can be difficult to study radiation-related risk of thyroid cancer in small populations exposed to low- to moderate-radiation doses.

Previously, Land et al. (5) reported results of a study of ultrasound-detected thyroid nodule prevalence and its relationship to radiation dose to the thyroid gland among a study population of 2,994 persons exposed at young ages to various levels of radioactive fallout from above-ground nuclear bomb tests carried out by the Soviet Union between August 1949 and September 1962 at the Semipalatinsk Nuclear Test Site (SNTS) in northeastern Kazakhstan. That study followed review and analysis of the evidence for exposure among the public from STNS fallout (6). The subjects for the 2008 article belonged to a study population of persons who had been screened for thyroid disease in eight different settlements in Kazakhstan near the SNTS and who had been under 21 years of age at some time between the first Soviet test on August 29, 1949 and the establishment, in 1957, of a Soviet registry of residents of fallout-affected villages. Screening for thyroid disease took place in August 1998 and was focused on three subgroups. The first subgroup consisted of 1,989 members of a formal, long-term study developed during the 1960s by the Kazakh Research Institute for Radiation Medicine and Ecology (IRME), who were screened in 1998 for thyroid nodules in one of seven villages (Bolshaya Vladimirovka, Dolon, Kanonerka, Karaul, Kaynar, Korostely and Sarzhal). The second subgroup consisted of 387 non-IRME residents of these villages who moved there after the cessation of aboveground test explosions in 1962. And the third group consisted of 618 residents of an eighth village, Novopokrovka; which although located near the 1949 fallout trace, was believed to be at a sufficient distance from it to avoid high levels of fallout. While subjects were screened in the above villages, some study population subjects lived in 11 other villages (Rubtsovok, Chubartau, Kyzyltukh, Charsk, Shemonakha, Leninogorsk, Znamenka, Semipalatinsk-City, Semiyarkha and the evacuation locations of Aayaguz and Sergiopol) at the time of exposure.

The 2008 risk analysis provided evidence for the prevalence of thyroid nodules related to the estimated external and internal radiation exposure of the thyroid gland as reconstructed from fallout deposition patterns, residential history and diet, including amounts and types of milk consumption. The 2008 dosimetric analysis, however, did not estimate uncertainties in individual dose. Such uncertainty is inherent in dose reconstructions of this type and originates from stochastic variation of physical dose-related parameters (e.g., the degree to which radioactivity is transferred to milk of individual dairy animals) or from lack-of-knowledge uncertainty about individual lifestyles and habits (e.g., individual rates of consumption of contaminated dairy foods). The 2008 study also did not explore, or attempt to correct for, the possible effects that uncertainties in dose reconstruction would have on the estimated dose response. The current analysis is an update of the 2008 study, based on a reduced sample size as discussed earlier and focused on explicitly accounting for shared and unshared sources of uncertainty in the reconstruction of individual doses to the thyroid gland from external and internal radiation sources. These uncertainties, typical of all historical dose reconstructions, inevitably result from a general absence of direct measurements of individual exposures and from the use of mathematical models to estimate environmental radioactivity concentrations in air, soil and terrestrial food products, e.g., milk and related dairy-based foods.

Since the publication of the 2008 analysis, other types of analyses of dose and dose effect for the populations exposed near the SNTS have been published. For example, Imanaka et al. (7) discussed the reconstruction of local fallout composition and gamma-ray exposure in Dolon. Grosche et al. (8) reported an investigation of mortality from cardiovascular diseases and its relationship to radiation exposure from exposure to SNTS fallout. Sigurdson et al. (9) discussed thyroid nodules, polymorphic variants in DNA repair and RET-related genes, with exposure to ionizing radiation. Finally, additional biodosimetry measurements in the form of EPR assays of tooth enamel have been reported (10), which add to the database established by previous investigators (11, 12). These recent additions to the literature, as well as our own analyses (2008 and the current article), increase our understanding of radiation health effects from the STNS (13–15).

METHODS

The 2008 investigation had three components: 1. ascertainment of nodule prevalence; 2. dose reconstruction; and 3. dose-response analysis. The first component included ascertainment of thyroid disease prevalence by ultrasound screening of local populations (with fine needle aspiration biopsy of suspicious nodules and cytopatho-logical determination of malignancy), and the reader is referred to the 2008 article (5) for details, as none of the methods or findings has changed.

In the current article the second component, dose reconstruction, relies on the fundamental mathematical dose assessment models for exposure to radioactive fallout used in 2008, but now also addresses dosimetric uncertainty and explicitly separates sources of shared and unshared errors. Methods for estimation of doses from external and internal irradiation by fallout from nuclear testing, with particular emphasis on fallout from the Nevada Test Site (NTS), have been discussed elsewhere in detail [e.g., Simon et al. (16, 17) and Beck et al. (18)], and formed much of the basis for the dose-estimation methods used in 2008 and in the current article. Modifications to the methods for the NTS dose reconstruction based on joint discussions between U.S. and Russian investigators were discussed by Simon et al. (19), Gordeev et al. (20, 21) and Beck et al. (18). Specific details about contamination from the SNTS were discussed by Gordeev et al. (20–22). The modifications of the 2008 dosimetry for the current study included: 1. Acquisition of new data on food consumption rates acquired by focus groups held in Kazakhstan; 2. Addition of minor pathways of exposure to the assessment model, e.g., intake of contaminated soil by dairy cattle; 3. Assignment of probability density distributions for animal milk transfer coefficients for radioiodine; and 4. Restructuring of the dosimetry algorithms into a two-dimensional Monte Carlo (2DMC) framework for the purposes of separating shared from unshared uncertainty and simulating multiple possibly true sets of population doses. These modifications are described in brief in the following subsections.

The third component, determination of the dose response, while using the same risk models as Land et al. (5), is implemented using a Bayesian model averaging (BMA) method. The primary goal of this article is to report the findings from the updated dosimetry and from the Bayesian risk analysis.

Study Population

As discussed in the 2008 publication, the original IRME-exposed population selected for studies of health effects of radioactive fallout from the SNTS in Kazakhstan is a roster of some 10,000 residents of 10 settlements near the SNTS, selected on the basis of soil sample radioactivity measurements during the period of above-ground nuclear test explosions at the SNTS (1949–1962). Because of migration, aging and mortality in that population, as well as logistical considerations associated with thyroid screening of persons located in settlements downwind of the SNTS, the 2008 study was based on 1,989 original exposed IRME subjects, 387 non-IRME residents examined in seven settlements and 618 non-IRME residents of a settlement (Novopokrovka) believed to have been essentially free from any substantial exposure to fallout. The final study population size in the current article is 2,376, including 1,602 of 1,989 original exposed IRME subjects, 303 of 387 non-IRME residents examined in 7 settlements, and 471 of 618 Novopokrovka residents. The reduced number of subjects reflects elimination of those original subjects whose residence histories were suspect and could not be verified, subjects for whom the year in which they relocated into or away from the area contaminated by fallout could not be ascertained, and subjects who were determined to have moved into the area after 1962.

Subject Recruitment and Informed Consent

As described by Land et al. (5), possible subjects for the 2008 analysis were contacted by mail during June of 1998, followed by a home visit shortly afterward to explain the study and obtain informed consent for thyroid screening by ultrasound and for finger-stick phlebotomy. Human subject protection review was provided by institutional review boards at the National Cancer Institute (Bethesda, MD) and the Semipalatinsk State Medical Academy (SSMA) (Semipalatinsk, Kazakhstan). Prior to phlebotomy and ultrasound screening, questionnaire-based interviews were used to acquire data on age, residential and medical history and to elicit recall of dietary consumption rates and patterns around the time of major fallout events from the SNTS, with emphasis on the exposure pathways of milk and milk-product consumption from cows, goats, sheep and horses grazing on local pasture land contaminated by radioactive fallout.

Thyroid Examination

In August 1998, on-site thyroid screening was carried out in eight settlements chosen for exposure history, population size and accessibility by vehicle. Screening was carried out by a bi-national team of medical specialists who traveled to each settlement. Radiologists screened the thyroid gland for nodule presence with high-resolution ultrasonography that could consistently identify 2 mm or larger lesions and measure nodules to within 1 mm in their largest dimension. Finger-stick phlebotomy was used to collect blood for evaluation of thyroid function by measuring thyroid stimulating hormone (TSH), using fluoroimmunoassay. Fine-needle aspiration biopsy, guided by ultrasound or palpation as appropriate, was recommended to individual subjects for the two largest of any nodules present that were 1 cm or greater in diameter, subject to informed consent. Malignancy was determined by microscopy review of Papanicolaou-stained slides. Within the study population of 2,376 subjects, 21 cases of confirmed thyroid cancer were reported (3 in males and 18 in females). Combining confirmed papillary cancers with possible follicular cancers, 28 cases were reported (4 males and 24 females), while after combining all suspicious thyroid neoplasms there were 35 total cases (7 males and 28 females).

Dose Reconstruction

1. Collection of additional food consumption data

The dose reconstruction used for the risk analysis of Land et al. (5) was based on individual information collected from basic questionnaires administered to the study population in 1998. However, because data on several key questions needed for accurately estimating doses were not obtained from the 1998 questionnaires, it was decided that an additional data collection campaign be conducted in 2007. However, because many years had elapsed since exposure, a strategy was developed to encourage accurate memory recall. In this work, a focus group interview was used to collect historical behavioral and food consumption data (23, 24).

Since many participants were too young at the time of the nuclear tests to be able to recall dietary consumption at the time of the tests, and since existing sources of archival data are limited, the interviews were conducted with parents and other village residents who cared for children during the time of exposure, ranging in age from 75–90 years at the time of interview in 2007. Eleven focus group interviews were conducted with 82 women from four villages: three groups in each of the villages of Karaul, Kainar and Kanonerka; and two groups in the smaller village of Dolon. These interviews yielded group-level estimates of age-, gender-, ethnicity- and village-specific dairy consumption patterns and daily-life activities in rural Kazakhstan during the 1950s. Since all of the major nuclear tests were conducted in the months of August to October (1949–1962), focus group questions targeted dairy consumption during that time of year. Focus group interviews were conducted separately for ethnic Kazakhs and Russians because of the potential effect of different consumption and living practices in the two ethnic groups. Of eight villages included in the 1998 field study, the above four villages (two primarily Russian and two primarily Kazakh villages) were selected for the focus group interviews to represent a range of moderate-to-high fallout exposure levels, as estimated.

The data collection pertained to relevant childhood behaviors, including time spent indoors and outdoors and consumption rates of milk and other dairy products. The data were collected for five age groups of children and adolescents, ranging from less than 1 year of age to 21 years of age. Dairy products considered included fresh milk and other products from cows, goats, mares and sheep. Men's focus group interviews were also conducted and pertained to construction materials of houses and schools, and animal grazing patterns and feeding practices. The data collection is described by Schwerin (23, 24), and findings are discussed in greater detail in Drozdovitch et al. (25).

In general, the dose reconstruction for the 2008 publication assumed much lower consumption rates of cows’ milk compared with our more recent focus group data, especially among Russian children, as well as for consumption of sour milk by children of both ethnicities, especially among Kazakhs. There was a good agreement between the two studies regarding the consumption rates of cottage cheese and koumiss (sour mare milk) for children aged 4–6 and 7–14 years, though not for younger children.

2. Exposure pathways

Because the disease end point of interest, in both the 2008 publication and in the current study, is thyroid nodular disease and thyroid cancer, the objective of the dose reconstruction is estimation of individuals’ fallout-related absorbed dose to the thyroid gland. As in the 2008 study, both external dose from fallout deposited on the ground and internal dose from intake of radioiodines (¹³¹I and ¹³³I) were estimated.

External dose is an important pathway and is well understood in terms of modeling. External exposure is modeled as the product of the air kerma, estimated from the time integral of the exposure rate and a correction to kerma, multiplied by a factor that describes the effectiveness of building shielding to reduce the outdoor exposure rate. The temporal dependence of the exposure rate, discussed by Simon et al. (19), is modeled by a ten-term exponential equation fitted to actual data and represents an improvement of the previous well known power function model of t^–1.2 (26). The number of hours spent indoors by persons of each age and ethnicity was approximately determined from focus group interviews discussed by Drozdovitch et al. (25). The shielding qualities of wooden homes (typical of those in predominantly Russian villages), adobe homes (typical of those in predominantly Kazakh villages) and in public schools have been described by Gordeev et al. (21).

Internal dose, the most important pathway of thyroid exposure, is a function of age at intake, the contamination level of dairy products (Bq/L or Bq/kg) and the rates of ingestion (mL/d or g/d) by study subjects. Types of dairy products included for this study were fresh milk from cows, goats, sheep and horses, koumiss (fermented mare's milk), sour milk, sour cream and fresh cheeses. The contamination of dairy products was estimated using models for ingestion rates of fresh pasture grass by dairy animals and ingestion of contaminated soil. Probability distributions assigned to feed-to-milk transfer coefficients (units of Bq/L per Bq/d), typically denoted as f_m, were based on data abstracted from a literature review (27) and experimental investigations conducted for this study (28). These probability distributions separated state-of-knowledge uncertainty from parameter variability.

Intake rates of each type of dairy product for Kazakhs and Russians, according to age group of children and for women during pregnancy and breastfeeding, were described by Drozdovitch et al. (25). Internal dose to infants during breastfeeding was estimated based on published transfer coefficients for healthy women (29).

3. Application of the two-dimensional Monte Carlo method

The primary difference, other than the study population size, between the dose reconstruction presented in the 2008 article and the current article is that the earlier reconstruction produced only a set of individual point estimates of radiation dose from external and internal radiation exposure for each subject, without any characterization or quantification of uncertainties in the reconstructed dose estimates. The current analysis utilizes a 2DMC approach that explicitly takes into account substantial and complex uncertainties in the individual parameters of the dose estimation model, including explicit separation of shared and unshared components (30, 31).

The 2DMC method simulates alternative, possibly true sets (or vectors) of doses for the entire study population, rather than producing a single set of “point” doses where uncertainty in dose estimation is not characterized. In this article, each simulated set of doses for the study population (one dose per person) is termed a “vector” of study population doses. Within each population dose vector, values of individual doses maintain proper inter-relationships such that the estimated doses for members of any subgroup of a study population that share common lifestyle attributes (e.g., persons living in the same village) maintain their proper correlation. The 2DMC procedure simulates inter-individual variability of possibly true doses within each population dose vector and captures the influence of uncertainty in the values of dosimetric parameters across multiple realizations of possibly true vectors of study population doses. Proper separation of inter-individual variability from lack of knowledge of parameter values that affects all subjects in the dose estimation defines the primary characteristic of the 2DMC approach, as well as its strength.

The calculation of each subject's dose uses conventional analytical dose estimation models, but prior to calculation, each model parameter is characterized as to whether it is shared among members of the entire study population, among members of subgroups, or is unique to each subject and therefore is totally unshared. Following this characterization, the state of knowledge about each parameter used for dose estimation is quantitatively described by a probability density function (PDF) that characterizes random inter-individual variability and uncertainty in the center and spread of the PDF, as well as how the PDF is shared among relevant subgroups of the study population. The calculations to produce multiple realizations of simulated individual doses follow a detailed Monte Carlo sampling plan that maintains separation of shared from unshared sources of errors (31). In this study, we have used the 2DMC method to generate 5,000 realizations of dose-vector pairs, each pair representing a realization of possibly true cumulative external and internal doses for each of the 2,376 individuals.

Because of the concern that each of the 5,000 vectors of 2,376 simulated individual doses might overestimate inter-individual variability of true doses and thus, might inadvertently introduce classical error into the analysis of dose response, we produced 5,000 vectors of 2,376 conditional individual mean and median doses using the 2DMC algorithm. The conditional mean and median doses for each person were obtained by resampling, 100×, the dose-estimation parameters exhibiting unshared uncertainty, after these parameters had been conditioned on a fixed set of shared parameter values. This fixed set of shared parameter values represents one of 5,000 unique sets of conditions of systematic/shared uncertainty. Resampling of the unshared parameter values 100× produces 100 alternative realizations of conditional dose estimates for a given person, from which the conditional individual median dose is obtained. This procedure was repeated 5,000 times for each new conditional set of shared parameter values to produce 5,000 sets of conditional individual mean and median doses (see Table 1, Fig. 1 and Supplementary Table S2; http://dx.doi.org/10.1667/RR13794.1.S1). Each set of conditional individual mean or median doses is assumed to be an “unbiased” central estimate of dose for the subgroup of individuals who share the same exposure attributes, when the specific set of values for shared parameters used to obtain a given vector of conditional individual median doses correctly represents the actual situation. When the vector of conditional individual mean or median doses consists of unbiased central estimates for members of specific population subgroups sharing the same exposure attributes, all remaining uncertainty is assumed to be random variation of the individual's unknown true dose about the conditional mean or median dose (i.e., all remaining dose uncertainty is 100% Berkson).

TABLE 1.

Ninety-Five Percent Uncertainty Range of the Cohort Distribution of Thyroid Doses Obtained from 5,000 Realizations of Cohort Dose Vectors, Each Comprised of 2,376 Conditional Individual Median Doses^a

	Overall cohort (N = 2,376)		Male (N = 973)		Female (N = 1,403)		Kazakh (N = 1,549)		Russian (N = 827)
	External thyroid dose (Gy)
Cohort dose	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%
Minimum (Gy)	0.0E+00	0.0E+00	0.0E+00	0.0E+00	0.0E+00	3.7E-05	0.0E+00	0.0E+00	0.0E+00	0.0E+00
Median (Gy)	2.2E-02	4.3E-02	2.4E-02	4.6E-02	2.1E-02	4.3E-02	2.8E-02	5.3E-02	1.0E- 02	2.5E-02
Mean (Gy)	4.1E-02	6.7E-02	4.1E-02	6.8E-02	4.1E-02	6.6E-02	4.3E-02	7.6E-02	3.9E-02	6.2E-02
Maximum (Gy)	3.1E-01	8.2E-01	3.0E-01	8.0E-01	3.0E-01	7.7E-01	3.0E-01	8.0E-01	3.0E-01	7.7E-01
Variance (Gy2)	2.3E-03	7.3E-03	2.3E-03	7.4E-03	2.3E-03	7.3E-03	1.7E-03	5.9E-03	2.4E-03	7.6E-03
	Internal thyroid radiation dose (Gy)
Cohort dose	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%
Minimum (Gy)	0.0E+00	0.0E+00	0.0E+00	0.0E+00	0.0E+00	3.4E-05	0.0E+00	0.0E+00	0.0E+00	0.0E+00
Median (Gy)	1.6E- 02	8.6E-02	1.5E- 02	8.2E-02	1.7E- 02	9.0E-02	2.0E-02	1.2E- 01	1.4E-02	7.9E-02
Mean (Gy)	4.4E-02	1.2E+00	4.3E-02	1.1E+00	4.4E-02	1.2E+00	5.2E-02	1.7E+00	4.0E-02	1.0E+00
Maximum (Gy)	4.5E-01	3.6E+01	3.9E-01	2.1E+01	4.3E-01	3.6E+01	4.4E-01	3.6E+01	4.3E-01	3.6E+01
Variance (Gy2)	3.1E-03	1.0E+01	3.2E-03	8.8E+00	3.0E-03	1.1E+01	3.4E-03	1.5E+01	2.9E-03	9.4E+00
	Total thyroid radiation dose (Gy)
Cohort dose	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%	2.50%	97.50%
Minimum (Gy)	0.0E+00	0.0E+00	0.0E+00	0.0E+00	0.0E+00	8.6E-05	0.0E+00	0.0E+00	0.0E+00	0.0E+00
Median (Gy)	6.6E-02	1.6E- 01	6.5E-02	1.6E- 01	6.6E-02	1.6E- 01	8.8E-02	2.0E-01	4.2E-02	1.4E-01
Mean (Gy)	9.5E-02	1.2E+00	9.4E-02	1.2E+00	9.5E-02	1.3E+00	1.1E- 01	1.8E+00	8.8E-02	1.1E+00
Maximum (Gy)	7.1E-01	3.6E+01	6.6E-01	2.1E+01	6.9E-01	3.6E+01	6.9E-01	3.6E+01	6.9E-01	3.6E+01
Variance (Gy2)	9.7E-03	1.0E+01	1.0E- 02	8.8E+00	9.5E-03	1.1E+01	8.3E-03	1.5E+01	9.7E-03	9.5E+00

^aEach of 5,000 vectors of 2,376 conditional individual median doses were obtained from 100× resampling of unshared parameters in the inner loop of the 2DMC dose reconstruction model to produce 100 random individual dose estimates per subject, each “conditioned” on a unique fixed set of outer loop parameter values that are shared by cohort subgroups. The set of shared outer loop parameter values was resampled 1× for each successive dose vector and the 100× inner loop resampling was repeated, until 5,000 vectors of conditional individual median doses were produced.

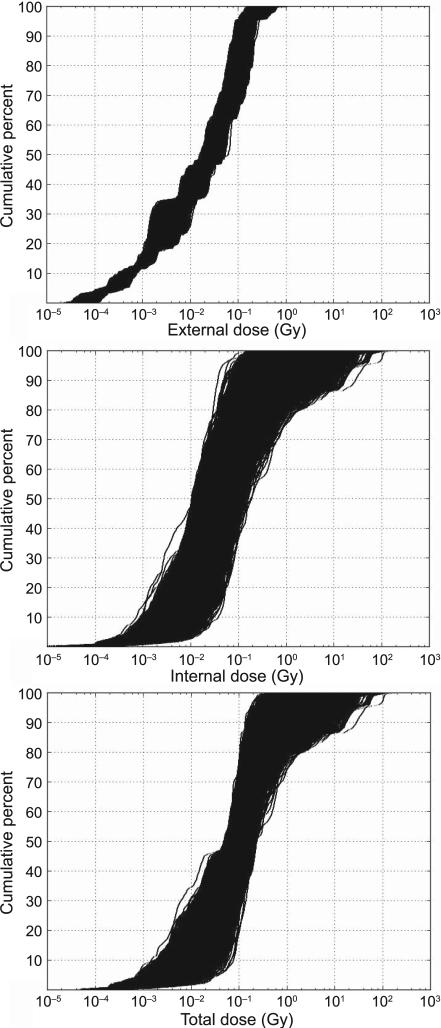
FIG. 1.

Cumulative percentage of thyroid dose for 5,000 dose vectors of 2,376 simulated conditional individual median doses, for external irradiation (top panel), internal irradiation (center panel) and total dose (sum of external + internal) (bottom panel).

The capability of multiple vectors of conditional individual median doses, when used with Bayesian model averaging methods to significantly reduce, if not eliminate, the effects of classical error, was demonstrated through a series of simulations tests (32). For this reason, our preferred approach for dose-response evaluation with the BMA approach relies on the use of the 5,000 vectors of conditional individual median doses. The results for the 2DMC simulation of conditional individual median doses are summarized in Table 1 and Fig. 1. Supplementary Tables S1 and S2 (http://dx.doi.org/10.1667/RR13794.1.S1) summarize the 2DMC production of 5,000 vectors of simulated individual doses and conditional individual mean doses, respectively.

4. Dose-response analysis

Only a few health risk studies have attempted to account for complex uncertainty in dose reconstruction by considering either a mixture of Berkson and classical measurement errors or mixtures of shared and unshared errors (33–35). The Bayesian approach used here is one of several types of risk estimation methods using multiple realizations of vectors of study population doses, with attributes similar to, for example, the Monte Carlo maximum likelihood method (35). Often, conventional dose-response analyses use the mean of multiple dose realizations per person in the regression, assuming that remaining uncertainty is associated with 100% Berkson error (36). A mixture of Berkson and classical measurement errors and limited shared errors was addressed by Li et al. (34), however, their mixture model cannot be applied to the Kazakhstan thyroid study due to the complexity and magnitude of the shared errors in this assessment.

As in Land et al. (5), we analyzed binary outcome data according to the following general family of models:

$$\mathrm{Odds}=\exp \left[\sum {\alpha }_i{X}_i\right]\times \left(1+\sum {\beta }_j{Y}_j\times \exp \left\{\sum {\gamma }_k{Z}_k\right\}\right).$$

Here, “Odds” is a function of nodule prevalence rate [Odds = rate/(1 – rate)]. The subscripted Greek letters α_i, β_j and γ_k denote unknown parameters, and the corresponding subscripted capital letters X_i, Y_j and Z_k denote potential risk factors, radiation dose (total dose = external dose + internal dose, or external and internal doses given separately), and effect modifiers, respectively. The exponential expression exp{α_iX_i} represents the baseline odds, i.e., when the radiation dose is zero. The “odds ratio” (OR) is the ratio of the odds to the baseline odds,

$$\mathrm{OR}=1+\sum {\beta }_j{Y}_j\times exp\left\{\sum {\gamma }_k{Z}_k\right\}$$

and the excess odds ratio (EOR) is the odds ratio minus 1. The parameter β_j represents the EOR per unit increment of the dose represented by Y_j, which may be total dose, external dose or internal dose, for values of the modifying factors Z_k such that $\sum {\gamma }_{\mathrm{k}}{\mathrm{Z}}_{\mathrm{k}}=0$. Throughout this article, the excess odds ratio (EOR) is considered be equivalent to the excess relative risk (ERR).

In this article, we use a Bayesian model averaging approach to estimate the dose response. In this method, none of the realizations of 5,000 vectors of 2,376 individual doses are considered to be absolutely equivalent to the unknown true dose vector, although we assume that some of the realizations may come closer to the unknown true dose vector than other realizations. The Bayesian method employed in this study obtains a posterior probability of the slope of a linear dose response via BMA (32) of each of the 5,000 realizations of external, internal and total dose vectors.

To perform Bayesian inference, we must formulate prior distributions for all uncertain model parameters used in logistic regression, along with their likelihood function. For prior distributions, we use a normal distribution with a large variance for the αs and γs to obtain a proper but noninformative prior. For a positive slope of the dose response, β, we use an exponential distribution with a large mean. Since uncertainty in dose estimation is represented by 5,000 dose vectors, we use a data augmentation approach to deal with multiple realizations of dose vectors. This is implemented in the form of a dose vector selection parameter, θ, that indicates which dose vector is used in the likelihood. The dose vector selection parameter has a multinomial distribution so that every dose vector has an equal a priori probability to be the possibly “true” dose vector [see ref. (32) for a more detailed description].

The posterior inference is obtained from a Markov chain Monte Carlo (MCMC) calculation. Bayesian parameter estimates and their corresponding 95% Bayesian credible intervals were obtained based on 40,000 posterior samples after 10,000 burn-in iterations (burn-in is an initial set that is not used for inferences). Along with the posterior inference for the slope of the dose-response parameter, β, a relative selection frequency (Bayesian weight) for a specific dose vector is obtained from the posterior distribution of the dose-vector index variable, θ. The Bayesian weight, $p(\theta =k\mid y,X,dosevecto{r}_k)∕{\sum }_{m=1}^{5,000}p(\theta =m\mid y,X,dosevecto{r}_m)$, k = 1,...,5,000, is a relative measure of the goodness-of-fit of each dose vector. For those dose vectors that are relatively close to the unknown vector of true doses, Bayesian weights will typically be relatively larger than those produced for the remaining dose vectors that are less precise approximations of the (unknown) vector of true dose.

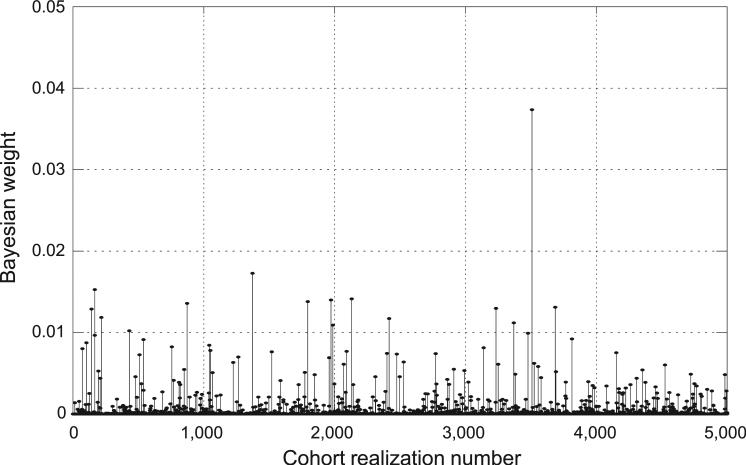
Figure 2 shows an example of Bayesian weights obtained using 5,000 vectors of 2,376 conditional individual median doses to evaluate the dose response for internal versus external exposure (Model 2). In this example, only 35% of the 5,000 dose vectors were given a nonzero weight by the Bayesian weighting algorithm. The overall Bayesian dose response in the example is determined by the top- weighted 210 dose vectors (4.2%) with relative Bayesian weights greater than 0.001, producing a cumulative Bayesian weight of 0.817.

FIG. 2.

An example of relative Bayesian weights obtained via Bayesian model averaging (BMA) of 5,000 vectors of 2,376 conditional individual median doses to evaluate dose response for internal vs. external exposures (Model 2). In this example, only 4% of the dose vectors have relative Bayesian weights greater than 0.001.

We evaluated the dose response using four approaches:

1. The use of conventional regression-based risk modeling with established software (Epicure, Risk Sciences International, Ottawa, ON) and the dose vector comprising 2,376 individual “best estimate” doses from the 2008 article, reflecting the reduced size of the current study population;

2. The use of the same regression-based risk modeling approach with the dose vector of 2,376 individual “mean” doses, in which each individual's mean dose is an average across that person's 5,000 dose realizations made in the current study;

3. The use of the same regression-based risk modeling approach with the dose vector of 2,376 individual “median” doses (obtained from the 5,000 dose realizations for each person);

4. A BMA estimation method using 5,000 population sets of 2,376 conditional individual “median” doses.

As described previously, we also evaluated the dose response with the BMA method using 5,000 vectors of simulated “possibly true” individual doses and 5,000 vectors of conditional individual mean doses. Based on extensive simulation tests discussed in Kwon et al. (32), the BMA method with conditional individual median doses produced the most reliable overall test results and is selected in this article as our preferred method for evaluating the dose response.

RESULTS AND DISCUSSION

Radiation Dose Estimates

This section discusses results from the 2DMC calculation of thyroid doses (Gy) for the 2,376 study subjects. As previously mentioned, 5,000 vectors of external and internal doses were computed, each vector representing a possibly true set of study population doses and each set containing one dose estimate per subject. The 2DMC dose reconstruction method produced 5,000 vectors of 2,376 simulated individual doses, conditional individual mean doses and conditional individual median doses. In this article, our primary evaluation of dose response is made using the conditional individual median doses with the Bayesian method. Extensive simulation tests demonstrated the overall superior performance of the BMA approach when used with multiple vectors of conditional individual median doses (32). The 2DMC results for the 5,000 vectors of conditional individual median doses are summarized in Table 1 and Fig. 1. The results for the 5,000 vectors of simulated individual doses and conditional individual mean doses are summarized in Supplementary Tables S1 and S2, respectively (http://dx.doi.org/10.1667/RR13794.1.S1).

Figure 1 presents cumulative probability distributions of all 5,000 vectors of conditional individual median doses for external dose, internal dose and total dose (Gy). The smaller variation among the 5,000 dose vectors for external irradiation compared to internal radiation can be clearly seen in this figure.

Table 1 provides information on the 95% uncertainty range for specific metrics of the population distribution of conditional individual median doses (e.g., population dose minimum, median, maximum and population dose variance) describing the inter-individual variability of conditional individual median doses within the study population, subdivided by sex and ethnicity, and for external dose, internal dose and total (external + internal) dose. In Table 1, the 95% uncertainty range has been obtained for each dosimetric end point by reporting the values occurring at the cumulative 2.5 percentile and 97.5 percentile of all 5,000 dose vectors.

At doses above 0.1 Gy, the dose from internal exposure generally dominates the total thyroid dose. For more than 90% of the 5,000 realizations of the population mean dose, internal exposure contributes more than 60% of the total. For nearly 99% of the 5,000 realizations, internal exposure contributes more than one half of the total study population mean dose. The internal dose also contributed the largest amount of dose uncertainty, a substantial amount of which reflects uncertainties in parameter values shared by members of multiple subgroups of the study population. For example, for external dose (Table 1), the 95% uncertainty range was less than a factor of two for the population median and mean dose and on the order of a factor of three for the population maximum dose and population dose variance. By contrast, the 95% uncertainty range is much larger for internal doses and total doses. For internal and total thyroid doses, the 95% uncertainty range for the population mean dose extends over a factor of 27 and 12.6, respectively. The 95% uncertainty range in the population maximum dose extends over a factor of 80 and 50, respectively and the 95% uncertainty in the population dose variance extends over three orders of magnitude.

For external, internal and total thyroid doses (Table 1), there are no appreciable differences in the distribution of individual doses between males and females or between ethnic groups. For external doses, Russians have modestly lower median doses than Kazakhs because of given differences in home construction materials and time spent outdoors. For internal doses, Russians have lower mean and median doses, though there is substantial overlap in the 95% uncertainty ranges of these dose quantities. In the case of internal doses, Russian doses are lower because of lower consumption of high-contamination dairy foods, e.g., goat, sheep and horse milk.

Random inter-individual variability of dose estimates for members of subgroups of the study population that share the same exposure attributes is eliminated when using conditional individual median doses. All uncertainty is due to shared sources of uncertainty in the parameters of the 2DMC dose-estimation procedure. As a result, the multiple vectors of conditional individual median doses produce markedly lower estimates of population dose variance [95% CI = 0.0097, 10 Gy² (Table 1)] than when multiple vectors of simulated individual doses are used [95% CI = 0.025, 81 Gy² (Supplementary Table S1: http://dx.doi.org/10.1667/RR13794.1.S1)] or when conditional individual mean doses are used [95% CI = 0.016, 33 Gy² (Supplementary Table S2: http://dx.doi.org/10.1667/RR13794.1.S1)].

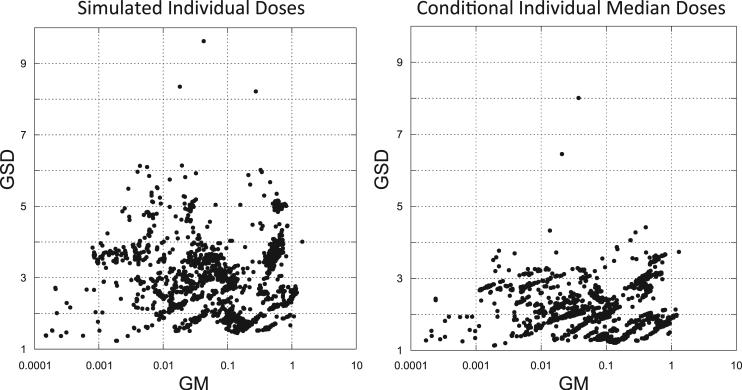
An understanding of the total uncertainty on a per person basis can be achieved by examining the geometric standard deviation (GSD) of dose for each subject across all of the 5,000 population dose vectors. In Fig. 3, plots are shown of all 2,376 individual doses summarized across all 5,000 dose realizations per person, each approximated as a lognormal distribution. Each individual's geometric mean dose (GM) is plotted against their associated geometric standard deviation (GSD). The larger the individual dose uncertainty, the larger the value of GSD. A comparison of simulated individual doses with conditional individual median doses shows a marked decrease in the dose GSD. The smaller GSD associated with the conditional individual median doses is due to the elimination of inter-individual variability in dose estimation contributed by unshared sources of error.

FIG. 3.

Geometric standard deviation (GSD) of simulated individual doses (Gy) (obtained from 5,000 realizations per study subject) plotted as a function of the geometric mean dose (GM) (left panel), and GSD of individual conditional median doses plotted as a function of geometric mean of the individual conditional median doses (right panel).

The higher values of GSD (with many exceeding 5.0) in the simulated individual doses (Fig. 3, left panel) are the result of large contributions from random and nonrandom sources of parameter uncertainties that are unshared across individuals in the study population. It is likely that these very large uncertainties will contribute to inadvertent classical errors in the dose-response analysis.

For the conditional individual median doses, dose uncertainties are contributed only by shared sources of parameter uncertainties. Most of the GSDs for conditional individual median doses (Fig. 3, right panel) are less than 3.0, with the majority of the GSDs being less than 2.5. Based on simulation tests conducted by Kwon et al. (32), Bayesian dose-response analyses using multiple vectors of conditional individual median doses are not expected to contain significant amounts of residual classical errors that would overestimate true inter-individual variability of dose and thus bias the slope of the dose response toward the null.

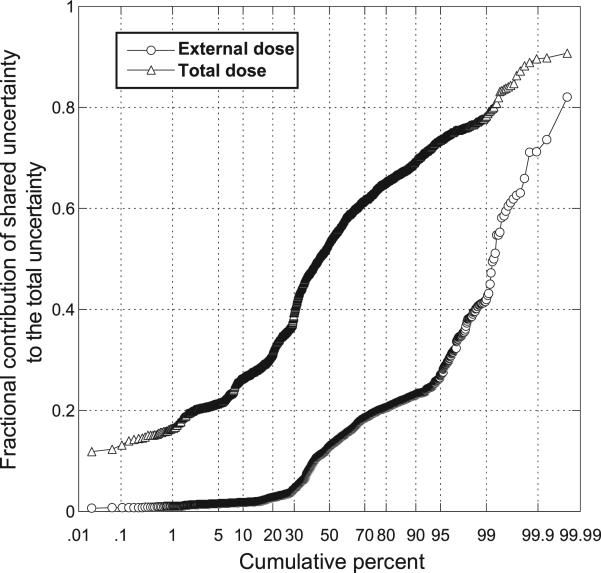
As shown in Fig. 4 and in Table 1, shared sources of uncertainty contribute substantially to the estimates of internal doses and total (internal + external) doses. By comparison, the contribution of shared sources of uncertainty to the estimation of external dose is relatively minor.

FIG. 4.

Cumulative probability plot of fractional contribution of shared uncertainty to the total uncertainty in individual external dose and total (external + internal) dose for each of 2,376 study subjects, determined as the ratio of variance of logarithms of conditional individual doses to the variance of logarithms of simulated individual doses (based on 5,000 realizations per study subject).

Table 2 compares the single vector of “best estimate” doses used in Land et al. (5) based on the original 2,994 subjects and on the current study population size of 2,376 subjects, with single vectors of individual median and mean values obtained from 5,000 dose realizations per subject. The variability of individual dose estimates produced using the single dose vectors composed of the “best estimates” from the 2008 study was markedly larger than what is produced using the individual mean and median doses obtained in the current study [each obtained from 5,000 dose realizations per subject (Table 2)]. The single dose vectors of individual mean and median doses also exhibit substantially lower values for the population dose maximum, mean and variance. For example, the population dose maximum drops from 10 Gy (in the 2008 analysis) to 4.2 Gy using individual mean doses and 1.1 Gy using individual median doses. The population dose variance drops from 0.56 Gy² using the former “best estimates” to 0.18 Gy² using individual mean doses and to 0.03 Gy² using individual median doses.

TABLE 2.

A Comparison of Summary Statistics for Single Vectors of Total (External + Internal) Thyroid Dose Expressing the Variability of Individual Doses within the Cohort

	Previous dose set (5)a	Previous dose set (5)a applied to current cohort	Current doses (individual mean values)b	Current doses (individual median values)b
			Number of subjects
Cohort dose distribution	2,994	2,376	2,376	2,376
Minimum (Gy)	0.00	0.00	0.00	0.00
Maximum (Gy)	10	10	4.2	1.1
Median (Gy)	0.085	0.11	0.12	0.096
Mean (Gy)	0.35	0.41	0.28	0.15
Variance (Gy2)	0.47	0.56	0.18	0.030

^aDoses from Land et al.(5) are a single vector of “best estimate” values, without uncertainty.

^bA single vector of individual mean or median doses obtained from 5,000 dose realizations per each of 2,376 subjects.

Dose-Response Analysis

Thyroid nodules

In this study population, a total of 748 thyroid nodules were found, 177 in males and 571 in females. Table 3 listed the nodules by sex, age at screening for thyroid disease and ethnicity. The primary results for thyroid nodules compare the slope of a linear dose response (ERR/Gy) between males and females (Model 1), between external and internal exposures to both sexes combined (Model 2) and between ethnic groups (Russians and Kazakhs, Model 3) as was reported in Land et al. (5). The dose-response results for the two variations of conventional regression (using a single vector of individual mean or median dose) and the BMA method using multiple vectors of conditional individual median doses are compared in Table 4, along with the previous results obtained using a single vector of “best estimate” doses (5). Supplementary results showing the dose response previously reported by Land et al. (5), and the BMA method using multiple vectors of simulated individual doses and conditional individual mean doses, are presented in Supplementary Table S3 (http://dx.doi.org/10.1667/RR13794.1.S1).

TABLE 3.

Distribution of Thyroid Nodules by Gender, Age and Ethnicity

		Nodules?
Subgroup	Sample size	Yes	No
Sex
Male	973	177	796
Female	1,403	571	832
Age at screening (years)
36-19	495	116	379
50-54	447	142	305
55-59	597	203	394
60-64	577	181	396
65-70	260	106	154
Ethnicity
Kazakh	1,549	460	1,089
Russian	827	288	539

TABLE 4.

Summary of Final Dose-Response Analyses for Nodule Prevalence, by Sex and Mode of Exposure

	Dose response evaluated using:
	Conventional regression (EPICURE )									Bayesian model averaging
	“Best estimate” doses [Land et al.(5)]			Individual mean dosesa (current article)			Individual median dosesb (current article)			5,000 Vectors of conditional individual median doses (current article)
Cohort size	N = 2,376			N = 2,376			N = 2,376			N = 2,376
Model description	Central estimate	95% CI		Central estimate	95% CI		Central estimate	95% CI		Central estimate	95% CI
		Lower	Upper		Lower	Upper		Lower	Upper		Lower	Upper
Model 1 (sex)
Baseline odds parametersc
Exp(α11): male subset 1, 3d	0.11	0.07	0.16	0.12	0.09	0.17	0.11	0.08	0.16	0.11	0.07	0.15
Exp(α12): male subset 2d	3.7E – 03	8.4E – 04	0.02	2.3E – 03	5E – 04	0.01	3.3E – 03	7.4E – 04	0.01	2.7E – 03	5.3E – 05	0.01
Exp(α21): female subset 1, 3d	0.73	0.63	0.85	0.78	0.68	0.89	0.74	0.63	0.87	0.75	0.64	0.85
Exp(α22): female subset 2d	0.12	0.07	0.19	0.12	0.08	0.19	0.11	0.07	0.18	0.12	0.07	0.17
α3: loge (age screened ÷56)e	2.64	1.77	3.51	2.37	1.51	3.23	2.32	1.47	3.17	2.33	1.48	3.16
Dose response (ERR/Gy)
β1: total dose (males)	4.79	1.75	7.83	4.83	2.48	9.33	11.2	3.97	18.5	9.99	2.33	19.07
β2: total dose (females)	0.23	–0.03	0.49	0.07	–0.08	0.29	0.52	–.26	1.29	0.35	1.1E – 05	1.00
Model 2 (external vs. internal dose)
Baseline odds parametersc
Exp(α11): male subset 1, 3d	0.09	0.06	0.14	0.12	0.08	0.17	0.11	0.07	0.16	0.10	0.05	0.14
Exp(α12): male subset 2d	3.3E – 03	7.3E – 04	0.02	2.4E – 03	5.3E–4	0.01	2.5E – 03	5.5E – 04	0.01	2.3E – 03	6.4E – 05	0.01
Exp(α21): female subset 1, 3d	0.73	0.63	0.84	0.77	0.67	0.89	0.76	0.66	0.88	0.75	0.64	0.86
Exp(α22): female subset 2d	0.11	0.07	0.18	0.12	0.08	0.19	0.12	0.07	0.19	0.12	0.07	0.17
α3: loge (age screened ÷56)e	2.44	1.57	3.32	2.37	1.51	3.23	2.34	1.49	3.20	2.37	1.47	3.20
Dose response (ERR/Gy)
β3: external	4.16	0.54	7.77	1.00	–0.76	3.25	0.85	–0.65	2.36	1.47	4.1E – 05	3.74
β4: internal	0.88	0.24	1.52	0.57	–0.44	1.27	2.91	0.13	5.69	3.59	0.11	9.73
Dose-response modifiers
Exp(γ1): sexe	0.21	0.11	0.39	0.13	0.04	0.43	0.16	0.06	0.42	0.16	0.03	0.28

^aNew dose data using 2,376 individual mean doses obtained from 5,000 dose realizations per person.

^bNew dose data using 2,376 individual median doses obtained from 5,000 dose realizations per person.

^cOdds = baseline × (1 + dose response × dose-response modifiers) = $\exp \{\sum {\alpha }_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}\}\times (1+\sum {\beta }_{\mathrm{j}}{\mathrm{Y}}_{\mathrm{j}}\times \exp \{\sum {\gamma }_{\mathrm{K}}{\mathrm{Z}}_{\mathrm{K}}\})$.

^dSubset 1 includes 1,602 IRME roster subjects screened in the villages of Bolshaya Vladimirovka, Dolon, Kanonerka, Karaul, Kaynar, Korostely and Sarzhal. Subset 2 includes 303 nonroster subjects from the same villages. Subset 3 includes 471 nonroster subjects screened in the village of Novopokrovka. (See description of “Study Population” in the Methods section of this article).

^e“Sex” = –1 and +1 for males and females, respectively; thus dose-response coefficients correspond to a population evenly divided by sex.

Comparison of dose response between males and females (Model 1)

All findings on the risk for thyroid nodules show that the ERR/Gy is markedly higher for males than for females and that this difference in risk is statistically significant. The dose response for females is not statistically significant (Table 4). This finding differs from what was reported for the study population of 2,994 subjects in Land et al. (5) (see Supplementary Table S3; http://dx.doi.org/10.1667/RR13794.1.S1).

The central estimates of ERR/Gy for males, based on 177 subjects with nodules, obtained from conventional regression analyses using either a single vector of individual median doses [ERR/Gy 11.2 (95% CI = 3.97–18.5)] or the BMA method using conditional individual median doses [ERR/Gy 9.99 (95% CI: 2.33–19.07)], are comparable to what has been reported for the risk of thyroid cancer from childhood exposures (0–18 years) to external radiation [ERR/Gy 7.7 (95% CI = 2.1–28.8)] (4). In general, the slope of the dose response for females, based on 571 subjects with nodules, is almost 30 times less than for males.

Comparison of dose response between external and internal exposure (Model 2)

Previously, Land et al. (5) showed that the slope of the dose response (ERR/Gy) for external exposure was higher (prior to modifying by sex), but not statistically significantly different from internal exposure. We obtain similar results to those reported in Land et al. (5) when using conventional dose-response analysis with a single vector of arithmetic mean dose per person.

However, when the single vector of individual median doses is used in the risk analysis, the central estimate of the slope of the dose response for internal exposures is a factor of about 5 higher than that obtained using the single-vector-individual mean doses and a factor of three higher than that obtained using the “best estimate” doses used in the 2008 study (Table 4). Using conventional regression with a single vector of individual median doses, the central value of the dose-response slope for internal exposure is more than three times that for external exposure. However, the differences in these results are not statistically significant.

In contrast to conventional dose-response analysis methods using regression-based methods with a single vector of individual dose estimates, the BMA method produced risk estimates for internal exposures that were greater than the risk estimates for external exposures. However, because of large overlap of 95% CIs, the difference in risk estimates between internal and external exposure was not statistically significant. Unlike the 2008 results, the dose responses for external exposure alone (Model 2, Table 4) using the dose estimates in this article were not statistically significant: the lower bound of the 95% CI of the ERR/Gy was either negative or approached zero.

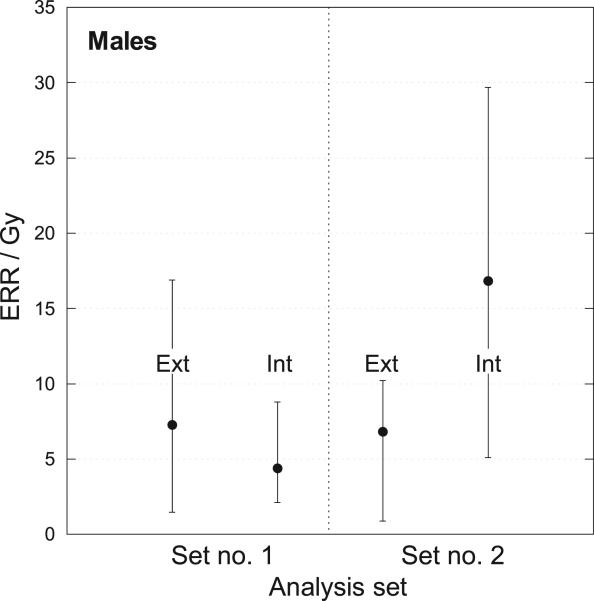
Evaluation of the dose-response differences in external and internal exposures for males and females separately, however, shows a marked difference (Figs. 5, 6). For example, for males (Fig. 5), the ERR/Gy is substantially larger than for females (Fig. 6) for both internal and external exposure. For males, the central values of the ERR/Gy for internal exposure (16.8–20.7) obtained with the Bayesian analysis were larger than those for external exposure (6.8), with substantial overlap of their 95% CIs (Fig. 5).

FIG. 5.

Estimates of ERR/Gy for males from external and internal exposure with 95% confidence intervals. Set no. 1: Conventional regression using mean dose per subject (from 5,000 realizations). Set no. 2: Bayesian analysis using 5,000 vectors of 2,376 conditional individual median doses.

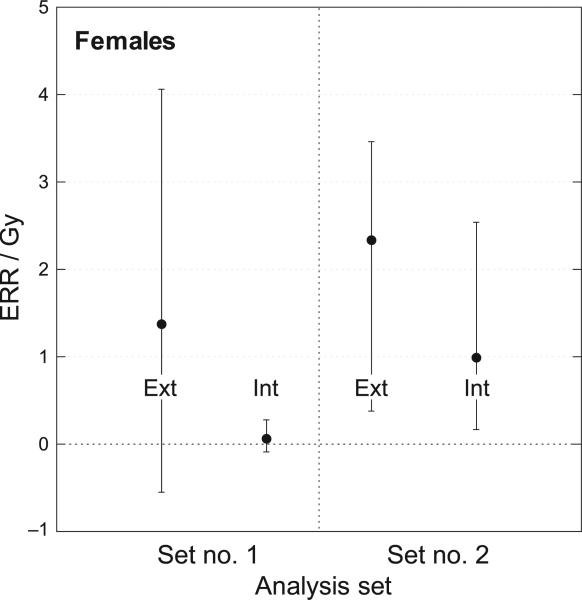
FIG. 6.

Estimates of ERR/Gy for females from external and internal exposure with 95% confidence intervals. Set no. 1: Conventional regression using mean dose per subject (from 5,000 realizations). Set no. 2: Bayesian analysis using 5,000 vectors of 2376 conditional individual median doses.

For females, the ERR/Gy for external exposure (2.34) obtained with the Bayesian analysis was greater than for internal exposure (0.99), but with substantial overlap of the 95% CIs. The Bayesian analyses of dose responses for females produced internal and external risk estimates with 95% CIs overlapping central values of the ERR/Gy (Fig. 6).

Ethnicity (Model 3)

The dose response was evaluated separately for Russians and Kazakhs because of differences in their baseline rates of disease (Model 3, Table 5). The slope of a linear dose response was evaluated using the BMA method with 5,000 vectors of conditional individual median doses. The slope of the combined gender dose response was quite similar for the two ethnic groups [Russians, ERR/Gy = 4.56 (95% CI = 1.04–8.61), Kazakhs, ERR/Gy = 3.23 (95% CI 0.47–6.70)], with the risk being marginally larger for Russians.

TABLE 5.

Dose-Response Analysis for Nodule Prevalence, by Ethnicity

Dose response was evaluated using Bayesian model averaging (BMA) with 5,000 vectors of conditional individual median doses
Cohort size	N = 2,376
Model description	Central estimate	95% CI
		Lower	Upper
Model 3 (ethnicity)
Baseline odds parametersa
Russians (RS)
Exp(α11): subset 1, 3b	0.38	0.28	0.48
Exp(α12): subset 2b	0.11	0.03	0.21
Kazakhs (KZ)
Exp(α21): subset 1, 3b	0.36	0.26	0.47
Exp(α22): subset 2b	0.04	0.02	0.06
α3: loge (age screened ÷56)c	1.95	1.10	2.82
Dose response (ERR/Gy)
β1: total dose (RS)	4.56	1.04	8.61
β2: total dose (KZ)	3.23	0.47	6.70

^aOdds = baseline × (1 + dose response × dose-response modifiers) = $\exp \{\sum {\alpha }_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}\}\times (1+\sum {\beta }_{\mathrm{j}}{\mathrm{Y}}_{\mathrm{j}}\times \exp \{\sum {\gamma }_{\mathrm{K}}{\mathrm{Z}}_{\mathrm{K}}\})$.

^bSubset 1 includes 1,602 IRME roster subjects screened in the villages of Bolshaya Vladimirovka, Dolon, Kanonerka, Karaul, Kaynar, Korostely and Sarzhal; subset 2 includes 303 nonroster subjects from the same villages: subset 3 includes 471 nonroster subjects screened in the village of Novopokrovka. (See description of “Study Population” in the Methods section of this article).

^c“Sex” = –1 and +1 for males and females, respectively; thus dose-response coefficients correspond to a population evenly divided by sex.

Thyroid carcinomas

In the previous study by Land et al. (5), the dose response for thyroid cancer was not reported because it was not statistically significant. In the current study, the linear dose response for thyroid cancer was reevaluated for:

1. 21 cases of confirmed papillary cancers only,

2. 28 cases of confirmed papillary cancers and suspected follicular cancers and

3. 35 incident cases of thyroid neoplasms (all types combined),

using the BMA method of risk estimation with all 5,000 sets of 2,376 conditional individual median doses (Table 6). The analysis for thyroid neoplasms and carcinomas was restricted to the Bayesian BMA approach with conditional individual median doses.

TABLE 6.

Thyroid Cancer Dose Response

Bayesian analysis with 5,000 vectors of conditional individual median dosesa Cohort size N = 2,376
	Neoplasms (35 cases)			Papillary cancers + suspected follicular cancers (28 cases)			Papillary cancers only (21 cases)
	Males = 7; females = 28			Males = 4; females = 24			Males = 3; females = 18
Dose response (EER/Gy)	Central estimate	95% CI		Central estimate	95% CI		Central estimate	95% CI
		Lower	Upper		Lower	Upper		Lower	Upper
Male	10.22	0.49	22.32	5.93	0	14.61	6.10	0	14.10
Female	1.66	0	6.02	4.33	0	13.31	3.82	0	11.69

^aEach of 5,000 vectors of 2,376 conditional individual median doses were obtained from 100× resampling of unshared parameters in the inner loop of the 2DMC dose reconstruction model to produce 100 random individual dose estimates per subject, each “conditioned” on a unique fixed set of outer loop parameter values that are shared by cohort subgroups. The set of shared outer loop parameter values was resampled 1× for each successive dose vector, and the 100× inner loop resampling was repeated, until 5,000 vectors of conditional individual median doses were produced. The thyroid doses used in this analysis were total doses (external and internal).

With so few cases, it is not surprising that the lower bound of the 95% CI for the slope of the thyroid cancer dose response is zero, indicating that the dose response is not statistically significant. An exception is with the dose response for males using seven cases of neoplasms. However, due to the very low number of cases reported for males, the results cannot be considered reliable. In general, the central risk estimates for males (ERR/Gy = 5.9– 10.2) and the upper 95% CIs for males and females (6–22) are quite similar to results reported for thyroid cancer in pooled childhood cohorts exposed to external radiation (4, 37) and children of mixed ages under age 18 exposed to Chernobyl fallout in Ukraine (38) and Belarus (39).

The central values of the ERR/Gy for females are lower than for males, a result that is consistent with what is found in this article for thyroid nodules. With the exception of the large differences observed for all neoplasms combined, the difference between the dose response for males and females for thyroid cancer is not statistically significant. The central values of ERR/Gy are within a factor of 1.3–1.6, which is much closer than the differences in central estimates of the dose response by sex obtained for thyroid nodules. In addition, the upper limits of the 95% CIs of the ERR/Gy for confirmed cases of thyroid papillary cancer in males and females are comparable (see Table 6).

CONCLUSIONS

Individual thyroid doses from external and internal radiation sources were reconstructed for 2,376 study subjects from fallout deposition patterns and residential history data and dietary history derived from interviews of subjects, family members and focus groups. The dietary input data included information about rates and types of dairy products consumed, recognizing that milk products are the primary route of exposure to fallout radioiodines. A BMA approach for risk analysis was employed using 5,000 realizations of the conditional individual doses generated by a 2DMC dose-estimation strategy (31). This dose-estimation strategy differentiates among dose-model parameters whose uncertainties are shared among members of subgroups of the study population and parameters whose uncertainties are specific to a given individual and are unshared. The risk estimation method evaluates the goodness-of-fit to the disease outcomes of the population for each of 5,000 simulated realizations of conditional individual median doses for all 2,376 study population members from external and internal radiation sources. The dose response estimated with the Bayesian method for internal exposures (in males and in males and females combined) is higher than reported in the 2008 analysis (5).

Unlike the 2008 analysis, the estimated dose response for thyroid nodules for internal dose from the analyses for both males and females combined, or for males only, is greater but not statistically different than that for external dose. A similar risk for internal and external exposure would agree with expectations that the dose delivered by the beta particles from internal radiation and the resulting damage to genetic material should be similar to the dose and damage caused by secondary electrons that deliver the dose from external photon irradiation.

We also found, over all the methods and dose realizations used in the dose-response analysis, there was a markedly higher ERR/Gy for males than females. While not completely understood, this result is likely related to the much higher baseline rate of nodules among females which, in itself, might reflect conditions of past iodine deficiency in Kazakhstan (40) and greater iodine requirements for women particularly during pregnancy (41). This finding may be peculiar to the population in Kazakhstan in the 1940s and 1950s and their diets and lifestyles, although given the information available, it is not possible to make a definitive explanation for the gender differences in the slope of the dose response.

The small number of thyroid neoplasms and thyroid cancers observed in this study population resulted in a slope of the dose response that was not statistically significant. However, for males, the central values of the ERR/Gy (ranging from 5.9–10.2) and the upper limit produced by the Bayesian dose-response analysis for males and females (6–22) are similar to what has been reported for thyroid cancer in other epidemiological studies involving external and internal radiation exposure to study populations comprised of children of mixed ages and young adults.

Although many revisions and modifications were made to the previous study by Land et al. (5), including reduction of the study population size from 2,994 to 2,376 subjects and revision of dose estimates based on improved knowledge of dietary habits, the largest differences were the result of simulation of thousands of 2DMC population dose vectors combined with the Bayesian model averaging method for risk analysis. This article represents a first-time application of these methods to address dose-estimation uncertainty in quantifying health risk from exposure to ionizing radiation. These methods provide a powerful strategy to disassociate shared from unshared sources of uncertainty in individual dose estimation. The possible presence of classical error within unshared sources of uncertainty is addressed using multiple realizations of study population vectors of conditional individual median doses with the Bayesian dose-response analysis. Unless explicitly accounted for, shared sources of uncertainty in dose estimation and classical error will introduce biases in the estimation of the dose response (42).

We believe that other health risk studies that depend on uncertain input data for estimating individual exposures and which rely heavily on mathematical models for reconstruction of individual doses in the absence of direct measurements can significantly benefit from use of the 2DMC dose reconstruction algorithm and the Bayesian dose-response strategies discussed here.