Abstract
We present a new multiscale method that combines all-atom molecular dynamics with coarse-grained sampling, towards the aim of bridging two levels of physiology: the atomic scale of protein side chains and small molecules, and the huge scale of macromolecular complexes like the ribosome. Our approach uses all-atom simulations of peptide (or other ligand) fragments to calculate local 3D spatial potentials of mean force (PMF). The individual fragment PMFs are then used as a potential for a coarse-grained chain representation of the entire molecule. Conformational space and sequence space are sampled efficiently using generalized ensemble Monte Carlo. Here, we apply this method to the study of nascent polypeptides inside the cavity of the ribosome exit tunnel. We show how the method can be used to explore the accessible conformational and sequence space of nascent polypeptide chains near the ribosome peptidyl transfer center (PTC), with the eventual aim of understanding the basis of specificity for co-translational regulation. The method has many potential applications to predicting binding specificity and design, and is sufficiently general to allow even greater separation of scales in future work.
Keywords: multi-scale modeling, molecular dynamics, ribosome exit tunnel, generalized ensemble, translation, PMF, coarse-grain, Monte Carlo
1. Introduction
It is often the case that we wish to predictively simulate the molecular interaction of something small (a peptide or other ligand) with something very large (a macromolecular complex). Molecular dynamics (MD) simulations that capture chemical atomic detail are crucial to this goal. For instance, the effect of individual water molecules near a surface may be critical to ligand affinity, yet the computational cost of simulating large systems in atomic detail can be a practical impossibility. New multiscale methods are essential to bridging the atomic scale with the much larger scale of macromolecular complexes.
One example of such a system is the ribosomal exit tunnel. The ribosome is a complex catalyst for the synthesis of new proteins. As nascent polypeptide chains are synthesized at the ribosome peptidyl transferase site (PTC), they emerge from the ribosome only after traversing a long tunnel.1,2
The ribosome exit tunnel is believed to act as a discriminating gate for protein sequences. Some peptide sequences have been shown to regulate their own translation process by directly interacting with components of the exit tunnel as they are being translate although the specific details of this molecular mechanism is unclear. For example, stalling of the SecM3–5 and tnaC6,7 peptides requires critical residues in the nascent peptide: a terminal Pro near the PTC site and a Trp near the constriction site, between ribosomal proteins L4 and L22 which protrude into the cavity at the tunnels narrowest point. Macrolide antibiotics are also known to bind near the constriction site, arresting translation, and inducing conformational changes in L22 observed in crystal structures.8
What is the molecular mechanism for peptide recognition in these stalling events? All-atom computer simulation is key to understanding this. There have been previous efforts to simulate the ribosome9 in atomic detail, yet this remains a challenge for all-atom molecular dynamics, due to its enormous size. Furthermore, studying sequence specificity requires multiple simulations to compare different sequences, and accurate free energy calculations incur even more computational cost.
Here, we present a multi-scale simulation approach we call the Multi-Scale Fragment Potential (MSFP) method, that aims to overcome some of these challenges. In MSFP, the ligand of interest is divided into fragments (a peptide into amino acids, for instance). First, all-atom molecular dynamics simulation is used to calculate the affinity of each fragment along the binding surface or other molecular environment as a 3D spatial potential of mean force (PMF). The fragment potentials are then used to locally bias conformational sampling in a coarse-grained model of the full ligand (a polypeptide chain, for example), allowing for efficient sampling of conformations and fragment sequences (different orderings and combinations of fragments). If desired, this process can be repeated iteratively, using predicted sequences and conformations from the coarse-grained sampling to seed further all-atom simulations.
In this report, we present a proof-of-principle study, using a reduced alphabet of single amino acid side chain analog PMFs constructed from large-scale MD simulations of single amino acid probes sampling the entire cavity of the ribosomal exit tunnel. In principle, the MSFP method is not limited to any particular molecular system. Here we use PMF maps of the ribosomal exit tunnel as a realistic example.
For the coarse-grained sampling, we use an efficient generalized ensemble Monte Carlo technique, which we describe in the Methods section. We demonstrate, for short polypeptide chains, how MSFP can obtain accurate estimates of free energy differences between sequences and conformational states, and with and without the inuence of the ribosomal exit tunnel PMFs. We discuss the differences between MSFP and existing multiscale methods, the approximations assumed in the method, and future directions of this work.
2. Methods
2.1. Theory
Here we rigorously define the approximations in the multiscale fragment approach. As we will see, there is a natural decomposition to the approximation that corresponds to the additive terms in the coarse-grained potential used in the MSFP method. This theoretical treatment is useful for substantiating the the method, and is a useful starting point for making accurate approximations.
2.1.1. The fragment approximation
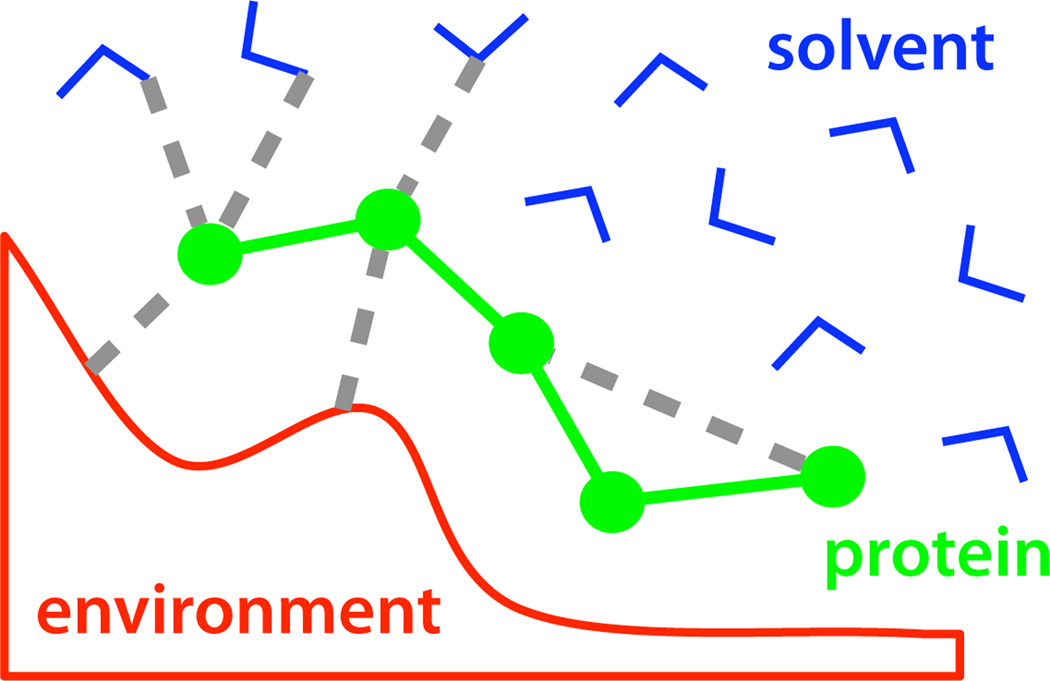
Consider the Hamiltonian ℋ(x) for a molecular system described by co-ordinates x = {p, s, e}, where p represents a set of protein coordinates, s represents a set of solvent coordinates, and e represents a set of ‘environment’ coordinates, for example, the atoms of a protein receptor or other molecular surface (Figure 1).
Here, Upp is the potential from the protein self-interactions, Ups is the potential due to all protein-solvent interactions, Upe is due to all protein-environment interactions, and so on. (Here, we are considering the ligand to be a polypeptide, but the treatment is general.)
Figure 1.
A molecular system is decomposed into protein, solvent, and environment co-ordinates.
Consider the partition function for this system at inverse temperature β = 1/kBT when we integrate out the solvent and environment coordinates to achieve a description of Z(p), the partition function as function of the protein coordinates alone.
| (1) |
For the time-being, we will consider the case where the environment coordinates are fixed with respect to the protein and solvent. In this case, Uee is constant and can be ignored, while Upp and Upe depend only on the protein coordinates, and Use depends only on the solvent coordinates. This yields
| (2) |
where
| (3) |
| (4) |
Here, Zp (p) is the Boltzmann factor due to protein self-interactions and the environment, and Zs(p) can be thought of as a solvation free energy term. Zs(p) contributes an extra “weight” to each conformation p due to interactions with the solvent.
Next, we introduce the fragment approximation. Suppose we have estimates for the partition functions Z(pi) = Zp(pi)Zs(pi) over a set of disjoint fragments {p1, p2, …, pn} = p. If we assume that each fragment is independent, then the partition function for the entire protein can be approximated as
To correct this approximation for the true Z(p), we would have to multiply by a correction factor
This correction factor represents the cooperativity of fragments as a function of the protein position p. Any non-additivity in the free energies is accounted for by Fcoop(p) = −β−1 log C(p). Note that we can separate the protein non-additivity of fragments and the solvent non-additivity:
If the protein-protein interactions are represented by an additive pairwise potential (as with most all-atom forcefields), then we can further reduce the cooperativity correction factor to the following form:
A similar approach, with the environment coordinates not fixed, leads to a similar expression, but with Zs (p) substituted with Zse(p) = ∫ ∫ds exp(−β[Ups(p, s) + Uss(s)])de exp(−β[Upe(p, e) + Use(s, e) + Uee(e)])
Now we can interpret the terms in the correction factor to have some intuitive meaning. The Boltzmann factor term on the left accounts for purely inter-residue interactions, mostly protein chain connectivity. The term on the right accounts for cooperativity (between fragments) due to solvent effects (hydrophobicity, charge screening, etc., and any mutual interaction of the solvent with the environment such as surface tension, molecular shape, etc.).
These two effects are exactly what we must add to the fragment potentials in order to construct an accurate coarse-grained model. In this paper, we use a simple dihedral potential with chain connectivity (described below) as a first approximation to a more detailed correction.
It is worth noting some useful features of the theory above. One is that it provides a framework for making successive many-body (2-, 3- and 4-body, say) corrections to the MSFP method, to systematically make corrections to a coarse-grained potential to improve the approximations. One way to do this is to simulate larger fragments (i.e. groups of smaller fragments) to quantify many-body interactions, at the cost of much more simulation. This kind of iterative approach is also a useful way to quantify the accuracy of any given coarse-grained approximation.
2.2. MD simulation of amino acid analogs in the ribosomal exit tunnel
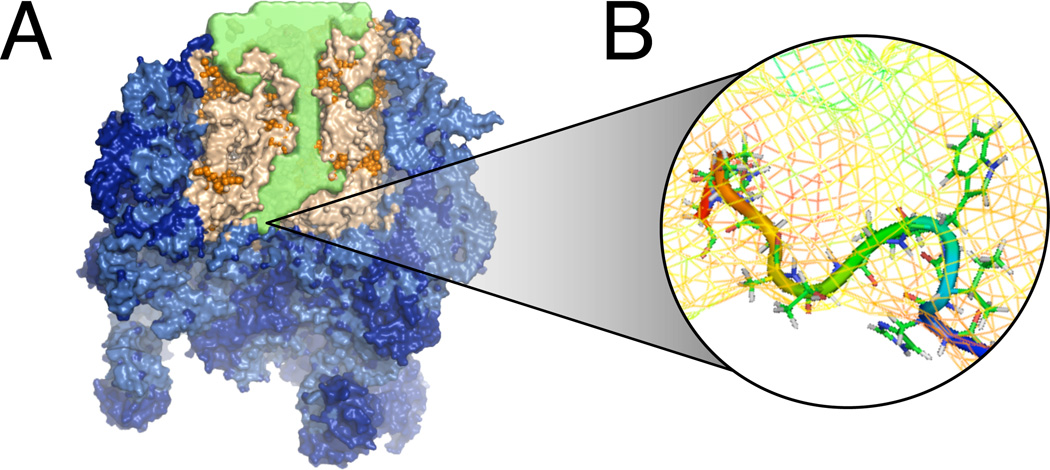
The MD simulation protocol is described as in.10 The model is built from a cut-out of the Haloarcula marismortui X-ray structure (pdb 1S7211), including the ribosome tunnel and nearby areas, explicit water and ions (Figure 3A). The inner surface of the ribosome tunnel was probed with small molecule analogs to amino acid sidechains. All-atom molecular simulations using the AMBER forcefield were performed with probe molecules exhaustively umbrella-sampled at a series of restrained grid points, which were then analyzed using WHAM,12,13 yielding comprehensive maps of the 3D potential of mean force (PMF) for the single amino acid sidechain analogs throughout the ribosomal exit tunnel. The resolution of these maps is 1Å, in the center-of-mass coordinate of the sidechain. It is important to note that while these 3D PMF maps are constructed from small molecule sampling, they are designed to capture the interactions of solely the single amino acid side chain with the chemical environment of the tunnel, including the effect of the solvent.
Figure 3.
(A) The cutout of the ribosome used for molecular simulation. In green is the accessible volume of the exit tunnel. (B) A close-up view of a conformation sampled by the coarse-grained chain potential using MSFP.
2.3. Coarse-grained MC sampling of protein chain
A Monte Carlo scheme was used to broadly sample conformational and sequence space under the influence of a coarse-grained potential. In this scheme, the peptide chain object is an all-atom structure, but with fixed bond lengths, which is convenient for transporting conformations from the coarse-grained phase back into all-atom simulations (Figure 3B). The form of the potential is
where x1, x2, …‥xn are the coordinates, and s(n) the amino acid, of each residue for chain index n. Usteric is a steric repulsion term calculated over all atoms in the structure as ∑i≠j Θ(rij − r0)(σij/rij)6, where rij is the distance between atoms i and j, Θ is the Heaviside step function, and σij are standard atomic radii. r0 is set to 1.2Å. Utrans is a harmonic potential that allows translations about an anchor point, which we tether to the backbone carbon of the last residue in the chain (nearest to the PTC). The PMF potential is a function of the side chain centroid, and is evaluated by linear interpolation from the grid of stored values. There is one PMF grid for each residue type: ALA, ASP, ILE, LYS, TRP. Udih is a backbone dihedral potential compiled from the top500 database.14 Note that in this model, there is no interaction of the chain with itself, except for simple sterics, respecting the distribution of dihedral angles.
Allowed move sets for the coarse-grained chain include: (i) chain growth or deletion by one residue, at the N-terminal end of the chain (ii) backbone dihedral (ϕ,ψ) rotations, (iii) random perturbations to side chain χ angles, (iv) mutation of a residues to a new amino acid, (v) translation of the entire chain.
The nascent peptide anchor location has been defined based on the crystal structure of a pre-translocational intermediate of Haloarcula marismortui (pdb 1KQS15) which includes the tRNA analog A76. We structurally aligned the pre-translocational intermediate to the ribosome structure on which we based our model (pdb 1S7211), and find little variation in the area of the PTC site, with especially the A and P loops structurally unchanged. It is believed that the polypeptide is attached close to atom 3OH of the tRNA analog A76.15 We use the location of this atom as an anchor point for the growing polypeptide chain in our MSFP simulation.
2.4. Flat-histogram generalized ensemble sampling
For enhanced efficiency, we sample from what can be called a generalized ensemble.16,17 Instead of a single potential, we sample from an ensemble of potentials, Uk, each with index k representing a binned macrostate of the chain that we wish to sample over. For this study, we have chosen states k ≡ (s, N), each representing a chain of length N where the Nth residue is amino acid s.
Consider a generalized ensemble of Hamiltonians
where β = 1/kBT, kB is the Boltzmann constant, T is temperature, and we have perturbed each Hamiltonian ℋk(x) by a weighting term gk. The generalized partition function for the entire ensemble is
where Zk is the unperturbed partition function for the ensemble indexed by k. To achieve uniform sampling across states k, we use the at-histogram method of Wang and Landau18 to iteratively converge upon weights gk = log Zk + C, for some arbitrary constant C. Once converged, the free energy of state k is obtained as −kBT · gk. In this algorithm, the number of times a state k is visited is stored as histogram counts Wk. Initially, all the gk are equal. Each time a state k is visited, gk is incremented by a small amount δ, and the histogram count Wk is increased by one. If the histogram is sufficiently at (when all Wk ≥ γ 〈Wk〉), δ is scaled to δ ← αδ, where 0 < α < 1, and 0 < γ < 1.
3. Results
3.1. Validation of the sampling algorithm
We simulated the sequence (Ala)5, using a sterics-only (no external PMF) coarse-grained potential, to validate the performace of the sampling. Here, the sequence stays fixed, but the chain is allowed to grow or shrink by one monomer at a time. The spring constant for the C-terminus tether was set as to produce fluctuations smaller than 0.1Å in the the anchored atom position. The at-histogram method ensures that that the simulation converges to a random walk in chain length.
In Wang-Landau histogram method, there is a trade-off in the initial choice of the weight increment δ. For accuracy, δ should be kept small, to achieve good resolution in the resulting histograms, as the free energy estimates are influenced more heavily by the sampling early in the simulation. However, as δ becomes small, the rate of convergence slows. By trial and error with the ALA5 sequence, we found that δ = 0.001, γ = 0.95, and α = 0.9, with weights updated every 100 MC steps, achieved a good balance and accuracy and speed. The free energies reach convergence within a few hours of real-time computation on a single processor of an 3 GHz Intel Xeon MacPro.
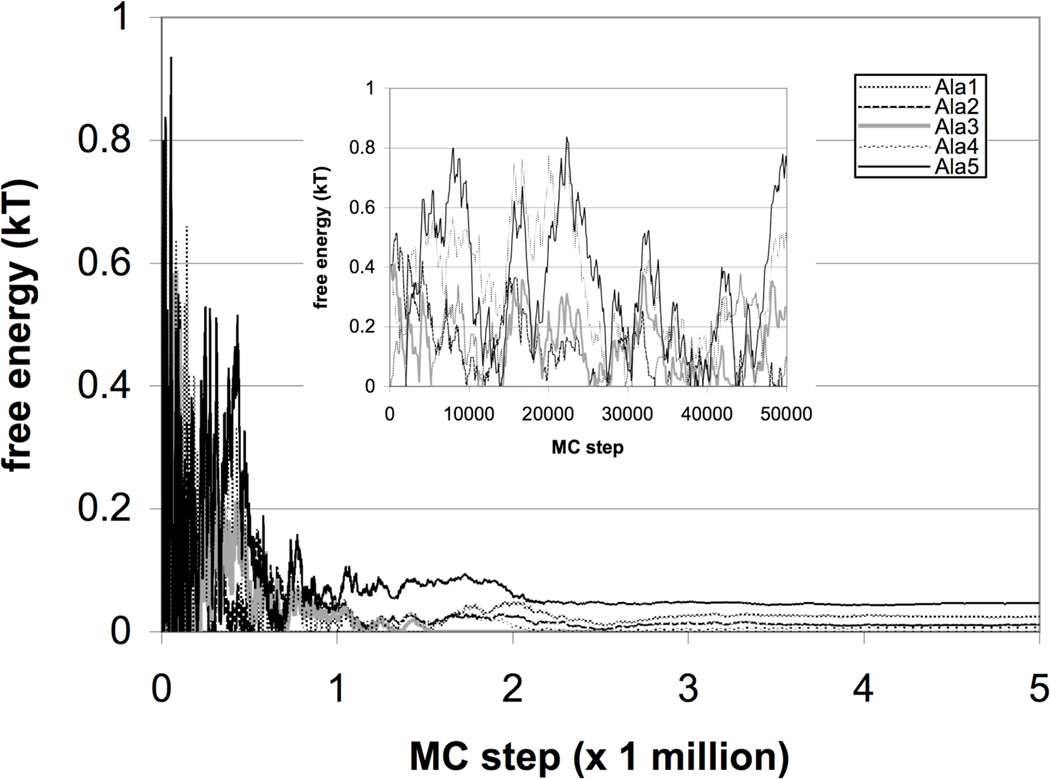
Because the only terms in the potential are dihedral preference and sterics, the only determinant of the free energies in this case is the accessible conformational volume, which should be roughly equal. After about 2 million MC steps, the computed free energies as a function of chain length converge to within < 0.1kBT from each other (Figure 2). These remaining free energy differences are due to both the accuracy resolution of the technique, and the slight differences in excluded volume for different chain lengths.
Figure 2.
Chain-growth sampling of Ala5 shows convergence of generalized ensemble sampling to within 0.1kBT the predicted values. The free energies are plotted with a reference state so that the lowest free energy is set to zero.
3.2. Sampling conformational and sequence space of peptide pentamers
Generalized-ensemble Monte Carlo using MSFP was performed across all sequences from the 5-letter alphabet of residues (A,D,I,K,W) and chain lengths ranging from 1 to 5 monomers, in both the absence and the presence of the computed PMF potential. The macrostates k = (N, s) were used for the Wang-Landau at-histogram algorithm. The MC parameters were those derived from our previous validation simulations above.
Pentamer sampling in the absence of the PMF (with dihedrals and sterics), produced an equilibrated trajectory, but with fluctuations in the weights slow to converge due to the number of possible macrostates. As expected, free energies were determined by the accessible conformational volume of each residue. But because the weight updating increment is not decreased until a sufficiently at sampling histogram has been achieved, the rate-limiting step for weight convergence is the sampling transition rates to unfavorable states. In this case, mutations to the bulky tryptophan residue had the lowest acceptances.
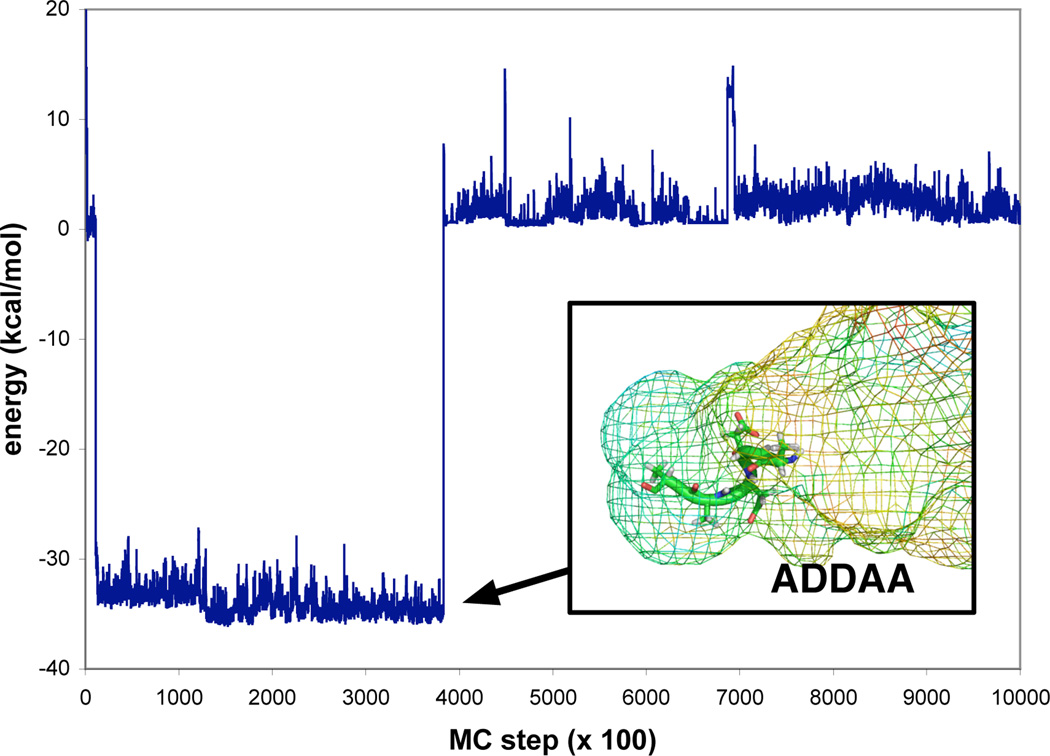
Pentamer sampling in the presence of the PMFs showed similar convergence behavior, but also showed strong specificity for particular peptide sequences and conformations during the coarse-grained trajectories that were simulated. Most notably, the sequence ADDAA sampled a conformational basin that was enthalpically favored by about 30 kcal/mol (Figure 4). With more sampling, and complete analysis will allow us to determine the entropic components of this binding affinity that our model predicts. For sequences predicted to have high affinity such as these, we can transport conformations back into detailed all-atom MD simulations of the ribosome, to test the predictions of MSFP. The role of water and/or entropic stabilization of peptides confined within larger macromolecules is important to many fundamental biological processes, and is an area of active research.
Figure 4.
An energy trace of MSFP sampling of nascent chains in the ribosomal exit tunnel. Generalized ensemble Monte Carlo sampling was performed across all sequences from the alphabet (A,D,I,K,W) and across all chain lengths up to 5-mers, in the presence of MD-derived PMFs for each residue type. A low-energy conformation for the sequence ADDAA was found to be exceptionally stable.
Some of the convergence issues we observe with the Wang-Landau algorithm can be ameliorated by augmenting the weight-updating procedure,19 or using more sophisticated generalized ensemble methods.16,20,21 Reference states for fragment PMFs may need to be validated and adjusted for optimal convergence.
4. Discussion
Many approaches have been developed for multiscale simulation,22,23 as well as coarse-grained models for proteins.24 The main goal of much of this work has been to develop accurate models that require fewer degrees of freedom, in order to speed up molecular simulations with minimal loss of accuracy in inter-particle interaction. Many of these methods rely on atomically detailed reference simulations. The Multiscale Coarse-Graining Method (MS-CG)25,26 is an approach for generating a consistent27,28 coarse-grained approximation to a many-body potential by using a force-matching technique from reference simulations. Inverse Monte Carlo approaches have also been used to optimize potentials for coarse-grained models using distributions calculated from atomistic reference simulations29,30
Two kinds of information are used to build a coarse-grained potential using the MSFP method: a potential of mean force derived from atomically detailed fragment simulations, and a potential that accounts for fragment cooperativity, mainly due to chain connectivity (although other cooperative effects are important). While large-scale fragment simulations are computationally feasible by a variety of methods,10,31 detailed simulation of a ligand’s self-interaction within its proper context (in this case, a nascent polypeptide in the unique environment of the ribosomal exit tunnel) can be prohibitively expensive. With the MSFP approach as presented here, we have instead modeled the polypeptide as a simple dihedral model with excluded volume to capture chain connectivity and sequence dependent torsional propensities. The statistical mechanical framework we present suggests a straightforward way to iteratively improve this simple chain potential to arbitrary accuracy, by using multi-body correction factors calculated from atomically detailed simulations.
In this paper, we have shown how the MSFP method can efficiently sample conformational and sequence space for polypeptides in a coarse-grained potential. Using generalized ensemble Monte Carlo sampling, we can obtain accurate estimates of free energy differences between chain macrostates. For this test problem, we have shown that some sequences are much more preferred than others, suggesting that MSFP could be a generally useful tool for ligand and/or peptide design that overcomes some of the traditional limitations of all-atom simulation.
Acknowledgments
We wish to thank M. Scott Shell, John Chodera, Xuhui Huang, the contributers of the Folding@Home distribution computing resource, and the Stanford Bio-X cluster. Authors gratefully acknowledge support from NIH and NSF, in particular Simbios (NIH U54 GM072970) and NSF FIBR (NSF EF-0623664).
References
- 1.Voss NR, Gerstein M, Steitz TA, Moore PB. Journal of Molecular Biology. 2006;360:893. doi: 10.1016/j.jmb.2006.05.023. [DOI] [PubMed] [Google Scholar]
- 2.Mankin AS. Trends in Biochemical Sciences. 2006;31:11. doi: 10.1016/j.tibs.2005.11.007. [DOI] [PubMed] [Google Scholar]
- 3.Nakatogawa H, Ito K. Cell. 2002;108:629. doi: 10.1016/s0092-8674(02)00649-9. [DOI] [PubMed] [Google Scholar]
- 4.Muto H, Nakatogawa H, Ito K. Molecular Cell. 2006;22:545. doi: 10.1016/j.molcel.2006.03.033. [DOI] [PubMed] [Google Scholar]
- 5.Nakatogawa H, Ito K. Chem Bio Chem. 2004;5:48. doi: 10.1002/cbic.200300751. [DOI] [PubMed] [Google Scholar]
- 6.Cruz-Vera LR, Rajagopal S, Squires C, Yanofsky C. Molecular Cell. 2005;19:333. doi: 10.1016/j.molcel.2005.06.013. [DOI] [PubMed] [Google Scholar]
- 7.Gong F, Ito K, Nakamura Y, Yanofsky C. Proceedings of the National Academy of Sciences. 2001;98:8997. doi: 10.1073/pnas.171299298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Auerbach T, Bashan A, Yonath A. Trends in Biotechnology. 2004;22:570. doi: 10.1016/j.tibtech.2004.09.006. [DOI] [PubMed] [Google Scholar]
- 9.Sanbonmatsu KY, Tung C-S. Journal of Structural Biology. 2007 Mar;157:470. doi: 10.1016/j.jsb.2006.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Petrone PM, Snow CD, Lucent D, Pande VS. Proceedings of the National Academy of Sciences. 2008 doi: 10.1073/pnas.0801795105. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ban N, Nissen P, Hansen J, Moore PB, Steitz TA. Science. 2000;289:905. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- 12.Kumar S, Bouzida D, Swendsen R, Kollman P, Rosenberg J. Journal of Computational Chemistry. 1992;13:1011. [Google Scholar]
- 13.Bartel C, Karplus M. Journal of Computational Chemistry. 1997;18:1450. [Google Scholar]
- 14.Lovell SC, Davis IW, Arendall IWB, de Bakker PIW, Word JM, Prisant MG, Richardson JS, Richardson DC. Proteins: Structure, Function and Genetics. 2003;50:437. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 15.Schmeing TM, Seila AC, Hansen JL, Freeborn B, Soukup JK, Scaringe SA, Strobel SA, Moore PB, Steitz TA. Nature Structural Biology. 2002;9:225. doi: 10.1038/nsb758. [DOI] [PubMed] [Google Scholar]
- 16.Park S. Phys. Rev. E. 2008;77:016709. doi: 10.1103/PhysRevE.77.016709. [DOI] [PubMed] [Google Scholar]
- 17.Lyubartsev AP, Martsinovski AA, Shevkunov SV, Vorontsov-Velyaminov PN. The Journal of chemical physics. 1992;96:1776. [Google Scholar]
- 18.Wang F, Landau DP. Physical Review E. 2001;64:056101. doi: 10.1103/PhysRevE.64.056101. [DOI] [PubMed] [Google Scholar]
- 19.Shell MS, Debenedetti PG, Pangiotopoulos AZ. Proteins: Structure, Function and Genetics. 2006;62:232. doi: 10.1002/prot.20714. [DOI] [PubMed] [Google Scholar]
- 20.Park S, Ensign DL, Pande VS. Physical Review E. 2006;74:066703. doi: 10.1103/PhysRevE.74.066703. [DOI] [PubMed] [Google Scholar]
- 21.Huang X, Bowman GR, Pande VS. Journal of Chemical Physics. 2008;128:205106. doi: 10.1063/1.2908251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ayton GS, Noid WG, Voth GA. Current Opinion in Structural Biology. 2007;17:192. doi: 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 23.Praprotnik M, Site LD, Kremer K. Annual Reviews of Physical Chemistry. 2008;59:545. doi: 10.1146/annurev.physchem.59.032607.093707. [DOI] [PubMed] [Google Scholar]
- 24.Tozzini V. Current Opinion in Structural Biology. 2005;15:144. doi: 10.1016/j.sbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 25.Izvekov S, Voth GA. Journal of Physical Chemistry B. 2005;109:2005. doi: 10.1021/jp0456685. [DOI] [PubMed] [Google Scholar]
- 26.Noid W, Chu J, Ayton G, Voth G. J. Phys. Chem. B. 2007 Jan;111:4116. doi: 10.1021/jp068549t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Noid W, Chu J, Ayton G, Krishna V, Izvekov S. J Chem Phys. 2008 Jan;128:244114. doi: 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Noid W, Liu P, Wang Y, Chu J, Ayton G. J Chem Phys. 2008 Jan;128:244115. doi: 10.1063/1.2938857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lyubartsev A, Laaksonen A. Phys. Rev. E. 1995 Jan;52:3730. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 30.Lyubartsev A. European Biophysics Journal. 2005;35:53. doi: 10.1007/s00249-005-0005-y. [DOI] [PubMed] [Google Scholar]
- 31.Clark M, Guarnieri F, Shkurko I, Wiseman J. J Chem Inf Model. 2006 Jan;46:23. doi: 10.1021/ci050268f. [DOI] [PubMed] [Google Scholar]