A Means to Accommodate Residual Limb Movement During Optical Scanning: A Technical Note

Abstract

A technique is described for correcting for subject movement while imaging the residual limb of a person with a transtibial amputation. Small reflective markers were placed on the residual limb, and then their motions tracked during scanning using two stationary cameras. The marker position measurements were used to generate appropriate translational and rotational transformation matrices so that limb motion could be corrected for during the 1.5-s scan interval. Evaluation tests showed good performance for moderate (2–4 mm) to high (5–8 mm) motion cases. The difference in mean absolute cross-sectional area between the test scan and a stationary reference scan was reduced by approximately one half when motion correction was used compared with when motion correction was not used. The algorithm broke down for exaggerated motion (≥9 mm) cases, particularly in areas outside the region encompassed by the markers. The developed method is useful in prosthetics research where high resolution shape measurement is needed, for example in cases where residual limb shape or volume change is of interest.

I. INTRODUCTION

The residual limb of a lower-limb amputee changes shape and volume over time. This change is relevant in prosthetics practice because shape and volume so strongly influence the fit of the prosthetic socket. In prosthetics research, efforts to quantify residual limb shape change from one time point to another have been made [1]–[3].

Measurement of short-term residual limb shape and volume change is challenging. Because the fluctuations are typically so small, less than a few percent [4], a high resolution modality is needed. Each 1.0% volume reduction for an average transtibial residual limb corresponds to approximately a 0.6 mm diameter difference [3]. Instantaneous shape acquisition is preferred so as to minimize error from subject movement. Subject movement is particularly important in investigations where the time course of residual limb shape and volume change is of interest. Residual limb volume increases quickly after socket doffing [3]. Though a number of imaging modalities have been used to image residual limbs, none simultaneously offer both high resolution and instantaneous acquisition. A commercial system using several digital cameras simultaneously (Ohio Willow Wood, Mt. Sterling, OH) offers instantaneous acquisition but lacks the capability to capture high curvature regions. High resolution methods, including optical scanning [3], laser scanning [5], [6], ultrasound [7]–[9], magnetic resonance imaging [10], computer tomography [11], [12], and spiral X-ray computer tomography [1], take between 1.5 s and several minutes depending on the technique. Even a 1.5-s interval is a relatively long time for a subject to remain still.

One way to improve performance of modalities with scan times that are not instantaneous is to monitor subject movement during scanning and then correct for it in postprocessing. The Polhemus electromagnetic field system (Fastrak, Polhemius, Colchester, VT) can be used in this way to track movement. The system tracks the position and orientation of a block-shaped sensor as it moves within a magnetic field. However, the sensor with attached cable must be positioned on the residual limb, preferably near the center of the region of interest. Presence of the large sensor interferes with residual limb image acquisition, making this method impractical.

The purpose of this research was to develop a means to correct for transtibial residual limb movement during optical scanning. Though we applied the developed technique to our custom scanner, the method is potentially applicable to other devices as well. The method and its capabilities are described.

II. METHODS

A. Scanner Design

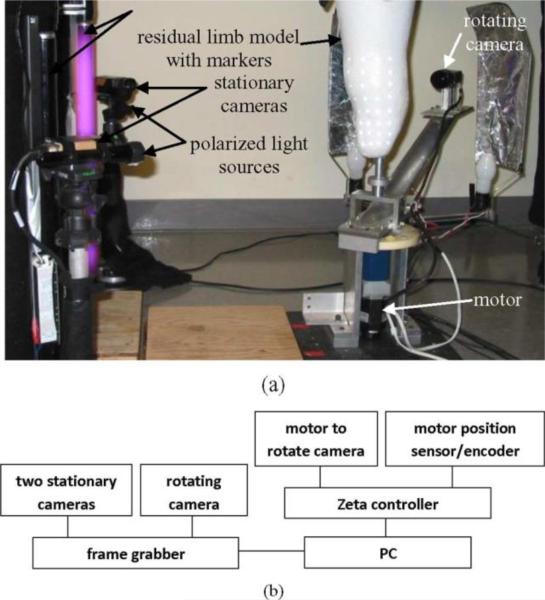
The scanner was a monochrome charged coupled device camera (KP-M1A, Hitachi Kokusai, Inc., Tokyo, Japan) with an 8-mm lens (Fijinon Corporation, Saitama City, Japan) attached to a thin-walled 5.1-cm-diameter aluminum cylinder (scanner arm) mounted to a motor (6 K, Compumotor, Parker Hannifin Corporation, Rohnert Park, CA) [Fig. 1(a)]. During residual limb scanning the camera was rotated approximately 290° around the residual limb using a motion controller (Zeta 1604, Compumotor) and PC (Precision 470, Dell, Round Rock, TX) while images were acquired (X64-AN 1, Coreco Imaging, Montreal, QC, Canada) [Fig. 1(b)]. A 290° interval ensured the entire residual limb surface was scanned. At the same time, this interval did not cause the scanner arm to contact the contralateral limb. The distance between adjacent pixels was 0.23 mm in the horizontal direction and 1.0 mm in the vertical direction. The mechanical design of the scanner minimized dynamic response in the scanner arm such that transients damped out within the first 30°, before image acquisition was initiated. Two light sources were positioned to illuminate the limb. The light sources were mounted on a mechanical cam attached to the base of the scanner arm so that they rotated with the arm. They moved out laterally, away from the arm central axis, during the central part of scanning so as to well illuminate the limb. They retracted in the very early and late phases of arm rotation (first 35° and last 35° , respectively) so that they did not contact the contralateral limb. Twenty-three images were acquired over the central 220° interval of camera rotation, a process that took approximately 1.5 s.

Fig. 1.

(a) Two stationary cameras monitored the positions of reflective markers placed on the limb. Rotating camera took 23 digital images during the central 220° of rotation around the residual limb. (b) Principal electronic components are shown.

Two stationary cameras (KP-M1A, Hitachi Kokusai, Inc.) tracked the motion of small markers placed on the residual limb, and these data were used to correct for subject movement. Sampling from the stationary cameras was performed at the same times at that from the rotating camera (23 images/1.5 s). The three sets of images were taken essentially instantaneously compared to the speed of residual limb movement. The two stationary cameras were positioned 90° apart [Fig. 1(a)]. The reflective markers (2 mm diameter, 0.1 mm thickness, 7610, 3M, St. Paul, MN) had an adhesive backing that allowed them to be easily positioned on the limb. A surgical skin marker (Viscot, East Hanover, NJ) was traced around each marker to enhance contrast and facilitate marker identification in image processing. Fluorescent and polarized light sources (DXE120M12, Dexin International, Inc., Covin, CA; 2-cell, Maglite, ON, CA; NT54-926, Edmund Optics, Barrington, NJ) were added [Fig. 1(a)] to enhance marker illumination since the markers were poorly illuminated when the rotating arm and attached light sources were on the opposite side of the residual limb. The fluorescent and polarized light sources did not interfere with the images acquired by the rotating camera.

B. Calibration

Each camera was independently calibrated using a modified application of the four-step Heikkila calibration procedure [13], [14]. Consistent with Heikkila's method, the procedure was initiated by determining intrinsic parameters, i.e., characteristics specific to the camera, from imaging a 2-D target multiple times from different positions. The 2-D target was a regular pattern of circles of known size and spacing mounted to a flat plate. Extrinsic camera properties, i.e., properties external to the camera including camera position and orientation, were determined by imaging a 3-D target, a 54.0-mm-diameter Delrin cylinder with a regular pattern of circles on the surface. The target was imaged at multiple rotating camera positions. Extending from Heikkila's method, we corrected for aberration in the lens and performed image reconstruction. These data also allowed the motor position encoder to be calibrated. Data were acquired simultaneously from all three cameras during calibration imaging.

An optimization procedure was then used to manipulate all parameters in the calibration model so as to minimize error in fitting of the data. Direct linear transformations were used. Calibration algorithms were run for each camera independently. Since the images were acquired simultaneously, the calibration could be coordinated across multiple cameras.

C. Motion Calculation and Correction

To calculate limb motion, image data from only the stationary cameras were used. It was assumed that the constellation of limb markers was rigid. This assumption was considered acceptable for this application since limb swelling over the course of the 1.5-s scanning interval was small.

Though common limb markers were not necessarily viewable by both stationary cameras at the same instant, since the constellation was assumed rigid, the transformations for both cameras were the same. Transformation parameters from one image to the next were calculated using an optimization procedure that for all markers in the constellation minimized the root mean square of the difference between the recorded position changes and those determined using the model.

The calculated motions were used to correct each silhouette image from the rotating camera, i.e., the location of the 3-D limb boundary points. The corrected points were then used to reconstruct the shape of the residual limb, using methods described previously [15]. For each coronal plane, the limb-boundary-tocamera segments from each of the 23 images encompassed the residual limb. Cartesian B-splines were formed for each coronal plane. B-splines were also used to assemble the data from adjacent planes so as to make a 3-D model.

D. Evaluation

A foam model of a transtibial residual limb was used to evaluate performance of the motion correction algorithm. The limb shape was from a transtibial amputee patient with a conical shape residual limb without undercuts. The distance from the patellar tendon to the distal end was 13.3 cm, and the circumference at the tibial tuberosity was 38.7 cm. The model was coated with white paint (V2192, Rust-Oleum, Vernon Hills, IL) to fill holes in the foam so as to make a smooth surface. The model was affixed to a rod at the proximal end so that its position could be controlled during testing. Five scans were performed. For the first scan, defined as the reference scan, the model was clamped in place at the proximal end so that there was no movement during scanning [Fig. 1(a)]. For the second scan, the model was displaced downward approximately 1 cm, rotated approximately 5°, and then reclamped in place. The other three scans were taken with different degrees of model motion over the course of the 1.5-s scan interval: approximately 2–4 mm, 5–8 mm, and mm for the third, fourth, and fifth scans, respectively. The motions were created by translating the rod at the proximal end of the model in an equilateral triangular pattern in the coronal plane while simultaneously rotating about the limb longitudinal axis approximately 5°. The 2–4 mm, 5–8 mm, and ≥ 9 mm distances corresponded to one side of the triangle. To accomplish these maneuvers, the rod was moved manually within a scaled reference frame connected to the support rails above the scanner.

Surfaces were generated without motion correction for all five scans, and with motion correction for the second, third, fourth, and fifth scans. Results from the second, third, fourth, and fifth scans were compared with the surface generated from the reference scan. To make this comparison, first the test scan and reference scan were aligned using a custom algorithm described in detail elsewhere [15]. The algorithm was an optimization procedure that used a weighted linear combination of maximized global similarity and maximized local shape similarity. Because the surfaces were described using B-splines, the shapes could be resampled after alignment, allowing a direct 1 to 1 comparison between cross sections at specified angular intervals. The absolute percentage differences in cross-sectional area between matched slices from the two models were calculated. This analysis was done for 175 slices at a 1.0-mm slice spacing. Using data from all 175 slices, a mean percentage absolute difference was calculated. This analysis was done for each test scan compared with the reference scan. The basis for using absolute area difference rather than volume difference was that volume difference can mask local shape distortion. By considering many slices and using the absolute difference in area for each slice, we achieved an assessment reflective of absolute mismatch.

III. RESULTS

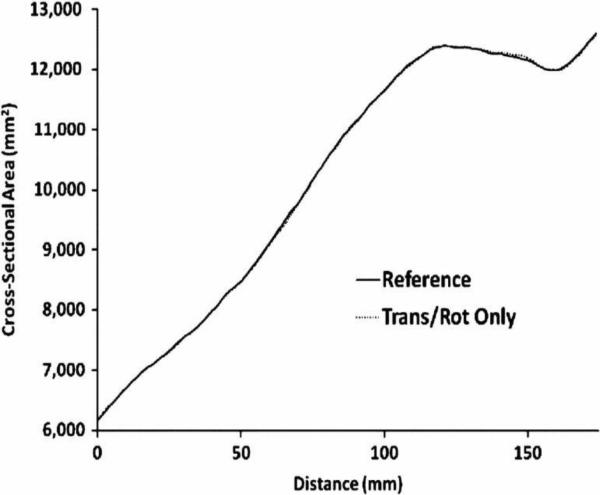
Comparison of the scan with an orientation change only (second scan) to the reference scan (first scan) showed comparable results. The cross-sectional area versus distance plots were similar (Fig. 2), and the mean absolute difference in cross-sectional area was small, 0.1% (Table I). This 0.1% difference was principally due to the resolution limitations of the scanner and to a lesser extent error in the alignment algorithm [15]. Results with and without motion correction were identical.

Fig.2.

Translationandrotationscancomparedwithreferencescan.Cross-sectionalareaversusdistanceplotsareverysimilar.Patellartendonisat124mmdistance.

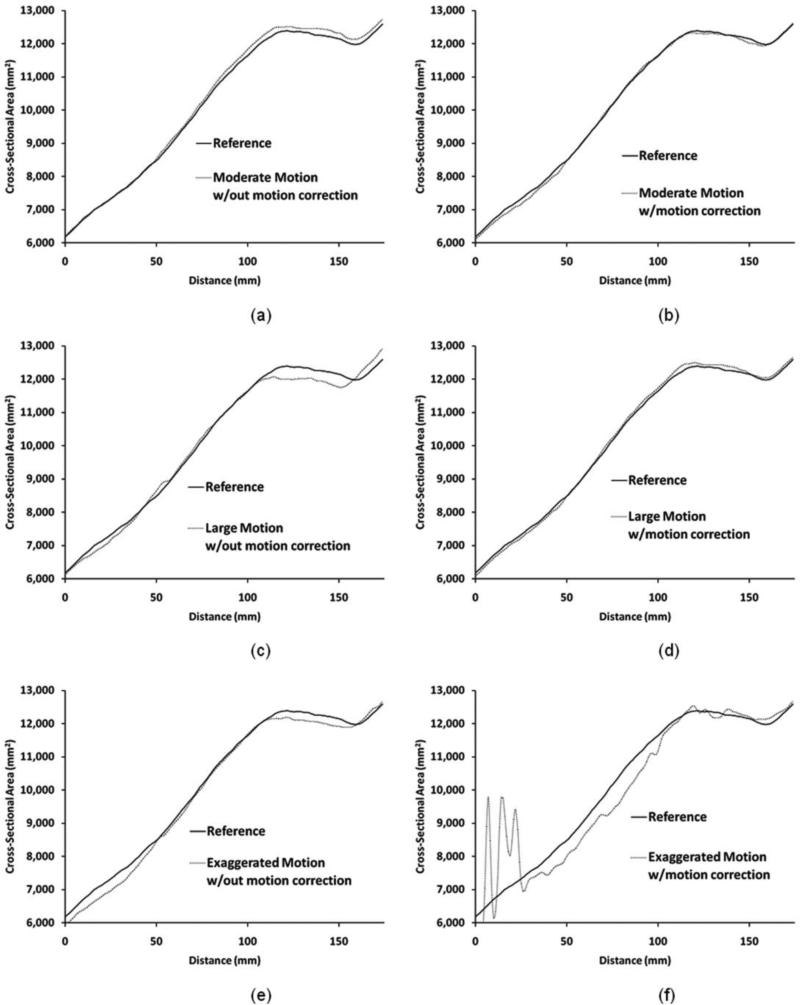
For the moderate and high motion cases (third and fourth scans, respectively), the motion correction algorithm performed well, improving the match of the cross-sectional area versus distance plots to the reference scan [Fig. 3(b) and (d)] compared to no motion correction [Fig. 3(a) and (c)]. The mean absolute difference in cross-sectional area was approximately cut in half when motion correction was used compared to when it was not used (Table I). For moderate motion the difference reduced from 1.0% to 0.6%. For high motion the difference reduced from 1.5% to 0.8%. No systematic proximal-to-distal change in the error was found.

Fig. 3.

Test scans compared with reference scan. For moderate and high displacements, scans with motion correction [(b) and (d)] showed results more comparable to the reference scan than for scans without motion correction [(a) and (c)]. For exaggerated motion [(e) and (f)], motion correction did not improve the result. Patellar tendon is at 124 mm distance.

For exaggerated motion (fifth scan), however, the motion correction algorithm was unsuccessful. The cross-sectional area versus distance plot showed substantial error [Fig. 3(f)], worse than that when no motion correction was used [Fig. 3(e)]. The error was worst at the distal end outside of the marker locations. The mean absolute difference in cross-sectional area was greater for motion correction (4.5%) compared with no motion correction (1.6%) for the exaggerated motion case (Table I).

IV. DISCUSSION

For imaging modalities that are not instantaneous, correcting for subject motion improves the quality and reliability of residual limb shape measurement. This correction is particularly important in assessment where the time course of residual limb shape and volume change is of interest. Each scan must be reliably collected. Researchers measuring shape immediately after doffing to infer residual limb shape before socket removal, 9 mm, the algorithm is no longer effective. This happens be-for example, must reliably obtain the first scan after doffing cause at large displacements the uniqueness of the solution and since limb volume increases quickly [3]. thus accuracy with which limb markers are found deteriorates.

The described method to correct for limb movement is limited in that it does not allow for excessive rotation or gross movement of the residual limb. Once motion is beyond approximately 9 mm, the algorithm is no longer effective. This happens because at large displacements the uniqueness of the solution and thus accuracy with which limb markers are found deteriorates. The solution becomes less stable. This limitation could potentially be reduced by incorporating marker position data from the rotating camera into the motion correction algorithm. However, it should be noted that once trained in our scanner, subjects experience only slight residual limb movement (< 2 mm) over the 1.5-s scan interval [3]. Thus, correcting for exaggerated motion is of limited relevance.

The markers placed on the limb potentially cause a slight distortion of the shape. However, since the markers are very thin (0.1 mm) and small (2.0 mm diameter) and since it is typically shape change from one scan to the next that is of interest in shape and volume change assessment, their presence is expected to have minimal impact. We have found that subjects walk comfortably in their prostheses with the markers in place.

The mean absolute difference in cross-sectional area calculated here for presentation in Table I reflects volume changes assuming the volume change for each section of limb is made positive. Actual volume differences are equal to or less than this calculation, thus in this sense our test was a worst case condition. Volume changes measured on a collection of transtibial amputees over a 35 min recovery interval after socket doffing ranged from 2.4% to 10.9% [3]. Thus the difference in absolute cross-sectional area here remaining after motion correct for no to moderate motion cases (0.1%–0.6%) is less than that after socket doffing. Therefore, the error is acceptable for measurement of limb volume change after doffing.

The motion correction algorithm did not completely eliminate the error for several reasons. First, the optical scanner had limited resolution due to the spacing between adjacent pixels. The alignment algorithm also introduced error but evaluation has shown this error to be minimal [15]. Our evaluations show the combined error from these two sources to be about 0.1%. Additional error is introduced from another source: marker position during part of the scan is lost because the rotating scanner arm obstructs the view from the stationary cameras (one at a time) during part of the scan. This loss of information deteriorates motion correction. This limitation could be reduced and motion correction improved by incorporating marker position information from the rotating camera into the motion correction algorithm. This remains an area of future work.