Investigations Concerning Cavitation and Frost Fatigue in Clonal 84K Poplar Using High-Resolution Cavitron Measurements^,

Frost- and drought-induced fatigue, which damages xylem vessels and makes them vulnerable to embolism, share a common mechanism.

Abstract

Both drought and freezing-thawing of stems induce a loss of hydraulic conductivity (percentage loss of conductivity [PLC]) in woody plants. Drought-induced PLC is often accompanied by physical damage to pit membranes, causing a shift in vulnerability curves (cavitation fatigue). Hence, if cavitated stems are flushed to remove embolisms, the next vulnerability curve is different (shifted to lower tensions). The 84K poplar (Populus alba × Populus glandulosa) clone has small vessels that should be immune from frost-induced PLC, but results demonstrated that freezing-thawing in combination with tension synergistically increased PLC. Frost fatigue has already been defined, which is similar to cavitation fatigue but induced by freezing. Frost fatigue caused a transition from a single to a dual Weibull curve, but drought-fatigued stems had single Weibull curves shifted to lower tensions. Studying the combined impact of tension plus freezing on fatigue provided evidence that the mechanism of frost fatigue may be the extra water tension induced by freezing or thawing while spinning stems in a centrifuge rather than direct ice damage. A hypothesis is advanced that tension is enhanced as ice crystals grow or melt during the freeze or thaw event, respectively, causing a nearly identical fatigue event to that induced by drought.

Water transport in xylem conduits of trees occurs while water is under tension (negative pressure; Tyree and Zimmermann, 2002). The xylem water-transport system is vulnerable to cavitation and embolism because tensile water is metastable, so if a gas bubble appears in a conduit it will rapidly expand to fill the conduit whenever the fluid tension is 0.1 MPa or greater, where a tension of 0.1 MPa is equivalent to vacuum pressure. A cavitation event occurs whenever a tensile water column breaks, which results in a water vapor-filled void. Because of Henry’s law of gas solubility in water, this vapor void will eventually equilibrate with air at atmospheric pressure, at which point the conduit is fully embolized (Tyree and Zimmermann, 2002). Embolism has been identified as a limiting factor of primary production (Hubbard et al., 2001). As a result, tree growth and fitness are probably negatively impacted temporarily or seriously limited permanently if embolism is extensive (Christensen-Dalsgaard and Tyree, 2013).

The two main factors causing cavitation and embolism are drought and frost (Mayr et al., 2003; Christensen-Dalsgaard and Tyree, 2013). Drought-induced cavitation is caused by the high xylem tension attributed to water stress. The high tension in the sap forces air bubbles into functional conduits from neighboring embolized ones through shared pit membranes (Jarbeau et al., 1995; Sperry et al., 1996; Hacke et al., 2001; Stiller and Sperry, 2002; Christman et al., 2012) according to an air-seeding mechanism (Sperry and Tyree, 1988; Cochard et al., 1992). Hence, the continuity of water flow is disrupted due to cavitation. Frost-induced cavitation, on the other hand, occurs when dissolved gases in the sap freeze out and create bubbles during ice formation because air is not soluble in ice (Mayr et al., 2003; Christensen-Dalsgaard and Tyree, 2013, 2014) but remains entrapped between ice crystals. Once the sap melts and tension is regenerated, the entrapped bubbles may expand to embolize the conduits instead of dissolving (Pittermann and Sperry, 2006). Current thinking is that freezing-induced embolism occurs when the tension exceeds a critical value determined by the surface tension of the bubbles, which mainly depends on the xylem water potential and the bubble radius (Yang and Tyree, 1992; Tyree et al., 1994; Hacke and Sperry, 2001). Larger bubbles may form in conduits with a larger diameter, so species with larger conduits are more vulnerable to frost-induced embolism (Langan et al., 1997; Davis et al., 1999; Pittermann and Sperry, 2006). Furthermore, enhanced loss of hydraulic conductivity (K_h) of trees may occur when stems are subjected to a combination of frost and drought causing low xylem water potential (Mayr et al., 2003; Willson and Jackson, 2006) and repeated freeze-thaw cycles (Sperry and Sullivan, 1992; Cox and Zhu, 2003; Mayr et al., 2003). However, even trees with small conduits are found to suffer severe embolism in winter (Sperry et al., 1988; Améglio et al., 2002) due mostly to freezing-drying of stems.

Resilient species are those that suffer no significantly different cavitation resistance before and after a cavitation-refilling cycle (Hacke et al., 2001; Christensen-Dalsgaard and Tyree, 2013). In contrast, species that are weakened by cavitation or frost are said to suffer cavitation fatigue or frost fatigue. Cavitation or frost fatigue is quantified by how much the vulnerability curve is shifted before versus after a fatigue-inducing event, and it is typically reported as a shift in P₅₀, which is either the pressure (negative value) or tension (positive value) that produces 50% loss of K_h. In the rest of this article, we will use T₅₀ to indicate the tension at 50% loss of conductivity or T_x to indicate the tension that induces x% loss of conductivity. Vulnerability curves (VCs) are usually measured by a centrifuge technique (Alder et al., 1997; Cochard et al., 2005), but most researchers measure just five or six points to determine a VC. High-resolution VC curves with nine to 27 points per curve can be collected quickly using the Cochard rotor. Recent studies have successfully used high-resolution VC to characterize the detailed shape of VCs, revealing dual Weibull curves (e.g. r- and s-shaped or dual s-shaped curves; Cai et al., 2014; Wang et al., 2014a) because a complex shape to a VC cannot be identified with just a few points. Furthermore, we used a centrifuge to induce tension while simultaneously freezing in order to study the combined impact of tension and freezing-thawing on frost fatigue and freeze-thaw-induced embolism.

In this article, we intend to investigate whether drought and freeze-thaw cycles could have an effect on the cavitation resistance in terminal shoots from adult trees of 84K poplar (Populus alba × Populus glandulosa), with high-resolution analysis of VCs and an artificial freeze-thaw simulation technique. Populus spp. are known to be water-demanding, drought-sensitive species with T₅₀ ranging from 1.07 to 2.5 MPa (Fichot et al., 2015) and vulnerable to winter damage (Feng et al., 2010). Among poplars, 84K poplar is known by foresters to be relatively resistant to water stress, low temperature, diseases, and insects (Zhou et al., 2007). As the main afforestation species in Shaanxi, Gansu, and Qinghai Province, 84K poplar is of great ecological importance.

RESULTS

Cavitation Fatigue

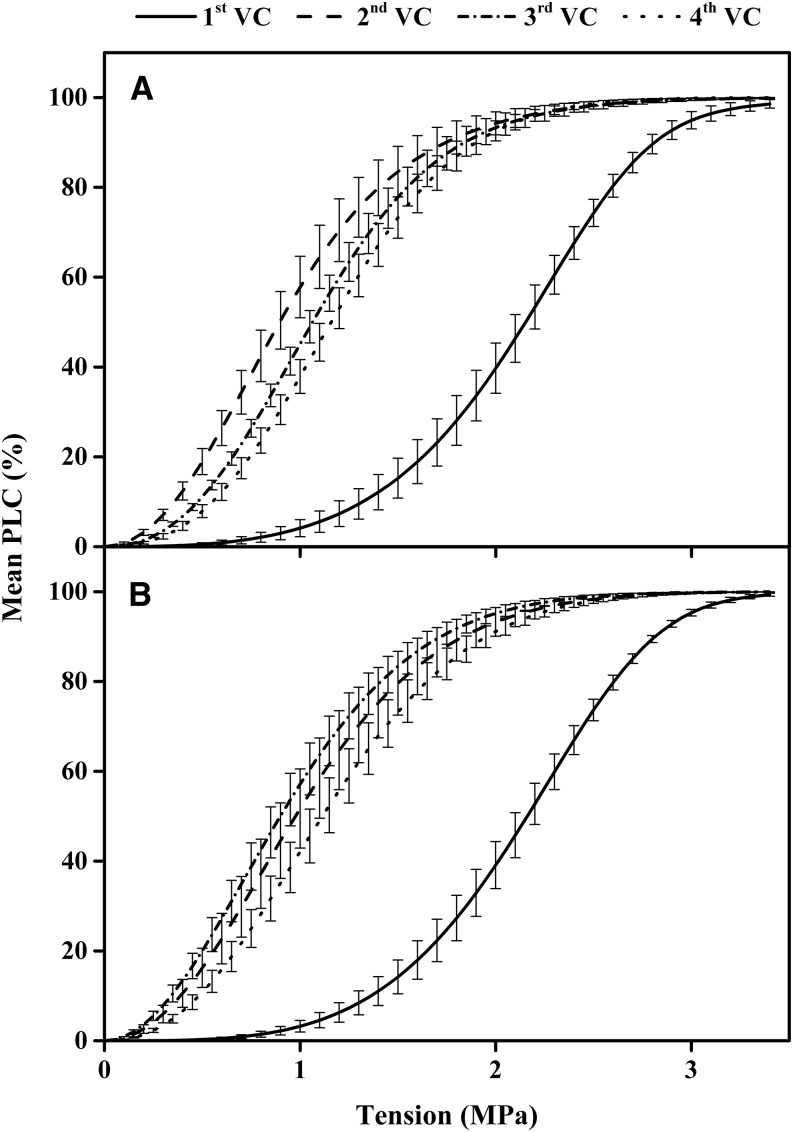
Vulnerability curves of 84K poplar stems were measured four times; the first VC was measured in flushed, native material, and the other three VCs were obtained on the same stem segments after exposure to three cycles of flushing with 0.1 m KCl and 0.01 m CaCl₂ solutions. All VCs were s shaped and fit Weibull curves with an average route mean square error (RMS_error) of 2.31% (for typical curves, see Supplemental Fig S1A). The recovery of K_h after each flush cycle averaged about 99.48% for all experiments (Table I). The mean values ± se of T_x at 10% increments of percentage loss of conductivity (PLC) are shown in Table II together with results of a significance test between KCl and CaCl₂ treatments. There was no significant difference between T_x values for KCl and CaCl₂ perfusions except between the second and third VCs, where CaCl₂ perfusion made the stems significantly more vulnerable from 10 to 50 PLC.

Table I. Percentage restoration of conductivity after flushing followed by VC measurement using 0.1 m KCl and 0.01 m CaCl₂ solution.

K_h numbers represents the ith flush followed by the ith VC measurement (i = 1, 2, 3, 4). The data are based on means ± se of seven samples (KCl) and six samples (CaCl₂).

Solution	Kh2/Kh1	Kh3/Kh1	Kh4/Kh1
KCl	100.2% ± 1.7%	100.2% ± 0.9%	95.4% ± 1.1%
CaCl2	98% ± 1.3%	103.1% ± 1.9%	100% ± 1.4%

Table II. Statistical analysis of VCs measured in the same stem undergoing four cycles of cavitation-refilling and VC measurements with 0.1 m KCl and 0.01 m CaCl₂ solutions.

Significance tests focus on the impact of salts (KCl versus CaCl₂) used for the flush. T_x represents the tension at which certain PLC was caused (10, 20,…90). The values are means ± se of seven samples using 0.1 m KCl solution and six samples using 0.01 m CaCl₂ solution. Significance levels (testing the impact of solution at any PLC): *P < 0.05.

PLC	First VC		Second VC		Third VC		Fourth VC
	Tx (KCl)	Tx (CaCl2)	Tx (KCl)	Tx (CaCl2)	Tx (KCl)	Tx (CaCl2)	Tx (KCl)	Tx (CaCl2)
10	1.38 ± 0.13	1.41 ± 0.11	0.38 ± 0.04	0.46 ± 0.05	0.48 ± 0.02	0.35 ± 0.03*	0.56 ± 0.04	0.50 ± 0.03
20	1.64 ± 0.11	1.66 ± 0.10	0.54 ± 0.05	0.63 ± 0.07	0.67 ± 0.02	0.52 ± 0.04*	0.75 ± 0.05	0.69 ± 0.05
30	1.82 ± 0.10	1.84 ± 0.09	0.68 ± 0.06	0.77 ± 0.09	0.81 ± 0.03	0.66 ± 0.05*	0.90 ± 0.05	0.86 ± 0.06
40	1.98 ± 0.09	2.00 ± 0.08	0.81 ± 0.07	0.90 ± 0.10	0.95 ± 0.04	0.79 ± 0.06*	1.04 ± 0.06	1.00 ± 0.07
50	2.12 ± 0.07	2.14 ± 0.07	0.93 ± 0.09	1.03 ± 0.11	1.08 ± 0.05	0.92 ± 0.07*	1.17 ± 0.06	1.13 ± 0.08
60	2.27 ± 0.06	2.28 ± 0.05	1.07 ± 0.10	1.16 ± 0.13	1.22 ± 0.06	1.06 ± 0.08	1.31 ± 0.06	1.28 ± 0.09
70	2.42 ± 0.05	2.43 ± 0.04	1.22 ± 0.11	1.31 ± 0.14	1.38 ± 0.08	1.21 ± 0.09	1.45 ± 0.07	1.44 ± 0.10
80	2.59 ± 0.05	2.60 ± 0.03	1.40 ± 0.14	1.49 ± 0.16	1.56 ± 0.09	1.41 ± 0.11	1.63 ± 0.08	1.63 ± 0.11
90	2.83 ± 0.08	2.82 ± 0.02	1.67 ± 0.17	1.74 ± 0.18	1.82 ± 0.12	1.68 ± 0.13	1.87 ± 0.09	1.91 ± 0.13

The shift of vulnerability curves to the left in Figure 1 indicated a loss of cavitation resistance (cavitation fatigue), but a shift to the right indicated a gain of cavitation resistance (recovery from cavitation fatigue). The significance of the shift in VCs was calculated two ways: shifts of mean VCs and shifts between stems (see Eq. 3 below). The results of significance tests based on shifts of means are shown in Table III. There were significant differences between the first versus second, first versus third, and first versus fourth VCs for both KCl- and CaCl₂-flushed stems and between the second and fourth VCs for KCl-flushed stems based on the means in Table II.

Figure 1.

Plotted mean vulnerability curves measured for the same stem exposed to four cycles of cavitation-refilling (flushing) and VC measurements with 0.1 m KCl solution (A) and 0.01 m CaCl₂ solution (B). Means and se (n = 7 for KCl values and n = 6 for CaCl₂ values) of all curves were computed. For the percentage recovery of K_h after flushes, see Table I.

Table III. Significance analysis results for the VCs quantified in Table II.

Significance tests focused on the differences between VC curve numbers (one, two, three, or four) based on the means in Table III for VC measurements with 0.1 m KCl solution or 0.01 m CaCl₂ solution. T_x represents the tension at which certain PLC was caused (10, 20,...,90). Letters i and j indicate the ith VC after the ith flushing and the jth VC after the jth flushing, respectively. The significance analysis of VCs with KCl solution was based on seven samples. The CaCl₂ solution VCs were based on six samples. Significance levels (testing the impact of solution at any PLC): *P < 0.05.

ith VC versus jth VC	Tx (KCl)									Tx (CaCl2)
	10	20	30	40	50	60	70	80	90	10	20	30	40	50	60	70	80	90
First versus second	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*
First versus third	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*
First versus fourth	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*	*
Second versus third
Second versus fourth		*	*	*	*	*	*
Third versus fourth

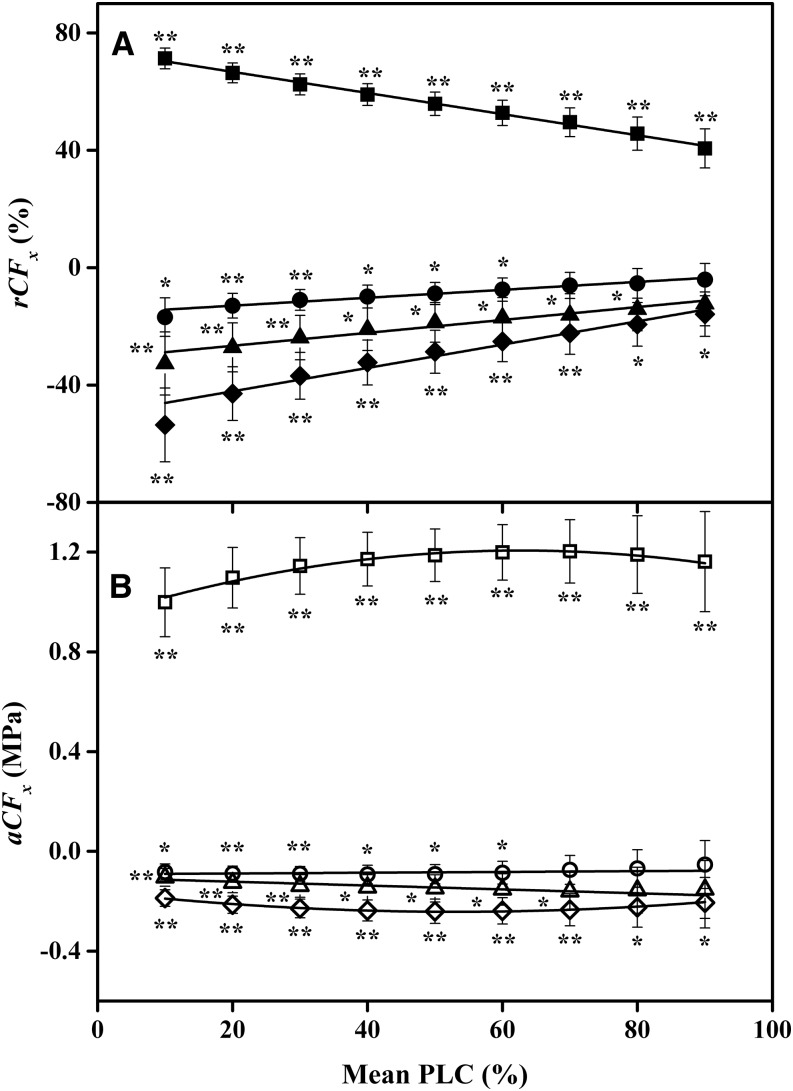
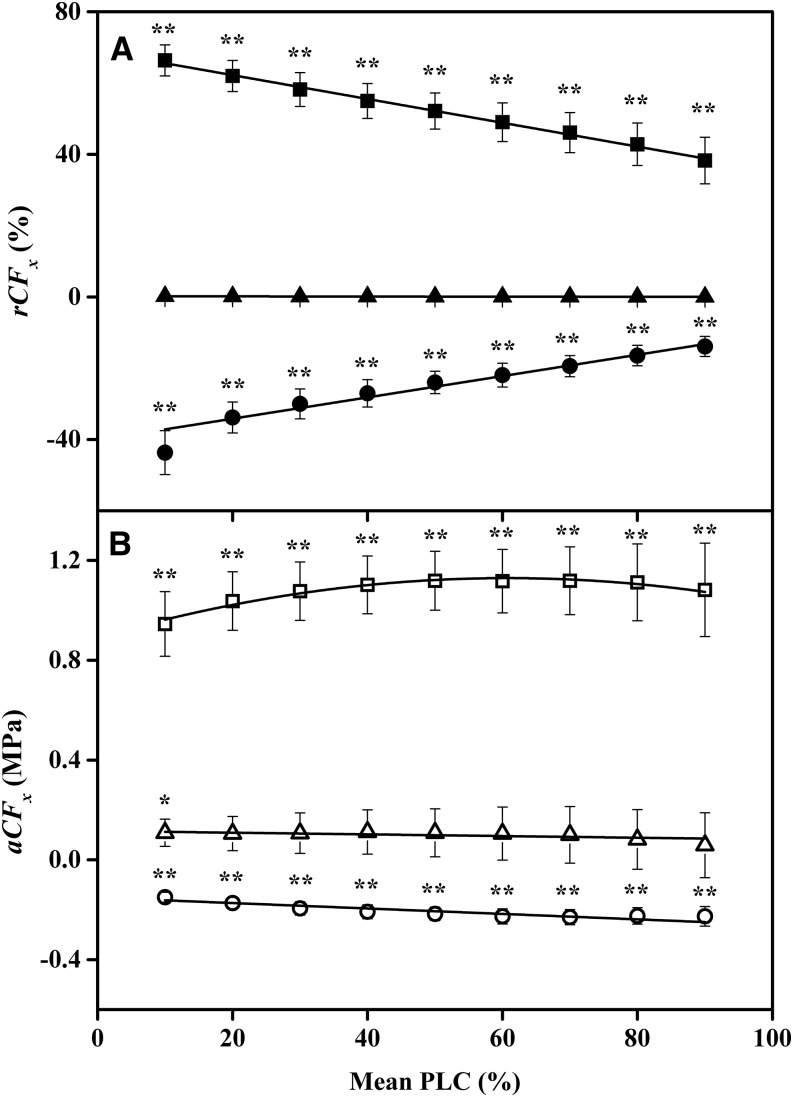
The significance test for shifts in the mean values of T_x were confounded by the population variability of VCs between individual stems. A stronger test of the shift in T_x values is obtained by using Equation 3B to compute the means shift of all individual branches and testing if the shift is significantly different from 0. The shifts can be computed as absolute cavitation fatigue shifts (aCF_x) or relative cavitation fatigue shifts (rCF_x) as defined in Equation 3, and these are shown as plots in Figures 2 and 3. Figures 2 and 3 demonstrate that there was a positive increase in cavitation fatigue (positive aCF_x or rCF_x) between the first and second VCs. But there were small but significant improvements (negative aCF_x or rCF_x) for most other cycles. Negative values of aCF_x or rCF_x indicate that the resistance to cavitation improved. Stems flushed by KCl solutions recovered more than stems flushed with CaCl₂ solutions (Figs. 2 and 3).

Figure 2.

Two quantitative measures of cavitation fatigue for KCl-flushed samples. The fatigue values were calculated from the mean of the differences in Equation 3B, which is considered a more powerful test of differences between VCs. A, Mean rCF_x versus x = the PLC at which rCF_x was evaluated. Squares compare first and second VCs, y = −0.3612x + 74.012 (r² = 0.9952, P = 2E-09); triangles compare second and third VCs, y = 0.2335x − 31.992 (r² = 0.9444, P = 1E-05); circles compare third and fourth VCs, y = 0.1436x − 16.341 (r² = 0.95, P = 8E-06); and diamonds compare second and fourth VCs, y = 0.43x − 52.274 (r² = 0.9489, P = 9E-06). B, Mean change in aCF_x versus x = the PLC at which aCF_x was evaluated. Squares compare first and second VCs, y = −7E-05x² + 0.0086x + 0.9352 (r² = 0.9758, P = 1E-5), although the individual points were not significantly different from each other (P = 0.334); triangles compare second and third VCs, y = −0.0006x − 0.1146 (r² = 0.7535, P = 0.0024); circles compare third and fourth VCs, y = 0.0004x − 0.099 (r² = 0.5669, P = 0.019); and diamonds compare second and fourth VCs, y = 3E-05x² − 0.0029x − 0.1636 (r² = 0.9877, P = 2E-6). Error bars indicate se. Symbols without asterisks were not significantly different from 0. The P values in the linear regressions give the probability that the slope is 0.

Figure 3.

Two quantitative measures of cavitation fatigue for CaCl₂-flushed samples. The fatigue values were calculated from the mean of the differences in Equation 3B, which is considered a more powerful test of differences between VCs. A, Mean rCF_x versus x = the PLC at which rCF_x was evaluated. Squares compare first and second VCs, y = −0.3333x + 68.857 (r² = 0.9961, P = 1E-09); triangles compare second and third VCs, y = −0.0018x + 0.1707 (r² = 0.9233, P = 4E-05); and circles compare third and fourth VCs, y = 0.3293x − 42.064 (r² = 0.9413, P = 1E-05). B, Mean change in aCF_x versus x = the PLC at which aCF_x was evaluated. Squares compare first and second VCs, y = −6E-05x² + 0.0078x + 0.8899 (r² = 0.9661, P = 4E-05), although the individual points were not significantly different from each other (P = 0.408); triangles compare second and third VCs, y = −0.0005x + 0.1225 (r² = 0.58, P = 0.017); and circles compare third and fourth VCs, y = −0.0009x − 0.1599 (r² = 0.8087, P = 0.001). Error bars indicate se. Symbols without asterisks were not significantly different from 0. The P values in the linear regressions give the probability that the slope is 0.

Frost Fatigue and Frost-Induced PLC

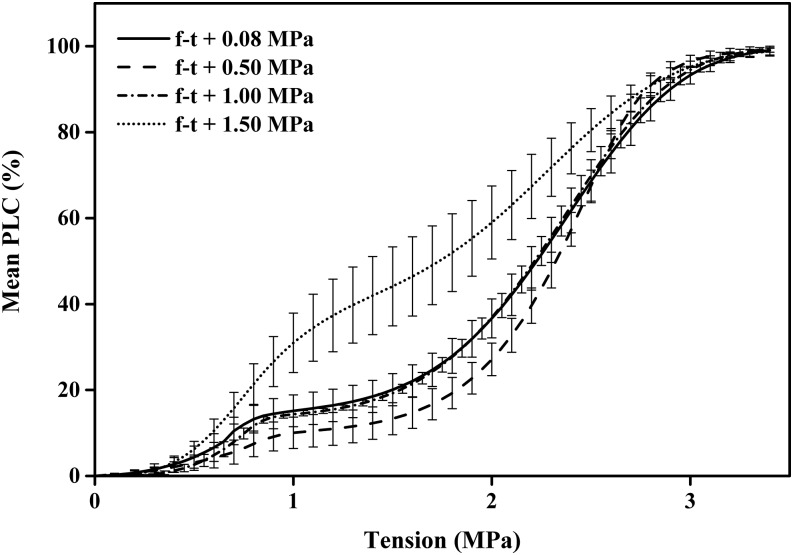
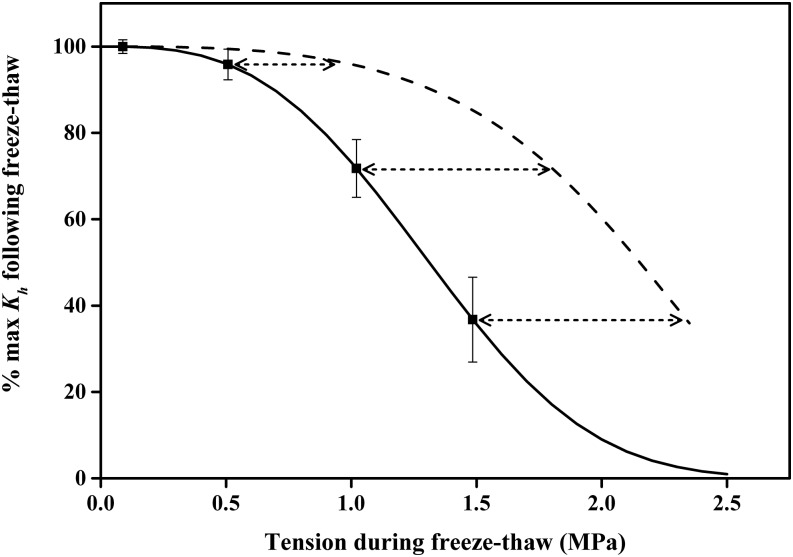
The vulnerability curves of 84K poplar were sigmoid curves in all experiments even after cavitation fatigue had occurred (Fig. 1; Supplemental Fig. S1A). In contrast, our freeze-thaw treatments caused significant change in the shape of the VCs measured after flushing. They changed from single to dual s-shaped Weibull curves (Fig. 4; Supplemental Fig. S1B; Eq. 2B). Freeze-thaw cycles were conducted on flushed stems at four different tensions (0.088, 0.5, 1, and 1.5 MPa) while the stems were spinning in a cavitron, and the mean flushed conductivity after the freeze-thaw event was 95% or greater of the original (Table IV). The highest two tensions were enough to cause some cavitation fatigue in the absence of freezing, but there was a synergy between the freeze-thaw event and cavitation fatigue causing a higher loss of maximum conductivity (Fig. 5) than expected from cavitation fatigue alone. At the lowest three tensions, the frost-fatigued curves were not significantly different and involved a shift in the 10% to 15% of most vulnerable vessels (Fig. 4). However, a freeze-thaw cycle at tension of 1.5 MPa caused a significant increase in frost fatigue.

Figure 4.

Vulnerability curves measured in stems following a freeze-thaw cycle (f-t) at varying tensions. Frost-induced embolism was removed by flushing before measuring the VCs; hence, the double s curves were caused by frost fatigue. Means of six to eight VCs were measured on flushed stems by the cavitron technique where each curve was fitted with a dual Weibull, then the mean and se of all six to eight best fit curves were computed.

Table IV. Percentage recovery of K_h after a freeze-thaw event in stems flushed with KCl at different freeze-thaw tensions.

The data are means ± se of six to eight samples. K_f-t, K_h recovered by flushing after the freeze-thaw event.

Kh	Freeze-Thaw Tension
	0.088 MPa	0.5 MPa	1 MPa	1.5 MPa
Kf-t/Kmax	100.85% ± 1.58%	98.68% ± 2.01%	97.11% ± 2.09%	95.4% ± 1.5%

Figure 5.

Squares show the impact of freezing on changes of K_h expressed as percentage of maximum conductivity (K_max) before freezing. Error bars indicate se (n = 6–8). The y axis can also be interpreted as 100% minus the PLC induced by freezing plus the tension on the x axis. The solid line is a Weibull equation fit of the squares. The dashed line shows the mean impact of tension alone, without freezing, on percentage maximum K_h. These values were replotted from the first VC in Figure 1A (100% − PLC induced by tension alone). The double arrows can be interpreted as the amount of tension added by the freezing or thawing of tissue.

The mean vessel diameter of 84K poplar was 28.7 ± 0.11 μm (n = 4,307) and hence should not be big enough to induce a loss of conductivity during a freeze-thaw event (Hacke and Sperry, 2001), and this fact is confirmed in the near-zero tension value shown in Figure 5; nevertheless, frost fatigue occurred even at the lowest tension (Fig. 4). However, increased tension caused a reduction in maximum K_h (Fig. 5), wherein the loss of K_h exceeded that due to tension-induced cavitation without freezing. This suggests that the freeze-thaw event caused an increase in tension (double-headed arrows in Fig. 5) during either the freezing or thawing or both as explained in “Discussion.”

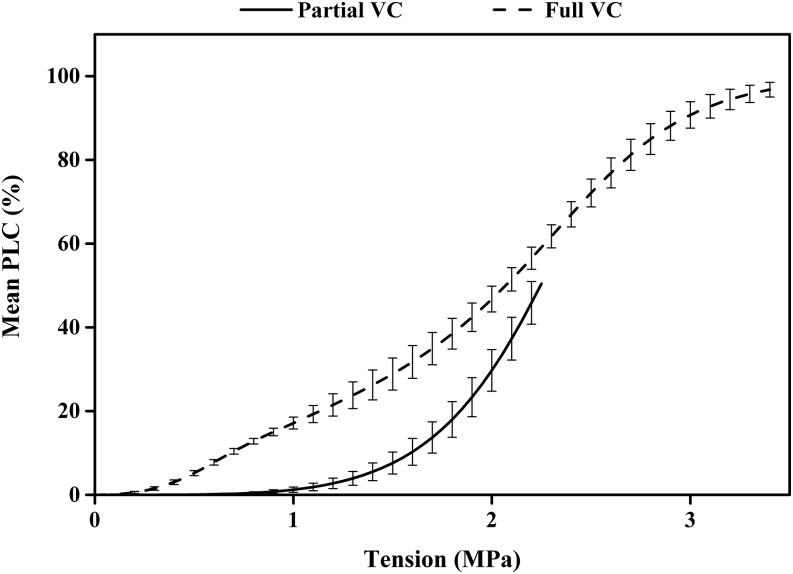
Frost-fatigue VCs looked very different from cavitation-fatigue VCs because the former transformed an s-shaped curve into a dual s-shaped curve, whereas cavitation fatigue shifted the entire s-shaped curve to the left in Figure 1, but it remained a simple s curve. We postulated that frost fatigue might damage only the most vulnerable vessels; hence, the nature of the damage might be duplicated by cavitation fatigue in only the lower half of the VC. To test this notion, we measured vulnerability curves of stems only to the 50 PLC value (Fig. 6, solid line), flushed the stem, and then measured the VC again (Fig. 6, dashed line). This procedure produced a dual Weibull curve strikingly similar to our frost-fatigue curve (Fig. 4, dotted line).

Figure 6.

Vulnerability curves measured before and after 50% embolism induced in stems. Means and se are shown for all six best fit curves before (solid curve) and after (dashed curve) 50% embolism was induced by a tension of about 2.25 MPa; the stems were flushed between the first and second curves. The dashed curve was fitted with a dual Weibull curve, which is the sum of two s-shaped Weibull curves.

Field Observations of Frost Fatigue

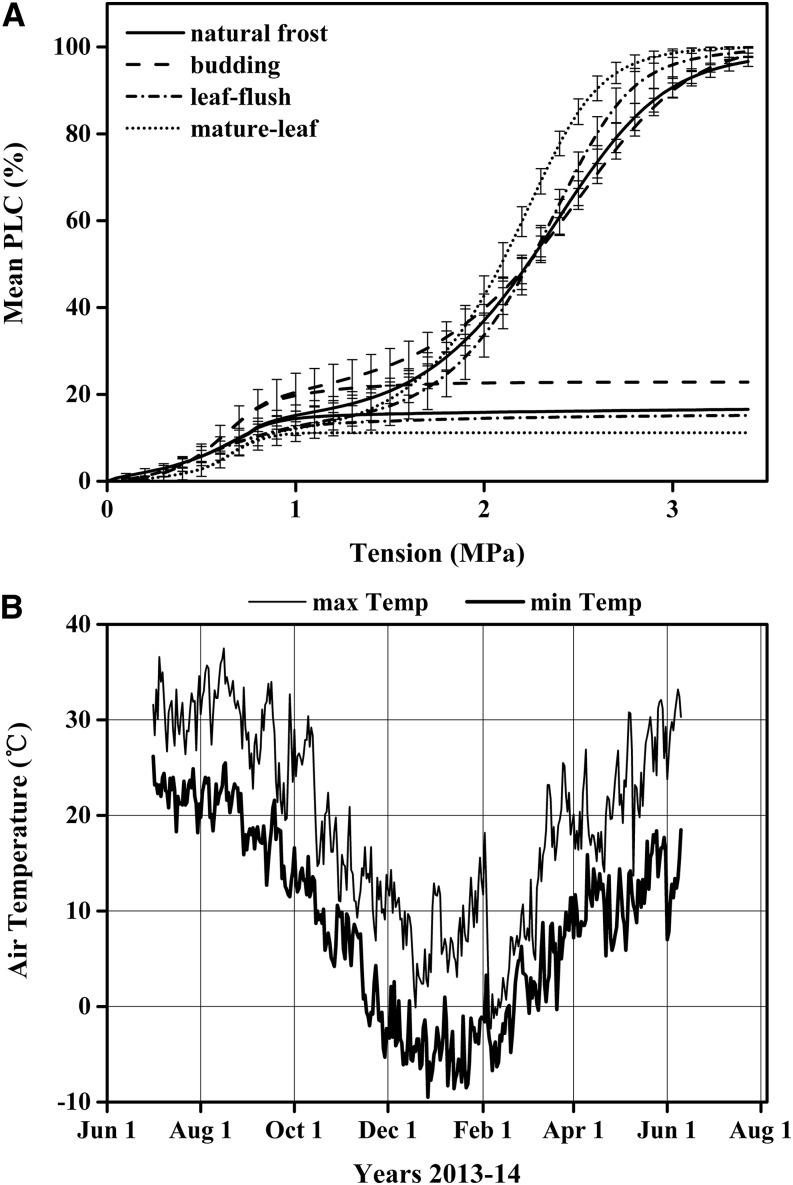
Vulnerability curves measured in four consecutive phenological phases were plotted in Figure 7A. The VCs were not significantly different from each other, no matter how many freeze-thaw cycles occurred during the winter (Table V). The frequency of frost events in the winter of this study can be deduced from the maximum and minimum temperatures shown in Figure 7B, but the stems might not have frozen every time the air temperature fell below 0°C because of supercooling. However, once leaves were fully expanded, values of T₆₀ to T₉₀ declined, perhaps because of the growth of new vessels in spring. The frost fatigue in early winter suggested that some of the early winter freezing events were enough to cause some frost fatigue that persisted into the spring. Comparison of Figure 7A with Figures 4 and 5 suggests that the first natural freezing events in trees might have been accompanied by an enhancement of xylem tensions of 0.5 MPa or greater at the time of the freeze-thaw events. Frost fatigue hydraulically damaged about 16% of the most vulnerable vessels (Fig. 7A). These freeze-thaw events caused no significant shift in the T₅₀ (Tables II and V); hence, the events reported here would not have been observed in previous studies that reported only the impact of frost damage on T₅₀ (Christensen-Dalsgaard and Tyree, 2013). High-resolution vulnerability curves are needed to document the cause of dual-s Weibull curves. At the beginning of our research on 84K poplar, dual-s Weibull curves were observed in June and July. By August, the 84K poplar shoots grew enough for cavitron-sized stem segments (0.274 m long × 6 mm diameter) to include only current-year shoots. Hence, when cavitation-fatigue experiments began in August, only s-shaped curves were observed (Fig. 1). When the trees flushed new leaves after winter, the vulnerability curves were still dual Weibull curves similar to those measured in the winter.

Figure 7.

A, Vulnerability curves measured when stems were in four phenological phases: natural frost, budding, leaf flush, and mature leaf. VC measurements in the natural frost stage were based on 12 samples. VC measurements in the budding and leaf flush stages were based on six samples. Mature leaf stage VC measurements were based on seven samples. The mean of these VCs was measured on flushed stems by the cavitron technique, where each curve was fitted with a dual Weibull curve, then the mean and se were computed from the individual Weibull curves. The dual Weibull fit is the sum of two Weibull curves; the first s-shaped Weibull curve of each phenological phase is plotted to its theoretical plateau for clarity, and the plateau values on the y axis = α in Equation 2B. B, Plot of minimum and maximum air temperatures recorded by a weather station 4 km from the location of the sampled trees.

Table V. Significance analysis of tensions at any given PLC in vulnerability curves of four phenological phases in stems collected from trees growing outdoors.

T_x represents the tension at which certain PLC was caused (10, 20,...,90). Data are based on means ± se. The same lowercase letters indicate significant differences at P > 0.05

Tx	Phenological Phase
	Natural Frost	Budding	Leaf Flush	Mature Leaf
T10	0.84 ± 0.12a	0.65 ± 0.07a	1.06 ± 0.26a	0.96 ± 0.15a
T20	1.47 ± 0.14a	1.17 ± 0.19a	1.52 ± 0.23a	1.56 ± 0.11a
T30	1.80 ± 0.11a	1.55 ± 0.21a	1.87 ± 0.12a	1.79 ± 0.09a
T40	2.05 ± 0.08a	1.96 ± 0.12a	2.07 ± 0.07a	1.95 ± 0.07a
T50	2.23 ± 0.07a	2.22 ± 0.06a	2.23 ± 0.05a	2.08 ± 0.05a
T60	2.39 ± 0.06a	2.41 ± 0.05a	2.36 ± 0.05a,b	2.20 ± 0.05b
T70	2.53 ± 0.06a	2.59 ± 0.04a	2.49 ± 0.06a	2.31 ± 0.04b
T80	2.71 ± 0.07a	2.77 ± 0.03a	2.63 ± 0.08a	2.44 ± 0.05b
T90	2.95 ± 0.07a	3.01 ± 0.05a	2.80 ± 0.10a,b	2.61 ± 0.06b

DISCUSSION

This study revealed two different fatigue responses in 84K poplar: a strong drought-induced cavitation fatigue and a weaker frost-induced fatigue. These will be discussed separately below.

Cavitation Fatigue: rCF_x and aCF_x

Many prior studies have described cavitation fatigue (Hacke et al., 2001, and refs. therein). The unique findings of our study were as follows. (1) Repeated cycles of cavitation and flushing do not cause additional damage (i.e. repeated cycles of cavitation and flushing did not increase the magnitude of fatigue; Fig. 1); rather, our data showed significant partial recovery (Figs. 2 and 3). (2) High-resolution measurements of VCs revealed a pattern of cavitation fatigue in which the rCF_x was a linear function of the T_x causing the fatigue (Figs. 2A and 3A), wherein the most vulnerable vessels exhibit the most relative cavitation fatigue. (3) When minor recovery from cavitation fatigue occurred after three cycles of cavitation and flushing, the biggest recovery occurred among the most vulnerable vessels. (4) Repeated cycles of flushing and cavitation showed that CaCl₂-flushed stems exhibited poorer recovery than KCl-flushed stems (Figs. 2 and 3).

With regard to the last finding, we compared stems flushed with CaCl₂ versus KCl to investigate the possible role of Ca²⁺ in stabilizing cell walls and pit membranes (Cosgrove, 1997; van Ieperen and van Gelder, 2006). Cell walls are weak ion-exchange resins containing mostly polyuronic acids that normally favor the accumulation of Ca²⁺ at the weak acid-exchange sites. Repeated flushing with concentrated KCl would gradually eliminate nearly all calcium absorbed to the exchange sites. Ca²⁺ might serve as a bridge between weak acid polymers that might add to the stability of pit-membrane pores that seed cavitation. Our results conclusively show that washing out Ca²⁺ by flushing with 0.1 m K⁺ enhanced rather than weakened cavitation resistance, from which we might conclude that putative pit-membrane pores actually shrunk. In contrast, flushing with Ca²⁺ made no difference compared with K⁺ and may actually retard recovery from cavitation fatigue.

Trends of rCF_x versus T_x had slopes significantly different from 0. In other Populus spp., the vulnerability to cavitation (measured by the b constant in the Weibull function) was linearly related to vessel diameter (Cai and Tyree, 2010). Hence, it can be hypothesized that the larger vessels have more rCF_x. More research is needed to confirm this relationship. Values of rCF_x in other species are also worth documenting in the future.

In our study, drought was induced artificially in a centrifuge, but it is generally assumed that soil-based drought events will have the same impact on cavitation fatigue, although there are few examples proving that assumption, with the notable exception of the well-documented case of sunflower (Helianthus annuus; Stiller and Sperry, 2002). In the case of sunflower, potted plants were dehydrated by withholding water, and the stem recovered from drought-induced cavitation fatigue within 4 d of rewatering, whereas the excised stems cavitated in a centrifuge showed weak or no recovery. Our study of 84K poplar also showed small but significant recovery from cavitation fatigue. More comparisons between whole plants and excised shoots need to be done to understand the mechanism of recovery in whole plants. In a survey study of seven species, Hacke et al. (2001) found that three species were resilient and four species were not resilient. Among those four species (Hacke et al., 2001), two were Populus spp. that exhibited cavitation fatigue in agreement with our 84K poplar clone. In contrast, Christensen-Dalsgaard and Tyree (2013) reported the Walker clone Populus spp. to be resilient in terms of T₅₀.

Absolute Frost-Fatigue Shift and Frost-Induced PLC

In contrast to cavitation fatigue, in which the prefatigued and postfatigued stems were both s shaped, frost fatigue changed the VC from an s shape to a dual s shape. Most previous studies of frost fatigue (Hacke and Sperry, 2001) have focused on increased PLC after a freeze-thaw event, and frost fatigue was measured as a shift of four- to five-point VCs of unfrozen versus frozen samples. Christensen-Dalsgaard and Tyree (2014) focused on shifts of T_25, T₅₀, and T₉₀ from VCs with six to seven points. Our study is unique in quantifying high-resolution curves with more than 20 points depending on the complexity of the curve. High-resolution curves are needed to accurately resolve complex curve shapes.

From previous studies, we would predict that 84K poplar would exhibit no PLC or frost fatigue following a freeze-thaw cycle because the vessel diameter of 84K poplar (28 μm) was below the critical diameter of 30 μm (Davis et al., 1999). Species with vessel diameters of 40 μm are typically 100% embolized after a freeze-thaw event, whereas species with vessel diameters between 30 and 40 μm are intermediate (Davis et al., 1999). Our results demonstrated that tension in combination with a freeze-thaw event caused more PLC than tension alone (Fig. 5). To our knowledge, our study is the first to demonstrate that species with vessels less than 30 μm in diameter are impacted when frozen under tension, which caused increased PLC and frost fatigue. It is not clear whether frost-induced embolism is always accompanied by frost fatigue, nor do we fully understand the mechanism of damage to pit membranes making them more vulnerable to cavitation after a freeze-thaw event.

Our results were consistent with the notion that a freeze-thaw event increased the centrifuge-induced background tension present in the stem segment during the experiment. Hence, more research is justified to test the hypothesis that cavitation fatigue and frost fatigue might both be manifestations of cavitation fatigue. The idea that a common mechanism existed between frost and cavitation fatigue was confirmed by the cavitation-fatigue experiment in which the first VC was taken only to 50% PLC because when these stems were flushed, the cavitation fatigue that resulted was strikingly similar to the frost-fatigue VC (compare Figs. 6 and 4).

Comparing the results in Figure 5 (dashed line minus solid line), one can conclude that the freeze-thaw cycle increased the tension by about 0.5 to 0.8 MPa (double-headed arrows in Fig. 5). Since water expands to form ice as it freezes and contracts as it thaws, one might presume that the frost fatigue occurred during the thaw. But this simple notion might be wrong because when Acer and Juglans spp. stems freeze, the tension often occurred during the freeze and positive pressure occurred during the thaw. Readers should consult previous work on Acer spp. for a detailed explanation for this notable behavior (Tyree, 1983; Johnson et al., 1987; Cirelli et al., 2008). Briefly, however, the development of tension is due to water migration into air-filled wood fiber cells to form ice (O’Malley and Milburn, 1983; Milburn and O’Malley, 1984) during the freeze event. The ice formation in the Milburn-O’Malley model is by vapor distillation from water in vessels to ice crystals growing in air-filled spaces, and the distillation process will induce tension in the liquid water. Our suggested interpretation of Figure 5 is as follows. In flushed stems, all wood fiber cells are filled with water, so freezing induces no extra tension; hence, there can be no freezing-induced PLC. But if the stems are put under tension before freezing, then air spaces are created in some fiber cells where ice can form, causing freezing-induced tension by the Milburn-O’Malley model (Tyree, 1983; Milburn and O’Malley, 1984); the enhanced tension would then induce cavitation before the vessels are totally frozen. However, the parsimonious explanation is that bubbles entrapped in ice expand during the thaw while ice melts under tension. We reject the parsimonious interpretation because a tension of 0.5 MPa should be enough to induce 100% embolism in all vessels because all vessels have air entrapped in ice. In contrast, the Milburn-O’Malley model predicts that tension will increase as the amount of air space for ice formation increases and the volume of air-filled fibers might increase with tension. Future research may resolve these conflicting ideas.

An alternative explanation is that ice crystal formation somehow damages pit membranes (Christensen-Dalsgaard and Tyree, 2014). For this to occur, ice crystals have to grow faster on one side of the pit membrane than the other. This is highly likely to occur if one side has water that can freeze but the other side has air because as water expands 10% to form ice, the pit membrane could be pushed toward the embolized side, causing tensile failure to the membrane. In contrast, if water and ice are present on both sides of the pit membrane, the pressure of ice might oppose each other equally, resulting in no damage. This idea about one-sided ice growth cannot be tested in 84K poplar because embolizing 50% of the vessels induced about the same amount of fatigue measured as a shift in vulnerability curve at the lower PLC values as frost fatigue.

Comparing Figures 1 and 6 reveals a shift of aCF_x (at x = 10 PLC) of about 1 MPa, and this shift is the same as the absolute frost-fatigue shift (aFF_x) at 10 PLC (Figs. 4 and 7). It could be argued that ice-induced damage to pit membranes ought to be quite different from cavitation damage. During a cavitation event, only one pore out of millions of pores connecting adjacent vessels needs to be plastically deformed to make a larger hole, which makes the vessels more prone to cavitation in subsequent VCs (Fig. 1). Based on surface tension arguments (Tyree and Zimmermann, 2002), we can say that the diameter (D) of a pit membrane pore that induces cavitation should be cos(θ) 4γ/ΔP, where ΔP is the pressure difference inducing cavitation across the pore, θ is the contact angle of the air-water interface at the pore surface, and γ is the surface tension of the solution at the pit pore. Frost or cavitation fatigue (aFF_x or aCF_x, respectively) equals the shift in ΔP to ΔP_f (i.e. from a normal to a fatigued pressure difference), inducing cavitation. Hence, D_f = D ΔP/ΔP_f. The shift of aCF_x at 10 PLC is ΔP = 1.5 to ΔP_f = 0.5 MPa, from which it follows that the most fatigued pore in the pit membrane is three times larger than the native pore (because ΔP/ΔP_f = 3). The magnitude of aCF_x = aFF_x in our study (at x = 10 PLC), which is a remarkable coincidence. One might argue that if the growth of ice crystals is poking holes in pit membranes, the holes ought to occur in thousands of membranes connecting adjacent vessels, and it seems unlikely that the shift aFF_x and aCF_x would be nearly identical. More experimental work might provide useful data to resolve these speculations.

We think much more can be learned about cavitation and frost fatigue through high-resolution measurement of vulnerability curves in a Cochard cavitron. At the time this study was completed, we could achieve fits to single or dual Weibull curves with RMS_error of about 2%. The RMS_error was primarily due to the error in the estimation of K_h and K_max because PLC = 100(1 − K_h/K_max). Subsequent to the completion of this study, we were able to increase the precision of measurements of K_h and K_max by a factor of 5 (Wang et al., 2014b). The increase of precision was achieved by using a regression method to estimate K_h values and by using a centrifuge that can control the temperature of the stem to ±0.04°C. Temperature control is important because K_h is inversely proportional to 1/viscosity of water, and the viscosity changes about 2.4% °C⁻¹. By using high-resolution measurements (more points) and high-precision measurements (more accurate K_h), future studies on cavitation and frost fatigue may reveal more about the mechanisms of damage and about the linkage, if any, between the two types of fatigue.

MATERIALS AND METHODS

Plant Material

The study was carried out on the clonal 84K poplar (Populus alba × Populus glandulosa) growing near Northwest A&F University in Yangling, Shaanxi, China (34°15′N, 108°4′E, elevation of 457 m). The sampling was conducted at intervals from August to April over a fall-winter-spring season in 2013 and 2014. All measurements were done on shoots that were not significantly water stressed before collection because no evidence of cavitation fatigue was observed in the first VC after flush. Shoots 90 to 120 cm in length were excised because preliminary air injection experiments indicated that maximum vessel length was less than 50 cm, and mean vessel length was about 6 cm; hence, the vessels are short enough relative to cavitron sample length to avoid the open-vessel artifacts reported by Wang et al. (2014a). The branches were enclosed in humidified black plastic bags after spaying leaves with water. Then, they were transferred to the laboratory within 15 min and submerged in water for at least 30 min to release tension. While submerged, a 27.4-cm-long segment was cut from each branch using fresh razor blades. Leaves were removed when present. These segments were exposed either to four consecutive cycles of cavitation-refilling or to a freeze-thaw cycle in combination with tensile water, imposed by spinning stems in a centrifuge. Additional experiments were done on the same species to compare laboratory results with field conditions throughout the winter and spring.

A VC defines the relationship between PLC and tension (T), where T = minus the xylem pressure potential. We used the whole vulnerability curves to quantify fatigue over nine equally spaced points on the y axis of the VC (for simple s-shaped curves). The cavitron technique was used to measure vulnerability curves. Both cavitation and frost fatigue were measured in terms of the shift of the vulnerability curve along the tension axis.

Flushing with Particle-Free Water

Clean flushing water was essential to prevent the plugging of pit membranes in the segments (27.4 cm long) because one objective was to carry out four repeated cycles of cavitation refilling on the same stem with two different solutions: 0.1 m KCl and 0.01 m CaCl₂. The clean water system described below could repeatedly restore K_max to 99.4% ± 0.6% of the first K_max.

An ultrapure water system (model GYJ1-10L-S; Huachuang) was used, which, according to specifications, produces water with less than 1 particle mL⁻¹ of greater than 10-nm diameter. Before flushing, freshly filtered water was produced each morning, reagent-grade KCl or CaCl₂ was added, and the water was stored in a stainless steel captive air tank (model 3400-002; SHURflo). The rubber bag inside the captive air tank was about 1.5 mm thick and comprised 90% of the surface area in contact with the salt solution. The lid and outlet tubing were stainless steel. Contrary to popular belief, stainless steel is not rust free; rust is easily observable in the rubber bag, but it does not adhere to the stainless steel surfaces. We recommend cleaning the tank twice per week to eliminate plugging rust particles formed gradually in the captive air tank. The SHURflo captive air tank was selected because it could be disassembled by removing six retaining bolts on the lid, allowing removal of the rubber bag and access to the stainless steel parts normally in contact with the salt solutions. All plastic and rubber tubing of the apparatus were cleaned with bleach to kill microorganisms, followed by flushing twice with purified water. Also, the solution in the tank was left unpressurized when not in use because air slowly permeates across the rubber bag. We observed that leaving the tank pressurized for 24 h made the water weakly effervescent, which could cause bubble formation in stem segments during a flush.

Cavitron Measurements

The measurements of K_h and VCs were carried out using a custom rotor designed by Cochard et al. (2005) based on the centrifuge technique (Alder et al., 1997). Design details have been described (Cai and Tyree, 2010).

Briefly, this technique makes it possible to measure the K_h while the stem segment is spinning at any given tension. A 27.4-cm segment is placed in the rotor mounted on the centrifuge. Both ends of the segment are placed in cuvettes filled with liquid (0.1 m KCl or 0.01 m CaCl₂) that could be replenished while spinning. A pressure difference generated by the different liquid levels of the cuvettes drives the liquid through the segment. Then, the rate of movement of the liquid in the stem could be measured directly by a continuous calculation of the volume change in the cuvettes within a certain time interval.

Prior to measurements, the stems were flushed with 0.1 m KCl or 0.01 m CaCl₂ at 40 p.s.i. (276 kPa) for 30 min to eliminate any native embolism. The length of time required to ensure that all conduits were refilled by the flush was determined in preliminary experiments as outlined below in “Refilling and Repeated Cavitation Cycles.” The rotor was rotated initially at 1,000 rpm (0.088 MPa) without a stem segment, and the thermostat was set a few °C below ambient room temperature in order to have improved temperature control during measurement. Once all conduits were refilled, K_max was measured at 1,000 rpm (0.088 MPa) in the cavitron after a stabilization time of 15 min. The tension caused by 1,000 rpm was too small to cause any embolism. Subsequently, a VC was obtained through stepwise increases in the spin rate of the centrifuge, subjecting the solution in the conduits to increasingly negative xylem pressures (tension = minus pressure). The K_h was collected after a 2-min stabilizing time at each 200-rpm increase. The PLC, which was attributed to embolized conduits, was computed from:

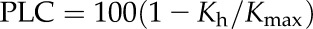(1)

The spin rate was increased until K_h was reduced to a point where the PLC was 90% or greater.

Vulnerability curves with nine or more points was deemed sufficient to characterize simple s-shaped Weibull curves. But 16 to 27 points are necessary to characterize a dual Weibull curve. Vulnerability curves, plots of PLC versus tension (T), were fitted to a single Weibull curve (Eq. 2A) or a dual Weibull curve (Eq. 2B) through CavAnal software written by M.T. Tyree (Cai et al., 2014):

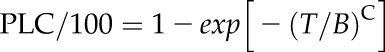(2A)

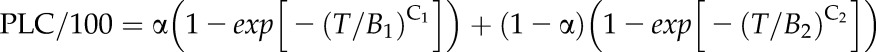(2B)

where the constants were calculated by minimizing RMS_error.

Computation of Cavitation Fatigue

Between any two cycles of cavitation and flushing of the same stem, cavitation fatigue was computed based on absolute shift of T_x (where x = 10, 20…90 PLC) from T_x,i to T_x,j, where i and j were the ith and jth VCs (j > i). So for aCF_x, we computed aCF_x = (T_x,i – T_x,j), and for rCF_x, we computed rCF_x = (1 – T_x,j/T_x,i). The means and se of each fatigue value were computed for all the stems in two different ways. The first was the difference of the means (Eq. 3A) of n values, and the second was the mean of the difference (Eq. 3B) for n values. The two values of 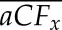are identical, but in the test of significance in the former, we are asking if the means are significantly different, whereas in the latter, we are asking if the difference is significantly different from 0, which was statistically more certain (see “Results”) because the phenotypic difference between individual stems is eliminated by computing the mean of the difference rather than the difference of the mean.

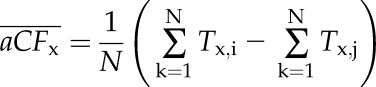(3A)

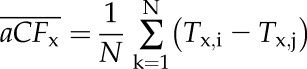(3B)

The mean rCF_x was computed from:

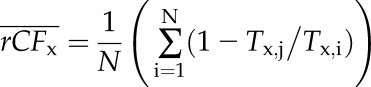(3C)

These computations allowed us to compute the fatigue shifts for up to four cycles of cavitation and flushing. Positive values of aCF_x and rCF_x measured loss in cavitation resistance, and negative values were interpreted as an increase in cavitation resistance.

Temperature Calibration

Temperature control during VC measurement is important because K_h changes 2.4% °C⁻¹ as stem temperature changes because of the effect of temperature on the viscosity of water. The Beckman-Coulter centrifuge has a temperature sensor and thermostatic temperature control, but the factory sensor is mounted too near the refrigeration coils; hence, large temperature differences were often observed between the factory sensor and the sensor we installed near the rotor. The temperature gradient was explained by the heat generated by the spinning-rotor motor (Wang et al., 2014b). In order to correct for temperature gradients, a custom temperature sensor based on an LM335 sensor chip was installed near the rotor midway between the refrigerated wall and the rotor. The temperature of the thermostat had to be adjusted down in order to achieve constant temperature in the rotor as rotor rpm increased. Experiments were done to test the adequacy of temperature control of the stem to within ±1°C.

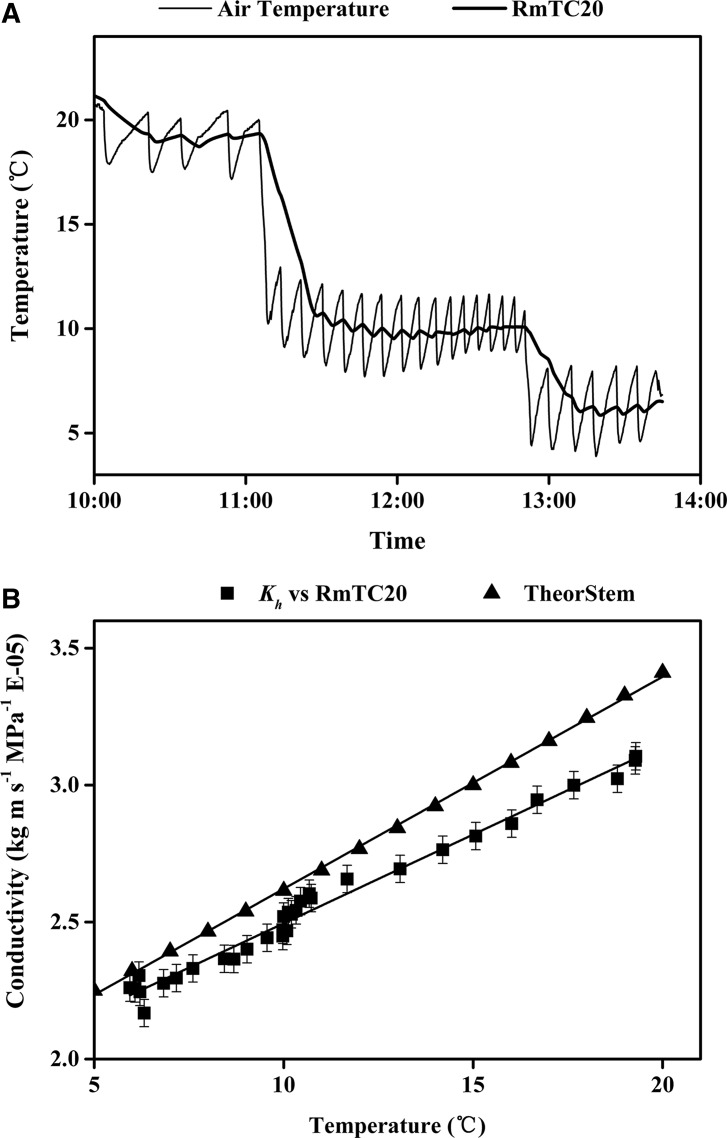
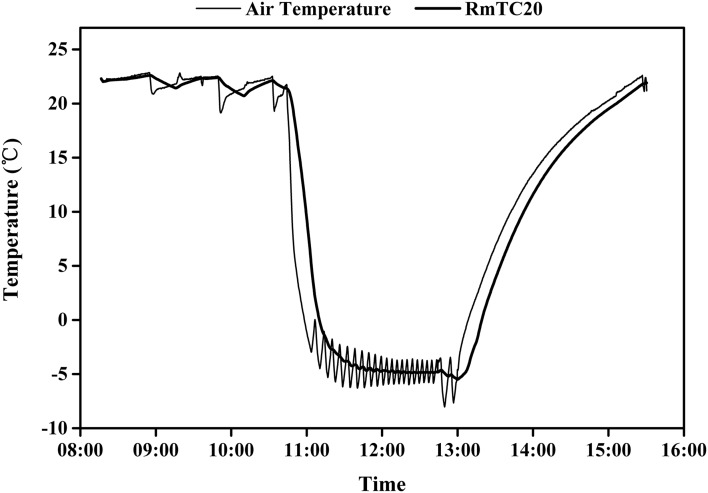
Additional experiments were done to ensure that we could stabilize the temperature of the stems within reasonable limits. K_h was measured at constant rpm while changing the thermostat temperature setting, which caused a corresponding rapid change in stem temperature, as confirmed by changes in K_h. The air temperature was logged every 10 s by our independent sensor while periodically measuring K_h at constant rpm. The stem K_h acts like a de facto thermometer because K_h changes in proportion to 1/viscosity of water. Preliminary experiments were performed to calibrate running mean values of air temperature to the stem thermometer. We found that a 20-min running mean of air temperature correlated satisfactorily with the change in K_h when air temperature was changing rapidly (Fig. 8). Even when the thermostatic temperature was set to a constant value, the instantaneous air temperature changed ±2°C as the refrigeration system turned on and off, but the 20-min running mean changed less (±0.5°C–1°C) when the refrigeration turned on and off more than once per 5 min.

Figure 8.

A, Tempo of change in air temperature and 20-min running mean of air temperature (RmTC20) measured 2 cm from the rotor during the experiment shown in B. B, K_h in stem versus RmTC20. The regression of K_h versus RmTC20 was y = 0.0648x + 1.8474 (r² = 0.9826, P ≤ 10⁻²³), and the close correlation means that the RmTC20 was an acceptable predictor of stem temperature. However, the dependence of K_h on stem temperature was less (bottom slope) than predicted from 1/viscosity of water in an ideal pipe (TheorStem), which had a regression of y = 0.0774x + 1.8472 (r² = 0.9994, P ≤ 10⁻²³).

Refilling and Repeated Cavitation Cycles (How Long Is Enough for Flushing?)

Preliminary experiments were done to determine the length of time required to refill the embolized conduits flushed at 276 kPa (40 p.s.i.). The original conductivity of each branch prior to flushing was measured at 1,000 rpm (0.088 MPa) in the cavitron. The stem was then subjected to alternating 5-min cycles of flushing and conductivity measurements until the conductivity stabilized (did not change for three consecutive cycles of flushing). Following this, the vulnerability curve of the stem was measured.

This cycle of flushing to K_max and measurement of a VC was repeated four times. Thirty minutes of flushing was enough to achieve a stable K_h. On average, K_h was returned to the same K_max as measured by the ratio of 100% K_flushed/K_max to within 99.4% ± 0.6%. If K_h failed to reach 93% or greater following a cavitation/flush cycle, then the data were thrown out.

Freeze-Thaw Cycles

The stems were directly flushed for 30 min at 276 kPa with 0.1 m KCl solution after collection. Unlike methods from other studies (Améglio et al., 2001; Willson and Jackson, 2006; Christensen-Dalsgaard and Tyree, 2013), we froze and thawed the plant material at known tensions in the stems while spinning in a cavitron. We chose tensions of 0.088, 0.5, 1, and 1.5 MPa to continue the frost-fatigue test. In experimentally simulated freeze-thaw cycles, the stems were exposed to freezing approximately for 2 h at −5°C (Fig. 9, thick line) and simultaneously to tensions (rpm) of 0.088 (1,000), 0.5 (2,400), 1 (3,400), and 1.5 MPa (4,100) following K_max measurements at 1,000 rpm. Then, the stems were thawed to room temperature at the same tension. The conductivity after freeze-thaw treatment was measured. Subsequently, the same stems were removed, flushed for 30 min, and a new VC was measured.

Figure 9.

Plot of temperature versus time for a typical freeze-thaw cycle. Air temperature (thin line) in the cavitron was collected every 10s. However, 20-min running mean air temperature (RmTC20; thick line) reflected more precisely the correct stem temperature (Fig. 8). The stems thawed more slowly than they froze because the centrifuge did not have active heating; hence, the stems and centrifuge were passively heated by the warm laboratory.

Partial versus Full Vulnerability Curve Comparison

In order to illustrate the connection between cavitation and frost fatigue in 84K poplar, two different vulnerability curves were measured. The liquid used for flushing was 0.1 m KCl. The first VC after flushing was stopped at 50% embolism, then the stem was removed and flushed again, and the VC was determined to more than 95% PLC.

Field Conditions

Four phenological phases from fall to winter and into the next spring, including a natural frost stage after the first freezing events of winter, budding stage, leaf flush stage, and mature leaf stage, were selected for VC measurements, in order to see if the trees growing outside showed a pattern of frost fatigue like that induced in cavitron experiments. In all four stages, stems were used to measure VCs directly after flushing for 30 min with 0.1 m KCl solution at 276 kPa.

Statistics

All statistical analyses were done with the SPSS 18.0 statistics package for personal computer (SPSS) using the 0.05 significance level. Comparisons of more than two groups between all means were made with one-way ANOVA and the Duncan test. Student’s t tests were used to compare means between two groups or differences of means from 0 when appropriate.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Typical examples of high-resolution VC curves with nine to 27 points measured by Cochard rotor.

Glossary

K_h

hydraulic conductivity

VC

vulnerability curve

T_x

tension that induces x% loss of conductivity

RMS_error

route mean square error

aCF_x

absolute cavitation fatigue shift

rCF_x

relative cavitation fatigue shift

aFF_x

absolute frost-fatigue shift

K_max

maximum conductivity

PLC

percentage loss of conductivity