Statistical estimation of physiological brain age as a descriptor of senescence rate during adulthood

Abstract

Mapping aging-related brain structure and connectivity changes can be helpful for assessing physiological brain age (PBA), which is distinct from chronological age (CA) because genetic and environmental factors affect individuals differently. This study proposes an approach whereby structural and connectomic information can be combined to estimate PBA as an early biomarker of brain aging. In a cohort of 136 healthy adults, magnetic resonance and diffusion tensor imaging are respectively used to measure cortical thickness over the entire cortical mantle as well as connectivity properties (mean connectivity density and mean fractional anisotropy) for white matter connections. Using multivariate regression, these measurements are then employed to (1) illustrate how CA can be predicated—and thereby also how PBA can be estimated—and to conclude that (2) healthy aging is associated with significant connectome changes during adulthood. Our study illustrates a connectomically-informed statistical approach to PBA estimation, with potential applicability to the clinical identification of patients who exhibit accelerated brain aging, and who are consequently at higher risk for developing mild cognitive impairment or dementia.

1. Introduction

Recent scientific research has shown that both healthy aging as well as various forms of brain pathology are associated with substantial changes in brain structure and connectivity (Thompson et al. 2003; 2004; Narr et al. 2005; Frisoni et al. 2007). As early as 1980, the rate of decreases in gray matter (GM) and white matter (WM) volumes per decade had been quantified in healthy human adults (Miller et al.). Pfefferbaum and Sullivan found ageing- and sex-related differences in WM diffusivity throughout the brain, particularly in the corpus callosum (Pfefferbaum et al. 2000; 2003). Importantly, it has been acknowledged that the human cortex experiences cortical thinning throughout the lifespan, and neuroimaging studies (Salat et al. 2004; Sowell et al. 2003; 2004) have measured cortical thinning rates and proposed their use as clinical biomarkers of increased risk for accelerated brain degeneration in adulthood, senescence and disease (Gur et al. 1999). Specifically, combining neuroimaging with computational neuroanatomy and statistical prediction models has allowed neuroscientists to assess the extent and severity of GM loss across adulthood. Such methods can allow individual subjects to be compared against the healthy population by evaluating the difference between their cortical thinning rate and the mean value of this quantity in healthy adults. This can allow one to identify adult individuals whose brains experience accelerated aging, i.e. whose brains appear to be significantly older than expected for the average person at their given chronological age based on structural and connectomic properties. In addition, this process can allow identification of such individuals at early stages of the accelerated senescence process, which can be useful in the context of timely clinical intervention. It is, thus, useful here to distinguish between chronological age (CA) and physiological brain age (PBA), the latter being clearly more difficult to assess than the former due to genetic and environmental factors which affect individuals differently. Such influences lead to statistical variability in PBA across healthy subjects even when CA is held constant. Given appropriate knowledge of brain structure changes across the lifespan in the healthy population, a person’s PBA can be estimated. Specifically, if the cortical thickness of an individual deviates substantially from the population mean at her/his CA, the direction of the deviation (i.e. the magnitude and sign of the statistical residual from the regression line) can be used to infer whether that subject’s PBA is substantially lower or higher than expected for an individual of their CA, the latter scenario being suggestive of accelerated aging.

Because of the often-reported relationship between cortical thickness and CA over extensive areas of the cortex (Walhovd et al. 2005; Fjell et al. 2009a; McDonald et al. 2009), the former measure can be used to estimate PBA. Nevertheless, though certainly useful to this end, cortical thickness is not the only measure which can be employed for PBA assessment because insight provided by other neuroanatomical correlates of brain aging can also contribute to the assessment of this phenomenon. Specifically, since aging-related changes in the human connectome are also likely to reflect brain aging, the inclusion of connectomic information in statistical models for PBA estimation is possibly informative. In this context, the purpose of this study is twofold: firstly, it aims to assess how changes in the connectivity density (CD) and fractional anisotropy (FA) of WM connections reflect aging-related changes in the human connectome throughout adulthood. Secondly, it provides evidence to the effect that connectomic information can be used to improve PBA statistical estimates above and beyond the extent to which this can be accomplished solely using cortical thickness measurements. Thus, in addition to demonstrating an improved statistical approach for PBA estimation, this study is the first to illustrate how aging affects human brain connectivity.

2. Methods

Subjects and data acquisition

The study cohort included N = 136 healthy adult subjects (42 males) with CAs between 18.6 and 61.1 (mean: 33.3 years, standard deviation: 11.6 years). Subjects provided their informed written consent as required by the Declaration of Helsinki, U.S. 45 CFR 46, and neuroimage volume acquisition was conducted with the approval of the local ethics committees at the respective research institutions where data were acquired. Participants were recruited by advertisements in local newspapers and campus flyers. Subjects were all healthy and had no history of neurological or psychiatric illnesses. No participant had a current or past psychiatric diagnosis (including substance abuse) or was taking medications for any medical reasons. Additional exclusion criteria for all participants included left-handedness, hypertension, neurological illness, metal implants, and a history of head trauma with loss of consciousness for more than 5 minutes. Neuroimaging data sets were fully anonymized, and no linked coding or keys to subject identity were maintained. For these reasons, in compliance with the U.S. Health Insurance Portability and Accountability Act (HIPAA; http://www.hhs.gov/ocr/privacy), this study does not involve human subjects’ materials. Structural T₁-weighted magnetic resonance imaging (MRI) and diffusion tensor imaging (DTI) volumes were acquired from each patient using a Siemens Trio Tim 3.0 T scanner. For MRI, an ultrafast ‘Turbo’ gradient-recalled MP-RAGE sequence (repetition time (TR) = 20 ms, echo time (TE) = 3 ms, flip angle = 25°, slice thickness = 1 mm, acquisition matrix = 256 × 256 × 256) was used. For DTI, a 12-channel coil and a sequence with the following parameters were used: TR = 9.4 s, TE = 88 ms, flip angle = 90°, slice thickness = 2 mm, number of gradient directions = 68, acquisition matrix = 128 × 128 × 128. Two non-diffusion weighted volumes were acquired for each subject (B₀-values: 0 s/mm² and 1000 s/mm²). The same scanner and sequence types were used for data acquisition from all subjects.

Cortical thickness and connectomic calculation

Using FreeSurfer software, the cortical surface was reconstructed as a triangular tessellation with ~300,000 vertices (average inter-vertex distance of ~1 mm) to produce a high-resolution, smooth representation of the GM/WM interface, as detailed extensively elsewhere (Fischl et al. 2002; Fischl et al. 1999; Dale et al. 1999). At each vertex v_i of the tessellation, cortical thickness was measured as the distance between the GM/WM boundary and the cortical surface. For each subject, DTI and MRI volumes were first co-registered using affine registration. Eddy current correction was then applied to each DTI volume, which was subsequently processed using TrackVis (http://trackvis.org) to reconstruct fiber tracts using deterministic tractography. Fiber bundles shorter than 15 mm were discarded.

Following cortical parcellation and WM tractography, the connectivity matrix of each subject’s brain was reconstructed. Let v_i and v_j be cortical mesh vertices linked by some WM connection c_ij. For each connection, the spatial coordinates associated with the extremities of c_ij (i.e. with v_i and v_j) were first identified. The corresponding entry indexed by i and j in the connectivity matrix C of the subject was updated to reflect the presence of a connection between the two vertices, and the process was repeated for each connection. The mean FA of c_ij was calculated as the average of FA values over all DTI voxels traversed by c_ij from one end of the connection to the other. Similarly, at each vertex on the cortical mesh, the mean FA of connections linking v_i to the rest of the brain was calculated. The CD at each vertex was computed as the sum of all reconstructed fibers linking it to the rest of the brain, divided by the surface area of the vertex neighborhood and by the total number of connections in the brain. Here, the neighborhood of some vertex v_i denotes the portion of the mesh surface containing points which are closest to v_i.

It is important to note that the generation of the connectivity matrix C did not involve the use of a predefined parcellation scheme. Because the extremity of each WM bundle is associated with some point v_i on the cortical mesh, the size of C is determined by the number of bundles reconstructed via tractography, rather than by the number of parcels in a parcellation scheme which is specified a priori. Because most parcellation schemes currently available comprise at most ~1,000 brain regions (Hagmann et al. 2008), the advantage of the present method for generating C lies in its ability to accommodate substantially more connectivity information than previously possible, and without the need for averaging of connectivity measures over the surface of each parcel, as is the case in conventional parcellation approaches. For example, in the present study, C was of size ~35,000 × 35,000 in each subject compared to at most ~1,000 × 1,000 in previous studies (Hagmann et al. 2008). Thus, the process of generating C using this approach carries with it the ability to specify connectivity information for each cortical location at a spatial resolution far greater than previously reported.

In all subjects, the total number of connections was smaller than the total number of cortical mesh vertices. Consequently, the calculation resulted in the presence of vertices with no assigned value for either CD or mean FA. To correct for this effect, cortical maps were smoothed across using a circularly symmetric Gaussian kernel on the folding surface with a full width at half maximum of 5 mm, a value which is more conservative—and possibly more appropriate—than in studies similar to ours (Salat et al. 2004; Fjell et al. 2009b). The maps were then averaged across subjects in FreeSurfer using a non-rigid, high-dimensional spherical averaging method to align cortical folding patterns (Fischl et al. 1999). This method involves (1) inflation of the cortical surface, (2) flattening of each hemisphere, and (3) morphing of each hemisphere into a surface which maintains the topological structure of the original surface, but has a closed-form coordinate system.

Statistical analysis

In many aging research studies, the desire to estimate cortical thickness and/or its rate of change (as statistical response variables) based on CA (as a statistical predictor variable) has been of preponderant interest. By contrast, the present study aims to explore the converse, i.e. the ability of cortical thickness and of brain connectomic properties to predict CA, and thereby also to estimate PBA, with potential clinical applications to the identification of clinical patients with accelerated brain aging. Implementing the procedures described in the previous two sections results in the association of three numerical values with each cortical location, namely cortical thickness, CD and the mean FA of connections linking each vertex to the rest of the brain; these quantities form a multivariate feature vector of size q = 3. The connections linking the vertex to the rest of the brain can be thought of as the set of connections which ‘innervate’ the cortical region represented by that vertex.

To investigate whether and to what extent the FA and CD measures are correlated, the Pearson product moment correlation coefficient between the two measures was first computed across subjects for each point on the cortex. Subsequently, the null hypothesis that there is no correlation between the two measures was tested using Student’s t test at α= 0.05 subject to the FDR correction for multiple comparisons. Because the null hypothesis was not accepted at any cortical location, it was deemed appropriate to include the two measures in the design matrix of the regression model described below.

Let Y be an N × 1 vector containing the CAs of the subjects in our sample of size N = 136. To explore the extent to which cortical thickness can predict the CA of each subject, one can form the standard set of multivariate regression equations Y = Xβ + ε, where Y contains the response variable values (subjects’ CAs), X is a design matrix containing q predictor variables, and where β and ε are vectors of regression coefficients and residuals, respectively. The least squares solution to this set of equations is β̂ = (X^TX)⁻¹X^TY. To account for the potential effect of sex as a confounding factor in the analysis, this predictor variable was initially coded as a binary variable in the design matrix. The effect of this predictor variable was then regressed out following a standard approach (Rencher 2002). Subsequently, the following statistical analyses were implemented.

In step 1, to test the omnibus null hypothesis that none of the independent variables predicts CA, one can compute Wilks’ Λ test statistic as Λ = |Y^TY − β̂^TX^TY|/|Y^TY − Nȳȳ^T|. This can be converted to an F statistic of the form F = [v_E(1 − Λ)]/(v_HΛ) and with v_H = q = 3 and v_E = N − q − 1 = 132 degrees of freedom (d.f.), cf. pp. 162–163 in (Rencher 2002). Here and throughout, v_H and v_E are the d.f. for the hypothesis and error, respectively. A split-half reliability analysis was implemented following standard classical test theory (Webb et al. 2006). Specifically, the original sample of size N was first divided into two subsets by randomly assigning each sampling unit (subject) to one of the subsets. The reliability coefficient ${\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^2={\sigma }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^2/({\sigma }_{\widehat{\mathit{\beta }}\mathit{X}}^2{\sigma }_{\mathit{Y}}^2)$—measuring the extent to which the regressors β̂X could reliably predict CA, i.e. Y—was computed for each subset. The Spearman-Brown prediction coefficient ${\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^{\ast }=2{\rho }_{\widehat{\mathit{\beta }},\mathit{X},\mathit{Y}}/(1+{\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}})$ was then used to assess the reliability of the regression model as a CA predictor. These calculations were repeated over 1,000 distinct random split-half assignment iterations, and the mean reliability coefficient 〈 ${\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^2$〉 and Spearman-Brown prediction coefficient 〈 ${\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^{\ast }$〉 over all 1,000 realizations were computed at each cortical location.

In step 2, we examined the ability of cortical thickness alone to predict CA. This can be accomplished using ‘leave-one-out’ regression, i.e. reduced-model regression involving the deletion of a single predictor variable from the design matrix (cf. pp. 330–332 in (Rencher 2002)). When removing exactly one variable (cortical thickness in this step) from the design matrix, the null hypothesis that the removed variable does not contribute above and beyond all other variables to the regression can be tested using an F statistic which has 1 and N − q − 1 d.f. When the numerator d.f. of the F-test is 1, such a statistic is the square of a t-statistic, given by $t={\widehat{\beta }}_j/(s\sqrt{g_{jj}})$, where j is the appropriate index of the predictor variable being deleted, g_ij is the j-th diagonal element of (X^TX)⁻¹ and s = (Y^TY − β̂^TX^TY)/(N − q −1)^1/2.

In step 3, we sought to determine whether two connectomic variables (CD and mean FA)—can predict CA above and beyond the extent to which cortical thickness can alone. In this case, the standard set of multivariate regression equations assumes the form ε = X′ β′ + ε′, where ε is the set of residuals from the regression performed in the first step of the analysis (i.e. the set of differences between the true CAs of the subjects and their CAs as estimated using cortical thickness alone). The primes in X′,β′ and ε′ are used to distinguish the design matrix, regression coefficients and residuals, respectively, in this step of our analysis from those in the first step. Thus, X′ is a design matrix containing two predictor variables (CD and mean FA), while β′ and ε′, are the regression coefficients and residuals, respectively, computed in the current step of the analysis. To test the omnibus null hypothesis that the connectomic variables do not predict CA above and beyond the extent to which cortical thickness alone can predict it, one can use an F statistic as previously explain, where F has v_H = q = 2 and v_E = N − q − 1 = 133 d.f.

Finally, in step 4, to investigate the distinct contribution of each connectomic variable to the estimation of CA, we implemented leave-one-out regression as previously explained, starting from the model containing only the connectomic variables and removing only one such variable at a time from the model. For all statistical tests included in this study, corrections for multiple comparisons were implemented using the false discovery rate (FDR) approach of Benjamini & Hochberg (1995).

3. Results

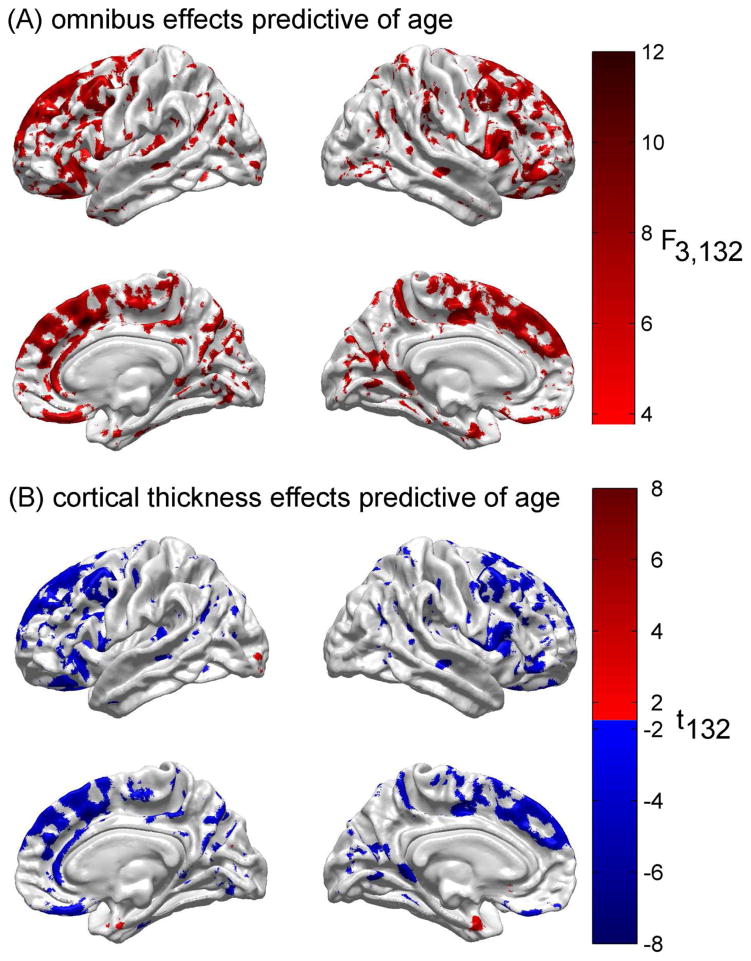
Figure 1A displays the results of the first step of the statistical analysis to determine the extent to which all three feature variables used can predict CA in adulthood. For each cortical location, this figure displays the F statistic for the omnibus test of the null hypothesis that none of the three independent variables (cortical thickness, CD and mean FA) predicts subject CA. Here and throughout, the displayed values of the test statistic are thresholded for both significance (using FDR < 0.05) and reliability (using $\langle {\rho }_{\widehat{\mathit{\beta }}\mathit{X},\mathit{Y}}^{\ast }\rangle >0.8$). The cortical maps reveal that the null hypothesis is rejected for large portions of the frontal lobe, both laterally, medially and ventrally. Additional areas where the omnibus null hypothesis is rejected include bilateral portions of the insula, parietal lobe (especially on the banks of the post-central sulcus and of the parieto-occipital sulcus), and occipital lobe. Regions where the F statistic is particularly large (F > 10) by comparison to other regions include the antero-medial and dorsal aspects of the superior frontal gyrus, triangular part of the inferior frontal gyrus (right hemisphere), as well as the straight and orbital gyri.

Fig. 1.

(A) Results of the statistical analysis to determine the extent to which all three feature variables (cortical thickness, CD and mean FA) can predict chronological age. For each cortical location, the F statistic with 3 and 132 d.f. is displayed for the omnibus test of the null hypothesis that none of the three independent variables predicts subject age. Here and throughout, the displayed values of the test statistic are thresholded for significance using FDR < 0.05. (B) Result of testing the null hypothesis that cortical thickness does not contribute to the regression model above and beyond all other predictor variables. The test statistic is Student’s t with 132 d.f. Some areas are colored in red, corresponding to t > 0, whereas others are colored in blue, indicating that t < 0. For areas colored in red, as cortical thickness increases, so does age. For areas colored in blue, as thickness decreases, age increases.

In Figure 1B, the distinct contribution of cortical thickness to the estimation of CA is examined (the second step of the analysis). This figure conveys the result of testing the null hypothesis that cortical thickness does not contribute to the regression model above and beyond all other predictor variables. The cortical maps confirm, as expected, that cortical thickness is a strong predictor of CA for most cortical locations where omnibus aging-related effects exist. For cortical locations where Student’s t > 0, increases in cortical thickness translate into increases in CA; conversely, for cortical locations where Student’s t < 0, decreases in cortical thickness translate into increases in CA. The latter is the case for most locations in questions, with a few notable exceptions such as the anterior extremity of the parahippocampal gyrus, bilaterally, and isolated portions of the left subcallosal gyrus and calcarine sulcus.

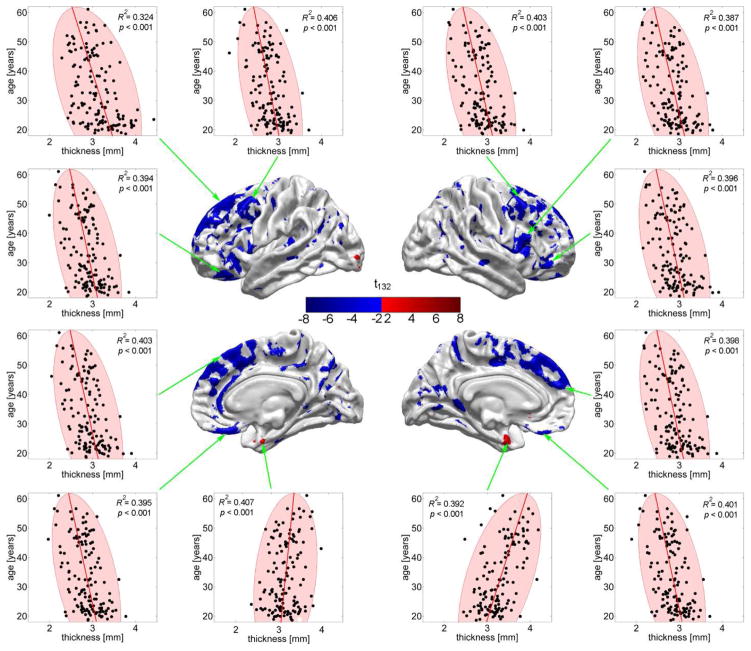
Figure 2 attempts to capture the results of the regression presented in Figure 1B in a more detailed, intuitive and visual manner. Specifically, Figure 2 contains two-dimensional (2D) plots of the response variable (CA, in years) plotted as a function of the most prominent predictor variable (cortical thickness, in mm) for all N subjects at 12 distinct cortical locations. All such locations were selected from among the set of points on the brain surface where the null hypothesis of Student’s t test—as described in step 2 of the statistical analysis—is not accepted. In each plot, an ellipse is drawn to indicate the 95% confidence region for the average thickness measure as a function of age. In other words, given the mean and standard deviation of the sample cortical thickness at the locations explored in each plot, the area of each ellipse indicates the 2D region in which 95% of all measurements are likely to be located. One property of the population sample being studied which is made obvious in Figure 2 is the approximately linear relationship between CA and cortical thickness within the available CA range (18.6 to 61.1 years), which illustrates the appropriateness of a linear regression model. Another property being featured is the presence of outliers in the population sample, as indicated by points located outside each confidence region. At all the cortical locations highlighted by the 2D plots, certain subjects are represented by points which are located outside the corresponding ellipse, which indicates that these subjects have cortical thickness values which are either significantly larger or smaller than expected for a healthy adult of their age. In the latter case, this may be indicative of accelerated senescence, and the methodological approach illustrated here may be useful for identifying individuals at high risk for neurological or neuropsychiatric illness.

Fig. 2.

CA (in years) as a function of cortical thickness (in mm) at 12 locations where thickness contributes to the regression above and beyond all other predictor variables (see text). Each dot represents a subject and ellipses are drawn to indicate the 95% confidence regions for thickness. The linear relationship between CA and cortical thickness within the CA range displayed (18.6 to 61.1 years) is apparent. Outliers (dots located outside the confidence interval) indicate the presence of subjects with atypical cortical thickness values given their CAs. Note the decrease in thickness at all highlighted locations, with the exception of two locations (bottom row, middle) where cortical thickening as a function of age is apparent.

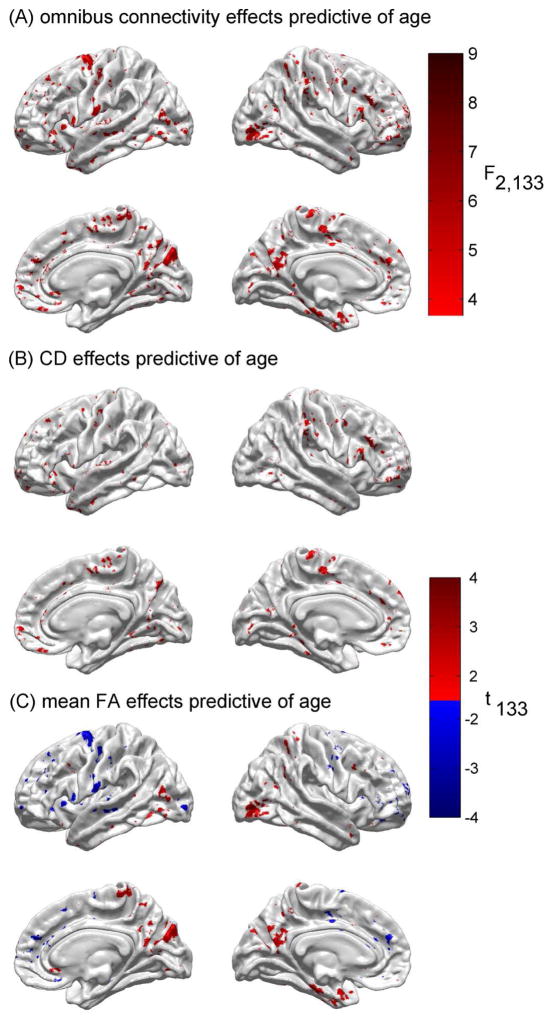
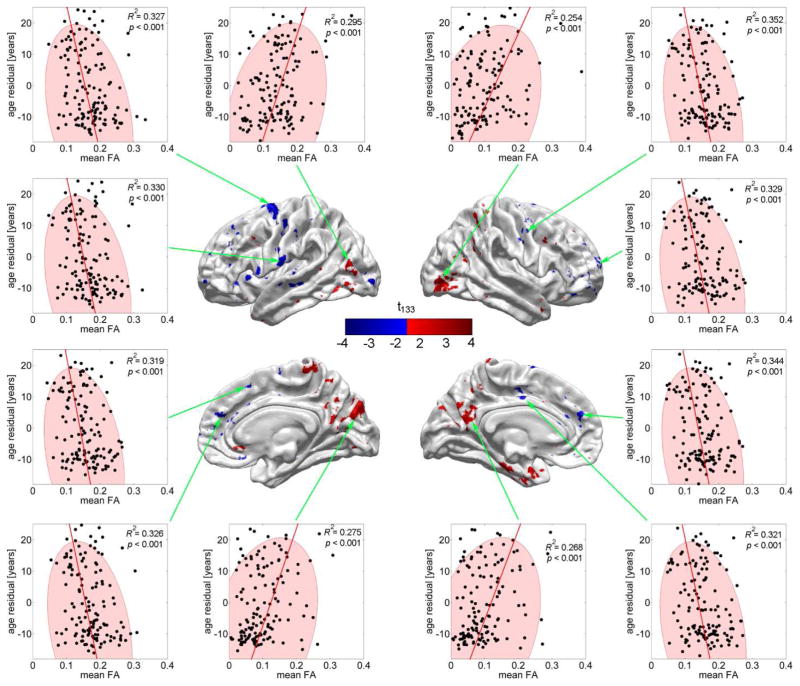
Figure 3A explores the results of testing the null hypothesis that neither of the connectomic variables predicts CA above and beyond the ability of cortical thickness to do so (the third step of the analysis). This figure indicates that the null hypothesis is rejected at a number of cortical locations, though particularly on portions of the paracentral lobules, on the banks of the occipito-parietal sulci, in the prefrontal areas of the superior frontal gyri, and on the anterior portions of the parahippocampal gyri.

Fig. 3.

(A) Results of testing the null hypothesis that neither of the connectomic variables predicts age above and beyond the ability of cortical thickness to do so. As in Figure 1A, the test statistic is the F statistic with 2 and 133 d.f. Color-coded arrows indicate prominent regions where the null hypothesis is rejected, namely the paracentral lobule of the right hemisphere (magenta), the anterior bank of the central sulcus in the left hemisphere (green), the banks of the parieto-occipital sulci (bilaterally, black), and the antero-medial aspects of the superior frontal gyri (bilaterally, cyan). (B) Results of testing the null hypothesis that CD alone cannot predict age above and beyond the ability of cortical thickness to predict it. As in Figure 1B, the test statistic is Student’s t with 133 d.f. (C) As in (B), for mean FA.

Figure 3B conveys the distinct contribution of each connectomic variable to the estimation of CA above and beyond the contribution of cortical thickness (the fourth step of the analysis). The null hypothesis is that the independent variable in question cannot predict CA above and beyond the ability of cortical thickness to predict it. Figure 3B indicates that, in the case of CD, the null hypothesis is rejected on portions of the paracentral lobules, on the banks of the occipito-parietal sulci, and in the prefrontal regions of the superior frontal gyri. Figure 3C shows that mean FA contributes significantly to the prediction of CA above and beyond the contribution of cortical thickness for areas such as the right paracentral lobule, the banks of the parieto-occipital sulci, the prefrontal aspect of the superior frontal gyri, etc.

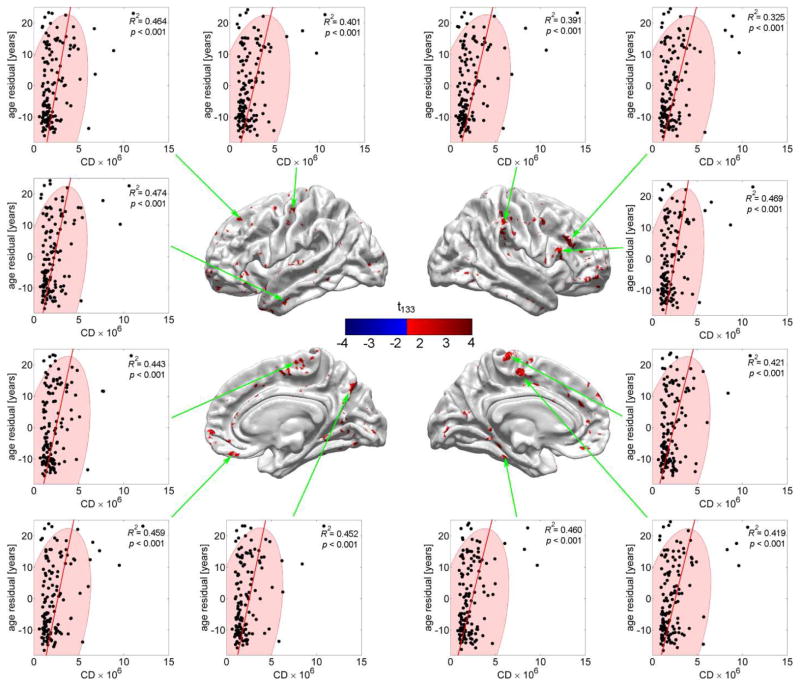
Figures 4 and 5 are similar to Figure 2 in that they attempt to illustrate the results of the regressions presented in Figures 3A and 3B in a more intuitive manner. Thus, both figures contain 2D plots of the response variable (residual CA, in years, after accounting for effects due to cortical thickness) plotted as a function of either CD (Figure 4) or mean FA (Figure 5). As in Figure 2, all N subjects are represented and all 12 highlighted cortical locations are selected from the set of points on the cortical surface where the null hypothesis of Student’s t test—as described in step 4 of the statistical analysis—is not accepted. Subjects represented by points located outside the confidence region have atypical CD (Figure 4) or mean FA (Figure 5), with potential implications as already mentioned.

Fig. 4.

Residual CA (in years) as a function of CD (scaled by 10⁶ for convenience) at 12 locations where CD contributes to the regression above and beyond cortical thickness (see text). Each dot represents a subject; ellipses are drawn to indicate the 95% confidence regions for CD. Note that (1) the residual CA can be either positive or negative, depending on whether thickness alone over- or underestimates CA, and that (2) there are outliers much farther outside the confidence region than in the case of cortical thickness (Figure 2) or mean FA (Figure 5).

Fig. 5.

As in Fig. 4, but where residual CA is plotted as a function of mean FA rather than CD. Note that there are both decreases in mean FA as a function of CA (Student’s t < 0, left and right columns), as well as increases (Student’s t > 0, middle, top and bottom).

4. Discussion

Interpretation

Comparison of Figures 1 and 3 in this article confirms that cortical thickness is the strongest predictor of PBA among the three feature variables selected. Thus, an important finding which emerges from examination of Figure 3 is that healthy brain aging throughout adulthood is associated with statistically significant changes in the connectomic properties of the brain even though not as extensively as cortical thickness. Additionally, we identify four principal cortical regions for which both the mean CD and the mean FA of the connections which link them to the rest of the brain are significantly affected by CA. Bilaterally, these are (A) the paracentral lobule, (B) the anterior wall of the central sulcus, (C) the banks of the parieto-occipital sulcus extending partially onto the cuneus and precuneus, and (D) the antero-medial aspect of the superior frontal gyrus.

Healthy aging is known to be associated with serotonin-modulated changes in glucose metabolism in the paracentral lobule, suggesting the presence of compensatory neurochemical processes prompted by aging-related loss of serotonin innervation (Goldberg et al. 2004). A neuroimaging study by Cheng et al. (2010) found aging-related FA loss in the right paracentral lobule and bilateral superior frontal gyrus in patients exhibiting abnormal WM microstructure and frontal disconnectivity. A spatial navigation study (Wenger et al. 2012) found that, in contrast to young subjects, older adults have reduced potential for experience-dependent cortical alterations in the left precuneus and paracentral lobule, suggesting that aging-related loss of spatial navigation skills may disproportionately affect connectivity between these structures and the rest of the brain. Thus, it appears that the aging-related connectivity alterations identified here between the anterior wall of the central sulcus (primary motor cortex), the paracentral lobule and the rest of the brain may partly reflect loss of motor acuity and serotonergic circuit degeneration throughout adulthood. Nevertheless, further study to test this hypothesis is required and the causality relationships involved in these aging-related connectomic alterations remain unclear.

In our study, both the mean CD and the mean FA of the connections linking the parieto-occipital sulcus to the rest of the brain are found to increase with CA (Figure 3). Such increases in connectivity with age have been reported by other authors as well (Lemaitre et al. 2012). In the case of the parieto-occipital sulcus, although a number of studies have attempted to identify its cortical functions, the precise role of this structure remains insufficiently delineated and it is thus challenging to interpret our findings involving this anatomical structure. The parieto-occipital sulcus is known to be the generative locus for the reactive alpha rhythm, whose amplitude and parameters are modulated by visual shape stimuli, spatial information transfer and other functions commonly associated with the dorsal visual pathway (Vanni et al. 1997). Whereas one study of target selection using reaching movements posited a role for the parieto-occipital sulcus and for surrounding anatomical areas in prehension (de Jong et al. 2001), another investigation suggested both proprioceptive as well as visual and non-visual reaching roles for this structure (Filimon et al. 2009). Ino et al. (2002) even proposed that mental navigation in humans is processed in the anterior bank of the parieto-occipital sulcus. Given the intriguing nature of our findings, it would thus be interesting for future studies to investigate whether aging-related increases in CD and mean FA associated with connections between the parieto-occipital sulcus and other brain areas are related to training or habituation processes taking place over the lifespan, or whether other causality mechanisms are involved instead.

Innovation

In contrast to previous studies which have aimed to estimate cortical thickness as a function of CA, we here explored the converse and novel approach of using cortical thickness and the connectivity properties of the cortex to predict CA, and thereby to estimate PBA. Specifically, the magnitude of each residual ε′ in the regression model described in step 3 of our statistical approach in the Methods section indicates the number of years by which the PBA of a given patient deviates from the mean PBA over healthy individuals who have the same CA as the patient in question. The sign of the residual indicates the direction of the deviation, with a negative residual indicating slower brain aging and a positive one indicating accelerated aging compared to the average rate. In the latter case, the approach illustrated in this study holds considerable translational impact because it can allow health professionals to identify patients whose brains are effectively older than they are expected to be compared to the average healthy population at that CA. This can direct clinicians’ attention to such patients for further examination and possibly for clinical intervention. Patients with accelerated aging may be at higher risk for conditions such as mild cognitive impairment or dementia, and the implementation of a statistical analysis approach such as ours may be of substantial use for the early identification of individuals who are likely to develop either of these conditions. In addition, as this analysis focuses upon structural brain changes which occur throughout adulthood, our study illustrates the growing need for age-stratified brain atlases, as outlined elsewhere (Van Horn and Toga 2009).

Comparison to previous studies

The pattern of cortical thickness changes which occur throughout the lifespan have been reported by numerous studies. Salat et al. (2004), for example, reported significant bilateral aging-associated cortical thinning in the superior frontal gyrus, medial occipital lobe, Broca’s and Wernicke’s areas, precentral gyrus, and significant bilateral cortical thickening in anterior cingulate and parahippocampal regions. A later study by Fjell et al. (2009b) reported high consistency of regional cortical thinning in aging across multiple samples, with substantial atrophy being observed over most of the cortex, with the exception of the anterior cingulate and inferior aspect of the medial frontal lobe, as in the study of Salat et al. In the present study, we similarly identify significant cortical thinning over the frontal lobe as well as cortical thickening in the anterior portions of the medio-ventral temporal lobes (e.g. parahippocampal gyri).

An important difference between our study and those of Salat et al. and Fjell et al. is that the decrease in cortical thickness which we have identified in the medial occipital lobe, in Broca’s area, in Wernicke’s area and in the precentral gyrus is not as significant and as spatially extended as in these two studies. Detailed comparison of our cortical atrophy maps (Figure 1) to those presented by Fjell et al. in Figure 3 of their article suggests that this discrepancy is likely due to the fact that our study does not include a substantial number of subjects older than 60. Specifically, our analysis involves a sample of 136 subjects with CAs in the range of 18.6 to 61.1 years (mean CA: 33.3 years, standard deviation of CA: 11.6 years). By contrast, Salat et al. base their analysis on a sample of 104 subjects with ages in the range of 18–93 years (mean CA: 56.4 years), whereas Fjell et al. use six distinct samples with various CA ranges and means. Thus, whereas Fjell et al. investigate cortical atrophy throughout both adulthood and senescence, it may be the case that the findings and conclusions of the present study are only applicable to adulthood due to the demographic profile of our sample. Examination of the characteristics associated with the six samples used by Fjell et al. and comparison of these characteristics with those of our own sample reveals that the Fjell sample whose demographics are most similar to ours is their Swedish sample (Sample No. 3), which consists of 106 subjects with CAs between 19 and 56 years (mean CA: 41.6 years). Not only is the CA range of the Swedish sample most similar to ours (19–56 years vs. 18.4–61.1 years), but the difference between the mean CA of the subjects in the Swedish sample and the mean CA of our own sample is 8.3 years. This is the lowest difference of CA means between our sample and any of the samples in the study of Fjell et al., which all contain a substantial number of subjects with CAs over 60 (with the exception of the Swedish sample).

Comparing our findings to those of Fjell et al. is relevant here because the mean cortical atrophy pattern exhibited by the Swedish sample of Fjell et al. (third row in Figure 3 of their article) is very similar to the cortical atrophy pattern displayed in Figure 1 of the present article. As in our case, the atrophy pattern in the Swedish sample of Fjell et al. exhibits significant atrophy over the lateral and medial aspects of the frontal lobes, though conspicuously less atrophy over occipital, parietal and temporal areas. What this may suggest is that, whereas the frontal lobe atrophies, on average, relatively early in life (i.e. before a CA of 60), most of the atrophy observed in other cortical regions by Salat et al. and by Fjell et al. in their other 5 samples becomes significant after this CA. Naturally, future research may clarify and provide further insight into the spatiotemporal variability of cortical atrophy patterns in the human cortex. In addition, the fact that suitable imaging volumes acquired from subjects over 61 were not available to us for this study constitutes a limiting factor of the study. Nevertheless, the agreement between the atrophy pattern of our sample as displayed in Figure 1 and that of the Swedish sample in Figure 3 of the article by Fjell et al. does suggest qualitative and quantitative agreement between our study on healthy aging and theirs, subject to the acknowledged limitations of our own approach and to the methodological differences between the two studies.

The atrophy pattern described in Figure 1 contains an age-related, anterior-posterior gradient of thinning with a strong frontal component. As pointed out by an anonymous reviewer, this result is in excellent agreement with at least two previous studies of longitudinal changes in cortical thickness due to normal aging. In one of these, Thambisetty et al. (2010) investigated thickness changes in older adults without dementia and concluded that ageing is associated with age-related decline in thickness exhibiting an anterior-posterior gradient with frontal and parietal regions, where decline rates are greater than in temporal and occipital regions. Similarly, a thorough review by Sullivan and Pfefferbaum (2006) concluded that the ageing-related decline of WM FA is linear from about age 20 onwards, and has a primarily frontal distribution, just as indicated by our study.

Limitations and caveats

The cross-sectional nature of the cohort whose neuroimaging measurements are used in this investigation must be acknowledged as a limitation. Specifically, our study does not take into account effects due to sex, ethnicity, intelligence, educational attainment, or to environmental factors which may influence PBA. Partly as a result of such drawbacks, the present investigation is best viewed as a pilot study which illustrates PBA estimation as a proof of concept. Additional studies with larger sample sizes are consequently needed in order to estimate and regress out the possible confounding effects of these factors (Ingalhalikar et al. 2014; Dennis and Thompson 2013). Similarly, one drawback of having a sample of moderate size (N = 136) with subjects whose CA varies over a wide range (18.6 to 61.1 years) is that, for some given CA, there are not enough subjects available here for the purpose of accurately assessing PBA variance in the healthy population for some fixed CA. Accordingly, given the structural and connectomic profile of a particular subject of interest, our cohort cannot be used as a normative sample for testing the hypothesis that the subject’s PBA is significantly different from the PBA of the healthy population at his/her CA. For these reasons, the cross-sectional nature of the sample and its relatively small size are two potential limitations which should be addressed by future studies aiming to use the PBA estimation approach in a clinical setting for the purpose of identifying human patients whose PBAs are significantly higher than expected given their CAs.

One methodological limitation of the PBA estimation approach is related to the loss of contrast between GM and WM in T₁-weighted MRI as a function of adult age, which may adversely impact the ability of tissue classification methods to segment the GM-WM boundary accurately. In the present case, tissue segmentation was performed based on spatial intensity gradients across tissue classes where the former are not simply reliant on absolute signal intensity, and previous studies of aging using this methodology have shown that the resulting segmentations can detect sub-millimeter differences between groups (Fischl et al. 2002; Fischl et al. 1999; Dale et al. 1999).

Another limitation of the present study is that it does not account for the potential confound of systematic differences in head movement patterns as a function of age. Such movement artifacts can impact measurements of FA, CD and GM thickness (Rohde et al. 2004; Freire and Mangin 2001). Avenues for addressing this challenge include (A) providing the ability to relate head position during MR scanning to an independent frame of reference (Qin et al. 2013), (B) using repeated scans of each subject to tease out motion-related effects (Ernst et al. 1999), or (C) implementing an MR sequence which implements intra-scan motion correction (Ugurbil et al. 2013; Herbst et al. 2014). In the present case, because none of these options was available to the imaging staff at the time of MR acquisition, we must acknowledge this as a potential limitation and draw attention to the fact that the results presented here must be interpreted with caution.

Finally, the use of linear regression in contrast to other approaches such as logistic or other forms of nonlinear regression may constitute a drawback of this study. Previously, both approaches have been used in neuroimaging studies of aging, and advantages as well as drawbacks associated with both techniques have been identified (Wang et al. 2009; Lerch et al. 2008; Dickerson et al. 2012). Because aging-related changes in the structural and connectomic variables considered here may exhibit either linear or nonlinear behaviors depending on metric type and age range, it may be challenging to argue persuasively in favor of applying a nonlinear regression model for all metrics considered here (Dickie et al. 2013). Our choice of linear regression is based on the consideration that linear models are more parsimonious and that their results are easier to interpret, whereas nonlinear models are less common and additionally require strong empirical justification. Given that the upper limit of the CA range is 61.1 years in our case, the use of linear regression is reasonable particularly because cortical thickness changes below a CA of ~60 do not exhibit clearly nonlinear behavior (Sowell et al. 2003).

5. Conclusion

Here we have proposed that connectomic metrics can be used in combination with cortical thickness to assess PBA in healthy aging over the course of adulthood. Using multivariate linear regression analysis, we illustrate the process of predicting CA and thereby estimating PBA while also concluding that healthy aging is associated with significant connectomic changes throughout adulthood. Whereas most aging research studies have attempted to estimate cortical thickness and its rate of change based on CA, one novel aspect of the present study is that it has explored the converse, i.e. the ability of cortical thickness and of brain connectomic properties to predict CA, and thereby also to estimate PBA. Though the sample size employed here is typical of pilot studies, both the statistical methodology and its demonstrated implementation are useful and may hold potential clinical applications for the identification of clinical patients with accelerated brain aging.