Abstract
The objective of the study was to assess the use of maximum (Vmax) and final propulsive phase (FPV) bar velocity to predict jump height in the weighted jump squat. FPV was defined as the velocity reached just before bar acceleration was lower than gravity (-9.81 m·s-2). Vertical jump height was calculated from the take-off velocity (Vtake-off) provided by a force platform. Thirty swimmers belonging to the National Slovenian swimming team performed a jump squat incremental loading test, lifting 25%, 50%, 75% and 100% of body weight in a Smith machine. Jump performance was simultaneously monitored using an AMTI portable force platform and a linear velocity transducer attached to the barbell. Simple linear regression was used to estimate jump height from the Vmax and FPV recorded by the linear velocity transducer. Vmax (y = 16.577x - 16.384) was able to explain 93% of jump height variance with a standard error of the estimate of 1.47 cm. FPV (y = 12.828x - 6.504) was able to explain 91% of jump height variance with a standard error of the estimate of 1.66 cm. Despite that both variables resulted to be good predictors, heteroscedasticity in the differences between FPV and Vtake-off was observed (r2 = 0.307), while the differences between Vmax and Vtake-off were homogenously distributed (r2 = 0.071). These results suggest that Vmax is a valid tool for estimating vertical jump height in a loaded jump squat test performed in a Smith machine.
Key points.
Vertical jump height in the loaded jump squat can be estimated with acceptable precision from the maximum bar velocity recorded by a linear velocity transducer.
The relationship between the point at which bar acceleration is less than -9.81 m·s-2 and the real take-off is affected by the velocity of movement.
Mean propulsive velocity recorded by a linear velocity transducer does not appear to be optimal to monitor ballistic exercise performance.
Key words: Linear velocity transducer, force platform, jump performance, swimming
Introduction
Jump ability has been described as an important factor for performance in many sports (Pérez-Gómez and Calvet, 2013). In swimming, this ability can be decisive (West et al., 2011). The narrow line between the success and failure (i.e., fractions of a second) of high-level swimmers indicates a need to optimise each part of the race. Starts and turns are the two skills most affected by jump performance (Bishop et al., 2013). A swimmer’s jump ability correlates well with performance at these two specific actions (Breed and Young, 2003; West et al., 2011) and it is common for a swimmer’s dry land training regimen to include several jumps, loaded or not, targeted at improving sports performance (Rebutini et al., 2014). Coaches, therefore, need tools to accurately monitor the jump ability of their athletes.
The force platform is among the most accurate measurement tools available to assess vertical jump performance (Linthorne, 2001) and is commonly regarded as the reference with which to compare other measurement tools (Cronin et al., 2004; Crewther et al., 2011). This device, nevertheless, has some practical limitations (it is difficult to transport and assessments are limited to laboratory conditions) and is more expensive than other measurement devices. These limitations have promoted the proliferating on the market of more economic and versatile measurement tools (e.g. accelerometers, linear position transducers, contact platforms, etc.) (McMaster et al., 2014).
Among these alternative devices, the linear position transducer is the most popular (Harris et al., 2010; Dugan et al., 2004). The linear position transducer is usually attached to the bar and calculates kinetic (force and power) and kinematic (velocity and acceleration) variables using bar displacement-time data. The instrument first differentiates these data and then double differentiates them to calculate velocity and acceleration, respectively. Force can then be calculated by multiplying the mass lifted and total acceleration (force = mass x [acceleration of the bar + 9.81 m·s-2]). Finally, power is calculated as the product of force and velocity. These manipulations of raw displacement-time data can, however, magnify the measurement error (Cormie et al., 2007; McMaster et al., 2014). Thus, linear velocity transducers as opposed to position transducers have been developed to minimise the number of calculations needed to obtain the kinetic and kinematic variables of interest. The first of these devices to appear on the market was used in the present study (T-Force System; Ergotech, Murcia, Spain). Linear velocity transducers directly measure bar velocity. A complete description of this system can be found in Sánchez-Medina and González-Badillo (2011).
Numerous studies have shown a good relationship between linear transducers and force platforms in the values of force, velocity and power they provide (Chiu et al., 2004; Cronin et al., 2004). For example, Crewther et al. (2011) observed significant correlations in force (r = 0.59 to 0.87) and power (r = 0.62 to 0.82) measurements made with a force platform and a linear position transducer during the loaded jump squat. However, a shortcoming of linear transducers is that they do not offer jump height measurements because they cannot determine the duration of the flight phase or the take-off velocity of the centre of mass. Different apparatuses can be used to calculate jump height (McMaster et al., 2014). The force platform predicts jump height from take-off velocity or flight time. Video capture devices can calculate the rise of the centre of mass by digitizing several anatomical landmarks. Jump mats and photo-cells are used to predict jump height based on flight time. Additionally reach-and-jump apparatuses (e.g. Vertec) directly measure jump height as the distance between reach height and the highest obtained jump.
It has been established that when light and medium loads are lifted during a traditional resistance training exercise (e.g. bench press or squat), deceleration at the end phase of the movement is greater than that would be expected due solely to the effect of gravity (Sánchez-Medina et al., 2010). This means that athletes must activate their antagonist muscles to apply force in the opposite direction to the load motion in order to stop the movement (Jarić et al., 1995). However during ballistic exercises (e.g. bench press throw or squat jump), in which resistance is accelerated throughout the entire range of motion, accelerations lower than gravity are not expected, because athletes do not have to apply force in the opposite direction of movement. However, the constant downward force exerted by the cable tension (≈ 5 N in our device) attached to the bar, as well as the friction force when the exercise is performed in a Smith machine, may induce a bar acceleration lower than gravity during the last movement phase. Accordingly, the velocity of the bar corresponding to the moment just before its acceleration is less than the acceleration of gravity, may be related to the take-off velocity of the centre of mass recorded by a force platform during a vertical jump.
A drawback of linear transducers is that they do not provide vertical jump height. Therefore, it would be interesting to find a way to predict jump height based on the movement velocity, which is directly measured by linear velocity transducers. In this context, this study aimed to predict jump height, derived from the subject’s take-off velocity estimated by a force platform (Vtake-off), from the maximum velocity of the bar (Vmax) or its final propulsive phase velocity (FPV), that is, the velocity attained by the bar just before its acceleration was lower than -9.81 m·s-2.
Methods
Study design
A correlation study was designed to predict jump height according to bar velocity. Subjects performed a loaded jump squat at 25%, 50%, 75% and 100% of body weight (BW) on a portable force platform with a linear velocity transducer attached to the barbell. The Vtake-off provided by the force platform data was used to estimate jump height. The two velocity values used to estimate jump height, Vmax and FPV, were provided by the linear velocity transducer.
Subjects
The study population was comprised of 30 swimmers, 23 women (age 16.0 ± 2.7 years, height 1.67 ± 0.06 m, body mass 57.6 ± 7.1 kg), and 7 men (age 18.0 ± 3.3 years, height 1.81 ± 0.04 m, body mass 68.2 ± 6.2 kg). All subjects were members of the Slovenian national team. Swimmers were requested to include loaded jump squat exercises in their dry land training schedule three months before the study outset. All subjects were informed of the procedures to be carried out and signed a written informed consent form prior to the investigation. For swimmers under 18 years, consent was obtained from their parents or guardians. The study protocol adhered to the tenets of the Declaration of Helsinki and was approved by the University Ethics Committee.
Procedures
Subjects visited the laboratory after refraining from strenuous exercise for a minimum of 48 hours. After body composition measurements, subjects completed a standardised warm-up based on jogging, joint mobility, dynamic stretching, six jumps without additional weight and one set of five jumps lifting 16 kg (this was the weight of the unloaded Smith machine bar) in the assessed exercise. This was followed by the test protocol in which subjects performed an incremental loading test at 25%, 50%, 75% and 100% of their own BW in a Smith machine. Load accuracy was at least 0.25 kg. Two attempts per load were allowed but only data for the best jump, or greatest Vtake-off, were entered in the analysis. Rest periods were one minute between tests using the same load and five minutes between tests using different loads.
The movement commenced from a standing position with the knees and hips fully extended, feet approximately shoulder-width apart, and the barbell resting across the back at the level of the acromion. The swimmers then slowly descended until the back of the thigh touched an elastic cord set at a knee angle of 90º (McBride et al., 2011). The knee angle was set with a manual goniometer. The subjects were instructed to maintain this position for two seconds before performing a purely concentric action in order to jump as high as possible (Markovic and Jaric, 2007). Movements such as countermovement or throwing the bar over the shoulders were not allowed. If any of these movements were observed, the jump was repeated after the corresponding period of rest.
The force platform and the linear velocity transducer were simultaneously used as follows:
Force platform: All jumps were performed on a portable force platform (AMTI, Watertown, MA, USA) mounted according to the manufacturer’s specifications. The device’s proper calibration was checked before and after each testing session. The force platform was positioned in the centre of the Smith machine and stabilized using a solid wooden base that was flush with the force platform surface. The ground reaction force, which was recorded with a frequency of 1,000 Hz, was used to calculate Vtake-off according to the impulse-momentum theorem. The impulse (force x time) recorded at each time point (1 millisecond) was divided by the subject’s mass to determine the system centre of mass change in velocity, which was then added to the system centre of mass prior velocity to give a new instantaneous velocity for that time interval. System centre of mass velocity at take-off was used to calculate jump height using the equation:
Jump height = (Vtake-off)2 / (2 x gravity)
Linear velocity transducer: A dynamic measurement system (T-Force System; Ergotech, Murcia, Spain) validated by Sanchez-Medina and González-Badillo (2011) was fixed perpendicularly to the bar with a tether to record its vertical instantaneous velocity at a frequency of 1,000 Hz. A complete description of this system is provided elsewhere (Sánchez-Medina and González-Badillo, 2011). Vmax was defined as the maximum instantaneous velocity attained during the concentric phase. FPV was defined as the bar velocity just before the acceleration of the bar was lower than -9.81 m·s-2. The propulsive phase of the repetition was defined as the interval between the beginning of the concentric movement and the time when bar acceleration is lower than gravity (-9.81 m·s-2) (Sánchez-Medina et al., 2010). Thus, FPV was the velocity recorded in the last millisecond of the propulsive phase.
Statistical analysis
Data are presented as mean ± standard deviation (SD). Prior to statistical analysis, the normal distribution of the data (Shapiro-Wilk test) and the homogeneity of variances (Levene test) were confirmed (p > 0.05). The Mann-Whitney U test was used to compare vertical jump performance in men and women. Analysis of variance (ANOVA) with repeated measures and Bonferroni post hoc comparisons were used to examine differences between the three velocities analysed (Vmax, FPV and Vtake-off) by sex (men and women) and load used (25%, 50%, 75%, and 100% of BW). Jump height (dependent variable) was predicted using Vmax or FPV as the independent variables through simple linear regression. The adjusted Pearson’s multivariate coefficient of determination (adj. r2), the standard error of the estimate (SEE), and the model equation are provided. Bland-Altman plots of mean differences were constructed to compare: a) Vtake-off with the two velocities recorded by the linear velocity transducer (Vmax and FPV); and b) jump height calculated from the force platform data with jump heights estimated by the two simple linear regression models. Significance was set at p < 0.05. All statistical tests were performed using the software SPSS version 20.0 (SPSS, Chicago, IL, USA) and Microsoft Excel 2007.
Results
The jump heights recorded in the male and female swimmers for each of the four loads are provided in Table 1. These data indicate that regardless of the load lifted, men jumped higher than women (p < 0.001).
Table 1.
Vertical jump heights recorded for men and women. Data expressed as mean (±SD).
| Load | Men (cm) | Women (cm) |
|---|---|---|
| 25% BW | 24.5 (3.6) | 17.5 (3.1) * |
| 50% BW | 17.9 (2.4) | 12.6 (2.4) * |
| 75% BW | 13.3 (1.3) | 8.8 (2.1) * |
| 100% BW | 9.7 (1.5) | 6.0 (1.7) * |
* p < 0.001 compared to men. BW = body weight
Differences in the three velocities (Vmax, FPV and Vtake-off) were significant for all loads lifted (25%, 50%, 75% and 100% of BW) in both sexes (p < 0.001). Pairwise comparisons revealed greater Vmax values compared with Vtake-off or FPV in all cases (Table 2). No differences were observed between FPV and Vtake-off, except when women lifted loads corresponding to 75% or 100% of BW, for which Vtake-off values were significantly higher (p < 0.05). Greater velocities for the four loads lifted were recorded in men (p < 0.01).
Table 2.
Maximum velocity (Vmax), final propulsive phase velocity (FPV) and take-off velocity (Vtake-off) by load and sex. Data expressed as mean (±SD).
| Sex | Variable | 25% BW | 50% BW | 75% BW | 100% BW |
|---|---|---|---|---|---|
| Men | Vmax (m·s-1) | 2.40 (.09) b.c | 2.09 (.06) b.c | 1.83 (.05) b.c | 1.62 (.05) b.c |
| FPV (m·s-1) | 2.26 (.09) a | 1.90 (.07) a | 1.56 (.06) a | 1.25 (.07) a | |
| Vtake-off (m·s-1) | 2.19 (.06) a | 1.87 (.05) a | 1.61 (.03) a | 1.38 (.04) a | |
| Women | Vmax (m·s-1) | 2.02 (.03) b.c | 1.78 (.03) b.c | 1.52 (.03) b.c | 1.34 (.03) b.c |
| FPV (m·s-1) | 1.85 (.03) a | 1.55 (.04) a | 1.24 (.03) a.c | 0.94 (.05) a.c | |
| Vtake-off (m·s-1) | 1.84 (.03) a | 1.57 (.03) a | 1.30 (.03) a.b | 1.07 (.03) a.b |
a, Significantly different versus Vmax. P < 0.05.
b, Significantly different versus FPV. P < 0.05.
c, Significantly different versus Vtake-off. P < 0.05.
Figure 1 depicts the regression models obtained to predict jump height from each of the two independent variables examined (Vmax or FPV). When Vmax was used as the independent variable, the model was able to explain 93% of the variance (Fexp = 1600.5, 1, 117 df), compared to 91% (Fexp = 1235.5, 1, 117 df) for the use of FPV as the independent variable.
Figure 1.
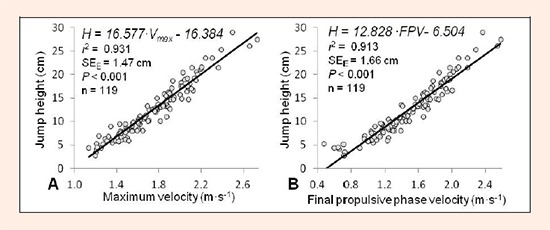
Simple linear regression models used to estimate jump height. Model obtained using as the independent variable maximum velocity (A) or final propulsive phase velocity (B). H = jump height (cm); Vmax = maximum velocity; FPV = final propulsive phase velocity; SEE = standard error of the estimate.
Bland–Altman plots comparing the use of the independent variables (Vmax and FPV) to estimate jump height (Vtake-off) are provided in Figure 2. The plots show that Vmax was significantly higher than Vtake-off (texp = 25.33; 118 df; p < 0.001), while Vtake-off was significantly higher than FPV (texp = 4.07; 118 df; p < 0.001). The systematic bias ± random error was 0.22 ± 0.09 m·s-1 for Vmax versus Vtake-off and -0.05 ± 0.12 m·s-1 for FPV versus Vtake-off. As also shown in Figure 2, the differences between Vmax and Vtake-off were homogenously distributed (r2 < 0.1), while heteroscedasticity was observed for FPV (r2 = 0.307).
Figure 2.
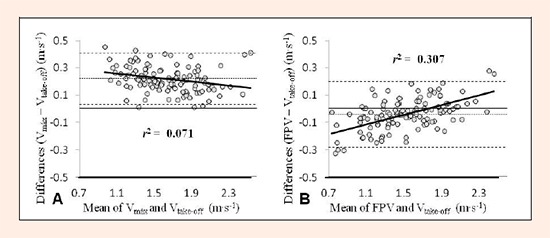
Bland–Altman plots showing differences between Vmax vs. Vtake-off (A) and FPV vs. Vtake-off (B). Each plot shows the mean difference and 95% limits of agreement (dashed lines), along with the regression line (solid line). Vtake-off = take-off velocity; Vmax = maximum velocity; FPV = final propulsive phase velocity.
Finally, Bland-Altman comparisons between jump height derived from the force platform data and jump height estimated from the regression models are illustrated in Figure 3. When Vmax was used as the independent variable, 95% limits of agreement were -2.9 cm to +2.9 cm while the corresponding limits for FPV were -3.3 cm to 3.3 cm. No significant differences were detected between real jump height and height estimated using the two prediction equations (both p > 0.99).
Figure 3.
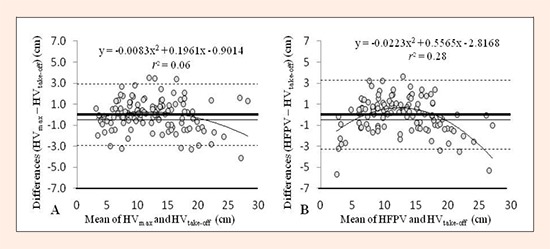
Bland–Altman plots showing differences between HVmax vs. HVtake-off (A) and HFPV vs. HVtake-off (B). Each plot shows the mean difference and 95% limits of agreement (dashed lines), along with the regression line (solid line). HVtake-off = jump height derived from take-off velocity; HVmax = jump height derived from maximum velocity; HFPV = jump height derived from final propulsive phase velocity.
Discussion
The main finding of our study was that both Vmax and FPV were able to reliably predict jump height. Notwithstanding, we feel that Vmax would be a more suitable indicator for several reasons: a) Vmax yielded the best-fit prediction (r2 = 0.931 vs. 0.913); b) the FPV data were heteroscedastic (r2 = 0.307). This means that FPV tended to be higher than Vtake–off for loads that can be moved at high velocities, while for heavier loads and thus a lower movement velocity, Vtake-off values increased. In contrast, differences between Vmax and Vtake-off showed no clear tendency (r2 = 0.071), indicated a more random distribution of differences; c) when Vmax was used as the independent, the standard error of the estimate was lower (SEE = 1.47 cm vs. 1.66 cm). This indicates a wider limits of agreement range in the Bland-Altman plot; d) for FPV as the independent variable, the regression model showed a tendency to underestimate jump height for extreme velocity values. This compromises the usefulness of this regression model when light and heavy loads are lifted; and finally e) from a practical standpoint, the determination of Vmax is less time consuming. This is because existing software does not provide the value of FPV and so the data for each repetition need to be exported to individually determine FPV. These results thus suggest that the prediction model adjusted for Vmax (jump height [cm] = 16.577·Vmax - 16.384, Figure 1) could be a valid tool to estimate vertical jump height.
Jump ability is a determinant of performance in many sports, including swimming (Bishop et al., 2013; West et al., 2011). In effect, ballistic exercises have been described to offer a greater stimulus for improving vertical jump performance compared to traditional resistance training exercises in well-trained athletes (Newton et al., 1999). Similarity with the athletic competition movement (Cormie et al. 2011) and the intense mechanical stimulus conferred by continued acceleration throughout the entire range of motion (Newton et al., 1996) determines that coaches prescribe ballistic exercises to induce adaptations that allow for greater transfer to athletic performance. This determines that training schedules targeted at improving athletic performance often include different types of jump (squat jump, counter movement jump, drop jump, etc.) with or without additional loads (Pérez-Gómez and Calvet, 2013; Rebutini et al., 2014). Moreover, given its close relationship with sports performance (Breed and Young, 2003; West et al, 2011), jump ability is also often used to monitor the training status of athletes (Cormie et al., 2010; Vuk et al., 2012). In this context, it is advisable that coaches have access to accurate tools to assess lower limb muscular power during such actions (Hori et al., 2007).
Although the force platform is a popular instrument to monitor jump ability (Linthorne, 2001), its use restricted to laboratory conditions, its difficult transport, and especially its price, make it unavailable to most coaches and physical trainers. However, new more portable and cheaper devices are appearing on the market, and these provide valuable information for coaches to plan and monitor the training of their athletes (McMaster et al., 2014). Among these devices, linear transducers of position and velocity are perhaps gaining most popularity in the field of physical training (Harris et al., 2010; Sánchez-Medina and González-Badillo, 2011). These devices enable the coach to record in real time the velocity and power generated by an athlete in each repetition. Based on this type of information, new training protocols can be designed in which the velocity of execution is the criterion for the intensity and volume of the training session (González-Badillo and Sánchez-Medina, 2010; González-Badillo et al., 2011; Sánchez-Medina and González-Badillo, 2011).
A drawback of these devices is that they do not provide jump height measurements. To address this problem, we here propose two equations to estimate jump height from the movement velocity of the bar recorded by a linear velocity transducer. Vmax showed the highest power of prediction (p < 0.001; r2 = 0.931; SEE = 1.47 cm). The data provided in Table 2 reveal that Vmax was significantly higher than Vtake-off for all the loads tested (P < 0.05). This was expected since the maximum velocity during a vertical jump is always detected immediately before take-off. Further, the difference between Vmax and Vtake-off appears to be unaffected by the velocity of execution, which is manifested by the negligible association shown in the Bland-Altman plot (r2 = 0.071) (Figure 2.A). The homoscedasticity of errors, generally defined as an r2 ≤ 0.1, has been identified as an important property by Atkinson and Nevill (1998).
The velocity reached just before acceleration of the bar was lower than gravity (-9.81 m·s-2), defined as the final propulsive phase velocity, also emerged as a good predictor of jump height (p < 0.001; r2 = 0.913; SEE = 1.66 cm). However, for the reasons indicated above, Vmax is a more useful tool for this purpose. Our results suggest that for loads lifted at low velocity, the time when acceleration of the bar is less than -9.81 m·s-2 could occur after take-off. This assumption is supported by the fact that Vtake-off was significantly higher than FPV when jumps were performed at low velocity (when women lifted loads equivalent to 75% and 100% of BW). Therefore, the validity of the mean propulsive phase velocity values, i.e., average velocity recorded from the start of the concentric movement until bar acceleration was lower than -9.81 m·s-2 (Sanchez-Medina et al., 2010), could be compromised in the case of ballistic exercises such as that assessed here.
Finally, we should mention that the prediction equations proposed in this paper are only valid for linear transducers working at a sampling frequency of 1,000 Hz. Today, other brands of linear transducers exist that work at a lower sampling frequency, typically 100 Hz. The use of a lower precision device to determine Vmax could underestimate jump height. Thus, recording Vmax across a time interval of 1 millisecond such as in our case will not be the same as recording this variable over 10 milliseconds. Our results are also restricted to jumps performed in a Smith machine. During free-weight squat jumps, horizontal bar displacement would likely lead to overestimation of vertical bar velocity (Cormie et al., 2007) and therefore of jump height.
Conclusion
Our findings indicate that maximum barbell velocity can be used to estimate vertical jump height using the equation: Jump height (cm) = 16.577·Vmax - 16.384 with an accuracy of 93.1%. Although the moment when bar acceleration drops below -9.81 m·s-2 is used to define the end of the propulsive phase in traditional resistance training exercises (e.g. squat or bench press), our data indicate that for loads lifted at low velocities (FPV < Vtake-off at 75% and 100% of BW in women) this will occur after take-off. This could compromise the validity of mean propulsive velocity to monitor ballistic exercises such as the jump squat examined here.
Acknowledgments
This study was supported by grants awarded by the Spanish Ministry of Science and Innovation (DEP2012-35774) and Ministry of Education, Culture and Sport (Predoctoral Grant FPU12/00360).
Biographies

Amador GARCÍA-RAMOS
Employment
Scholarship holder (FPU12/00360). Department of Physical Education and Sport, University of Granada, Spain.
Degree
MSc
Research interests
Sport biomechanics, resistance training, altitude training.
E-mail: amagr@ugr.es

Igor ŠTIRN
Employment
Associate Professor. Department of Kinesiology, University of Ljubljana, Slovenia.
Degree
PhD
Research interests
Neuromechanics of human movement, strength and conditioning, aquatic sports and exercising.
E-mail: igor.stirn@fsp.uni-lj.si

Paulino PADIAL
Employment
Lecturer in Sports Training. Department of Physical Education and Sport, University of Granada, Spain.
Degree
PhD
Research interests
Strength training, sport performance and training in combat sports.
E-mail: ppadial@ugr.es

Javier ARGÜELLES-CIENFUEGOS
Employment
Sports Performance Analysis Department. Spanish Sports Council, Sierra Nevada High Performance Centre, Granada, Spain.
Degree
MSc
Research interests
Sport performance analysis, biomechanics, resistance training.
E-mail: javier.arguelles@csd.gob.es

Blanca DE LA FUENTE
Employment
Head of Sports Performance Analysis Department. Spanish Sports Council, Sierra Nevada High Performance Centre, Granada, Spain.
Degree
PhD
Research interests
Swimming biomechanics, performance analysis, altitude training.
E-mail: blanca.delafuente@csd.gob.es

Vojko STROJNIK
Employment
Professor. Department of Kinesiology, University of Ljubljana, Slovenia.
Degree
PhD
Research interests
Neuromechanics of human movement, motor control, strength and conditioning.
E-mail: Vojko.Strojnik@fsp.uni-lj.si

Belén FERICHE
Employment
Lecturer in Sport Training. Department of Physical Education and Sport, University of Granada, Spain.
Degree
PhD
Research interests
Sport training, altitude training.
E-mail: mbelen@ugr.es
References
- Atkinson G., Nevill A.M. (1998) Statistical methods for assessing measurement error (reliability) in variables relevant to sports medicine. Sports Medicine 26(4), 217-238. [DOI] [PubMed] [Google Scholar]
- Bishop C., Cree J., Read P., Chavda S., Edwards M., Turner A. (2013) Strength and Conditioning for Sprint Swimming. Strength and Conditioning Journal 35(6), 1-6. [Google Scholar]
- Bland J.M., Altman D.G. (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1(8476), 307-310. [PubMed] [Google Scholar]
- Breed R.V., Young W.B. (2003) The effect of a resistance training programme on the grab, track and swing starts in swimming. Journal of Sports Science 21(3), 213-220. [DOI] [PubMed] [Google Scholar]
- Chiu L.Z.F., Schilling B.K., Fry A.C., Weiss L.W. (2004) Measurement of resistance exercise force expression. Journal of Applied Biomechanics 20(2), 204-212. [Google Scholar]
- Cormie P., Deane R., McBride J.M. (2007) Methodological concerns for determining power output in the jump squat. Journal of Strength and Conditioning Research, 21(2), 424-430. [DOI] [PubMed] [Google Scholar]
- Cormie P., McGuigan M.R., Newton R.U. (2010) Adaptations in athletic performance after ballistic power versus strength training. Medicine and Science in Sports and Exercise 42(8), 1582-1598. [DOI] [PubMed] [Google Scholar]
- Cormie P., McGuigan M.R., Newton R.U. (2011) Developing maximal neuromuscular power: part 2 - training considerations for improving maximal power production. Sports Medicine 41(2), 125-146. [DOI] [PubMed] [Google Scholar]
- Crewther B.T., Kilduff L.P., Cunningham D.J., Cook C., Owen N., Yang G.Z. (2011) Validating two systems for estimating force and power. International Journal of Sports Medicine 32(4), 254-258. [DOI] [PubMed] [Google Scholar]
- Cronin J.B., Hing R.D., McNair P.J. (2004) Reliability and validity of a linear position transducer for measuring jump performance. Journal of Strength and Conditioning Research 18(3), 590-593. [DOI] [PubMed] [Google Scholar]
- Dugan E.L., Doyle T.L., Humphries B., Hasson C.J., Newton R.U. (2004) Determining the optimal load for jump squats: a review of methods and calculations. Journal of Strength and Conditioning Research 18(3), 668-674. [DOI] [PubMed] [Google Scholar]
- González-Badillo J.J., Marques M.C., Sánchez-Medina L. (2011) The importance of movement velocity as a measure to control resistance training intensity. Journal of Human Kinetics 29, 15-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Badillo J.J., Sánchez-Medina L. (2010) Movement velocity as a measure of loading intensity in resistance training. International Journal of Sports Medicine 31(5), 347-352. [DOI] [PubMed] [Google Scholar]
- Harris N.K, Cronin J., Taylor K.L., Boris J., Sheppard J. (2010) Understanding position transducer technology for strength and conditioning practitioners. Strength and Conditioning Journal 32(4), 66-79. [Google Scholar]
- Hori N., Newton R.U., Andrews W. A., Kawamori N., McGuigan M.R., Nosaka K. (2007) Comparison of four different methods to measure power output during the hang power clean and the weighted jump squat. Journal of Strength and Conditioning Research 21(2), 314-320. [DOI] [PubMed] [Google Scholar]
- Jarić S., Ropret R., Kukolj M., Ilić D.B. (1995) Role of agonist and antagonist muscle strength in performance of rapid movements. European Journal of Applied Physiology and Occupational Physiology 71(5), 464-468. [DOI] [PubMed] [Google Scholar]
- Linthorne N.P. (2001) Analysis of standing vertical jumps using a force platform. American Journal of Physics 69(11), 1198-1204. [Google Scholar]
- Markovic G., Jaric S. (2007) Is vertical jump height a body size-independent measure of muscle power? Journal of Sports Sciences 25(12), 1355-1363. [DOI] [PubMed] [Google Scholar]
- McMaster D.T., Gill N., Cronin J., McGuigan M. (2014) A brief review of strength and ballistic assessment methodologies in sport. Sports Medicine 44(5), 603-623. [DOI] [PubMed] [Google Scholar]
- McBride J.M., Haines T.L., Kirby T.J. (2011) Effect of loading on peak power of the bar, body, and system during power cleans, squats, and jump squats. Journal of Sports Science 29(11), 1215-1221. [DOI] [PubMed] [Google Scholar]
- Newton R.U., Kraemer W.J., Häkkinen K. (1999) Effects of ballistic training on preseason preparation of elite volleyball players. Medicine and Science in Sports and Exercise 31(2), 323-330. [DOI] [PubMed] [Google Scholar]
- Newton R.U., Kraemer W.J., Häkkinen K., Humphries B.J., Murphy A.J. (1996) Kinematics, kinetics and muscle activation during explosive upper body movements. Journal of Applied Biomechanics 12(1), 31-43. [DOI] [PubMed] [Google Scholar]
- Pérez-Gómez J., Calbet J.A. (2013) Training methods to improve vertical jump performance. The Journal of Sports Medicine and Physical Fitness 53(4), 339-357. [PubMed] [Google Scholar]
- Rebutini V.Z., Pereira G., Bohrer R.C., Ugrinowitsch C., Rodacki A.L. (2014) Plyometric long jump training with progressive loading improves kinetic and kinematic swimming start parameters. Journal of Strength and Conditioning Research (In press). [DOI] [PubMed] [Google Scholar]
- Sánchez-Medina L., González-Badillo J.J. (2011) Velocity loss as an indicator of neuromuscular fatigue during resistance training. Medicine and Science in Sports and Exercise 43(9), 1725-1734. [DOI] [PubMed] [Google Scholar]
- Sánchez-Medina L., Pérez C.E., González-Badillo J.J. (2010) Importance of the propulsive phase in strength assessment. International Journal of Sports Medicine 31(2), 123-129. [DOI] [PubMed] [Google Scholar]
- Vuk S., Markovic S., Jaric S. (2012) External loading and maximum dynamic output in vertical jumping: the role of training history. Human Movement Science 31(1), 139-151. [DOI] [PubMed] [Google Scholar]
- West D.J., Owen N.J., Cunningham D.J., Cook C.J., Kilduff L.P. (2011) Strength and power predictors of swimming starts in international sprint swimmers. Journal of Strength and Conditioning Research 25(4), 950-955. [DOI] [PubMed] [Google Scholar]


