Testing for effects of climate change on competitive relationships and coexistence between two bird species

Abstract

Climate change is expected to have profound ecological effects, yet shifts in competitive abilities among species are rarely studied in this context. Blue tits (Cyanistes caeruleus) and great tits (Parus major) compete for food and roosting sites, yet coexist across much of their range. Climate change might thus change the competitive relationships and coexistence between these two species. Analysing four of the highest-quality, long-term datasets available on these species across Europe, we extend the textbook example of coexistence between competing species to include the dynamic effects of long-term climate variation. Using threshold time-series statistical modelling, we demonstrate that long-term climate variation affects species demography through different influences on density-dependent and density-independent processes. The competitive interaction between blue tits and great tits has shifted in one of the studied sites, creating conditions that alter the relative equilibrium densities between the two species, potentially disrupting long-term coexistence. Our analyses show that long-term climate change can, but does not always, generate local differences in the equilibrium conditions of spatially structured species assemblages. We demonstrate how long-term data can be used to better understand whether (and how), for instance, climate change might change the relationships between coexisting species. However, the studied populations are rather robust against competitive exclusion.

1. Introduction

Competition is defined as the negative effects which one organism has upon another by consuming, or controlling access to, a resource that is limited in availability [1]. At the species level, competition may lead to exclusion if one species experiences a greater competitive effect from another species than within its own species [2,3]. Theoretical [3] and empirical [4,5] investigations have indicated the importance of both competition and the environment in predicting species composition, diversity and niche overlap in ecological communities. However, conclusive demonstrations of competitive exclusion are rare.

Climate fluctuations are known to affect the distribution, behaviour and phenology of plants and animals [6]. Recent climatic changes have been reported to disrupt tight trophic interactions between consumers and resources in fish–plankton [7], insect–plant [8] and bird–insect systems [9], and climate change is one of the largest current threats to biodiversity [10]. It has recently been hypothesized that climate change may affect the coexistence of competing species [11]; however, few studies have so far incorporated the climate effect in a classical competitive framework, and those that do have dealt with plant communities [12,13]. To do so requires the analysis of long-term data on the dynamics of competing species together with corresponding climate data. We do so here for the first time, to our knowledge, using long-term data on competing bird species (tits).

It is important to differentiate between the effects that short- and long-term environmental changes may have on species coexistence. Short-term environmental variation represents fluctuations around some stationary point (e.g. the annual variation in monthly temperature around the long-term mean for that month), whereas long-term variation represents a change in position of this stationary point (e.g. an increase or decrease in the long-term average temperature for a given month).

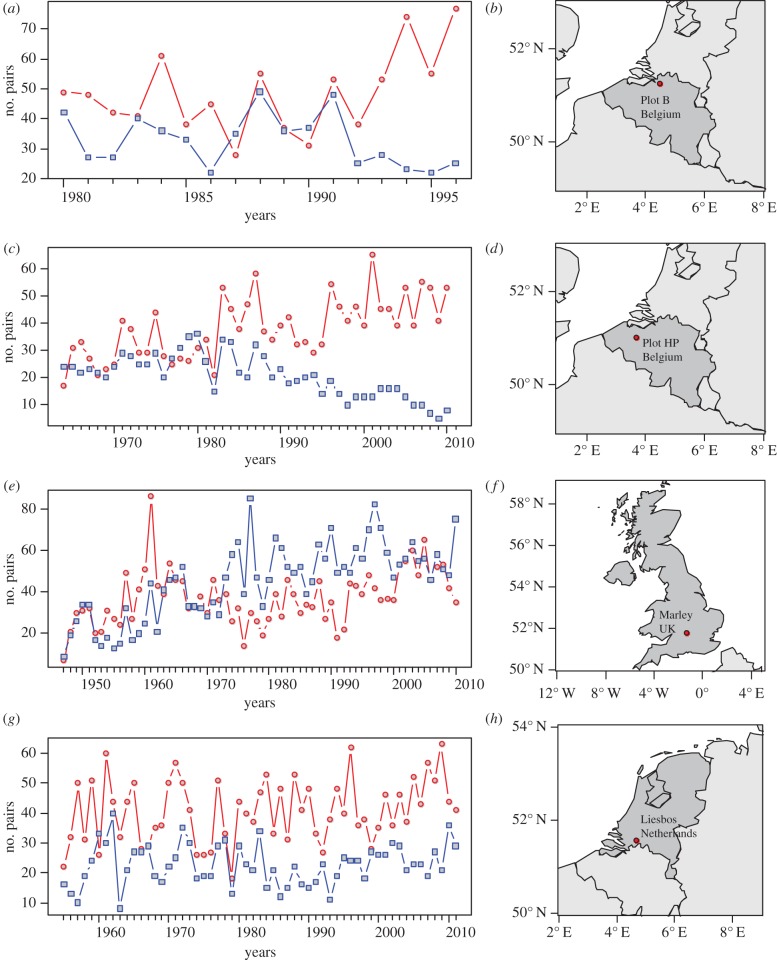
Here, we study the effect of year-to-year variation in climatic condition on the competitive interaction between two European tit species, the blue tit (Cyanistes caeruleus; BT) and the great tit (Parus major; GT). During the breeding season, GTs and BTs compete for food. Because BTs consume smaller instar of the same caterpillar species as eaten by the GT [14–16], they can pre-emptively consume available prey and hence outcompete GTs for food. Although this has an impact on GT reproductive success [17], it does not have an effect on GT breeding numbers. During winter, both GTs and BTs use cavities for night roosting. When only large-holed nest-boxes are available, GTs competitively exclude BTs from the nest-boxes, even when these are superabundant, and hence outcompete BTs. Providing small-holed nest-boxes that can be used by BTs but not by GTs results in an increase BT numbers roosting in nest-boxes [18,19] and an increase in BT breeding density, implying that interspecific competition for cavities as roosting sites during winter has an effect on BT breeding population size. We used data from four sites in western Europe (figure 1) where counts of breeding pairs of the two species have been collected for more than 15 years, and where both species were sufficiently numerous to test our hypotheses (see electronic supplementary material, table S5). Finding suitable data series for these species represents a major challenge, due to various anthropogenic habitat changes over time. For example, changes to forest structure and/or changes in the number of nest-boxes available in study plots have occurred in a number of the potential study populations across Europe. The time series we investigated represented the few available lacking such large-scale alterations, to avoid confounding results.

Figure 1.

Data and location of the available long-time series on breeding density of GTs and BTs in Europe. (a,c,e,g) Census data were collected annually for both species in all plots. Data are presented in number of breeding pairs over time (years) of both species: BTs (blue lines with square symbols) and GTs (red lines with dot symbols). (b,d,f,h) On the location maps, the dots present the location of the different study sites (electronic supplementary material, table S7). (Online version in colour.)

To assess the impact of climate change on the strength of competition between these two species, we estimate how the parameters of a competition model vary due to climate change (see Material and methods). For this, we use a discrete-time (annual reproduction) setting, assuming a Gompertz density-dependent feedback framework, where intra- and interspecific competition affects each species's population density, N_i,t (where t indicates the year). While studying fish population, Myers et al. [20,21] argued that density dependence was best approximated by the discrete-time Gompertz model (i.e. log-linear dependence on density). Such log-linear density dependence in the survival was later on demonstrated for another population [22,23]. Note that the log-transformation has the fortunate effect that the addition of a given number of individuals at low abundance will have larger effect than adding the same number of individuals at high abundance. The Gompertz model is written as

1.1

where r_i is the maximum per capita (intrinsic) growth rate for species i, K_i is the local equilibrium density in the absence of heterospecifics and α_ij represents the per capita effect of species j on the growth rate of species i. Typically, K, r and α are considered constants for a given species, location and environmental condition, respectively. However, if the environment changes, these parameters might also change. We therefore estimate how these parameters vary with the environment at any given time, employing an appropriate combination of additive and non-additive statistical models. Using Akaike's information criterion corrected for small sample size (AICc), we select among competing models that are flexible enough to include terms that show whether model parameters vary with short- and/or long-term environmental variation. Having selected the most appropriate model for each site, we assess the effect these changing parameter values have on positive equilibrium densities when necessary (stable coexistence: if and only if α_ii × α_jj is larger than α_ij × α_ji).

The aims of this paper are therefore (i) to assess whether the strength of competition between GTs and BTs is changing over time, (ii) to establish if this change, if any, is linked to any changes in climatic variables and (iii) to forecast the consequences of the change in the strength of competition for species coexistence.

2. Material and methods

The study was conducted on GTs and BTs breeding populations from four sites in western Europe (figure 1). GTs and BTs are small cavity-nesting passerines that readily accept nest-boxes if these are available in large numbers. In the semi-natural woodlands where the two species breed, nest cavities are often a limiting resource due to forest management, and nest-boxes are commonly provided by researchers, volunteer bird-ringers and the general public. In the study, boxes with a large entrance hole (approx. 32 mm) suitable for both tit species were provided in excess (more than five boxes per hectare; electronic supplementary material, table S7), so that GT breeding density was not limited by cavity availability. In Plot B, small-holed nest-boxes (entrance hole approx. 26 mm; accessible to BT but not to GT) were also present throughout the study. The presence of small-holed boxes reduces interspecific competition for roosting sites during winter and results in an increase of BT breeding density [17]. During the breeding season, boxes were checked at least once a week and the number of pairs was recorded as the number of first clutches found in nest-boxes (figure 1; electronic supplementary material, table S7). Census data were collected annually for both species in all plots. We assumed that immigration and emigration rates were approximately equal (the simplest assumption in this case) and did not have an important effect on the dynamics we observed. For one of the Belgian populations we studied (Plot HP), this has been tested. Plot HP was part of a regional study that included seven study plots over a 15-year period, during which time all nestlings were banded, and many recaptured breeding. In all study plots and for both GT and BT, the exchange of immigrants among neighbouring sites was balanced [24].

Climate data were taken from regional weather stations located near the study sites (see electronic supplementary material, table S7). Monthly temperature, spring (average for March, April and May) and winter temperature (average for December, January and February) were calculated from these. We used the winter index for the North Atlantic Oscillation (NAO) as a global index affecting all study populations (winter NAO: December, January, February [25,26]; and spring NAO: March, April, May). We also used the Beech Crop Index (BCI) from The Netherlands as an environmental variable for Plot B, Plot HP and Liesbos (BCI is a measure for the amount of beech seeds present in the winter and correlates with crop size of several other tree species fed on by tits [27]). All these indices were shown to affect GT and/or BT population dynamics in different ways at the local population scale.

In three sites intra- and interspecific competition could be detected within and between the focal species (Plot B and Plot HP in Belgium, Marley Wood in the UK). In the remaining site, however, available data did not allow for adequately fitting models that included terms for both intra- and interspecific competition for both species (Liesbos in The Netherlands).

(a). Theoretical model

Equation (1.1) can be re-parametrized as follows:

2.1

where a_i0 = r_i, a_ii = −r_i/K_i and a_ij = −r_iα_ij/K_i. That is, the ecological parameters can be expressed as statistical parameters: r_i = a_i0, K_i = −a_i0/a_ii and α_ij = a_ij/a_ii. On the log-scale, and slightly rearranged, the model becomes

2.2

To account for possible nonlinearities, we also considered a threshold model [28], after testing for additivity/non-additivity [29] (see also below):

2.3

The environmental variable E_t is used to partition the effect of position over a ‘low’ or ‘high’ environmental regime (for instance, if E interacts with N_i, (1 + a_ii) will differ from (1 + b_ii), as can a_i0 from b_i0 while a_ij will remain unchanged; a_ij = b_ij). The threshold level (θ) of covariate E that separates the two regimes was chosen by minimizing the generalized cross-validation (GCV) score among models that spanned the restricted range of E.

Such a linear (or piecewise linear) model formulation was used for our statistical modelling procedure. Coefficients (1 + a_ii) and (1 + b_ii) (the latter represented as a threshold-dependent parameter) were estimated as the full term within the parentheses.

(b). Statistical modelling

All analyses were performed using R v. 3.0.2 software [30]. We developed a model incorporating inter- and intraspecific competition and environmental variables (to limit the number of degrees of freedom, we used only one climate or environmental variable per model). We tested potential interactions between the explanatory variables using Bürmann's expansion [29]. This non-parametric method yields a test for the null hypothesis that the variables have additive effects only, as well as testing for interactions between each pair of variables. Following this, we apply a threshold non-additive formulation (as given by equation (2.3)) where the response changes according to whether the climate covariate is above or below some threshold level, θ. The threshold level (θ) is found by minimizing the GCV score over an interval defined by the 20–80 percentiles of the covariate. We then assess the significance of the threshold effect identified through the above procedure using a non-parametric permutation test (see §2c for more detail).

The most appropriate model, given the data, was selected using the Akaike's information criterion corrected for small sample size (AIC_c). The selected model was that with the lowest values of AIC_c, and factors were considered to lead to a significant change in the model when they led to ΔAIC_c ≥ 2 (electronic supplementary material, table S8). In summary, for each system and for any particular climatic or environmental covariate, we tested for non-additivity (see below), and only if the test rejected non-additivity did we proceed to fit a threshold model and test for threshold effects, so as to ensure that the non-additivity detected may be adequately described by a threshold model. The AIC selection was then used to select the final model among competing threshold models. Thus, the tests were used for the sole purposes of screening and validating which climatic or environmental covariates may be appropriate threshold variables, and only then was AIC used to rank the models.

(c). Additivity, non-additivity and threshold modelling

Two numerical and continuous covariates may interact with each other (in our case temperature and intra-specific competition). A formal test has been developed to check the additivity assumption that is implicit in linear regression modelling (Bürmann test [29]). Once a threshold effect is detected through the above procedure, we conduct a non-parametric permutation test to assess its statistical significance, with the null hypothesis that there is no change of covariate effect in different regimes defined by the level of the threshold variable. We randomly shuffle the threshold variable repeatedly, but keep the other variables unchanged and refit the model to the shuffled dataset for a number of replications (e.g. n = 500) to obtain a sample of test statistics (e.g. log-likelihood). The p-value of the permutation test is then calculated as the proportion of times when the test statistic from the shuffled dataset exceeds that from the original (unshuffled) dataset. The null hypothesis of no threshold effect is rejected if the permutation p-value is less than 0.05. A similar technique for testing threshold effects in spatial distribution change was adopted by Liu et al. [31].

Once non-additivity is detected, it is necessary to somehow model it appropriately. In such circumstances, one modelling approach is to partition one of the two interacting covariates in two levels, below and above a certain threshold. In other words, the model formulation (threshold non-additive formulation) is composed of two additive formulations where the response changes according to an environmental force (e.g. temperature) above or below this threshold level. In this procedure, there is no a priori knowledge of where the threshold may be. This is overcome by carrying out a grid search throughout the entire range of the interacting covariate and selecting the threshold that produces the best model, where the best model is that which minimizes the GCV score. In short, the GCV is a measure of the predictive squared error of the model [32]. Low values indicate the best compromise between model complexities (i.e. number of parameters) and fit to the observed data. To conduct this analysis, we used a linear version (L. C. Stige 2012, personal communication) of the univariate threshold GAM function [28] developed by K.-S.C. This approach has previously been successfully used in several studies (e.g. [32]).

(d). Dynamical properties

Point estimates for population parameters [r_i, K_i], theoretical equilibrium densities [N_i*] and eigenvalues [λ_i] for the three study plots with statistical support for interspecific competition were calculated. Eigenvalues are derived from the Jacobian matrix (B) of the linearized system evaluated around the interior equilibrium, with elements

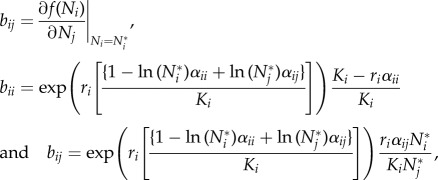where f(N_i) is given as equation (1.1) and N* = exp(A⁻¹K) gives the 2 × 1 vector containing species-specific equilibrium population densities.

3. Results

Parametrization of model (1) for the four different time series (table 1) documented the existence of both intra- and interspecific competition between GTs and BTs in three of the four sites and predicted coexistence of GTs and BTs in all study plots. Parameter estimates for r_i, K_i, α_ij as given in equation (1.1) are presented in table 1 and electronic supplementary material, table S6, for each of the four sites. The results of the analyses of the community models (for both GTs and BTs) with respect to possible effects of temperature on competitive coexistence are reported below for each study site (figure 2 and table 1; electronic supplementary material, table S1).

Table 1.

Derivation of population dynamical stability properties. Point estimates for population parameters [r_i, K_i] (in log-normal scale), equilibrium densities in number of breeding pairs [N_i*] and eigenvalues [λ_i] for the three study plots with statistical support for interspecific interactions (α_ij). All systems are feasible [all N_i* > 0] and locally stable (all |λ_i| < 1), such that populations will return to equilibrium following a small perturbation. Plot B shows a shift in relative abundances of the two species across the temperature threshold (θ), but no change in feasibility or local stability conditions. We created 1000 bootstrap samples and estimated the parameters for the corresponding model in each sample. By definition, the system is locally stable when (α_ii · α_jj > α_ij · α_ji). In our case, (α_ii · α_jj = 1) and (1 > α_ij · α_ji). Models formulations are summarized in electronic supplementary material, table S1.

location	speciesi	ri	Ki	αij	Ni*	λi	significance of 1 > αij · αji	interpretation
Plot HP	GT	3.77	5.11	0.51	43.27	0.83	p < 0.001	stable coexistence
	BT	2.24	5.84	0.84	14.22	0.05
Plot B	GT (TempSpring < θ)	5.20	4.70	0.25	47.45	−0.51	p < 0.001	stable coexistence
	BT (TempSpring < θ)	6.20	6.21	0.74	28.98	0.40
	GT (TempSpring ≥ θ)	5.20	4.70	0.25	41.49	0.75	p < 0.001	stable coexistence (tending towards unstable; see text)
	BT (TempSpring ≥ θ)	4.65	9.51	1.51	49.49	−0.34
Marley Wood	GT	2.16	4.55	0.25	35.76	0.85	p < 0.001	stable coexistence
	BT	1.59	7.05	0.90	45.64	0.45
Liesbos	GT	3.29	3.81	0.06	36.94	0.14	p < 0.001	stable coexistence
	BT	2.00	2.32	−0.21	21.59	0.14

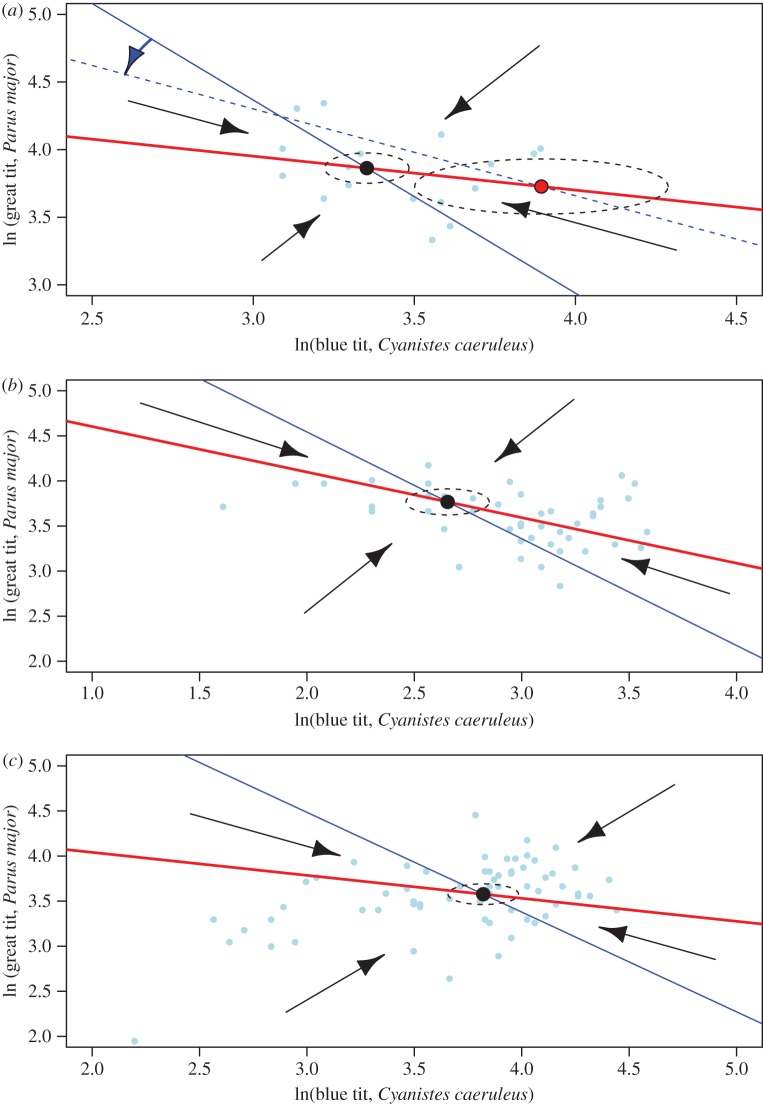
Figure 2.

Zero-growth isoclines for sympatric populations of GTs (bold red lines) and BTs (blue lines). Big black dots show estimated stable equilibrium points (ln(N*) in table 1) and small light blue dots show the census data. The dotted ellipses correspond to the standard deviation around the equilibrium calculated by bootstrap methods (electronic supplementary material, table S6). α is α_ij. In Plot B, BT population shows a threshold interaction with an environmental variable (mean temperature conditions in spring; (a)). For BT, there is a different isocline (and equilibrium state) for temperatures below (blue line) and above (blue dotted line) the threshold of mean spring temperature of 9.7°C. The blue curved arrow indicates the direction of the change of the BT isocline with an increase of temperature over the threshold and the big red dot the corresponding new equilibrium point. In Plot HP, the equilibrium is unaffected by the environmental variables modelled (b). At Marley Wood, the community equilibrium point is unaffected by the environmental variables modelled (c). (Online version in colour.)

In Plot B (Peerdsbos, Belgium), the best models selected included intra- and interspecific terms; for BTs, the model also included a threshold effect related to spring temperatures (March to May). The parameter for the interspecific term a₁₂, expressing the effect of BT numbers on GT per capita growth rate (equation (2.2); electronic supplementary material, table S2) is not significantly different from 0. This indicates a non-significant per capita interspecific effect on the growth rate of GTs (α_ij, equation (1.1)). By contrast, the term a₂₁, expressing the effect of GT numbers on BT per capita growth rate, is highly significant (equation (2.2); electronic supplementary material, table S2). Furthermore, as shown by the Bürmann and permutation tests, long-term climate change had a biologically important effect on population and community dynamics, as demonstrated by a threshold type response of model parameters associated with a change in the relevant climate variable (equation (2.3); electronic supplementary material, table S2). For BT, all parameters of equation (1.1) changed with spring temperature: in the context of this analysis, we emphasize that r₂ decreased (6.20 to 4.65), while K₂ increased (electronic supplementary material, table S6), resulting in a reduction of intra-specific competition. On the other hand, interspecific competition as expressed by α₁₂ (the effect of GT numbers on BTs) increased. When spring temperatures were warmer than the estimated threshold temperature of 9.7°C, α₁₂ = 1.51; in years in which spring temperatures were below the threshold level α₁₂ = 0.74 (table 1; electronic supplementary material, tables S1, S2 and S6). Therefore, spring temperature affected both intra- and interspecific competition for BTs in Plot B but in opposite directions. GT intrinsic growth rate (r₁) increases with increasing temperature. The net result is that colder springs (Temp_Spring,t < θ) are associated with GTs having higher equilibrium densities than BTs (N*_GT > N*_BT), while this relative abundance ranking is switched during warmer springs (Temp_Spring,t ≥ θ; N*_BT > N*_GT) (table 1). The zero-growth isoclines are shown in figure 2a.

In Plot HP (Ghent, Belgium), the best models selected by AICc include both intraspecific (a_ii) and interspecific (a_ij) interaction terms for both species. Both estimates for the interspecific terms a₁₂ and a₂₁ (equation (2.2)) are significantly different from 0 (electronic supplementary material, table S3). While March temperature was found to be important in driving population fluctuations of both GTs and BTs, there were no associated temporal thresholds in this climate variable, with coexistence (and parameter values) maintained across the observed range of climate fluctuations all else equal. The resulting zero-growth isoclines are shown in figure 2b, with parameter estimates and equilibrium conditions outlined in table 1 and electronic supplementary material, table S3.

In Marley Wood (UK), the best model includes both intra- and interspecific terms for GTs (electronic supplementary material, tables S4 and S8). However, another almost equally good model includes only the intraspecific term (electronic supplementary material, table S8). A similar result is found for BTs, where the best model includes both intra- and interspecific terms (electronic supplementary material, tables S4 and S8) with an equivalent model including only the intraspecific term (electronic supplementary material, table S8). The parameters for the interspecific terms a₁₂ and a₂₁ (equation (2.2) are not significantly different from 0 (electronic supplementary material, table S4). Both tit species were affected by temperature (May and June for GT and BT, respectively). There was no threshold effect of climate fluctuations on these populations. The resulting zero-growth isoclines are shown in figure 2c with parameter estimates and equilibrium conditions outlined in table 1 and electronic supplementary material, table S4.

In Liesbos (The Netherlands), the best model includes only the intraspecific terms for GTs (electronic supplementary material, table S1). The second best includes both interspecific and intra-specific terms, and is presented in electronic supplementary material, table S5. The parameter for the interspecific term a₁₂ is not significantly different from 0 (equation (2.2); electronic supplementary material, table S5). For BTs, the best model includes both intraspecific and interspecific terms (electronic supplementary material, tables S5 and S8). However, competing models include either only the intra- or the interspecific term (electronic supplementary material, table S8). The parameter for the interspecific term a₂₁ is not significantly different from 0 (and positive; see electronic supplementary material, table S5), suggesting there is no evidence for competition between these species at this site (therefore zero-growth isoclines are not shown). Both species were affected by temperature (May for GT and April for BT). GT numbers were also affected by the BCI, but no threshold effect of climate fluctuations on these populations was detected (table 1; electronic supplementary material, table S5).

All species pairs were found to be at a locally stable equilibrium (table 1). Under observed conditions, population growth rates were close to 1. Recent climate change (warmer springs) has not qualitatively changed these patterns, but has altered the relative abundances (equilibrium densities) of BTs and GTs in one area.

4. Discussion

Using the best available long-term population time series coupled with environmental covariates, we have demonstrated local differences in the responses of two sympatric competitors to short- and long-term climate change. While there is considerable spatio-temporal heterogeneity in our data—both within patch local conditions and variation in temperature across time—short-term climate fluctuations (temperatures during spring) were found to drive population fluctuations in all four study sites, whereas competition between BTs and GTs was detected in three of the four sites. In Plot B (Peerdsbos, Belgium), long-term climate fluctuations also modified density-independent and density-dependent population processes to affect the long-term equilibrium behaviour of the system. The nonlinear effect of long-term changes in spring temperature interacted with population processes to swap the relative abundances of GTs and BTs in Plot B, Belgium: GTs have higher abundance in cooler springs, while BTs are predicted to be more abundant in warmer springs. These changes in mean density, if maintained, may result in trophic cascades [33] or, in extreme cases, extinction cascades [34], leading to further restructuring of the local foodweb. The distribution and (a)symmetry of pairwise competition values have strong effects on patterns of species loss in competitive communities [35,36] and food webs [37]; thus, any climate-induced shifts in competition, as observed here, can be expected to filter through the whole ecosystem, driving direct and indirect changes across multiple trophic levels. The equilibrium densities are system attractors, with short-term fluctuations (driven by, for example, annual temperature variation) around these points. The threshold effect identified in Plot B leads to a change in the local equilibrium point when spring temperature is above the threshold temperature in any year. However, if the temperature drops below the threshold in subsequent years, the equilibrium point will also change correspondingly (electronic supplementary material, figure S2). The populations tracking these shifting equilibria may struggle to match them in the short-term, through under- or over-compensatory dynamics, until longer-term changes in conditions settle down and populations fluctuate around a new, more persistent equilibrium point (e.g. [38–40] for further illustration and discussion of this point).

Our results generate two important questions. (i) Why do we observe an effect of spring temperatures on community dynamics in only one of four study plots? (ii) What mechanism(s) can cause this change?

To answer the first question, while we cannot provide a specific mechanism, it is useful to underline a number of differences between Plot B and the other three plots. Nest-boxes were provided in excess in all sites (electronic supplementary material, table S7) with a range of 5.3 (Liesbos) to 14.4 (Plot B; 9.6 large-holed and 4.8 small-holed) nest-boxes per hectare. Plot B has the highest density (availability) of nest-boxes, which might suggest the lowest levels of intra- and interspecific competition for this resource. This aspect is not necessarily reflected in our parameter estimates: Plot B has neither the highest K_i estimates nor the lowest α_ij estimates in the sites we considered. However, Plot B was part of a long-term experiment to test for the effects of differences in intra- and interspecific competition between GTs and BTs in Antwerp [17]. The experimental treatment in Plot B provided a surplus of large-holed nest-boxes (diameter 32 mm; used by both GTs and BTs) and a surplus of small-holed nest-boxes (diameter 26 mm; used by BTs only). In the other three study sites, only large-holed nest-boxes were available. The presence of small-holed boxes results in a BT density that is 1.5–2 times higher than in their absence [18,41]. Furthermore, in plots with small-holed nest-boxes and increased BT density (as in Plot B), BT nestling and adult female body mass (and hence probability of survival) is lower than in plots without small-holed nest-boxes and low BT density [17]. Experimental manipulations indicate that values for r increased when small-holed boxes were present [17]. This is confirmed in our analysis with r_BT values calculated for Plot B of 6.20 and 4.65 being much larger than in Plot HP (2.24), Marley Wood (1.59) and Liesbos (2.00), where only large-holed nest-boxes were present (table 1). Finally, local recruitment rates and dispersal are also impacted by the presence of small-holed nest-boxes [17]. All these differences between Plot B and the other three plots will probably translate into differences in how changing spring temperatures impact upon the interactions between GTs and BTs. In their comparison between 24 long-term studies of GTs and BTs across Europe, Visser et al. [42] found that the most rapid change in lay date of GTs and BTs was in Plot B. Matthysen et al. [43] showed that with increasing temperatures GTs and BTs not only advanced lay date but also strongly reduced the proportion of breeding pairs that initiate second clutches, effects that again can impact GTs and BTs in different ways.

Temperature-dependent rates of caterpillar growth represent one possible mechanism involved in the observed effect of spring temperature on the interaction between GTs and BTs in Plot B. During warm springs, the caterpillar food peak advances, tracked in parallel by both species [42,43]. This in itself should not induce a change in competition, but in warm springs the caterpillar food peak also becomes narrower [44]. Several studies have shown differential use of prey sizes and prey categories by this species pair. In general, BTs eat smaller prey than GTs, and if the time period during which BTs have a competitive advantage (because younger instar are smaller) is shortened, this would intensify competition [14,15].

We used data on the number of each species observed in nest-boxes, raising the question of the significance of our result for the overall population (breeding in cavities and in nest-boxes). In all areas we studied, nest-boxes were present in surplus. GTs and BTs used natural cavities exceptionally where breeding success is generally lower than in nest-boxes [45]. As nest sites are typically a limiting factor for population growth in managed forests over most of Europe [45,46], we speculate that competition for nest sites in areas without nest-boxes is likely to have a similar effect.

BTs and GTs represent a species pair that has received considerable ecological interest over the years. Surprisingly few field studies that have tracked these species in forest habitats across Europe have been able to maintain a relatively constant study site, with changes to, for instance, forest structure and/or the number of nest-boxes over time restricting the length and number of population time series that are amenable to long-term investigation. Analysing those long-term data that are available and relevant, we have shown for the first time that climate change can affect the outcome of competitive interactions between coexisting species in the field. Specifically, we have provided an example where the relative abundances of each species are expected to change as a consequence of long-term climate change. It follows that climate change might have profound community effects resulting from changing competitive relationships between competing species [33–36,47,48]. Previous work on population dynamics, species interactions and environmental variation has tended to focus on the assumptions that the environment may fluctuate around some mean value and affect maximum population growth rate additively (but see [3,12,13,38,49]). Here, we have extended this view by demonstrating that changing climate can indeed change equilibrium conditions, moving the system to a new state where a previously less abundant species becomes relatively more abundant (BT). Such variation of competitive relationships may result in changes in relative fitness for the competing species (e.g. nestling survival) across environments as, for instance, demonstrated for flycatchers [50]. Our results highlight the need for future research—both empirical and theoretical—that considers how both short- and long-term environmental variation impact upon the form and outcome of species interactions.