Social evolution in the shadow of asymmetrical relatedness

Abstract

The persistence of altruism and spite remains an enduring problem of social evolution. It is well known that selection for these actions depends on the structure of the population—that is, on actors' genetic relationships to recipients and to the ‘neighbourhood’ upon which the effects of their actions redound. Less appreciated, however, is that population structure can cause genetic asymmetries between partners whereby the relatedness (defined relative to the neighbourhood) of an individual i to a partner j will differ from the relatedness of j to i. Here, we introduce a widespread mechanism of kin recognition to a model of dispersal in subdivided populations. In so doing, we uncover three remarkable consequences of asymmetrical relatedness. First, altruism directed at phenotypically similar partners evolves more easily among migrant than native actors. Second, spite directed at dissimilar partners evolves more easily among native than migrant actors. Third, unlike migrants, natives can evolve to pay costs that far outstrip those they spitefully impose on others. We find that the frequency of natives relative to migrants amplifies the asymmetries between them. Taken together, our results reveal differentiated patterns of ‘phenocentrism’ that readily arise from asymmetries of relatedness.

1. Introduction

For 50 years, inclusive fitness theory [1,2] has proved invaluable to our understanding of the evolution of cooperation and conflict. In its simplest form, it states that a social action will evolve when R_ijB − C > 0, where C is the lifetime fitness cost of the action to an actor i, B is the lifetime fitness benefit to a recipient j and R_ij is the genetic relatedness of i to j. This principle, known as Hamilton's rule, provides a powerful account of the evolution of altruism (C > 0, B > 0) and spite (C > 0, B < 0)—namely, that actors can compensate for their costs by helping recipients who may bear identical copies of causal alleles and by harming those who may not.

A resurgence of interest in the effects of population structure has, however, refined our understanding of Hamilton's rule. Interactions not only have consequences for actors and recipients, but also for the neighbourhood, which consists of those individuals whose fitness is affected by any altered level of local competition resulting from an interaction [3–10]. In many simple population structures, we can capture this with Hamilton's rule by defining 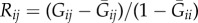, where G_ij is the coefficient of consanguinity (CC) between i and j, an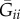d and 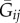are, respectively, the average CCs between i and i's neighbourhood and between i and j's neighbourhood [8]. Formalized in this way, relatedness accounts for both the primary (actor–recipient) and secondary (neighbourhood) effects of an interaction. Moreover, it supplies an intuitive interpretation of ‘positive’ and ‘negative’ relatedness: R_ij > 0 when i is more likely to share alleles with j than with j's neighbourhood, and R_ij < 0 when i is more likely to share alleles with j's neighbourhood than with j.

So specified, relatedness changes both with the consanguinity between actor and recipient and with the consanguinity between actor and neighbourhood. Significantly, such relatedness will tend to be asymmetrical (R_ij ≠ R_ji) [11,12] whenever partners have different consanguinities to the other's neighbourhood 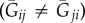, despite having the same consanguinity to one another (G_ij = G_ji). Thus, when partners take both the roles of actor and recipient, i may value j less than j may value i for reasons that are not intrinsic to either party. Limited dispersal will cause such an asymmetry, because the genotypes of native-born individuals will be better represented in their neighbourhood than those of recent immigrants. We illustrate this phenomenon in figure 1, which considers interactions between native and migrant partners in two different neighbourhoods.

Figure 1.

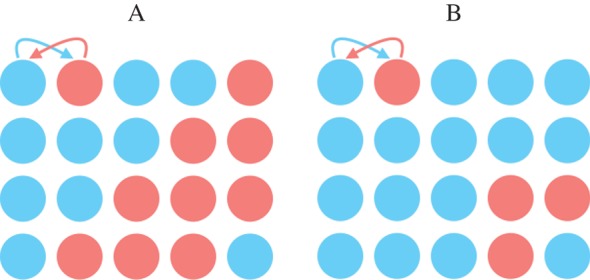
Symmetrical and asymmetrical relatedness in the model. Consider a focal pair of partners living on two different demes, A and B. In both demes, consanguinity is known with certainty and the partners act simultaneously on each other, as indicated by the arrows. We also assume that the secondary effects of the primary interaction evenly affect the entire deme. The sole difference between demes A and B is the composition of the neighbourhood. Deme A consists of an even mixture of native (blue circles) and migrant offspring (red circles), whereas deme B consists of four times as many native as migrant offspring, and it is this difference that causes asymmetries of relatedness between the partners. In deme A, relatedness between the native and migrant partners is symmetrical. That is, relatedness is the same from the native actor/migrant recipient perspective as from the migrant actor/native recipient perspective. In deme B, however, relatedness between the native and migrant is asymmetrical: relatedness is much lower from the native actor/migrant recipient perspective than it is from the migrant actor/native recipient perspective.

To allocate altruistic and spiteful behaviour, many species rely on mechanisms of kin recognition [11,13–15]. These mechanisms exploit natural covariation between genetic identity and cues—both contextual and phenotypic—to regulate an actor's behaviour. For instance, juvenile Belding's ground squirrels (Spermophilus beldingi) tend to emerge from their burrows 25 days from birth, and so can accidentally find their way into the burrows of non-relatives. Consequently, dams will foster about 75% of unrelated juveniles experimentally introduced into their burrows within 25 days of having produced a litter, but will reject nearly 80% of unrelated juveniles introduced outside of this temporal window [16]. Moreover, female yearlings appear to distinguish full- from half-sisters, despite having been reared together as littermates [16].

The latter finding suggests that, in addition to other cues, female Belding's ground squirrels use phenotype matching, a mechanism of kin recognition common to a wide range of taxa (including mammals, birds, amphibians, insects and possibly microbes [11,13–15]) that generates estimates of relatedness by comparing actor, recipient and neighbourhood phenotypes that are correlated with genotypes [11,17]. Importantly, the genotype–phenotype relationship need not be causal, but simply correlational. Hence, individuals can acquire phenotypes through the local environment (e.g. a nest-specific song), and they can learn the phenotypes of others. In phenotype matching, similar partners (judged relative to the neighbourhood phenotype) are perceived as positively related and dissimilar ones as negatively related [11,17,18]. Consequently, asymmetrical perceptions of relatedness should occur when one phenotype of a pair is better represented in the neighbourhood than is the other phenotype [11]. Hence, individuals bearing more common phenotypes should behave differently from individuals bearing rare phenotypes when interacting with similar and dissimilar conspecifics.

The relevance of the neighbourhood is often overlooked, and we believe that it can have profound consequences for the direction in which social evolution proceeds. Our objective here, then, is to assess the effects of asymmetrical relatedness—caused by variation among actors in consanguinity to the neighbourhood—on the evolution of social behaviour. We study this in a subdivided population with partial migration that generates genetic and phenotypic variation. Actors can then use this variation to decide how much to help or harm their partners. Our analysis employs a simple inclusive fitness model.

2. Material and methods

(a). Population structure

We work with an infinite island model with demes of K randomly mixing haploid, asexual breeders. We use a Wright–Fisher model [19,20] with non-overlapping generations. In each generation, the breeders produce a large number of offspring and then die. The offspring interact in random pairs on the natal deme, after which they disperse to a random deme at a small rate m. Migration introduces genetic and, as we show below, phenotypic variance into the neighbourhood: most demes will be uniform but a small number will have individuals with locally rare genotypes and phenotypes. We suppose that migrating offspring from a single breeder travel in a ‘bud’ so that in the rare cases when a bud succeeds in finding a distant deme, a significant number of clonal immigrants join the deme offspring population. We let q be the average size of a successful bud, measured as a proportion of the total deme offspring. Thus, following a budding event, q is the probability that an immigrant will occupy each breeding spot.

Following migration, the offspring on each deme (native and recent immigrant) compete for the K breeding vacancies, based on their fitness as determined by the interactions. We label both parental and offspring generations by the dispersal status of the parent (native or migrant) and distinguish them by their class: breeder (parent) and actor (offspring). Thus, a ‘migrant actor’ is the offspring of a migrant breeder.

(b). Social Interaction

At the interaction stage, each offspring gives a fitness bonus B to its partner at a cost C, where B and C are constrained to lie on a trade-off curve (figure 2a). The choice of the (B, C) pair for each actor is based on its estimate of relatedness to its partner. To determine the evolutionary stability of a (B, C) pair, we calculate the inclusive fitness effect W_IF of a mutant actor who plays a variant strategy (B + b, C + c) for small increments b and c (see the electronic supplementary material). If this is non-zero, the (B, C) pair cannot be convergence stable [21] and the population can be invaded. Using Hamilton's rule, the inclusive fitness effect of an interaction will have the form

2.1

The numerator of the last expression displays the effect as the sum of the primary (the first term) and the secondary (the second term) inclusive fitness effects of the interaction. Here G is the CC of the actor to its partner (chosen at random from the offspring on the deme) and 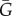is the CC of the actor to those offspring whose probability of winning a breeding spot will be affected downstream by the primary fitness effects (i.e. the secondary recipients). In this case, these are the offspring, native and migrant, who will be competing for the next-generation breeding spots on that deme.

Figure 2.

Assumptions of the model. (a) We assume that the actual benefit–cost ratio shows diminishing returns and so is constrained to a trade-off curve like the one depicted (C = B²). The actual benefit–cost ratio is the slope B/C of the (blue) line drawn from the origin, whereas the marginal benefit–cost ratio is the slope b/c of the tangent (red) line. (b) For the signalling system, we assume that native signals (blue curve) are distributed with mean 0 and variance σ² = 1 and migrant signals (red curve) are distributed with mean μ = 2 and variance σ² = 1.

(c). Phenotype matching

While we are assuming that interactions are at random, we will also assume that actors have information about their relatedness to their partners and are able to use that to condition their behaviour. In our model, this is gained through phenotype matching. To build a phenotype matching mechanism into our model, we suppose that an offspring produces a signal (such as a contact call [22]) learned from its parent as a function of the parent's deme of origin. Since migration is rare, we can assume that native offspring on a deme are clonal, and of course any immigrant bud will also be clonal. Thus, a deme with a migrant bud has two kinds of signals (native and migrant) and we assume that the immigrants keep the migrant signal for only one generation. That is, an immigrant who becomes a breeder has migrant offspring, but any of these who become breeders in the next generation adopt the native signal. We take the signals to be normally distributed with variance σ² and means of 0 and μ for the native and migrant signals, respectively (figure 2b). We also assume that native and migrant offspring know their own identity (as native or migrant) and, in addition, that natives know whether or not there is a migrant bud on the deme. However, the identity of a partner can only be estimated from the partner's signal. Although these assumptions do not necessarily reflect the mechanistic details of phenotype matching in any particular species, they do provide a simple way to rigorously model the essential parts of a phenotype matching system: a reliable correlation between consanguinity and signal value, information about own phenotype, information about partner phenotype and information about the distribution of phenotypes in the neighbourhood [11,17]. In any case, our model is biologically plausible because this kind of information is readily available and the mechanism for its use is cognitively simple.

On demes containing an immigrant bud, with proportion q migrant and 1 – q native offspring, the inclusive fitness effects (equation (2.1)) for a native and migrant actor are

2.2

and

2.3

Here G_N(s) and G_M(s) are the CCs of a native and migrant actor to a partner bearing signal s, and since migration is rare and can be neglected for this purpose, the secondary effect CCs and 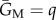are simply the proportion of the deme offspring that are of the actor's genotype. We are interested in the sign of the inclusive fitness effect, and so equations (2.2) and (2.3) work only with the numerator of equation (2.1), as is common practice.

The CCs G_I(s) are calculated from the probability densities P_N(s) and P_M(s) that an offspring bearing a signal s is a native or a migrant, respectively. Since migration is rare, we can assume that in a deme that has just received a migrant bud, the native and immigrant populations are both clonal and

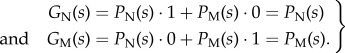2.4

We obtain the P_I(s) from Bayes' Theorem

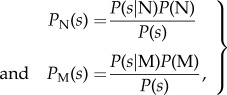2.5

where P(s|N) and P(s|M) are the probabilities that a native and a migrant bear a signal s, and P(N) = 1 − q and P(M) = q are the frequencies of native and migrant offspring on the deme. Assuming, as seems reasonable, that P(s|N) and P(s|M) are proportional to D_N(s) and D_M(s), the density functions for native and migrant signals, we have

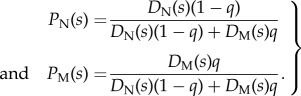2.6

3. Results

Our purpose here is to compare the behaviour of native and migrant offspring when interacting with partners of the same perceived CC. That is, where on the B–C graph (figure 2a) will a native and a migrant play when interacting with a partner of CC G_N(s) = G_M(s) = G? The answer, from equations (2.2) and (2.3), is that a native actor will play where the slope of the B–C graph is

3.1

and a migrant actor will play where the slope is

3.2

As expected, equations (3.1) and (3.2) show that the equilibrium (B, C) pair for a native differs from that for a migrant when interacting with a partner of the same CC. Note that when the denominator of either of these expressions is zero (G = 1 – q or G = q) the strategy will sit on the vertex of the curve (figure 2a) at the transition point between altruism and spite. In the standard case of no budding, there will only be a single migrant breeder and we have q = 1/K.

A significant special case arises when signals have vanishingly small variance so that the actor knows the identity of its partner. Putting the G_IJ in place of the G_I(s) in equations (2.2) and (2.3) gives us the inclusive fitness effects W_NN = q(b − c), W_NM = − (1 − q)b − qc, W_MN = − qb − (1 − q)c and W_MM = (1 − q)(b − c), and these provide the evolutionarily stable strategy (ESS) conditions for the marginal effects. For the case of no budding (q = 1/K), these conditions are presented in table 1 alongside the payoffs when constrained to the trade-off curve C = B². These results show, not surprisingly, that interactions between like partners (native/native and migrant/migrant interactions) are altruistic, while those between unlike partners (native/migrant and migrant/native interactions) are spiteful. In the latter case, however, they display two striking asymmetries. First, the ESS conditions for native actors differ from the ESS conditions for migrant actors. Indeed, only when the neighbourhood is restricted to the actor and recipient alone (K = 2) do migrant and native behaviours become symmetrical, as expected. Second, and by corollary, native actors can evolve to absorb costs that exceed those they spitefully impose on migrant partners, whereas migrant actors must inflict larger costs on native partners than they are themselves willing to bear. In other words, natives can evolve spite more easily than migrants, and can tolerate ‘extreme’ costs in the process. In the electronic supplementary material, we show that these asymmetries hold over a range of benefit–cost trade-off functions.

Table 1.

Evolutionarily stable strategy (ESS) conditions for social interactions on a deme of size K when partner identity is known and there is no budding (q = 1/K). The ‘marginal ESS' portion at the left presents the ESS conditions for the marginal effects and the ‘actual ESS' portion at the right presents the corresponding payoffs for the trade-off curve C = B² (see the electronic supplementary material). Although interactions between individuals of the same type (open cells) share the same ESS conditions, those between individuals of different types (shaded cells) do not.

More generally, evaluation of equations (3.1) and (3.2) establishes three significant patterns when native and migrant actors are interacting with partners of the same CC: (i) migrants are more altruistic than natives, (ii) natives are more spiteful than migrants and (iii) natives are often able to absorb costs that surpass the harm inflicted on recipients, whereas migrants are not. These patterns are illustrated in figure 3 for the trade-off curve C = B². This figure also displays the effect of K on the C/B line. It shows that the asymmetries between native and migrant actors grow with deme size, which, of course, is already predicted in the ‘actual ESS’ column of table 1. Moreover, deme size has a larger effect on native than on migrant behaviour. This is because, with increasing deme size, the range of evolutionarily stable costs borne by a native actor increases towards infinity while the range of evolutionarily stable costs borne by a migrant actor decreases towards zero.

Figure 3.

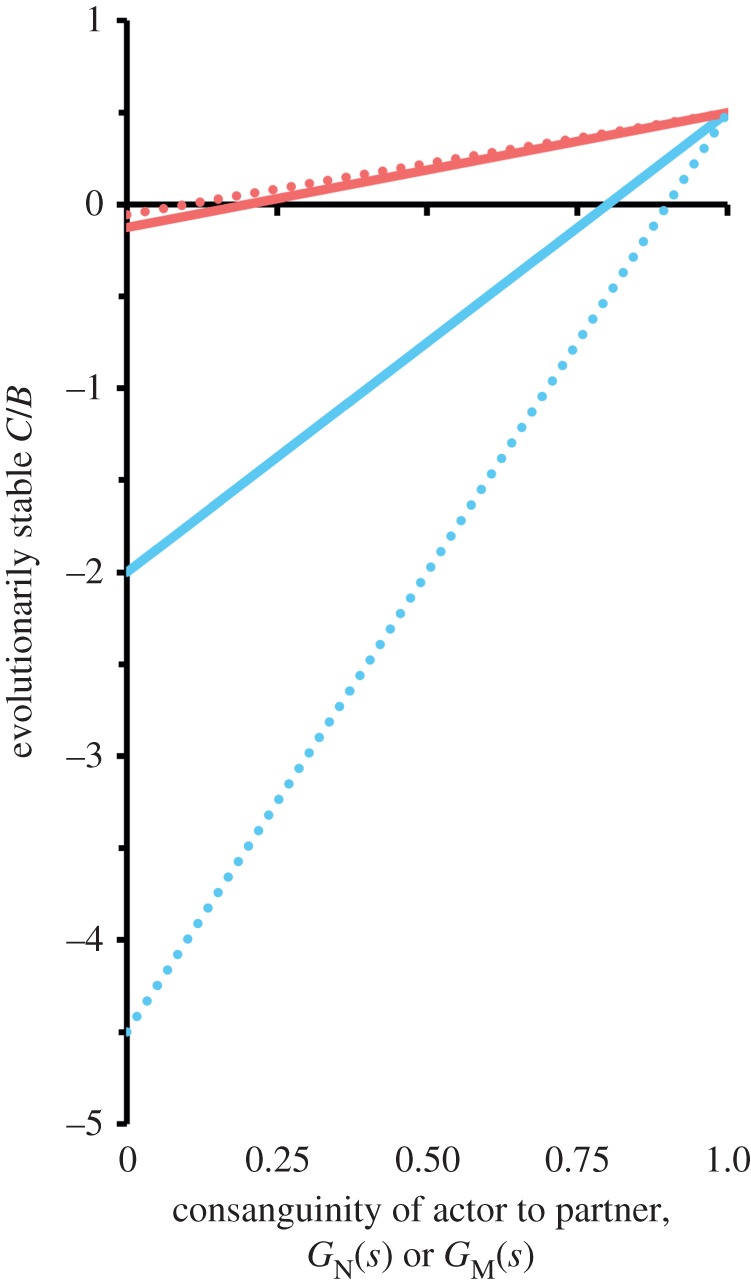
Evolutionarily stable cost/benefit (C/B) ratios change with consanguinity and deme size K. Evolutionarily stable C/B ratios for the signal model with no budding (q = 1/K) are plotted against consanguinity G between interactants for native (blue) and migrant (red) actors for the trade-off curve C = B². The C/B ratios increase with G for both types of actor. However, these ratios differ between native and migrant actors when interacting with partners of the same CC (i.e. G_N(s_N) = G_M(s_M)). Finally, deme size (solid lines, K = 5; dashed lines, K = 10) has a greater effect on native than on migrant behaviour.

4. Discussion

Our work extends prior analysis of the effects of dispersal on social evolution in subdivided populations [4–6,9,10,23] by demonstrating that differing consanguinities to the neighbourhood cause asymmetries of relatedness between partners that are subsequently realized by kin recognition systems. Put simply, we found that individuals bearing locally common phenotypes (natives) were less helpful to similar partners and more harmful to dissimilar ones than were individuals bearing locally rare phenotypes (migrants).

Our purpose was to show how social evolution can depend on an actor's relationships to both its partner and to the neighbourhood, which may be as broad as an entire population or as narrow as a nest. To the extent that the neighbourhood extends beyond the interacting pair, is genetically structured, and information about this structure is available and used, we can anticipate asymmetries in the behaviour of locally common and rare phenotypes. Taken together, our findings reveal alternative patterns of behaviour that can be described, by the way of analogy to human ethnocentrism, as phenocentric: cooperation evolves between phenotypically similar partners and conflict evolves between dissimilar ones. Holding ecological conditions constant, our model generates three clear predictions. First, actors bearing rare phenotypes will tend to be benevolent (and more so) towards a wider range of partner phenotypes than will actors bearing common phenotypes. Second, actors bearing common phenotypes will tend to be maleficent (and a great deal more so) towards a wider range of partners than will actors bearing rare phenotypes. Third, an increase in the proportion of individuals who bear common phenotypes will magnify these differences.

In the model, we assumed that the native knows there is a migrant on the patch. This comes from the assumption that among the large number of offspring, individuals have many opportunities to observe signals in the neighbourhood. If such opportunities are limited, a native actor's assessment of the probability that there is a migrant on the patch will be based on sampling a reduced number of signals and this will affect both the actor's estimate of its consanguinity to its partner as well as its estimate of its average consanguinity to the neighbourhood, and that enters into the inclusive fitness calculation through the secondary effects of the interaction. The overall effect of reducing this information by a factor of, say, 2 or 5 is to increase the actor's estimate of its consanguinity to both its partner and its neighbourhood, but in such a way that its behaviour—its tendency to be altruistic or spiteful—sees little change.

Our findings depart in interesting ways from previous models that considered only the actor–recipient relationship or that assume actors have at best limited information about their partners or the neighbourhood. For example, El Mouden & Gardner [10] also produced an inclusive fitness model of dispersal in a subdivided population; however, actors were endowed with the knowledge that they had (or had not) emigrated but could not infer the genetic identities of their partners beyond chance expectation. Hence, native actors would rightly assume that they were more closely related to their partners than would migrant actors. The authors found that altruism evolves among natives and selfishness (but not spite) evolves among migrants, a pattern that is nearly opposite to our own. The key differences between the two models revolve largely, if not exclusively, around the kinds of information that individuals use: actors in our model could discriminate their partners more precisely than could actors in the El Mouden and Gardner model. Consequently, we expect that examples of behavioural distinctions between common and rare phenotypes in the real world will better conform to our model than to another only to the extent that individuals fully use phenotypic information of both partner and neighbourhood to estimate relatedness.

This supposition may go some way to explaining why spite evolves so easily in our model when performed by natives—far more so than does altruism when carried out by either native or migrant—than it seems to in nature. Spite may in fact be rare, but this may only be because the circumstances in which we might observe it are specific. For instance, the extreme spite of our model requires (i) the use of a phenotype matching mechanism that is conditioned on local neighbourhood phenotypes, (ii) a phenotypically common actor and (iii) a phenotypically rare recipient. Interestingly, some species of bacteria that discriminate positive from negative relatives do tend to behave more spitefully than altruistically [15]. It is hence possible that relevant cases of spite have been overlooked.

Consequently, the best hope of testing our model is in species that show genetic structure to their social networks and that use phenotype matching mechanisms that rely on both partner and neighbourhood phenotypes. For example, there are species, such as the great reed warbler (Acrocephalus arundinaceus), the Columbian ground squirrel (Spermophilus columbianus) and the weaver ant (Oecophylla smaragdina), that appear to integrate neighbourhood phenotypes into at least some evaluations of relatedness [17]. But the clearest evidence in support of our predictions comes from the Argentine ant (Linepithema humile). When placed together in an arena, individuals drawn from genetically homogeneous colonies are more aggressive towards conspecifics drawn from heterogeneous colonies than the converse, often with fatal results [24]. Moreover, increasing experience with members of hostile colonies attenuates this asymmetry [25]. Humans, too, parallel our results—particularly when different ethnic groups come into contact. Ethnic majority groups manifest greater prejudice against minorities [26]. Indeed, individuals of the majority ethnic group are most often the perpetrators and individuals of minority groups the victims of ethnically motivated hate crimes (see the electronic supplementary material). Conversely, minority groups show more favouritism towards members of their own groups than do majority groups [27]. Furthermore, ethnic minorities are more likely to co-reside with individuals outside of the nuclear family in cooperative relationships, even after researchers have accounted for demographic and acculturation effects [28,29]. Finally, increasing contact with ethnic out-groups reduces prejudice against them [30] and changes ethnic categorization [31]. Despite the evolutionary novelty of encounters between genetically distant ethnic groups, these arrangements may nevertheless be attributable, at least in part, to shifting perceptions of relatedness produced by a phenotype matching mechanism. Whether this is the case remains to be seen.

Funding statement

We acknowledge funding from the Natural Sciences and Engineering Research Council of Canada to P.D.T. and the Social Sciences and Humanities Research Council of Canada to D.B.K.

Authors' contributions

The authors contributed equally to the work. D.B.K. conceived of the analysis, D.B.K. and P.D.T. designed the model, P.D.T. analysed the model, and both authors wrote and approved the paper.

Competing interests

We have no competing interests.