Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2015 May 6;12(106):20141365. doi: 10.1098/rsif.2014.1365

A novel collagen gel-based measurement technique for quantitation of cell contraction force

Tianrong Jin 1, Li Li 2, Richard C M Siow 2,†, Kuo-Kang Liu 1,†,✉
PMCID: PMC4424670  PMID: 25977960

Abstract

Cell contraction force plays an important role in wound healing, inflammation, angiogenesis and metastasis. This study describes a novel method to quantify single cell contraction force in vitro using human aortic adventitial fibroblasts embedded in a collagen gel. The technique is based on a depth sensing nano-indentation tester to measure the thickness and elasticity of collagen gels containing stimulated fibroblasts and a microscopy imaging system to estimate the gel area. In parallel, a simple theoretical model has been developed to calculate cell contraction force based on the measured parameters. Histamine (100 µM) was used to stimulate fibroblast contraction while the myosin light chain kinase inhibitor ML-7 (25 µM) was used to inhibit cell contraction. The collagen matrix used in the model provides a physiological environment for fibroblast contraction studies. Measurement of changes in collagen gel elasticity and thickness arising from histamine treatments provides a novel convenient technique to measure cell contraction force within a collagen matrix. This study demonstrates that histamine can elicit a significant increase in contraction force of fibroblasts embedded in collagen, while the Young's modulus of the gel decreases due to the gel degradation.

Keywords: collagen gel, human aortic adventitial fibroblast, histamine, cell contraction force, nano-indentation, elasticity

1. Introduction

The collagen contraction assay was firstly reported by Bell et al. [1] and has been described as fibroblast-populated collagen lattice (FPCL). The mechanism for fibroblast contraction is mediated by the control of myosin light chain (MLC) phosphorylation status through the action of MLC kinase (MLCK) [2]. As reviewed by Dallon & Ehrlich [3], raised intracellular calcium levels leads to calmodulin-dependent MLCK activation, which results in MLC phosphorylation and actin–myosin crossbridge formation and filament sliding.

Human aortic adventitial fibroblasts (HAoAF) are resident in the adventitia of the aorta and they have been employed in experimental models of arterial remodelling and restenosis [4]. Histamine is an agonist that elicits increases in intracellular calcium and is released by basophils and mast cells during inflammatory responses. It acts on cells via a family of G protein-coupled histamine receptors, histamine receptor H1–H4. Several studies have shown that human fibroblasts express H1 receptor and can be activated via histamine binding, resulting in phospholipase C activation and production of inositol triphosphates (IP3) and diaglycerol (DAG) [5,6]. The increase of IP3 causes calcium release from the internal stores and consequently triggers fibroblast contraction via activation of MLCK [7].

Several approaches have been developed to measure cell contraction forces in vitro; among these, collagen gel contraction assay (CGCA) and traction force microscopy (TFM) are the most common techniques. For the both methods, cell contraction forces are measured indirectly based on measurement of deformation of the matrix surrounding the cells, such as a cell-embedded collagen gel or cell-seeded polymer substrate. However, the CGCA technique is used for the measurement of forces in populations of cells, while TFM is more suited for the measurement of forces in single cells.

When CGCA is used for assessing contraction forces, cells are embedded within the collagen matrix, which provides cells with a physiological environment. Collagen is a key component of the extracellular matrix that facilitates cell migration and contraction [8]. Cell-embedded collagen gels are easily constructed and the measurement of their contraction is straightforward. Conventional techniques used to measure collagen gel contraction rely on imaging only the gel area from a top view. The estimation of contraction is often expressed by the area changes of the gels between the beginning and end of the treatment or cell contraction period [9,10]. To improve the measurement of cell contraction kinetics for time-dependent changes, time-lapse-video-based imaging techniques have been developed to record changes in gel areas continuously while the cells contract [11]. Although the versatility of the CGCA method facilitates general use, it does not provide quantification of cellular contraction forces, since the mechanical properties of the collagen matrix will dictate the measurement accuracy of the cellular contraction forces. The elasticity of the disc-shaped collagen gel can be influenced by the cell treatments and the same amount of gel radius shrinkage may result from very different cellular contraction forces. Moreover, in the normal physiological environment, cells do not merely contract in a two-dimensional manner, therefore, measuring the radius of the gel disc only from the top view will not provide an accurate assessment of the magnitude of cellular contraction.

Alternatively, TFM was developed to measure single cell contraction forces by observing the underlying elastic polymer substrate (e.g. polyacrylamide gel) embedded with multiple fluorescence microbeads [12–14]. A number of mathematical models have been developed to facilitate the estimation of contraction force based on the relative motion of the beads. However, the stiffness of the gel substrate can be altered by cell differentiation and biochemical treatments during the measurement and this may affect the accuracy of the force measurement. More importantly, it is more technically challenging to obtain results using the TFM method and measurements do not provide a true physiological model because the assessment of cellular contraction based on a two-dimensional surface, instead of a three-dimensional gel matrix.

To improve the accuracy of CGCA force measurements, a culture force monitor (CFM) system was developed by attaching strain gauges at the edges of a cell-embedded collagen gel to directly assess cell contraction [15–20]. Cellular contraction force can be measured continuously without influence of the elastic variation of collagen gel. Single cell contraction force can thus be approximately estimated by the measured force divided by the total number of the embedded cells. However, the measurement was only limited to a random uniaxial stress as the strain gauges could only measure the contraction in single directions.

Having taken into account the variation in elasticity of the collagen matrix, we re-designed the collagen gel-based assay technique to quantify cell contraction forces with a significantly higher degree of accuracy. The method essentially correlates the relationship between gel deformation and embedded cell contraction force. The elastic modulus and thickness of each collagen gel were routinely quantified by a bespoke nano-indentation tester and the data were used as input parameters for a simple mathematical model that correlates cell contraction force with gel properties, including radius, thickness and elasticity, which varied throughout the different treatments. The single cell contraction force can also be determined providing that the total cell number embedded in the gels are known. In this study, we have also applied the new gel-based sensing technique to investigate the contraction force of HAoAF treated with the agonist histamine or following co-treatment with ML-7, a well-established inhibitor of MLCK, to attenuate fibroblast contraction.

2. Material and methods

2.1. Cell culture

Cryopreserved HAoAF were purchased from PromoCell GmbH at passage 2. Cells were cultured at 37°C in a 95% air/5% CO2 atmosphere using phenol red-free Dulbecco’s modified Eagle's medium (DMEM) supplemented with fetal calf serum (FCS, 10%), penicillin (100 IU m l−1), streptomycin (100 µg ml−1) and l-glutamine (2 mM). Cells at passage 7–9 were used in all experiments.

2.2. Collagen gel contraction assay

2.2.1. Collagen gel assay

Confluent HAoAF cultures were detached from flasks using trypsin/EDTA and cell number determined using a haemocytometer. After centrifugation, cells were re-suspended in DMEM containing 10% FCS at densities of between 0.5 × 106 and 2.5 × 106 cells ml−1 and mixed with culture medium containing collagen I on ice at a ratio of 1 : 9, resulting in the final DMEM containing 1.76 mg ml−1 collagen I, 2 mM l-glutamine, 100 IU ml−1 penicillin, 100 µg ml−1 streptomycin and 5% FCS. The cell suspension was transferred into 35 mm Petri dishes (1.2 ml dish−1, achieving cell densities between 0.06 × 106 and 0.3 × 106 cells gel−1) and incubated in a cell culture incubator for 20 min to polymerize the gel before addition of a further 1.5 ml DMEM containing 5% FCS. After incubation for 16 h, the culture medium was replaced with fresh DMEM containing 5% FCS and collagen gels were dislodged from the edge of the dish using a sterile spatula. Gel thickness and elasticity measurements were conducted 48 h later. In experiments to address the effects of histamine on cell contraction, fibroblasts were re-suspended in DMEM containing 10% FCS at a density of 1.8 × 106 cells ml−1 (achieving a cell density of 0.216 × 106 cells gel−1) and incubated for 16 h before treatment of cells in the presence or absence of the MLCK inhibitor ML-7 (25 µM) for 30 min. Some dishes were then stimulated with the agonist histamine (100 µM) to elicit cell contraction. Collagen gels were then immediately dislodged from the dish using a sterile spatula with gel thickness and elasticity measurements conducted 5 h later.

2.2.2. Experimental measurements

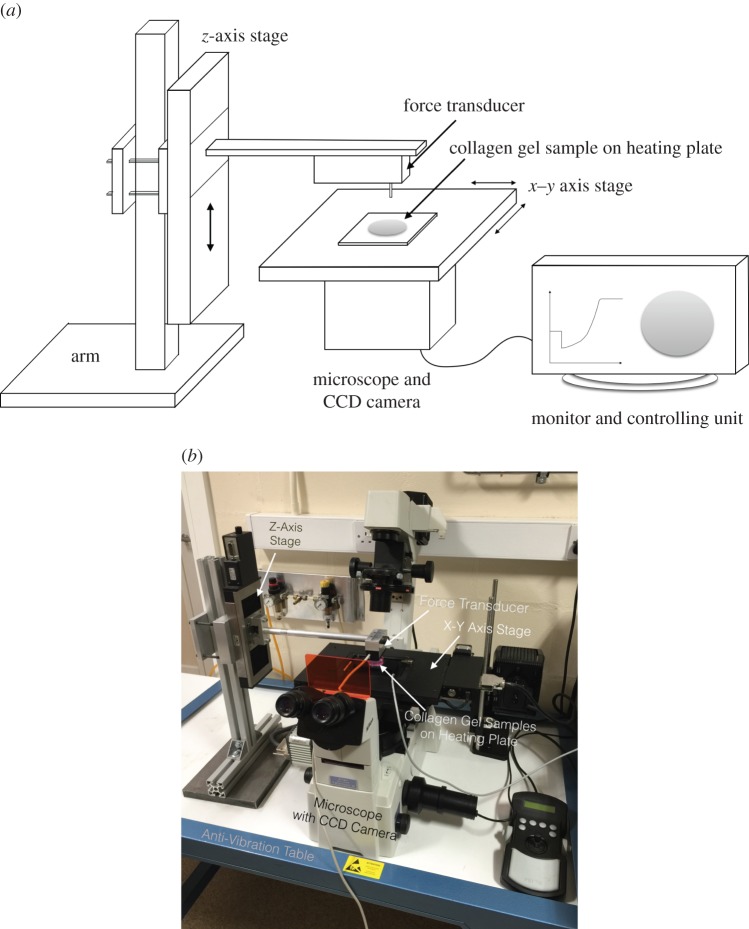
A depth-sensing nano-indentation tester was developed to quantitatively measure the thickness and Young's modulus of the cell-embedded collagen gel, which were used as input parameters to estimate contraction force (§2.3.2). As shown in the figure 1, the system is mainly comprised of a force transducer (406A, Aurora Scientific Inc.) attached with a cylindrical flat punch or indenter (ca 1 mm in diameter), Z-axis step motor linear stage (UTS 100CC with ESP301 Motion Controller, Newport), XY-axis stage (ProScan III, Prior Scientific) and a temperature control heating plate (Temp. Control, iBidi). All components are mounted on an inverted microscope (TE2000-S, Nikon) and controlled by Labview software (National Instrument). The system has ultimate force and displacement resolutions of 10 nN and 100 nm, respectively. The force transducer senses the force via the cylindrical indenter. The mechanical properties of collagen gels were measured by the system described. Nano-indentation of collagen gel was performed at a controlled indentation speed of 40 µm s−1. Force and displacement were recorded simultaneously during the loading/unloading indentation cycles. When the thickness and elasticity were measured, collagen gel was plated in the 35 mm Petri dishes with no culturing medium on the heating plate at 37°C. The whole system was placed on an anti-vibration table (Wentworth Laboratories Ltd). Ten random positions were picked and measured to generate 10 different force–displacement (F–D) curves for analysis. The thickness of the gel was measured based on the displacement difference between the gel's top surface and the Petri dish surface, while the gel's elasticity was measured based on the analysis of the indentation F–D curves (§2.3.1).

Figure 1.

Figure 1.

Open in a new tab

(a) Schematic of the depth-sensing nano-indentation system for force–displacement measurement. (b) Image of nano-indentation system. (Online version in colour.)

In parallel, a computerized CCD-enhanced camera (ORCA-ER, Hamamatsu) has been used to measure the radius of the disc-shaped hydrogel, from the vertical top view, and the radius change before and after cell contraction can be determined by referencing the culturing area of the Petri dishes. The measurement accuracy of the radius was up to 1 µm.

2.3. Theoretical analysis

2.3.1. Young's modulus of collagen gel

Young's modulus of collagen gel is modelled by employing nonlinear strain-dependent elasticity [21]:

2.3.1. 2.1

where E0 is Young's modulus at strain Inline graphic. To estimate Young's modulus, it is necessary to find a suitable connection between the F–D curve and the modulus. When a cylindrical punch indenting a flat elastic substrate (collagen gel), a linear relationship derived from Hertz contact theory can be expressed as [22]:

2.3.1. 2.2

where E* is the reduced modulus of collagen gel, r is the radius of the cylindrical indenter, D is the displacement or depth of the indenter into the collagen gel surface and F is the force measured by the force transducer. For two elastic bodies in contact, the reduced modulus can be also described as follows according to Hertz contact theory [23]:

2.3.1. 2.3

where ν is the Poisson's ratio and E is Young's modulus of the indented collagen gel. The subscript i refers to the properties of the cylindrical indenter. Hydrogel can normally be considered as an incompressible material, i.e. ν = 1/2, and the indenter is regarded as perfectly rigid, i.e. Ei = ∞, and thus equation (2.3) can be simplified as follows:

2.3.1. 2.4

Combining (2.1), (2.2) and (2.4), the following equation can be derived:

2.3.1. 2.5

For the strain 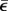Inline graphic can be approximately calculated as the ratio of the displacement of the indenter to the measured thickness of the collagen gel, H, i.e. 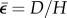Inline graphic. Hence, by using nonlinear least square regression to fit 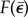Inline graphic with D based on equation (2.5), Young's modulus E0 of the collagen gel can be estimated from each measured F–D curve.

2.3.2. Contraction force

A simple theoretical model has been developed to estimate cell contraction force based on the force balance between cell contraction and gel deformation. Figure 2 shows the thickness (h0 and h1) and radius (r0 and r1) of a disc-shape collagen gel at the beginning and end of contraction. Young's modulus E0 of the collagen gel is described by the linear elastic mechanics as:

graphic file with name rsif20141365-e6.jpg 2.6

where dσ and dɛ represent stress and strain, respectively, generated by cell contraction to the gel. During the entire contraction process, the contraction force acts perpendicularly on the circumference surface which area can be expressed as 2πr · h. Hence the stress dσ can be calculated by radial contraction force dF per unit area as the equation:

graphic file with name rsif20141365-e7.jpg 2.7

where r and h are the immediate radius and thickness of collagen gel. Correspondingly, the strain dɛ can be expressed as the deformation of collagen gel in the radial direction.

graphic file with name rsif20141365-e8.jpg 2.8

Hence, combing equations (2.6), (2.7) and (2.8), Young's modulus E0 can be expressed as:

graphic file with name rsif20141365-e9.jpg 2.9

Here, the average thickness can be expressed as h = (h0 + h1)/2 if the gel thickness change is approximately linear during the contraction process. After rearranging equation (2.9) with integration, the final overall contraction force therefore can be presented as:

graphic file with name rsif20141365-e10.jpg 2.10

The model simply correlates the overall cell contraction force F with the measured material parameters, including Young's modulus, thickness and radius of collagen gel. The single cell contraction force is approximately calculated as the overall contraction force divided by the counted cell numbers.

Figure 2.

Figure 2.

Open in a new tab

Schematic of theoretical model for collagen gel before and after contraction.

3. Result

3.1. Young's modulus of collagen gel

Typical indentation curves and their corresponding nonlinear fitting curves are represented in figure 3a. The first 25% of the indentation depth to the gel thickness (i.e. strain up to 0.25) is selected to estimate Young’s modulus of the collagen based on the minimum least square fitting of equation (2.5) with the experimental force–strain data. Figure 3b shows Young’s modulus for HAoAF-embedded collagen gels for controlled gels and treated gels at a cell density of 0.216 × 106 cells gel−1. After treatment with histamine, Young’s modulus of the collagen gels was decreased by 41.2% compared with the untreated gels, while treatment with ML-7 shows the inhibitory effect of decreasing elasticity (ca 59.3%).

Figure 3.

Figure 3.

Open in a new tab

(a) Typical Young's modulus fitting of collagen gel contraction measurement from force–strain curve. (b) Data denote mean±s.e.m. of Young's modulus of collagen gel with/without histamine and ML-7. P-value was calculated using one-way ANOVA with Bonferroni post hoc test. **p < 0.05; *p < 0.5.

3.2. HAoAF contraction force after histamine and ML-7 treatment

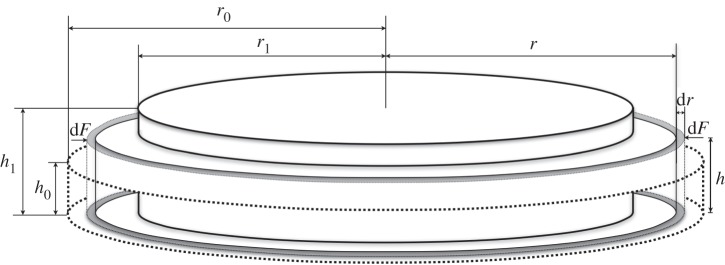
The images shown in figure 4b,c demonstrate the shrinkage of the HAoAF-embedded collagen gels treated by histamine with/without ML-7 compared with the untreated gel (figure 4a). The shaken gel sizes/radii can be calculated by counting the pixels of the gel images referencing the culturing area of the Petri dishes. By substituting the measured radius, Young's modulus and thickness of collagen gels into equation (2.10), HAoAF contraction force can then be estimated. Figure 5 shows that when cells were treated with histamine (100 µM), there was a nearly threefold increase in contraction force from 0.3 ± 0.04 to 0.89 ± 0.02 mN of overall contraction force. In the meantime, the contraction forces of single cells were calculated by the overall contraction force divided with the total number of cells embedded in the collagen gel. The single cell contraction force correspondingly increased from 1.41 ± 0.4 nN to 4.15 ± 0.5 nN when histamine was added. The MLCK inhibitor ML-7 (25 µM) attenuated the increase in contraction force by 60%.

Figure 4.

Figure 4.

Open in a new tab

Photographs of the typical HAoAF-embedded collagen gel after treatments. (a) Controlled collagen gel, (b) agonist histamine (100 µM) stimulated collagen gel, (c) histamine stimulated collagen gel with the presence of MLCK inhibitor ML-7 (25 µM). The areas circled with black solid lines in (a–c) represent the culturing areas of 35 mm Petri dishes. The areas circled with coloured dash lines in (a–c) denote the sizes of collagen gels, which were calculated by referencing the culturing area of Petri dishes. (Online version in colour.)

Figure 5.

Figure 5.

Open in a new tab

HAoAF were embedded into collagen gels at a density of 0.216 × 106 (cells gel−1). (a) Overall contraction force and (b) single cell contraction force per gel with/without histamine and ML-7. Data denote mean±s.e.m. from three independent measurements, p-value was calculated using one-way ANOVA with Bonferroni post hoc test. ***p < 0.005.

3.3. Cell-density effect on contraction force

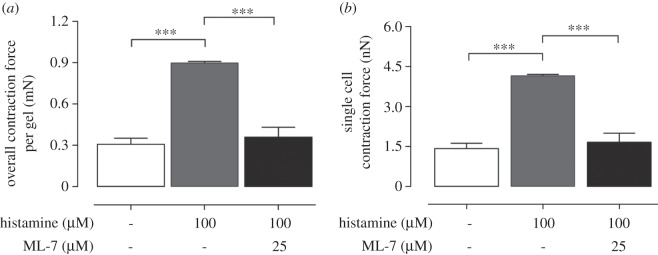
In the study, a constant volume of collagen gel was embedded with different cell densities to examine whether cell density could potentially have an influence on single cell contraction force. As shown in figure 6, the gel contraction forces determined for three different cell densities, i.e. 0.06, 0.12 and 0.3 × 106 (cells gel−1), have been measured after 48 h. The result shows that the overall contraction force calculated as determined by linear regression increases in a linear manner with the seeding densities of fibroblasts. As a result, the cell densities within the gels can be assumed to have no significant influence on the single cell contraction force measurements.

Figure 6.

Figure 6.

Open in a new tab

Cellular contraction force at different cell densities. (a) Overall contraction force of HAoAF at three different cell densities, i.e. 0.06, 0.12 and 0.3 × 106 (cells gel−1). (b) Single cell contraction force of the three cell densities. Data denote mean±s.e.m. from four independent measurements, p-value and R2-value in (a) were calculated based on the linear regression model.

4. Discussion

This study describes a novel method to assess cellular contraction force in vitro using a collagen gel-based sensing technique to demonstrate cell contraction force changes in fibroblasts treated with the agonist histamine, which increases intracellular calcium to elicit contraction, and attenuated by the MLCK inhibitor ML-7. It is worth highlighting that conventional collagen gel contraction assays have been mainly based on the observation of the change of cell-embedded collagen gel area [24], although a few studies have included measurement of the gel thickness [25]. However, Young's modulus of the gel should be regarded as one of the key parameters required to estimate the cell contraction force, as described mathematically by equation (2.10). The result (figures 3 and 5) demonstrates the significant increase in cell contraction force after histamine treatment, despite Young's modulus of collagen gel decreasing. Since the treatment conditions or state of cell differentiation may alter the gel elastic modulus, careful characterization of the gel elasticity before and after the culturing period are critical to accurately determine the cell contraction forces.

A significant increase in single cell contraction force by histamine treatment has been demonstrated using this novel technique by combining nano-indentation with mathematical modelling of collagen gel contraction. As reported in the literature [7], histamine can elicit an extensive contraction of cells as measured using CGCA. However, adding ML-7, a MLCK inhibitor, to the collagen gel can significantly attenuate the cellular contraction elicited by histamine, confirming that the fibroblast contraction was mediated via MLC phosphorylation [26]. Overall, the order of magnitude of cell contraction forces measured using this novel technique was comparable with those values determined by other methods, e.g. CFM [20,27].

As shown in figure 6, the single cell contraction force was demonstrated to be cell-density independent. As the histamine-treated collagen gels were only allowed to contract for 5 h before the measurement, the cell proliferation during this period was negligible and cell numbers can be reasonably assumed to remain constant throughout the measurements. The single cell contraction force can therefore be calculated by dividing the overall contraction force by the known initial number of cells. However, for longer term measurement (more than 24 h) in the cell-density contraction experiments, it was noticeable that cells were aligned on the bottom of the Petri dishes. This implies that there may be a potential cell number loss and the collagen gel liquid content may be reduced [1]. Moreover, the cell proliferation rate during long-term treatment could cause a significant increase in cell number within the gels. Assessment of total DNA content would be a possible way to verify that the final number of cells within the gels remained constant until the end of assay.

Nevertheless, from the results shown in figure 6b, the single cell contraction force can be calculated by the initial cell seeding number as there was no significant force difference measured between the different cell densities. We have shown that 0.1 × 106 cell gel−1 is an ideal cell seeding density for the long-term contraction force measurement while a higher cell seeding density, e.g. 0.3 × 106 cell gel−1 will be desirable for shorter periods of measurement (less than 24 h). This is because with same amount of cells embedded, contraction assays performed soon after seeding (less than 6 h) will generate less overall contraction force than measurements taken after a longer period (24 h) due to cell proliferation. Therefore, increasing cell seeding density would provide a greater overall contraction force and result in more accurate measurements of cell contraction force.

The novel technique reported in this study is applicable to assess forces generated by any cell type that can be cultured within a three-dimensional collagen gel and responds to agonist stimulation leading to cell contraction. For example, assessment of forces elicited by vascular smooth muscle cells may indicate the likelihood of a treatment causing contractile responses that may lead to hypertension [28] while assessment of contraction forces in dermal fibroblasts may provide insights into the wound healing potential of drugs, anti-wrinkling properties of therapeutic compounds or suitability of three-dimensional gel matrices for tissue-engineering of skin substitutes [29–31]. These are only a few potential applications where the novel technique to assess cellular and gel contraction forces may provide important information for future bioengineering and clinically relevant therapeutic strategies.

5. Conclusion

This study has demonstrated a novel technique to quantify cellular contraction force when cells are embedded in a three-dimensional collagen gel matrix. The histamine-induced contraction of fibroblasts through MLCK activation and MLC phosphorylation, determined in cells seeded in a collagen gel, are in agreement with observations previously reported [27]. Moreover, the alteration in the collagen gel elasticity before and after histamine treatment was measured. The nonlinear theoretical fittings of collagen gel elasticity are in agreement with the experimental data. The measurements have confirmed that the mechanical property changes of the gel matrix should be taken into account to accurately measure cell contraction forces using gel contraction assays.

Acknowledgement

This work was supported by a grant from Leverhulme Trust (PRG-2012-738) awarded to K.-K.L. and a grant from the British Heart Foundation (FS/09/037/27827) awarded to R.C.M.S. We would also like to thank Prof. Giovanni E. Mann and Dr Ron Jacob, Cardiovascular Division, King's College London, for their insightful suggestions and technical support.

References

  • 1.Bell E, Ivarsson B, Merrill C. 1979. Production of a tissue-like structure by contraction of collagen lattices by human fibroblasts of different proliferative potential in vitro. Proc. Natl Acad. Sci. USA 76, 1274–1278. ( 10.1073/pnas.76.3.1274) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Ehrlich HP, Rockwell WB, Cornwell TL, Rajaratnam JB. 1991. Demonstration of a direct role for myosin light chain kinase in fibroblast-populated collagen lattice contraction. J. Cell. Physiol. 146, 1–7. ( 10.1002/jcp.1041460102) [DOI] [PubMed] [Google Scholar]
  • 3.Dallon JC, Ehrlich HP. 2008. A review of fibroblast-populated collagen lattices. Wound Repair Regen. 16, 472–479. ( 10.1111/j.1524-475X.2008.00392.x) [DOI] [PubMed] [Google Scholar]
  • 4.Travis JA, Hughes MG, Wong JM, Wagner WD, Geary RL. 2001. Hyaluronan enhances contraction of collagen by smooth muscle cells and adventitial fibroblasts: role of CD44 and implications for constrictive remodeling. Circ. Res. 88, 77–83. ( 10.1161/01.RES.88.1.77) [DOI] [PubMed] [Google Scholar]
  • 5.Liang W, McDonald P, McManus B, van Breemen C, Wang X. 2003. Histamine-induced Ca2+ signaling in human valvular myofibroblasts. J. Mol. Cell. Cardiol. 35, 379–388. ( 10.1016/S0022-2828(03)00010-5) [DOI] [PubMed] [Google Scholar]
  • 6.Johnson CL, Johnson CG, Bazan E, Garver D, Gruenstein E, Ahluwalia M. 1990. Histamine receptors in human fibroblasts: inositol phosphates, Ca2+, and cell growth. Am. J. Physiol. 258, C533–C543. [DOI] [PubMed] [Google Scholar]
  • 7.Horie M, et al. 2014. Histamine induces human lung fibroblast-mediated collagen gel contraction via histamine H1 receptor. Exp. Lung Res. 40, 222–236. ( 10.3109/01902148.2014.900155) [DOI] [PubMed] [Google Scholar]
  • 8.Ahearne M. 2014. Introduction to cell–hydrogel mechanosensing. Interface Focus 4, 20130038 ( 10.1098/rsfs.2013.0038) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Jeng JH, Lan WH, Wang JS, Chan CP, Ho YS, Lee PH, et al. 2006. Signaling mechanism of thrombin-induced gingival fibroblast-populated collagen gel contraction. Br. J. Pharmacol. 147, 188–198. ( 10.1038/sj.bjp.0706462) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Yanase M, et al. 2003. Functional diversity between Rho-kinase- and MLCK-mediated cytoskeletal actions in a myofibroblast-like hepatic stellate cell line. Biochem. Biophys. Res. Commun. 305, 223–228. ( 10.1016/S0006-291X(03)00726-5) [DOI] [PubMed] [Google Scholar]
  • 11.Nakamura Y, Hirano S, Suzuki K, Seki K, Sagara T, Nishida T. 2002. Signaling mechanism of TGF-β1-induced collagen contraction mediated by bovine trabecular meshwork cells. Invest. Ophthalmol. Vis. Sci. 43, 3465–3472. [PubMed] [Google Scholar]
  • 12.Dembo M, Wang Y-L. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76, 2307–2316. ( 10.1016/S0006-3495(99)77386-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Butler JP, Tolić-Nørrelykke IM, Fabry B, Fredberg JJ. 2002. Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol.-Cell Physiol. 282, C595–C605. ( 10.1152/ajpcell.00270.2001) [DOI] [PubMed] [Google Scholar]
  • 14.Yang Z, Lin J-S, Chen J, Wang JH. 2006. Determining substrate displacement and cell traction fields—a new approach. J. Theor. Biol. 242, 607–616. ( 10.1016/j.jtbi.2006.05.005) [DOI] [PubMed] [Google Scholar]
  • 15.Delvoye P, Wiliquet P, Levêque J-L, Nusgens BV, Lapière CM. 1991. Measurement of mechanical forces generated by skin fibroblasts embedded in a three-dimensional collagen gel. J. Invest. Dermatol. 97, 898–902. ( 10.1111/1523-1747.ep12491651) [DOI] [PubMed] [Google Scholar]
  • 16.Kolodney MS, Wysolmerski RB. 1992. Isometric contraction by fibroblasts and endothelial cells in tissue culture: a quantitative study. J. Cell Biol. 117, 73–82. ( 10.1083/jcb.117.1.73) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Eastwood M, McGrouther DA, Brown RA. 1994. A culture force monitor for measurement of contraction forces generated in human dermal fibroblast cultures: evidence for cell–matrix mechanical signalling. Biochim. Biophys. Acta 1201, 186–192. ( 10.1016/0304-4165(94)90040-X) [DOI] [PubMed] [Google Scholar]
  • 18.Eastwood M, Porter R, Khan U, McGrouther G, Brown R. 1996. Quantitative analysis of collagen gel contractile forces generated by dermal fibroblasts and the relationship to cell morphology. J. Cell. Physiol. 166, 33–42. () [DOI] [PubMed] [Google Scholar]
  • 19.Freyman T, Yannas I, Pek Y, Yokoo R, Gibson L. 2001. Micromechanics of fibroblast contraction of a collagen–GAG matrix. Exp. Cell Res. 269, 140–153. ( 10.1006/excr.2001.5302) [DOI] [PubMed] [Google Scholar]
  • 20.Campbell BH, Clark WW, Wang JH. 2003. A multi-station culture force monitor system to study cellular contractility. J. Biomech. 36, 137–140. ( 10.1016/S0021-9290(02)00325-1) [DOI] [PubMed] [Google Scholar]
  • 21.Tatara Y. 1991. On compression of rubber elastic sphere over a large range of displacements—part 1: theoretical study. J. Eng. Mater. Technol. 113, 285–291. ( 10.1115/1.2903407) [DOI] [Google Scholar]
  • 22.Johnson KL. 1987. Contact mechanics. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 23.Heinrich H. 1881. Über die Berührung fester elastischer Körper. J. Die Reine Angew. Math. 92, 156–171. [Google Scholar]
  • 24.Zhu Y, et al. 2001. Contraction of fibroblast-containing collagen gels: initial collagen concentration regulates the degree of contraction and cell survival. In Vitro Cell. Dev. Biol. 37, 10–16. () [DOI] [PubMed] [Google Scholar]
  • 25.Kurosaka H, Kurosaka D, Kato K, Mashima Y, Tanaka Y. 1998. Transforming growth factor-beta 1 promotes contraction of collagen gel by bovine corneal fibroblasts through differentiation of myofibroblasts. Invest. Ophthalmol. Vis. Sci. 39, 699–704. [PubMed] [Google Scholar]
  • 26.Matsumoto H, et al. 2007. Comparison of gel contraction mediated by airway smooth muscle cells from patients with and without asthma. Thorax 62, 848–854. ( 10.1136/thx.2006.070474) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Fujimura T, Hotta M, Kitahara T, Takema Y. 2011. Loss of contraction force in dermal fibroblasts with aging due to decreases in myosin light chain phosphorylation enzymes. Archiv. Pharmacol. Res. 34, 1015–1022. ( 10.1007/s12272-011-0619-9) [DOI] [PubMed] [Google Scholar]
  • 28.Wynne BM, Chiao CW, Webb RC. 2009. Vascular smooth muscle cell signaling mechanisms for contraction to angiotensin II and endothelin-1. J. Am. Soc. Hypertens. 3, 84–95. ( 10.1016/j.jash.2008.09.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Brown RA, Sethi KK, Gwanmesia I, Raemdonck D, Eastwood M, Mudera V. 2002. Enhanced fibroblast contraction of 3D collagen lattices and integrin expression by TGF-β1 and -β3: mechanoregulatory growth factors? Exp. Cell Res. 274, 310–322. ( 10.1006/excr.2002.5471) [DOI] [PubMed] [Google Scholar]
  • 30.Grinnell F. 2003. Fibroblast biology in three-dimensional collagen matrices. Trends Cell Biol. 13, 264–269. ( 10.1016/S0962-8924(03)00057-6) [DOI] [PubMed] [Google Scholar]
  • 31.Ahearne M, Wilson SL, Liu K-K, Rauz S, El Haj AJ, Yang Y. 2010. Influence of cell and collagen concentration on the cell–matrix mechanical relationship in a corneal stroma wound healing model. Exp. Eye Res. 91, 584–591. ( 10.1016/j.exer.2010.07.013) [DOI] [PubMed] [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES