Investigating biomechanical noise in neuroblastoma cells using the quartz crystal microbalance

Abstract

Quantifying cellular behaviour by motility and morphology changes is increasingly important in formulating an understanding of fundamental physiological phenomena and cellular mechanisms of disease. However, cells are complex biological units, which often respond to external environmental factors by manifesting subtle responses that may be difficult to interpret using conventional biophysical measurements. This paper describes the adaptation of the quartz crystal microbalance (QCM) to monitor neuroblastoma cells undergoing environmental stress wherein the frequency stability of the device can be correlated to changes in cellular state. By employing time domain analysis of the resulting frequency fluctuations, it is possible to study the variations in cellular motility and distinguish between different cell states induced by applied external heat stress. The changes in the frequency fluctuation data are correlated to phenotypical physical response recorded using optical microscopy under identical conditions of environmental stress. This technique, by probing the associated biomechanical noise, paves the way for its use in monitoring cell activity, and intrinsic motility and morphology changes, as well as the modulation resulting from the action of drugs, toxins and environmental stress.

1. Introduction

Depending on the cell type and environment, cells often undergo continuous morphological and motility changes. Cytoplasm and subcellular components self-organize to change shape and also provide the basis for cellular motility. These processes, though superficially simple, are highly complex and represent nature's unique solutions to challenges posed by mechanics, thermodynamics and biochemistry. Diverse biological processes ranging from embryogenesis, fetal and organ development to immune response against inflammation and wound healing involve movement or migration of cells [1]. Cellular motility also plays a crucial role in many diseases, including in tumour invasion and spread (metastasis) of cancer. Therefore, understanding and targeting cell motility is a topical strategy in reducing morbidity and fatality in cancer treatment [2]. Cellular morphology also provides an indication of the conditions being experienced by the cells as well as that of the various biological processes operative in cells [3].

The attachment–detachment of cells to the underlying substrate and extracellular matrix (ECM) takes place through focal adhesion points which involve binding of integrin mediators to ECM molecules, leading to the formation of focal complexes [4]. Integrin receptors are connected to the cytoskeleton through actin networks which influence reorganization of the cytoskeleton, hence, the cell structure itself [5]. These processes have biomechanical consequences and can be used to model the behaviour of cells. Assuming environmental factors as input, cells (both individually and collectively) represent physical dynamical systems which respond to the input (stimuli) by modulating their motility and morphological characteristics. These biomechanical manifestations are often stochastic and, thus, call for a tool for sensing and interpretations. Techniques based on optical microscopy [6–8], micromanipulation [9], modified atomic force microscopy (AFM) [10] and optical traps [11] have been used to understand the mechanics of focal adhesion [12]; however, analysis of stochastic aspects of cellular motility and morphology is missing. Thus, there is a need for the development of a biomechanical noise probing technique that could be simple, non-invasive and real-time. In this paper, we use one of such techniques, based on quartz crystal microbalance (QCM), to study the biomechanical noise associated with human neuroblastoma cells.

In the past few decades, the QCM [13] has emerged as an important tool for highly sensitive, label-free, gravimetric measurements of physical processes involving physical adsorption and desorption of a variety of analytes. The QCM can be mechanically abstracted as a single degree-of-freedom spring-mass-damper system such that any attachment/detachment of analyte on the crystal manifests in the form of a change in resonant response that is read out using external electronics. This property of QCM has been extensively used to perform measurements on biological systems in liquid environments. In the presence of liquid, acoustic oscillations of the QCM couple to the surrounding liquid media, and the viscoelastic properties of the media at the interface [14] have predictable effects on the frequency (f) and dissipation (D) characteristics of the QCM. A range of biological systems have been probed using the QCM, including the physi/chemisorption of proteins and lipids [15], binding and reaction kinetics of biomolecules [16], cell attachment–detachment and spreading [17–20], etc. Descriptive models [21,22] have been proposed to correlate adsorption–desorption and binding studies using the QCM but for complex systems such as cells, a quantitative description using conventional analysis (f−D) techniques is often inadequate. When such systems are influenced by actively driven dynamic and non-equilibrium processes such as motility and morphological perturbations, fluctuations in the QCM response as a function of time are seen. There is, therefore, the possibility of using the resulting recorded fluctuations in response as a means of characterizing such dynamic and complex biological systems.

It can be hypothesized that movement of cells on the surface can result in biomechanical noise that can couple to the response of the QCM and be conspicuously evidenced in terms of enhanced levels of fluctuations in the recorded QCM response. Sapper et al. [23] previously reported that the effect of biomechanical noise on frequency fluctuations in a QCM is several orders of magnitude higher than that contributed by other noise sources. By calculating the power spectral density (PSD) of the QCM frequency fluctuations in the case of attached mammalian cells, the authors were able to qualitatively associate frequency fluctuation data with cell motility. In a separate study, Tarantola et al. [24] studied motility of different cancer cell lines using the same technique. In both the studies, outcome of the fluctuation analysis was compared with a similar analysis on the electric cell–substrate impedance sensing data. Pax et al. [25] studied the fluctuations in the QCM response due to the periodic contractions of rat cardiac myocytes and extracted the beating rates through subsequent PSD analysis.

In this paper, neuroblastoma cancer cells are studied using a time-domain fluctuation analysis technique (Allan deviation measurements) applied to the measured QCM response. The case study of neuronal cells (from the differentiated human neuroblastoma cell line) is considered where their interactions with the sensor surface are monitored, while subjecting the cells to external heat stress which eventually leads to apoptosis. This study provides insights into the mechanical response of the particular type of cancer cells owing to the change in local temperature. By combining separate optical studies with QCM data, it is possible to correlate the observed changes in single cell state and morphology as well as total surface coverage of the cells to the QCM frequency fluctuation data. Thus, the paper establishes the basis for the use of time-domain QCM frequency fluctuation analysis for sensing biomechanical noise output of cells, deciphering and monitoring physical behaviour of cells and cell–substrate interactions and the changes induced owing to environmental stress. The results indicate that this technique can be expanded to other case studies on cellular systems and the effect of varying environmental conditions on their mechanical behaviour.

2. Material and methods

2.1. Quartz crystal microbalance set-up

AT-cut plano-plano thickness shear mode Cr/Au coated 5 MHz quartz crystals, 1 inch in diameter (see schematic in figure 1a) are used. Crystals were fitted into a dedicated Kynar^® flow-cell, part of the standard QCM200^® instrument from Stanford Research Systems. The flow-cell volume is approximately 150 µl. Crystal electrodes are isolated from the flow media, and electrical connections to the interface electronics are achieved through spring-loaded contact pins. During experiments, the series resonance frequency and crystal resistance is logged and then later processed off-line. The gate-time (sampling time) of the instrument was set to 1 s. The temperature of the flow-cell was controlled by a heater with the whole set-up being placed inside an environmental chamber with fully humidified atmosphere at 37°C and 5% CO₂ during the length of the experiments on the live cells. The environmental chamber was placed on a vibration isolation table, and the attached electrical cables, connecting the crystal to the measurement set-up (outside the chamber), were fitted with foam dampers at points of contact with the chamber to prevent external vibrations arising from the humidifier or other sources from impacting measurement.

Figure 1.

(a) Schematic of a quartz crystal top surface with circular Cr/Au electrode, and (b) cross-sectional schematic view of a SH-SY5Y human neuroblastoma cell adhering to the poly-l-lysine (PLL) coated crystal. (Relative dimensions not to scale.) (Online version in colour.)

2.2. Cell-culture and crystal chip preparation

Experiments were carried out using SH-SY5Y cells, a human neuroblastoma cell line, commonly used to study neuronal function and behaviour [26]. Cells were adherent with neurite outgrowth. Moreover, the cells tended to grow in clusters resulting in patchy surface coverage of the culture dish. Cells were cultured at 37°C in a humidified atmosphere in a medium containing 87% Dulbecco's modified Eagle's medium (Gibco), 10% heat-inactivated fetal bovine serum, 2% B-27 (Gibco) and 1% antibiotic–antimycoticum (Gibco). The addition of 10 nM staurosporine (Sigma) to the culture medium triggered cell differentiation into a neuroblast-like cell type, which arrests proliferation and results in a stable population [27]. The cells studied in this work do not undergo cell division but nevertheless change their shape both as a result of movement and environmental stress [28–30]. Thereafter, the required number of cells were reseeded on autoclaved, poly-l-lysine (PLL, Sigma)-coated quartz crystals placed inside a 35 mm culture dish (Greiner). Prior to the seeding of cells, the quartz crystals were incubated with aqueous PLL (0.02 m/v %) solution for 2 h at 37°C to facilitate adherence of cells to the surface. A schematic of a cell attached to a PLL-coated quartz crystal is shown in figure 1b.

In order to study cell motility, the number of cells seeded on the quartz crystal should result in relatively sparse coverage to minimize the influence of cell compression and contact inhibition [28]. Therefore, two extreme cell concentrations were chosen to study cell behaviour and motility. Approximately 5700 and 51 700 cells per cm² were seeded onto the quartz crystal containing cell culture dishes. These seeding densities resulted in a surface coverage of approximately 3.6% (surface coverage i) and approximately 30.7% (surface coverage ii), respectively, which was measured by quantifying the cell population over a relatively large area (approx. 0.5 cm²) of the quartz crystal using optical images to remove the influence of local heterogeneity owing to cell colonies/clusters. Experiments for intermediate surface coverages, 13.0% (surface coverage iii) and 22.5% (surface coverage iv) along with control experiments were also performed. Cells were allowed to attach to the substrate over 24 h. Thereafter, cell attachment and viability were checked using a light microscope.

Crystals demonstrating good attachment of cells on the surface were then chosen for individual experiments. These crystals were placed inside the pre-warmed flow-cell which was filled with cell culture medium carefully avoiding introduction of air bubbles, which can interfere with the QCM readings. The flow-cell was sterilized with 70% ethanol prior to cell experiments and thereafter kept under sterile cell culture conditions to exclude contamination of the cells throughout the experiments. The flow-cell was then placed inside the environmental chamber, connections to electronics were made and data recording with the QCM was initiated after an initial stabilization period of approximately 20 min. During QCM measurements, there was no flow of the medium to preclude flow-related perturbations.

2.3. Hyperthermia induced, time-lapse live cell experiments

Changes in cellular morphology and motility were studied in SH-SY5Y cells seeded onto a 35 mm glass-bottom dish (MatTek, USA) with a surface coverage of approximately 30.7%. Hyperthermia was induced by gradual temperature increase from 37°C to 45°C in an environmental chamber (humidified atmosphere with 5% CO₂) of a Leica microscope allowing for live cell, time-resolved phase-contrast imaging using a 400× objective. Time-lapse recording was started simultaneously with the initiation of temperature increase. The temperature was measured in the air chamber, and a final temperature of 45°C was recorded after 50 min. Time-lapse video recording was carried out capturing one frame every 20 s. For cell tracking, image sequences were pre-processed using threshold adaptation, background subtraction, followed by using an unsharpening mask and binarization in ImageJ (NIH, USA) [31]. For every frame, boundaries were drawn using the marking tool in ImageJ and shape parameters such as centroid, area and circularity were obtained. Centroid positions were superimposed on the optical frames to visualize the track of selected cells and further processing on the data was performed to calculate distance travelled, mean-squared displacement and speed.

3. Results and discussion

3.1. Heat stress experiments

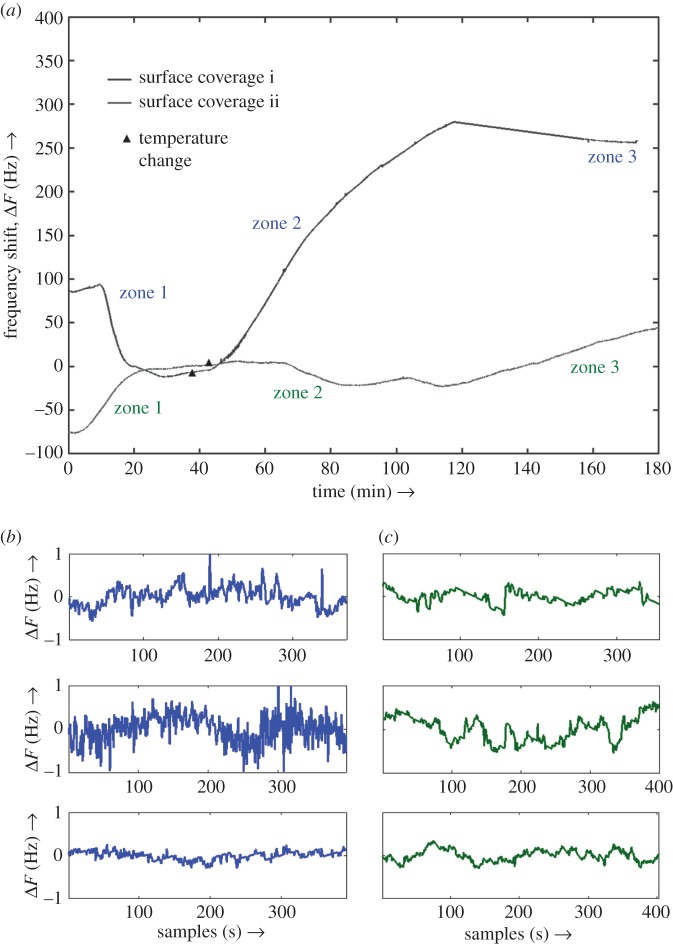
Cell-covered QCM crystals were prepared as detailed earlier (Material and methods) and loaded into the flow chamber. After the recordings on the QCM crystal stabilized, the temperature of the heater was ramped up from 37°C to 45°C. This change in temperature induces stress resulting in changes in the cell shape and texture indicating apoptotic processes and ultimately resulting in apoptosis (as shown in the later sections). Data were recorded beyond the time after the temperature monitor (attached to the exterior of flow cell) reached the final set temperature to allow for equilibration and compensate for any thermal lag. After every experiment, the crystals were viewed under the microscope to confirm that the cells have undergone apoptosis triggered by the heating process and formed typical spherical shapes alongside with detachment from the surface. Frequency data for two such experiments are shown in figure 2a. As the temperature was increased, both crystals showed a gradual positive frequency shift (ΔF) indicating a change in mass loading (Δm) on the surface. The frequency shift for the larger cell population (approx. 250 Hz) was much greater than the one observed for the smaller cell population (approx. 50 Hz) as expected roughly from the Sauerbrey equation (, where F₀, A, ρ_q, μ_q are the unloaded crystal resonance frequency, active crystal area, i.e. area constrained by the electrodes, density of quartz and shear modulus of quartz, respectively). It should be noted that the Sauerbrey equation has limited validity in this case and a more elaborate model is necessary for quantitative correlation to the experiment owing to the complex nature of the physical system under investigation. While accurate prediction of changes based on frequency data alone is challenging owing to the complex nature of the interfacial surface, the changes could be qualitatively interpreted as owing to rupture of the strong adhesion bonds of cells as they progress towards apoptosis, which are slowly replaced by loose physisorption, both for the cells that remain on the surface and those that sink after complete detachment. This observation is consistent with previous experiments on studying cell apoptosis using the QCM [17].

Figure 2.

(a) Frequency shift plots for two different surface coverages: 3.6% (surface coverage i) and 30.7% (surface coverage ii) of SH-SY5Y human neuroblastoma cells on different quartz crystals. Markers indicate the point of commencement in temperature increment of the flow-cell from 37°C to 45°C in order to apply heat shock to the adherent cells. Three different zones are also annotated which roughly define three different stages of the experiments. Zone 1 is where cells are healthy, zone 2 is immediately after the temperature is increased and represents transition to cell apoptosis, whereas zone 3 is the stage just before the experiment is concluded with final stages of apoptosis. Increase in frequency in both the cases indicates decrease in mass loading (i.e. cell detachment from the surface) with time. (b,c) (Two columns of three plots each.) Snapshots of frequency fluctuations in zone 1, zone 2 and zone 3 (top to bottom) for the two cases of varying surface coverage. In all cases, the trendline has been adjusted for representation purposes only. Note that in the case of larger surface coverage, the signal is more ‘noisy’ in zone 2, whereas it is least in zone 3. In the case of lower surface coverage, differences in the frequency fluctuations in three different zones are relatively smaller than the former case. (Online version in colour.)

3.2. Biomechanical noise and frequency fluctuations

Frequency and dissipation readings provide valuable information on changes occurring at the crystal–liquid interface and have proven to be especially useful in ligand binding experiments. While cell adhesion, spreading, detachment and morphological changes in the presence of an analyte have been previously studied by QCM using the frequency-dissipation approach [18–20,32], dynamic changes or fluctuations in these parameters have been given little attention. Fluctuations in QCM parameters have been shown to correlate with the subtle changes in mass and viscous loading at the interface [23,24]. Cell–substrate interactions probed using the QCM involve constant attachment and detachment at focal adhesion points, morphological changes and cell–cell interactions which can result in perturbations in viscoelastic loading on the QCM. These variations, representing the biomechanical noise contribution of the seeded cells, are recorded as frequency fluctuations in the QCM data.

Based on QCM frequency measurements, three zones are defined on the basis of variability in environmental and interfacial conditions. Zone 1 is defined as the time period starting from the point where data recording is commenced, and the system is held at 37°C. This zone corresponds to the case where cells are viable and kept in ideal culture conditions. Zone 2 is defined as the zone starting immediately after the temperature is increased and up to the point where all cells are in the late stages of apoptosis owing to hyperthermia. Zone 3 is defined as the region where the environment has reached the final phase following cell death owing to the heat shock treatment in zone 2. The frequency fluctuation data for both experiments are plotted in figure 2b,c. It is clear, even by visual examination, that the amplitude of frequency fluctuations is reduced significantly for zone 3 compared with zone 1 for higher cell coverage. An increased amplitude of frequency fluctuations indicates large-scale activity on the surface, which is to be expected when the cells are healthy and mostly stable in clusters (colonies) compared with when they are largely static (apoptotic). Both frequency shift and fluctuation amplitude changes for the smaller surface coverage are relatively indistinguishable and do not shed much light qualitatively. However, to establish more quantitative insights into these observations, time-domain frequency stability analysis is employed.

3.3. Time-domain biomechanical noise analysis

3.3.1. Two sample Allan deviation

Frequency fluctuations (arising from biomechanical noise) can be characterized either by performing frequency domain analysis (calculating PSD) of the data or by analysing the Allan variance in the time domain. Although interconvertible, Allan variance is chosen over PSD as it is more convenient to interpret in terms of the experimental set-up used in this work, which owing to use of a frequency counter, outputs observed frequency as a time series. A complete PSD-based analysis for the experiments is also provided in the electronic supplementary material to provide a comparison with previous studies.

A quantitative measure of frequency stability is established by analysing the Allan variance (see the electronic supplementary material) for the datasets corresponding to the various cases of cell coverage in zones 1–3. The Allan variance is chosen over standard M-sample variance as it is convergent for most types of noise processes and can also help distinguish different noise mechanisms. An overlapped Allan variance, for M fractional frequency values, is employed to provide higher statistical confidence (see electronic supplementary material).

Plots showing overlapped Allan deviation as a function of averaging time show a power-law dependence as a function of averaging time (τ) with characteristic slopes μ(σ_y(τ) ∼ τ^μ/2) in such plots and, thus, can be readily identified. White noise (f⁰) describes μ = −1, flicker noise (1/f) describes μ = 0, random walk frequency-modulated noise (1/f²) describes μ = 1, whereas frequency drift describes μ = 2 [33,34]. While the frequency fluctuation data shown in figure 2 are linear drift compensated, there is no pre-processing of the frequency fluctuation data used to calculate overlapped Allan deviation. Furthermore, error estimates for 1-sigma confidence intervals are calculated for all the three zones. Figure 3a shows the sigma-tau plot for the high surface coverage cell experiment where the difference between the Allan deviation values (fluctuation levels) for three different zones is very clear. This agrees well with the frequency fluctuations observed in the three zones. Furthermore, the deviation plot for each zone is considered separately and slopes between every pair of adjacent points are obtained using linear fitting. Relevant plots are shown in figure 3a(ii,iii,iv). Similarly, figure 3b represents sigma-tau plots for the low cell surface coverage. In this case, for short averaging times, the Allan deviation values are very close to each other while they diverge a bit for longer averaging times.

Figure 3.

(i,ii) Log–log overlapped Allan-deviation plots for the larger and smaller surface coverages respectively. From (i)—(i), it is quite evident that the fluctuation levels for all averaging times (τ) are highest for zone 2, intermediate for zone 1, whereas levels are lowest for zone 3. This indicates when cells are alive, owing to their activity, fluctuation levels are higher when compared with when cells are dead. Also, when cells are in a stressed state higher fluctuation levels are observed. (i): (ii–iv) Individual linear fitting curves (black, continuous and slightly offset for clarity) for three zones. Similarly, from (ii), (i) it is evident that while fluctuation levels for shorter averaging times are higher for both zone 1 and zone 2, fluctuation levels are only slightly higher for zone 2. Linear fitting (ii–iv) indicate nature of noises (power-law type) for different zones as in the previous case. (Online version in colour.)

3.3.2. Interpretation of log–log overlapped Allan deviation plots

Individual deviation values for each time factor are calculated and can be used to compare the fluctuation levels between different zones. In table 1, Allan deviation values for the shortest averaging time (1 s) are used for representation. In the case where cells are cultured on the QCM, it is quite evident that deviation values are the maximum for zone 2, are the least for zone 3 and lie in-between these two values for zone 1. The relative difference between deviation values is clear between high and low surface coverage of cells. In all the cases though, for zone 3, fluctuation values are which approximately corresponds to the baseline fluctuation level. To determine the effect of heating on the fluctuation levels, two control experiments, without any cells, were performed with, first, just water and, second, with the cell culture medium. All other conditions were kept the same. Log–log plots of deviation values for the control experiments are shown in figure 4c,d. Clearly, there is very little change in the fluctuation levels when the temperature is increased implying that the observed noise levels (figure 4a,b) are generated owing to the presence of the cells on the surface. Experiments with intermediate cell coverage of 13.0% (surface coverage iii) and 22.5% (surface coverage iv) were also performed. Both the experiments agree with the trends in the frequency fluctuation data observed with the high and low surface coverage experiments. For averaging factors τ = 2 s, 4 s, a similar table is formulated with similar trends seen (see electronic supplementary material). For larger averaging times (more than or equal to 8 s), the plots start to intersect pointing towards the fact that values must be interpreted with care as drift processes start to dominate. To understand the contribution of different noise sources at various timescales, we can separate the contribution of device noise from the biomechanical noise emerging from the activity of the cells themselves by comparison with respect to control experiments. Some of the principal device noise could be evidenced as thermal noise or flicker noise with noise contributions from the crystal and the amplifier, along with sensor drift owing to changes in environmental conditions. Physical processes associated with cellular activity such as attachment–detachment of individual focal contacts, morphological changes in response to external environmental conditions and internal cellular processes, migration of cells on the surface, cluster dynamics of cells, fluctuations in the viscoelasticity of the fluid owing to cell activity and external environmental perturbations are expected to contribute to the measured frequency fluctuations. Each of the above processes are expected to operate on different timescales, for example, attachment–detachment between ECM and cells are much faster ( for spontaneous dissociation of a closed bond at a focal adhesion site can range from fraction of seconds to tens of seconds [35]), whereas motility and cluster dynamics can be relatively slower. As shape changes are sensitive to external conditions, any fast external processes will influence the cell morphology at a similar rate. A plot of Allan deviation slopes for different averaging times can be found in the electronic supplementary material. Nevertheless, in order to correlate and verify predictions from the time-domain frequency analysis with cell behaviour, optical imaging experiments were carried out.

Table 1.

Two sample overlapped Allan deviation values at τ = 1 s for different zones and varying surface coverage.

experiment	zone 1 (10−8)	zone 2 (10−8)	zone 3 (10−8)
surface coverage i (30.7%)	2.248	116.2	1.122
surface coverage ii (3.6%)	1.172	1.310	0.899
surface coverage iii (13.05%)	2.31	3.2	1.024
surface coverage iv (22.5%)	1.67	99.186	1.612
control-DI water	0.861	0.865	0.742
control-cell culture	0.975	0.888	0.742

Figure 4.

(a,b) Log–log overlapped Allan-deviation plots for surface coverage iii (13%) and iv (22.5%), whereas (c,d) are overlapped Allan-deviation plots for control experiments. All the steps are common in control experiments with the exception of absence of any seeded cells. In (c), the surrounding media is DI water, whereas in (d) the surrounding media is cell culture. (Online version in colour.)

3.4. Correlating frequency fluctuation data with optically recorded cellular mechanical behaviour

3.4.1. Observing a sample cell

The aim of this section is to correlate the frequency fluctuation analysis with cellular changes and behaviour in terms of motility, substrate adhesiveness and morphology resulting from hyperthermia. Therefore, cells were exposed to increasing temperature under conditions comparable to those used during the QCM experiment, and optical images were obtained using a phase-contrast microscope to extract information on morphology and motility.

Figure 5a–h shows eight selected time points for the same cell sample exemplifying the drastic cellular changes due to hyperthermia. The position of the same cell which moves on the surface and changes in morphology is marked with a star/asterisk). Significantly, the size of the nucleus increases on increasing the temperature and thereafter, the nucleus shrinks (figure 5e,f) until distinction from the cytoplasm is not possible any more (figure 5g,h). Furthermore, pigmentation of the nucleus becomes uneven showing darker spots as visible in figure 5c–h. Nuclear swelling and chromatin aggregation have been observed in the context of apoptosis induced by hyperthermia [36,37]. In the same images, similar abnormal coloration of the cytoplasmic region is observed that is likely triggered by the aggregation and rearrangement of cytoskeletal proteins caused by the heat treatment. Several other changes in the morphology can be seen including reduced branching of neurites and blebbing (bubble-shaped protrusions) as highlighted by the white arrows in figure 5f,g. The cell size sharply decreases after prolonged heat treatment as seen in figure 5e–h with gradual rounding of the cell shape indicating apoptosis and ultimate detachment from the surface indicated by halo around each cell.

Figure 5.

(a–h) Phase-contrast optical images of cells seeded on a PLL-coated glass surface. Temperature is increased from 37°C to 45°C over a period of 150 min during which cells changes morphology, ultimately shrink and become round which is characteristic of apoptosis.

3.4.2. Cell tracking analysis

For further quantification of cellular movement during heat stress treatment, we performed cell tracking analysis. Figure 6a–c represents the frames recorded at the beginning, during and at the end of the optical imaging experiment, respectively. Individual cell movement tracks are labelled and coloured in the frames. One clear observation from cell tracking is that the motion of cells changes from being directed (elongating and reaching out in a particular direction) with a nearly linear displacement track towards localized, confined movement. This change occurs simultaneously with the change in cell shape outlined in §3.4.1.

Figure 6.

(a–c) Phase-contrast images of SH-SY5Y cells at different time instances during the heating process. Coloured lines represent the tracks of various cells undergoing heat-induced stress. In (b), arrows are indicating the direction of motion of individual cells, whereas in (c), they are indicating the final positions of the cells. (d) Mean-square displacement plots of cells prior to the heat-stress phase of the experiment (first 16 min) indicating the presence of at least two categories of cell movements, fast and slow, while, a close fit to MSD(Δt) = 4DΔt + (νΔt)² is performed to extract diffusion coefficients and speed values. Similarly, (e) is MSD log–log plot for the last stage of experiment (150th–190th min). (f) Mean and standard deviation values for normalized change in the cell spreading (apparent overlap area) of the cells under consideration are plotted against time which peak almost halfway through and then rapidly decrease until the cells become spherical. (g) Total surface coverage shows a similar trend. (Online version in colour.)

To identify the movement of cells during the heat stress stage of the experiment, mean-square displacement (MSD) for each cell is calculated using the following expression for two-dimensional motion:

3.1

where, x(t), y(t) are the spatial position loci of a cell. By plotting the MSD versus Δt, the motion can be characterized as either confined random walk (figure 6d) using MSD(Δt) = 4DΔt^α or as a superposition of directed motion and diffusion using MSD(tΔ) = 4DΔt + (vΔt)², where D is the diffusion constant and α < 1. During the first 16 min of the time-lapse experiment, the temperature was not observed to increase more than 0.2°C and allows us to assume that cells are exposed to normal culture conditions. Cell motility was characterized during this phase to make the following heat-induced changes apparent and comparable. Roughly, two groups of cells were identified, one with faster motility and directed motion (v ∼ 1.5 μm min⁻¹), whereas the other shows a slower movement (v ∼ 0.38 μm min⁻¹) with a diffusion constant of D ∼ 2 × 10⁻² μm² s⁻¹ for both. These observed motilities take cell–cell interactions into account which slows down the overall speed and causes observed differences between the groups.

As discussed before, cellular motility depends on many environmental factors such as temperature, cell culture medium [38] and substrate properties such as rigidity, microstructure [39] and coating [40] as well as being dependent on the cell type or cell line and the seeding density. In particular, it has been shown that cellular confluency influences cellular behaviour and cell morphology as higher cell densities compromise the individual cell area impacting on cell morphology and motility [41]. Many intracellular processes are involved in cell migration. In the direction of cell migration, a leading edge is formed by extending flat membrane processes composed of an inner actin criss-cross network called lamellar ruffling. This is accompanied by the cell–substrate interactions in order to form adhesion points at the leading processes. Then, the cell body, including cytoplasm and organelles, is shifted, whereas the trailing cell rear is retracted. Thereby, temperature affects cell motility and related characteristics such as lamellar ruffling protrusion as shown by Shelden et al. [30] for human neuroblastoma cells. Lamellar ruffling has been observed to increase for temperatures up to 40°C (mild hyperthermia) but declines for further temperature increase. Furthermore, Hartmann-Petersen et al. [38] have studied cellular process domains as well as mean cell speed and area in murine fibroblasts under temperature conditions of 37–40°C and demonstrated an increase of characteristic values proposing the assumption that cells at slightly higher temperatures are more spread out and motile.

Similar observations have been made for the cell motility of 3T3 cells showing a peak between 36.5 and 38.5°C, with strongly declining motility towards lower or higher temperatures [36]. It is commonly known that prolonged treatment of cells at hyperthermic temperatures compromises cell viability and effectively triggers apoptosis. Treatment of cells with temperatures as high as 43°C for at least 1 h has been shown by Luchetti et al. [37] to already trigger apoptosis in human neuroblastoma cells. This is accompanied by changes in cell morphology such as blebbing, nuclear swelling, chromatin margination and changes in the cell shape eventually followed by cell rounding. Cytoskeletal proteins undergo aggregation and rearrangements leading to the final breakdown of microtubules. Additionally, cellular membrane characteristics are altered leading to cellular adhesiveness impairment [42,43].

The observed motility of cells along with the constant morphological readjustments within and around clusters continuously varies the viscoelastic loading of the QCM and contributes to the fluctuations in resonant frequency observed. Even when cells are observed under healthy and stable conditions, there is constant motility contributing to the variations in resonance frequency. Thus, as cells are stressed, their motility increases initially and then drops. Further, during the final part of the experiment, the remaining small and round cell bodies appear to describe random motion. To quantitatively characterize this cellular motion in order to find out whether this motion could contribute to the noise levels, images from 120 frames between 150th and 190th minutes were used. Fitting the tracking data to the above equations revealed that cells have a diffusion constant of approximately from 10⁻² to 10⁻³ μm² s⁻¹ indicative of Brownian motion (figure 6e). This confirms the hypothesis of cellular detachment as the temperature increases. Thus, following the final stages of apoptosis, cells are eventually either loosely attached or completely detached. The detached cell body is located above the penetration depth region, which accounts for the reduced fluctuations observed in zone 3 in the QCM experiments.

Apart from the cell motility data, another observable factor that correlates well with the fluctuation analysis is the cellular spreading obtained from the apparent cellular overlap area. To calculate the relative change in the spreading, we normalize instantaneous apparent overlap area with respect to final apparent overlap area where sphericity is observed for each cell. The procedure is repeated for the whole sample set and, mean and standard deviation values were calculated for the recorded frames. From figure 6f, it is quite evident that cellular spreading reaches a maximum midway, and this is also where maximum deviation values are observed. Depending on the immediate vicinity and state of the cells, some show a larger change in spreading, whereas others do not. As the cells undergo apoptosis, we observe an almost uniform overlap area across the sample set with reduced deviation values. Cells attach to surfaces through focal adhesion points and therefore a change in the spreading is likely to result in the increase of these focal contact points, leading to larger perturbations per cell. Also, as the spreading changes, viscoelastic loading near the QCM surface will also change. All this effectively changes the loading conditions of the QCM. It is clear from the calculations that the total surface coverage (figure 6g) increases by 34% first as the temperature increases and eventually decreases by 67% (relative to the initial surface coverage).

Both the motility and morphological data obtained from parallel optical experiments qualitatively correlate with the frequency fluctuations observed in the QCM. The prediction from the fluctuation analysis that on heating an initial increase in fluctuations is a result of an increase in activity as proved by the concomitant increase in motility and contact area (morphology change) observed in optical experiments. Similar observations of increased motility on a slight increase of temperature before declining in another cell line [36] boost the validity of our time-domain fluctuation analysis. Overall, the fluctuation analysis and its classification into the three different zones map directly to the cell state induced by thermal stress.

This paper provides a framework for establishing the relationship between fluctuations observed in QCM frequency data and biomechanical processes such as cell motility and shape change, not otherwise established through the standard analysis of QCM frequency shift and dissipation data. In order to establish a quantitative correlation between the observed frequency fluctuations and biomechanical processes, a predictive mathematical model for cellular biomechanical noise must be developed. The viscoelastic loading on the QCM includes contributions from: (i) viscoelastic loading of cells which is dependent on the attachment/detachment through focal contacts and, hence, the ‘activity’ of the cells (general model presented in the electronic supplementary material, information §A) and (ii) changes in the liquid loading owing to the movement and change in the apparent contact area of the cells resulting in the squeezing in or squeezing out of cell-culture within the approximately 250 nm decay length of the resulting shear acoustic wave generated in fluid. As the cells are well adhered to the surfaces in zone 1 and during most of zone 2, the cell–substrate distance is assumed to be more or less the same for the overall population. The results in this paper motivate a more detailed study and model development to establish the quantitative correlation between specific cellular biomechanical processes with the observed resonator frequency fluctuations as a logical next step.

4. Conclusion

Understanding motility and cell behaviour in response to stress is vital for studying several physiological processes and diseases. Cell motility and morphology are important measurable facets of cellular biomechanics while also being correlated with several underlying biochemical processes. These processes are also indicative of the physical state of the cell, and, any variations in the state induce variation in the biomechanical activity of the cell, often, describing apparently stochastic behaviour. In this work, we have studied the motility and cell behaviour of living neuroblastoma cells and the effects of thermal stress on them by QCM. Time-domain frequency fluctuation analysis is employed to provide insights into the complex behaviour of neuroblastoma cells and these data are optically correlated with changes in motility and morphology. The fluctuation analysis reveals three distinct types of behaviour which included the prediction of an increased state of activity of cells following an increase of temperature before a decrease of activity on account of cell death. Furthermore, the experiments provide interesting insight into the nature of cell–substrate interactions under healthy conditions and in response to thermal stress. The high degree of correlation between the frequency fluctuation data and optically recorded mechanical behaviour also provides the basis for future studies using the QCM as a means of inferring the nature of physical processes underlying cell–substrate interactions by quantifying the associated biomechanical noise.