A century of transitions in New York City's measles dynamics

Abstract

Infectious diseases spreading in a human population occasionally exhibit sudden transitions in their qualitative dynamics. Previous work has successfully predicted such transitions in New York City's historical measles incidence using the seasonally forced susceptible–infectious–recovered (SIR) model. This work relied on a dataset spanning 45 years (1928–1973), which we have extended to 93 years (1891–1984). We identify additional dynamical transitions in the longer dataset and successfully explain them by analysing attractors and transients of the same mechanistic epidemiological model.

1. Introduction

Mechanistic mathematical models are being used increasingly in the study of infectious diseases at the population level and are considered to be powerful tools for predicting epidemiological dynamics [1–3]. Successful modelling of observed epidemic patterns requires access to high-quality data, including disease incidence [4,5] (or disease-induced mortality [6,7]), demography (especially birth rates [8,9]) and changes in contact patterns (e.g. resulting from school vacations [10–12]).

In 1973, London & Yorke [11,12] published monthly measles incidence rates for New York City (NYC) spanning 1928–1973. These data have been extensively studied [4,5,11–15]. We extend the dataset to produce a time series of reported measles cases and concurrent demographic data (total population and total births), which spans the 93 years 1891–1984 (and for much of the incidence time series we increase the temporal resolution from monthly to weekly). Our process of data acquisition, compilation and quality-checking is detailed in §2 and all the data are available in the electronic supplementary material for this paper.¹

Measles exhibits recurrent epidemics, the frequency and amplitude of which change over long timescales. Much research over the last 40 years has attempted to reveal the biological and dynamical processes that give rise to these changing epidemic patterns, especially the transitions evident in NYC measles dynamics [5,11,14–18]. In this paper, by more than doubling the length of the NYC measles time series, we substantially enhance the opportunity to test hypotheses concerning the mechanisms that drive childhood disease transmission patterns.

We model measles dynamics in NYC using the susceptible–infectious–recovered (SIR) model, which is applicable to diseases for which acquired immunity is permanent [1,2,19]. There has been considerable debate in recent years concerning the most appropriate formulation of the SIR model for childhood infections such as measles [20–26]. We follow Krylova & Earn [6,27], who showed that for measles, the simplest sinusoidally forced SIR model—when suitably parametrized—makes identical predictions to more complicated versions of the model that include realistically distributed latent and infectious periods (details in §3.1).

2. Data compilation

The monthly measles data published by London & Yorke [11,12] span the years 1928–1973. We compiled data of finer temporal resolution (weekly), and extended the time series back to 1891, using a variety of documents stored at the NYC Academy of Medicine Library.² We also extended the monthly measles data forward to 1984 using vital statistics records available on the NYC Health Department website.

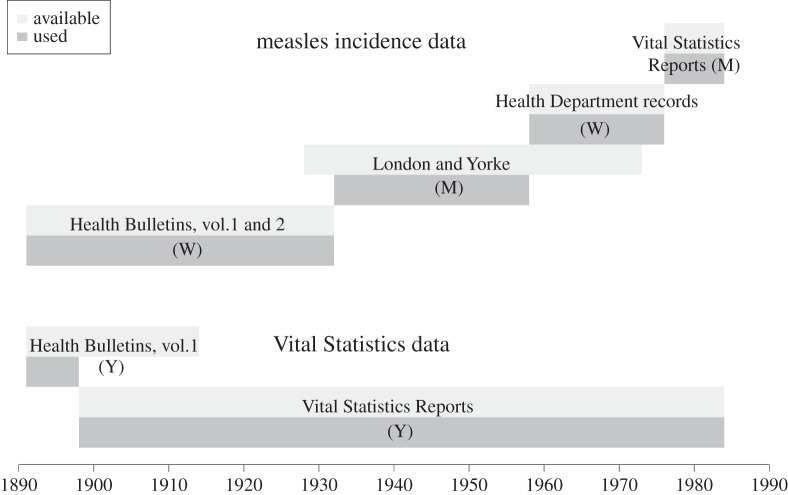
Figure 1 summarizes the data sources, including those from which we extracted birth rates. Below we briefly explain some of the issues involved in preparing the full time series for the analyses described in §3. Much greater detail about the data is provided in the electronic supplementary material, §S1.

Figure 1.

Summary of data available (light grey) and used (dark grey). W, M and Y indicate weekly, monthly and yearly sources, respectively. See electronic supplementary material, §S1 for a detailed description of sources and data compilation.

2.1. Adjustments and normalization

2.1.1. Births

Our data sources typically report vital statistics in NYC as a whole, but the boundary of NYC changed in 1898. Until the end of 1897, NYC included only the island of Manhattan. In January 1898, the city limits were redefined to include The Bronx, Brooklyn, Queens and Richmond. The Vital Statistics Reports are derived from census data and include yearly numbers of total population, births, deaths and infant mortality. We assume these data are reliable, but they extend back only to 1898 [28]. The weekly Health Bulletins include total population estimates and weekly birth counts for Manhattan only, and extend back to 1891. In order to merge these two sets, we aggregate the weekly birth counts yearly, and rescale the birth numbers such that the per capita birth rate from 1891 to 1898 meets a linear extrapolation of the per capita birth rate from 1898 to 1900. From 1900 to 1935, the Vital Statistics Reports present births and total population numbers only at 5-year intervals, representing the average of yearly values in each interval. For these years, constant values are used over each 5-year interval.

2.1.2. Infant mortality

The Health Bulletins do not contain infant mortality data, and we therefore extrapolate per capita infant mortality rates for 1891–1898 from 1898 to 1905 data. Infant mortality was very substantial in the early part of the time series. In 1898, 24% of all reported deaths were infants (in sharp contrast to 2% in 1984).

2.1.3. Measles cases

The NYC Health Department Weekly Bulletins normally reported the city-wide total number of measles cases, but in 1915 measles cases were reported only for three hospitals within the city. We rescaled the aggregated case reports for these three hospitals so that their yearly total matched the reported yearly sum in the 1915 Vital Statistics Report (see the electronic supplementary material, §S1.14 for details).

For most of the period for which we have measles data (1891–1984), we have weekly reports, but we have only monthly incidence for 1932–1958 and 1976–1984. In order to work with a weekly time series for the full length of the dataset, we created weekly time series from the monthly data as follows:

• — generate a series of weekly dates that occur on the same day of the week as the dates in the weekly time series segment preceding the monthly data;

• — for each new weekly time point, set its measles incidence equal to the number of cases reported for the month within which it falls, divided by the number of weekly points that fall within that month; and

• — at this stage, the artificially weekly time series contains four-to-five week blocks of constant incidence. To remove this spurious step-like structure, we smooth the artificial portion of the weekly time series with a 5-point moving average.

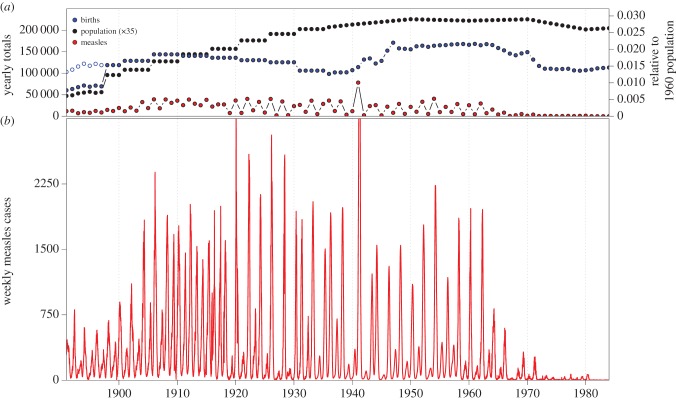
Figure 2 shows the resulting weekly measles times series, together with annual births and total population.

Figure 2.

NYC vital statistics and measles case report data, 1891–1984 (for compilation details see §2 and electronic supplementary material, §S1). (a) Annual births, estimated total population and reported measles cases. The NYC population was 1 657 000 in 1891 and peaked at 7 903 000 in 1950. Annual births peaked at 171 174 in 1947. Open circles indicate adjusted births, accounting for the change in the boundary of NYC in 1898 (see §2.1). (b) Weekly measles cases (as reported, except 1932–1958 and 1976–1984, for which weekly cases were estimated from monthly data; see electronic supplementary material, §S1). Two peaks are cut off in this plot (4671 cases reported for the week ending 31 Jan 1920 and 5016 cases estimated for the week ending 22 Mar 1941). (Online version in colour.)

2.2. Consistency checks

There is some temporal overlap among the various source documents (figure 1), which facilitates some cross-checking. From 1911 to 1932, we compared the yearly aggregated measles case reports from the Vital Statistics Reports with yearly sums of the data we acquired from the weekly Health Bulletins. From 1928 to 1932, we compared monthly aggregated case data from London & Yorke [11] with monthly sums of the weekly reports from the Health Bulletins. Finally, from 1958 to 1973 we compared monthly aggregated case data from London & Yorke [11] with monthly sums of the weekly reports from the Health Department records. In all cases, there is excellent agreement between previously published data and our newly digitized data (see the electronic supplementary material, §S1.8).

3. Analysis

In this section, we describe the tools that we use to examine measles dynamics in NYC. We begin with the SIR model (§3.1), and explain how we use the effective basic reproduction number 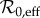(§3.2.1) and the estimated amplitude of seasonal forcing α (§3.2.2) to predict the periodicity of measles incidence in NYC (§3.3). We estimate 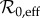and α as functions of time to generate an SIR-predicted frequency structure for measles in NYC throughout the time period 1891–1984. In §4, we compare the observed frequency structure of the incidence time series (using a continuous wavelet transform) with the SIR-predicted frequency structure.

3.1. The susceptible–infectious–recovered model

The deterministic SIR model [1,19] can be written [27]

3.1a

3.1b

3.1c

where S, I and R denote the numbers of susceptible, infectious and recovered (immune) individuals, respectively. Equations (3.1a,b) do not depend on the state variable R, so the full dynamics of the system can be described in two dimensions and the third equation can be ignored. The parameters are the rates of transmission (β) and recovery (γ), as well as the per capita rates of birth (ν) and death (μ). The mean infectious period is T_inf = 1/γ. As discussed below, N₀ refers to the population size at a particular ‘anchor time’ t₀ (as opposed to the current total populations size N = S + I + R). We will interpret the ‘birth rate’ ν more generally as the per capita rate of susceptible recruitment (relative to N₀) [2,4,5,13,27]. Here μ represents the per capita rate of death from natural causes (disease-induced mortality is assumed to be negligible).

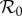. The basic reproduction number 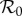is the average number of secondary cases caused by a primary case in a wholly susceptible population [1,29]. If births balance deaths, then for the SIR model 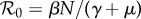[1]. In our situation (3.1), typically ν ≠ μ and [27]

3.2

We assume that the susceptible recruitment rate ν changes slowly enough that 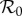can be defined at a given time by treating ν as a constant. Secular changes in ν can induce dynamical transitions [2,4,5,13,27], as we discuss in §3.3.

3.1.1. Seasonality

To account for seasonally varying transmission arising from aggregation of children in schools [2,5,11,15], we assume the transmission rate is seasonally forced,

3.3

where β₀ is the mean transmission rate, α is the amplitude of forcing and time t is measured in years. We use the simple sinusoidal forcing function (3.3) rather than more realistic term-time forcing [5,17] because the two yield virtually identical dynamics (for different α values) [5,27]. Introducing time-dependence into the transmission rate generally affects the basic reproduction number 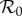[30,31]; however, for the SIR model (3.1), inserting the mean transmission rate β₀ in place of β in equation (3.2) is correct [32].

3.1.2. Susceptible–infectious–recovered versus susceptible–exposed–infectious–recovered

Most previous work on measles dynamics has been based on the SEIR model (e.g. [4,5,14,15]), which includes an additional class (E) of exposed individuals who are infected but not yet infectious. Because the mean latent period for measles (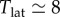 days, [1]) is long relative to the mean infectious period ( 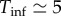days, [1]), it is natural to assume that the SEIR model will represent measles dynamics better than the simpler SIR model, which includes no latent period. However, Krylova & Earn [27] showed that the SIR model displays virtually identical dynamics to the SEIR if the length of the mean generation interval ( 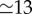days) is used for the mean infectious period in the SIR model. This dynamical correspondence holds also for versions of the SIR and SEIR model with realistically distributed stage durations, rather than the exponential distributions implied by equation (3.1) [27]. We therefore use the SIR model (3.1) with T_inf = 13 days.

3.2. Parameter estimates

Table 1 summarizes our estimated parameter values. There are two categories of parameters, those that are assumed to be fixed and those that vary in time. Our analysis in §3.3 involves predicting the dynamical effects of changes in 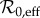(which depends on changes in susceptible recruitment ν through births B and proportion vaccinated p, §3.2.1) and changes in the amplitude of seasonal forcing α.

Table 1.

Demographic and disease parameter estimates for NYC.

parameter	meaning	estimate	source
fixed parameters
γ−1	mean generation time	13 days	[1,27]
μ	natural death rate	0.02 yr–1	[5]
N0	population in 1960	7 782 000	[28]
ν0	births in 1960 /N0	0.0214	[28]
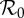
	basic reproduction number in 1960	17	[1,4,5]
parameter	meaning	range	source
time-varying parameters
B	births per year	98 507–171 174	[28]
Dinfant	infant deaths per year	1540–16 609	[28]
p	proportion vaccinated	0–0.66	[33]
ν	susceptible recruitment per year	0.00473–0.0214	equation (3.4); §3.2.1
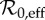
	effective	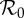3.86–17.5	equation (3.5); §3.2.1
α	amplitude of seasonal forcing	0.11–0.21	equation (3.3); §3.2.2

Following previous work [4,5,27], we estimate 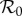in 1960 by assuming the standard estimate for England and Wales in 1960 [1, p. 70] also applies to NYC. Susceptible recruitment in 1960, ν₀, arises entirely from births because the measles vaccine was not yet available and immigration of susceptibles into NYC was negligible (most immigrants would have been immune).

Note that the natural death rate indicated in table 1 yields a mean lifetime μ⁻¹ = 50 years, which is much shorter than the true mean lifetime. This intentional discrepancy accounts partially for the long tail in the implicitly assumed exponential distribution of lifetimes. Our results are insensitive to the value of μ because most people contract measles as children, and immune individuals do not affect transmission.

3.2.1. Effective basic reproduction number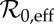

Because our estimate of 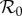(equation (3.2)) is for 1960, we take our ‘anchor time’ to be t₀ = 1960. Susceptible recruitment (ν) is defined in terms of births (B), infant mortality (D_infant), the population size at the anchor time (N₀) and vaccine uptake (p),

3.4

Infant mortality is deducted here because it represents a large reduction in new susceptibles early in the NYC time series (see §2.1). The effective 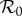is [2,5,27]

3.5

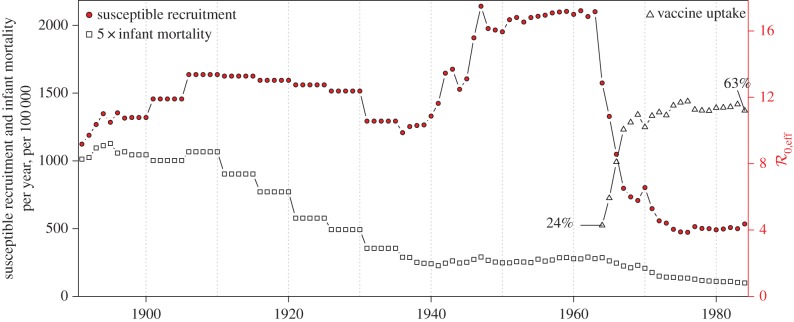
Thus, the time series 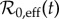is strictly proportional to ν(t) (figure 3).

Figure 3.

Susceptible recruitment ν(t) in NYC, as defined by equation (3.4). From the scaling given in equation (3.5), the effective basic reproduction number 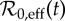is proportional to ν(t) and its value is indicated on the right axis. Annual infant mortality (scaled by five for clarity) and estimated annual vaccine uptake (since 1964) are also shown. (Online version in colour.)

3.2.2. Seasonal forcing amplitude

We estimate the seasonal forcing amplitude α as a function of time using the method of Krylova [6, ch. 4]. Krylova improved on the earlier method of Fine & Clarkson [34] for estimating β(t) by allowing for reporting delays, accounting for natural mortality, and removing the restriction that the generation interval must be equal to the observation interval, requiring instead that the generation interval is an integer multiple of the observation interval.

Krylova's method [28, ch. 4] begins by reconstructing the time series of the number of susceptible individuals in the population via

3.6

The symbols here refer, for the time interval from t to t + Δt, to the number of susceptibles (S_t), the proportion of newborns vaccinated (p_t), the number of births (B_t, adjusted for infant mortality), the proportion of cases reported (ρ_t), the number of cases reported (C_t), the number of deaths from natural causes (D_t) and the total population size (P_t). The time interval between reports is Δt (one week in our case) and the average reporting delay is T_report (taken to be two weeks). Following Fine & Clarkson [34], we infer the reporting efficiency ρ_t by assuming that all surviving individuals eventually contract measles (hence we estimate ρ_t as a moving average of measles cases divided by a moving average of susceptible recruitment).

As in the Fine & Clarkson [34] algorithm, an estimate of the proportion of the population susceptible is required at a single time point. We assumed that at time t = 1900 this proportion was S₀/P₀ = 0.05, which is near the endemic equilibrium of the unforced SIR model [1]. Our results are not sensitive to the precise value of S₀ assumed. A bad guess leads to an obvious spurious trend in the reconstructed susceptible time series. See Krylova [6, p. 134] and deJonge [35, p. 16] for greater detail on this issue.

After reconstructing the full time series of susceptibles {S_t}, the transmission rate at time t is estimated via [6, eqn 4.12]

3.7

Krylova's method requires that the disease generation interval be an integer multiple of the observation interval. The mean generation interval for measles γ⁻¹ = 13 days, and following [6,34] we approximate this as T = 2 weeks (table 1).

Given the full time series {β_t}, the seasonal pattern for a given year y containing reporting dates t_i, i = 1, … ,52, can be expressed

3.8

where angle brackets refer to the average over the 52 reporting dates in year y. The underlying pattern of seasonality should not vary substantially from year to year (since population contact structures do not change significantly from year to year). To reduce the noise in the inferred seasonality, 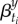, we obtain the median seasonal pattern over a 9 year period centred on the focal year y. Thus, we replace eac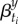h with

3.9

The estimated seasonal pattern (3.9) is our observational equivalent of the term α cos 2πt in the sinusoidally forced transmission rate (3.3) that we use in the SIR model (3.1). However, in order to use the sinusoidally forced SIR model to make predictions, we must estimate the amplitude (α) of sinusoidal forcing to which the observed forcing pattern (3.9) is equivalent. 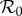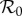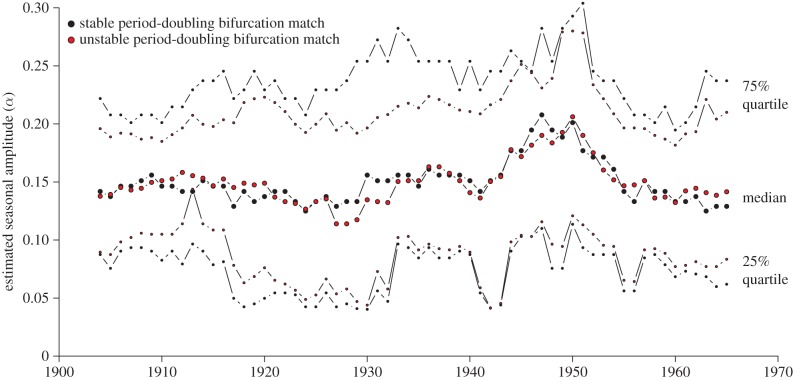Previous work [5] has indicated that such an equivalence does exist and can be found by matching stable or unstable period doubling bifurcation points—along the main branch of the bifurcation diagram—that occur when forcing the SIR model with a sinusoidal versus observed seasonal pattern; the match is accomplished by making a sequence of bifurcation diagrams with different sinusoidal forcing amplitudes (α) until an α value is found that yields a bifurcation diagram in which the focal bifurcation occurs at the same 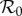value as in the bifurcation diagram made with the observed seasonal forcing pattern. We separately matched stable and unstable period doubling bifurcations and found negligible difference in the estimated α. We also varied the averaging window from 5 to 13 years and found no significant differences from the 9 year window specified above. In order to quantify uncertainty in one α estimate, we computed 25% and 75% quartiles of the seasonal pattern in (3.9) along with the median. For these quartiles, we matched the stable and unstable period doubling bifurcations, as we did for the median. Our estimated α time series is shown in figure 4.

Figure 4.

Estimates of the amplitude (α) of seasonality of measles transmission, from 1904 to 1965, based on 9-year time windows around each year (details in §3.2.2). The measles incidence data after 1970 (after mass vaccination was in full force) is much noisier and estimating α is much more difficult. We assume α remained roughly constant after the final point shown in the graph. (Online version in colour.)

We estimate α only from 1900 to 1970. We avoid pre-1900 data due to the previously mentioned change in reporting area in 1898 (§2), and lack of data outside Manhattan. We do not produce estimates beyond 1970 because case sampling is worse, resulting in poor and unreliable reconstruction. Since we use 9-year windows to produce estimates, and data from 1900 to 1970, we produce α estimates for the years 1904–1965. The temporal progressions of both our predictor parameters (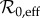 and α) are shown in a figure in §3.3.3 for the full time series.

3.3. Transition analysis

Previous work has shown that analysis of the deterministic SIR model (3.1) is sufficient to predict changes in the frequency structure of observed temporal patterns of infectious disease incidence [2,4,5,27] or mortality [6] observed over many decades. The methodology has been described in detail previously [27, §2.2]. Here we briefly summarize our analysis as we apply it to the newly extended NYC measles times series, emphasizing the aspects of our approach that differ from previous transition analyses.

3.3.1. Features of the data that we would like to explain

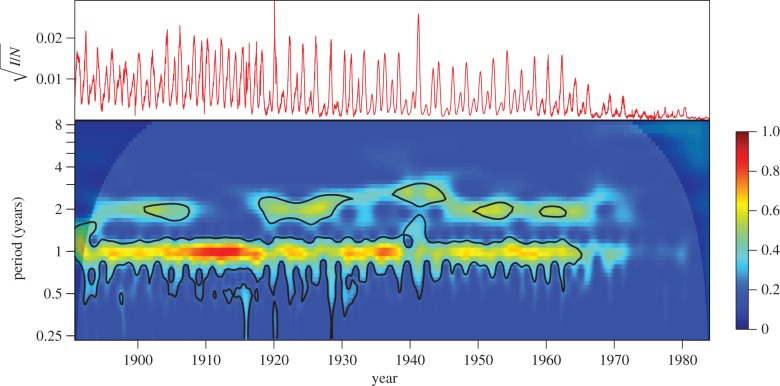
Figure 2 presented all the data used for our analyses. Figure 5 displays the normalized NYC measles time series again, but in two different ways that highlight the changes in frequency structure that we seek to understand. The top panel of figure 5 shows weekly normalized measles on a square root scale, suppressing epidemic magnitude in favour of exposing periodic structure. The bottom panel of the figure shows the corresponding continuous wavelet transform [36–40], which reveals the dominant frequencies at each point in time.

Figure 5.

Observed measles dynamics in NYC from 1891 to 1984. (a) Square root of measles case reports, normalized by total concurrent population. (b) Colour depth plot of a continuous wavelet transform of the square root of normalized observed NYC measles cases (colour warmth scales with spectral power and 95% significance contours are shown in black). Shaded regions in the upper left and right indicate the cone of influence [36]. (Online version in colour.)

The main features of the wavelet transform in figure 5 are two spectral peaks at almost all times. Throughout most of the time series, there is a peak at a period of 1 year. The period of the second peak varies between 2 and 3 years (and is absent from about 1912 to 1915). Can we explain the existence and spectral position of these peaks over the course of the time series?

3.3.2. Attractor and transient periods as functions of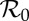

For any given parameter set and initial conditions, the solution of the SIR model (3.1) yields predicted dynamics that can be compared with the observed time series. In particular, two periods can usually be extracted from (non-chaotic) SIR solutions: (i) the period of the attractor that is reached asymptotically and (ii) the period of the transient during approach to the attractor. The attractor period—or resonant period—of the SIR model is always an integer multiple of the 1-year forcing period and is typically inferred from bifurcation diagrams of the stroboscopic map associated with the model [5]. The transient period—or non-resonant period—can be a time of any length and is obtained by a linear perturbation analysis of the associated attractor [4]. (For an attractor with period k, its transient period T_k is given by 2πk/|Arg(λ_k)|, where λ_k is the dominant eigenvalue of the associated stroboscopic map [4,13].) Both resonant and non-resonant periods are expected to be observed in real incidence time series because demographic stochasticity sustains transient dynamics [4,41].

Naively, there are many model parameters (β, γ, ν, μ, N₀, α) and possible initial conditions (S₀, I₀) to consider when attempting to make predictions using the SIR model (3.1). However, the relationship between susceptible recruitment and effective reproduction number (equation (3.5)) can be exploited [2,4,5,27] to reduce the relevant number of parameters to one: predictions can be made from the SIR model (3.1) by considering only how periodicity of solutions varies as a function of the basic reproduction number 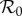(equation (3.2)) with all other parameters fixed (provided the amplitude of seasonality α can be taken to be constant throughout the observed time series).

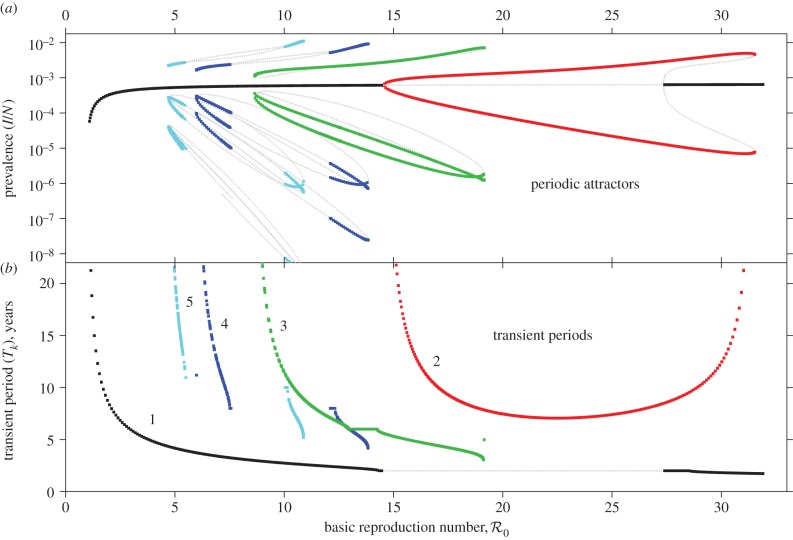
Figure 6 presents predicted NYC measles dynamics as a function of 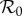. The top panel is a bifurcation diagram for the SIR model (3.1) and the bottom panel shows the transient periods associated with each attractor. From these diagrams, we can read off the predicted attractor and transient period for any given 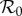. For 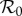values for which multiple attractors coexist, predicted dynamics are history-dependent and demographic stochasticity can lead to switching among attractors [5,44]; however, in real incidence time series we are unlikely to detect attractors with periods other than 1 or 2 years, for a number of reasons:

• (i) attractors with periods longer than 2 years typically have small attracting basins,

• (ii) long-period attractors typically have unrealistically low prevalence levels,

• (iii) brief excursions of long-period attractors will not be distinguishable from noise and

• (iv) in the presence of noise, some long-period attractors are indistinguishable from lower period attractors.

Figure 6.

Attractor analysis diagram for measles parametrized for NYC, constructed using XPPAUT [42]. This figure is similar to Krylova [6, fig. 9], but the seasonal amplitude here is α = 0.12 rather than α = 0.08. (a) For each value of 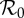on the x-axis, yearly values of the infected SIR compartment are shown (on a log-scale) from long-term solutions of the system (ignoring transient dynamics). The light grey lines show repellers, which can have important influences on dynamics [43]. Parameter values used are μ = ν = 0.02 yr⁻¹, α = 0.12, 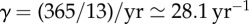. Longer period attractors exist for this parametrization of the SIR model, but their basins of attraction are small and they have not been observed in real-world systems. Our analysis is focused on the main branch, which shows, from left to right, a stable period doubling and an unstable period doubling bifurcation. (b) Transient periods associated with each of the attractors displayed in (a), computed as in [4,27]. (Online version in colour.)

The predicted transient periods for non-annual attractors are all very long; in practice, only the transient period associated with the annual attractor is likely to be observable. The degree of spectral power generated by a transient varies with the system's proximity to the associated attractor. During time intervals when the system is very close to the attractor, the transient period can be undetectable (we demonstrate this effect through stochastic simulations in the electronic supplementary material, §S2).

3.3.3. Attractor periods as functions of both 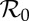and α

For the era (1928–1972) of NYC measles dynamics that has been studied previously [4,5,11,27], it was reasonable to assume that the amplitude of seasonal forcing (α) was roughly constant. With our much longer time series going back to 1890, this approximation is less likely to be valid. We therefore estimated the amplitude of time-varying seasonality in §3.2.2. To make use of estimates of both 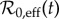and α(t), we need a two-dimensional equivalent of figure 6, showing how attractors and transients vary as functions of both 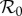and α.

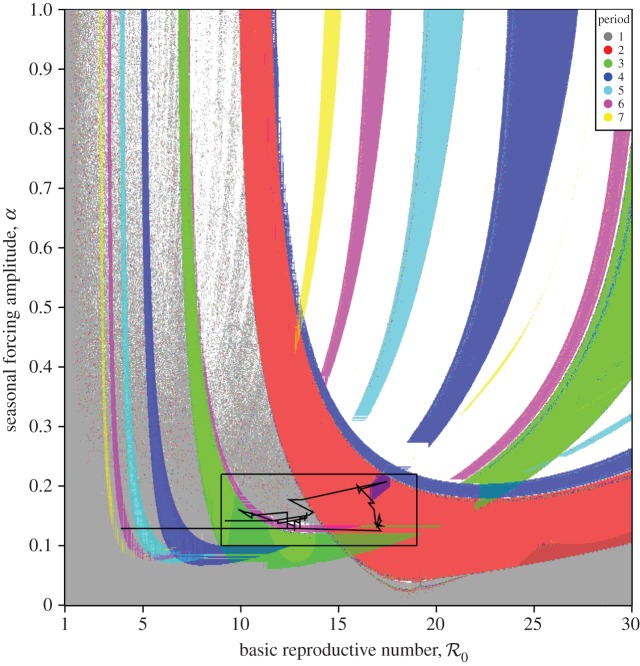
Figure 7 presents a two-dimensional bifurcation diagram for the SIR model (3.1), which shows the regions of the 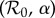parameter plane in which attractors of various lengths exist. The black curve shows the estimated trajectory of NYC measles in this parameter plane (based on the median value of α shown in figure 4). The boxed region is shown on a larger scale in figure 8, and the last two digits of many years are marked along the 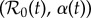curve.

Figure 7.

Periodic attractors in the sinusoidally forced SIR model (§3.1) as a function of basic reproduction number 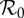and seasonal amplitude α (μ = ν = 0.02 yr⁻¹, γ = 28.1 yr⁻¹). The black curve shows the trajectory of NYC measles in this parameter plane, based on our estimates of 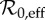and α for the period 1891–1984. The colour of each point represents the period (in years) of the attractor to which the SIR system has converged. Partial colour transparency allows us to display the existence of multiple attractors for given 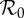and α. A systematic exploration of the full range of initial conditions for each parameter pair 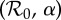was not computationally feasible, but we integrated the model from the initial state variables S₀ = 10⁻¹ and I₀ = 10⁻³. We computed the grid by row from left to right, right to left, and by column from top to bottom, and bottom to top. In each case, after the initial point on a row or column, we use the final conditions of the simulation for one point as the initial conditions for the next. Results from all four grid computations are overlaid. White regions on the plot indicate either periods longer than shown in the legend or lack of simulation convergence to any periodic attractor.

Figure 8.

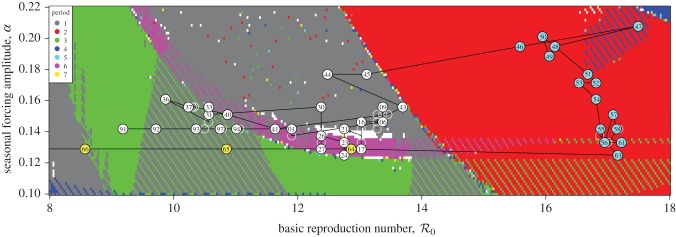
Zoomed-in and enhanced version of the boxed region in figure 7. The estimated yearly parameter time series 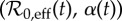is overlaid on the colour-coded attractor plot. Different epochs have been marked with different coloured circles; 1891–1945 white, 1946–1963 teal and 1964–1984 yellow. The number in each circle is the last two digits of year t for t in the range 1891–1984 (some years are marked with white circles and no year for readability). Where more than one resonant period is possible (depending on initial conditions), coexistence of multiple attractors is shown with alternating stripes.

4. Results

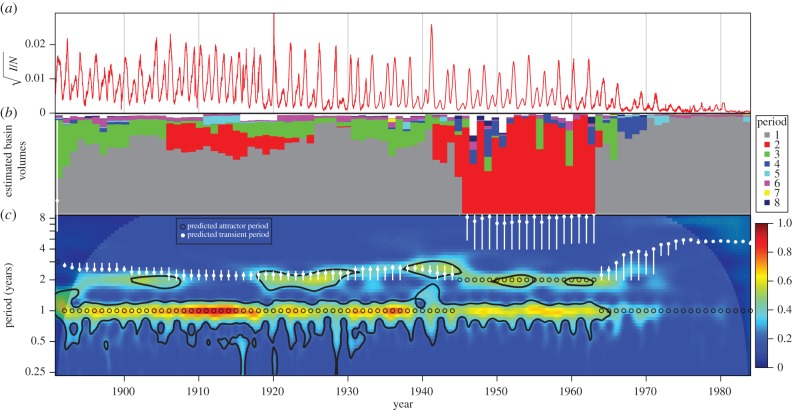
We summarize our results in figure 9. As in figure 5, figure 9a,c shows the NYC measles incidence time series and wavelet spectrum, which we aim to explain using the SIR model (equation (3.1)).

Figure 9.

Comparison of predicted versus observed measles dynamics in NYC from 1891 to 1984. (a) Square root of measles case reports, normalized by total concurrent population. (b) Approximate volumes of basins of attraction near the observed NYC measles incidence for each year from 1891 to 1984. For each year, we display the proportion of 10 000 simulations that reach each period. See §4 for details. (c) Colour depth plot of a continuous wavelet transform of the square root of normalized observed NYC measles cases (colour warmth scales with spectral power and 95% significance contours are shown in black). The predicted attractor and transient periods are overlaid (only the periods of annual and biennial attractor transients are short enough to appear on this graph and to be observable). Unfilled black circles indicate predicted attractor periods that are consistent with the observed data.

Figure 9b shows predicted attractor periods for each year from 1891 to 1984. For each year, the SIR model was solved for 10 000 distinct initial states and the period of the attractor to which the solution converged was recorded. The coloured bands show the proportion of runs that converged onto an attractor of the period indicated in the legend; thus the relative lengths of the coloured bands can be viewed as estimates of the relative volumes of the basins of attraction associated with each periodic attractor. The collection of initial states for a given year (t) was chosen as follows:

• — the initial proportion susceptible (S₀) was varied from 80% to 120% of the proportion that would be susceptible at equilibrium (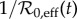) if the system were unforced;

• — the initial prevalence (I₀) was varied throughout the range of observed weekly incidence (before 1963 for the pre-vaccine era and after 1963 for the vaccine era);

• — a 100 × 100 grid of initial states was considered in the region of the (S₀, I₀) plane specified above. For each grid point, the model parameters were set according to table 1, except that the estimated 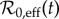(figure 3) was used in place of 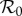, and the seasonal amplitude (α) was chosen at random from a uniform distribution between the lower and upper quartile of the estimated α(t) (figure 4) for the year in question.

In years for which multiple attractors are predicted, any of these attractors could occur in a particular realization of the underlying stochastic process. In each year, we take the predicted attractor period to be that of the attractor to which the greatest number of simulations converged. Black circles indicate these attractors on the wavelet spectrum. White vertical bars identify the possible ranges of transient periods associated with these attractors (an annual attractor for most of the time series, but a biennial attractor from 1946 to 1963). The heavy white dot on the white bars indicates the median transient period for the simulations associated with the given year.

The qualitative agreement between predicted and observed spectral peaks in figure 9 is very good. In greater detail

• 1891–1945

  • Observed behaviour: the wavelet spectrum has a substantial peak at a period of 1 year throughout this time interval, and a secondary peak near a period of 2 years is evident except during 1909–1917. From 1909 to 1917, the incidence time series shows very similar annual epidemics.
  • Predicted periods: panel b shows that an annual attractor exists throughout this year range with a larger estimated basin of attraction than other attractors. Other longer period attractors with smaller estimated basins of attraction coexist with the annual for some years (also see figure 8, white circles). The median predicted transient period varies between 2.20 and 2.58 years over this time span and is slightly longer than the observed (2 year) secondary peak period before about 1905.
  • Interpretation: since the wavelet spectrum does not show power near period 3 at the beginning of the time series (excluding information inside the cone of influence), we conclude that the real system was near the period 1 attractor initially. The system appears to remain near the period 1 attractor for the duration of this time interval, which can be explained by the consistently high volume of attraction of the annual attractor. Where they exist, longer period coexisting attractors might influence the dynamics, but their effects would likely be indistinguishable from noise because the temporal segments in question are too short for multiple cycles of these longer period attractors to be completed. The power near period 2 throughout this time interval is always close to the predicted transient period associated with the period 1 attractor. The power observed at a transient period in an infectious disease time series varies significantly, as stochasticity affects the proximity of the system to the periodic attractor. The temporary absence of power near period 2 is a phenomenon that we have reproduced with the estimated parameter values using stochastic simulations (electronic supplementary material, §S2).
• 1946–1963

  • Observed behaviour: there is substantial power at precisely periods 1 and 2 years throughout this time interval.
  • Predicted periods: the greatest estimated basin volume throughout this interval is occupied by a period 2 attractor, with coexisting longer period attractors also present (also see figure 8, teal circles).
  • Interpretation: the multi-year attractors that are identified always display power at a 1-year period in addition to the period of the attractor because the multi-year epidemic pattern involves epidemics every year. Since a biennial attractor is the most probable throughout this time interval, we expect to see the observed power at 1 and 2 years.
• 1964–1984

  • Observed behaviour: the wavelet diagram shows power near period 1 year throughout the time interval, and power near periods 2 and 3 years up to 1973. The time series appears very noisy and a dramatic drop in incidence is evident beginning in 1965.
  • Predicted periods: an annual attractor exists throughout this time interval, with sporadically coexisting attractors of periods 3–6 years. No biennial attractor is predicted (also see figure 8, yellow circles).
  • Interpretation: vaccination was introduced in NYC in 1963, accounting for the dramatic drop in cases. As cases drop, dynamics are governed more by demographic and extrinsic stochasticity than periodic attractors. This accounts for the weakness of spectral peaks. We conclude that the system transitioned from a biennial attractor to an annual attractor near the beginning of this time interval, which is consistent with predicted behaviour. The weak spectral peak at period 1 year until 1980 suggests that the system remained near the annual attractor until the end of the time series.

5. Discussion

The NYC measles incidence data published in 1973 by London & Yorke [11,12] has inspired a great deal of research on infectious disease dynamics [2,4,11,14,15]. Given the impact of the London and Yorke time series (monthly reported measles cases from 1928 to 1972), we were motivated to extend the dataset to more than twice its previous length (1891–1984), and in so doing we obtained long spans of higher quality (weekly rather than monthly) data. To complement the measles data, we compiled annual birth and population data for NYC for same year range. We collected data from a number of distinct sources, which contained some overlapping years, allowing us to perform sanity checks and either verify data quality or make minor corrections.

Previous work [4,5,27] has used mechanistic epidemic models to understand transitions in measles dynamics in NYC from 1928 to 1972. These analyses made predictions of dynamical transitions based on changes in the effective basic reproduction number 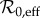(estimated from changes in susceptible recruitment arising from births and vaccination), and a fixed amplitude of seasonal forcing (α). For our analysis of transitions in the newly extended time series, we generalized this approach to allow for changes in both 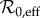and α and estimated both over the course of the observed time series.

There is excellent agreement between our SIR model predictions of dominant periods and the observed frequency structure in the data quantified by a continuous wavelet transform (figure 9). All observed transitions can be explained using the deterministic SIR model by a combination of changes in birth rate, vaccination and the effect of demographic stochasticity preventing transient oscillations from damping out [41,45].

We did not, in this paper, attempt to predict the relative magnitudes of the observed spectral peaks in the NYC measles wavelet spectrum. Doing so requires analysis of the stochastic SIR model, either by simulation [2,4] or by analytical or semi-analytical methods that have begun to be applied to infectious disease dynamics in recent years [16,46].

We did point out an unusual feature of the new earlier segment of the NYC measles time series from 1909 to 1917, namely the complete lack of spectral power at any period other than 1 year, even though an observable transient period near 2 years is predicted. As a proof of principle, we showed in electronic supplementary material, §S2 that precisely this behaviour can be reproduced in stochastic SIR simulations, but we did not quantify the probability of such behaviour occurring. One possible direction for future work would be to examine the wavelet spectra of large numbers of realizations of the stochastic SIR model with the parameters estimated for NYC measles (including the vaccine era during which demographic stochasticity plays a much larger role); analysing such a collection of simulations would allow us to estimate the probability distribution of relative transient power at each point along the time series, and more generally the probability of observing a time series very similar to the real data. This would be computationally expensive, but seems likely to be enlightening and could substantially enhance our understanding of dynamical transitions in recurrent patterns of infectious disease epidemics.

Funding statement

We were supported by an Ontario Graduate Scholarship (K.H.) and the Natural Sciences and Engineering Research Council of Canada (D.J.D.E.).