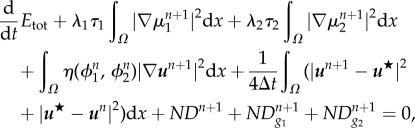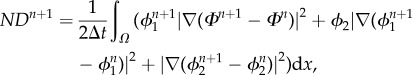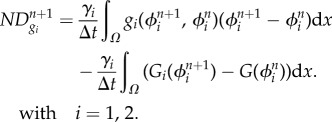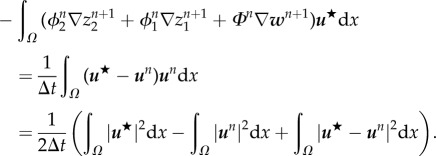Multicomponent model of deformation and detachment of a biofilm under fluid flow

Abstract

A novel biofilm model is described which systemically couples bacteria, extracellular polymeric substances (EPS) and solvent phases in biofilm. This enables the study of contributions of rheology of individual phases to deformation of biofilm in response to fluid flow as well as interactions between different phases. The model, which is based on first and second laws of thermodynamics, is derived using an energetic variational approach and phase-field method. Phase-field coupling is used to model structural changes of a biofilm. A newly developed unconditionally energy-stable numerical splitting scheme is implemented for computing the numerical solution of the model efficiently. Model simulations predict biofilm cohesive failure for the flow velocity between 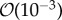and 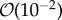m s⁻¹ which is consistent with experiments. Simulations predict biofilm deformation resulting in the formation of streamers for EPS exhibiting a viscous-dominated mechanical response and the viscosity of EPS being less than 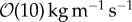. Higher EPS viscosity provides biofilm with greater resistance to deformation and to removal by the flow. Moreover, simulations show that higher EPS elasticity yields the formation of streamers with complex geometries that are more prone to detachment. These model predictions are shown to be in qualitative agreement with experimental observations.

1. Introduction

Biofilms are microbial aggregates embedded in a self-produced matrix of extracellular polymeric substances (EPS). They are ubiquitous in nature and carry out important functions in biological systems [1] and engineering applications [2,3]. On the other hand, biofilms may play detrimental roles such as contributing to the fouling of industrial infrastructure and harbouring pathogens in water distribution systems. Biofilms also cause dental plaque and contamination of medical devices and implants, and can increase antibacterial resistance [2,4]. It is estimated that up to 80% of clinical infections are biofilm associated [4].

Biofilms often form in hydrated environments where they are subjected to fluid flow-driven shear forces. External fluid flows can cause biofilm deformation, breakup and detachment, which can have significant effects on biofilm structure and function, and drastically change biofilm activity [5]. Thus, understanding and predicting biofilm constitutive behaviour (i.e. stress-related deformation and detachment) is of prime importance for many applications. For example, biofilm control is important for improving the efficiency of water and waste water treatment, dental plaque removal and cleaning medical materials and surfaces in hospitals. However, it is not fully understood how biofilms respond to external flow environment, and how mechanical properties of different components of the biofilm contribute to its structural stability.

Rheological studies have shown that biofilms exhibit viscoelastic behaviour [6–8]. Conceptually, biofilms are made of dispersions of colloidal particles (cells, mineral precipitates, debris) in an EPS hydrogel composed primarily of cross-linked polysaccharides and proteins [9,10]. Based on this observation, Alpkvist & Klapper [11] used an immersed boundary method to model biofilm deformation and detachment under fluid shear stress. Their novel approach treated the biomass as a viscoelastic, breakable network of springs embedded in fluid flow, and simulations demonstrated how a ‘mushroom’-shaped biofilm detached under the impact of flow.

In [12–14], a phase-field approach [15,16] was used to model biofilm interaction with external flow using a one-fluid multiphase formulation. In these papers, the biofilm was treated as a single incompressible fluid consisting of a polymer network. The mixing or cohesion energy was described using free-energy-based thermodynamic interactions and intermolecular forces between the different phases [12,13]. Each phase or component was described by a volume fraction or concentration that played the role of a phase-field variable. Other biofilm constitutive and fluid–structure interaction models have also been developed using discrete and continuum approaches [17–24]. (For comprehensive reviews, see [25–27] and references therein.) Kinetic theory [28] and network theory [29] polymer models were also implemented recently to study complex constitutive behaviour of biofilms.

Many of these models focus on slow timescale events such as biomass growth or decay, whereas only a few papers have considered fast flow–biofilm interaction or biomass detachment [11,13,25,26,28], and tried to delineate the effect of viscoelasticity of biomass on the constitutive behaviour and failure of the biofilm under different flow conditions. Yet, previous experimental studies indicate that biofilm sloughing detachment (i.e. one of biomass loss mechanisms) is significant for determining the quasi-stationary state of biofilms. Here, the growth of a biofilm is balanced by its detachment, as opposed to erosion of a small number of cells [25]. Hence, it is important to incorporate a realistic representation of the mechanical properties and constitutive relations in biofilm models [25,26].

In this paper, a novel biofilm model for studying the effect of mechanical properties of biofilm on its interaction with a fluid flow environment is developed. Biofilm is assumed to be an incompressible complex fluid made of a ternary mixture of bacteria, EPS and solvent phases. Biomass growth and decay are neglected, because timescales of these events are of the order of hours and minutes and we are interested in the hydrodynamic process affecting biofilm deformation and detachment which is of the order of seconds [26]. An energy-based system is obtained by using energetic variational principles [30–32] and phase-field method to simulate interactions between biofilms and fluid flows. The energetic variational procedure is used to derive the coupled system, in which individual phases are coupled together using the phase-field approach to take into account their mechanical effects. As a result, the model describes biofilm heterogeneity by incorporating biofilm's structural variability. This is important, because distributions of bacterial cells and EPS are highly non-uniform. Specifically, viscoelastic properties of EPS are taken into account, and the bacterial phase is represented as a viscous fluid. In reality, biofilm viscoelastic deformation may occur at timescales varying from seconds to days [25]. In our model, the timescale of the biofilm viscoelastic response is determined by the value of the viscoelastic relaxation parameter, separating solid-like and fluid-like responses from each other [6].

The new model is used to predict how mechanical properties of the biofilm influence the formation of filamentous structures known as streamers, which can enhance the mass transfer [22] and cause catastrophic flow clogging effects [33]. Simulations show that the model is capable of determining the effects of mechanical properties of the components of the biofilm on fluid–biomass interaction. The effects of structural heterogeneity on biofilm deformation and detachment are also studied. Numerical results are shown to be in a qualitative agreement with experiments reported in the paper. The model also predicts cohesive failure of the biofilm leading to biomass detachment. Cohesive failure is shown to be effected by the intrinsic properties of the biofilm. Indeed, the model predicts that the resistance of the biofilm to the external fluid flow is largely attributed to the viscous force of the EPS network. Simulation results indicate that a biomass with lower viscosity of the EPS tends to bend and form streamer-like structures that can detach owing to shear stress of the flow. Longer EPS elastic relaxation results in rippling the surface of the biofilm and formation of complex streamers under relatively strong flow shear stress. This implies that a biofilm with a more elastic EPS network tends to be unstable under flow and that small perturbations applied to the biofilm interface may result in formation of secondary complex structures.

This paper is organized as: §2 provides experimental motivation for the model and describes experimental fluid–biofilm structure interaction data. The derivation of the model is presented in §3. The numerical scheme developed to solve the model equations is described in appendix A. Simulations and predictive results are discussed in §4. Finally, conclusions are discussed in §5.

2. Experiments to test the mechanical properties of biofilms

Experiments were performed to obtain a better understanding of how the mechanical properties of a biofilm influence its response to fluid flow. In particular, we assessed how different shear stress conditions affect biofilm detachment. For this purpose, we used biofilms obtained from a mixed culture membrane biofilm reactor (MBfR) [34]. Biofilm samples were obtained from a 250-ml MBfR, inoculated with activated sludge from a local wastewater treatment plant. Acetate was continuously supplied to the reactor and pressurized air was supplied to the lumen of the hollow-fibre membranes. The reactor contained a bundle of 480 individual hollow-fibre membranes, each with an 80-µm external diameter. The biofilm reached a thickness of several millimetres after 60 days. At that time, a biofilm portion of around 3–5 mm in thickness was removed from the membrane bundle and sectioned, parallel to the membrane, into outer and bottom layers. Each layer had a similar thickness and was tested in the flow cell. The biofilm sample was added to a rectangular cavity in an acrylic support, which then was inserted into the flow cell (figure 1a). Tests were carried out under non-growth conditions. The total time, from placement of the biofilm in the flow cell until the end of testing of the biofilm section, was less than 3 h. MBfR applications are promising biofilm-based technologies where biofilm management sets important challenges for the performance of the system (e.g. biofilm start-up times, optimal biofilm thickness, detachment control) [34].

Figure 1.

Biofilm–fluid flow interaction experiments. (a) Experimental scheme. (b) Lower effective viscosity, η = 10³ kg m⁻¹ s⁻¹. (c) Higher effective viscosity, η = 10⁵ kg m⁻¹ s⁻¹. t = 0 (before beginning flow), t = 60 s of flow shear, t = 120 s (30 s after stopping flow). (Online version in colour.)

Biofilm effective viscosity was determined by shear rheometry using a parallel plate rotational rheometer (Viscoanalyser, ATS Rheosystems, Bordentown, NJ) as described elsewhere [35]. The viscosity was estimated in the linear viscoelastic regime (i.e. mechanical properties are not affected by the applied stress level) over a stress range of 0.1–5 Pa. The biomass obtained from different depths of the MBfR biofilm has different effective viscosities (between 10³ and 10⁵ kg m⁻¹ s⁻¹). We compared their response with flow-driven stress. Constant water flow rates were imposed for 90 s in the channel using a peristaltic pump (Cole-Palmer, Chicago, IL). The biofilm deformation in response to fluid flow was recorded over time using a stereomicroscope. Image analyses were used to determine biofilm structure [5]. The mean flow velocities tested in the system were u = 0.001, 0.005 and 0.02 m s⁻¹. These conditions imposed laminar flow, with a Reynolds number (Re) = 5.6, 27.8 and 111.1, respectively, based on the empty channel width and mean velocity.

Negligible deformation of the less viscous biofilm was observed at the lowest flow regime (Re = 5.6). Higher deformation of this biofilm occurred with increased flow velocity (Re = 27.8 and 111.1), resulting in significant detachment (sloughing) at the highest flow velocity tested (Re = 111.1) as shown at t = 60 s (figure 1b). Less viscous biofilm showed more significant deformation and detachment than more viscous biofilm. In the latter, significant deformation occurred only at the highest flow regime (Re = 111.1) as shown at t = 60 s (figure 1c). Some detachment by erosion was also observed. Namely, superficial biofilm was observed to detach and elongate to form moving structures, such as oscillating streamers (figure 1c). Although in both biofilms an initial elastic response was clear, residual deformation was observed after the stress was removed (figures 1b,c, t = 120 s).

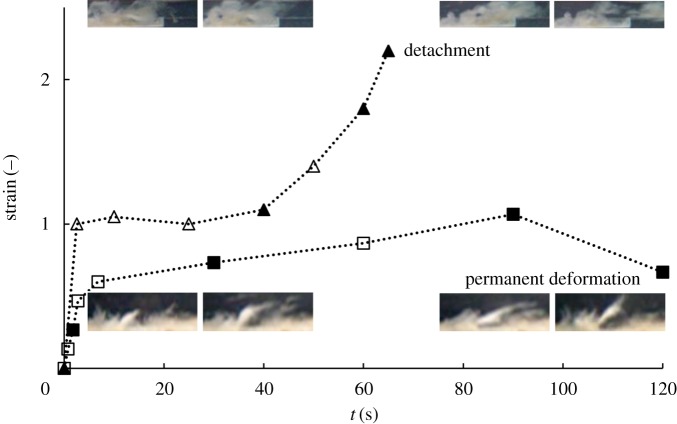
Analysis of biofilm deformation under the highest flow condition is presented in figure 2. Strain over time is shown for the sloughing event observed in the lower viscosity biofilm and a biofilm streamer formed in the biofilm with higher viscosity, respectively. Deformation was estimated by tracking a representative biofilm section using image analysis, as illustrated. After an initial period of elastic strain, viscous creep led to detachment and irreversible deformation of a streamer structure. Viscoelastic mechanical stretching at high Re produced biofilm failure and streamer formation in a short timescale. The viscoelastic relaxation time λ is the characteristic timescale separating elastic and viscous-dominated behaviour, and can be estimated as the time required for viscous creep to equal elastic deformation. The deformation results suggest an apparent λ of the order of magnitude of 60 s (figure 2). Although a remarkable commonality in λ has been reported for a wide variety of biofilms in the range of 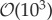s [6], the transient viscoelastic response of the biofilm was very different and more rapid than estimated in other biofilms and may be due to differences in structural composition [36].

Figure 2.

Biofilm consecutive response over time at u = 0.020 m s⁻¹, leading to detachment and streamer formation. Triangles for less viscous biofilm (η = 10³ kg m⁻¹ s⁻¹) and squares for more viscous biofilm (η = 10⁵ kg m⁻¹ s⁻¹), closed symbols follow the images sequence. (Online version in colour.)

Biofilm resistance to mechanical stress is largely determined by biofilm viscoelasticity. On the one hand, in a short timescale, an elastic response absorbs stress energy through reversible deformation. On the other hand, long-lasting stress leads to energy dissipation by viscous flow and non-reversible deformation. This dual behaviour helps to adjust the biofilm structure to respond to external loads.

Generally, biofilms become established under flow-driven shear forces that do not cause substantial elastic deformation. However, when constant stress is maintained for long timescales compared with λ, biofilms fail to resist the imposed shear and show viscous deformation. Biofilm detachment occurs when the applied force exceeds biofilm cohesiveness. In the elastic regime, higher fluid shear stress and sustained storage of elastic strain can quickly produce loadings higher than the ultimate strength of the biofilm and produce biofilm failure. Elasticity is important for biofilm development, because elastic elongations of the biofilm following the flow can act as precursors of streamers. These structures can form steady streamers in laminar and turbulent flows [37]. Streamlined elastic deformation reduces the drag on biofilm structures, but more flexible (i.e. more elastic) structures can vibrate and develop oscillations more prone to breakage and detachment [22]. In low Re creeping flows (), highly viscous deformation has been proposed as a main driver for streamer formation usually observed at timescales much larger than the viscoelastic relaxation timescale [38]. Under higher flow, shear viscous creep can produce biofilm necking and strain accumulation resulting in cohesive failure [39]. Rapid biofilm failure can also be attributed to nonlinear effects owing to shear rate dependence of mechanical properties (e.g. strain-hardening, shear-thinning) [10,39].

These experimental results showed that the mechanical response of the biofilm to flow-driven stress was dependent on the hydrodynamic regime and the biofilm mechanical properties, and suggested a viscoelastic behaviour under short-term flow fluctuations. Owing to biofilm variability in structure and constitution (i.e. differences in the proportion and in the mechanical parameters of the components), mechanical features of biofilm should be expected to vary, as shown by the biofilm rheometric characterization. This justifies the need to develop models that capture in more detail viscoelastic behaviour and heterogeneity of biofilms.

3. Modelling biofilm

Here, we introduce a system of partial differential equations to model biofilm deformation under different flow conditions in the form of a heterogeneous, multicomponent complex fluid consisting of three phases: bacteria, EPS and an effective solvent, which all have different mechanical properties.

The energetic variational approach, which is based on the first and second laws of thermodynamics, has been successfully applied to model complex fluids [30–32,40]. Using Hamilton's least action principle (LAP; or principle of virtual work) and Rayleigh's maximum dissipation principle (MDP), the conservative and dissipative forces are obtained from the total energy functional of the system [41–43]. This force–balance law expands the conservation of momentum principle to include dissipation and couples model equations, allowing for a systematic inclusion of different physical interactions between the components [26].

We use this approach and a phase-field coupling [30] to combine representations of different components of biofilm and to include their mutual interactions as follows. First, we derive the equations for a two-phase system representing a mixture between bacteria and EPS following an energy law [30]. Phase-field variable ϕ₁ is used in this system to represent the volume fraction of EPS. We use an Oldroyd-B formulation [44] to represent the viscoelastic contribution of the EPS network. In particular, we use a Eulerian description of the strain. This allows one to account for the impact of EPS on the biomass mixture by incorporating contribution of the elastic energy into the chemical potential. Then, a single set of governing equations is defined on the entire domain in a purely Eulerian framework [45].

Next, we model the biofilm as a three-phase mixture made of solvent and the binary complex fluid previously defined. In what follows, we introduce another phase-field variable ϕ₂, and use the same approach for deriving an energy conserved system.

3.1. Two-phase biofilm mixture

We assume in the initial two-phase biofilm mixture that bacterium behaves like a Newtonian fluid, and that EPS is a viscoelastic substance. The free energy of the mixed system consists of internal and kinetic energies. The internal energy is accounted for by the mixing energy of the mixture and the elastic-free energy of the viscoelastic polymer in the EPS. The volume fraction of the EPS in the biofilm is denoted by ϕ_n(x, t) and that of bacteria by ϕ_b(x, t). It follows from the incompressibility constraint and volume continuity that ϕ_n(x, t) + ϕ_b(x, t) = 1, with .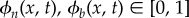

We introduce a new variable 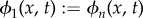, hence 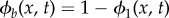. Note that 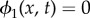represents pure bacteria while 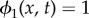represents pure EPS. 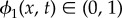represents mixtures of bacteria and EPS.

The mixing energy between the bacteria and EPS is determined by intermolecular forces. We assume it extends over the entire domain according to Cahn & Hilliard [15] and introduce it into the system as biofilm cohesion energy [17]:

3.1

This energy functional represents competition between a homogeneous bulk mixing energy density term G₁(ϕ₁) that establishes total separation of the phases into pure components and a gradient distortional term 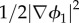that represents weakly non-local interactions between components and penalizes spatial heterogeneity. The bulk mixing energy and the gradient terms contain the ‘phobic’ and ‘philic’ tendencies between the mixture constituents, respectively. The constant γ₁ balances the competition between both effects, whereas λ₁ defines the magnitude of the cohesion energy inside the total energy. The cohesion energy incorporates the concept of a viscous biofilm and the formation of physical links and entanglements such as in a polymer network. Parameter values of γ₁ and λ₁ have to be chosen judiciously [30]. At low volume fraction, phases are unstable and tend to separate [17]. The energy density has a minimum at a volume fraction of ϕ₁ = ϕ_1,0 where attraction force is balanced by repulsive packing interaction [17]. See also figure 3.

Figure 3.

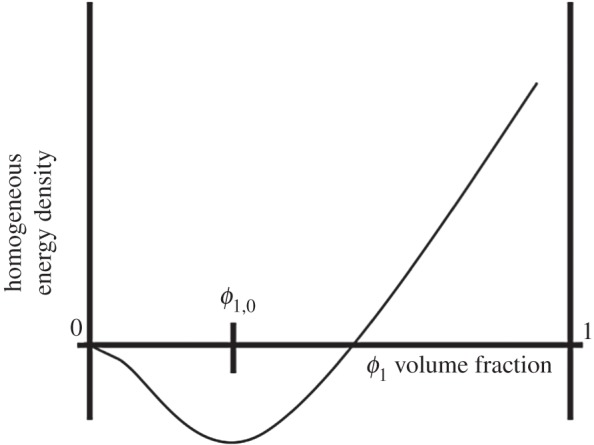
Form of the mixing energy density G₁(Φ₁).

We include the elastic-free energy from the induced extra stress tensor. To account for the viscoelastic rheology of the EPS the Oldroyd-B model is adopted, which is a Hookean dumbbell model and an extension of the upper-convected Maxwell model, well suited to describe the time-dependent flow of dilute solutions of polymers [46]. In particular, we adopt the formulation presented in [44], where the authors established local and global existence of classical solutions without using an artificial damping mechanism.

To this end, the elastic energy functional of the EPS is defined by

3.2

This elastic energy functional is associated with the deformation-gradient tensor F (strain). In (3.2), λ_Φ is the elastic relaxation time. If we assume that 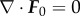, then for all later time, we have that [44]. Thus, where Φ is a vector. Elastic materials have a natural Lagrangian description, whereas fluid flow is conventionally solved in a Eulerian framework. A Eulerian description of F is incorporated to compute the evolution of the biofilm strain [44,45]. This approach allows one to represent the system in a purely Eulerian frame. In the two-dimensional case, Φ = (Φ₁, Φ₂) and F = ∇ × Φ with

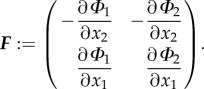3.3

The kinetic energy accounts for the mixture transport and is defined as

3.4

where ρ is the mixture density and u is the velocity field. For the sake of simplicity, we assumed that the densities of the phases are equal. This is justified, because biofilms are composed mostly of water and can be regarded as an incompressible material with constant density [10,13].

The total energy of the two-phase mixture system is expressed as the sum of the kinetic, cohesion and elastic energies [30]

3.5

From the total energy action functional, conserved and dissipative parts of the system are obtained using the LAP and the MDP with incompressibility of flow [30,41]. One source of dissipation of the system is from the viscous stress term 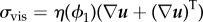, where 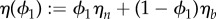is the effective viscosity of the mixture. The system also contains an additional dissipation term in the phase-field transport equation, given by a generalized Fick's law which is the mass flux proportional to the gradient of the chemical potential μ₁ defined as 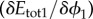. Here, 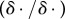denotes the variational derivative. This variational derivative leads to the conserved Cahn–Hilliard phase transport equation [15]. The general procedure for deriving the governing equations from the least-action principle has been outlined in [47,48]. In the following, therefore, we simply list the equations for our particular governing system

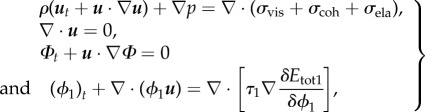3.6

where p denotes the hydrostatic pressure and τ₁ is a mobility parameter that determines the relaxation of the mixing interface [30]. The cohesion and elastic stress tensors (σ_coh, σ_ela) were derived from the corresponding energy terms [30,44]

3.7

Then, the resulting system is as follows

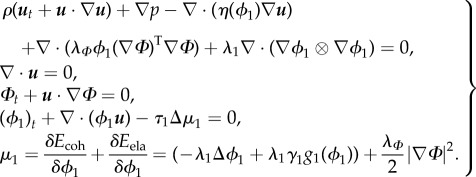3.8

where 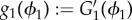. Defining an auxiliary unknown

3.9

we can rewrite

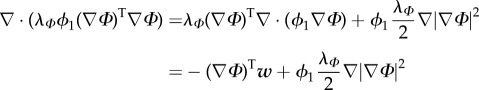3.10

and

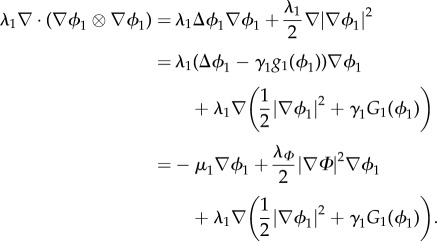3.11

Then, we have that

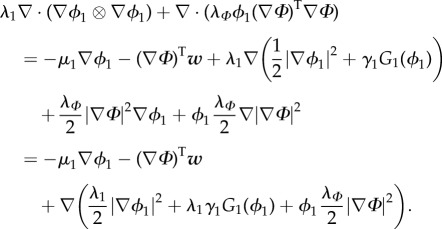3.12

Finally, system (3.8) is rewritten as

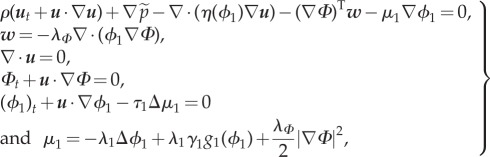3.13

with

3.14

This PDE system has the following boundary conditions. For ϕ₁, Φ, μ₁ and the auxiliary unknown w, we assume Neumann boundary conditions: 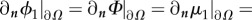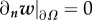, where n is the normal vector to the boundary. For u, we assume the non-slip boundary condition: 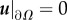. Taking into account the equalities

(in the second relation the incompressibility constraint 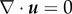has been used), we can redefine again the pressure term as

From now on, we use p instead of 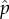to simplify the notation, and we can rewrite system (3.15) as

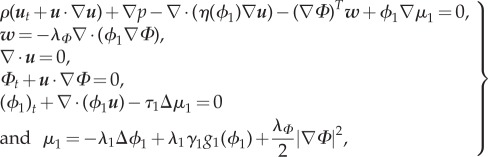3.15

with

3.16

Here, we show that system (3.15) is strictly dissipative. Indeed, after taking the inner product of (3.15)₁ with u, (3.15)₂ with p, (3.15)₃ with w, (3.15)₄ with Φ_t, (3.15)₅ with μ₁ and (3.15)₆ with (ϕ₁)_t, we obtain the following dissipative energy law

3.17

3.2. Three-phase biofilm mixture

We now introduce a second phase field function 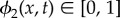to model mixing of the previous two-phase viscoelastic mixture of the EPS and bacteria with the solvent. ϕ₂(x, t) is defined as the volume fraction of the binary mixture, whereas (1 − ϕ₂(x, t)) denotes the volume fraction of solvent in the biofilm. ϕ₂(x, t) = 0 represents pure solvent and ϕ₂(x, t) = 1 represents the pure EPS–bacteria mixture. Then, the total energy of the ternary mixture system is described by the sum of the kinetic, elastic, and two cohesion energies [30]

3.18

where

3.19

3.20

Here, E_coh2 is the cohesive energy density describing mixing forces between the EPS–bacteria mixture and the solvent. It describes the competition between the homogeneous mixing energy density G₂(ϕ₂) and the term 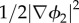that penalizes spatial heterogeneity. γ₂ and λ₂ are balancing constants. In this case, there is a factor ϕ₂ included in equation (3.19), because the energy is only logically defined in the regions where there is EPS–bacteria mixture (i.e. in this expression, ϕ₂ plays the role of a localizer).

Let us define the effective viscosity of the mixture as 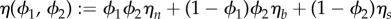, and the chemical potential associated with ϕ₂ as 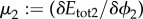. The following system is obtained by implementing the procedure used to derive the system (3.15)

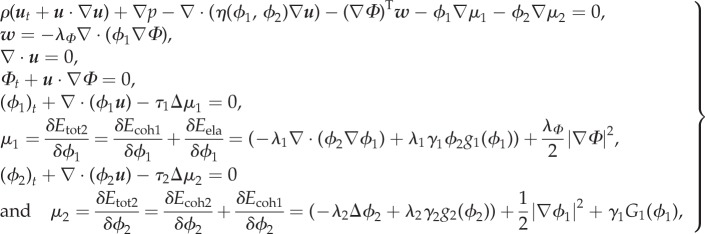3.21

where 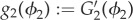and τ₂ is a mobility term.

In this new system of PDEs, we use the same boundary conditions as in the two-phase mixture case and add homogeneous Neumann boundary conditions for ϕ₂ and μ₂: .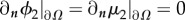

The total energy of the system (3.21) is also dissipative. This can be shown by taking the inner product of (3.21)₁ with u, (3.21)₂ with p, (3.21)₃ with w, (3.21)₄ with Φ_t, (3.21)₅ with μ₁, (3.21)₆ with (ϕ₁)_t, (3.21)₇ with μ₂ and (3.21)₈ with (ϕ₂)_t. The following energy law is obtained

3.22

4. Simulation results

Our study focuses on fast events and conditions leading to biofilm deformation and detachment resulting in formation of streamers. Simulations were carried out using a novel numerical scheme given by equations (A 3)–(A 5) in appendix A.1 computationally implemented using finite-element software FreeFem++ [49]. A representative physical domain L_x1 × L_x2 (1 × 1 mm) and values of physical parameters found in the literature (table 1) were used. Biofilms characterized as viscoelastic fluids are estimated to consist of 80% or more water, with cells and EPS comprising the rest of the biomass [10]. Thus, we considered an initial solvent volumetric fraction in the biofilm mixture ϕ_s = 0.8, whereas bacteria and EPS concentrations were both set to ϕ_b = ϕ_n = 0.1. Simulations were performed using an initial biofilm structure consisting of a protrusion from a smooth biofilm, resembling precursor of a streamer.

Table 1.

Model physical parameters.

parameter	symbol	value
domain dimensions	Lx1 × Lx2	10−3 × 10−3 (m)
solvent density	ρ	103 (kg m−3)
magnitude of Ecoh1	λ1	10−1 (kg m s−2)
magnitude of Ecoh2	λ2	10−1 (kg m s−2)
balance inside Ecoh1	γ1	102
balance inside Ecoh2	γ2	102
mobility binary mixture	τ1	10−5 (kg−1 s)
mobility ternary mixture	τ2	10−5 (kg−1 s)

A triangular spatial mesh of size 1.25 × 10 ⁻⁵ m and a time-step size of Δt = 10⁻⁴ s were used. The inflow condition, as a flow rate constant in time, was prescribed at x = 0, a periodic (cyclic) boundary was imposed at x₁ = 0 and x₁ = L_x1, in order to minimize edge effects on the calculated flow pattern. The velocity profile and hydrodynamic conditions in the whole domain are detailed in figure 4. For flow between parallel plates, it is reasonable to assume an axis-symmetric system and consider half of a fully developed parabolic velocity profile with a maximum velocity u_max at the top boundary. We considered a velocity range between u_max = 0.001 and 0.01 m s⁻¹.

Figure 4.

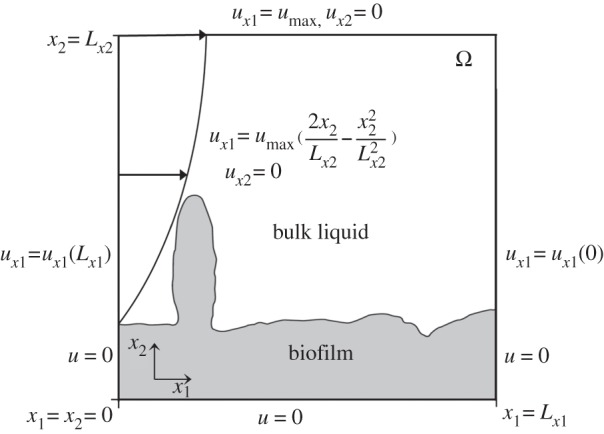
Model physical domain and hydrodynamic boundary conditions.

In order to reduce the computational cost of the system, we used linearized approximations of in (A 3)₄ and in (A 3)₆. This allowed dividing the problem (A 3) into three substeps, computing in the first substep the pair , then 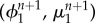, and finally 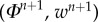. Although with these approximations we cannot assure the strictly dissipative character of the system, the good performance of the simulations suggested that the physical dissipation neutralized the appearance of numerical instabilities. The cohesion potentials were approximated using a linear second order in time approximation introduced in the Cahn–Hilliard framework in [50]

4.1

For a detailed survey on properties and approximations of potential terms in energy-based systems, we refer readers to [51,52].

Mechanical parameter values reported in the literature such as the shear moduli and the viscosity vary by orders of magnitude. For instance, the biofilm effective viscosity typically ranges between 10 and 10⁶ kg m⁻¹ s⁻¹ [6]. On the other hand, the elastic relaxation timescale appears to have little variation, typically of the order of minutes [6]. Simulations to study the effect of these mechanical properties and flow-driven stress were performed using numerical scheme (A 3)–(A 5).

4.1. Effect of the biofilm viscosity

We first studied the effect of the biofilm viscosity on its mechanical response to fluid flow. We considered three different viscosity conditions with values listed in table 2. The parameter values of EPS and bacterial viscosities are chosen to be consistent with viscosity values measured elsewhere [53,54]. In addition, the EPS viscosity values used in simulations represents the lower end of the typical biofilm viscosity range [6]. The solvent was assumed to be water. A short viscoelastic relaxation time λ_Φ = 10⁻³ s, relative to the simulations timescale (s) was used to capture the characteristic behaviour of the biofilm and to save computational time.

Table 2.

Mechanical parameters for viscosity simulations.

	ηn(kg m−1 s−1)	ηb (kg m−1 s−1)	ηs (kg m−1 s−1)	λΦ (s)
case 1	1	10−2	10−3	10−3
case 2	10	10−1	10−3	10−3
case 3	102	10−1	10−3	10−3

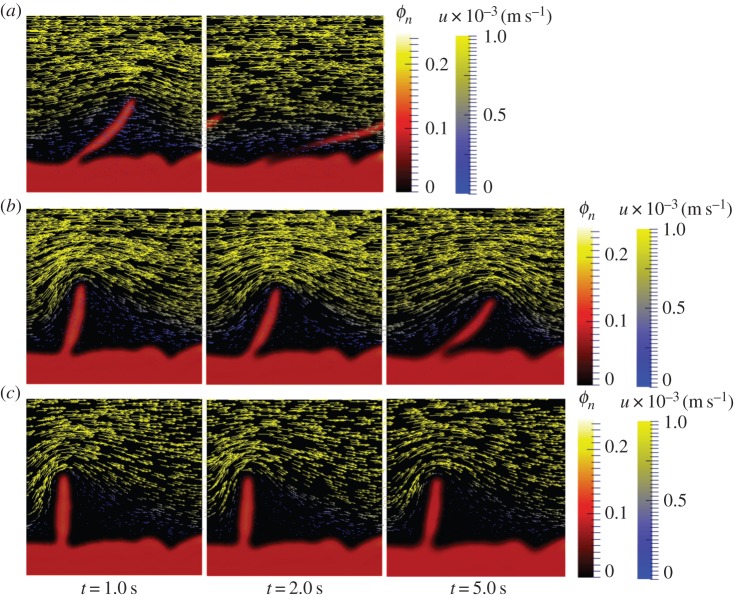
The dynamics of the volume fraction of EPS ϕ_n showed different biofilm deformation over time for the studied cases (figure 5). In case 1, we observed how a detachment was produced, leading to formation of streamers through fracture failure of the ‘tail’ of the protrusion of the biofilm (figure 5a between t = 1.0 and 2.0 s). This simulation assumed a less viscous state of the biofilm. In cases 2 and 3, it was observed that the higher the viscosity of the EPS, the lower the scope of deformation caused by the same flow. The biofilm structure in case 2, deformed more than in case 3 (figure 5b,c). This was owing to the higher effective viscosity of the biofilm in case 3, resulting in a higher resistance to mechanical stress as observed in the experiments. Both protrusions in case 2 and 3 remained stable after a longer simulation time, deformed but did not detach. This suggested that for timescales longer than the relaxation timescale, streamers may form owing to mechanical degeneration as formation of highly viscous jets. With a higher viscosity, detachment due to fluid shear is resisted by slow deformation [55]. In these simulations, the EPS concentration was the same as that of bacteria, but with a much higher viscosity which therefore determined the magnitude of the effective viscosity. This is true in viscoelastic fluid biofilms; the polymer network composition and the water content determine the mechanical response, and no colloidal effects are expected owing to a low cell density [10].

Figure 5.

Effect of biofilm viscosity increase on biofilm–flow interaction at u_max = 0.001 m s⁻¹. Velocity profile and biofilm volumetric fraction Φ_n over time. (a) Case 1, η_n = 1 kg m⁻¹ s⁻¹. (b) Case 2, η_n = 10 kg m⁻¹ s⁻¹. (c) Case 3, η_n = 10² kg m⁻¹ s⁻¹.

The flow velocity field was also influenced by the biofilm structure. In the simulation with lower EPS viscosity, some biofilm flow-through was observed (case 1). On the other hand, with a much higher viscosity, the biofilm mixture deformed very slowly and behaved like a wall, significantly affecting the flow pattern and preventing any flow from penetrating through (case 3). Theoretical and experimental studies have shown that the viscoelastic biofilm gel-like matrix largely minimizes flow advection [56]. However, because of structural and local heterogeneities, biofilms contain zones behaving like a solid or a liquid rather than a viscoelastic gel [57]. Within fluidic areas, advection may have a significant role (e.g. for mass transport of solutes such as nutrients or antimicrobials).

The simulations did not show differences between the evolution of ϕ_n and ϕ_b. Bacteria and EPS phases showed similar spatial–temporal dynamics in all tested conditions. The EPS distribution was mostly coherent with that of bacteria, and both remained together in the mixture (data not shown). A similar trend was found in a recent multicomponent study of fluid–biofilm interaction [13]. In model simulations, the coherence between EPS and bacteria is determined by the parameter choice in the cohesion energy, based on the fact that the EPS and bacteria are bounded as EPS is produced by cells. In biofilms, the EPS and bacteria dynamics are also dictated by cell growth. However, in the simulations, a short timescale was used to assess the viscoelastic mechanical response and growth was neglected. For longer timescales, growth effects can be included in the model through reactive terms [13].

4.2. Effect of the extracellular polymeric substances elasticity

Mechanical properties and conformational dynamics of the EPS polymer network are key to understanding biofilm response to mechanical stress. To assess the elastic component of deformation, the timescale of the elastic relaxation λ_Φ was varied. A longer stress relaxation indicates more elastic behaviour. In order to study the effect of EPS elasticity on biofilm deformation and detachment, we considered conditions leading to flexible precursor structures of streamers. Conditions listed in table 3 were tested.

Table 3.

Mechanical parameters for elasticity simulations.

	ηn (kg m−1 s−1)	ηb = ηs (kg m−1 s−1)	λΦ (s)
case 4	1	10−3	10−3
case 5	1	10−3	1
case 6	1	10−3	102

The evolution of ϕ_n over time is presented in figure 6. With increased relaxation time, a more elastic response was observed within the simulation timescale, and biofilm compression and channelling was observed. The timescale of the process was of the order of a second (L_x1/u), which is much larger than λ_Φ in case 4, so that the fluid elements adjust to the flow and no viscoelastic effects were observed (only viscous deformation). In case 5, λ_Φ is similar to the simulation timescale, and in case 6, λ_Φ is much longer than the simulation timescale. In both these cases, viscoelastic effects were manifested. The simulated biofilm protrusions deformed more and developed into finer streamers over time compared with that of case 4. With higher elasticity, more complex configurations were observed, which became unstable and collapsed with the flow over time (figure 6b,c). These simulations suggested the elastic behaviour of EPS may produce the biofilm adaptation to flow shear stress and local structural heterogeneities [57].

Figure 6.

Effect of elastic relaxation increase on biofilm–flow interaction at u_max = 0.001 m s⁻¹. (a) Initial structure at t = 0. EPS volumetric fraction Φ_n at t = 1.0 s, (b) Case 4, λ_Φ = 10⁻³s. (c) Case 5, λ_Φ = 1 s and (d) case 6, λ_Φ = 10² s.

In low Reynolds number flows, it has been hypothesized that biofilm streamers form from an elastic degeneration mechanism [37], or from the flow in highly viscous liquid states [38], and streamer appearance timescales are similar to that of biofilm growth process. However, we observed the formation of streamers in a short timeframe, as a consequence of elastic deformation of a precursor followed by viscous behaviour leading to a virtually stabilized length in experiments (figures 1 and 2). The biofilms we studied were subjected to strong flow shear and showed a stress relaxation timescale much shorter than that of growth. This is consistent with streamer formation reported in other's experiment [39]. Together with the model simulations and the experiments, we suggested that high viscosity combined with low elasticity of EPS may be needed to form stable biofilm structures. Again, no significant differences between the evolution of ϕ_n and ϕ_b were observed in these simulations, indicating mechanical consistency between the bacterial and EPS dynamics.

4.3. Effect of the flow stress

Simulations to study the influence of flow shear on the biofilm mechanical response were performed by imposing different flow velocities. Biofilm conditions previously simulated in case 2 were chosen. The effective viscosity of the biofilm was shown to be within the typical range reported in [6]. Similar to experiential observations (figures 1 and 2), simulations showed that biofilm deformation increased with increase in flow velocity to u_max = 0.002 and 0.004 m s⁻¹ (figure 7). After the flow was stopped in simulations, the simulated biofilm protrusion remained in the deformed shape similar to the ones shown in (figure 7a,b). This indicated the mechanical response of the biofilm in case 2 was dominated by the viscous stress.

Figure 7.

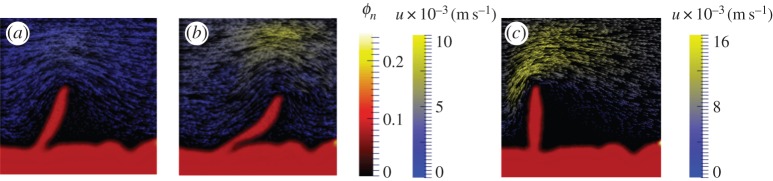
Effect of flow stress on biofilm for case 2, η_n = 10 kg m⁻¹ s⁻¹. EPS volumetric fraction Φ_n at t = 1.0 s. (a) u_max = 0.002 ms⁻¹. (b) u_max = 0.004 ms⁻¹. (c) u_max = 0.008 ms⁻¹, η_n = 10³ kg m⁻¹ s⁻¹.

In §2, our experimental results showed deformation and detachment of biofilms under different conditions. We ran simulations with higher viscosities and flow velocities similar to the ones in the experiments. For instance, simulations were run for the same biofilm structure but with the EPS viscosity of η_n = 10³ kg m⁻¹ s⁻¹ (lowest experimentally obtained effective viscosity) and u_max = 0.004 and 0.008 m s⁻¹. The simulated biofilm protrusion showed negligible deformation as shown in figure 7c for u_max = 0.008 m s⁻¹. This result again implied the biofilm's resistance to deformation introduced by flow shear can be largely attributed to its viscosity [55].

5. Conclusions

This paper describes a novel model for studying biofilm interaction with fluid flow, derived using the combination of the energetic variational approach and phase-field method. The model represents biofilm as a ternary complex fluid made of heterogeneously distributed bacteria, EPS and solvent phases. Biofilm viscoelastic constitutive response to mechanical stress is represented using energy conserved Eulerian formulation. The model is based on continuum mechanics and is obtained from physical principles without using heuristic arguments. It is thermodynamically consistent and satisfies an overall dissipative energy law, which usually guarantees well-posedness [30,58]. The phase field coupling avoids the need to track the interface explicitly [30,41] which is difficult when topological change of the interface is involved. Specifically, biofilm detachment is simulated using the phase-field modelling method. The unconditionally energy-stable splitting scheme introduced in this paper allows one to solve the model equations at low computational cost. Our model and models in [12–14] all use a phase-field approach to couple components of biofilm. The difference is that our model is based on physics laws, and it is shown to have system energy decrease over time. Further mathematical analysis of the model will be the subject of future study.

As opposed to previous models, biofilm–fluid interaction in our model is simulated in the Navier–Stokes flow regime without assuming that all biofilm phases are locked together and advect with the same velocity. We also assume that underlying mechanical characteristics of the biofilm determine observed biofilm responses to shear stresses imposed by external flow. Simulating topological changes of a biofilm such as biofilm sloughing detachment by using the phase-field approach simplifies computational implementation of the model. Using physical energy laws allows the model equations to be derived without using empirical arguments. As a result, mechanical responses of individual biofilm components to forces from the external environment can be assessed. Moreover, the model takes into account non-uniform distributions of different biofilm phases providing better understanding of deformation and detachment of realistic heterogeneous biofilms.

The simulated biofilm–fluid interaction qualitatively agrees with experimental observations. Based on the model simulations, the following new biological insights were obtained. The model showed that within the range of flow velocity between 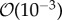and 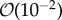m s⁻¹, EPS viscosity about 100 kg m⁻¹ s⁻¹ or higher provided strong structural support, resulting in small deformation of the biofilm. Simulations showed that an increasing elasticity of the EPS (with relaxation time ranging from 0.001 to 100 s) could lead to formation of filamentous structures such as streamers even at low Reynolds number flow (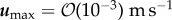) when the effective viscosity of EPS is less than 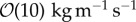. Thus, the model predicts that the resistance of the biofilm in response to the fluid flow is largely due to the viscous resistance of the EPS network. Simulation results also indicate that a biofilm with the EPS with lower viscosity tends to bend and form streamer-like structures which can detach under shear stress from the flow. Higher EPS elastic relaxation results in rippling of biofilm surface and formation of complex streamers under higher shear stress. This implies that a biofilm with more elastic EPS network tends to be unstable under flow and that small perturbations applied to the biofilm may result in formation of secondary complex structures. For the timescale used in simulations, experiments in biofilms with lower viscosity also showed streamer formation and detachment. This demonstrated that the model can be used to predict the cohesive failure of the biofilm by taking into account flow shear stresses and biofilm viscoelasticity.

In our experiments, only bulk average properties were measured. Recent studies have shown that the same biofilm can exhibit mechanical properties spread over several orders of magnitude, and that local heterogeneity strongly depends on external conditions such as shear stress history [57]. In addition, biofilm mechanical parameters in theoretical models are typically obtained using bulk macroscopic approaches and considered as averages. The model presented in this paper incorporates the effect of local variations and distributions of mechanical properties in a biofilm providing a better understanding of the mechanisms of biofilm deformation and detachment. In particular, effects of viscosity and elasticity of different components of the biofilm can be evaluated.

Simulations of biofilm's response to fluid flow described in this paper used model parameter values of viscosity and elastic relaxation time taken at the low end of experimental measurements. The model simulations were not able to assess scenarios with higher viscosity or elastic relaxation parameters, because higher hydrodynamic stress led to ill-conditioned matrices. Stability problems are known to appear in viscoelastic systems for more elastic regimes, i.e. high Weissenberg number in non-Newtonian fluids. It is beyond the scope of this study to develop specific numerical techniques to resolve these issues. Nevertheless, the mechanical parameter values used are adequate for simulating biofilm response to flow shear. The constitutive model considered in this paper establishes well-posedness for the deformation gradient without adding damping mechanisms or dissipative effects [44]. The Oldroyd-B system works well for steady shear flow under moderate induced strains. Under large strain rates it is not able to represent non-linear features of polymer solutions such as shear-stress-dependent viscosity and normal stress differences [46]. The incorporation of these properties may be also important for the simulation of biofilm fluid–structure interaction. We plan to investigate nonlinear viscoelastic models in future.

To summarize, simulations demonstrate that the model described in this paper is capable of characterizing effects of the mechanical parameters of the different components of the biofilm in the fluid–biomass interaction. In particular, simulations were used to study the mechanical role of EPS and formation of biofilm streamers. Lastly, extension of this model can also be used to study other biological and biomedical problems, including growth of a blood clot in blood flow. Understanding how blood clots, consisting of various types of blood cells and fibrin network, maintain their structural integrity under stress from blood flow is of great medical importance [59,60].

Appendix A

A.1. Numerical methods

For the sake of simplicity, simulations were carried out in a two-dimensional setting, although the variational formulation describing fluid mixtures with viscoelastic properties [44] can be directly applied to three-dimensions with increased computational cost. In this section, an accurate and efficient numerical scheme to approximate the coupled nonlinear PDEs system (3.21) is presented. Because we were concerned with the computational cost of the system, we designed a splitting scheme that divides the computation of the system into two different steps, which satisfies a discrete version of the dissipative energy law (3.22). We assumed a uniform partition of [0, T]: t_n = nΔt, with Δt = T/N denoting the time step and aⁿ denoting an approximation of a(t_n). A general scheme is presented, where the approximation considered for the convective term is

A 1

that satisfies the property

A 2

We used the following expression for the homogeneous part of the cohesion energy densities [17]

Then, the proposed algorithm reads

Step 1. Find 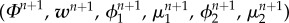such that

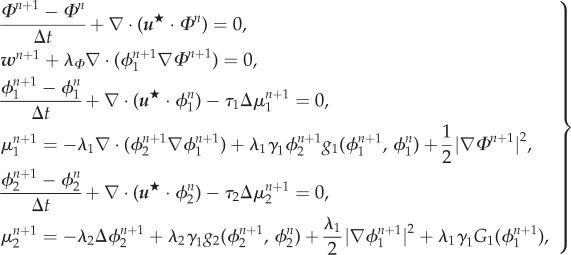A 3

where

A 4

Step 2. Find 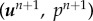such that

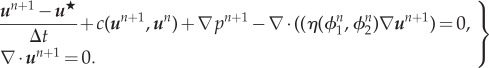A 5

Theorem A.1. —

The numerical scheme (A 3)–(A 5) is unconditionally energy-stable, i.e. the total energy of the system is dissipative and satisfies a discrete version of the energy law (3.22):

A 6

where the numerical dissipation introduced in the system is

A 7

and

A 8

Proof —

Consider the key relation (A 4)

Testing by we obtain

Using the previous relation and taking the inner product of (A 5)₁ with uⁿ⁺¹, (A 5)₂ with pⁿ⁺¹, (A 3)₁ with wⁿ⁺¹, (A 3)₂ with , (A 3)₃ with , (A 3)₄ with , (A 3)₅ with and (A 3)₆ with , we finally obtain (A 6) ▪