An anthropologically based model of the impact of asymptomatic cases on the spread of Neisseria gonorrhoeae

Abstract

Neisseria gonorrhoeae (GC) remains a serious burden in many high-sexual-activity, undertreated populations. Using empirical data from a 2009 study of GC burden among pastoralists in Kaokoveld, Namibia, we expand the standard gonorrhoea transmission model by using locally derived sexual contact data to explore transmission dynamics in a population with high rates of partner exchange and low treatment-seeking behaviour. We use the model to generate ball-park estimates for transmission probabilities and other parameter values for low-level (i.e. less than approx. 1200 copies/20 µl PCR reaction) asymptomatic infections, which account for 74% of all GC infections found in Kaokoveld in 2009, and to describe the impact of asymptomatic, low-level infections on overall prevalence patterns. Our results suggest that GC transmission probabilities are higher than previously estimated, that untreated infections take longer to clear than previously estimated and that a high prevalence of low-level infections is partially due to larger numbers of untreated, asymptomatic infections. These results provide new insights into the natural history of GC and the challenge of syndromic management programmes for the eradication of endemic gonorrhoea.

1. Introduction

Dynamic compartmental models have been effective tools for understanding the transmission system of contagious infections [1,2], including gonorrhoea [3]. Gonorrhoea (GC) presents special challenges to building an effective compartmental model, including lack of knowledge of the epidemiologic impact of asymptomatic infections, an incomplete understanding of immune response to gonorrhoea infection and the complexity of modelling contact network structures. Getting empirical data for any of these is very difficult.

The earliest GC models [3,4] accounted for asymptomatic disease by including an equation to represent a third health status (susceptible, symptomatic and asymptomatic). They accounted for variability in sexual contact frequencies by assuming two sub-groups differentiated by sexual activity levels. In these models, the high-activity group—responsible for the persistence of GC, despite R₀ values of apparently less than 1 across the rest of the population—is referred to as the ‘core’ group [3,5,6]. Since its development, the core-group concept has been defined and applied in many different ways [7] but there is a lack of consensus regarding its value for measuring, predicting and intervening on real GC epidemics. Furthermore, Rothenberg et al. [8] argue that the concept of a core group is too simplistic because it considers only individual risk behaviours and not confounding influences of risk associated with one's group membership or environment.

More recent models have questioned the assumption that contact between core and non-core-group members is random—certainly an oversimplification of reality—and thus, have expanded the complexity of contact pattern algorithms. In their GC model, Garnett & Anderson [9] defined a single parameter (ɛ) of assortative mixing to represent the proportion of all contacts that individuals reserve for their own group. Jacquez et al. [10] and Simon & Jacquez [11] introduced the concept of preferred mixing, in which a proportion (r_i) of total contacts are reserved for members of one's own group, with all other contacts (1 − r_i) randomly proportioned within the total population, allowing for different activity groups to have different amounts of within-group preference.

Despite the inclusion of greater biological and behavioural complexity, these models still struggled to reflect real epidemiologic patterns because good estimates for some parameters were still not known. Garnett et al. [12] responded to this problem by fitting a GC transmission model with parameter values drawn from empirical data. Their model described GC transmission in a clinic population in Newark, New Jersey; it included two infected/infectious states (symptomatic and asymptomatic), four sexual activity groups (instead of the simple ‘core’ and ‘non-core’ dichotomy) and an embedded expression for assortative sexual mixing among the activity groups. The model was informed by empirical data from the Newark clinic population; of course, nearly all the study subjects were symptomatic. The model used data from the National Health and Nutrition Examination Survey to estimate parameters for contact patterns. Ultimately, they found this empirically driven model only matched real world patterns when transmission probabilities and asymptomatic disease parameters were set unrealistically high and that the model was highly sensitive to small changes in parameter values. The goal of this paper is to enrich and expand the approach of Garnett et al. especially to shed more light on the role of asymptomatic individuals and to re-examine the transmission parameters.

1.1. A model of GC transmission in Kaokoveld, Namibia

We present a model of GC transmission among a remotely living population of semi-nomadic pastoralists in Kaokoveld, northwestern Namibia, among whom condom use is rare and treatment is often inaccessible. In 2009, one of us (A.H.) undertook a cross-sectional, empirical study of GC burden, reproductive health and sexual behaviour and contacts in Kaokoveld [13]. Like Garnett et al. [12], our GC model includes four sexual activity groups and parameter estimates based on empirical data. Also, by collecting our empirical data cross-sectionally, rather than targeting treatment-seeking participants, we likely captured a more realistic view of the prevalence of asymptomatic GC cases in Kaokoveld.

Our model makes several advancements on Garnett et al.'s work. First, our empirical data come from a population of sexually active adults within a closed sexual network, not a subpopulation of symptomatic patients attending a clinic. Therefore, our estimated ranges for several parameters—including proportion of asymptomatic infections (θ_k), number of contacts (c_ki) and preferred mixing (r_i)—are backed by a richer dataset.

Second, because our field protocol included the collection of urethral/vaginal swabs for qPCR-based GC diagnostics, we were able to quantify bacterial loads for each participant in the sample. This information led to the inclusion of a novel complexity: a third infected/infectious status that is exclusively asymptomatic and low bacterial load. Figure 1 presents a histogram of DNA quantities among 431 urethral or vaginal samples from our study participants [13]. Participants whose sample quantities had fewer than 1125 copies/20 µl qPCR reaction were categorized as having ‘low-level’ infections, according to the distinct cut-off in the data in figure 1. This is very close to the presumed ID₅₀ dose for GC of 1000 copies [14]. Sixty-four per cent of participants (n = 276) were GC positive; 74% of these cases were low-level.

Figure 1.

Histogram of DNA quantity in 431 urethral or vaginal samples from participants in Kaokoveld, Namibia, 2009. Quantities of 1125 copies or more were categorized as ‘high-level’ infections, according to a distinct cut-off in the data. This is very close to the ID₅₀ dose for GC as reported by Todar [14].

In Kaokoveld, where most GC infections are asymptomatic and people therefore seldom seek treatment, we found a high prevalence of low-level infections [13]. Though the transmission probability of low-level infections is likely lower than that of high-level infections, their high prevalence suggests they are important in maintaining endemic levels of GC in this population. By adding this additional infection status and using qPCR assays to quantitate GC DNA levels, we observed infections at a finer resolution. Third, our interviews included questions about numbers and names of sexual partners, which guided our parameter estimates for contact rates and preferred mixing.

It is not the goal of this paper to derive point estimates of the unknown transmission probabilities and infection durations. Given the high number of unknown parameters and uncertainties in our sample's representation of the full population, such a goal is not achievable. Rather, following the path-breaking work of Garnett et al. [12], we will show that only specific ranges of parameters yield the high prevalences we found in our sample. The goals of this paper include descriptions of these ranges, of our paths to calculating them, and of their implications for understanding nuances in the spread of GC.

This research programme focused on the following four questions:

• (1) In a population where most people, not just a small core group, have multiple and concurrent partners, how do we model contact structure?

• (2) How accurate are previous estimates of transmission probability?

• (3) What are the characteristics of low-level infections?

• (4) How does the addition of a low-level status of GC infection to the compartmental model affect overall prevalence?

We will first expand on and clarify these questions, then describe our model including descriptions of its various parameters and our estimates of these parameters, describe how our analysis of this model shed light on each of the four questions, discuss the sensitivity of our results and finally discuss model limitations and future directions.

1.1.1. Question 1 (modelling contact structure)

Unlike many western populations, having multiple, concurrent partners is culturally acceptable and commonly practiced among the Kaokoveld pastoralist tribal groups. Populations that broadly condone partner concurrency challenge the notion of a GC-sustaining, high-activity ‘core’ group. Our empirical dataset includes data on recent sexual partners for all participants in the Kaokoveld study. Thus, we have a unique ability to use detailed field-collected data to estimate parameters for contact frequency and mixing—two crucial but difficult to estimate parameters—for our model.

1.1.2. Question 2 (accuracy of previous estimates of transmission probability)

Garnett et al. [12] were concerned that their transmission probability estimates were ‘too high’: (male-to-female (β₁) = 0.8 and female-to-male (β₂) = 0.6) because they exceeded the values reported by Hooper et al. [15] and Platt et al. [16], who used culture-based methods to estimate transmission probability and duration. We attempted to address that concern in our model, suspecting that an additional infectious status with transmission probability (albeit a much lower one) might help drive overall prevalence.

1.1.3. Question 3 (characteristics of low-level infections)

The observation of highly prevalent, asymptomatic, low-level GC cases in the Kaokoveld empirical dataset was an unexpected finding that yielded a number of new questions. For example: How long does it take for high-level infections to decrease into low-level infections? How long do low-level infections last before they resolve? We use our model to generate ball-park estimates of (i) the rate at which high-level asymptomatic infections decrease into low-level infections (ψ_k), (ii) the transmission probability of low-level infections (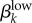), and (iii) the duration of low-level infections before they resolve (γ_k).

1.1.4. Question 4 (impact of low-level infections on overall prevalence)

Low-level infections are highly prevalent in Kaokoveld; this is likely to be true in any high-activity population where people rarely receive antibiotic treatment for their GC infections. With prevalence as high as 42% (men) and 53% (women), low-level infections likely have an impact on overall transmission patterns.

The distribution of GC in Kaokoveld, as we view it from our 2009 dataset, is really just a snapshot of a dynamic process of transmission, self-limiting infection and disease resolution. Our model provides an opportunity to estimate these unknown characteristics of low-level GC infection (e.g. transmission and duration) under the biological and sociological conditions of Kaokoveld. We hope that our ability to include in our model more complete data on sexual behaviour, contact structures and bacterial load will yield sharper estimates of the transmission parameters of GC in larger, urban populations.

2. Material and methods

2.1. Empirical dataset from Kaokoveld, Namibia, 2009

An eight-month field study was undertaken in 2009 among the semi-nomadic, remotely living pastoralists of Kaokoveld, in northwestern Namibia. We recruited 445 participants and had complete data (including GC status) for 431 participants. These data were collected as part of an ecological and behavioural study of sexually transmitted diseases that explored GC epidemiology in a high-activity, remote population with very limited access to treatment. Treatment in Kaokoveld is exclusively through syndromic management [17,18]. Urethral (male) and vaginal (female) swabs were collected in the field and tested for GC-specific DNA using qPCR, a highly sensitive molecular technique that enables DNA quantitation [13]. Thirteen per cent of men and 17% of women had high-level GC infections. The striking result from the Kaokoveld study was the high prevalence of low-level GC infections found: 42% of men and 53% of women.

2.2. Description of the model

Building on the foundational work of Garnett et al. [12], we present an ordinary differential equation system to model the transmission dynamics of endemic GC—in our case for a high-activity, undertreated population in remote Namibia (figure 2). The model was analysed using Matlab R2012a.

Figure 2.

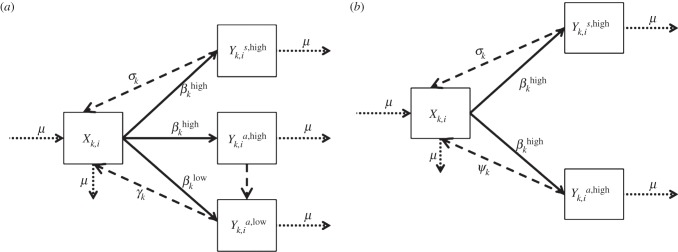
Diagram of the model of gonorrhoea transmission in Kaokoveld, Namibia, 2009 compared to a gonorrhoea model without low-level infections: to explore our question about the role of low-level infections in maintaining overall gonorrhoea prevalence in Kaokoveld, we compared outcomes from running our full model (a) with outcomes from running the model after removing low-level infection status (b). When low-level status is removed, asymptomatic, high-level infections return directly to susceptible status.

Individuals in our model fall into one of four health categories: susceptible (X), symptomatic high-level-infected (Y^s,high), asymptomatic high-level-infected (Y^a,high) or asymptomatic low-level-infected (Y^a,low). Participants with low-level GC infections were no more likely to report genito-urinary symptoms than people who tested negative for GC and/or chlamydia; therefore, we have no symptomatic low-level category in our model. Individuals in the model are categorized by sex (k = 1 (males), k = 2 (females)) and activity group (i). Though partner concurrency is normative in Kaokoveld, there is still wide variability in contacts per unit of time among participants. We therefore follow Garnett et al. [12] and allow four activity groups. These activity groups represent four levels of contact frequency, ranging from highest (i = 1) to lowest (i = 4) activity, but with different mean contact rates for men and women in each activity group (i.e. c_1,i ≠ c_2,i).

Heterosexual sex is assumed; previous research [19] and our own field interviews indicate that non-vaginal modes of sexual contact (e.g. anal and oral) are culturally rejected and rarely practiced in the study population. With a few exceptions (identified below), our parameter values come directly from the 2009 Kaokoveld field study dataset. See electronic supplementary material, appendix A, for the model equations and for a full description of the model. Final parameter estimates are reported in table 1.

Table 1.

Table of final parameter estimates.

parameter	symbol	definition	men (k = 1)	women (k = 2)
preferred mixing	ri	the proportion of total contacts of the ith activity group that are reserved for members of the same activity group	i = 1: 5/7 = 0.71 i = 2: 1/6 = 0.17 i = 3: 4/15 = 0.27 i = 4: 1/2 = 0.50	i = 1: 5/7 = 0.71 i = 2: 1/6 = 0.17 i = 3: 4/15 = 0.27 i = 4: 1/2 = 0.50
entry and exit from population	μ	per-day proportion of the population that enters and exits the population of reproductively active adults	0.00013	0.00013
contacts	ck,i	per-day mean number of sexual contacts within the past six months of members of the kth sex and ith activity group	i = 1: (13.38 × 2/365) = 0.0743 i = 2: (6.88 × 2/365) = 0.0382 i = 3: (3.23 × 2/365) = 0.0179 i = 4: (0.85 × 2/365) = 0.0047	i = 1: (8.867 × 2/365) = 0.0486 i = 2: (6.6 × 2/365) = 0.0362 i = 3: (4.4 × 2/365) = 0.0241 i = 4: (2.483 × 2/365) = 0.0081
recovery from symptomatic high-level infections,	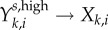σk	reciprocal of the mean number of days between onset of symptoms and receiving clinic treatment for members of the kth sex	(1/21) = 0.0476	(1/24) = 0.0416
recovery from asymptomatic, low-level infections,	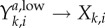γk	reciprocal of the mean number of days a low-level infection persists in members of the kth sex until it spontaneously resolves	(1/333) = 0.003	(1/333) = 0.003
transmission probability of high-level infections		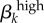the probability that a susceptible person of the kth sex will be infected during a single sexual contact with a member of the other sex who has a high-level GC infection	0.95 (male-to-female)	0.8 (female-to-male)
transmission probability of low-level infections		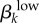the probability that a susceptible person of the kth sex will be infected during a single sexual contact with a member of the other sex who has a low-level GC infection	0.5	0.3
proportion of asymptomatic infections	θk	the proportion of infected people of the kth sex that has a high-level, asymptomatic infection	0.78	0.95
rate of movement from asymptomatic high-level infection to low-level infection, Yk,ia,high → Yk,ia,low	ψk	reciprocal of the mean number of days for the kth sex between the onset of infectiousness to the reduction of infection level below ID50 dose	(1/250) = 0.004	(1/333) = 0.003
number of people in each activity group (initial conditions)	Nk,i	the number of people in each activity group, based on proportion of population Nk,i, given a population size of 1000 men and 1000 women	N1,I = 1000 i = 1: 36 i = 2: 118 i = 3: 452 i = 4: 394	N2,I = 1000 i = 1: 81 i = 2: 86 i = 3: 195 i = 4: 638

2.3. Parameter values

A goal of this paper is to use the survey data collected and more general information about Kaokoveld to construct and study a model of the spread of GC in rural Kaokoveld. There are three types of parameters that are central to building such a model: the entry and exit rates into the sexually active population, the distribution of the levels of sexual activity among the males and females of Kaokoveld and the parameters that summarize how the different groups mix for sexual activity.

2.3.1. Population parameters

2.3.1.1. Entry/exit from population (μ)

Our model considers only sexually active individuals. Our entry/exit parameter is the average number of individuals who become (stop being) sexually active in a given period divided by the number of sexually active people in the study population. Little demographic data exist for rural Kaokoveld specifically, but there are regular censuses at the district level (Kunene district). A Namibian Ministry of Health and Social Services demographic study [20] reported that the median age of first sexual intercourse in the Kunene district is about 17.5 for both men and women (Table 5.6 in the report). The age of sexual debut is slightly earlier in the rural areas of Kunene, including Kaokoveld (approx. 16–17 years old). Tables 5.7.1 and 5.7.2 of the Namibia Demographic and Health Survey [20] show that men and women are typically still sexually active into their late fifties.

Based on these estimates and data for age-stratified population numbers in Namibia [20,21], we estimate that about 23 000 Namibians turn 16.5 each year and that the total population between the ages of 16.5 and 60 is about 500 000 (electronic supplementary material, appendix B, table I); thus, new 16-year-olds make up 4.6% of the sexually active population. The daily entry and exit rate into the sexually active population is 0.046/365, μ = 0.00013.

To keep the population dynamics from complicating the disease transmission dynamics, we assume, as all other such modelling efforts do, that the size of the sexually active population is constant for our model simulations; thus, we work with daily entry/exit rate μ = 0.00013. Our sensitivity analyses indicate our results are not sensitive to small changes in μ.

2.3.1.2. Contact rates (c_k,i)

We next focus on the contact rate per person—the number of sex partners per person per period. All survey participants were asked to provide the names of all sexual contacts within the last six months—the longest range of time that participants could accurately recall contact information. For both men and women, we identified break points to divide the participants into four activity groups for each sex. We denote by c_k,i the mean number of contacts for persons of sex k = 1,2 in activity group k = 1,2,3,4 (electronic supplementary material, appendix B, table IV).

The challenge in constructing a population model of contacts from the mixing data collected arises from the fact that the total number of contacts reported by the men in the sample (683) is more than twice as large as the total number reported by women (305). We needed to make adjustments as our closed population model must have the number of contacts of men with women equal to the number of contacts of women with men.

Such a discrepancy can arise from two sources: those in the sample may have misreported their contact history (men over-reporting and/or women under-reporting), or the sample was not representative of the sexual activity levels of those in the underlying population. We claim that the women's numbers are where adjustments needed to be made. We do not think men were over-reporting because the survey asked detailed questions about sexual behaviour that enabled data triangulation and made it difficult to fabricate partnerships. We detected over-reporting by men a few times but found that it only occurred among very young men who had only recently begun sexual activity. While our survey design deterred over-reporting attempts by men during the interview process, it could not identify under-reporting by women. Thus, we assume from our methods that women's contact data, on the whole, were less reliable than the men's. Although there is little research on the sexual behaviour norms of Kaokoveld, the existing literature, as well as our own field knowledge [13], show that concurrency is common and culturally acceptable among most women as well as men [19] and that women use this freedom to select partners that provide material and emotional support [22].

We took two steps to use the survey data to build a consistent contact structure into our model. First, to balance the number of men and women, we added 13 more women and distributed them evenly among all but the highest contact rates. This brought the number of women in the sample to 221, equal to the number of men, and it brought the number of women's contacts up to 399.

Second, we looked for a closed subsample within the whole sample—individuals in the total sample who reported partners that were also participants in the study. This yielded a subsample of 76 women and 70 men. The majority of partnerships in this subsample were reported by both partners. Eleven of the men (16%) in this subsample did not report contacts that women in the sample had reported, and 13 of the women (17%) did not report contacts that men in the subsample had reported. Electronic supplementary material, appendix B, table II, shows a contact matrix for this subsample where we included the contacts that were reported by only one partner. The result is a contact matrix with 103 contacts. The row and column headings in electronic supplementary material, table II, indicate one of the four activity groups.

We created a matrix of contact between men and women in each activity group in this subsample from electronic supplementary material, table II. Electronic supplementary material, appendix B, table III, shows that the fraction of contacts reported by men with each activity group of women is fairly consistent between the subsample and the full sample. This gave us an additional reason to trust the reporting by men more than women. Given that men reported 683 contacts in the full sample and 103 in the subsample, we multiplied each cell value in our subsample of contact structure (electronic supplementary material, table II) by 683/103. This preserved the distribution of the number of men in each male activity group and generated a unique multiplier for each activity group (c₂₁ = 1.2, c₂₂ = 2.2, c₂₃ = 2.2, c₂₄ = 1.7) for the underrepresented numbers of women's contacts in the full sample. By multiplying these values by the total number of women in each activity group, we generated a total number of contacts for women that are symmetric to that reported by men. Final values for the total number of women and the total number of contacts in our model are presented in electronic supplementary material, appendix B, tables IV and V.

As an additional check of this approach, we also ran a version of the model where we adjusted men's contact rates based on women's reports. We then ran the model over a wide range of transmission probability estimates (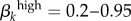 and 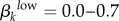) and found that no model runs using values generated from women's reports produced infectious steady states that came close to matching empirical values from Kaokoveld (electronic supplementary material, appendix B, table VI and figure I). This further supports our decision to use men as the reliable sex to balance contact rates in our model.

2.3.1.3. Mixing parameter (ρ_jk,i)

The c_kj's discussed above keep track of the average number of contacts in each activity group j for each sex k. The next parameter in modelling the sexual contact structure is the mixing parameter, which keeps track of who has sex with whom, in particular, what fraction of activity group i's contacts are with individuals in (opposite sex) group j. There are two extremes for such matrices. In one (‘associative mixing’), members of group i mix only with members of the corresponding group i. At the other extreme is random or proportionate mixing in which the fraction of a group i member's (say, male) contacts with female members of group j is simply the fraction of all females in the study population that are in group j, i.e. the relative size of group j. Classically, proportionate mixing has been the most common model assumption.

In their study of the spread of GC in New Jersey, Garnett et al. [12] used a combination of these two mixing specifications. They assumed that each activity group reserved a fraction ρ of contacts for members of the corresponding opposite sex group with the rest of their contacts randomly distributed among all four activity groups (see [3]). We added a bit more flexibility in our contact pattern model by allowing each activity group j to reserve a different fraction (r_j) for within-group mixing with the rest proportionately distributed among all four activity groups. Jacquez et al. [10] called this ‘preferred mixing’.

We used the Kaokoveld survey to generate contact matrices that describe contact patterns in rural Kaokoveld. In fact, we once again used the 146-participant subsample of those 103 contacts for which both partners reported the contact in the survey. The resulting 4 × 4 contact matrix is presented in electronic supplementary material, appendix B, table II. If contacts were random, this contact matrix would have a χ² of zero. Instead, its χ² is 13.7. We calculated what integer values we could subtract from the diagonal entries of this contact matrix (i.e. the cells that represent the number of contacts between men and women of the same activity group) so that the resulting matrix would have as small a χ² as possible. We divided these subtracted numbers by the total number of contacts in each group to get the reserved fraction r_i for each group. See table 1 for final values.

2.3.2. Disease parameters

2.3.2.1. Transmission probability of symptomatic and asymptomatic high-level infections ()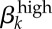

This parameter (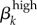) is the mean probability that a single contact with a sex k′ person infected with a high-level infection will lead to a new infection. We cannot estimate this directly from our dataset because we do not have accurate estimates of the number of sex acts per person or the GC statuses of participants' contacts. However, values for GC transmission in the literature estimate male-to-female transmission at 0.5 by Platt et al. [16] and female-to-male at 0.2–0.5 by Hooper et al. [15]. Garnett et al. [12] could not maintain endemic GC in their model to match levels seen in Newark without increasing these probabilities to 0.8 and 0.6, respectively. Though Garnett et al. were concerned that these values were ‘too high’, our estimations suggest that these higher values may be closer to reality for many settings. Platt et al. [16] and Hooper et al.'s [15] empirically derived estimates were based on culture detection methods, which are very insensitive compared with molecular assays that are now the standard. Additionally, in Kaokoveld, GC transmission—especially male-to-female—is likely to be at the high end of realistic estimates because of the frequency of partner exchange, minimal condom use and a preference for dry sex. Thus, we expect that the appropriate estimates for disease transmission lie somewhere in this higher range.

2.3.2.2. Transmission probability of asymptomatic low-level infections ()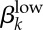

We assume that low-level infections have a lower transmission probability than high-level infections. However, because our empirical work in Kaokoveld was the first to report on the observance of high prevalence of low-level infections among an undertreated population, there are no reliable estimates for this parameter. We use our model to generate estimates for low-level transmission probabilities.

2.3.2.3. Recovery from symptomatic high-level infection (σ_k)

In the Kaokoveld dataset, the vast majority of participants who reported having had symptoms in the prior six months sought treatment at a clinic. Only symptomatic people receive treatment because local sexually transmitted disease (STD) care is through syndromic management; no screening or partner notification programme exists. Thus, individuals in our model recover from symptomatic infection faster than they do from other categories of infection because they received antibiotics.

We identified survey participants who reported having had GC symptoms within the past six months [13]. From these individuals' data, we estimated the number of days between symptom recognition and travel to the clinic. We separated this parameter by sex, because women in our study typically took longer to seek treatment. We estimated a duration average of 11.7 days for men and 14.5 days for women. These numbers are roughly estimated because people in our study population do not keep a specific record of dates. It takes several days after treatment begins (i.e. day of clinic attendance) for the antibiotics to clear the infection completely, and our field interviews indicate that that there was variability in which antibiotics were dispensed during the data collection period. Therefore, our estimates for recovery from symptomatic high-level infection (σ_k) are likely low and oversimplified, but offer a starting point for calibrating the model.

2.3.2.4. Rate of movement from Y_k^a,high → Y_k^a,low (ψ_k)

This parameter estimates the rate at which asymptomatic high-level infections diminish into low-level infections. Like 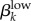, this value is unknown because asymptomatic low-level infections had not been reported prior to the Kaokoveld study. It has been assumed that untreated people are infectious for six months [12], but this estimate was derived when culture was still the diagnostic gold standard. Low-level infections were not likely to be detectable and so previous values given for duration of infectiousness of untreated infections might actually be an estimate of how long it takes for an untreated infection to diminish below the ID₅₀ dose. We use our model to test this assumption.

2.3.2.5. Recovery from asymptomatic infection (γ_k)

This is the rate at which low-level infections diminish to the point of complete resolution and an infected person becomes susceptible again. Because this parameter is part of movement in and out of the low-level infectious state, we again do not have reliable estimates for this parameter. We use our model to explore reasonable values.

2.3.2.6. Proportion of high-concentration infections that are asymptomatic (θ_k)

Very few men and even fewer women with high-level GC infections in the Kaokoveld study reported symptoms. Given the lack of screening and partner notification programmes in Kaokoveld, people who do not perceive symptoms do not receive antibiotic therapy. These people stay infected and infectious longer than people who receive antibiotic treatment. The proportion of asymptomatic—and therefore untreated—individuals in a population will likely have a strong influence on transmission dynamics and endemic levels of GC.

All participants in the empirical study were asked whether they were currently experiencing (i) abnormal discharge or (ii) dysuria (i.e. pain or itching during urination). Answers to these two questions were tightly correlated [13], so the variables were aggregated. Among participants with high-level GC infections, 78% of men and 95% of women were asymptomatic; this is a much higher rate of asymptomatic infection than usually reported in the literature, but studies among similarly rural [23] and resource poor populations [24] find similarly low rates of symptom reporting. In our model, θ₁ = 0.78 and θ₂ = 0.95.

3. Results and discussion

3.1. Calibration and validation

3.1.1. Question 1. How does contact structure affect GC prevalence in our model?

We use the function ρ_ki for preferred mixing, with a term (r_i) for proportion of within-group contacts for each activity group, to capture nuances of within-group preference in a tractable way. For sake of comparison, we compared three mixing formulations: preferred mixing with r_i as in the final model, random (or proportionate) mixing with r_i = 0 for all i and associative mixing with r_i = 1 for all i.

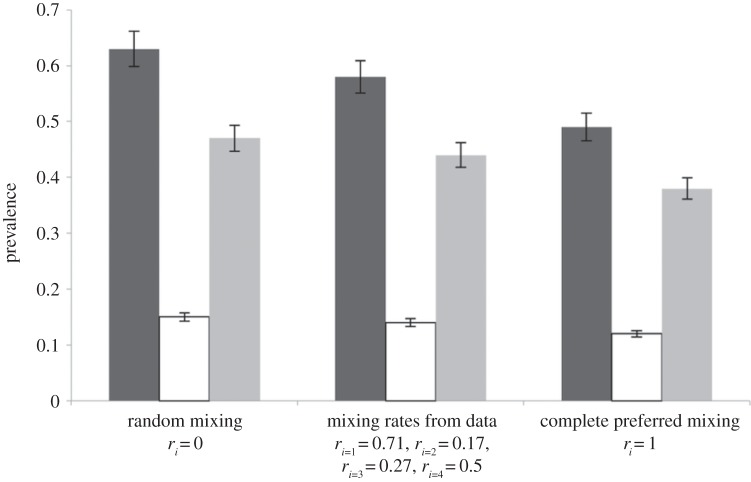
We found that prevalence decreased as within-group preference increased (figure 3). Total prevalence was highest under conditions with completely random contact structure—expected because this is the case in which low-activity individuals mix the most with high-activity individuals (e.g. [25]).

Figure 3.

Prevalence is higher when contact structure is random: we ran the model three different ways: first, we assumed random mixing (r_i = 0); second, we used our empirically derived estimates for r_i; third, we assumed assortative mixing (r_i = 1). Trends were the same for men and women so prevalences are not reported by sex. Total prevalence (black) decreases as contact structure becomes less random. The change in overall prevalence is due mostly to decreases in low-level infections (grey), while high-level infections (white) change little.

3.1.2. Question 2. Are male-to-female transmission probabilities higher than previously estimated?

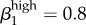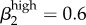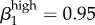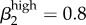Regarding our parameters for high-level transmission probability, we were not able to reflect the endemic levels in Kaokoveld if we reduced transmission below Garnett et al.'s values of (male-to-female) and ; in fact, we get closer to Kaokoveld prevalence levels when we increase high-level transmission above Garnett et al.'s values to and (figure 4a,b; electronic supplementary material, appendix B, table VII). We used the model to generate rough estimates of transmission probabilities for the low-level infected status as well. This is the first time this status has been presented in a model of GC transmission, so we used our calibration process to define reasonable estimates (figure 4a; electronic supplementary material, appendix B, table VII). Our estimates for low-level transmission probabilities to match Kaokoveld prevalence levels centred around 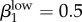and .

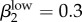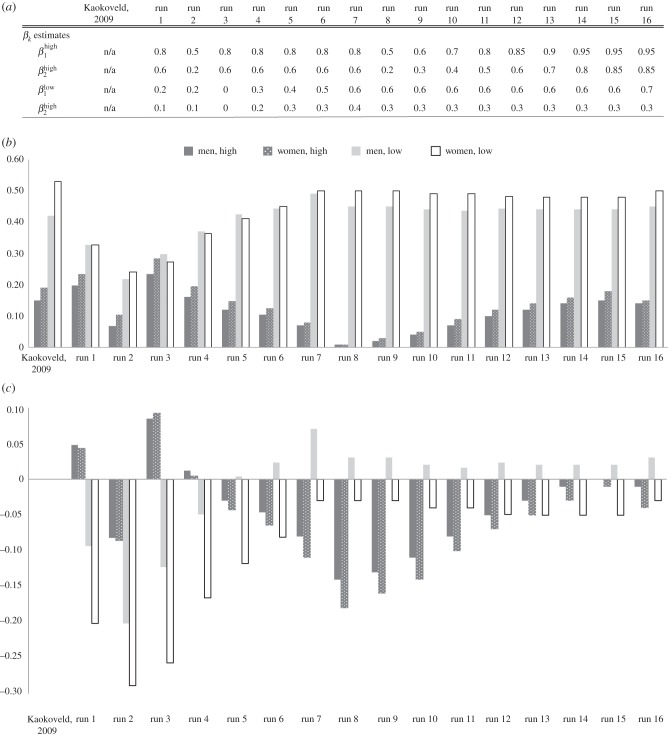
Figure 4.

(a–c) Calibrating transmission probabilities for high- and low-level Neisseria gonorrhoeae infections: transmission probabilities for high-level infections from our model are higher than those estimated by Garnett et al. [12], but closer to Garnett et al.'s estimates than previously reported in the literature. Low-level transmission probability estimates are lower than high-level estimates but maintain the same pattern of male-to-female transmission being higher than female-to-male. (a) β_k estimates we used for each run. (b) Prevalence outcomes from each run for high- and low-level infections for men and women, along with the Kaokoveld prevalences for comparison. (c) Difference in prevalence outcomes between each run and the prevalences from our empirical study in Kaokoveld.

To find the best estimates for 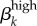and 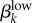, we ran approximately 40 simulations with a range of different β values. In figure 4a–c, we present a summary of some of our runs (once we determined rough estimates for other parameters) to illustrate our pattern for calibrating these transmission parameters. Figure 4a lists all β_k values used in each run. Figure 4b shows the prevalence outputs from each run, along with a comparison to prevalence levels in the Kaokoveld sample. Figure 4c shows the difference between prevalence outputs from each run and Kaokoveld prevalence.

Run 1 (figure 4a) uses Garnett et al.'s [12] final values for high-level infections (β_k^high) and 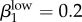, 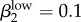. We also ran the model (Run 2) with parameter values for β_k^high (β₁^high = 0.5 and β₁^high = 0.2) as reported by Hooper et al. [15] and Platt et al. [16] to demonstrate that these β_k values cannot sustain infections levels seen in our Kaokoveld sample. Our simulations systematically used different β_k values to find the combination of transmission parameters that yielded closest model-generated prevalences to the Kaokoveld sample values. Given our choices of the other model parameters and of the β_k's we sampled, we found the closest fit to the Kaokoveld sample values in Run 15: 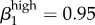, , 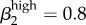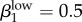and 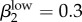. Deviations from these values led to poorer fits to the Kaokoveld data.

Our results suggest that differences in transmission risk between men and women persist among diminishing, lower transmissibility infections, which might help explain the greater prevalence of low-level infections among women in Kaokoveld. This result also suggests that the β values estimated by Garnett et al. are not unrealistically high.

Some discussion of the existing empirical evidence for transmission probabilities is helpful here. The studies used to inform GC transmission models were conducted when the gold standard for GC diagnosis was culture [15,16]. Culture has largely been replaced by molecular techniques, which are more sensitive and can detect GC DNA at much lower quantities. Therefore, it is likely that many cases were not detected in those early studies, reducing the transmission probabilities that they generated.

Hooper et al. also found that female-to-male transmission probability differed between two different demographic groups in their study. Thus, it is also possible that among some high-activity populations—especially ones with high levels of partner exchange [26], low rates of condom use and a preference for dry sex [27]—transmission probabilities for both sexes are higher than previously estimated.

We do not assume that our estimates are universally appropriate because transmission probability is context-dependent and is likely best represented by some range, which is influenced by many factors, including bacterial load, infection duration and frequency of past infections in the population. It probably also depends on the environment and culture of the underlying population. Unique behavioural characteristics in Kaokoveld, including limited access to treatment, minimal condom use, preference for dry sex and high frequency of partner exchange, could easily affect the underlying transmissibility of GC among the population.

Finally, it is important to note that our values for high-level GC transmission may seem strange because they are so much higher than previously suggested values from empirical studies or models. However, these rates only apply to transmission of the highest concentration infections in the model population, which account for about 26% of the infections in the model. Our low-level transmission probability estimates account for 74% of the infections. If the transmission parameters are reduced to a weighted average for each direction (male-to-female and female-to-male), we get β₁ = 0.62 and β₂ = 0.43, which are closer to previous estimates. Thus, the actual problem of prior β_k estimates not being high enough to account for observed prevalences in high-risk communities may not have been with the estimates being inaccurate so much as there being an oversimplification with using a one-level β_k parameter, as well as a general lack of information about asymptomatic cases. In this vein, a considerable body of work on the transmission of HIV, for example, stresses the role of heterogeneity in a number of important epidemiologic and biologic factors, including the sex of the infected partner, the type of sex act and the time since that partner's infection occurred [28,29]. To capture this heterogeneity, a single beta just will not do.

3.1.3. Question 3. What are the characteristics of low-level infection status?

The high prevalence of low-level GC infections in Kaokoveld (42% of men, 53% of women) motivated the construction of this model to define low-level associated transmission characteristics of GC and explore their effect on overall prevalence in Kaokoveld or other similarly undertreated populations with high endemic GC levels.

Given our choices of the β_k's, our model-generated prevalence came closest to matching the Kaokoveld prevalence when we set parameter values for which (i) women (σ₂ = 24 days) were infectious at the symptomatic, high-level infection stage longer than men (σ₁ = 21 days) and (ii) both men and women's asymptomatic high-level infections lasted longer than the six months typically estimated for untreated, asymptomatic infection (γ_k = 10.9 months). Also, women (ψ₂ = 10.9 months) remained in the low-level stage longer than men (ψ₁ = 8.2 months) before returning to susceptible status. All final parameter values are reported in table 1.

These numbers are greater than estimates previously generated, but there are very few estimates from empirical data of the natural history of gonococcal infection, and none that were obtained in the absence of treatment where highly sensitive diagnostics were used to diagnose and quantify GC infections. An early study of untreated, incarcerated women found that after four months of monitoring, less than half the participants became culture negative [30]; it follows that infection duration is at least four months, probably longer. Most aspects of the study design suggest that disease duration was heavily underestimated. First, the study recruited already infected, symptomatic participants—unknown numbers of days of infectiousness were lost at the beginning of the infection. Second, participants' GC was considered resolved when cultures became negative, even though all ‘cleared’ participants still reported having symptoms—this insensitive diagnostic technique was likely not catching infections as they diminished in titre.

There are also no reliable data for untreated GC duration for men. Handsfield et al. [31] tracked asymptomatically infected men, but they were treated by day 165 (5.4 months); our results indicate that infections last at least that long.

Most model-based research estimates infection duration to be six months, which is derived from an attempt to find the duration of infection that would fit a population where the proportion of cases that are asymptomatic is 40–60% [31,32]. These studies were conducted among urban populations in a clinic setting where we do not expect their proportions for asymptomatic cases to match the proportions found in highly remote populations. There are two reasons for this: first, clinic-collected samples are usually biased towards symptomatic cases because asymptomatically infected people are less likely to seek treatment for an STD. Second, other studies of healthcare-seeking behaviour have shown that infected people in high-risk settings are more likely to disregard genito-urinary symptoms [24] and in rural areas (where clinic access is poor) even fewer seek treatment [23]. Regardless of whether a particular GC infection is symptomatic (i.e. the person has characteristic discharge, dysuria, abdomen pain, etc.), if the infected person does not recognize those conditions as infection symptoms nor seeks treatment for them, the infection is, functionally, asymptomatic and will have a longer duration of infectiousness than treated infections and will attenuate in the manner we model herein.

Our estimates need to be backed up by other empirically backed models and direct measures, but they do shed light on aspects of GC epidemiology that are very difficult to study empirically—especially the impact of asymptomatic disease on driving transmission, particularly where GC infections are rarely treated and infectiousness persists longer.

3.1.4. Question 4. What role do low-level infections play in overall gonorrhoea prevalence?

Because low-level infections were highly prevalent among men and women (there were more men and women with these infections than there are GC negative people in our sample), we presumed they played an important role in driving overall transmission. We predicted that if we removed this compartment from our model, we would see a significant drop in overall prevalence.

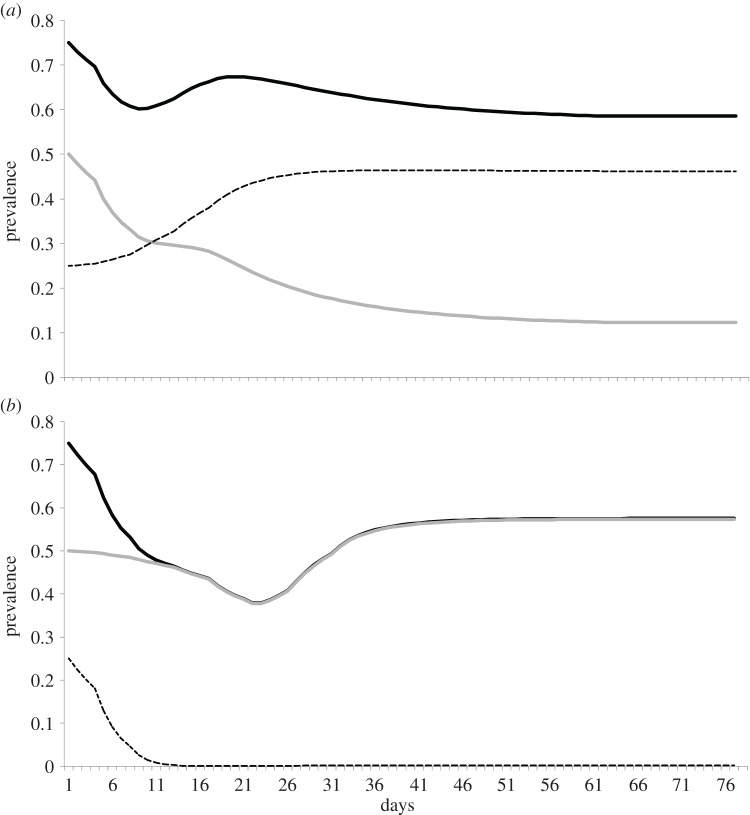
After calibrating the model for a closest match to Kaokoveld prevalence patterns, we ran the model without a low-level infection compartment (i.e. asymptomatic high-level infected individuals moved directly back to being susceptible, figure 2). However, we found in these runs that overall prevalence remained the same, but was driven entirely by high-level infections (figure 5) because, when we removed the low-level infection compartment from the model, infected individuals did not spend several additional months in the low-level infectious stage, which means they became susceptible to a new infection sooner. In this version of the model, people's individual infections are shorter, but reinfection frequency increases and, over time, people spend more time in a state of high infectiousness.

Figure 5.

Removing low-level infections from the model increases high-level infections and does not reduce overall prevalence: (a) equilibrium prevalence when we run our model with parameters that best match the Kaokoveld conditions. Total prevalence (solid black) is 58% and is composed of 46% low-level infections (dashed) and 12% high-level (symptomatic and asymptomatic combined) infections (grey). When low-level infections are removed (b), and die out from initial conditions, prevalence remains the same and is composed almost entirely of asymptomatic high-level infections. Symptomatic infections increase as well but stay below 4% prevalence.

Our model illustrates the impact of low-level infections on the prevalence of high-level infections and contributes to an old but patchy discussion on the importance of immunity in GC epidemiology. Studies of similarly high-activity, low-treatment populations do not report prevalences as high as we found in Kaokoveld [33,34]. Our model suggests that, without the added stage of low-level infection, prevalence of high-level infections in Kaokoveld (and, presumably similar populations) would be much higher. Instead, we argue that high GC prevalence in undertreated populations is mostly composed of long-duration, low-level infections, which have the effect of decreasing both the number of potential opportunities to become reinfected and the possibility of facing a new, severe infection.

As one of our reviewers pointed out, ‘there is an interesting parallel to HIV epidemiology, previously unrecognized in the setting of gonorrhoea: the importance of low-degree, high-concurrency sexual networks; a high-infectivity group (or perhaps phase); and a low-infectivity group that might be important for endemic maintenance of infection. The parallel would be complete if people are most infectious soon after acquiring gonorrhoea’.

3.2. Sensitivity and uncertainty analyses

We conducted two kinds of uncertainty and sensitivity analyses to determine the relative influence of the 31 model parameters of the transmission dynamics on the equilibrium values of the eight outputs: the final prevalences of uninfected males and females (X), of symptomatic high-level males and females (Y^s,high), of asymptomatic high-level males and females (Y^a,high) and of asymptomatic low-level males and females (Y^a,low). Uncertainty analyses assess the prediction imprecision in the outcome variable due to uncertainty in estimating the value of input parameters. Sensitivity analyses quantify how changes in the value of input parameters alter the value of an outcome variable. Uncertainty and sensitivity analyses are necessary to explore the behaviour of a model as complex as the one presented here, especially because the uncertainty in estimating the values of many of the input parameters compounds the complexity of the model. For both sets of analyses, we explored the effects of each parameter on the eight output estimates representative of transmission in this system. We present both analyses to assess the sensitivity and prediction uncertainty for each parameter.

3.2.1. Sensitivity and uncertainly analyses: elasticity

The sensitivity analysis, which is the simplest approach, involved changing the value of each parameter while holding the other parameters fixed. This parameter sensitivity measure (elasticity) was estimated by determining the mean percentage change in each output from a 1% change in the parameter of interest, relative to the values in the base run (electronic supplementary material, appendix C, table VII). This approach is quick and simple, but it explores only a small region of the full parameter space.

The most sensitive parameter was the proportion of high-concentration infections that are asymptomatic (θ_k). A 1% change in θ₁ resulted in a 4% decrease in men's symptomatic high-level infections; increasing θ₂ by 1% resulted in a 19% decrease in symptomatic high-level-infected women. There were also major effects on the asymptomatic high-level men and women. Our values for θ₁ and θ₂ are higher than those usually reported in the literature. However, as we indicated above, because of our face-to-face interviews, our collection of urethral and vaginal samples, and our use of molecular diagnostics instead of culture, we are comfortable with the values of θ₁ = 0.78 and θ₂ = 0.95 for our Kaokoveld sample. Due to local variability in the biological characteristics of individual epidemics and accessibility of treatment, we expect values for θ_k to differ among populations.

The other input parameters whose elasticities exceeded 0.58 in absolute value were (table 2): transmissibility of high-level infection (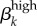) and disease duration parameters (σ_k, ψ_k, γ_k). The 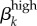sensitivity suggests a narrow range of accurate estimates for these transmission probabilities. No population or contact parameters were especially elastic, and the numbers with low-level infection or no infection were not particularly sensitive to parameter values.

Table 2.

Ranked parameter elasticities with absolute value greater than 0.58%. θ_k, proportion of high-level infections that are asymptomatic; σ_k, recovery rate from symptomatic, high-level infections; γ_k, recovery rate from asymptomatic, low-level infections; 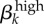, transmission rate of high-level infections; ψ_k, recovery rate from asymptomatic, high-level infections. Note the insensitivity of population and contact parameters.

high-level, symptomatic men		high-level, symptomatic women		high-level, asymptomatic men		high-level, asymptomatic women
parameter	elasticity value	parameter	elasticity value	parameter	elasticity value	parameter	elasticity value
θ1	−3.7	θ2	−19.08	ψ1	−1.27	ψ2	−1.26
σ1	−1	σ2	−0.99	γ1	0.91		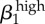0.9
γ1	0.93		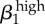0.93		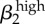0.85	θ2	0.88
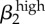	0.87	γ2	0.91	θ1	0.82	γ2	0.87
ψ2	−0.79	ψ1	−0.84	ψ2	−0.84	ψ1	−0.82
γ2	0.67	γ1	0.71	γ2	0.65	γ1	0.68

3.2.2. Sensitivity and uncertainly analyses: partial rank correlations

To explore the effect of varying the values of all input parameters across their whole range simultaneously, we used Latin hypercube sampling (LHS) and partial rank correlation (PRC) [35,36]. In LHS, a probability distribution for each of the 31 input parameters is chosen and the support of each of these distributions is divided into N equivalent segments (N = 2000). We then ran the model 2000 times to compute the eight outcomes of interest, each time choosing at random and independently, without replacement, a value for each of the 31 parameters from the 2000 subintervals. (After these 2000 runs, each of the 2000 subintervals comprising the distribution for each of our 31 parameters had been sampled only once.)

To carry out the PRC process, we assigned ranks to our 2000 subintervals for each of our 31 parameters from 1 to 2000 in the natural increasing order. This yielded a 2000 × 31 integer-valued input matrix. We also assigned integer ranks to the values of the corresponding outputs. Next, we constructed a 2000 × 1 matrix of the output variables generated by each of these 2000 runs and then rank-transformed this column matrix by replacing the value of the outcome variable of the ith run by its relative size (rank) among the 2000 output variables of all 2000 runs. Finally, we used the rank-transformed input matrix and the rank-transformed output matrix to calculate the Spearman or rank correlation coefficient and the partial rank correlation coefficient (PRCC). The magnitude of the PRCC indicates the importance of the uncertainty in predicting the value of the outcome variable, and the result for each input and output variable is a number between −1 and +1. The sign of the PRCC indicates whether the input parameter has a negative or positive effect on the outcome variable. PRCC is adequate for uncertainty and sensitivity analysis of nonlinear and monotonic relationship between inputs and outputs.

Electronic supplementary material, appendix C, table VIII, gives the values of all the input–output combinations that had a significant PRCC (p < 0.001). Table 3 lists the combinations that had significant PRCCs with absolute value greater than 0.35. As expected, the parameters with high elasticities also had high PRCCs (θ_k, σ_k, ψ_k, γ_k). But other input variables and output variables now play a role, including the average number of contacts of women in the lowest activity group (c₂₄), the fraction of men in the second lowest activity group (N₁₃) and their average number of contacts (c₁₃) and the fraction of activity that high-activity men and women had with each other (r₁). Unlike the results for elasticities, some of these parameters increased the uncertainty in estimates of the equilibrium numbers of asymptomatic and uninfected men and women.

Table 3.

Significant PRCC values with absolute value more than 0.35 after 2000 model runs^a. r_k, proportion of contacts with partners from the same activity group; N_ik, number of men or women in i activity group; c_ik, contact rate; 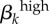, transmission rate of high-level infections; 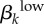, transmission rate of low-level infections; γ_k, recovery rate from asymptomatic, low-level infections; θ_k, proportion of high-level infections that are asymptomatic; σ_k, recovery rate from symptomatic, high-level infections; ψ_k, recovery rate from asymptomatic, high-level infections.

estimate of susceptible men		estimate of susceptible women		estimate of high-level, symptomatic men		estimate of high-level, symptomatic women		estimate of high-level, asymptomatic men		estimate of high-level, asymptomatic women		estimate of low-level, asymptomatic men		estimate of low-level, asymptomatic women
parameter	PRCC	parameter	PRCC	parameter	PRCC	parameter	PRCC	parameter	PRCC	parameter	PRCC	parameter	PRCC	parameter	PRCC
ψ2	0.7723	c24	−0.9537	σ1	−0.9805	σ2	−0.9687	ψ1	−0.8898	ψ2	−0.9059	γ1	−0.9218	c24	0.9045
r1	−0.7445	ψ2	0.7387	γ1	0.6996	θ2	−0.7743	γ1	0.8403	γ2	0.7633		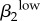0.8166	γ2	−0.8241
ψ1	0.7007	ψ1	0.5701	ψ2	−0.6851	γ2	0.6044	ψ2	−0.8371	c24	0.7355	r1	0.6439	ψ2	0.5922
γ1	0.6643	γ2	0.5196	θ1	−0.6582	γ1	0.5267	γ2	0.7364	ψ1	−0.6783	ψ1	0.6297		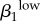0.4832
N13	−0.623	r1	−0.5112	γ2	0.5768	ψ1	−0.513		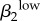−0.6564	γ1	0.6737	N13	0.509	γ1	−0.445
c13	−0.5009	r4	0.3978		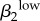−0.5121	c24	0.5071		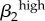0.4812		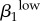−0.4508	γ2	−0.4279	r1	0.3636
	−0.4988		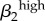		0.3574		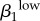		−0.4134		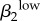−0.4456	c13	0.4175
γ2	−0.4949
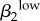	−0.4838
c24	−0.458

^aAll values, p < 0.001.

4. Model limitations and future directions

There are several limitations to conclusions we can draw from the key insights of our model. First, even with high transmission probabilities and long infection durations, our model outputs for high- and low-level GC prevalences among women were lower than our empirical values. A likely contributing reason for this is that women were under-reporting their number of contacts. Although we were able to account for this somewhat by estimating new contact rates using multipliers derived from men's more accurate contact rates, it seems that we are still underestimating the amount of partner concurrency among women in Kaokoveld.

Second, it is tempting to draw conclusions about immunity to GC from our model. These results and our empirical data from Kaokoveld do not measure immunity but are consistent with previous observations of an incomplete immune response to GC infections. Plummer et al. [37] show that immunity is strain-specific and incomplete. In their study, female sex workers were significantly less likely to be reinfected with the same strain of GC and the longer a woman engaged in sex work, the less frequently she was infected. It has also been proposed that untreated infections will have a stronger immune response than those that resolve more quickly as a result of antibiotic intervention [31]. Adding the potential for immunity would be an important advancement on the model because it would allow us to make predictions about how specific intervention programmes will affect population-wide acquired immunity. In a resource poor setting, where treatment is limited and erratic, immunity to disease can play a very important, protective role.

Third, while our model allows for low-level infections to generate from (i) exposure from a contact with another low-level infection and (ii) a diminished asymptomatic high-level infection, we do not allow for a new high-level infection to result from exposure to a low-level infection. However, this may be an important component of GC transmission, happening when a person with a low-level infection has sexual contact with a person who has never been exposed to that strain before. As age-discordant couples are common in Kaokoveld [19] (A. Hazel 2009, unpublished field interviews), it is possible that many GC cases among the youngest adults were the result of contact with an older adult who has a low-level infection. It is necessary to further explore if these contacts are important for maintaining the 15% prevalence for high-level infections in Kaokoveld and are, therefore, ideal targets for prevention interventions. This is especially important because it could help explain—in addition to the problem of under-reporting by women—why our model outputs for high-level infections in women were lower than the survey indicated.

5. Conclusion

Using the approach pioneered by Hethcote & Yorke [3], and especially by Garnett et al. [12], we present a model of GC transmission that is the first to include a compartment for reduced-infectiousness disease status (figure 2). By constructing this model using (i) extensive empirical, cross-sectional data about sexual activity and contact structure based on interviews in rural Kaokoveld and (ii) sensitive, quantitative diagnostic GC assays of urethral or vaginal swabs of the interviewees, we were able to interrogate old assumptions about transmission probabilities and infection duration. Our model supports Garnett et al.'s findings [12] that the transmissibility of high-level infections is higher than past epidemiologic studies have reported, further suggesting that the estimates derived from culture-based studies are not reliable. Finally, we described the transmission and duration of a new infectious stage of GC that is the result of untreated, unresolved asymptomatic infections. These explorations provide corroborating insights into the importance of immunity in shaping patterns of endemic GC.

The original fieldwork in Kaokoveld was completed when treatment options were strictly limited to symptomatic people. This is still the case, but these studies—yielding reliable prevalence measures and empirically backed theoretical transmission models—have the potential to inform STD care to the Kaokoveld communities and similarly remote, undertreated populations. With parameter estimates that are backed by empirical validation, we can build from our current model to predict future risk based on behavioural or epidemiologic transitions. This is an important future step because the Kaokoveld pastoralists, like many remotely living subsistence-based populations, are facing economic, cultural and environmental changes that are likely to have an impact on health and healthcare access [38,39].

Funding statement

We thank our funding sources: Interdisciplinary Program in Infectious Diseases (NIH T32 A1049816), the Robert Wood Johnson Health and Society Small Grant Program, the Wenner-Gren Dissertation Fieldwork Grant, American Philosophical Society's Lewis & Clark Fund, Complex Systems Approaches to Population Health & Health Inequalities (University of Michigan Center for the Study of Complex Systems and the Center for Social Epidemiology and Public Health) and the University of Michigan's Rackham Graduate School and the School of Natural Resources and Environment.