Hierarchical analysis and multi-scale modelling of rat cortical and trabecular bone

Abstract

The aim of this study was to explore the hierarchical arrangement of structural properties in cortical and trabecular bone and to determine a mathematical model that accurately predicts the tissue's mechanical properties as a function of these indices. By using a variety of analytical techniques, we were able to characterize the structural and compositional properties of cortical and trabecular bones, as well as to determine the suitable mathematical model to predict the tissue's mechanical properties using a continuum micromechanics approach. Our hierarchical analysis demonstrated that the differences between cortical and trabecular bone reside mainly at the micro- and ultrastructural levels. By gaining a better appreciation of the similarities and differences between the two bone types, we would be able to provide a better assessment and understanding of their individual roles, as well as their contribution to bone health overall.

1. Introduction

Cortical and trabecular bone are arranged within a hierarchical structure in the osseous tissue: this diversity of structures allows the skeleton to perform its mechanical and metabolic functions. Different factors, such as bone mass, geometry, material properties, cortical to trabecular proportion, molecular composition, microstructure and architecture, contribute to the tissue's strength and quality [1–3].

Collagen fibres, as an organic component, and carbonated apatite crystals, as a non-organic component, contribute to bone's strength by resistance against loads applied to its structure [1]. The mineral phase is the main determinant of stiffness, whereas collagen content governs its post-yield ductility. The mechanical properties of bone are ultimately determined by the mineral content and its distribution pattern within the collagenous matrix, as well as the tissue's structural, microstructural and nanostructural organization [4].

Composed primarily of osteons of concentric lamellae, cortical bone is remarkably stiff and contributes substantially to the tissue's mechanical strength. On the other hand, trabecular bone is arranged in a mosaic of angular segments of parallel sheets of lamellae and shows a greater rate of metabolic activity, lower modulus and larger surface-area-to-volume ratio [2,5–7].

Extensive research has been conducted to distinguish cortical from trabecular bone [4,7–30]. Although a variety of animal models and analytical techniques have been employed to assess the differences between these two structural components—especially in the context of endocrine, dietary and stress variables—few studies have compared them in a comprehensive manner. Bigi et al. [13] have reported the CO₃ and Ca/P content of trabecular and cortical bone in mouse. Bagi et al. [15] analysed the yield load and stiffness of cortical bone in mouse based on bone volume fraction. Toolan et al. [31] analysed the effects of bisphosphonates on the mechanical behaviour of rat bones. Hodgskinson et al. [19] and Kuhn et al. [11] reported the hardness and Ca, CO₃, C/PO₄ and Ca/P content for trabecular and cortical bone of bovine. Limited data have been reported on pig and dog [22,32]. The majority of work on human contains mineral density, bone volume fraction, tissue modulus and module of elasticity [7,21,23–27,29,30]. These studies have produced inconsistent results and have only provided snapshots of the vast spectrum of data on which to base an exhaustive comparison (table 1).

Table 1.

A chronological snapshot of comparative hierarchical properties of cortical and trabecular bones.

level	indices	ref.	bone type	testing technique	cortical bone	cancellous bone
macro-structure	ash (inorganic) content %	[13]	rat femur/tibia	thermogravimetry	66.4 (0.3)	62.0 (0.3)
		[21]	steer vertebra/tibia	gravimetry	67.86	64.55
	protein content (%)	[21]	steer vertebra/tibia	gravimetry	28	31.09
	bone mineral density (BMD) (g cm−3)	[17]	mouse femur/tibia	μCT	1.089 (0.017)	0.745 (0.102)
		[28]	human (black) tibia	peripheral QCT	0.229 (0.088)	1.188 (0.043)
			human (white) tibia		0.255 (0.053)	1.117 (3.6)
	bone tissue density (ρT) (g cm−3)	[22]	rat vertebra/femur	gravimetry	2.066 (0.005)	1.908 (0.011)
		[21]	human vertebra/tibia	gravimetry	1.91	1.87
			steer vertebra/tibia	gravimetry	1.995 (0.01)	1.93 (0.22)
	stiffness (N mm−1)	[15]	rat femoral midshaft	three-point bending	47.24 (6.59)	—
		[31]	rat femoral midshaft	three-point bending	588 (75)	—
			rat vertebra	compression	—	1327 (336)
	failure load (N)	[15]	rat femoral midshaft	three-point banding	160.09 (30.80)	—
microstructure	BV/TV (mm3 mm−3)	[15]	rat femur	μCT	0.46	0.11 (0.04)
		[17]	mouse femur/tibia	μCT	—	0.25 (0.06)
		[20]	fetal pig mandibular	μCT	—	24.14 (4.14)
	mod. of elasticity (GPa)	[30]	human iliac crest (23 year)	three-point bending	3.76 (1.68)	3.03 (1.63)
			human iliac crest (63 year)	three-point bending	5.26 (2.09)	4.16 (2.02)
		[7]	human tibia	four-point bending	6.75 (1.00)	5.72 (1.27)
		[29]	human proximal tibia	three-point banding	5.44 (1.25)	4.59 (1.6)
	yield strength (YS) (GPa)	[27]	human femur	compression	0.109	0.089
nanostructure	tissue modulus (GPa)	[32]	porcine femur	microindentation	11.6 (9.5)	5.9 (4.3)
				nanoindentation	16.4 (1.3)	21.5 (2.1)
		[25]	human vertebrae/tibia	nanoindentation	25.8 (0.7)	13.4 (2.0)
		[26]	human femur	acoustic microscopy	17.73 (0.22)	17.5 (1.12)
				nanoindentation	20.02 (0.27)	18.14 (1.7)
		[4]	human femur	nanoindentation	21.2 (5.3)	11.4 (5.3)
	hardness (GPa)	[25]	human vertebrae/tibia	nanoindentation	0.736 (0.034)	0.468 (0.079)
		[4]	human femur	nanoindentation	0.234–0.76	0.234–0.76
composition	CO3 (−)	[13]	rat femur/tibia	FT-IR	3.8 (0.2)	2.3 (0.2)
		[11]	bovine femur/tibia	chemical analysis	5.33 (0.1)	5.33 (0.18)
	C/PO4 (−)	[11]	bovine femur/tibia	chemical analysis	0.17	0.17
	Ca (mg g−1)	[19]	bovine femur	colorimetry	271	257
		[23]	child vertebrae/femur	gravimetry	194	47.4
	HPO4 (%)	[11]	bovine femur/tibia	FT-IR	20.3 (0.2)	20.7 (0.2)
	PO4	[11]	bovine femur/tibia	FT-IR (%)	9.6 (0.1)	8.7 (0.1)
		[23]	child vertebrae/femur	chemical analysis (mg g−1 of bone)	24.1	90.3
	Ca/P (−)	[13]	rat femur/tibia	spectrophometry	1.63 (0.2)	1.5 (0.2)
		[11]	bovine femur/tibia	chemical analysis	1.64 (0.02)	1.58 (0.06)

Given the complex nature of bone, a comparison between its cortical and trabecular components should consider the hierarchical arrangement of structural properties for these two distinct tissues. Recent technological advancements have allowed researchers to evaluate bone's properties at ultra-, micro- and nanostructural levels, facilitating new insights into the tissue's material properties. Moreover, by considering the relative influences of certain structural parameters on bone strength and modulus, the tissue's mechanical properties can be predicted by mathematical modelling with single- and two-parameter power-law or linear functions [33–37]. However, owing to the heterogeneity and anisotropic material properties of cortical and trabecular bone, these methods cannot fully predict the mechanical properties of bone. In recent years, several methods have been proposed to overcome this shortcoming [38–43]. One of the methods considered for this purpose is the continuum micromechanics approach [44,45]. Continuum micromechanics is the analysis of heterogeneous or anisotropic materials at the level of the individual material elements forming these materials [44,45]. It has been used in several applications including modelling of defects in solids [46], mechanical properties of composites [47], electroelastic moduli of piezoelectric composites [48] and recently in modelling of mechanical properties of bone [40,42,43].

The aim of this study is to explore the hierarchical arrangement of structural properties in cortical and trabecular bone and to determine a mathematical model that accurately predicts the tissue's mechanical properties as a function of these indices (figure 1). By gaining a better appreciation of the similarities and differences between the two bone types, we will be able to provide a better assessment and understanding of their individual roles, as well as their contribution to bone health overall [11,18].

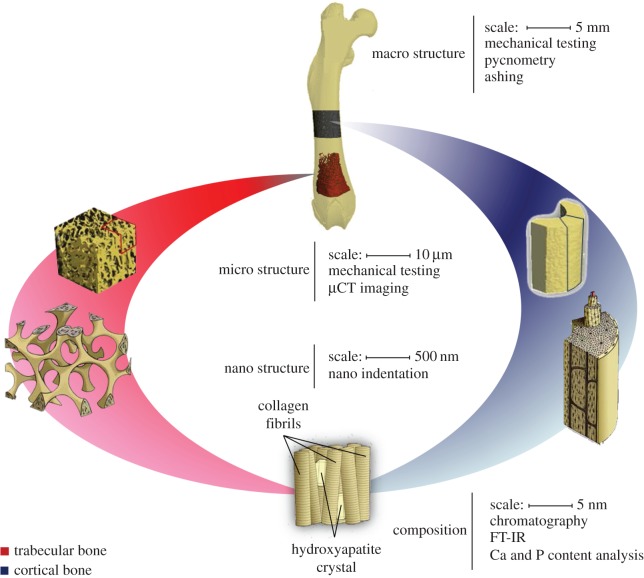
Figure 1.

An illustration of the hierarchical nature of cortical and trabecular bone.

2. Material and methods

2.1. Specimen preparation

The study protocol was approved by the Institutional Animal Care and Use Committee at Beth Israel Deaconess Medical Center, Boston, MA. Thirty Sprague–Dawley female rats (20 weeks old) were obtained from Charles River Laboratories (Charlestown, MA, USA) and euthanized via CO₂ inhalation. Cylindrical samples of diaphyseal cortical bone (height 6.85 ± 0.85 mm) and distal metaphyseal trabecular bone (height 5.17 ± 0.65 mm) specimens were obtained from each femur (figure 2). Additionally, secondary specimens for embedding were obtained by cutting 1-mm-thick diaphyseal and distal metaphyseal sections from all femurs. The specimen preparation protocol has been published in detail elsewhere [49]. All specimens underwent cleaning via sonic agitation (Fisher Scientific International, Hampton, NH, USA) while suspended in distilled water for 20 min, followed by centrifugal removal of excess water and marrow at 9g for 15 min. The details of the analytical methods will be presented in hierarchical fashion as follows.

Figure 2.

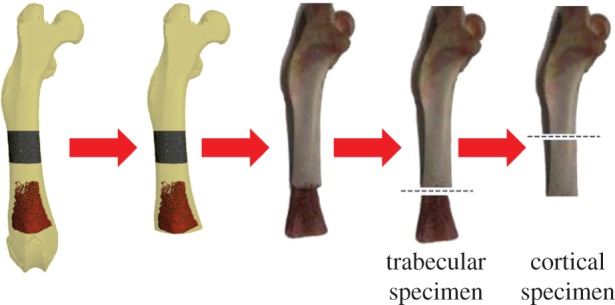
An illustration of the preparation process for cortical and trabecular specimens.

2.2. Macrostructural properties

2.2.1. Extrinsic structural properties

All cylindrical specimens underwent uniaxial compression (INSTRON 8511, Instron Corporation, Norwood, MA, USA) for determination of properties through analysis of the load–displacement curve. Structural stiffness was defined as the slope of the linear portion of the curve, whereas yield load was represented at the point where the curve ceased to be linear. The point with the highest load value represents the ultimate load.

2.2.2. Bone tissue density (ρ_t)

Bone mass and tissue volume (TV) of cylindrical specimens were measured by a precision scale (AnalyticalPlus, Ohaus, Pine Brook, NJ, USA) and gas pycnometry (AccuPyc 1330, Micromeritics, GA, USA). Bone tissue density was calculated by dividing bone mass by bone tissue volume.

2.2.3. Mineral and matrix content

In order to determine the mineral (ash mass/dry mass) and matrix (1 − (ash mass/dry mass)) contents, the cylindrical specimens were dried at 70°C for 24 h and ashed at 600°C for 96 h (Furnace 48000, Thermolyne, Dubuque, IA, USA). It has been shown that some parts of mineral evaporate at 600°C and quantitatively contribute to 6.6% of mineral weight. Therefore, the measured mineral content should be multiplied by 1.066 to show the actual mineral content in the bone.

2.3. Microstructural properties

2.3.1. Morphometric indices

Bone volume fraction (BV/TV) and bone-surface-to-volume ratio (BS/BV) of the trabecular and cortical cylindrical specimens were assessed using micro-computed tomography (µCT40; Scanco Medical AG, Brüttisellen, Switzerland—tube energy and current, 55 kVp and 145 µA, respectively; integration time, 250 ms; and isotropic voxel size, 20 µm).

2.3.2. Apparent material properties

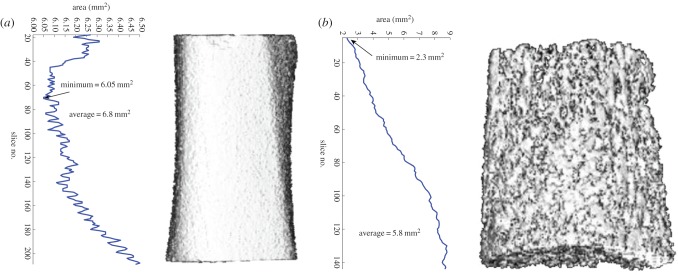
Apparent mechanical properties were calculated from the stress–strain curves obtained from uniaxial compression testing. The minimum cross-sectional areas for cancellous and cortical bone specimens were calculated from µCT images (figure 3). The modulus of elasticity (E) was determined from the slope of the linear portion of the curve, while the point where the curve ceased to be linear was designated as the yield strength (YS). The point with the highest strength value represented the ultimate strength (US).

Figure 3.

Calculation of minimum cross-sectional area for (a) cortical and (b) trabecular specimens. (Online version in colour.)

2.4. Nanostructural properties

2.4.1. Nanoindentation

The secondary specimens were dehydrated with ethyl alcohol, embedded in epoxy resin and polished. The midsections of the trabecular elements and the cortical shells were selected as indentation sites using a Berkovich indenter (Hysitron Triboindenter, Minneapolis, MN, USA) to avoid boundary condition errors. Thirty-five indentations distributed across the cross section of each sample were done and the results were averaged per sample.

2.5. Compositional properties

2.5.1. Total protein and collagen content

Following uniaxial compression testing, cylindrical specimens were subjected to amino acid analysis. For this purpose, specimens were powdered using a Spex mill (SPEX Freezer/Mill; SPEX Industries Inc., NJ, USA) and lyophilized to recover cortical and trabecular bone powder. The matrix analysis was performed with an amino acid analyser (Beckman System 7300; Beckman Coulter Inc., CA, USA). The amino acids were separated by ion-exchange chromatography followed by post-column derivatization using ninhydrin for detection. Signals at 440 and 570 nm wavelengths were integrated, and the concentration of each ninhydrin-reactive component was recorded.

2.5.2. Phosphate (PO₄), hydrogen phosphate (HPO₄), carbonate (CO₃), carbonate/phosphate and protein/mineral content

Fourier transform infrared (FT-IR) spectroscopy was performed on cylindrical specimens using a spectrometer (Perkin-Elmer, Waltham, MA, USA). The spectra were curve-fitted in the ν₄ PO₄, ν₂ CO₃ and amide band domains (Galactic GRAMS Software, Salem, NH, USA). The ν₄ PO₄ domain shows five main phosphate bands at 600, 575 and 560 cm⁻¹ for PO₄ groups in an apatite lattice, and 617 and 534 cm⁻¹ for non-apatitic environments corresponding to surface location (figure 4a) [50]. The ν₂ CO₃ domain was decomposed into three bands at 879, 871 and 866 cm⁻¹ related to types A and B carbonate, and carbonate ions in non-apatitic environments, respectively (figure 4b) [51]. The amide–ν₃ carbonate domain (1300–1800 cm⁻¹) was decomposed into seven bands at 1750, 1670, 1640, 1550, 1510, 1450 and 1410 cm⁻¹. The relative intensity of the mineral and protein bands has proven to be an accurate measure of the mineral-to-protein ratio [52].

Figure 4.

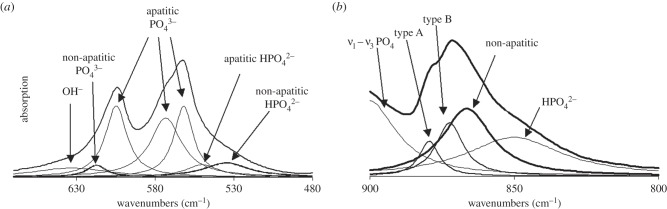
(a) Infrared spectrum in the ν₄ PO₄ domain of a synthetic nanocrystalline apatite (maturation time 3 days, exempt of foreign ions). Curve-fitting (Lorentzian band shape) showing the different absorption bands and their attribution. (b) Infrared spectrum in the ν₂ CO₃ domain of a synthetic nanocrystalline apatite (maturation time 3 days, prepared in the presence of carbonate ions). Curve-fitting (Lorentzian band shape) showing the different absorption bands and their attribution.

2.5.3. Calcium and phosphate (PO₄) content

Calcium content was determined using an NBX electron microprobe (Cameca Instrument, Nampa, ID, USA) on isolated mineral crystals pressed into a flat pellet (beam voltage, 10 keV; beam current, 30 nA; and a rastered beam, 64 × 64 µm) [53,54]. On the other hand, a modified Fiske and Subbarow colorimetric method at the peak absorption of 660 µm was used to quantify the phosphate content [55–57].

2.6. Statistical analysis

Normality of continuous data was assessed by using the Kolmogorov–Smirnov test. Comparative analyses were performed by one-way analysis of variance (ANOVA), with bone type (cortical and trabecular) as independent variables, and outcome measures from different testing modalities as dependent variables. In addition, a regression analysis was conducted to determine the correlation between axial stiffness derived from experiments and that derived from the micromechanics model. Statistical analysis was performed using the PSAW software package (version 19.0; SPSS Inc./IBM, Chicago, IL, USA). Two-tailed values of p < 0.05 were considered statistically significant.

2.7. Mathematical modelling

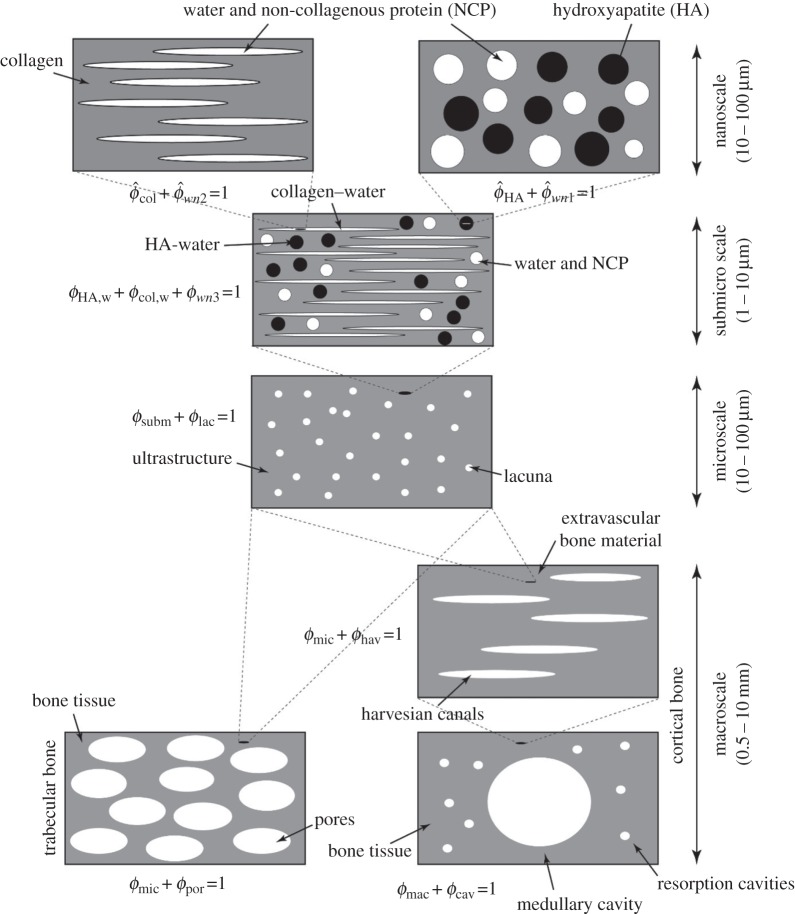
Bone has a hierarchical structure [58,59]; therefore, each level of hierarchy plays a significant role in the mechanical properties of bone structure. Figure 5 shows the four levels of hierarchy inspired from material composition and structure of the bone: nanoscale (10–100 nm), submicroscale (1–10 µm), microscale (10–100 µm) and macroscale (0.5–10 mm). The objective of mathematical modelling is to relate macrostructural mechanical properties of bone to its elementary components, namely hydroxyapatite (HA) crystals, collagen, non-collagenous proteins (NCPs) and water.

Figure 5.

Micromechanics representation of hierarchical structure of bone with four levels of hierarchy from nano- to macroscale.

A micromechanics approach is ideal for modelling the mechanical properties of bone owing to the tissue's heterogeneity and complex structure. The basic concept behind it is to hierarchically label the representative volume elements (RVEs) in the bone structure. Based on the micromechanics approach framework, the RVEs should have two main aspects: first, the characteristic dimension of these volume elements (l) should be considerably larger than the characteristic length (d) of the elements constructing them and at the same time extremely smaller than the characteristic dimensions (L) of the architecture built by the RVEs (i.e. 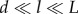). Second is the ability of RVEs to be divided into phases with constant material properties.

At each level of hierarchy, the phases and their properties are defined (volume fractions ϕ and elastic stiffnesses c). Based on the linear elasticity estimate of continuum micromechanics and assuming constant elastic modulus for the phases in the RVEs, the homogenized stiffness of RVEs, 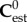, can be determined as [44,45]

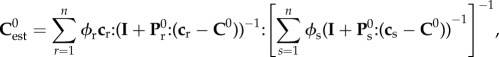2.1

where n is the number of phases in the RVEs, c is the phase stiffness, I is the fourth-order unity tensor and C⁰ is the homogeneous elastic matrix stiffness which is included in the phases. Tensor P⁰ is related to the Eshelby tensor [60] (P⁰ = S^0Esh: C^0,−1), which characterizes the interaction between phases in the RVEs.

In micromechanics modelling, the elastic stiffness of RVEs found in each level of hierarchy will be used as phase stiffness for the analysis of subsequent levels. There are several estimates in the literature for choosing C⁰. The Mori–Tanka scheme [61,62] is the model which chooses C⁰ = C^matrix, meaning that there is an inclusion phase consisting of small particles embedded in the continuous-matrix phase. This model, which is best suited for particle-reinforced composites, has an explicit solution. The self-consistent scheme [63,64] is the model which chooses 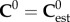, meaning that the phases are dispersed with the stiffness properties of homogenized RVEs. For the self-consistent scheme, equation (2.1) is reduced to a set of nonlinear equations. Here, the micromechanics representation of each phase and corresponding elastic modulus tensors are derived.

2.7.1. Nanoscale

2.7.1.1. Interaction of water and non-collagenous proteins with hydroxyapatite

At the nanostructural level, HA crystals, water and NCPs (figure 5) interact with each other. At this level, phases are dispersed, thus warranting the use of a self-consistent scheme

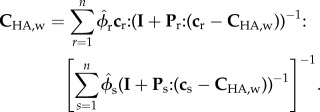2.2

HA minerals are platelet shaped [65–68], and water is considered to have a spherical shape. Volume fractions of HA and water are 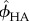and 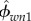, with a sum equal to 1,

2.3

Platelet-shaped HA minerals make the RVE matrix anisotropic. Using Laws formula [69,70] for determining the P tensor in a transversely isotropic matrix, the P tensor can be found for water and HA (appendix A.1). Assuming isotropic material properties for water and HA, the corresponding elastic matrices can be written as

2.4

and

2.5

where K_HA, G_HA, K_w and G_w are the isotropic stiffness properties of the HA and water. I^vol and I^dev are, respectively, the volumetric and deviatoric part of the fourth-order unity tensor (I^vol = 1/3δ_ijδ_kl and I^dev = I − I^vol). For highly mineralized tissues, radial stiffness was shown to be equal to axial stiffness [71], which means that HA isotropically contributes to the bone tissue stiffness. For the exploration of the volume fraction–radial stiffness relation to the point where the volume fraction of HA is equal to 1, the isotropic elastic stiffness of HA is equal to 100 GPa. Based on the relation: C_11,HA = E_HA(1 − v_HA)/((1 + v_HA)(1−2v_HA)) and assuming v_HA = 0.27 [72], the elastic modulus, bulk modulus and shear modulus of HA can be found as 79.76, 57.8 and 31.4 GPa, respectively (table 2). Equation (2.2) leads to five coupled nonlinear equations, which should solve simultaneously to reach five constants of the transversely isotropic matrix C_HA,w.

Table 2.

Isotropic mechanical properties of bone elementary components.

component	elastic modulusa (Gpa)	Poisson's ratio (v)	bulk modulus, K (GPa)	shear modulus, G (GPa)	reference
hydroxyapatite	79.76	0.27	57.8	31.4	[71]
collagen	5.4	0.28	4.1	2.1	[73]
water and non-collagenous protein	0	0.49	2.3	0

^aOnly two of these parameters are independent. The other two can be found based on universal relations for isotropic material.

2.7.1.2. Interaction of water and non-collagenous proteins with collagen

At this level, fibrillar collagen molecules are attached to each other, and the space between them is filled with water and NCPs. Considering collagen molecules as a matrix and the interspace water and NCPs as an inclusion, from the Mori–Tanaka scheme, the corresponding stiffness can be written as

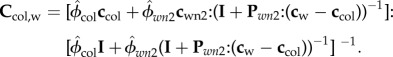2.6

Assuming isotropic material properties for the collagen matrix, the corresponding elastic modulus matrix can be written as

2.7

where K_col and G_col are, respectively, the bulk modulus and shear modulus of the collagen stiffness matrix (table 2). Because the matrix is isotropic, the P_col tensor is defined based on the cylindrical inclusions embedded in an isotropic matrix (appendix A.2). Volume fractions of phases are 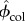and 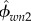for collagen and water, respectively, where

2.8

2.7.2. Submicroscale

At this level, the organic and mineral phases interact with water and with each other. Stiffness matrices of mineral and organic phases come from RVEs at the nanolevel. Dispersion of the phases in the RVEs warrants the use of a self-consistent scheme:

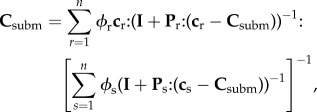2.9

where C_subm is the stiffness of submicroscale. Volume fractions of phases occupying the RVEs are ϕ_HA,w, ϕ_col,w and ϕ_wn3, where

2.10

Spherical phase inclusions are chosen for mineral and water phases (i.e. P_min = P_w = P_sph) and cylindrical phase inclusions are chosen for organic phases (i.e. P_mat = P_cyl; appendix A.1).

2.7.3. Microscale

At a microstructural level, lacunae containing osteocytes are enclosed by the continuous bone matrix. From the Mori–Tanaka scheme, considering the bone material as a matrix and lacunae as spherical inclusions with volume fractions of ϕ_subm and ϕ_lac, the stiffness of bone material at the microscale, C_mic, becomes

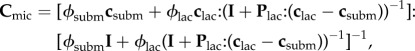2.11

where c_lac = 3K_wI^vol + 2G_wI^dev, P_lac = P_sph for a transversely isotropic matrix and

2.12

The non-zero terms of P_lac are presented in appendix A.1.

2.7.4. Macroscale

The structure of cortical and trabecular bone becomes different at this level. Therefore, the modelling has been divided into cortical and trabecular bone (figure 5). The Haversian canals contain blood vessels and nerve cells; therefore, it is reasonable to assign water stiffness to them (c_hav = 3K_wI^vol + 2G_wI^dev). The volume fractions of phases in the RVEs are ϕ_hav and ϕ_mic, where

2.13

For cortical bone, considering bone microstructure as a matrix and Haversian canals as inclusions and using the Mori–Tanaka scheme, the stiffness matrix can be written as

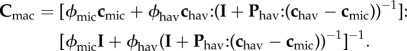2.14

Finally, to model the stiffness of trabecular and cortical bone structure (C_bone), porosities in trabecular bone have considered as spherical inclusions, and medullary cavity and restoration cavities in cortical bone have been considered as cylindrical inclusions in a transversely isotropic matrix (P_por = P_sph, P_cav = P_cyl). Because porosities and cavities are vacant, their stiffnesses are set to zero (c_por = c_cav = 0). Using the Mori–Tanaka scheme, from equation (2.1) C_bone can be written as

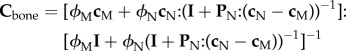2.15

and

2.16

where subscript M stands for mac and mic and subscript N stands for cav and por regarding cortical and trabecular bone, respectively.

2.7.5. Elementary-phase stiffness values and modelling parameters

Having a micromechanics model in hand, the elementary-phase stiffness values of the bone structure should be determined (i.e. K_HA, G_HA, K_col, G_col, K_w, G_w,). Table 2 shows the values which are chosen for the model. The phase stiffness matrices can be built based on these properties (c_HA, c_col, c_w). Then, the tissue-specific composition data should be determine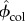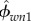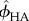d: , , and 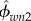for nanoscale; ϕ_HA,w, ϕ_col,w and ϕ_wn3 for submicroscale; ϕ_subm and ϕ_lac for microscale; and ϕ_mic, ϕ_hav, ϕ_mac, ϕ_cav (cortical bone), ϕ_por, ϕ_mic (trabecular bone) for macroscale.

First, the volume fractions of bone elementary components ϕ_col, ϕ_HA and ϕ_wn are determined from experimental data. Having mineral density (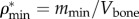) as a ratio of mineral mass m_min to bone volume V_bone, found from μCT analysis (table 3) and the mass density of HA as ρ_HA = 3 g cm⁻³ [74] the volume fraction of HA can be obtained as

2.17

Table 3.

Composition and axial module of elasticity of cortical and trabecular bone.

structure	BV/TV (Φbone)	mineral density (mg cm−3)	ΦHA (equation (2.17))	Φcol (equation (2.18))	Eexp (MPa)
cort.	0.681	1031.404	0.344	0.363	11 547.87
cort.	0.582	1039.963	0.347	0.39	6807.52
cort.	0.502	1023.679	0.341	0.361	3681.35
cort.	0.539	991.172	0.33	0.261	6882.1
cort.	0.593	1035.283	0.345	0.331	6558.1
cort.	0.533	1024.222	0.341	0.363	4533.97
cort.	0.71	1033.027	0.344	0.335	11 201.11
cort.	0.714	1008.662	0.336	0.267	9516.63
cort.	0.68	1016.562	0.339	0.3	10 884.01
cort.	0.682	1013.443	0.338	0.295	9975.74
cort.	0.628	1008.42	0.336	0.277	10 449.87
cort.	0.626	1003.777	0.335	0.27	9012.52
cort.	0.543	1048.647	0.35	0.328	4197.04
cort.	0.53	1024.542	0.342	0.36	5574.04
cort.	0.723	1053.653	0.351	0.282	10 903.1
cort.	0.642	1033.69	0.345	0.332	11 500.08
cort.	0.698	1025.488	0.342	0.356	11 729.17
cort.	0.699	1062.7	0.354	0.284	9000.9
cort.	0.576	1009.146	0.336	0.289	5197.7
cort.	0.578	1020	0.34	0.315	7664.45
trab.	0.444	789.609	0.263	0.218	2982.19
trab.	0.451	786.057	0.262	0.211	2243.71
trab.	0.509	709.283	0.236	0.194	2482.5
trab.	0.536	753.249	0.251	0.205	6346.28
trab.	0.443	682.138	0.227	0.155	3186.72
trab.	0.483	696.437	0.232	0.185	814.56
trab.	0.452	657.295	0.219	0.173	3184.05
trab.	0.533	651.083	0.217	0.218	5576.47
trab.	0.391	598.734	0.2	0.344	698.32
trab.	0.375	591.434	0.197	0.189	598.32
trab.	0.485	617.37	0.206	0.118	341.62
trab.	0.455	671.77	0.224	0.163	828.85
trab.	0.548	685.158	0.228	0.16	871.05
trab.	0.444	685.957	0.229	0.169	2396.38
trab.	0.414	618.033	0.206	0.182	3866.67
trab.	0.449	615.078	0.205	0.155	3264.69
trab.	0.496	688.174	0.229	0.177	4191.65
trab.	0.472	659.889	0.22	0.164	2884.53
trab.	0.368	631.535	0.211	0.196	1707.21
trab.	0.458	598.071	0.199	0.334	915.11

Bone mineral content (BMC), which is the ratio of mineral mass (m_min) over dry bone mass (m_dry), is determined using ashing analysis). Taking the mass density of organic matrix as ρ_org ≈ ρ_col = 1.41 g cm⁻³ [74,75], ϕ_org reads as

2.18

Here, the mass densities of protein and collagen are assumed to be the same. Approximately 90% of the mass density of protein is collagen [59,74], therefore ϕ_col = 0.9ϕ_org (table 3). Then, the volume fraction of water and non-collagenous protein can readily be found as

2.19

The total volume fraction of water and non-collagenous proteins can be written as

2.20

At nanoscale observation, volume fractions of HA and collagen (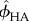 and 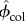) can be found as

2.21

and

2.22

Using equations (2.3), (2.8), (2.10), (2.20), (2.21) and (2.22) and assuming water contents in the two considered RVEs at the nanolevel are the same (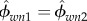), and also the water contents at the nano- and microlevels are equal (ϕ_wn3 = ϕ_wn/2), the volume fraction composition at the nano- and submicroscale can be found as

2.23

2.24

2.25

At the microlevel, the volume fraction of the lacunae is defined as the area of lacunae in the examined area divided by the total area. Here, ϕ_lac is assumed to be 2% [76–78]. The volume fraction of Haversian canals is defined as the ratio of the area of Haversian canals to the total considered area. ϕ_hav varies from 2% to 5% for healthy cortical bone [79], and here it is assumed to be 3% [80]. At last, for determining the volume fraction at the macrolevel (cortical and trabecular bone), ϕ_mac (cortical) and ϕ_mic (trabecular) are assumed to be equal to bone volume fraction (BV/TV). The experimental data for bone volume fraction can be found in table 3.

2.8. Finite-element analysis

µCT-based finite-element analysis was performed, for both trabecular and cortical bone, to evaluate the proposed micromechanics model. The models were meshed with eight-node linear hexahedral elements. The material was assumed to be linear elastic with the elastic modulus taken from experimental tissue modulus results for each sample (table 4). The number of elements ranged from 110 000 to 630 000 for trabecular samples and from 990 000 to 1 900 000 for cortical bone samples. To mimic the mechanical testing conditions, the lower surface of the models was fixed, whereas a linear displacement load was applied at the upper surface of the model. Then, the reaction forces at the superior surfaces were evaluated to determine the apparent elastic modulus of the samples.

Table 4.

Macro-, micro-, nano- and compositional-level properties of rat cortical and trabecular bone found by this study.

variable	modality	units	cortical bone	cancellous bone	p value
bone tissue density	pycnometry	g cm−3	2.17 (0.017)	2.16 (0.07)	0.78
mineral content	gravimetry	%	66.63 (7.64)	68.90 (9.94)	0.42
matrix content	gravimetry	%	28.97 (7.64)	26.55 (9.93)	0.42
stiffness	mechanical testing	N mm−1	7199 (270)	719 (68)	<0.001
yield load	mechanical testing	N	737 (110)	43 (23)	<0.001
bone volume fraction	μCT imaging	mm3 mm−3	0.59 (0.03)	0.37 (0.04)	<0.001
bone-surface-to-volume ratio	μCT imaging	mm2 mm−3	3.84 (0.19)	14.44 (2.91)	<0.001
modulus of elasticity (E)	mechanical testing	GPa	8.50 (2.86)	2.47 (1.68)	<0.001
yield strength (YS)	mechanical testing	GPa	0.13 (0.02)	0.03 (0.01)	<0.001
tissue modulus	nano-indentation	GPa	18.98 (5.73)	18.27 (3.77)	0.46
hardness	nano-indentation	GPa	0.74 (0.25)	0.73 (0.21)	0.72
total protein	amino acid analysis	%	11.80 (4.11)	11.57 (3.43)	0.90
total collagen	amino acid analysis	%	10.50 (3.84)	9.58 (3.27)	0.59
collagen content in protein	amino acid analysis	%	88.57 (2.04)	82.04 (3.20)	<0.001
PO4 (non-apatitic)	FT-IR	%	10.42 (1.95)	9.52 (1.30)	0.25
HPO4	FT-IR	%	30.60 (4.74)	28.91 (4.80)	0.44
CO3	FT-IR	%	3.63 (1.48)	2.56 (1.12)	0.11
C/P	FT-IR	—	0.056 (0.002)	0.058 (0.003)	0.09
protein-to-mineral ratio	FT-IR	—	0.77 (0.09)	0.70 (0.05)	0.89
Ca content	chemical analysis	µg mg−1 of bone	261.19 (100.40)	298.61 (20.135)	0.29
PO4 content	chemical analysis	µg mg−1 of bone	18.74 (5.46)	19.26 (4.23)	0.76

3. Results

At the macrostructural level, no differences were observed between cortical and trabecular bone regarding tissue density (ρ_t), as measured by gravimetric methods (p = 0.78), and mineral and matrix contents, as assessed by ash content (p = 0.42 and 0.41, respectively). Nonetheless, stiffness and yield load values were significantly greater in cortical bone (p < 0.001 for both cases; table 4).

Cortical bone has a larger volume fraction (p < 0.001) and a smaller bone-surface-to-volume ratio (BS/BV; p < 0.001) than trabecular bone. Apparent mechanical properties showed that the cortical bone modulus of elasticity (E) and yield strength (YS) values were approximately four times greater than those of trabecular bone (p < 0.001 for both cases). Both bone types failed at the segment of the smallest cross section (table 4).

At the nanostructural level, no significant differences in tissue modulus and hardness were observed between the two bone types (p = 0.46 and 0.72, respectively; table 4). Cortical bone demonstrated higher modulus variability than trabecular bone (standard deviation was 5.73 GPa for cortical bone and 3.77 GPa for trabecular bone; figure 6). Amino acid analysis indicated no differences in total protein and collagen levels between the two bone types (p = 0.59 and 0.90, respectively). However, collagen content in cortical specimens was on average 7% greater than that of trabecular bone specimens (p < 0.001, table 4).

Figure 6.

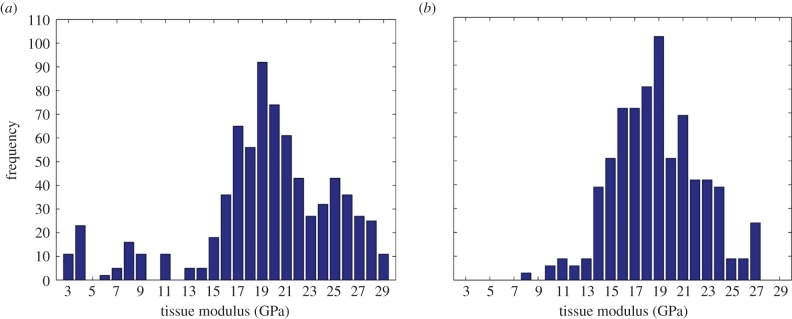
Tissue modulus frequency plots. (a) Cortical bone; (b) trabecular bone. (Online version in colour.)

Non-apatitic phosphate (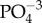 ) content did not differ between groups (p = 0.25), neither did the HPO₄ content in the hydrated surface layer (p = 0.44). Carbonate (CO₃) content also showed no difference among trabecular and cortical specimens (p = 0.01).

There were no differences between groups in carbonate-to-phosphate (C/P) and protein-to-mineral ratios (p = 0.09 and 0.89, respectively). Additionally, there were no differences in calcium and phosphate contents of the two bone types (p = 0.29 and 0.76, respectively; table 4).

The mathematical model's validation is based on elastic moduli values obtained during mechanical testing (table 3). The R² between the experimental and modelling axial stiffness values is 0.82, which shows relatively high agreement between the results (figure 7). The average values of axial elastic modulus (C₃₃) found from micromechanics modelling for cortical and trabecular bone are 8.40 and 3.02 GPa, respectively. Experimental results show these values to be 8.34 and 2.85 GPa for cortical and trabecular bone, respectively. Based on the continuum micromechanics approach, the elastic tensor for rat cortical and trabecular bone can be evaluated as

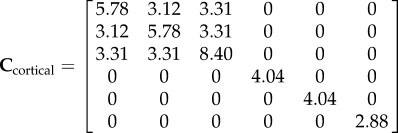3.1

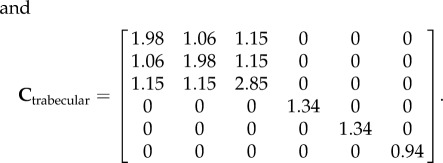3.2

Figure 7.

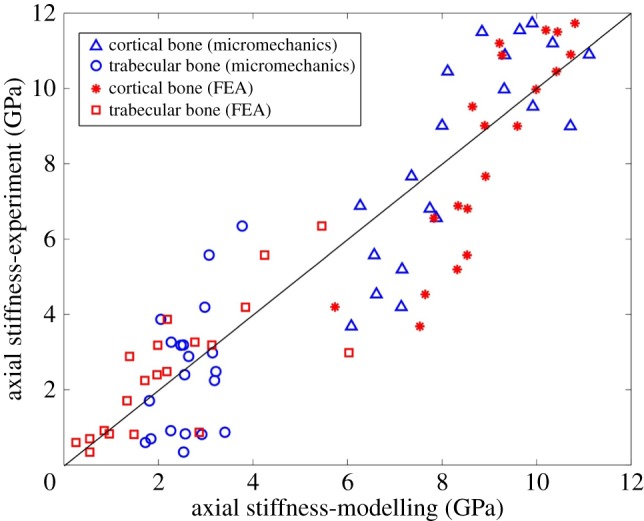
Comparison of axial elastic stiffness between micromechanics modelling and finite-element modelling with experiments for cortical and trabecular bone. FEA, finite-element analysis. (Online version in colour.)

Axial displacement contours of cortical and trabecular bone samples were obtained using finite-element analysis, as shown in figure 8. The axial displacement contour distribution in cortical bone is more regular than that in trabecular bone. The elastic moduli derived from finite-element analysis are shown in figure 7. There was a strong correlation between finite-element analysis results and mechanical testing results (R² = 0.84).

Figure 8.

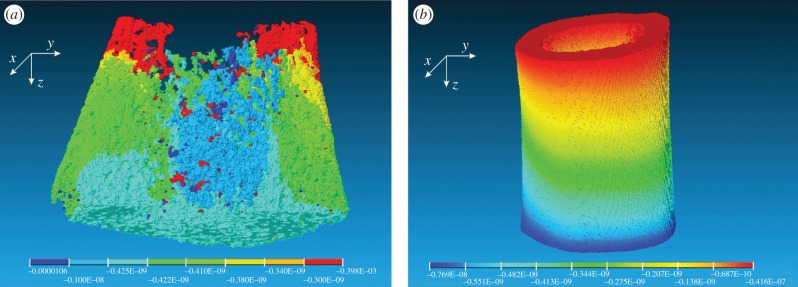
Axial displacement contours of (a) trabecular bone and (b) cortical bone obtained from finite element analysis.

4. Discussion

The aim of this study was to explore the hierarchical nature of the two major bone types in rats. By using a variety of analytical techniques, we were able to characterize the structural and compositional properties of cortical and trabecular bone, as well as to determine the best mathematical model to predict the tissue's mechanical properties.

Our hierarchical analysis demonstrated that the differences between cortical and trabecular bone reside mainly at the micro- and macrostructural levels. Our findings are consistent with those of previous studies: modulus of elasticity and yield strength values were significantly lower in trabecular bone specimens [7,24,26,27,29,30]. Although not evidenced in our study, Choi & Goldstein [7] made the same asseveration, emphasizing the higher mineral density values seen in trabecular bone. These findings can be explained by the configuration of lamellar/collagen fibres within the tissue, along with other microstructural characteristics that altogether support the fact that tissue morphology, and not just mineral density, plays a major role in determining the mechanical properties of cortical bone. The wide range of apparent elastic moduli can be explained by the wide range of bone volume fraction in the samples. Another factor causing the high degree of dispersion could be the way of calculating the apparent modulus: the resultant force is divided by the minimum cross-section area to determine the apparent elastic modulus (figure 3). Therefore, some of the apparent elastic moduli for trabecular bone are larger than those of cortical bone.

As shown by previous studies that also used FT-IR, carbonate content is significantly greater in cortical bone [13]. This finding may be explained by the critical role played by this ion during mineralization, coupled to the fact that cortical bone undergoes less remodelling over time. Khun et al. [11] described the differences in the mineral content and crystal maturation process in young and old animals, which mirror those seen in cortical and trabecular bone, respectively. For this reason, the differences between the mineral crystals may be attributed to their age, as well as to contrasting extents of post-translational modifications in the collagen structure [12,13,19,81]. The higher protein-to-mineral ratio and collagen content in protein seen in cortical bone seems to be similarly linked to its mechanical properties. The intermolecular cross-linking of collagen strongly determines the way fibrils are arranged to ultimately provide matrices with tensile strength and viscoelasticity [82,83]. Although a weak trend was evidenced in the carbonate-to-phosphate ratio between bone types, this finding further demonstrates the reigning similarities of cortical and trabecular bone at the compositional level.

Analysis performed at the nanostructural level yielded results that were consistent with previous reports in the literature, where hardness is basically considered to be similar between both bone types [19,25,32]. Hodgskinson et al. [19] described a strong relationship between calcium content and hardness, all equally similar across specimens compared in this study.

The purpose of mathematical modelling was to predict the bone's mechanical properties (i.e. anisotropic elastic moduli) as a function of the elementary components of the bone. For mathematical modelling, two approaches have been proposed in the literature for attributing the anisotropy to the bone structure, namely ‘mineral-reinforced collagen matrix’ [84–86] and ‘collagen-reinforced mineral matrix’ [71,87,88]. Both these approaches have been incorporated in the proposed model; the choice of platelet-shaped HA as an inclusion imposes anisotropy at the nanoscale and the choice of cylindrical-shaped collagen molecules as an inclusion imposes anisotropy at the submicroscale (figure 5). Regarding the shape of the elementary constituents of bone, it has been shown that HA crystals have plate-like shapes [89]. In this study, the HA crystals are assumed to be plate-like, which affects the Eshelby tensor and eventually the micromechanics model. Other approaches have employed spherical shapes to model HA inclusions [41]. The results of mathematical modelling are highly dependent on the choice of the mechanical properties of bone elementary components (i.e. HA and collagen). Here, we used the data from Katz & Ukraincik [72] and Yang et al. [73] for HA and collagen, respectively. These values also have been used by Hellmich & Ulm [71] and Hamed et al. [90] for multi-scale modelling of bone, and the results have shown good agreement with experimental findings. As seen in figure 7, finite-element modelling results better correlate with the mechanical testing results, especially for trabecular bone samples (R² = 0.56 for finite-element modelling versus R² = 0.2 for micromechanics modelling). The reason is that micromechanics modelling provides more crude results, as the bone structure become more disorganized.

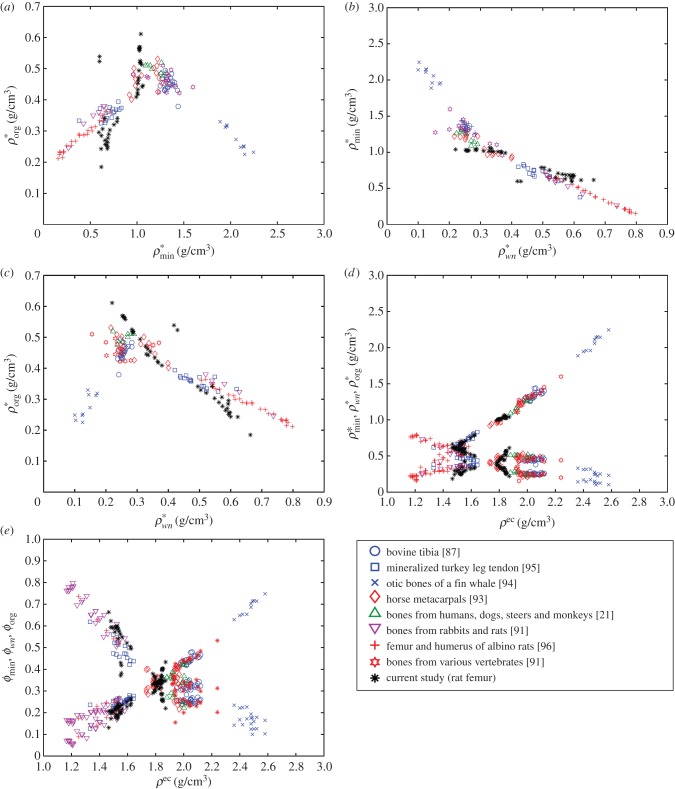
For comparison, bone mineral, organic and water densities and bone volume fractions of the samples are plotted along with the results of other organs and species in the literature [21,79,91–97] (figure 9). These plots were first reported by Vuong & Hellmich [97] to verify the universal relation among the bone constituents. As outlined in Vuong & Hellmich [97], these figures can be divided into two regions and be presented by bilinear functions. Figure 9a–c is plotted based on mineral (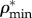), organic (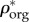) and water and non-collagenous protein 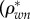) densities. Alternatively, extracellular bone density can be found as

3.3

Densities of bone composition elements (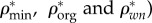 are plotted versus extracellular bone density in figure 9d. The volume fractions of bone constituents (ϕ_min, ϕ_org and ϕ_wn) versus extracellular bone density are shown in figure 9e. In figure 9a, in the region with positive slope, the organic density (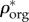) is increased by increasing extracellular bone mineral density (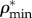). This region is represented by growing organisms and species, whereas the region with negative slope represents the adult organisms [97]. Figure 9a–e shows that the reported results in this study for bone composition densities and volume fractions are comparable to previous studies in the literature. In addition, our results further validate the universal relation between different bone composition elements [97].

Figure 9.

Relation between (a) apparent mineral (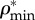) and organic (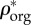) densities, (b) apparent water and non-collagenous proteins (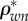) and mineral (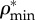) densities, (c) apparent water and non-collagenous proteins (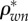) and mineral (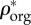) densities, (d) apparent densities and (e) volume fractions of mineral (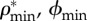), organic (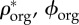) and water and non-collagenous proteins (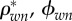) versus extracellular bone density (ρ^ec).

In this study, we did not consider the potential differences in geometry in the two bone types being compared. We strongly believe that it would be relevant to address the roles of lacunae and osteons in the structural properties of trabecular and cortical bone. In addition, the inferior resolution of FT-IR at very small scales introduces another limitation to our study [18]. In spite of these shortcomings, this study provides a comprehensive framework for trabecular and cortical bone properties that can be expanded upon in future studies.

Appendix A

A.1. P-tensor in a transversely isotropic matrix

For a detailed derivation of the P-tensor for anisotropic matrices, please refer to [70,98]. For a transversely isotropic material, the non-zero terms of the stiffness matrix C are C₁₁ = C₂₂,C₃₃,C₁₂,C₁₃ = C₂₃,C₄₄ = C₅₅ and C₆₆ = 1/2(C₁₁ − C₂₂). For spherical inclusions, the non-zero terms of the P-tensor can be found as

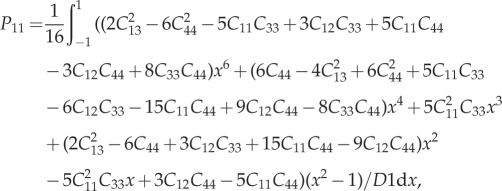A 1

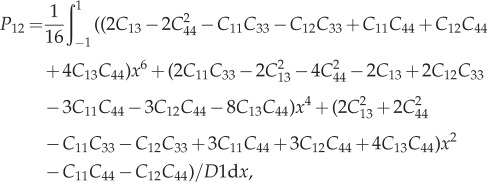A 2

A 3

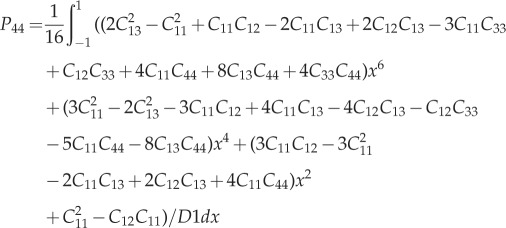A 4

and

A 5

where

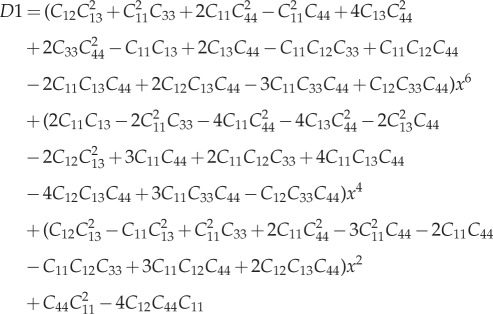A 6

and

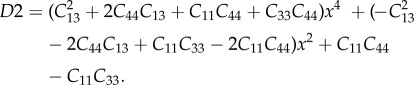A 7

For cylindrical inclusions, the non-zero terms of the P-tensor are written as

A 8

A 9

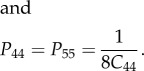A 10

For platelet-shape-like inclusions the P-tensor becomes

A 11

A.2. P-tensor in an isotropic matrix

For isotropic material, the stiffness matrix can be written as C = 3kI^vol + 2μI^dev, where k and μ are the bulk and shear modulus, respectively, and I^vol and I^dev are the volumetric and deviatoric part of the fourth-order unity tensor (I^vol = 1/3δ_ijδ_kl and I^dev = I−I^vol). The P-tensor in an isotropic matrix for cylindrical inclusions can be written as [45,98]

A 12

where the Eshelby tensor has the following non-zero terms:

A 13

A 14

A 15

A 16

A 17

Funding statement

This work was supported in part by the Qatar National Research Foundation (QNRF; NPRP 5-086-2-031) and departmental funding from the Children's Hospital Orthopaedic Surgery Foundation.