Abstract
Spatial reaction–diffusion models have been employed to describe many emergent phenomena in biological systems. The modelling technique most commonly adopted in the literature implements systems of partial differential equations (PDEs), which assumes there are sufficient densities of particles that a continuum approximation is valid. However, owing to recent advances in computational power, the simulation and therefore postulation, of computationally intensive individual-based models has become a popular way to investigate the effects of noise in reaction–diffusion systems in which regions of low copy numbers exist. The specific stochastic models with which we shall be concerned in this manuscript are referred to as ‘compartment-based’ or ‘on-lattice’. These models are characterized by a discretization of the computational domain into a grid/lattice of ‘compartments’. Within each compartment, particles are assumed to be well mixed and are permitted to react with other particles within their compartment or to transfer between neighbouring compartments. Stochastic models provide accuracy, but at the cost of significant computational resources. For models that have regions of both low and high concentrations, it is often desirable, for reasons of efficiency, to employ coupled multi-scale modelling paradigms. In this work, we develop two hybrid algorithms in which a PDE in one region of the domain is coupled to a compartment-based model in the other. Rather than attempting to balance average fluxes, our algorithms answer a more fundamental question: ‘how are individual particles transported between the vastly different model descriptions?’ First, we present an algorithm derived by carefully redefining the continuous PDE concentration as a probability distribution. While this first algorithm shows very strong convergence to analytical solutions of test problems, it can be cumbersome to simulate. Our second algorithm is a simplified and more efficient implementation of the first, it is derived in the continuum limit over the PDE region alone. We test our hybrid methods for functionality and accuracy in a variety of different scenarios by comparing the averaged simulations with analytical solutions of PDEs for mean concentrations.
Keywords: hybrid modelling, stochastic reaction–diffusion, pseudo-compartment, multiscale modelling
1. Introduction
Diffusion of macromolecules and larger entities is the result of a rapid number of collisions with solvent molecules. Often, the detailed information about the solvent molecules is not known, and the macromolecule (particle) appears to move stochastically. The motion of an individual particle can be simulated in two different ways [1]: those in which trajectories are defined on continuous domains and those in which trajectories are defined by a random walk on a lattice. Stochastic simulation of individual particles is appropriate on timescales that are much larger than the time between solvent molecule collisions and, in such circumstances, the particle trajectories may resemble a Wiener process (Brownian motion). Coarse-graining the continuous domain into a lattice of compartments, between which particles undergo a random walk, is a simplification that may be appropriate if the lattice spacing is not too large as to impair good spatial resolution. Both off-lattice [1–3] and on-lattice [4–9] individual-based stochastic simulations have remained popular paradigms for stochastic diffusion simulations.
It is also common for mathematical models of diffusive processes to treat diffusion using deterministic continuous partial differential equations (PDEs) [10]. That is, it is assumed that the copy numbers of particles are so large that a continuous distribution of particles can be defined which evolves deterministically [11]. The effect on the time derivative of the concentration distribution of particles owing to the random motion of individuals is represented by a Laplacian term in the governing equation. Other effects, such as particle flow, reactions and other interactions can be incorporated into this mathematical framework by the introduction of additional terms in the governing PDEs. The simplicity with which diffusion can be represented in these deterministic models has, in part, lead to its popularity in modelling complex physical behaviour. This is notably the case in mathematical modelling of biological processes [12–14] owing to the importance of diffusion of either chemicals and/or cells in many biological environments. Some deterministic PDE models have the distinct advantage over stochastic models of diffusion that they are analytically tractable, so that the particle dynamics may, in some circumstances, be predicted without numerical simulation [15]. In addition, when numerical solutions are required, there exists a plethora of well-established techniques at hand [16].
While PDE interpretations of the diffusion mechanisms are convenient and popular, they lack the ability to appropriately represent systems in which stochasticity is inherent [17]. For example, fluctuations in the number of particles in a system are especially important for systems in which one or more of the constituent species is in low abundance [18]. Such situations appear frequently in biological applications owing to the small spatial scales that are often involved and can lead to dynamics that are significantly different from a deterministic model which may be postulated based purely on macroscopic considerations and assuming large copy numbers [19–24]. The effects of stochasticity have been investigated in spatially extended systems of the type we consider in this paper [6,7,18,25]. Owing to the increase in computer capabilities, stochastic simulation techniques for reaction–diffusion systems have found popularity and have been implemented in a number of freely available simulation packages [26–30].
Individual-based simulations (off- and on-lattice stochastic simulations) of diffusion are capable of capturing stochastic effects which PDEs cannot. However, this is at the cost of computational effort which becomes an insurmountable barrier very quickly as copy numbers increase [18]. For extended domains, in which concentrations of particle species vary dramatically, a computationally feasible model may require localized regions in which diffusion is modelled using a continuous PDE (for regions in which concentration is high) and an individual-based simulation (for regions in which concentration is low). For example, in the modelling, calcium-induced calcium releases small numbers of ions that bind to and facilitate the opening of ion channels thus inducing the release of numbers of orders of magnitude more calcium ions. An individual approach is appropriate for the initial binding, but infeasible for modelling the concentration of ions after the release [31]. Similar multi-scale issues occur in the spatio-temporal modelling of cellular signal transduction [32], in actin dynamics in filopodia [33] and in the formation of morphogen gradients in the early embryo [34–37].
The importance of efficient and accurate hybrid algorithms for coupling models of diffusion between different regions of space has resulted in a large body of research in the past decade. Most of the models that couple the PDE paradigm with compartment-based stochastic simulations involve the use of significant overlapping regions and/or the averaging of particle flux in order to simulate the necessary boundary condition for the PDE [38–41]. Ferm et al. [42] also have a method of coupling a PDE to a compartment-based simulation that employs operator splitting and τ-leaping for the time evolution of the compartment-based model where possible. Recently, hybrid models of stochastic diffusion in which on- and off-lattice models are coupled between different regions of space have been proposed [32,33,43–45]. Central to these models is the ability to treat individual particles as they migrate from one regime to the other. The individual treatment of particles allows for the extension of these coupling algorithms to low copy number regimes. This type of coupling technique was also recently applied to the coupling of a PDE with particles undergoing off-lattice Brownian dynamics [46,47].
In this paper, we develop hybrid algorithms that couple a PDE in one region of the domain to a compartment-based model in the other. This allows particle concentrations to be resolved on a fine scale in regions of the domain where an individual-based description is required, but at a much coarser scale in regions where particle numbers are large enough to warrant a continuum description. Rather than balancing flux at the interface we use a method that is similar to the ghost-cell method [44]. A defining characteristic of this method is the individual treatment of particles as they cross the interface. In our coupling method, a small region of the PDE domain adjacent to the compartment-based region is allowed to contribute particles to the compartment-based regime as if it were itself a compartment. We will refer to this as a pseudo-compartment. The treatment of this pseudo-compartment is complicated. From the perspective of the PDE region, it contains a continuous probability distribution representing the distribution of particles. However, from the perspective of the compartment regime, the pseudo-compartment has compartment-like properties. That is, it contains particles that can jump into their neighbouring compartment according to standard compartment-based rules for diffusion. The pseudo-compartment's duality allows for particles to behave correctly as they cross individually between the two different regimes. When particles cross over the interface, an indicator function with the mass of a single particle is added to the probability distribution in the region of the pseudo-compartment.
A one-dimensional graphical representation of this approach is given in figure 1.
Figure 1.

In the left-hand side of the domain, ΩP, the distribution of particles is modelled as a PDE. On the right-hand side, ΩC, the particle density is modelled with a compartment-based approach. The concentration of particles in each compartment, Ci for i = 1,…,K, of ΩC is represented by a dark blue rectangle (numbers of particles can be found by multiplying by the compartment width, h). The probability density in ΩP is represented by the light blue curve. The two regimes interact through the movement of particles from the left-most compartment in ΩC, C1, to the pseudo-compartment, C−1, (whose average particle concentration is represented by the height of the green box on the right of ΩP) and vice versa. The height of the green rectangle is calculated by integrating the PDE solution over the region [0, h) and dividing by h. Thus the ‘number of particles’ in the pseudo-compartment can be calculated by multiplying the height of the green box by h. (Online version in colour.)
We present two separate methods (which we refer to as pseudo-compartment methods (PCMs)) for conceptualizing and implementing this coupling scheme. The first method is necessary for the precise coupling of systems with low copy numbers. The second method is a mathematically justified simplification of the first for situations in which large particulate copy numbers are present within the PDE domain. We demonstrate these coupling mechanisms in one dimension only, but they are easily generalized to higher-dimensional problems with (hyper)-planar interfaces.
2. Algorithms
2.1. Overview of algorithms for deterministic and compartment-based stochastic diffusion
In this section we will provide an overview of the two different modelling regimes that will be used in our hybrid algorithm, highlighting any intricacies in their definition or implementation.
2.1.1. Compartment-based modelling
We denote the region in which we employ the compartment-based regime ΩC. In this region, we partition the domain into K regular compartments of length h. We choose h to be sufficiently small that particles in each compartment can be considered to be well mixed, reacting only with particles in their current compartment. We do not keep detailed information about the specific location of each particle, rather we simply store the number of particles of each type in each of these compartments. While this produces a significant saving on computational intensity in comparison with Brownian dynamics models (in which the position of each individual is stored and/or updated at each step), we lose information about the specific location of each of the particles in a compartment and are forced to assume that each particle is distributed uniformly throughout the compartment.
Considering a general system of N species and M chemical reactions, a propensity function, αi,j(t), i = 1,…,K and j = 1,…, M + 2, is assigned to each reaction in each compartment (including the two ‘diffusive reactions’ by which particles leave compartment i). The propensity functions are defined such that ai,j(t)dt is the probability that the jth reaction occurs in the ith compartment during the infinitesimally small time interval [t, t + dt]. The propensity function for a specific reaction in a particular compartment depends on the number of reactant particles available in that compartment (for all but zeroth-order reactions), the method by which they combine, the kinetic rate constant and (for all but first-order reactions) the size of the compartment, h [1]. Similarly, for each species, we can characterize the diffusive jumps of particles between compartment i and its two nearest neighbouring compartments as a set of first order interactions with propensities
| 2.1 |
for j = M + 1, M + 2. Here, DA denotes the macroscopic diffusion coefficient of species A and Ai is the copy number of species A in compartment i. Equation (2.1) is specific for regular square lattices with no sensing of neighbouring compartments. For unstructured meshes, the jumping propensity αi,j between two lattice points can be calculated by considering a finite-element discretization of the appropriate PDE over the mesh or, in special cases by considering first passage time problems. For details on the derivation of transition rates on unstructured meshes, the reader is referred to references [7–9]. Such a discretization justifies the notation αi,j (i.e. a dependence on the destination for the jump). In other scenarios, even on regular lattices (where the particles being modelled are cells, for example) jump rates can depend explicitly on the number of particles in neighbouring compartments in order to mimic ‘volume-filling’ or ‘density-dependent’ effects [6]. Although we do not explicitly deal with these scenarios in this work, it would be straightforward to do so.
There are two predominant mechanisms for simulating the time evolution of the system. In the time-driven approach, a fixed time step Δt is designated, and each reaction j in compartment i occurs with probability αi,jΔt. This method is simple to implement, but less efficient than the alternative event-driven algorithm. In order to ensure accuracy in the time-driven algorithm, the time step must be chosen to be sufficiently small that single particles do not undergo multiple diffusion or reaction events in a single step. This can lead to very small choices of Δt and consequently many time steps in which no reaction/diffusion events occur. In comparison, an event-driven algorithm simulates the evolution of the system by choosing the time step between reaction/diffusion events from an exponential distribution. The most commonly cited example of such a simulation scheme is the Gillespie's direct method (DM) [48] in which the time for the next reaction of any sort, τ, is chosen from an exponential distribution with parameter α0 (where 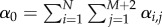 is the sum of all the propensity functions). In practice, τ is simulated according to the following formula
is the sum of all the propensity functions). In practice, τ is simulated according to the following formula
| 2.2 |
where r1 is uniformly distributed in (0, 1). The event that takes place τ units of time from the current time is chosen from a weighted probability proportional to each of the event propensities αi,j.
There are efficient adaptations of Gillespie's original algorithm available depending on context [49–53]. These algorithms are mathematically identical and differ only in the computational bookkeeping required to implement them. An efficient algorithm designed specifically for spatially extended systems is the next subvolume method from Elf & Ehrenberg [54], and an adaptation of the next reaction method from [52] (which is itself based on Gillespie's original first reaction method [55]). For simplicity and efficiency, we choose Gillespie's DM (event-driven) in order to evolve particle numbers in ΩC, although we note that our algorithms can be trivially modified to incorporate the alternative event-driven simulation methods discussed above or time-driven evolution.
2.1.2. Partial differential equation-based modelling
We denote the region in which we solve the PDE as ΩP. In this region, we solve the relevant one-dimensional PDE numerically, but to a high degree of accuracy. In particular, we solve the PDE
| 2.3 |
where R(p) represents a set of, as yet unspecified, reactions.
A zero-flux boundary condition is implemented on the PDE at the interface between the two regions. This is because flux of particles over this interface is not governed by a continuous diffusive flow of particles but rather a discrete jumping processes that mimics it. It is important to ensure that there is consistency between the methods by which particles transfer back and forth between regimes, because any imbalance can create significant numerical artefacts.
In the examples that follow, we discretize the PDE-domain, ΩP, into a regular grid with spacing Δx, where Δx ≪ h. In order that the time step which we take is not restricted by the requirement for stability of the PDE solver, we employ the θ-method with θ ≤ 1/2 which is unconditionally stable. In particular, we choose θ = 1/2 (Crank–Nicolson method) which gives a solution that is second-order accurate in space. Note that the coupling algorithm that follows is independent of the method that is used to solve the PDE, providing that method is sufficiently accurate.
2.2. Low copy number coupling technique: algorithm 1
In both hybrid algorithms presented here, it is important to note that, while we implemented the Gillespie's DM for the compartment-based simulation (event-driven) and a Crank–Nicolson method for solving the PDE part of the simulation (both for accuracy reasons), the choice of methodology does not affect the results of the coupling (but may affect the accuracy of the individual simulations).
It is common to think of the PDE description of diffusion as the evolution of a continuous concentration. However, at low concentrations, this quantity is not well defined. Here, we consider a situation in which there may be insufficient particles to satisfy the continuum limit. According to the definition of concentration, p(x,t), given NP identical particles in total over the concentration distribution, the probability distribution of finding any particular particle, p′(x,t), is given by p′(x,t) = p(x,t)/NP. The distribution p′(x,t) is well defined for low copy numbers and behaves in a similar way to the concentration (albeit normalized by NP). In this situation, the continuous distribution which is solved by the PDE cannot be interpreted as a concentration. Instead, we consider p′(x,t) as the probability density to find each of the NP particles that are within the PDE domain (we denote the number of compartment particles NC such that total number of particles is N = NP + NC). We specify that in the continuum limit, as NP → ∞, the PDE should describe the concentration of particles. As such, we define the continuous distribution p′(x,t) to be the probability density to find each of the NP PDE-based particles at position x, scaled by the number of particles, such that 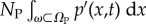 is the expected number of particles in an arbitrary subset, ω, of ΩP.
is the expected number of particles in an arbitrary subset, ω, of ΩP.
Our first algorithm (which is appropriate for situations in which the copy numbers are low) progresses asynchronously. The compartment-based regime is updated in an event-driven manner, whereas the PDE domain is updated in a time-driven manner. We use the model design shown in figure 1 and describe here how to couple the transition of particles between the PDE and compartment-based regimes using the pseudo-compartment, C−1.
Particle numbers in region ΩC are updated according to jump propensities given in equation (2.1). We extend the definition of these jump propensities to include transitions to and from the pseudo-compartment, C−1, that lies inside the PDE domain. When a particle is chosen to jump left from compartment C1 in ΩC, into the pseudo-compartment, C−1, its mass is incorporated into the PDE solution. The expected number of particles within the pseudo-compartment is increased by one by adding 1/h to the PDE distribution in [−h,0).
In ΩC, the propensity for a jump from compartment to neighbouring compartment is given by equation (2.1). We modify the propensity to jump from the pseudo-compartment, C−1, into its neighbouring compartment, C1, in ΩC, in order to take account of the expected number of particles in C−1. The jump propensity from C−1 to C1 is therefore given by
| 2.4 |
where 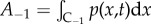 is the expected number of particles in the pseudo-compartment. For convenience in what follows, we denote the normalized number of particles in C−1 as a−1 = A−1/NP.
is the expected number of particles in the pseudo-compartment. For convenience in what follows, we denote the normalized number of particles in C−1 as a−1 = A−1/NP.
Jumps from C−1 to C1 occur as compartment-based events in the algorithm. This means that in each small time interval (t, t + dtp) in which the PDE is updated, none of the PDE-based particles can jump into ΩC. Because p(x,t) is the scaled probability distribution describing the probability of finding these particles in the PDE regime, the new distribution must be conditioned on the event that none of these particles jumped into the compartment-based regime during the PDE update interval (t, t + dtp). After running the PDE solver on the distribution p(x,t), a change of δp(x,t) must be made to reflect the fact that none of the remaining NP particles transferred into C1 via C−1.
In the small time step dtp, each of the expected A−1 particles inside the pseudo-compartment should be capable of jumping over the interface with a probability of Pjump = Ddtp/h2. By definition
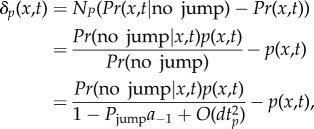 |
2.5 |
where Pr indicates the probability for a single particle. Pr(no jump|x,t) depends on whether the particle in question is inside or outside the pseudo-compartment, C−1
| 2.6 |
Therefore,
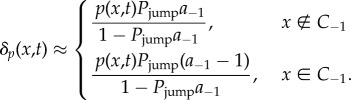 |
2.7 |
As dtp → 0, Pjump → 0 and we find that
 |
2.8 |
The PDE is therefore solved with an additional source term of size p(x,t)Da−1/h2, throughout the domain and a sink term inside the pseudo-compartment of size −p(x,t)D/h2. These additional terms ensure that the probability distribution inside the PDE domain redistributes correctly as a result of not finding pseudo-compartment particles available for jumping in a given time step.
Changes in the compartment-based regime have an impact on the PDE only when particles cross the interface. We have already discussed the change to the relatively straightforward indicator function addition of density to the PDE when particles cross from C1 to C−1. However, when particles cross from C−1 to C1, it would be erroneous to simply subtract 1/h from the PDE distribution in C−1 (reversing the operation for the transfer of particles in the opposing direction). This is because we assume that each of the particles in the PDE region has the same distribution function p(x,t)/NP. Therefore, taking any one of these NP identical particles across the boundary into ΩC will result only in a rescaling of this distribution. Recognizing that we lose a single particle's worth of mass, the distribution p(x,t) in ΩP should now represent the probability distribution of NP − 1 identical particles, so we can calculate the rescaled distribution as
A cartoon schematic illustrating the algorithm is given in figure 2. The algorithm is also outlined in detail in table 1. It may seem odd that particles appear to be allowed to transfer from the entire PDE domain while being allowed only to transfer back into the more localized C−1. This restriction is predicated on the assumption that all particles in the PDE regime have the same distribution which is proportional to the PDE solution, p(x,t). However, when a particle travels from C1 in the compartment-based regime into C−1 in the PDE regime, its position is known. This breaks the assumption that all particles in the PDE are identical. This issue has been documented previously [46]. It results in an increase in the variance of the number of molecules near the interface. In [46], the variance error can be controlled by adding in an ‘overlap’ region in which particles may be in the form of either regime (PDE and off-lattice particle-based). The pseudo-compartment in this manuscript plays a similar role to this ‘overlap’ region. In the pseudo-compartment, whereas density is updated using the PDE, particles are transferred by the evolution of the PDE (into the remainder of the PDE regime) and by lattice-based rules (into the compartment-based regime). This complication is unavoidable for algorithms of this nature. The variance is also naturally reduced by increasing the number of particles (see algorithm 2).
Figure 2.
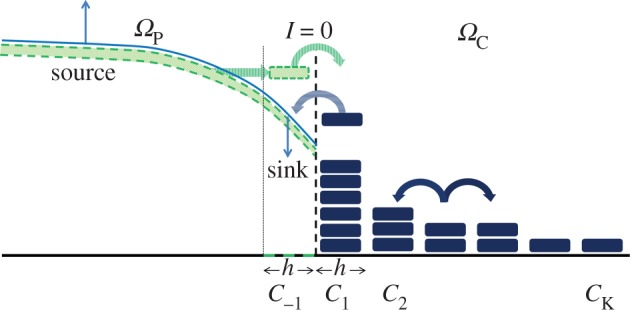
A cartoon schematic illustrates the most important features of algorithm 1 in one dimension. In ΩC, to the right of the interface, particles are represented as individuals in compartments (dark blue rectangles) with each individual adding 1/h to the density in that compartment. Particles can jump to neighbouring compartments within ΩC (dark blue block arrows). In ΩP, to the left of the interface, density is represented by a ‘continuous’ function (light blue curve). Particles in the left-most compartment in ΩC (adjacent to the interface) can jump into the PDE regime (blue horizontally striped arrow) where they are added by means of an indicator function to the PDE solution in the region [−h,0)—the pseudo-compartment. The PDE does not include information about the specific location of individuals and, so when a particle jumps from the pseudo-compartment into ΩC, it must first be realized in the pseudo-compartment by subtraction of its contribution to the whole PDE followed by an instantaneous jump over the interface. Every instance in which a particle does not jump from the pseudo-compartment into ΩC, the conditional probability to find particles in the distribution must necessarily be adjusted, so that more weight lies outside of the pseudo-compartment. This effect results in a net source of distribution outside of the pseudo-compartment in the PDE and a balancing net sink of distribution inside the pseudo-compartment such that the total number of particles is conserved in the absence of reactions. (Online version in colour.)
Table 1.
Algorithm for the coupling of the compartment-based regime with the PDE-based regime in the case of low copy numbers (algorithm 1).
| (i) | Initialize the time, t = t0 and set the final time, tfinal. Specify the PDE-update time step dtP and initialize the next PDE time step to be tP = t + dtP. |
| (ii) | Initialize the number of particles in each compartment in ΩC, Ai for i = 1, …, K, and the distribution of probability density in ΩP, p(x,t0), for x ∈ ΩP. |
| (iii) | Calculate the propensity functions for diffusion between the compartment regimes as αi,j = AiD/h2 for i = 1…K and j = M + 1, M + 2 and for reactions as αi,j for i = 1…K and j = 1, …, M using the usual mass action kinetics. |
| (vi) | Calculate the propensity function for diffusion from the pseudo-compartment, C−1, in ΩP into the adjacent compartment, C1, in 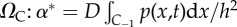 (equation (2.4)). (equation (2.4)). |
| (v) | Calculate the sum of the propensity functions, 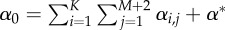 . . |
| (vi) | Determine the time for the next ‘compartment-based’ event tC = t + τ, where τ is given by equation (2.2). |
| (vii) | If tC < tP then the next compartment-based event occurs: |
| (a) Determine which event occurs. Each event occurs with probability proportional to its propensity function (see [48]). | |
(b) If the event corresponds to αi,j for i = 1…K and j = M + 1, M + 2 then move a particle from compartment i in the direction specified by j. If the particle crosses the interface into pseudo-compartment C−1, then add a particle's worth of mass to the region C−1 i.e. 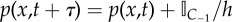 . Here, . Here,  is the indicator function which takes the value 1 in C−1 and 0 elsewhere. is the indicator function which takes the value 1 in C−1 and 0 elsewhere. |
|
| (c) If the event corresponds to propensity function α* then place a particle in C1. To remove this particle from the PDE solution, simply rescale the solution i.e. p(x,t + τ) = p(x,t)(NP − 1)/NP. Update NP and NC to reflect the exchange of particles between regimes. | |
| (d) Update the current time, t = tC. | |
| (viii) | If tP < tC then the PDE regime is updated: |
| (a) Update the PDE solution according to the numerical method described in §2.1.2 using p(x,t) as the previous value of the solution. | |
| (b) Add the auxiliary source and sink terms (see equation (2.8)) to the numerical solution of the PDE. | |
| (c) Update the current time, t = tP and set the time for the next PDE update step to be tP = tP + dtP. | |
| (ix) | If t ≤ tfinal, return to step (iii). |
| Else end. |
In algorithm 1, changes to the PDE solution are as a result of diffusion, auxiliary source/sink terms for changes in conditional probability, events where a particle moves from the pseudo-compartment, C−1, to the first compartment, C1, in the compartment-based regime, ΩC, and events where a particle moves in the opposite direction from C1 to C−1. All of these changes may be represented formally in the following PDE (in one dimension)
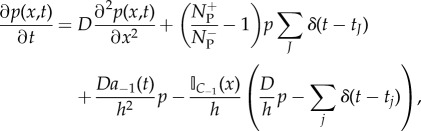 |
2.9 |
where 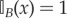 if x ∈ B and zero otherwise, tj are instants when particles jump from compartment to PDE, tJ are instants when particles jump from PDE to compartment and
if x ∈ B and zero otherwise, tj are instants when particles jump from compartment to PDE, tJ are instants when particles jump from PDE to compartment and 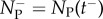 and
and 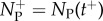 represent numbers of particles in ΩP immediately before and after times in which the number discontinuously jumps at respective moments tJ (they can be thought of as left and right limits of Np(t) respectively). Note that
represent numbers of particles in ΩP immediately before and after times in which the number discontinuously jumps at respective moments tJ (they can be thought of as left and right limits of Np(t) respectively). Note that  . As a common sense check, we can integrate over the ΩP to derive an equation for the change in the total number of particles represented by the PDE regime, NP
. As a common sense check, we can integrate over the ΩP to derive an equation for the change in the total number of particles represented by the PDE regime, NP
 |
2.10 |
As expected, the number of particles changes by integer amounts at the discrete times when particles enter or leave the domain.
2.3. High copy number coupling technique: algorithm 2
The algorithm presented in §2.1.2 is accurate for both high and low copy numbers. However, its complexity leads to computational overheads which may prove costly, especially in situations in which copy numbers of species are relatively high, and a less sophisticated coupling method would suffice. For this reason, we derive the following coupling method (which we refer to as algorithm 2) as a limiting case of our original algorithm, valid only for the scenario of high copy numbers.
We predict the benefits of these hybrid methods to be greatest for applications that have regions in which there are low copy numbers (requiring individual-based simulation) and other regions of high copy numbers (in which a PDE description will be more efficient). In particular, the copy numbers at the interface should be high in order to justify the use of the PDE there. Arguably if the copy numbers are low at the interface, then the interface is positioned incorrectly.
In order to derive our simplified algorithm, we allow NP → ∞. This implies that times between transfer events (particles crossing from C−1 to C1 and vice versa) are low: 0 < tj+1 − tj ≪ 1 and 0 < tJ+1 − tJ ≪ 1. Let us define a small time, δt, such that
(1) the number of transfer events that occur between t and t + δt is large, but is also
(2) significantly smaller than the total number of particles in the pseudo-compartment.
Satisfying point 1 ensures that individual jump events may be averaged over (t, t + δt) and satisfying point 2 ensures that δt is small on the scale of diffusion allowing for PDE solver time discretization to be implemented at a later stage on the majority of non-jumping particles. Both points 1 and 2 may be satisfied for sufficiently large NP. Integrating equation (2.9) from t to t + δt, dividing by δt and taking the limit as δt → 0, we find
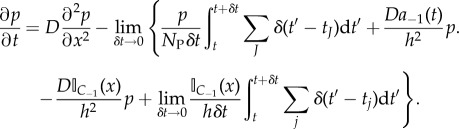 |
2.11 |
For each C−1 → C1 transfer event, we approximate 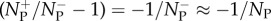 , because NP is large. It should be noted that in order to obtain equation (2.11) from equation (2.9), one requires δt be sufficiently small that temporally varying dependent variables are constant on (t, t + δt), that is
, because NP is large. It should be noted that in order to obtain equation (2.11) from equation (2.9), one requires δt be sufficiently small that temporally varying dependent variables are constant on (t, t + δt), that is 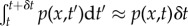 and similarly for a−1(t) and 1/NP(t). The large number of transfer events that occur between t and t + δt mean that the fluctuations in the number of transfer events are negligible and, as such, they can be predicted deterministically using the propensities given in §2.2 (equations (2.1) and (2.4))
and similarly for a−1(t) and 1/NP(t). The large number of transfer events that occur between t and t + δt mean that the fluctuations in the number of transfer events are negligible and, as such, they can be predicted deterministically using the propensities given in §2.2 (equations (2.1) and (2.4))
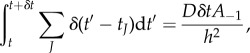 |
2.12 |
and
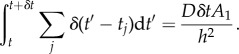 |
2.13 |
Substituting equation (2.12) into equation (2.11) and recalling that A−1 = a−1NP, we find the second and third terms on the right-hand side of equation (2.11) cancel each other. Consequently, we see that changes in the PDE as a result of hybridization with the discrete subdomain (i.e. not including the Laplacian diffusion operator) are confined to within the pseudo-compartment.
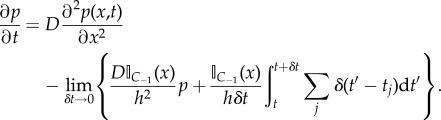 |
2.14 |
Substituting equation (2.12) into the second term on the right-hand side of equation (2.14), we obtain (correct to O(h2) accuracy; as accurate as the compartment-based simulation)
 |
2.15 |
In order to find equation (2.15), it should be noted that
 |
2.16 |
where x0 is at the centre of C−1 and px(x0, t) = O(h) (owing to the no flux boundary condition placed on the PDE at the interface between the two subdomains). Evaluating the limit δt → 0, we obtain
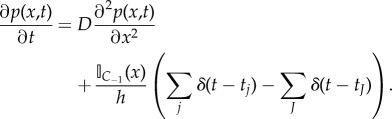 |
2.17 |
If the number of particles within the pseudo-compartment, A−1, becomes large then it will have a small relative variance and hence can effectively be assumed to be deterministic (albeit not necessarily integer valued).
Equation (2.17) is the motivating representation for algorithm 2, which is valid for large NP. Transfer events from ΩP and ΩC are calculated in the same way as algorithm 1, however, their effect on the PDE domain is different. The source and sink terms in algorithm 1, required for conditional probability changes in the PDE distribution as a result of periods of ‘no jump’, are no longer part of algorithm 2. In algorithm 2, as particles transfer from C−1 to ΩC particles are withdrawn from the PDE assuming that they were from the pseudo-compartment in the same way that they are added when particles transfer from ΩC to C−1 (as indicated in equation (2.17)).
Unsurprisingly, for large NP, we obtain a near deterministic hybrid simulation in both subdomains. Using equations (2.12) and (2.13), equation (2.15) becomes
| 2.18 |
The last two terms in equation (2.18) represent a lattice approximation to a free diffusive flux over the interface, a desired outcome of algorithm 2.
A cartoon schematic illustrating the simplified algorithm for large copy numbers (algorithm 2) in one dimension is given in figure 3.
Figure 3.

A cartoon schematic illustrates the most important features of algorithm 2 in one dimension. In ΩC, to the right of the interface, particles are represented as individuals in compartments (dark blue rectangles) with each individual adding 1/h to the density in that compartment. Particles can jump to neighbouring compartments within ΩC (dark blue block arrows). In ΩP, to the left of the interface, density is represented by a ‘continuous’ function (light blue curve). Particles in the left-most compartment in ΩC (adjacent to the interface) can jump into the PDE regime (blue horizontally striped arrow) where they are added as an indicator function to the PDE solution in the region [−h,0)—the pseudo-compartment (green dashed line). Pseudo-particles (hatched green rectangles with dashed borders) corresponding to the mass of the PDE in the pseudo-compartment are allowed to jump right (green vertically striped arrow) into the first compartment in ΩC. When a particle leaves the pseudo-compartment an indicator function of mass corresponding to one particle is removed from the PDE in that region. (Online version in colour.)
Table 2 describes the algorithm used to interface the two regimes. Note that when removing a pseudo-particle from the PDE regime in step (vii)(c) we enforce the condition that p(x,t) > 1/h forall x ∈ C−1 to ensure that when we remove an indicator function corresponding to a particle's worth of mass that we do not make the PDE solution negative. In practice, this condition will rarely be enforced, because the PDE region should be used to describe regions of the domain that have sufficiently high density that the individual-based model becomes inefficient. We note, however, that with a fixed interface this will not always be possible and that this restriction may lead to slight inaccuracies in the solution.
Table 2.
Algorithm for the coupling of the compartment-based regime with the PDE-based regime in the case of high copy numbers.
| (i) | Initialize the time, t = t0 and set the final time, tfinal. Specify the PDE-update time step dtP and initialize the next PDE time step to be tP = t + dtP. |
| (ii) | Initialize the number of particles in each compartment in ΩC, Ai for i = 1, …, K, and the distribution of probability density in ΩP, p(x,t0), for x ∈ ΩP. |
| (iii) | Calculate the propensity functions for diffusion between the compartment regimes as αi,j = AiD/h2 for i = 1…K and j = M + 1, M + 2 and for reactions as αi,j for i = 1…K and j = 1, …, M using the usual mass action kinetics. |
| (iv) | Calculate the propensity function for diffusion from the pseudo-compartment, C−1, in ΩP into the adjacent compartment in 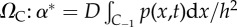 (equation (2.4)). (equation (2.4)). |
| (v) | Calculate the sum of the propensity functions,  . . |
| (vi) | Determine the time for the next ‘compartment-based’ event tC = t + τ, where τ is given by equation (2.2). |
| (vii) | If tC < tP then the next compartment-based event occurs: |
| (a) Determine which event occurs according to the method described in the text (see [48]). | |
(b) If the event corresponds to αi,j for i = 1…K and j = M + 1, M + 2 then move a particle from compartment i in the direction specified by j. If the particle crosses the interface into pseudo-compartment C−1 then add a particle's worth of mass to the region C−1 i.e.  . Here . Here 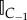 is the indicator function which takes the value 1 in C−1 and 0 elsewhere. is the indicator function which takes the value 1 in C−1 and 0 elsewhere. |
|
(c) If the event corresponds to propensity function α* and p(x,t) > 1/h forall x ∈ C−1 then place a particle in C1. Remove a particle's worth of mass from the PDE solution in the region C−1 i.e. 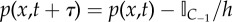 . . |
|
| (d) update the current time, t = tC. | |
| (viii) | If tP < tC then the PDE regime is updated: |
| (a) Update the PDE solution according to the numerical method described in §2.1.2 using p(x,t) as the previous value of the solution. | |
| (b) Update the current time, t = tP and set the time for the next PDE update step to be tP = tP + dtP. | |
| (ix) | If t ≤ tfinal, return to step (iii). |
| Else end. |
We have shown that, theoretically, algorithm 1 simplifies to algorithm 2 in the case of large NP. In the following section, we demonstrate this empirically on a number of simple test problems. We also demonstrate the strong agreement between the hybrid simulations of both algorithms and known exact analytical solutions.
3. Results
Here, we assesses the accuracy of our proposed algorithms in simulating three straightforward test problems of increasing complexity. In all the example simulations that follow, we choose dtp, Δx = 0.005 and h = 0.05, so that for every compartment, there are 10 PDE mesh points. These parameters will be systematically varied later in this section in order to determine the error behaviour of the algorithm.
3.1. Test problem 1: uniform particle distribution
In test problem 1, we demonstrate that our proposed algorithms are capable of maintaining a steady-state distribution of particles. We consider the diffusion of non-interacting particles on a domain with reflective boundaries which will maintain a steady-state distribution. We assume that all N particles are initially uniformly distributed across the domain and move with diffusion coefficient D = 1/400, in non-dimensionalized units. The PDE that we solve in ΩP is the diffusion equation with zero-flux boundary conditions at either end.
Figure 4 demonstrates that a uniform steady state is maintained by both algorithms. The disparity between the PDE solution and the analytical solution close to the interface in figure 4c is transient and oscillates either side of the analytical solution as time progresses (see electronic supplementary material, movies S1 and S2 corresponding to algorithms 1 and 2, respectively).
Figure 4.
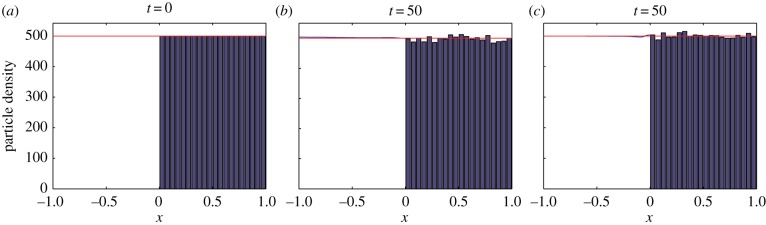
Maintenance of (a) an initially uniform steady state by (b) algorithm 1 and (c) algorithm 2. In each subfigure, the blue curve is the solution of the PDE in ΩP, the blue histograms represent the concentration of particles in each of the compartments in ΩC and the red curve represents the analytical solution of the mean-field model. Note that the blue curve is difficult to see because, for the most part, it lies underneath the analytical solution. The number of particles is N = 1000. The simulation results are averaged over 100 repeats. (Online version in colour.)
3.2. Test problem 2: particle redistribution
As a further example of the propriety of our algorithms, we consider a situation in which particles are initially uniformly distributed in either ΩP or in ΩC with no particles in the complementary region. We note that the situation in which all the particles are in ΩC and hence the concentration in the compartment-based region is much higher than that in the PDE region is not the ideal situation in which to employ our algorithm. However, it is important to show that our algorithm is robust to such situations. In physical terms, each of these simulations corresponds to particles, artificially kept in one half of a box, being allowed to diffuse into the other half of the box.
The mean-field model corresponding to this situation can be formulated as an initial-boundary-value problem
| 3.1 |
with zero-flux boundary conditions
| 3.2 |
and initial conditions
| 3.3 |
or
| 3.4 |
depending on which side of the box we wish to initialize the particles. This equation can be solved using separation of variables and Fourier series. For initial condition (3.3), the solution is given by
 |
3.5 |
For initial condition (3.4), the minus in front of the sum is replaced with a plus.
In figure 5, we compare the analytically derived density to the density produced using our algorithms given initial condition (3.3). We see a favourable comparison between the solution according to our algorithms and the mean-field solution. A comparison of the densities through time for algorithm 1 and 2 can be seen in electronic supplementary material, movies S3 and S4, respectively. In electronic supplementary material, movies S5 and S6, we present the same comparison but for a single realization of algorithms 1 and 2, respectively. In electronic supplementary material, figure S1, we compare the particle density of the two algorithms against the analytical solution of the mean-field model for initial condition (3.4). The comparison is again favourable.
Figure 5.
Particles initially in the left-hand half of the domain (a) spread diffusively (with diffusion coefficient D = 1/400) throughout the domain eventually reaching steady state. By t = 1000, the system is assumed to have reached steady state. (b,c) Show the particle density profile according to algorithm 1 at times 250 and 1000, respectively. (d,e) Show the same comparison for algorithm 2. Figure descriptions and particle numbers are as in figure 4. The simulation results are averaged over 100 repeats. (Online version in colour.)
3.3. Test problem 3: a morphogen gradient formation model
In this final test problem, we model the formation of a morphogen gradient by considering basic first-order reactions. Morphogen is produced at x =−1 with rate Dλ. We implement this production as a flux boundary condition in the PDE region of the model
| 3.6 |
We also allow the morphogen to decay uniformly across the domain with rate μ and we implement a zero-flux boundary condition at x = 1. These zeroth-order (production) and first-order (degradation) reactions allow for the description of the mean dynamics of the fully stochastic model by a PDE
| 3.7 |
This is the mean-field PDE which we expect the density to satisfy across the whole domain. The analytical solution for the expected evolution of the density for this system (with boundary condition analogous to equation (3.6)) can therefore be found explicitly as
| 3.8 |
where
 |
3.9 |
gives the steady state of the morphogen gradient and
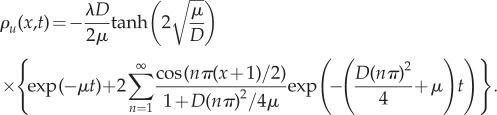 |
3.10 |
Because equation (3.7) is the PDE, we would expect the mean-field density of the fully stochastic model to satisfy, we use this as the PDE we solve in ΩP in our hybrid model. In ΩC, we implement the usual diffusive ‘reactions’ and additional mono-molecular decay reactions in each compartment and a zero-flux boundary condition at x = 1.
In figure 6, we compare the analytically derived density to that produced using our algorithms given an initially empty domain. We increase the value of the diffusion coefficient by a factor of 10 (in comparison with previous simulations) to D = 10 × h2 = 1/40 (in order to achieve a sensible steady-state profile). We choose λ = 1000 and μ = 0.1, giving a rate of influx of particles into the domain of Dλ = 25. As in previous examples, we see a favourable comparison between the solution according to our hybrid algorithms and the expected mean-field solution given by equations (3.8)–(3.10). A comparison of the densities through time for algorithms 1 and 2 can be seen in electronic supplementary material, movies S7 and S8, respectively.
Figure 6.
A morphogen gradient forms through a combination of influx at the left-hand boundary and decay of morphogen particles throughout the domain. Panel (a) shows the initially empty domain. By t = 60, the system is assumed to have reached an approximately steady state. Panels (b,c) show the particle density profile according to algorithm 1 at times 15 and 60, respectively. Panels (d,e) show the same comparison for algorithm 2. Figure descriptions are as in figure 4. The simulation results are averaged over 100 repeats. (Online version in colour.)
A more quantitative study of the similarities between the solution of our algorithms and the analytical solutions is presented in §4.
4. Error analysis
Here, we revisit the comparison between the mean particle densities predicted by our hybrid algorithm and the expected values given by the corresponding deterministic model. It is our aim in developing our algorithms that the error between the hybrid methods and the deterministic solution should be of the same order of magnitude as the accuracy associated with the individual numerical simulation techniques. In particular, we developed our algorithms in order that the stochastic model should not ‘see’ (i.e. be influenced by) the interface. Because it is well established that the descriptions of particle density in ΩP and ΩC are valid representations of diffusion, we address the question ‘can our algorithms correctly simulate the flux over the interface?’ In order to test this, we compare
| 4.1 |
the expected number of particles in ΩC in the deterministic model to
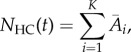 |
4.2 |
the expected number of particles in ΩC in the hybrid models. Here,  represents the mean number of particles in the ith compartment averaged over 100 repeats of the hybrid algorithms. For completeness, we also compare
represents the mean number of particles in the ith compartment averaged over 100 repeats of the hybrid algorithms. For completeness, we also compare
| 4.3 |
the expected number of particles in ΩP in the deterministic model to
| 4.4 |
the expected number of particles in ΩP in the hybrid models.
The results for test problem 1 are shown in figure 7. In simulations generated by our hybrid algorithm 2, the mass in the PDE-based regime is very similar to the expected mass given by the uniform solution of the diffusion equation. The same is true of the mass in the compartment-based regimes. Results are quantitatively indistinguishable (excepting for expected stochastic variation) for algorithm 1, although, for brevity, we do not explicitly show the corresponding figures.
Figure 7.

Error plots for the uniform particle distribution maintenance example. In panel (a), we display the normalized (i.e. divided by the total number of particles in the domain) expected value of the total mass in ΩP given by the analytical solution (red, dashed line, NDP(t)/(NDP + NDC(t))) and the normalized average mass in ΩP according to our hybrid algorithm 2 (black line, NHP(t)/(NHP + NHC(t))). In panel (b), we display the same comparison but for the mass in the compartment-based regime (i.e. NDC(t)/(NDP + NDC(t)) (red, dashed line) and NHC(t)/(NHP + NHC(t)) (black line)). The masses generated by our hybrid algorithm are averaged over 100 repeats as in previous density comparison figures. No systematic bias is discernible even for simulations run over longer time periods and with more particles. (Online version in colour.)
In figure 8, we display similar comparisons for test problem 2, in which the particles are initialized uniformly in ΩP only. As the simulation evolves, we see that the expected mass predicted by the hybrid algorithm matches closely the expected mass given by the analytical solution in both ΩP and ΩC. Further, the insets demonstrate that the relative error between the masses generated by the analytical solution and the hybrid model are low and have no systematic bias, but instead fluctuate about their expected values. Similar results hold for the initial condition in which the particles are initialized uniformly in ΩC only (see electronic supplementary material, figure S2). As in figure 7, because the results of the simulations of our two hybrid algorithms are quantitatively similar, we present only the simulation results from our second hybrid algorithm.
Figure 8.

Error plots for test problem 2, in which all particles are initially in ΩP. In (a), we display the normalized expected value of the total mass in ΩP given by the analytical solution (red, dashed line, NDP/(NDP + NDC) and the normalized average mass in ΩP (black line, NHP/(NDP + NDC) according to our second hybrid algorithm. In (b), we display the same comparison but for the compartment-based regime. In each panel, the inset displays the evolution of the relative error (i.e. (NHP−NDP)/NDP or (NHC−NDC)/NDC, respectively) throughout the simulation. Again, the masses generated by our hybrid algorithm are averaged over 100 repeats. (Online version in colour.)
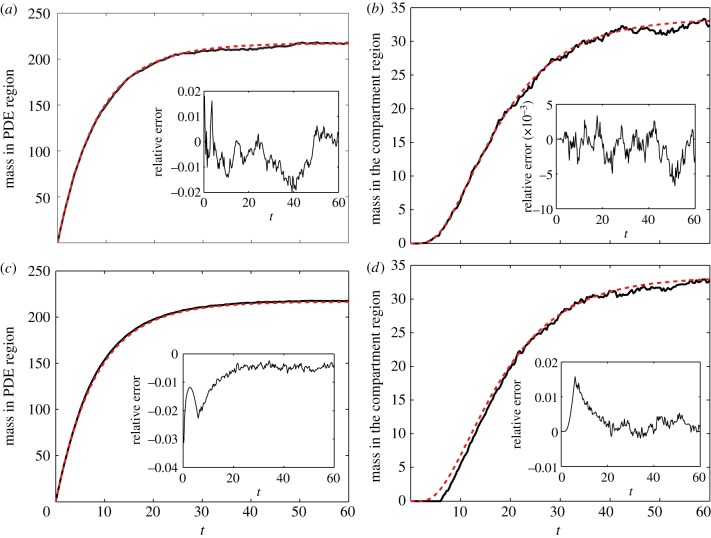
Finally, in figure 9, we display similar comparisons between the mass in each of the regimes for both of the hybrid algorithms we have developed when simulating the formation of a morphogen gradient (test problem 3). Again, a comparison of the results from the hybrid algorithm and the analytical solution shows good agreement, especially for long times. However, there is a clear disparity between the mass in ΩC for algorithm 2 and the expected mass in that region (figure 9d). In particular, the hybrid algorithm under-represents the expected mass in the compartment-based regime for early times. Although it is not clearly visible in figure 9c owing to the scale of the axes, there is a corresponding over-representation of the expected mass in ΩP at early times for algorithm 2. This is not the case for algorithm 1 (figure 9a,b).
Figure 9.
Error plots for the morphogen gradient formation example for (a,b) algorithm 1 and (c,d) algorithm 2. (a) and (c) refer to mass in the ΩP and (b) and (d) to mass in ΩC. Figure descriptions are as in figure 8. (Online version in colour.)
The reason for this disparity is a technical one. Recall that in algorithm 2, in order to avoid negative solution values, a particle is not allowed to be removed from the pseudo-compartment, C−1, until the PDE solution across that compartment has a value of at least 1/h. This avoids the possibility that the removal of a pseudo-particle may send the value of the PDE solution in C−1 negative. As the domain is initially empty and fills from the PDE region, there is a significant period of time in which mass should be flowing over the interface, but is restricted from doing so by an artificial barrier in our approximate algorithm 2. The flow of particles into ΩC is, therefore, retarded in comparison with the analytical solution for which, of course, no such barrier exists. In algorithm 1, however, we see no such problem (cf. figure 9b), because mass which is moved across the interface is removed from the whole of ΩP, rather than just the pseudo-compartment. This justifies our assertion that algorithm 2 is suitable for simulations in which the number of particles at the interface are high, whereas algorithm 1 is suitable for situations in which there may be low copy numbers at the interface. We explore the ramifications of these results further in the discussion.
In order to determine the robustness of our coupling mechanism, we performed further analysis of the error for test problems 1 and 2 (‘maintenance of a uniform steady’ state and ‘particles flowing from ΩP to ΩC’, respectively). Specifically, we investigated the emergence of error associated with the discretization parameters dtp (the time discretization associated with PDE updates) and h (the compartment size in ΩC; figure 10a,b, respectively). The time-averaged relative error in the expected number of particles in ΩC simulated using our hybrid simulation was determined by comparing with the same quantity predicted by a continuous mean-field analytical PDE solution to the respective test problems. In order to reduce the effect of stochastic fluctuation on the error measurement, we averaged the particle numbers over 100 repeat simulations each with N = 1000 particles for each of the test problems. Owing to the computational intensity of these algorithms with such larger particle numbers and the wide variety of simulation parameters, we conducted our error analysis using algorithm 2. We expect the error behaviour to be the same for algorithm 1, because the source of error we have identified (see below) should affect both algorithms in a similar manner.
Figure 10.
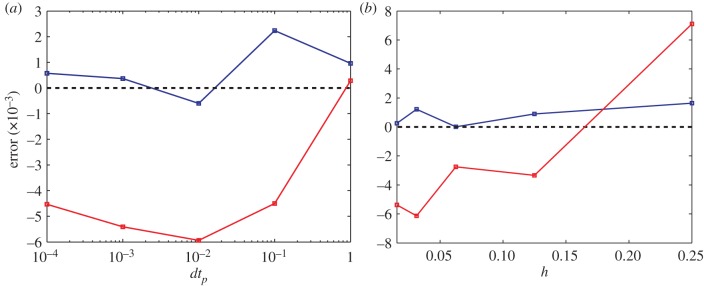
Error in compartment-based particle numbers varies with (a) PDE step size, dtp, and (b) compartment size, h, for both test problem 1 (blue) and test problem 2, in which all the particles are uniformly distributed in ΩP (red). For (a), simulation parameters are as given previously with dtp varying in steps of powers of 10 from 10−4 to 1 (note the log-scale on the horizontal axis.). For convenience in (b), we chose Δx = 1/256 and varied h in powers of two from 1/64 to 1/4. In test problem 1, final simulation time was 50 (as in figure 7), whereas in test problem 2, the final simulation time was 250. (Online version in colour.)
The results of varying both h and dtp separately are shown in figure 10. On the vertical axis, error is defined as 〈(NDC − NHC)/NDC〉 where, as before, NDC is the known expected number of particles in ΩC and NHC is the averaged simulated number of particles in the same region. The angle brackets denote the time average of the relative error recorded at unit time intervals throughout the simulation. A positive error indicates a net bias in the simulations for particles towards ΩP, whereas a negative error indicates a net bias for particles towards ΩC.
Test problem 1 contains smaller sources of error than test problem 2. These errors have a consistent order of magnitude as that of expected stochastic fluctuations as a result of finite copy number. The difference in the magnitude of the error between test problem 1 and test problem 2 can be attributed to the way in which mass transfer is balanced or unbalanced. For test problem 1, net diffusive transfer of mass into the pseudo-compartment from the PDE is zero as is the net transfer of particles between the pseudo-compartment and ΩC. In test problem 2, there is a net transfer of mass into the pseudo-compartment from the PDE regime and a net transfer out to the compartment-based regime. The systemic sources of error that we have identified in our method result from a non-zero net particle flux over the interface. The PCM results in these errors being very small.
While still very small, a comparatively larger error associated with the hybrid modelling approach is observed in cases of non-zero net flux (in which the well-mixed assumption does not strictly hold within the pseudo-compartment). Increasing both h and dtp results in an increase in relative error in test problem 2 (figure 10). The reason for this increase is not directly related to the hybrid model but rather to the individual single-scale models used. Significant increases in the error for test problem 2 can be seen when dtp is increased beyond  . Similarly, an O(h2) error is expected for large compartment sizes, h. In both cases, the effective diffusion is reduced (in comparison with that expected by the equivalent continuous PDE) as a result of discretization error in the PDE and compartment region, respectively. The reduction of effective diffusion leads to a reduction in the net diffusive flux over the interface, regardless of the implementation of the interface itself. The increase in error with increasing h and dtp is therefore, a manifestation of discretization error in the simulation methods employed in ΩC and ΩP, respectively.
. Similarly, an O(h2) error is expected for large compartment sizes, h. In both cases, the effective diffusion is reduced (in comparison with that expected by the equivalent continuous PDE) as a result of discretization error in the PDE and compartment region, respectively. The reduction of effective diffusion leads to a reduction in the net diffusive flux over the interface, regardless of the implementation of the interface itself. The increase in error with increasing h and dtp is therefore, a manifestation of discretization error in the simulation methods employed in ΩC and ΩP, respectively.
The sign of the relative error in test problem 2 is negative for low h and low dtp. This is a manifestation of a small increase in diffusive flux caused by our algorithm pseudo-compartment. The cause of this error is due to the breakdown of the assumption that mass in C−1 is evenly distributed. Indeed, in test problem 2, mass flowing into C−1 from the remainder of ΩP is instantaneously considered to be evenly spread in C−1 for the purposes of consideration of jumping into ΩC. Instead, this mass lies a small distance away from the expected position at the centre of the node on the side which is furthest from the interface. This erroneous evenly distributed assumption results in a slightly increased net flux of particles over the interface that would otherwise be expected. The reason that this source of error is not prevalent in test problem 1 is because there is no net flux of particles flowing into or out of C−1 that would contribute to such an error. The effect of this error is always to create a net increased bias over the interface in the direction of the net flow (an overall negative relative error in the case of test problem 2). It is important to note that this error is common at the interface of hybrid models of this type. The inclusion of the pseudo-compartment rather than a clean interface forces particles that would contribute to this error to have a decreased number of transfer events associated with them and therefore compound a much smaller error (see for example, the two regime method Flegg et al. [43]).
Fine details of the error and its dependence on the small model parameters Δx, dtp and h is complex and difficult to determine owing to other algorithmic factors (for example, particles need to wait between PDE time steps to be considered for C−1 → C1 when they are near the edge of C−1). It is also unclear if the reflecting boundary at I plays any role as a source of error for particular discretization parameters. Some of these issues may be responsible for complex error behaviour in figure 10 for small h and small dtp. On the other hand, details of fluctuation of the error for small h and small dtp are of the order of fluctuations that are expected as a result of finite copy number and may not be systemic in nature.
Importantly, for small h and dtp, while there is a bias for particles to flow over the interface in the direction of net flow, this bias is still very small. The authors recommend the use of parameters Δx, dtp and h that individually minimize the discretization error of the PDE and compartment-based methods used. The interface should create a bias approximately proportional to h in the direction of net flow but this bias is significantly reduced owing to the dual nature of the pseudo-compartment. For completeness, the authors recommend that dxp ≪ h to maintain the approximation of a PDE in ΩP although it would appear that the method is robust when this approximation is relaxed. Indeed, if dxp = h, one would expect no interface-related error at all, because transfer into the pseudo-compartment from the ‘PDE’ is concentrated at the node at the centre of the pseudo-compartment. In this case though, the PDE becomes more closely described as a diffusion master equation on a lattice.
5. Discussion
We have introduced two algorithms which allow a coupling between a continuum PDE description of particle density in one region of the domain and a discrete stochastic compartment-based description in another. Using a pseudo-compartment in the PDE regime, which has properties of both descriptions, we were able to couple the two simulation methodologies together in such a way that the expected flux across the interface is maintained. We evidenced this through a series of examples, demonstrating good correspondence between the expected mass in each of the modelling regions (averaged over several repeats of the hybrid simulation algorithms) and the mass in those regions determined by the corresponding fully deterministic mean-field model. We also analysed the errors in the coupling method over a wide range of model parameter values and found them to be small (always less than 1%) even at the extremes of the parameter regimes in which the single-scale models we employ on either side of the interface are not expected to work well.
Our method relies on a knowledge of the deterministic PDE description to which the mean of the compartment-based simulations corresponds. While this is easy to obtain in the examples we have studied, when higher-order reactions are introduced to the stochastic model, there is no longer an exact closed-form representation of the expected particle density as a PDE in terms of the first moment alone. In order to obtain a self-contained equation, we must make moment closure assumptions, which means that the PDE description will no longer correspond exactly to the mean behaviour of the compartment-based system. However, in situations where particle numbers are sufficiently large the closed PDE description will often be a close match to the expected densities of the compartment-based model and, as such, we expect that our algorithms will still be applicable. Furthermore, large particle numbers are precisely the regime in which we want to make use of the PDE description, further improving the applicability of our algorithms.
It is precisely this consideration that will provide the motivation for our next work on this subject to develop a hybrid method with an adaptive interface. In order to make the hybrid algorithm as efficient as possible, the interface should be able to move, so that only regions with sufficiently low concentrations are represented by the compartment-based model and regions with high concentration are consistently represented with the PDE-based model. This would ultimately allow for algorithm 2 to be used in all cases for efficiency reasons. A good set of rules that could be used to move an interface was explored in reference [45]. This will increase the computational efficiency of the algorithm, because we will no longer be simulating the individual particle movements in the discrete model when the continuum description can be tolerated. There is also scope to interface the algorithms we have developed in this manuscript with algorithms designed to couple compartment-based models and molecular-based models [43,44] in order to build a ‘three-regime method’. Another important extension of this work is to consider compartment-based models on irregular lattices which will allow us to capture more complex and realistic domain geometries.
For the sake of clarity in this manuscript, we presented the algorithms themselves and the illustrative examples in a single dimension; however, the algorithm is easily adapted to higher-dimensional problems with (hyper)-planar interfaces. We therefore expect our algorithms to be highly applicable to stochastic simulations of systems in which molecular populations are high in some regions and low in others, meaning that neither a fully deterministic-continuum nor a fully-stochastic-individual-based model is appropriate. Our algorithms provide significant increases in speed in comparison with fully stochastic models and more accurate and representative modelling in comparison with fully deterministic models.
Supplementary Material
References
- 1.Erban R, Chapman SJ. 2009. Stochastic modelling of reaction–diffusion processes: algorithms for bimolecular reactions. Phys. Biol. 6, 1–18. ( 10.1088/1478-3975/6/4/046001) [DOI] [PubMed] [Google Scholar]
- 2.Andrews SA, Bray D. 2004. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys. Biol. 1, 137–151. ( 10.1088/1478-3967/1/3/001) [DOI] [PubMed] [Google Scholar]
- 3.van Zon JS, ten Wolde PR. 2005. Simulating biochemical networks at the particle level and in time and space: Green's function reaction dynamics. Phys. Rev. Lett. 94, 128103 ( 10.1103/PhysRevLett.94.128103) [DOI] [PubMed] [Google Scholar]
- 4.Drawert B, Lawson MJ, Petzold L, Khammash M. 2010. The diffusive finite state projection algorithm for efficient simulation of the stochastic reaction–diffusion master equation. J. Chem. Phys. 132, 074101 ( 10.1063/1.3310809) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lampoudi S, Gillespie DT, Petzold LR. 2009. The multinomial simulation algorithm for discrete stochastic simulation of reaction–diffusion systems. J. Chem. Phys. 130, 094104 ( 10.1063/1.3074302) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Baker RE, Yates CA, Erban R. 2010. From microscopic to macroscopic descriptions of cell migration on growing domains. Bull. Math. Biol. 72, 719–762. ( 10.1007/s11538-009-9467-x) [DOI] [PubMed] [Google Scholar]
- 7.Yates CA, Baker RE, Erban R, Maini PK. 2012. Going from microscopic to macroscopic on non-uniform growing domains. Phys. Rev. E 86, 021921 ( 10.1103/PhysRevE.86.021921) [DOI] [PubMed] [Google Scholar]
- 8.Yates CA, Baker RE. 2013. Importance of the Voronoi domain partition for position-jump reaction–diffusion processes on non-uniform rectilinear lattices. Phys. Rev. E 88, 054701 ( 10.1103/PhysRevE.88.054701) [DOI] [PubMed] [Google Scholar]
- 9.Engblom S, Ferm L, Hellander A, Lötstedt P. 2009. Simulation of stochastic reaction–diffusion processes on unstructured meshes. SIAM J. Sci. Comput. 31, 1774–1797. ( 10.1137/080721388) [DOI] [Google Scholar]
- 10.Murray JD. 2003. Mathematical biology II: spatial models and biomedical applications, vol. 2 of Interdisciplinary mathematics. New York, NY: Springer. [Google Scholar]
- 11.Berg HC. 1993. Random walks in biology. Princeton, NJ: Princeton University Press. [Google Scholar]
- 12.Field RJ, Noyes RM. 2010. Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. J. Chem. Phys. 60, 1877–1974. ( 10.1063/1.1681288) [DOI] [Google Scholar]
- 13.Adomian G. 1995. The diffusion–Brusselator equation. Comput. Math. Appl. 29, 1–3. ( 10.1016/0898-1221(94)00244-F) [DOI] [Google Scholar]
- 14.Schnakenberg J. 1979. Simple chemical reaction systems with limit cycle behaviour. J. Theor. Biol. 81, 389–400. ( 10.1016/0022-5193(79)90042-0) [DOI] [PubMed] [Google Scholar]
- 15.Zauderer E. 1983. Partial differential equations of applied mathematics. New York, NY: John Wiley & Sons. [Google Scholar]
- 16.Thomas J. 1995. Numerical partial differential equations, vol. 22 New York, NY: Springer. [Google Scholar]
- 17.Erban R, Chapman SJ, Maini P. 2007. A practical guide to stochastic simulations of reaction–diffusion processes. (http://arxiv.org/abs/0704.1908) [DOI] [PubMed]
- 18.Gillespie DT, Hellander A, Petzold LR. 2013. Perspective: stochastic algorithms for chemical kinetics. J. Chem. Phys. 138, 170901 ( 10.1063/1.4801941) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Swain PS, Elowitz MB, Siggia ED. 2002. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl Acad. Sci. USA 99, 12 795–12 800. ( 10.1073/pnas.162041399) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Elowitz MB, Levine AJ, Siggia ED, Swain PS. 2002. Stochastic gene expression in a single cell. Sci. Signal. 297, 1183–1186. ( 10.1126/science.1070919) [DOI] [PubMed] [Google Scholar]
- 21.Ghosh S, Ghosh P, Basu K, Das SK. 2007. Modeling the stochastic dynamics of gene expression in single cells: a birth and death Markov chain analysis. In IEEE Int. Conf. on Bioinformatics and Biomedicine, BIBM 2007, Silicon Valley, CA, 2–4 November, pp. 308–316. Piscataway, NJ: IEEE. [Google Scholar]
- 22.Tian T, Burrage K. 2004. Bistability and switching in the lysis/lysogeny genetic regulatory network of bacteriophage λ. J. Theor. Biol. 227, 229–237. ( 10.1016/j.jtbi.2003.11.003) [DOI] [PubMed] [Google Scholar]
- 23.Vilar JMG, Kueh HY, Barkai N, Leibler S. 2002. Mechanisms of noise-resistance in genetic oscillators. Proc. Natl Acad. Sci. USA 99, 5988–5992. ( 10.1073/pnas.092133899) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gonze D, Halloy J, Goldbeter A. 2002. Robustness of circadian rhythms with respect to molecular noise. Proc. Natl Acad. Sci. USA 99, 673–678. ( 10.1073/pnas.022628299) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Woolley TE, Baker RE, Gaffney EA, Maini PK. 2011. Power spectra methods for a stochastic description of diffusion on deterministically growing domains. Phys. Rev. E 84, 021915 ( 10.1103/PhysRevE.84.021915) [DOI] [PubMed] [Google Scholar]
- 26.Ander M, et al. 2004. Smartcell, a framework to simulate cellular processes that combines stochastic approximation with diffusion and localisation: analysis of simple networks. Syst. Biol. 1, 129–138. ( 10.1049/sb:20045017) [DOI] [PubMed] [Google Scholar]
- 27.Hattne J, Fange D, Elf J. 2005. Stochastic reaction–diffusion simulation with MesoRD. Methods Biochem. Anal. 21, 2923–2924. ( 10.1093/bioinformatics/bti431) [DOI] [PubMed] [Google Scholar]
- 28.Ramsey S, Orrell D, Bolouri H. 2005. Dizzy: stochastic simulation of large-scale genetic regulatory networks. J. Bioinform. Comput. Biol. 3, 415–436. ( 10.1142/S0219720005001132) [DOI] [PubMed] [Google Scholar]
- 29.Drawert B, Engblom S, Hellander A. 2012. URDME: a modular framework for stochastic simulation of reaction–transport processes in complex geometries. BMC Syst. Biol. 6, 76 ( 10.1186/1752-0509-6-76) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sanft KR, Wu S, Roh M, Fu J, Lim RK, Petzold LR. 2011. Stochkit2: software for discrete stochastic simulation of biochemical systems with events. Bioinformatics 27, 2457–2458. ( 10.1093/bioinformatics/btr401) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Flegg MB, Rüdiger S, Erban R. 2013. Diffusive spatio-temporal noise in a first-passage time model for intracellular calcium release. J. Chem. Phys. 138, 154103 ( 10.1063/1.4796417) [DOI] [PubMed] [Google Scholar]
- 32.Klann M, Ganguly A, Koeppl H. 2012. Hybrid spatial Gillespie and particle tracking simulation. Bioinformatics 28, i549–i555. ( 10.1093/bioinformatics/bts384) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Erban R, Flegg MB, Papoian GA. 2013. Multiscale stochastic reaction–diffusion modelling: application to actin dynamics in filopodia. Bull. Math. Biol. 76, 799–818. ( 10.1007/s11538-013-9844-3) [DOI] [PubMed] [Google Scholar]
- 34.Wolpert L. 1969. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 25, 1–47. ( 10.1016/S0022-5193(69)80016-0) [DOI] [PubMed] [Google Scholar]
- 35.Tostevin F, Ten Wolde PR, Howard M. 2007. Fundamental limits to position determination by concentration gradients. PLoS Comput. Biol. 3, e78 ( 10.1371/journal.pcbi.0030078) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kicheva A, Pantazis P, Bollenbach T, Kalaidzidis Y, Bittig T, Jülicher F, González-Gaitán M. 2007. Kinetics of morphogen gradient formation. Science 315, 521–525. ( 10.1126/science.1135774) [DOI] [PubMed] [Google Scholar]
- 37.Bollenbach T, Kruse K, Pantazis P, González-Gaitán M, Jülicher F. 2005. Robust formation of morphogen gradients. Phys. Rev. Lett. 94, 1–4. ( 10.1103/PhysRevLett.94.018103) [DOI] [PubMed] [Google Scholar]
- 38.Flekkøy EG, Feder J, Wagner G. 2001. Coupling particles and fields in a diffusive hybrid model. Phys. Rev. E 64, 066302 ( 10.1103/PhysRevE.64.066302) [DOI] [PubMed] [Google Scholar]
- 39.Alexander FJ, Garcia AL, Tartakovsky DM. 2002. Algorithm refinement for stochastic partial differential equations. I. Linear diffusion. J. Comput. Phys. 182, 47–66. ( 10.1006/jcph.2002.7149) [DOI] [Google Scholar]
- 40.Moro E. 2004. Hybrid method for simulating front propagation in reaction–diffusion systems. Phys. Rev. E 69, 060101 ( 10.1103/PhysRevE.69.060101) [DOI] [PubMed] [Google Scholar]
- 41.Wagner G, Flekkoy EG. 2004. Hybrid computations with flux exchange. Phil. Trans. R. Soc. Lond. A 362, 1655–1666. ( 10.1098/rsta.2004.1405) [DOI] [PubMed] [Google Scholar]
- 42.Ferm L, Hellander A, Lötstedt P. 2010. An adaptive algorithm for simulation of stochastic reaction–diffusion processes. J. Comput. Phys. 229, 343–360. ( 10.1016/j.jcp.2009.09.030) [DOI] [Google Scholar]
- 43.Flegg MB, Chapman SJ, Erban R. 1974. The two-regime method for optimizing stochastic reaction–diffusion simulations. J. R. Soc. Interface. 9, 859–868. ( 10.1098/rsif.2011.0574) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Flegg MB, Hellander S, Erban R. 2014. Convergence of methods for coupling of microscopic and mesoscopic reaction–diffusion simulations. (http://arxiv.org/abs/1304.7393) [DOI] [PMC free article] [PubMed]
- 45.Robinson M, Flegg M, Erban R. 2014. Adaptive two-regime method: application to front propagation. J. Chem. Phys. 140, 124109 ( 10.1063/1.4868652) [DOI] [PubMed] [Google Scholar]
- 46.Franz B, Flegg MB, Chapman SJ, Erban R. 2012. Multiscale reaction–diffusion algorithms: PDE-assisted Brownian dynamics. SIAM J. Appl. Math. 71, 714–730. [Google Scholar]
- 47.Franz B, Xue C, Painter KJ, Erban R. 2013. Travelling waves in hybrid chemotaxis models. Bull. Math. Biol. 244, 98–106. ( 10.1007/s11538-013-9924-4) [DOI] [PubMed] [Google Scholar]
- 48.Gillespie DT. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361. ( 10.1021/j100540a008) [DOI] [Google Scholar]
- 49.Cao Y, Li H, Petzold L. 2004. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J. Chem. Phys. 121, 4059–4067. ( 10.1063/1.1778376) [DOI] [PubMed] [Google Scholar]
- 50.Yates CA, Klingbeil G. 2013. Recycling random numbers in the stochastic simulation algorithm. J. Chem. Phys. 138, 094103 ( 10.1063/1.4792207) [DOI] [PubMed] [Google Scholar]
- 51.McCollum JM, Peterson GD, Cox CD, Simpson ML, Samatova NF. 2006. The sorting direct method for stochastic simulation of biochemical systems with varying reaction execution behavior. Comput. Biol. Chem. 30, 39–49. ( 10.1016/j.compbiolchem.2005.10.007) [DOI] [PubMed] [Google Scholar]
- 52.Gibson MA, Bruck J. 2000. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. A 104, 1876–1889. ( 10.1021/jp993732q) [DOI] [Google Scholar]
- 53.Li H, Petzold L. 2006. Logarithmic direct method for discrete stochastic simulation of chemically reacting systems. Technical report. University of California Santa Barbara. See http://www.engr.ucsb.edu/_cse.
- 54.Elf J, Ehrenberg M. 2004. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst. Biol. 1, 230–236. ( 10.1049/sb:20045021) [DOI] [PubMed] [Google Scholar]
- 55.Gillespie DT. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434. ( 10.1016/0021-9991(76)90041-3) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.