Building a Pan-Genome Reference for a Population

Abstract

A reference genome is a high quality individual genome that is used as a coordinate system for the genomes of a population, or genomes of closely related subspecies. Given a set of genomes partitioned by homology into alignment blocks we formalize the problem of ordering and orienting the blocks such that the resulting ordering maximally agrees with the underlying genomes' ordering and orientation, creating a pan-genome reference ordering. We show this problem is NP-hard, but also demonstrate, empirically and within simulations, the performance of heuristic algorithms based upon a cactus graph decomposition to find locally maximal solutions. We describe an extension of our Cactus software to create a pan-genome reference for whole genome alignments, and demonstrate how it can be used to create novel genome browser visualizations using human variation data as a test. In addition, we test the use of a pan-genome for describing variations and as a reference for read mapping.

1. Introduction

Areference genome is a genome assembly used to represent a species. Reference genomes are indispensable to contemporary research primarily because they act as a common coordinate system, so that genes, variations, and other functional annotations can be described in common terms (Coffey et al., 2011; ENCODE Project Consortium et al., 2011; 1000 Genomes Project Consortium, 2010).

In this article we explore creating a pan-genome reference from a set of genomes. We start from a set of genomes in a genome alignment (Paten et al., 2011b), which partitions the genomes' subsequences into homology sets that we term blocks. The problem is to find an ordering of the blocks that as closely as possible reflects the ordering of the underlying genome sequences. We call such an ordering a pan-genome reference because it indexes every block, something that any individual genome within the population almost certainly does not. Though potentially useful for many of the things reference genomes are currently used for, our principal motivation is to produce better visualizations of variation and closely related species data within a genome browser (Meyer et al., 2013), in which one reference genome is used as the coordinates to display data for a species and for which a pan-genome display would allow a more complete view of the data.

Closely analogous to the problem of building a pan-genome reference of aligned input genomes, a great deal of previous work has focused on methods for ancestral reconstruction. Most relevant to this work is the (rearrangement) median problem. The median problem is, informally, to find for a set of genomes and a given edit operation a median genome whose total pairwise edit distance from each of the other sequences is minimal (Tannier et al., 2009). Naively it might be assumed that good solutions to the median problem might have utility for finding an intra-species pan-genome reference. However, in the median problem the edit operations are not necessarily restricted to maintain sequence colinearity while during evolution complex selective pressures often work to achieve exactly this (Kirkpatrick, 2010). For example, consider the three signed permutations: A, d, B, e, C and A, −e, B, −d, C and A, B, e, −d, C. Assume that the capital letters A, B, and C represent very large subsequences of the genome, and the lowercase letters, d and e, represent short subsequences. In each of the sequences the large subsequences maintain their colinearity with respect to one another, and ignoring the short subsequences no edits appear to have occurred. However, when incorporating the short subsequences, the optimal median sequence under either the double-cut-and-join (DCJ) or reversal edit operations is A, −e, −B, −d, and C; the other sequences are each one operation away. This optimal median sequence contains an inversion of the large sequence B, which may make it biologically implausible to be a common ancestor, e.g., if there is a single gene with exons spanning A, B, and C. This tendency to lose colinearity has led to the study of “perfect” rearrangement scenarios, in which common intervals of ordered subsequences present in the input are conserved (Berard et al., 2009).

However, current algorithms for finding perfect rearrangement scenarios require the common intervals to be prespecified, do not allow copy number variation, and require the common intervals to exist in all the inputs. This makes them inappropriate when there is no prior expert knowledge to define the intervals, or when representing large populations, where copy number variation is present and missing data and unusual variants break many intervals that would otherwise be common.

Related to our approach, methods to derive consensus orderings of sets of total and partial orders have been extensively considered, particularly in the domain of social choice (Fagin et al., 2002; Kendall, 1938). In general, the inputs to such problems are sequences or structures equivalent (in their most general form) to directed acyclic graphs (DAG), and the output is a consensus (partial) ordering. In such work, algorithms often work to minimize the consensus' (weighted) symmetric difference distance or Kemeny tau distance (Kendall, 1938) (informally, the number of out of order, discordant, pairs). Recently, such consensus ordering procedures have been adapted to create consensus genetic maps from sets of individual subpopulation maps (Bertrand et al., 2009). The problem formalized here has similarity to such approaches, with the important difference that it explicitly models the double-stranded nature of DNA, allowing us to account for the cost of sequences being inverted with respect to one another.

In what follows we will formalize the basic problem, prove its NP-hardness, describe a principled heuristic decomposition of the problem using cactus graphs (Paten et al., 2011a), give heuristic algorithms for the problem's solution, demonstrate the algorithms performance using simulation, and explore a pan-genome reference for the human major histocompatibility complex (MHC), including its utility for visualization, variant description and read mapping.

2. Methods

2.1. The pan-genome reference problem

2.1.1. Genome sequences

Let 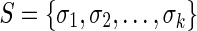be the input DNA sequences, with lengths 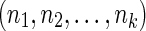. For simplicity we assume here that the DNA sequences are linear, though extensions to allow additional circular sequences are straightforward. Due to the double-stranded nature of DNA, we distinguish the 5′ and 3′ ends of each sequence element. We denote a tuple 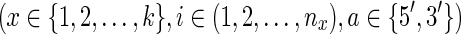as 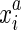, giving the coordinate of the a end of the ith element in σ_x. For any DNA sequence σ_x the ends are oriented consistently, so that for all i > 1 the 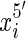end is adjacent (contiguous) in the sequence to the 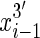end and, for all i < n_x the 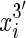end is adjacent in the sequence to the 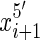end. We use signed notation to distinguish ends, hence 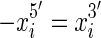and . 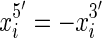The set of all end coordinates is S.

2.1.2. Alignment

The end coordinates in S are partitioned by their alignment relationships. To represent this we define the alignment relation ∼ ⊂ S². The alignment relation is an equivalence relation, that is, one that is transitive, symmetric, and reflexive. We denote the equivalence classes for ∼ as S/∼, and write 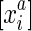to represent an equivalence class containing 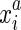. We also constrain the alignment relation to force the pairing of opposite ends. Firstly, we assume if 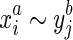then 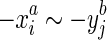, we call this strand consistency. Secondly, we assume if 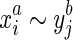then neithe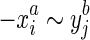r or 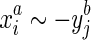, which we term strand exclusivity. Due to strand consistency, for all 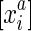in S/∼ there exists 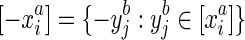, the reverse complement of 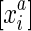. Due to strand exclusivity, for all 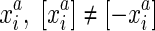. Combining these two statements it follows that |S/∼| is even. The set 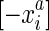can be equivalently denoted 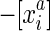, so that the reverse complement of X in S/∼ is −X. We call each member of S/∼ a side, and each pair set of forward and reverse complement sides a block. Note that the alignment relation allows for copy number variation, that is, arbitrary numbers of coordinates from sequences in the same genome can be present in a block.

2.1.3. Sequence graphs

Let G = (V, E) be a (bidirected) sequence graph. A bidirected graph is a graph in which each edge is given an independent orientation for each of its endpoints (Medvedev and Brudno, 2009). The vertices are the set of blocks, 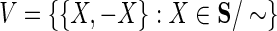. The edges, 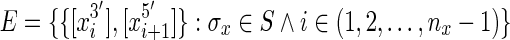, encode the adjacencies (biologically the covalent bonds) between contiguous ends of sequence elements. Each edge is a pair set of sides rather than a pair set of vertices, therefore giving each endpoint its orientation (Fig. 1A). The cardinality and size of G are clearly at most linear in the size of S.

FIG. 1.

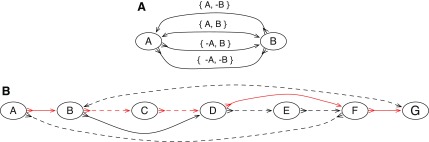
An illustration of a pan-genome reference on a sequence graph. (A) A bidirected graph representing the four ways two blocks can be connected. The arrowheads on the edges indicate their endpoints: the sides of the vertices. (B) An example pan-genome reference on a sequence graph. There are two sequences, indicated by the color of the edges. The red sequence, represented by the thread A, B, C, D, F, G, and the black sequence, represented by the thread A, −F, −E, −D, −B, G. The red thread visits the edges {−A, B}, {−B, C}, {−C, D}, {−D, F}, and {−F, G}, and the black thread visits the edges {−A, −F}, {F, −E}, {E, −D}, {D, −B}, and {B, G}. Neither thread includes all the blocks. A pan-genome reference, indicated by the dotted edges, is A, −F, −E, −D, −C, −B, G. The dotted edges and the edges {−B, D} and {−D, F} are the edges consistent with the given pan-genome reference.

A sequence of sides 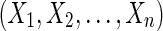is a thread. If the elements in 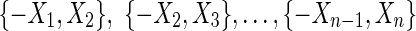are edges in the graph then the thread is a thread path. We use a sequence of sides, rather than vertices, because the sides orient the vertices, distinguishing forward and reverse complement orientations. For example, for each sequence 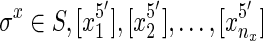is a thread path in G, because for all 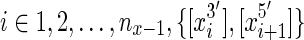(equivalently 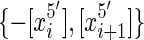) is an edge in G.

A transitive sequence graph, 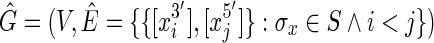, includes the sequence graph G as a subgraph but additionally includes edges defined by transitive adjacencies, that is, pairs of ends connected by a thread path. The cardinality (vertex number) of 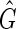is the same as G, but the size (edge number) of 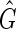is worst-case quadratic in the size of S. A sequence graph encodes input sequences and an alignment; a transitive sequence graph models the complete set of ordering and orientation relationships between the blocks implied by the input sequences (Supp. Fig. 1, Supplementary Material is available online at www.liebertpub.com/cmb).

2.1.4. Pan-genome references

A pan-genome reference F is a set of non-empty threads such that each block is visited exactly once (Fig. 1B). Intuitively, not all pan-genome references are equally reasonable as a way of summarizing S, because they will not all be equally “consistent” with the set of adjacencies, 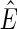. An edge {X, Y} is consistent with a pan-genome reference F if and only if there exists a thread in F containing the subsequence 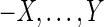(Fig. 1B). Given a weight function 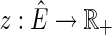, which maps edges to positive real valued weights, the pan-genome reference problem is to find a pan-genome reference in 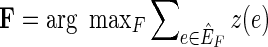, where 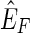is the subset of 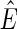consistent with F.

2.1.5. Exponential weight function

Although many possible weight functions exist, inspired by the nature of genetic linkage, we define z({X, Y}) = z′(X, Y) + z′(Y, X), where 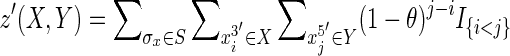, in which I_{i<j} is the indicator function that is 1 for pairs of i and j for which i < j else 0, and the parameter θ is a real number in the interval [0, 1). The θ parameter intuitively represents the likelihood that an adjacency between two directly abutting sequence elements is broken or absent in any other randomly chosen sequence, and is defined analogously to its use in the LOD score (Griffiths et al., 1999) used in genetics. For θ > 0, the score given to keeping elements in a sequence in the same order and orientation in the pan-genome reference declines exponentially with distance separating them.

To make it clear that an intermediate value of θ is desirable we can look at what happens at extreme values of the parameter. As θ approaches 1 the weight function becomes dependent only on edges in the sequence graph. Figure 2 demonstrates a limitation with considering only these edges, which is similar to that described for edit operations in the introduction. At θ = 0 all transitive adjacencies are equally weighted, however this can lead to longer sequences having undue influence on the solution; Figure 2 also gives an example of this limitation when weighting all adjacencies equally. One issue not dealt with by the definition of z are the evolutionary interdependencies between the input sequences. It is possible to adjust the weights given to adjacencies given a phylogenetic tree that relates the input sequences (or the genomes they derive from). However, where homologous recombination is present a weighting based upon a phylogenetic tree is insufficient and yet more complex strategies are needed.

FIG. 2.

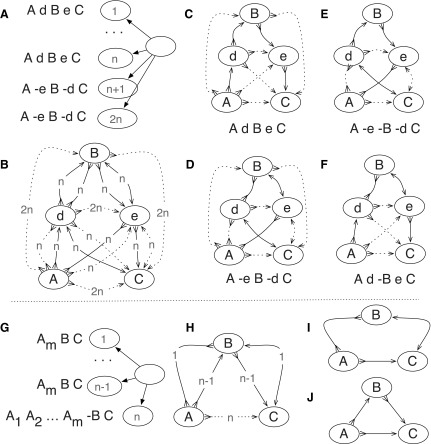
(Top) An illustration of why it is not always sufficient to consider only abutting adjacencies. (A) There are five blocks, A, B, C, d, and e, reprising their roles from the example given in the introduction. The input contains n copies of the sequence A, d, B, e, C, and n copies of the sequence A, −e, B, −d, C. (B) The bidirected graph representation of this problem, with the number of adjacencies supporting each edge labeled, the abutting adjacencies shown as solid lines, and the nonabutting adjacencies shown as dotted lines. If only solutions that start with A and end with C are of interest, there are four maximal solutions, shown in (C, D, E, F). Solutions (C) and (D) each have 4n abutting adjacencies and 10n nonabutting adjacencies. Solutions (E) and (F) each also have 4n abutting adjacencies but only 6n nonabutting ones. For θ <1 the (C) and (D) solutions are optimal. As θ approaches 1, the weight of nonabutting adjacencies approaches 0 and all four solutions become equally weighted, despite (E) and (F) having B in the reverse orientation. (Bottom) An illustration of why θ should be greater than 0. (G) There are m + 2, blocks, the input contains n − 1 copies of the sequence A_m, B, C and 1 copy of the sequence 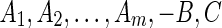. (H) The bidirected graph representation of the problem, where the sequence of blocks has been reduced to just a single vertex for convenience. The two maximal solutions are shown in (I, J), corresponding to the two distinct input sequences. If m > n and θ is 0 then the solution with B in the reverse orientation (I) is optimal, despite this orientation being observed only once. By increasing θ the alternative solution with B in the forward orientation becomes optimal.

2.2. NP-hardness of the pan-genome reference problem

We show the pan-genome reference problem is NP-hard, demonstrating that the pan-genome reference problem can be projected onto the problem of finding maximum weight subgraphs of a bidirected graph that do not contain characteristic classes of simple cycle.

An M, N bidirected simple cycle, henceforth abbreviated to an M, N-cycle, is a simple cycle in a bidirected graph containing M vertices such that M ≥ N; M − N of the vertices have both their sides incident with an edge in the cycle (we call these balanced vertices), and the other N vertices have only one side incident with edges in the cycle (we call these unbalanced vertices). An M, N-cycle is odd if N is odd, else we call it even. We say a bidirected graph is strongly acyclic if it contains no M, 0-cycles or odd M, N-cycles. Let 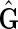be the set of all strongly acyclic subgraphs of 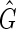of maximum weight. The following lemma shows the relationship between maximum weight strongly acyclic subgraphs and maximum weight pan-genome references.

Lemma 1. There exists a surjection f : 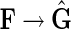, such that for all F in F, .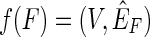

Proof. Let 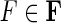, the threads in F orient all the vertices, partitioning the sides into two sets according to if they appear in a pan-genome reference thread or not. By definition, the consistent edges and this bipartition of the sides form a bipartite graph. If there exists an odd M, N-cycle in f (R), then it defines an odd cycle in this bipartite graph (a contradiction), hence f (R) contains no odd M, N-cycles.

A pan-genome reference induces a partial <_F order on the vertices. If there exists an M, 0-cycle , as these edges are consistent with F, this implies that both 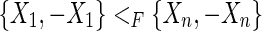and 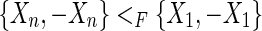, but a partial order is antisymmetric (a contradiction), therefore f (R) contains no M, 0−cycles.

As f (F) is strongly acyclic, if it is not in 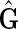then it must be possible to add an edge to f (F) without creating an M, 0-cycle or odd M, N-cycle. Assume therefore that f (F) is a subgraph of some 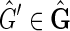. Let {X, Y} be an edge in 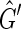but not in f (F). By definition, {X, Y} has nonzero weight. Between {X, −X} and {Y, −Y} of the three other possible edges, {{X, −Y}, {−X, Y}, {−X, −Y}}, one must be in 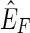, else F is not a maximum weight solution to the pan-genome reference problem, because in this case there must exist two threads in F, one that contains X or −X and one that contains Y or −Y, and these two threads can be concatenated together to create a new pan-genome reference additionally consistent with one of the four possible edges between {X, −X} and {Y, −Y}. 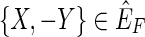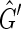If then contains a 2, 1-cycle {{X, −Y},{Y, X}}, if {−X, −Y} then 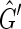contains a 2, 0-cycle {{−X, −Y}, {Y, X}} and if {−X, Y} then 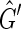contains a 2, 1-cycle {{−X, Y}, {Y, X}}. In all cases therefore we derive a contradiction, therefore .

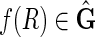It remains to prove that for every member of 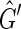in 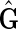there exists F such that 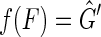. For 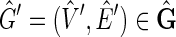a side bicoloring is a labeling function color, such that each vertex and edge's sides are colored such that one is black and the other is red, that is, it creates a bipartition of the sides of the graph.

To construct such a coloring for 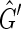use a depth first search. In each connected component of 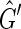pick an unlabeled vertex and color one of its sides red and the other black. The depth first search recurses from this vertex such that for each edge of the form {X, Y } if X is colored red and Y is unlabeled then Y is colored black and −Y is colored red and vice versa if X is colored black. If during this recursion an edge is encountered such that both sides are already labeled then the depth first search has traversed an M, N-cycle. Further, if the sides of this edge are labeled with the same color then the depth first search has failed to produce a side bicoloring. Suppose we encounter such a cycle in 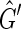; either there are two excess black sides or two excess red sides, as only the last edge encountered does not have sides of distinct colors. Each balanced vertex contributes a black and a red side while each unbalanced vertex contributes either two black sides or two red sides, therefore N ≥ 1. Furthermore, as there are only two excess vertices of one color, N must be odd, implying 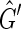is not strongly acyclic, therefore there exists a side bicoloring of 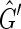. Given a side bicoloring of 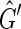let 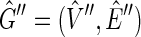be a digraph, such that 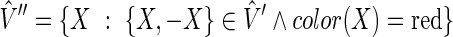and 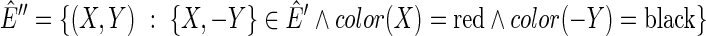, where (a, b) is a directed edge from a to b. The graph 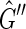is isomorphic to 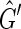, except that the arbitrary orientations of the sides within the vertices have been reassigned so that there is only one type of edge in the graph (Fig. 3). A directed cycle in 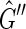would be an M, 0-cycle, but as 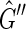is strongly acyclic it must contain no directed cycles, therefore 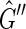is a DAG. Any topological sort 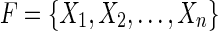of the vertices of 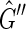is a pan-genome reference for which .   ■

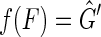FIG. 3.

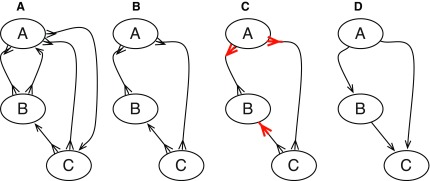
(A) A bidirected graph with three vertices A, B, and C. (B) A subgraph of (A) containing no M, 0-cycles or odd M, N-cycles. (C) A side bicoloring of (B). (D) A digraph for (C).

Theorem 1. The pan-genome reference problem is NP-hard.

Proof. The problem of finding a maximum weight strongly acyclic subgraph of a bidirected graph is polynomial-time reducible to the pan-genome reference problem, because, by the previous lemma, the consistent subgraph of any solution to the pan-genome reference problem is a maximum weight strongly acyclic subgraph. It remains to prove that the problem of finding a maximum weight strongly acyclic subgraph of a bidirected graph is NP-hard. We prove this by reduction of the minimum feedback arc set problem (Karp, 1972), which is to find a smallest set of edges in a directed graph that when removed results in a graph containing no directed cycles. Using the demonstration in the previous lemma, a digraph can be equivalently represented as a side bicolored bidirected graph. An unbalanced vertex in an M, N-cycle is red if the endpoints of the edges incident with it in the cycle are colored red, or else it is black. Suppose there exists an M, N-cycle in a side bicolored bidirected graph with i balanced vertices, j unbalanced red vertices, and k unbalanced black vertices. As in a side bicolored bidirected graph each edge has one red endpoint and one black endpoint; the total number of red and black endpoints is equal, therefore i + 2j = i + 2k, thus k = j and therefore it is not possible to construct an odd M, N-cycle in a side bicolored bidirected graph. As a directed cycle in a digraph corresponds to an M, 0-cycle in the equivalent side bicolored bidirected graph, the minimum feedback arc set problem is thus polynomial-time reducible to the problem of finding a maximum weight strongly acyclic subgraph of a side bicolored bidirected graph (i.e., eliminating M, 0-cycles).   ■

An alternative, similarly simple proof of NP-hardness uses the elimination of odd M, N-cycles rather than the M, 0-cycles, reducing the maximum bipartite subgraph problem (Newman, 2008].

2.3. Algorithms for the pan-genome reference problem

We have established the pan-genome reference problem is NP-hard, and now, given that knowledge, we describe a principled—and to our knowledge novel—heuristic to decompose the problem using cactus graphs, and briefly describe two straightforward algorithms to build and refine a pan-genome reference.

2.3.1. Cactus decomposition of the pan-genome reference problem

A cactus graph of the type introduced in Paten et al. (2011a) describes a sequence graph in a hierarchical form. For a sequence graph G, a pair of sides X and Y form a chain interval if there exists a thread path of the form 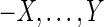, but no thread path of the form 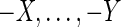or 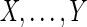. Chain intervals represent intervals that are “fundamental” in the sense that all the simple threads for all the sequences in S follow the traversal rules defined above. It is reasonable therefore to search for reference sequences that preserve all such intervals.

The chain interval relation defines a partition of the vertices into a set of disjoint chains. A chain is a thread such that all and only pairs of form (X_i, X_j) for which j−i ≥ 1 define a chain interval; we call each chain interval of the form (−X_i, X_i+1) a link. Chains can be arranged hierarchically, because one child chain may be contained within the link of a parent chain. We call two chains siblings if either they are both children of the same parent chain link, or both are not contained within any parent chain link (i.e., they are at the highest level of the hierarchy). For a thread the two sides X₁ and −X_n are stubs. A net is an induced subgraph of G defined by the set of stubs for a maximal set of sibling chains and (if they exist) the pair of sides that define the containing parent link (Fig. 4A). A graph in which the nodes are the nets and the edges are the oriented vertices of a sequence graph forms a cactus graph (Fig. 4B).

FIG. 4.

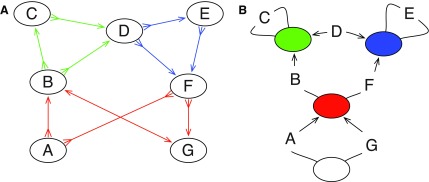
(A) The bidirected graph from Figure 1B rewritten to show the nets as colored side subgraphs. (B) The cactus graph representation of the blocks and nets in (A), with the white net containing the highest level chains. The edges represent the blocks; the vertices represent the nets. The arrowheads on the edges indicate endpoints that are links.

To construct a reference that respects all chain intervals we create a pan-genome reference independently for each net, treating each pair of chain stubs as equivalent to blocks in the previous exposition. Additionally, the pan-genome reference for each child net with a parent link must be composed of a single thread whose stubs are the sides of the parent link. This reduces the maximum size of the pan-genome reference problem to that of the largest net in the sequence graph, which as the sequence graph for alignments of variation data is often relatively sparse, has [in our experience and in accordance to random graph theory (Erdos and Rényi, 1960)] size only approximately logarithmically proportional to the number of vertices in the graph. It also facilitates parallel execution, because each net can be computed in parallel.

2.3.2. Greedy and iterative sampling algorithms for the pan-genome reference problem

Given the decomposition, we build a pan-genome reference for each subproblem using an initial greedy algorithm, before iterative refinement that employs simulated annealing.

In overview (see the source-code for more details), a pan-genome reference F is composed, starting from the empty set, by greedily adding one member of V to F at a time, each time picking the combination of insertion point and member of V that maximizes consistency with elements already in the F. The algorithm is naively |V|³ time (as each insertion is |V|² time), though by heuristically ignoring weights less than a specified threshold (the weight declines exponentially with sequence separation), and using a priority queue to decide which member of V to add next, it can be improved |V|log(|V|) in practice.

Given an initial reference F the procedure progressively searches through a sequence of neighboring permutations, where for a reference F a neighboring permutation is created by removing an element from F and then inserting it either in the positive or negative orientation as a prefix, suffix, or coordinate between elements in the reduced F, potentially including the elements original coordinate. The algorithm incorporates simulated annealing by using a monotonically decreasing temperature function to control the likelihood of choosing neighbouring, lower scoring permutations. As the temperature tends to zero the algorithm becomes greedy and we can search for a local minima, while as the temperature tends to positive infinity all permutations become equally probable and the search becomes a random walk. Each iteration of sampling, in which the repositioning of every block is considered once, is naively |V|² time, but, as for the initial greedy algorithm, is improved to |V|log(|V|) in practice. By decreasing the temperature monotonically, and independently of the score, we heuristically ensure that the total number of iterations of this procedure is constant.

3. Results

3.1. Simulation experiments

To test the algorithms described we use a simple simulation of a rearrangement median problem. We start with a single linear chromosome, represented as a signed permutation of 250 elements, which we call the original median. We then simulate either 3, 5, or 10 leaves, treating each leaf with a set number of random edits. For convenience we simulate only translocations and inversions, which results in each leaf remaining a single contiguous chromosome, and apply an equal number of translocations and inversions. Note, for simplicity, we did not assess copy number changes (e.g., duplicative rearrangements), but doing so would be interesting.

We performed two sets of simulations, in the first we did not constrain the length of the subsequence of elements inverted or translocated. In such a scenario only a few edits are sufficient to radically reorder the genome and break many resulting ordering relationships. In the second scenario we constrained the lengths of inverted subsequences to 2 or 1, and constrained the length of translocated subsequences to just 1. In this scenario relatively large numbers of rearrangements are required to breakup the ordering of the original median. Intuitively, the former scenario seems more likely when the genomes are more distantly related, and synteny relationships have been lost, the latter seems much more plausible for closely related genomes, for example, when studying genomes within a population or between subspecies.

To find solutions to the pan-genome reference problem we use a combination of the algorithms described above, first using the greedy algorithm, then refining it with iterative sampling, performing 1000 iterations of improvement and setting θ = 0.1 (values of theta between 0.5 and 0.001 made little difference to the result). We call this combination Ref. Alg. in the results that follow, and look at results for 3, 5, and 10 leaf genomes, to see how increasing data alters the resulting solutions. To compare performance of our solutions we compare them to the original median, and to a median genome inferred using the AsMedian program (Xu, 2009) (using default parameters), which finds optimal solutions to the DCJ median problem with three leaves. We assess performance by looking at two metrics. Firstly, the DCJ distance, which gives the minimum number of edits needed to translate one genome into another by DCJ edits. Secondly, viewing the medians as two signed, partial order relations A and B on the blocks, the symmetric difference distance, defined as 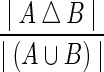. This gives the proportion of order plus orientation relationships not common to the two medians.

Figure 5A–D shows the results of simulating unconstrained, arbitrary translocations and inversions. Unsurprisingly, Ref. Alg. constructs medians that are substantially farther from the leaves or the original median in terms of DCJ distance than the results of AsMedian (avg. 44% and 103% more overall than Ref. Alg. with three leaves, respectively, from the leaves and original median). Furthermore, in terms of symmetric difference distance, the AsMedian solutions are on average 52% closer to the original median (though not the leaves) than those constructed using Ref. Alg. with three leaves. This clearly demonstrates that using the Ref. Alg. for sequences whose ordering have been turned over by large rearrangements produces poor results, and that ancestral reconstruction algorithms can be used more effectively for moderate numbers of edits in this scenario, with the caveat that they may construct a multi-chromosomal ordering of the data.

FIG. 5.

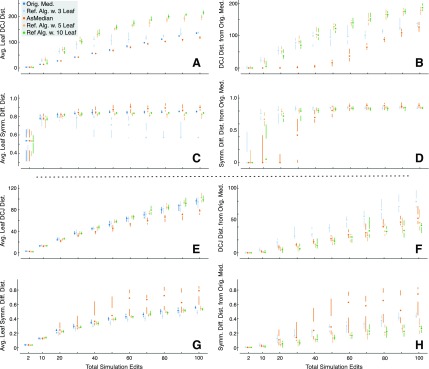
(Top) Simulation results using arbitrary inversion and translocation operations. Each plot shows the total number of operations (a mixture of 50% inversions and 50% translocations) versus either the DCJ distance (top two plots) or symmetric difference distance (bottom two plots). The left plots give the average distance from the leaf genomes and the right plots give the distance from the original “true” median genome. Series shown include the original median genome (left plots only), the inferred median genome from the AsMedian program (Xu, 2009) using three leaves, and the inferred median genomes using our combined reference algorithms, using, separately, 3,5, and 10 leaf genomes as input. Simulations used 10 replicates for each fixed number of edits, points give median result, lines show max and min quartiles. (Bottom) Simulation results using short inversion and translocation operations, laid out as in the top panel.

Figure 5E–H shows the results of simulating short edits, demonstrating a striking converse to the unconstrained case. In terms of DCJ distance, the Ref. Alg. with 5 and 10 leaves is actually able to outperform the AsMedian program in terms of distance to the original median (Ref. Alg. with five leaves requires 20% on avg. fewer DCJ edits than AsMedian), while in terms of symmetric distance, Ref. Alg. with three leaves is able to find solutions that are as close to the leaves as the original median and substantially closer to the original median than the AsMedian results (Ref. Alg. with three leaves is 31% closer on avg. than AsMedian in terms of symmetric difference distance to the original median). Furthermore, adding more leaves improves the results substantially (Ref. Alg. with 10 leaves is 52%, 44% closer, on average, to the original median in terms of avg. DCJ and symmetric difference than Ref. Alg. with 3 leaves). These results demonstrate that if edits have largely maintained the linear ordering of the sequences then, even when the sequences have been subject to substantial numbers of edits, Ref. Alg. is competitive with an ancestral reconstruction method in terms of DCJ, while ensuring that all elements appear in an ordering that is closer, in terms of ordering and orientation, than an optimal ancestral reconstruction method.

3.2. Creating a pan-genome reference for the major histocompatibility complex (MHC)

To test the utility of the described pan-genome in practice, we created a pan-genome reference, abbreviated P. Ref., for the MHC region, exploring P. Ref.'s utility for visualization, variant description, and mapping. We used 16 human assemblies and the chimpanzee genome as an outgroup (see Supplementary Data). The 16 human assemblies include the primary reference sequence for the MHC, which is a single haplotype named PGF. To generate the Cactus alignment we used its default parameters and set θ = 10⁻⁴ (tested θ values between 10⁻² and 10⁻⁶ produce similar results). The pan-genome reference P. Ref. covers just over five megabases, and with respect to it the samples collectively contain tens of thousands of indels and hundreds of more complex rearrangements.

3.2.1. A pan-genome visualization of MHC

To produce better visualizations of variation and closely related species data within a genome browser, we converted P. Ref. into a consensus nucleotide sequence by creating a consensus sequence for each block and then concatenating these subsequences together in the order of the pan-genome reference. Figure 6 shows example prototype browser screenshots for the MHC. Each shows the alignment of a query genome with respect to P. Ref. (along the horizontal axis). Each screenshot shows a sequence of alignment “snake tracks,” arranged vertically, one for each of the aligned query genomes. Each alignment snake is a sequence of blue/red rectangles (depending on strand) connected together by lines. The rectangles represent subsequences of a query genome aligned to the reference, the lines represent the adjacencies between these aligned subsequences. The red tick marks within the rectangles represent single nucleotide variations (SNVs). The top panel of Figure 6 shows indels; as no sequence apart from P. Ref. contains all the blocks, only the P. Ref. browser can show the contents of all the segregating indel subsequences. The middle panel of the figure shows a segregating combination of an inversion and deletion. The chromosome reference sequence for the human reference genome (PGF) has the inversion, but P. Ref., being a comprehensive consensus, both includes the subsequences missing from the chromosome reference sequence and orients the inversion according to the majority of the samples. In the bottom panel a tandem duplication is shown. All the human assemblies are either incomplete or have two copies of the tandemly duplicated subsequence, however, P. Ref. alone, containing a single copy of the tandem duplication subsequence, is able to cleanly display the event using the semantics of the alignment snake track in which each query subsequence is shown aligned to only one reference subsequence.

FIG. 6.

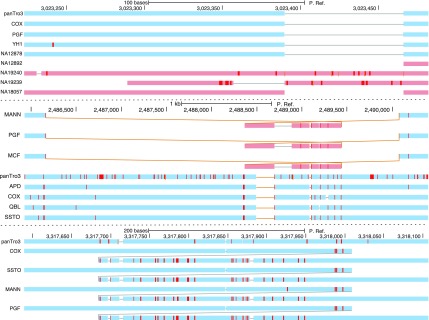
Prototype UCSC pangenome reference browser screenshots. (Top) Indels. (Middle) A segregating inversion. (Bottom) An apparently fixed tandem duplication. For reasons of space some samples are omitted from the screenshots. The human reference genome is PGF, the chimpanzee genome is panTro3, and details of the other samples are in the Supplementary Material.

3.2.2. P. Ref. contains ∼6% of recurrent bases that are absent in PGF

Given the relatively small number of samples, recurrent bases (present in two or more samples) are likely segregating at a reasonable frequency in the population. An important category of recurrent (segregating) bases are those that PGF fails to represent (i.e., not in PGF). On average each human sample has 68,525 (1.84%) such bases. Summing across the samples, 329,190 recurrent bases in the MSA (5.88% of columns and nonrecurrent bp) do not contain bases in PGF (see Supplementary Material section 5 and Supplementary Fig. 2).

3.2.3. P. Ref. is inclusive of all recurrent segregating indels and has fewer SNVs

The absence of many recurrent bases from the primary reference, PGF, is reflected in the relative ratio of insertions and deletions when compared to P. Ref. With respect to PGF the rate of insertions of the samples averages 2.8 × 10⁻⁴ per bp overall, and is similar to the rate of deletions, averaging 2.6 × 10⁻⁴ per bp overall. Conversely, the rate of insertions with respect to P. Ref. is much lower, averaging only 0.5 × 10⁻⁴ per bp overall, while the rate of deletions is much higher, at 5.3 × 10⁻⁴ per bp overall (Fig. 7A and B). This demonstrates a key difference between PGF, or likely any existing biological sample, and P. Ref., in that P. Ref. includes all recurrent segregating bases, while any biological sample is likely to have approximately equal numbers of insertions and deletions with respect to any other sample (Supplementary Material section 6).

FIG. 7.

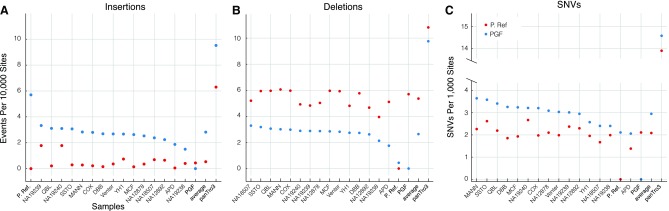
A comparison of indel and SNV rates between P. Ref. (red dots) and PGF (blue dots). (A–C) The number of insertions/deletions/SNVs per site (position) of each sample, as predicted by the Cactus MSA with respect to PGF and P. Ref.

Where as the pan-genome reference makes a tradeoff between insertions and deletions, for SNVs picking the consensus base has a clear advantage in reducing the number of events that need to be described per sample, thereby aiding data compression. With respect to PGF the SNV rate differs between samples from between 0.0021 to 0.0036 SNVs per bp. With respect to P. Ref. the SNV rate differs between samples from between 0.0014 to 0.0027 SNVs per bp. In every sample there are fewer SNVs with respect to P. Ref. than to PGF, the difference being 29% on average (Fig. 7C and Supplementary Material section 6).

To check that variants we predicted were of high fidelity (and that therefore the alignment was reasonable) we compared them to dbSNP. Overall, the MSA made 22,360 indel predictions of which 14,575 (65%) were confirmed, accounting for 34% of all short indels currently in the dbSNP/1KGP data. For more details, please see Supplementary Material section 7 and Supplementary Fig. 3 and Supplementary Table 1.

3.2.4. RNA alignments: P. Ref. contains all RefSeq transcripts that mapped to the MHC region as well as additional transcripts missing from PGF

Any reference genome must contain a set of representative gene structures for the species. We took the RefSeq human transcripts (Pruitt et al., 2012) and aligned them independently to PGF and P. Ref, using stringent identity and coverage parameters and keeping only the best alignments for each transcript (see Supplementary Material section 8). Requiring 95% of the transcript to be aligned at 95% identity, we find 210 RefSeq genes whose transcripts all align to both the MHC region of PGF and P. Ref. better than the remainder of PGF (Supp. Table 2). We find no transcripts that align to the PGF and not to P. Ref., but three genes with transcripts that align to P. Ref. but not to PGF. One of these genes, HLA-DQB1, has three RefSeq transcripts, of which only one (NM_001243962) did not map to PGF. By reducing the required identity for this transcript to 90%, we were able to obtain a reduced stringency match.

3.2.5. The HLA-DRB hypervariable region: P. Ref. includes segregating HLA-DRB genes not in PGF

The remaining two genes with transcripts that mapped to P. Ref. but not to PGF (HLA-DRB3 and HLA-DRB4) were entirely missing from PGF. Interestingly, both mapped to P. Ref. within large indels contained within a region that corresponds to the HLA-DRB hypervariable region. In P. Ref. the HLA-DRB hypervariable region (Traherne, 2008) contains a large number (29 events) of large insertions with respect to PGF; Supplementary Figure 4 shows this region in a prototype P. Ref. genome browser, while Supplementary Figure 5 shows the entire MHC for P. Ref. All the expected HLA genes in this region are present (known genes HLA-DRB5, HLA-DRB1, and pseudogenes HLA-DRB9 and HLA-DRB6), as well as the two extra HLA genes (HLA-DRB3, HLA-DRB4) described, and also pseudogenes (HLA-DRB2, HLA-DRB7, HLA-DRB8) that are recurrent in the input samples and known to be segregating in humans but not present in PGF (Stewart et al., 2004, Traherne et al., 2006, Horton et al., 2008).

3.2.6. Short read mapping: More reads map to P. Ref. than to PGF, but fewer reads map uniquely

Earlier we demonstrated that P. Ref. is inclusive, having relatively few insertions with respect to the input samples. However, the cost of including segregating but potentially rare subsequences in a pan-genome reference is the inclusion of potentially rare breakpoints. Such rare breakpoints could disrupt more common subsequences and potentially make mapping and annotation more difficult. To assess the tradeoffs made, we test P. Ref. as a target for mapping experiments. In brief, we constructed versions of P. Ref. excluding a held out sample and then compared mappings made with BWA (Li and Durbin, 2009) of the held out sample's reads to PGF and the held out P. Ref. (see Supplementary Material section 9). We mapped Illumina unpaired and paired reads. For each paired read we required that both its ends mapped in the proper orientation given the pairing constraint and were separated by at most 1000 bases, calling such reads properly paired.

We find that on average 5,958 (0.6%) more unpaired reads and 13,828 (0.5%) more paired reads map to P. Ref. than to PGF (Supp. Fig. 6). Of note, this is in reasonable agreement with the average proportion of bases in these samples (0.89%) that are recurrent but do not map to PGF.

Converse to an increase in the numbers of mapping reads, we find on average per sample 9,656 (0.26%) fewer unpaired reads and 6,413 (0.25%) fewer paired reads map uniquely to P. Ref. than map uniquely to PGF. To analyze this reduction we investigated reads that map uniquely to PGF but non-uniquely to P. Ref., calling such reads PGF mapping discordant. Supplementary Table 3 shows characteristics of these reads; we find that 73% of the bases to which such reads map are labeled repetitive, which is 1.4 times the average. We also find that there are three fold more SNVs in the dbSNP/1KGP data called at these bases than on average. We hypothesize this enrichment for SNVs is due to the absence of an orthologous sequence in PGF that is present in the sample being mapped (Supp. Fig. 7). This missing ortholog then results in the appearance of unique mapping to its paralog. This is important, as such SNVs, being located on a paralogous sequence, will have altered linkage properties with respect to surrounding SNVs.

4. Discussion and Conclusion

We defined a problem useful for creating a pan-genome reference between closely related genomes, proved it is NP-hard, and described principled heuristics to find (approximate) solutions. We demonstrated in simulations the tradeoffs between optimizing for conserved order relationships and minimizing DCJ operations. In addition, we have demonstrated the method's utility in constructing visualizations of variation data in the UCSC browser, providing a view of the alignment not typically possible from any input genome. Finally, though our primary motivation in this article is visualization, pan-genome references, being comprehensive and consensus orderings, are likely to prove useful for other purposes, here we have explored uses of P. Ref. for describing variations, genes, and as a target for mapping. Where reference genomes are currently used for computational convenience, for example, in read compression, and are not integral for biological interpretation, a pan-genome reference may present a useful alternative to current reference genomes. Additionally, given that (sequence) graphs do not have an implicit linear decomposition, having a pan-genome coordinate system on such graphs could prove useful in processing multiple alignments.

We have demonstrated the relationship of the pan-genome reference problem to a method for ancestral reconstruction, but the pan-genome reference problem also has close similarities with sequence assembly problems, which have variants explicitly described on bidirected graphs (Medvedev and Brudno, 2009). In particular, the scaffolding problem given paired reads involves arranging a set of “scaffold” sequences in a partial order to essentially maximize the numbers of consistently ordered, oriented, and spaced paired reads. Apart from the additional constraint on spacing, the scaffolding problem with paired reads can be defined equivalently to the pan-genome reference problem.

Acknowledgments

We acknowledge the support of the followings grants: ENCODE DAC (Data Analysis Center), subaward on NHGRI grant #U01HG004695 to European Bioinformatics Institute; ENCODE DCC (Data Coordination Center), NHGRI grant #U41HG004568; Browser (Center for Genomic Science), NHGRI grant #P41HG002371; and Gencode, subaward on NHGRI grant #U54HG004555 to Sanger Center.

Author Disclosure Statement

The authors declare that no competing financial interests exist.