Model Reduction by Manifold Boundaries

Abstract

Understanding the collective behavior of complex systems from their basic components is a difficult yet fundamental problem in science. Existing model reduction techniques are either applicable under limited circumstances or produce “black boxes” disconnected from the microscopic physics. We propose a new approach by translating the model reduction problem for an arbitrary statistical model into a geometric problem of constructing a low-dimensional, submanifold approximation to a high-dimensional manifold. When models are overly complex, we use the observation that the model manifold is bounded with a hierarchy of widths and propose using the boundaries as submanifold approximations. We refer to this approach as the manifold boundary approximation method. We apply this method to several models, including a sum of exponentials, a dynamical systems model of protein signaling, and a generalized Ising model. By focusing on parameters rather than physical degrees of freedom, the approach unifies many other model reduction techniques, such as singular limits, equilibrium approximations, and the renormalization group, while expanding the domain of tractable models. The method produces a series of approximations that decrease the complexity of the model and reveal how microscopic parameters are systematically “compressed” into a few macroscopic degrees of freedom, effectively building a bridge between the microscopic and the macroscopic descriptions.

Models of complex systems are often built by combining several microscopic elements together. This constructionist approach to modeling is a powerful tool, finding widespread use in many fields, such as molecular dynamics [1–3], systems biology [4–6], climate [7,8], economics [9], and many others [10–12]. Nevertheless, it is not without its pitfalls, most of which arise as models grow in scale and complexity. Overly complex models can be problematic if they are computationally expensive, numerically unstable [13], or difficult to fit to data [14]. These problems, however, are only manifestations of a more fundamental issue. Specifically, although reductionism implies that the system behavior ultimately derives from the same fundamental laws as its basic components, this does not imply that the collective behavior can easily be understood in terms of these laws [15,16]. The collective behavior of the system is typically compressed into a few key parameter combinations while most other combinations remain irrelevant [17]. The system therefore exhibits novel behavior that emerges from the collective interactions of its microscopic components. Extracting the emergent physical laws directly from the microscopic model, however, remains a nontrivial problem. A systematic method of simplifying complex models in a way that reveals the emergent laws governing the collective behavior would be a welcome tool to many fields.

The problem we consider here is to construct a simpler description of a system for a fixed set of predictions. A variety of model reduction techniques have been applied with consistent success, such as exploiting a separation of scales [18–20], clustering or lumping similar components into modules [21–23], or other methods to computationally construct a simple model with similar behavior [13,24]. Many methods have been developed by the control and chemical kinetics communities focused on dynamical systems [13,18–20,25], with recent applications to systems biology [24,26–29].

Existing methods are only partial solutions for two reasons. First, automatic methods often produce “black boxes” that do not explain the connection to the underlying physics or provide explanatory insights. Second, techniques that do give explanatory insights are only applicable to limited situations. These methods typically involve identifying some simplifying approximation, such as a mean-field approximation or expansion in a small parameter, and fail when such approximations cannot be identified. For example, the renormalization group (RG) is a powerful tool for producing a series of effective theories to describe a system’s behavior at different observation scales [30,31]; however, it requires that the system exhibit an emergent scale invariance or conformal symmetry.

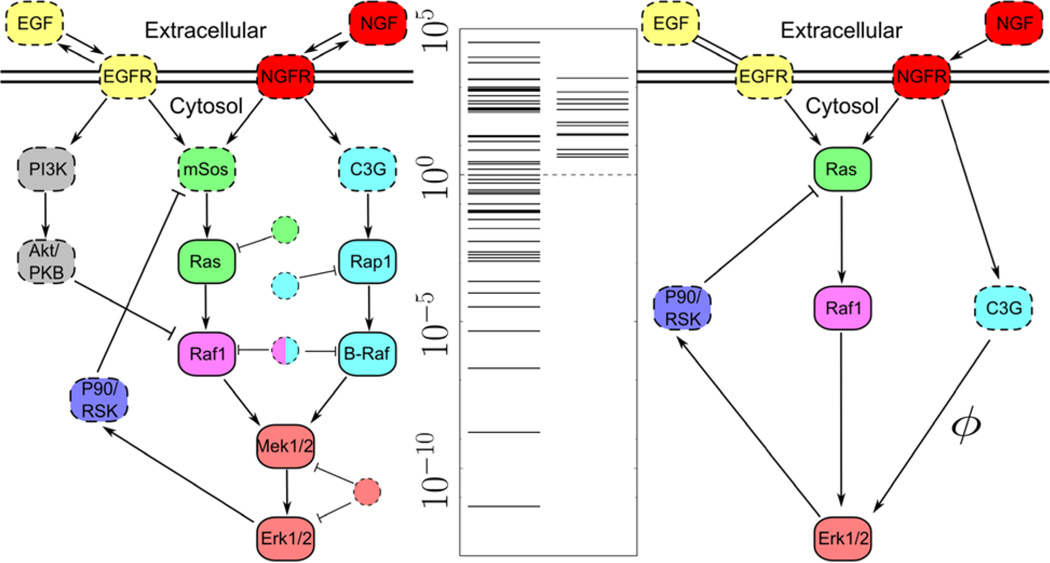
As a concrete example, we consider a model of biological signaling by the epidermal growth factor receptor (EGFR) summarized in Fig. 3 [32,33]. This model is formulated as a dynamical system, consisting of 15 independent differential equation and 48 parameters describing the kinetics of several biochemical reactions, which can be fit by least squares to experimental data [32,33]. However, most parameter combinations are irrelevant for explaining model behavior, and parameter estimation leads to huge uncertainties in the inferred parameter values, a phenomenon known as sloppiness. Sloppiness has been observed in models of systems biology [32–34], insect flight [35], interatomic potentials [36], particle accelerators [37], and critical phenomena [17]. Ideally, one would like to remove the irrelevant parameters so that the parameters in the reduced model can be estimated and given a physical interpretation. The aforementioned techniques, however, cannot be applied to this nor to many other sloppy models.

FIG. 3.

Original and reduced EGFR models. The interactions of the EGFR signaling pathway [32,33] are summarized in the leftmost network. Solid circles are chemical species for which the experimental data were available to fit. Manifold boundaries reduce the model to a form (right) capable of fitting the same data and making the same predictions as in Refs. [32,33]. The FIM eigenvalues (center) indicate that the simplified model has removed the irrelevant parameters identified as eigenvalues less than 1 (dotted line) while retaining the original model’s predictive power.

There are several challenges to systematically simplifying complex models. First, it is often parameter combinations rather than individual parameters to which the model is insensitive. Typically, a model is sensitive to all parameters individually and the insensitivity only arises because of their compensatory nature. The relevant parameter combination can be a nonlinear combination of individual parameters. Consequently, the relevant combination often depends strongly on the parameter values, which are in turn very sensitive to noisy data. Even if irrelevant combinations could be identified, systematically removing the combination from the model is not straightforward—simply fixing a parameter combination does not really make the model conceptually simpler.

To overcome these challenges, we use an information theoretical approach, applicable to diverse classes of models. Consider an arbitrary probabilistic model P(ξ|θ) for observing a vector of random variables ξ given a parameter vector θ. The range of physically allowed parameter values describe a family of related models. We seek a reduced model with fewer parameters that can approximate the full family described by the original. We anticipate such a reduction to exist for models with more parameters than “effective degrees of freedom” in their observations, a condition to be made more precise shortly. Qualitatively, we understand such models have more complexity in their description than in their predictions, which leads to large uncertainties in inferred parameter values.

The insensitivity of model predictions to changes in parameters is measured locally by an eigenvalue decomposition of the Fisher information matrix (FIM), g_μν = −〈(∂² log P)/(∂θ_μ∂θ_ν)〉, where 〈·〉 means the expectation value. Sloppy models have eigenvalues exponentially distributed over many orders of magnitude, quantifying an extreme insensitivity to coordinated changes in the microscopic parameters and indicating a novel collective behavior that is largely independent of the underlying, microscopic physics [17].

We now employ a parameter-independent, geometric interpretation [14,38–40]. The FIM acts as a Riemannian metric on the space of probability distributions, so that the family described above is equivalent to a manifold of potential models. When a model has many more parameters than effective degrees of freedom in its emergent behavior, the manifold is bounded with a hierarchy of widths, qualitatively described as a hyper-ribbon [14,40]. Indeed, the widths of this hyper-ribbon are a measure of the number of effective degrees of freedom in the model. If the narrowest widths are sufficiently small, then it can be accurately approximated by a low-dimensional, reduced model, analogous to approximating a long, narrow ribbon by either a two-dimensional surface or a one-dimensional curve.

In this Letter we use the boundaries of the model manifold itself as approximations, which we refer to as the manifold boundary approximation method (MBAM). Given a statistical model P(ξ|θ) and set of parameters θ, we first calculate the FIM and identify the eigendirection with smallest eigenvalue, i.e., the least relevant parameter combination. Second, we numerically construct a geodesic from the initial parameters in this irrelevant direction until a boundary is identified as described in Refs. [14,40] and in the Supplemental Material [41]. Third, having found the boundary numerically, we identify it with a limiting approximation in the mathematical form of the model. Evaluating this limit removes one parameter combination from the model. Fourth, the simplified model is calibrated by fitting its behavior to that of the original model. This process is repeated until the model is sufficiently simple.

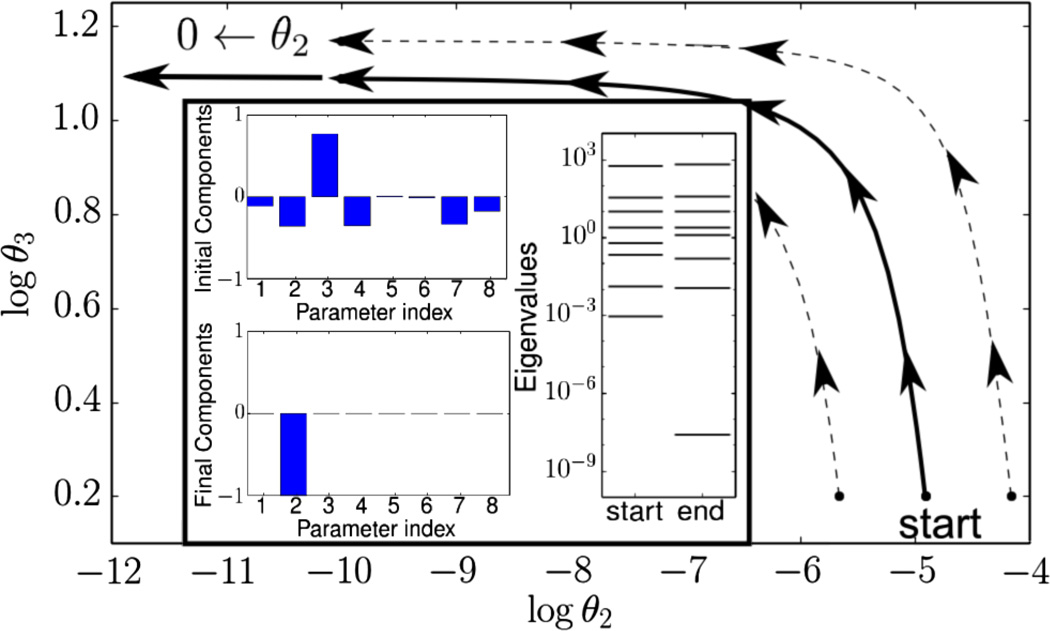
Consider an illustrative example: a model given by the sum of exponentials, $y(t,A,\lambda )={\sum }_{\mu }^N{A}_{\mu }\text{exp}(-{\lambda }_{\mu }t)$, with parameters θ = (A_μ, λ_μ) ≥ 0 and predictions at time points t_m, which are fit to data by least squares. This functional form appears in many contexts, such as radioactive decay, chemical kinetics, and statistical mechanics partition functions. Following the methods in Refs. [14,40], geodesics are calculated as paths through the parameter space as illustrated in Fig. 1. These paths are nonlinear and amenable only to numerical approximation. However, as the geodesic paths approach the boundary of the model manifold, they straighten out to reveal a well-defined, physically relevant limiting case.

FIG. 1.

Identifying the boundary limit. For the exponential model in the text with eight parameters, initially, the least sensitive parameter combination involves many parameters and is difficult to remove (inset, top left). By following a geodesic to the manifold boundary (solid line), the combination rotates to reveal a limiting behavior; here, only one parameter (an exponential rate) becomes zero (inset, bottom left). As the boundary is approached, one eigenvalue of the FIM approaches zero (inset, right). Once the smallest eigenvalue becomes well separated from the other eigenvalues, the limiting behavior becomes apparent. This limit is largely independent of the starting point; nearby parameter values all map to the same simplified model (dashed lines).

We identify the limiting case by monitoring the eigenvalues and eigenvectors of the FIM matrix along the geodesic path. Initially, the least sensitive combination involves nearly all of the individual parameters. As the boundary is approached, however, the smallest eigenvalue separates from the others and approaches zero. When it is well separated from the other eigenvalues, the components of that eigendirection have rotated to reveal the limit corresponding to the manifold boundary (θ₂ → 0 in Fig. 1). Physically, this limit is interpreted to mean the time scale of one exponential is slower than that of the experiment. Analytically evaluating this limit results in a new model with one less parameter and a slightly different functional form. Using this model as a starting point, the process is repeated until all of the irrelevant parameters have been removed, one at a time, as conceptually illustrated in Fig. 2.

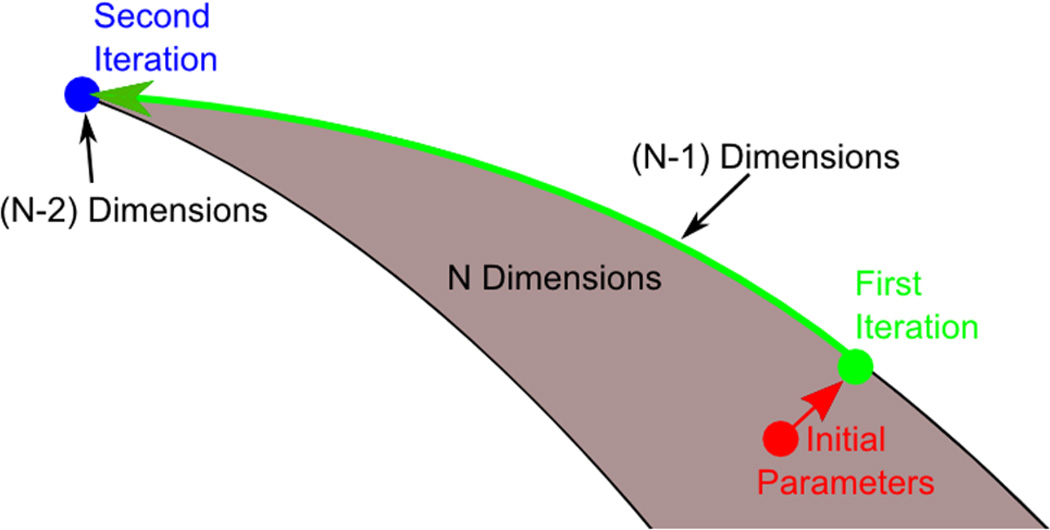
FIG. 2.

Approximating the manifold by its boundary. A high-dimensional, bounded manifold may be approximated by a low-dimensional manifold. Parameter degrees of freedom are systematically removed, one at a time, by approximating the full manifold by its boundary. After several approximations, the reduced model is represented by a hypercorner of the original manifold that preserves most of the original model’s behavior.

Iterating this process for the exponential example reveals that all boundaries of the model manifold correspond to physically simple limits. They include λ_μ → 0, so that Ae^−λt → A as we have seen. Additionally, λ_μ → ∞, so that Ae^−λt → 0 for t > 0, as well as A_μ, λ_μ → A_ν, λ_ν, so that two terms merge together. Repeated evaluation of these limits yields a reduced model of the form $ỹ(t,Ã,\tilde{\lambda },\tilde{B})={\sum }_{\mu }^{N\prime }{Ã}_{\mu }\text{exp}(-{\tilde{\lambda }}_{\mu }t)+\tilde{B}$, where N′ < N and we have denoted the reduced parameters with a tilde. The number of terms in the reduced model will depend on the time points t_m and the desired fidelity to the original model’s predictions.

Although the boundary is identified using a linear combination of parameters, evaluating the limit in the model can identify nonlinear combinations in the reduced model. For example, two parmeters may become infinite in such a way that only their ratio is retained in the final model. The combination depends on the functional form of the model so that the reduction is customized to the specific system (see examples in the Supplemental Material [41]). It appears to be a general feature that these limiting approximations have simple physical intepretations, such as well-separated time scales in the exponential model.

Because inferred parameters often have large uncertainties, knowing true parameters as a starting point for geodesics is often unrealistic. Large uncertainties imply that many different parameter values lead to the same model behavior, i.e., occupy a small region on the model manifold. This “compression” of large regions of parameter space into indistinguishable predictions is analogous to universal behavior in other systems, such as near critical points or phase transitions [17]. Model reduction reflects this property by compressing the parameter space along the geodesic into a few, relevant parameter combinations. Inspecting Fig. 1, all of the parameter values that lie along a geodesic path map to the same point on the boundary. Similarly, points on other nearby geodesic paths map to the same boundary but with slightly different parameter values. Thus, by construction, the large parameter uncertainties are compressed along the geodesic into the relevant parameters of the reduced model. Repeating the model reduction process with different initial parameter values but with similar model predictions therefore leads to the same reduced model. We explicitly check this argument with the models considered here for several initial parameter values with statistically equivalent behaviors. We find the final reduced model is indeed robust to the starting point.

We now return to the complicated EGFR model. This model already employs the most “obvious” approximations, using Michaelis-Menten reactions and ignoring spatial variations in concentrations and flucutations in particle number. That is, the model already employs quasi-steady state approximations, mean-field approximations, and a type of thermodynamic limit. It also excludes many other details that a biological expert would consider irrelevant (a comprehensive model of the same system involves 322 chemical species and 211 reactions [43]). In spite of these approximations, most of the parameters in the model remain irrelevant when fit to data, as illustrated by the FIM eigenvalues in Fig. 3, but it is not immediately clear what else can be removed.

Applying the MBAM further simplifies the model from 48 to 12 parameters and from 15 to 6 independent differential equations as summarized in Fig. 3. These approximations are more diverse than those in the exponential model, reflecting the increased complexity and lack of symmetry of this system, but are nevertheless all amenable to analytic evaluation and physical interpretation. They include limits in which reactions equilibrate, turn off, saturate, or never saturate, as well as several singular limits. They also include more subtle limits in which reaction rates become small while their downstream effects become large in a balanced way. The FIM eigenvalues reveal that the simplifications have removed the irrelevant parameters while retaining the predictive flexibility of the original model. Indeed, the lack of small eigenvalues indicates that all of the parameters can be connected to some aspect of the system’s emergent behavior, as we discuss below.

As a final example, we consider a Boltzmann distribution of a one-dimensional (for simplicity) chain of Ising spins. This model typically is written as a Hamiltonian (H = −J∑_μs_μs_μ+1 − h∑_μs_μ) with two parameters (J and h). These parameters are the relevant combinations under a RG coarsening and therefore describe the emergent physics. However, they are a poor model of the microscopic correlations among the spins s_μ. We therefore generalize this model as H = −∑_μJ_μs_μs_μ+1 to reflect a more flexible microscopic formulation.

The manifold boundaries of this model are given by J_μ → ±∞ (see Supplemental Material [41]). These limits are again both physically intuitive and simple to evaluate, corresponding to the scenario of either perfectively correlated or anticorrelated nearest neighbor spins (ferromagnetic or antiferromagnetic order, respectively). These limits remove a spin degree of freedom from the model and couple next-nearest neighbors with an effective interaction. Removing all of the odd spins corresponds to predictions on long length scales and can be accurately described by the effective Hamiltonian of the form $H_{\text{eff}}=-{\sum }_{\mu }^{N/2}{\tilde{J}}_{2\mu }{s}_{2\mu }{s}_{2\mu +2}$. This model corresponds to a hypercorner of the original manifold in which half of the coupling constants become infinite, and is equivalent to a single iteration of a block-spin renormalization procedure. This basic result generalizes to arbitrary dimension (allowing us to recover the typical criticality described by RG in higher dimensions). Similar results also hold for alternate microscopic versions of the model. For example, a microscopic Hamiltonian given by H = −∑_μαJ_αs_μs_μ+α yields simplifying limits that remove the high-frequency spin configurations as in the momentum-space RG. Unlike RG, however, the MBAM is not limited to systems with self-similar behavior.

The connection to the renormalization group provides a motivation for interpreting reduced models generally. RG makes systematic the removal of short distance degrees of freedom within the context of field theories and solidifies the concept of effective field theories. Similarly, the MBAM is a technique for constructing effective models in more general contexts. Returning to the EGFR model, we see that the simplified model treats C3G as directly influencing Erk concentration. This interaction is not direct in the reductionist sense, but is mediated by a chain of reactions (C3G → Rap1 → BRaf → Mek → Erk) described by eight parameters. However, the simplified model has a single “renormalized” parameter describing the effective interaction. We can trace the macroscopic parameter ϕ back to its microscopic origin through the limiting approximations

$$\varphi =\frac{(k_{\text{Rap}1\text{To}\mathrm{B}\text{Raf}})(K_{\mathrm{m}\mathrm{d}\mathrm{B}\text{Raf}})(k_{\mathrm{p}\mathrm{B}\text{Raf}})(K_{\mathrm{m}\mathrm{d}\text{Mek}})}{(k_{\mathrm{d}\mathrm{B}\text{Raf}})(K_{\mathrm{m}\text{Rap}1\text{To}\mathrm{B}\text{Raf}})(k_{\mathrm{d}\text{Mek}})}.$$ (1)

Notice that ϕ condenses the many microscopic parameters into a single relevant, nonlinear combination. Each microscopic parameter can be important to the system’s emergent behavior, but only through its effect on ϕ. The simplified model, therefore, contains real biological insights and Eq. (1) serves as the basis for understanding and predicting the functional effects of microscopic perturbations, such as mutations or drug therapies, on the system’s macroscopic behavior.

The MBAM method is different from other reduction techniques in its aim to remove parameters rather than physical degrees of freedom. These are not unrelated since parameters generally codify the relationship among physical degrees of freedom. There are three advantages to this abstraction. First, it allows simplification of relationships among physical degrees of freedom even if they cannot themselves be removed, e.g., removing edges from the network in Fig. 3. Second, it allows the use of information geometry as a unified language for exploring model families regardless of the actual physics. Finally, approximations among physical degrees of freedom can usually be interpreted as a limiting case of a parameter, so there is no loss in generality. Consequently, most simplifying approximations that are specific to a particular model class are naturally subsumed as special cases, as we have already seen for the renormalization group. Similarly, we can recover in other instances mean-field approximations, steady-state approximations, continuum limits, thermodynamic limits, etc. The MBAM is therefore not only an alternative method of model reduction, but a unifying and generalizing principle of which many existing methods are special cases.

There are three conditions that a statistical model must satisfy for this method to be applicable. First, it must be a parametric model with a FIM. Second, we require that the model be sloppy. Models that are not sloppy will not have a thin manifold and cannot be easily approximated. This essentially restricts the information content of the model predictions; i.e., models must have fewer effective degrees of freedom in the predictions than the parameters. Third, it is necessary that the model manifold be bounded with a hierarchy of boundaries. For example, the manifold for fitting time series on 0 < t < 1 to polynomials y(t) = ∑_μθ_μt^μ subject to the constraint ${\sum }_{\mu }{\theta }_{\mu }^2<1$ is an ellipsoid with a hierarchy of widths but without a hierarchy of edges; i.e., there are no corners.

Although we cannot give sufficient conditions for this hierarchical structure, there is considerable evidence that it is shared by many models. Complex models are often constructed by combining many simple physical principles. These physical principles typically have limiting cases: chemical reactions saturate, equilibrate, or turn off; magnetic moments correlate or anticorrelate; time scales separate; etc. Combining these principles into a complex model then leads naturally to the desired hierarchical structure. The general use of limiting approximations, which we now understand to be special cases of manifold boundaries, is strong evidence for the universality of this hierarchical structure. More broadly, physics is made up of a hierarchy of theories, many of which are understood as limiting cases of more microscopic theories, e.g., thermodynamics as a limit of statistical mechanics or Newtonian mechanics as a limit of quantum mechanics. The relationship between these microscopic or macroscopic theories is the same as that between the microscopic or macroscopic models we have considered here.

In this Letter we have used information geometry to understand how model behavior is compressed into a few effective degrees of freedom. We have seen that manifold boundaries correspond to limiting approximations that can be identified and evaluated to systematically remove irrelevant parameter combinations from complex models. This approach makes minimal assumptions and unifies many other existing model reduction techniques. It goes beyond available methods, however, and allows the simplification of more general models. As the tension between microscopic complexity and emergent simplicity is a central theme in most all of science, and complex systems research specifically, this approach will be useful for extracting effective models of emergent behavior in many fields and for understanding how microscopic details are compressed into macroscopic parameters.