More powerful genetic association testing via a new statistical framework for integrative genomics

Abstract

Integrative genomics offers a promising approach to more powerful genetic association studies. The hope is that combining outcome and genotype data with other types of genomic information can lead to more powerful SNP detection. We present a new association test based on a statistical model that explicitly assumes that genetic variations affect the outcome through perturbing gene expression levels. It is shown analytically that the proposed approach can have more power to detect SNPs that are associated with the outcome through transcriptional regulation, compared to tests using the outcome and genotype data alone, and simulations show that our method is relatively robust to misspecification. We also provide a strategy for applying our approach to high-dimensional genomic data. We use this strategy to identify a potentially new association between a SNP and a yeast cell’s response to the natural product tomatidine, which standard association analysis did not detect.

1 Introduction

Missing heritability is a major issue in genetic association studies and refers to the fact that for many traits, only a small proportion of their variance in the population can be explained by the genetic variants identified so far (Manolio et al., 2009; Visscher and Montgomery, 2009; Bansal et al., 2010). There are many possible causes, but recent experimental work by Bloom et al. (2013) suggests that missing additive heritability may arise partly because there is insufficient statistical power to detect SNPs with small but nonzero effects.

Our interest in this problem was motivated by a study of the genetic basis of drug response. One major goal of personalized medicine is to target treatments to those patients who will see the greatest benefits. To begin to understand the mechanisms of patient-specific drug response, Perlstein et al. (2007) collected expression and genotype data on yeast segregants before exposing them to a variety of small molecules. Using standard methods they identified several genetic variants responsible for segregant-specific responses to some of the drugs, but noted that identifying additional functional polymorphisms was a major area of future interest. We were interested in incorporating the expression information into association testing in order to detect variants associated with yeast cell drug response that were missed by standard analyses.

Integrative genomics, this joint analysis of outcome and genotype data with additional types of genomic information, offers a promising general approach to more powerful association studies (Chen et al., 2008; Emilsson et al., 2008). Most existing integration methods use the additional information to filter the SNPs, for example by removing SNPs that are not significantly associated with outcome-associated genes. The power gain then comes from the reduced multiple testing burden (Ware et al., 2013). While sensible, the statistical properties of this approach are unclear because it requires a number of ad-hoc decisions, such as the thresholds for deciding which genes are associated with the outcome and with SNPs. Furthermore, it is unclear how to control for multiple comparisons or false discovery rates when the filtering steps are performed on the same set of samples.

In this paper we propose a new method for integrating expression data into genetic association studies. Intuitively, expression data should provide more information about SNPs that are associated with the outcome by regulating the transcription of outcome-associated genes. We indeed show that compared to standard non-integrative methods, our approach can have increased power to detect just these SNPs, which we will refer to as outcome-associated expression SNPs, or o-eSNPs. Furthermore, we use standard estimating equation theory to provide a valid inferential procedure. When a particular set of genes is of interest, our method can be applied to detect o-eSNPs that are associated with the outcome through genes in that set. For a more unbiased discovery procedure, our method can also be applied genome-wide by considering one gene at a time, where to reduce the multiple testing burden imposed by the huge number of pairwise tests we can restrict ourselves to testing only those SNPs located cis to each gene.

In Section 2 we specify our procedure, discuss its assumptions, describe its estimation and inference, and present strategies for analyzing high-dimensional genomic data, where the number of genes may exceed the sample size. In Section 3 we explain why our method can have more power to detect o-eSNPs. In simulations in Section 4, we explore its performance under model misspecification, in Section 5 we apply our method to the yeast drug response experiment of Perlstein et al. (2007), and the paper ends with a discussion in Section 6.

2 Integrative analysis

2.1 Method

For the i^th subject, i = 1, …, n, let Y_i be the outcome of interest, G_ij, j = 1, …, p be the expression of the j^th transcript, and X_il, l = 1, …, r be additional non-genomic covariates, such as clinical or environmental measurements or principal components derived from the genotype data, to control for population stratification (Price et al., 2006). Also let G_i = (G_i1, …, G_ip)^T and X_i = (X_i1, …, X_ir)^T.

We focus on testing the association between the outcome and a set of SNPs S_ik, k ∈ 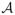, where S_ik is the number of minor alleles at the k^th SNP and we assume that | 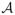|< n. Letting | 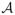| = 1 corresponds to testing one SNP at a time, which is standard practice in genome-wide association studies. We also allow | 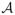| > 1 in order to test sets of SNP, such as those located near the same transcript or belonging to the same pathway. Letting S_i = (S_ik, k ∈ 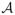)^T, we posit that in general the relationship between Y_i, G_i, X_i, and S_i can be modeled as

$$g\{\mathrm{E}(Y_i\mid {\mathbf{G}}_i,{\mathbf{S}}_i,{\mathbf{X}}_i)\}={\alpha }_{\mathit{int}}+{\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X+{\mathbf{S}}_i^T{\mathit{\alpha }}_S+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i+{\mathbf{S}}_i^T{\mathbf{A}}_{SX}{\mathbf{X}}_i,$$ (1)

$${\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i={\beta }_{\mathit{int}}+{\mathbf{S}}_i^T{\mathit{\beta }}_S+{\mathbf{X}}_i^T{\mathit{\beta }}_X+{\mathbf{S}}_i^T{\mathbf{B}}_{SX}{\mathbf{X}}_i+{\mathbf{X}}_i^T{\mathbf{B}}_{XX}{\mathbf{X}}_i+{\epsilon }_i,$$ (2)

where g is a link function and ε_i is a random error term.

The outcome model (1) describes the effect of G_i and X_i on Y_i, where α_G, α_X and α_S are the regression coefficients of the main effects of transcript expressions, covariates and SNPs, and A_GX and A_SX represent the effects of interactions. The transcript model (2) describes the regulation of G_i by S_i and X_i, where β_S and β_X are the regression coefficients of the main effects of the SNPs and covariates and B_SX and B_XX represent interaction effects. Since G_i may depend on both S_i and X_i, including the ${\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i$ term in (1) requires including the ${\mathbf{X}}_i^T{\mathbf{B}}_{XX}{\mathbf{X}}_i$ term in (2). For example, if G_i = γ_int +Γ_SS_i + Γ_XX_i + ε_i, then A_GX ≠ 0 implies that B_XX ≠ 0. The proposed models are quite general by specifying gene-and SNP-environment interactions, but additional terms, such as gene-gene interactions, could also be added, or the interaction terms could be dropped to reduce the number of parameters.

We propose the following procedure to test the association between S_i and Y_i:

1. Estimate α̂_G and Â_GX by fitting (1) under the assumptions that α_S = 0 and A_SX = 0.

2. Use these estimates in (2) to estimate β̂_S and B̂_SX.

3. Use a Wald test based on these estimates to test β̂_S = 0 and B_SX = 0.

Under the null hypothesis of no association, α_S, A_SX, β_S, and B_SX are all zero, so our procedure gives a valid test for association between S_i and Y_i. We are interested in the particular alternative that S_i is associated with Y_i through regulation of the expression of G_i (S_i are o-eSNPs). In this case, β_S is nonzero and B_SX may be as well. If we had measurements on gene methylation, we could also similarly include these measurements in models (1) and (2) to identify SNPs that affect Y_i through methylation.

Our framework is similar to a mediation analysis model (Baron and Kenny, 1986; Hayes, 2009; VanderWeele and Vansteelandt, 2010), with two major differences. First, in contrast to mediation analysis, we are not interested in assigning causal interpretations to any of our parameters, and instead are concerned solely with increasing the power of association testing. Second, to our knowledge our approach is novel in its use of unknown parameters in the outcome of the transcript model (2) to reduce p transcript expression levels to a scalar summary. Most mediation models only consider a single mediator, and those that allow more than one require estimating the indirect effect of S_ik on each transcript separately (Preacher and Hayes, 2008; VanderWeele and Vansteelandt, 2014). Models used in the analysis of expression quantitative trait loci (Brem et al., 2002; Morley et al., 2004; Cai et al., 2013) also study the effect of genotype on every measured transcript. Our approach is instead only concerned with a particular scalar function of the transcripts. It requires estimating fewer parameters, and does not require modeling the individual transcript-SNP associations.

2.2 Assumptions

The good performance of our procedure requires two assumptions. First, there can be no unmeasured covariates that confound either the effect of the SNPs on the outcome, or the effect of the transcripts on the outcome. This is in contrast to standard analysis, which only requires adjusting for confounders of the SNP-outcome association. We study violations of this assumption in Example 4 of Section 4, where we find that at least in our simulation settings, the type I error is still maintained and in some cases our integrative analysis still has improved power compared to standard analysis.

Second, our method works best when there is no direct effect of the SNPs on the outcome, such that the SNPs act only through regulating gene expression. Indeed, Kenny and Judd (2014) recently noted that in the absence of a direct effect, testing the indirect effect in a mediation analysis can be dramatically more powerful than testing the total effect. They considered a single mediator in a simulation study and gave a heuristic explanation of the phenomenon. In Section 3 we show analytically, for multiple mediators, that our test can be more powerful than standard analysis. Furthermore, even when a direct effect exists (α_S ≠ 0), we show in Example 2 of Section 4 and Web Appendix A that our test can sometimes still have increased power.

2.3 Estimation and inference

Let θ = (α_int, α_G, α_X, A_GX) and τ = (β_int, β_S, β_X, B_SX, B_XX) be vectors of the unknown parameters, let θ̂ and τ̂ denote their estimates, and let μ_i(θ) and η_i(τ) be the mean functions of (1) and (2), respectively. When the dimensions of G_i and X_i are small enough, we can simultaneously fit models (1) and (2) by solving the estimating equation

$${\mathbf{U}}_n(\mathit{\theta },\mathit{\tau })=\frac{1}{n}\sum _i{\mathbf{u}}_i(\mathit{\theta },\mathit{\tau })=\left[\begin{array}{l}\frac{1}{n}{\sum }_i\frac{\partial g^{-1}({\mathit{\mu }}_i)}{\partial \mathit{\theta }}\{Y_i-g^{-1}({\mathit{\mu }}_i)\}\hfill \\ \frac{1}{n}{\sum }_i\frac{\partial {\mathit{\eta }}_i}{\partial \mathit{\tau }}({\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i-{\mathit{\eta }}_i)\hfill \end{array}\right]=\mathbf{0}.$$

Step 1 of our procedure obtains θ̂ and Step 2 obtains τ̂, and it is easy to see that U_n(θ̂, τ̂) = 0. Standard generalized estimating equation theory (Diggle et al., 2013) then gives that

$$\sqrt{n}\{{(\widehat{\mathit{\theta }},\widehat{\mathit{\tau }})}^T-{(\mathit{\theta },\mathit{\tau })}^T\}\to N\{\mathbf{0},\mathbf{J}{(\mathit{\theta },\mathit{\tau })}^{-1}\mathbf{V}(\mathit{\theta },\mathit{\tau })\mathbf{J}{(\mathit{\theta },\mathit{\tau })}^{-1}\},$$

where ∂U_n/∂(θ, τ) → J(θ, τ) and $\sqrt{n}{\mathbf{U}}_n(\mathit{\theta },\mathit{\tau })\to N\{\mathbf{0},\mathbf{V}(\mathit{\theta },\mathit{\tau })\}$, and we use this distribution to implement the Wald test in Step 3 of our procedure. The Jacobian J can be estimated by evaluating ∂U_n=∂(θ, τ) at θ̂ and τ̂ and V(θ, τ) can be estimated by the sample covariance matrix of the u_i(θ̂, τ̂).

It is worth considering the special case of case-control sampling, which is common in genome-wide association studies of binary outcomes Y_i. In this setting, fitting a logistic regression in the outcome model will still give valid estimates and inference (Prentice and Pyke, 1979), but we must modify the estimating equations for the transcript model. We adopt the weighting method of Monsees et al. (2009): if P is the prevalence of the outcome, n₁ is the number of cases, n₀ is the number of controls, and n = n₁ + n₀, we solve

$${\mathbf{U}}_n(\mathit{\theta },\mathit{\tau })=\left[\begin{array}{l}\frac{1}{n}{\sum }_i\frac{\partial g^{-1}({\mathit{\mu }}_i)}{\partial \mathit{\theta }}\{Y_i-g^{-1}({\mathit{\mu }}_i)\}\hfill \\ \frac{P}{n_1}{\sum }_{i:Y_i=1}\frac{\partial {\mathit{\eta }}_i}{\partial \mathit{\tau }}({\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i-{\mathit{\eta }}_i)+\hfill \\ \frac{1-P}{n_0}{\sum }_{i:Y_i=0}\frac{\partial {\mathit{\eta }}_i}{\partial \mathit{\tau }}({\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i-{\mathit{\eta }}_i)\hfill \end{array}\right]=\mathbf{0},$$

where here g⁻¹(x) = 1=(1 + e^−x) is the canonical link function for logistic regression. One disadvantage of this approach is that we must have a priori knowledge of the prevalence P, but good estimates are available for many well-studied diseases. Another disadvantage is that this probability weighting method can give parameter estimates with relative large variances (Monsees et al., 2009). We may be able to improve our results by using secondary phenotype analysis methods proposed by Lin and Zeng (2009) and He et al. (2012).

2.4 Strategies for high dimensional data

In most genomic applications the number of transcripts exceeds the sample size, so the estimating equations do not have a unique solution. This high-dimensional transcript issue is unique to our method and is a not a problem for non-integrative analyses. If the mechanism underlying the outcome is known to proceed via a certain pathway, or a certain pathway is of particular interest, one approach is to perform integrative analysis using only the transcripts in the pathway. We refer to this as the pathway approach.

On the other hand, we may want a more unbiased o-eSNP detection procedure. An alternative approach to reducing dimensionality is to fit our integrative model one transcript at a time. This type of marginal analysis is popular in gene expression profiling experiments. We refer to this as the pairwise approach, because it quantifies the association between the outcome and each transcript-SNP or transcript-SNP set pair. Because of the complicated dependencies between these tests, we adjust for multiple comparisons using the Bonferroni correction. However, this may be too conservative, especially when we conduct all possible pairwise tests. One way to reduce the number of tests is to consider only pairs that are in cis. This is sensible because cis-SNPs are likely to function by regulating transcription and so are exactly the type of SNPs our method is designed to detect.

In general, the two assumptions discussed in Section 2.2 that are required by our integrative method may not hold when using these high-dimensional approaches. First, it is likely that some confounders of the transcript-outcome association have not been accounted for, because there are probably many genes that affect both the outcome and the genes in the model, but which themselves have not been included in the model. In addition, it is likely that there are direct effects between the SNP or SNP set and the outcome, for example through the confounding genes. However, in simulations and in Web Appendix A we show that our method can still perform well. In particular, we study the performance of the pairwise approach in simulations in Example 6 of Section 4.

3 More powerful o-eSNP detection

We show analytically that our procedure can have more power than standard analysis for detecting o-eSNPs. For simplicity we consider a single SNP, no other covariates, and scalar continuous Y_i under the ordinary linear model, though similar calculations can be performed for generalized linear models. We also assume that Y_i, G_i, and S_i have been centered to mean zero, so that the intercept terms disappear. Finally, we let α_S = 0 and A_SX = 0, so model (1) becomes $Y_i={\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\epsilon }_{i1}$ and model (2) becomes ${\mathbf{G}}_i^T{\mathit{\alpha }}_G={\beta }_S{S}_i+{\epsilon }_{i2}$, where ${\epsilon }_{i1}~N(0,{\sigma }_1^2)$ and ${\epsilon }_{i2}~N(0,{\sigma }_2^2)$ are independent of G_i, S_i, and each other. We compare our integrative analysis to the usual approach of directly regressing Y_i on S_i according to $Y_i={\beta }_S^{\ast }{S}_i+N(0,{\sigma }^{\ast 2})$. If our integrative model is true, ${\beta }_S^{\ast }={\beta }_S,{\sigma }^{\ast 2}={\sigma }_1^2+{\sigma }^2$, and the null hypothesis of no association between S_i and Y_i is equivalent to β_S = 0 in the integrative model and ${\beta }_S^{\ast }=0$ in the usual linear model.

Let β̂_S be the estimate of β_S from our integrative analysis, and let ${\widehat{\beta }}_S^{\ast }$ be the estimate of ${\beta }_S^{\ast }$ obtained from linear regression. Since both estimates are asymptotically unbiased and normal, to show that the integrative method has greater power we must show that $var({\widehat{\beta }}_S)<var({\widehat{\beta }}_S^{\ast })$. It is easy to see that $var({\widehat{\beta }}_S^{\ast })=({\sigma }_1^2+{\sigma }_2^2)/var(S_i)$. Next let G = (G₁, …, G_n)^T and S = (S₁, …, S_n)^T. Then

$$\begin{array}{l}\sqrt{n}({\widehat{\beta }}_S-{\beta }_S)=\sqrt{n}{({\mathbf{S}}^T\mathbf{S})}^{-1}{\mathbf{S}}^T(\mathbf{G}{\widehat{\mathit{\alpha }}}_G-\mathbf{S}{\beta }_S)\\ =\sqrt{n}{({\mathbf{S}}^T\mathbf{S})}^{-1}{\mathbf{S}}^T(\mathbf{G}{\mathit{\alpha }}_G-\mathbf{S}{\beta }_S)+{({\mathbf{S}}^T\mathbf{S})}^{-1}{\mathbf{S}}^T\mathbf{G}({\widehat{\mathit{\alpha }}}_G-{\mathit{\alpha }}_G)\sqrt{n}\\ \to N\{\mathbf{0},{\sigma }_2^2/var(S_i)\}+var{(S_i)}^{-1}{\mathbf{\sum }}_{SG}N\{0,{\sigma }_1^2{\mathbf{\sum }}_{GG}^{-1}\},\end{array}$$

where α̂_S is the estimate of α_S from fitting the outcome model, Σ_SG = E(S^TG), and Σ_GG = E(G^TG). Since the two normal distributions in the last line are independent,

$$var({\widehat{\beta }}_S)={\sigma }_2^2/var(S_i)+{\sigma }_1^2{\mathbf{\sum }}_{SG}{\mathbf{\sum }}_{GG}^{-1}{\mathbf{\sum }}_{GS}/var{(S_i)}^2,$$

where Σ_GS = E(G^TS), so $var({\widehat{\beta }}_S)<var({\widehat{\beta }}_S^{\ast })$ when ${\mathbf{\sum }}_{SG}{\mathbf{\sum }}_{GG}^{-1}{\mathbf{\sum }}_{GS}/var(S_i)<1$. For example, when the genes are independent this condition reduces to ${\sum }_{j=1}^p\text{cor}{(S_i,G_{ij})}^2<1$.

In other words, we gain the most power if the G_i are weakly correlated with S_i. This is sensible, because otherwise the expression data would add little additional information. In the extreme case where they are perfectly correlated, our integrative analysis would be no different from a standard analysis. On the other hand, while the integrative approach has more relative power for weak correlations, its absolute power can be low if the correlations are too low, as in the extreme case where cor (S_i, G_ij) = 0 we also have β_S = 0. In the ideal setting, the correlations are weak but β_S is still large, which is only possible when G_i is highly associated with Y_i so that α_G is large.

So far we have assumed that the SNP functions entirely through regulating gene expression. In Web Appendix A we show that our procedure can sometimes also have greater power than standard analysis for detecting SNPs that also function through non-regulatory mechanisms. One reviewer raised the question of whether accounting for these direct effects might improve the power of our integrative approach. We also analytically and numerically compare two such methods. One turns out to have the same power as standard analysis. The other can be more powerful than our procedure for o-eSNPs with large direct effects but is always worse for detecting those without direct effects.

4 Model misspecification and simulations

4.1 Types of misspecification

Our integrative approach requires us to model the relationship between expression and genotype and expression and the outcome. This is contrast to standard analysis methods, which only require specifying the outcome-genotype relationship. Here we study different model specifications in six simulated examples.

Briefly, we constructed Example 1 so that both the integrative and the standard models were correctly specified. We constructed Examples 2 through 4 so that only the standard analysis model remained valid. Specifically, Example 2 allowed a direct effect of a SNP on the outcome not mediated through transcriptional regulation, Example 3 allowed for measurement error in the gene expression measurements, and Example 4 omitted some important genes from the integrative analysis and included unimportant ones. Examples 2 and 4 illustrate the consequences of violating the assumptions required by our method, discussed in Section 2.2. In Example 5 we misspecified both the integrative and standard models by allowing interaction terms, and in Example 6 we considered high-dimensional SNPs and genes. Details are given below.

4.2 Analysis methods

For all data generating mechanisms, when the number of genes p was small we implement our integrative procedure using the linear univariate integrative model

$$\begin{array}{ll}\hfill g\{\mathrm{E}(Y_i\mid {\mathbf{G}}_i,S_i,{\mathbf{X}}_i)\}& ={\alpha }_{\mathit{int}}+{\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X,\\ \hfill {\mathbf{G}}_i^T{\mathit{\alpha }}_G& ={\beta }_{\mathit{int}}+{\beta }_S{S}_i+{\mathbf{X}}_i^T{\mathit{\beta }}_X+{\epsilon }_i\end{array}$$

for each of the q SNPs. When p > n we used this model in the pairwise fashion discussed in Section 2.4. We compared to the standard marginal generalized linear model

$$g\{\mathrm{E}(Y_i\mid S_i,{\mathbf{X}}_i)\}={\beta }_{\mathit{int}}^{\ast }+{\beta }_S^{\ast }{S}_i+{\mathbf{X}}_i^T{\mathit{\beta }}_X^{\ast },$$

specifically the linear model for continuous Y_i and the logistic model for binary Y_i.

As a comparison, we also considered what we refer to as the overlap method: we first identified genes associated with the outcome, and then for each SNP we identified genes associated with that SNP. In both cases we set the significance threshold using false discovery rate control (Benjamini and Hochberg, 1995) at the 5% level. We assessed the significance of each SNP by calculating the p-value for the overlap between the two gene sets using Fisher’s exact test. To calculate the gene-SNP associations under case-control sampling we used the weighting scheme described in Section 2.3. Similar overlap procedures have been proposed in other integrative genomics applications (He et al., 2013).

4.3 Simulation settings

For each setting we generated continuous Y_i according to Y_i = m_i(θ) + ε_i for some mean function m_i(θ), where ε_i ~ N (0, 4). We generated binary Y_i according to logit P(Y₁ = 1 | G_i, S_i, X_i) = −α_int + m_i(θ), where α_int was such that marginal prevalence was around 31%. In Examples 1–5 we generated n = 200 samples for the continuous outcome and n₁ = 100 cases and n₀ = 100 controls for the binary outcome, and we doubled these in Example 6. We studied the power and type I error of the the integrative, standard, and overlap analysis methods mentioned above, averaged over 250 simulations.

Example 1

We independently generated 100 SNPs under Hardy-Weinberg equilibrium using additive coding (0, 1, or 2), with minor allele frequencies of 10%, and r = 2 clinical covariates from standard normals. We then generated p = 10 transcripts according to ${\mathbf{G}}_i={\mathbf{S}}_i^T{\mathbf{\Gamma }}_S+{\mathbf{X}}_i^T{\mathbf{\Gamma }}_X+{\mathit{\epsilon }}_i$, where Γ_S and Γ_X were 100 × p and r × p coefficient matrices, respectively, and ε_i ~ N (0, 4Σ). We set Σ equal to the sample correlation matrix of 10 observations drawn from a p-dimensional standard normal with independent components. We independently set each entry of Γ_S and Γ_X to zero with probability 0.5 and generated the nonzero entries uniformly from [−1, 0.05] ∪ [0.05, 1]. We let $m_i(\mathit{\theta })={\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X$ and α_int = −3. We independently generated the components of α_G uniformly between [−0.7, −0.05] ∪ [0.05, 0.7], and the components of α_X from a standard normal. Finally we generated a single additional SNP, for a total of q = 101, to be unassociated with Y_i, by adding a row to Γ_S that was drawn from a standard normal and then made orthogonal to α_G.

Example 2

We followed Example 1 but let $m_i(\mathit{\theta })={\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X+{\mathbf{S}}_i^T{\mathit{\alpha }}_S$ and α_int = −5.8. We let each entry of α_S have magnitude 0.75 and the same sign as the corresponding entry of β_S =Γ_Sα_G, so that the total effect of each SNP was always stronger than its indirect effect through the transcripts.

Example 3

We followed Example 1 but assumed that instead of observing G_i we only observed G_i + ε_i, where the measurement error ε_i was a p-dimensional mean-zero normal with a covariance matrix whose jk^th entry equaled 2 · 0.5^|j−k|.

Example 4

We followed Example 1 but simulated 15 instead of 10 genes. We added rows to Γ_S and Γ_X to make them q × 15 and r × 15 coefficient matrices, respectively. We set the covariance matrix of the error term ε_i equal to 4 times the sample correlation matrix of 10 observations drawn from a 15-dimensional standard normal with independent components. We then replaced the upper 10 × 10 block of this covariance matrix by the Σ used in Example 1. We simulated the Y_i using the first 10 genes, as in Example 1, but in our analysis we used only the first 5 and the last 5 genes. In other words, we misspecified G_i with five false negatives and five false positives. Because the G_i were all correlated, this example simulates the presence of unmeasured confounders of the transcript-outcome association.

Example 5

We followed in Example 1 but let $m_i(\mathit{\theta })={\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X+{\mathbf{S}}_i^T{\mathit{\alpha }}_S+{\mathbf{G}}_i^T{\mathbf{A}}_{GS}{\mathbf{S}}_i+{\mathbf{G}}_i^T{\mathbf{A}}_{GX}{\mathbf{X}}_i+{\mathbf{S}}_i^T{\mathbf{A}}_{SX}{\mathbf{X}}_i$ and α_int = −4.3. To generate A_GS and A_SX we randomly set each entry to zero with 10% probability, and then sampled the nonzero entries uniformly from [−0.5, −0.05]∪[0.05, 0.5]. To generate A_GX we set entries to zero with 30% probability.

Example 6

We generated q = 10, 000 SNPs and two cis-genes for each SNP by multiplying the number of minor alleles by coefficients generated from standard normals, for a total of p = 20, 000 genes. To each gene we added normally distributed error terms such that the covariance between the j^th and k^th genes was 16 · 0.5^|j−k|. We generated X_i as in Example 1 and let $m_i(\mathit{\theta })={\mathbf{G}}_i^T{\mathit{\alpha }}_G+{\mathbf{X}}_i^T{\mathit{\alpha }}_X$ and α_int = 16. We randomly set each of the components of α_G to be zero with 99.9% probability, and we drew the nonzero entries uniformly from [−5, −1] ∪ [1, 5]. This resulted in 14 SNPs associated with Y_i. We independently generated the components of α_X from a standard normal. We applied our pairwise integrative analysis to each SNP and its cis genes. We used a Bonferroni adjustment to correct for multiple testing in both the integrative and standard analyses. We did not implement the overlap method because it requires regressing each of the 20,000 genes on each of the 10,000 SNPS, and would have been computationally cumbersome.

4.4 Results

Table 1 reports the type I errors of testing the SNP that was unassociated with Y_i. The integrative and standard analyses both maintained the type I error at the nominal 0.05 level, for all of the model misspecifications. The overlap method was extremely conservative.

Table 1.

Average type I errors at nominal 0.05 level. Integration: proposed method; Standard: standard univariate regression analysis; Overlap: overlap method.

Example	Linear			Binary
	Integrative	Standard	Overlap	Integrative	Standard	Overlap
1	0.040	0.052	0.000	0.052	0.040	0.000
2	0.036	0.028	0.000	0.036	0.060	0.000
3	0.040	0.052	0.000	0.040	0.040	0.000
4	0.056	0.044	0.000	0.032	0.032	0.004
5	0.060	0.056	0.000	0.036	0.028	0.000

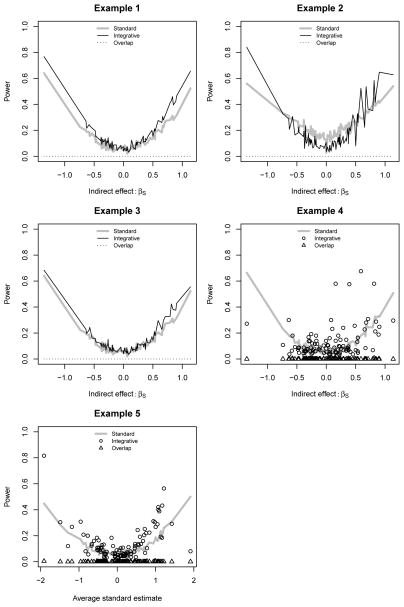
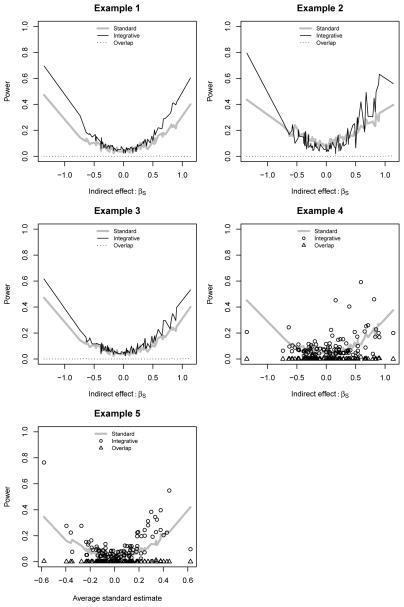
Figures 1 and 2 illustrate the average power curves for identifying the other 100 SNPs that we simulated to be associated with Y_i. In each example, the overlap procedure had almost no power to detect any of the SNPs. This was because the gene-SNP associations were usually too weak to detect, and when they were detected, the overlap between the outcome-associated and the SNP-associated genes was not significant because there were only 10 genes. The overlap method is thus more suitable for high-dimensional expression data, but was too computationally prohibitive to implement in Example 6. In the ideal setting of Example 1, integration indeed was more powerful than standard analysis.

Figure 1.

Average power curves for linear outcomes. Integration: proposed method; Standard: standard univariate regression analysis; Overlap: overlap method.

Figure 2.

Average power curves for binary outcomes. Integration: proposed method; Standard: standard univariate regression analysis; Overlap: overlap method.

Our method was not always preferable in Example 2, which included direct effects that our integrative model could not detect. When the magnitude of the direct effect exceeded the magnitude of the indirect effect, standard analysis had more power. However, when the β_S were large enough, our integrative procedure was still more effective. We discuss the consequences of direct effects in greater detail in Web Appendix A.

The effect of the measurement error in Example 3 was to reduce the power gain of integration over standard analysis. For example, with binary outcomes the power of integration to detect a SNP with β_S ≈ 1.5 decreased from 70% to 60%. However, this was still higher than the 40% power of the standard logistic regression of Y_i on S_i. There were no additional negative consequences of measurement error, most likely because we assumed a measurement error model that was linear in the true covariates G_i. In this case the error could be absorbed by the intercepts and the random error terms of the integrative outcome and transcript models, with reduced power as the only downside. Nonlinear measurement error could have more complicated effects, similar to those studied in Example 5.

It is more difficult to characterize the consequences of the misspecified gene set in Example 4. The effect of including genes not associated with the outcome is simply to increase the variance of the final estimate and to reduce power, but the effect of not including important genes obviously differs for different SNPs. For example, we lose power to detect SNPs associated with the outcome through the genes left out of the gene set. This is why in our pairwise approach we advocate testing multiple gene-SNP pairs for each SNP.

Both the integrative and standard analysis models were misspecified in Example 5 due to the omission of interaction terms. In fact the importance of each SNP is more difficult to quantify in this setting, since both the main effects and interaction terms need to be taken into account. For simplicity, in the X-axes of the power curves for Example 5 we ordered the SNPs by their average effect sizes as estimated using the standard analysis methods. Though standard analysis was more effective for a few SNPs, the preponderance of SNPs were still more easily detected by our integration.

For the pairwise analysis of the high-dimensional data in Example 6, Table 2 gives the true positive rates, defined as the proportion of the outcome-associated SNPs that were detected, the false discovery rates, defined as the proportion of the detected SNPs that were not associated with the outcome, and the total number of SNPs detected. We defined the false discovery rate to be zero when no SNPs were detected. Even with the Bonferroni adjustment over twice as many tests, pairwise integrative analysis had much higher power to detect outcome-associated SNPs, with much lower false discovery rates, than standard analysis.

Table 2.

SNP detection in high-dimensions (Example 6), after Bonferroni correction to give a family-wise error rate of 0.05. We simulated a total of 14 o-eSNPs. Integration: proposed method, 20,000 tests; Standard: standard univariate regression analysis, 10,000 tests. Performance metrics (SD): TP = true positive rate, FD = false discovery rate; Median size is reported (interquartile range).

Outcome	Method	TP	FD	Size
Continuous	Integration	34.86(7.77)	1.14(4.69)	5(2)
	Standard	1.2(2.97)	5.2(22.25)	0(0)
Binary	Integration	12.4(6.72)	0.13(2.11)	2(1)
	Standard	0.14(1)	0(0)	0(0)

5 Data analysis

We used our integrative analysis method to explore the genetic basis of drug resistance in yeast cells. Perlstein et al. (2007) measured expression levels of 6228 genes from 104 yeast genotyped segregants at baseline. They then treated the segregants with 94 different small molecules at different concentrations and for different amounts of time and recorded the segregant final yields. We focused on the natural product tomatidine, which has been found to have anticarcinogenic potential, as well as a variety of other health benefits (Friedman, 2013). Our goal was to detect o-eSNPs associated with response to tomatidine. We focused on the shortest time point (68 hours in 3.4M tomatidine), when we felt the effect of baseline gene expression on final yield would be the strongest.

We first imputed missing expression values using the averages of the values of the 10 nearest neighbors, using the BioConductor package impute, and then averaged observations with the same gene symbol. Next, following Lee et al. (2006) we identified 584 blocks of highly correlated markers, and within each block we selected a representative marker SNP with the lowest proportion of missing data.

Using final yield as the outcome, we applied our integrative analysis, using the pairwise approach, to all SNPs and their cis-genes. As discussed in Section 2.4, this approach is unlikely to satisfy the assumptions stated in Section 2.2, but simulations and Web Appendix A show that our approach can still perform well. Following Brem et al. (2002), we defined a SNP and a gene to be in cis if they are located within 10kb of each other, which resulted in 6,628 total pairs that included all 584 marker SNPs. There was a single pair that remained significant after Bonferroni correction for 6,628 tests (p-value cutoff of 7.5 · 10⁻⁶). This pair had a p-value of 3.3 · 10⁻⁶, was located on chromosome 8, consisted of the gene YHR005C (GPA1) and the SNP NHR001C, and suggests that NHR001C may affect the response to tomatidine by regulating the expression of GPA1, a G protein involved in the yeast mating pathway. In contrast, simply regressing final yield on NHR001C gave a p-value of 4.1 · 10⁻³, which would not pass a Bonferroni correction for 584 tests (p-value cutoff of 8.6 · 10⁻⁵). This potential o-eSNP would not have been discovered with standard analysis.

6 Discussion

We have proposed a new statistical framework for integrating outcome, gene expression and genotype data, and we showed analytically and in simulations that under certain conditions, integration can provide more powerful detection of outcome-associated expression SNPs (o-eSNPs). Using our approach, we discovered in yeast a potentially new association between response to tomatidine and the SNP NHR001C.

Our method requires that all confounders of both the SNP-outcome and the transcript-outcome associations be included in the regression models. It also works best if the associations between the SNPs and the outcome are entirely mediated through regulation of gene expression. Violations of the first assumption may result in low power or inflated type I error, while violations of the second can result in low power. However, simulation Examples 2 and 4, and our analytic work and further simulations in Web Appendix A, suggest that our approach can still be effective.

In Section 2.3 we describing fitting our approach using estimating equations composed of the sum of independent and identically distributed terms. However, some widely used models cannot be fit using such estimating equations. Chief among them is the Cox model for survival outcomes, whose estimating equation is a continuous-time martingale. Integrative analysis can still be performed using Cox regression as the outcome model, but more work is needed to rigorously derive the asymptotic distribution of the resulting estimates.

Our pairwise approach described in Section 2.4 may miss SNPs with trans-regulatory relationships. Ideally we would be able to fit our integrative model using all genes, and even all genotyped SNPs, and indeed modifications of existing high-dimensional regression techniques such as the lasso may allow us to achieve simultaneous estimation and variable selection. However, in the practical application of our approach it is vital to be able to quantify the uncertainty of our parameter estimates. Methods for assigning p-values to sparse regression estimates is currently an active area of research (Zhang and Zhang, 2011; Javanmard and Montanari, 2013; van de Geer et al., 2013) and we believe that in the future it may be possible to apply some of these developments to our integration method.

One limitation of our approach is the difficulty of correctly specifying the relationships between the different data types. Though our simulations suggest that we can still gain power under misspecified models, we can also consider semiparametric models of the form

$$g\{E(Y_i\mid {\mathbf{G}}_i,{\mathbf{S}}_{ik},{\mathbf{X}}_i)={\alpha }_{\mathit{int}}+{\alpha }_1({\mathbf{G}}_i,{\mathbf{X}}_i)+{\alpha }_2({\mathbf{X}}_i),{\alpha }_1({\mathbf{G}}_i,{\mathbf{X}}_i)={\alpha }_{\mathit{int}}+{\beta }_1({\mathbf{S}}_i,{\mathbf{X}}_i)+{\epsilon }_i\},$$

where α₁, α₂, and β₁ are unspecified functions. For example, we can use kernel-based methods (Wu et al., 2011) to estimate nonlinear functions of SNP sets and genes.