Multiscale Polar Theory of Microtubule and Motor-Protein Assemblies

Abstract

Microtubules and motor proteins are building blocks of self-organized subcellular biological structures such as the mitotic spindle and the centrosomal microtubule array. These same ingredients can form new “bioactive” liquid-crystalline fluids that are intrinsically out of equilibrium and which display complex flows and defect dynamics. It is not yet well understood how microscopic activity, which involves polarity-dependent interactions between motor proteins and microtubules, yields such larger-scale dynamical structures. In our multiscale theory, Brownian dynamics simulations of polar microtubule ensembles driven by cross-linking motors allow us to study microscopic organization and stresses. Polarity sorting and cross-link relaxation emerge as two polar-specific sources of active destabilizing stress. On larger length scales, our continuum Doi-Onsager theory captures the hydrodynamic flows generated by polarity-dependent active stresses. The results connect local polar structure to flow structures and defect dynamics.

Nonequilibrium materials composed of self-driven constituents—active matter—present novel physics to understand and may one day provide new technologies such as autonomously moving and self-healing materials [1–5]. One central example is mixtures of cytoskeletal filaments and molecular motors, which are important for their ability to form self-assembled cellular structures, such as the mitotic spindle and cell cortex. Reduced in vitro systems show that biofilament and motor-protein mixtures can form self-organized patterns, such as vortices and asters, reminiscent of cellular structures [6–8]. Recently, Sanchez et al. [9] synthesized mixtures of microtubules (MTs), multimeric kinesin-1 motor complexes, Adenosine Triphosphate (ATP), and a depletant. In bulk, extended MT bundles spontaneously form, which continuously stretch, bend, and fracture, leading to large-scale flows. When condensed onto an oil-water interface, the MTs form a nematically ordered active surface characterized by turbulentlike motions and motile disclination defects.

Understanding reduced filament-motor systems is an important step towards comprehending more complex active systems. Therefore, theoretical studies have investigated aspects of MT–motor-protein assemblies at different scales [10–14]. Inspired by the experiments of Sanchez et al. [9], Giomi et al. [15,16] and Thampi et al. [17–19] have studied liquid crystal hydrodynamic models driven by an apolar active stress [20]. While apolar models reproduce qualitative features of these experiments, MTs have polarity and cross-linking motors move directionally; hence, aligned MTs must have different interactions than antialigned MTs, and activity-driven material stresses and fluxes should reflect the polarity of these interactions. We investigate this through multiscale modeling, first discovering two separate microscopic sources of active and extensile stresses, one induced by motor-driven polarity sorting of antialigned MTs, and another from relaxation of cross-link tethers between polar-aligned MTs. We formulate a Doi-Onsager model [21–24] with fluxes and stresses reflecting these effects, and use this to study the interfacial experiments of Sanchez et al. [9]. Simulations show persistent folding flows and defect birth and annihilation, arising from active stresses occupying geometrically distinct regions. Having properly accounted for drag of the bounding fluids, we find a well-defined characteristic length scale from linear theory, which agrees well with feature sizes in our simulations.

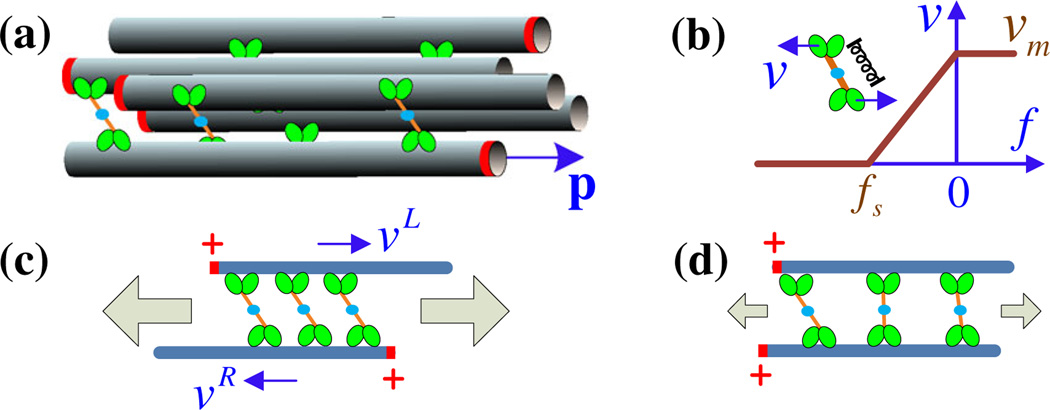
We outline the basic model in Fig. 1. Every MT has a plus-end-oriented director p, the same length l, and diameter b [Fig. 1(a)]. Nearby MTs are coupled by active plus-end-directed cross-links consisting of two motors connected by a springlike tether. Motor velocities are controlled by a piecewise linear force-velocity relation [Fig. 1(b)]. For antialigned MTs [Fig. 1(c)], the two motors move in opposite directions, stretching the tether to slide the MTs towards their minus ends, which is termed polarity sorting [10]. Conversely, for polar-aligned MTs the two motors move in the same direction, with little or no net sliding, and the retarding force on the leading motor causes stretched tethers to relax [Fig. 1(d)].

FIG. 1.

(color online). (a) Schematic of a cluster of polar-aligned and antialigned MTs, with their plus ends marked by red rings. Cross-linking motors walk on neighboring MTs at speed υ and (b) exert springlike forces, with a linear force-velocity relation. (c) An antialigned MT pair being polarity sorted by active cross-links. The left- (right-)pointing MT moves right (left) with velocity υ^L (υ^R). (d) A polar-aligned MT pair upon which cross-link forces are relaxing due to the force-velocity relation. In both, the gray arrows characterize the magnitude of an induced extensile stress.

Microscopic model

We first perform 2D Brownian dynamics (BD) Monte Carlo (MC) simulations of MTs driven by explicit motors with binding and unbinding kinetics [25]. The main purpose is to quantify local MT pair interactions, with long-ranged hydrodynamics neglected due to its high computational cost. We represent MTs as perfectly rigid rods, and assume a reservoir of ideal motors at fixed chemical potential. The motors bind to (unbind from) two filaments simultaneously, and unbind immediately upon reaching the plus end of either MT. At equilibrium, the average number of motors cross-linking MTs i and j is 〈N_ij〉 ~ ρ² ∫ ds_i ∫ ds_j exp {−[u_c(s_i, s_j)/k_BT]}, where ρ is the linear binding-site density on a single MT, u_c is the quadratic potential for cross-link extension, and s_i,j parametrizes the MT arclength [25]. The number of motors that bind or unbind is sampled from a Poisson distribution with the correct average number of events in each time interval so that the equilibrium distribution is recovered for static cross-links. Bound motors are inserted by first selecting pairs of MTs then sampling from the appropriate bivariate normal distribution to choose motor end points. The motor on each cross-link end point moves with a linear force-velocity relation [40]: υ = υ_m max (0, min(1, 1 + f / f_s)), where f is the magnitude of the cross-linking force, υ_m is the maximum translocation velocity, and f_s is the stall force. After the MC cycle, we compute all the forces and torques from motors, short-range repulsion, anisotropic local fluid drag by the solvent, and random thermal forces, to evolve MT positions and orientations forward in time [25,41]. The BD MC simulations are nondimensionalized using the length b, energy k_BT, and time τ = D/b², where D is the diffusion coefficient of a sphere of diameter b. Our model is similar to that of Head et al. [14], but new in our work are algorithmic improvements for handling cross-links and neglect of filament elasticity that allows us to simulate larger systems and measure the stress tensor.

Extensile stress and its origins

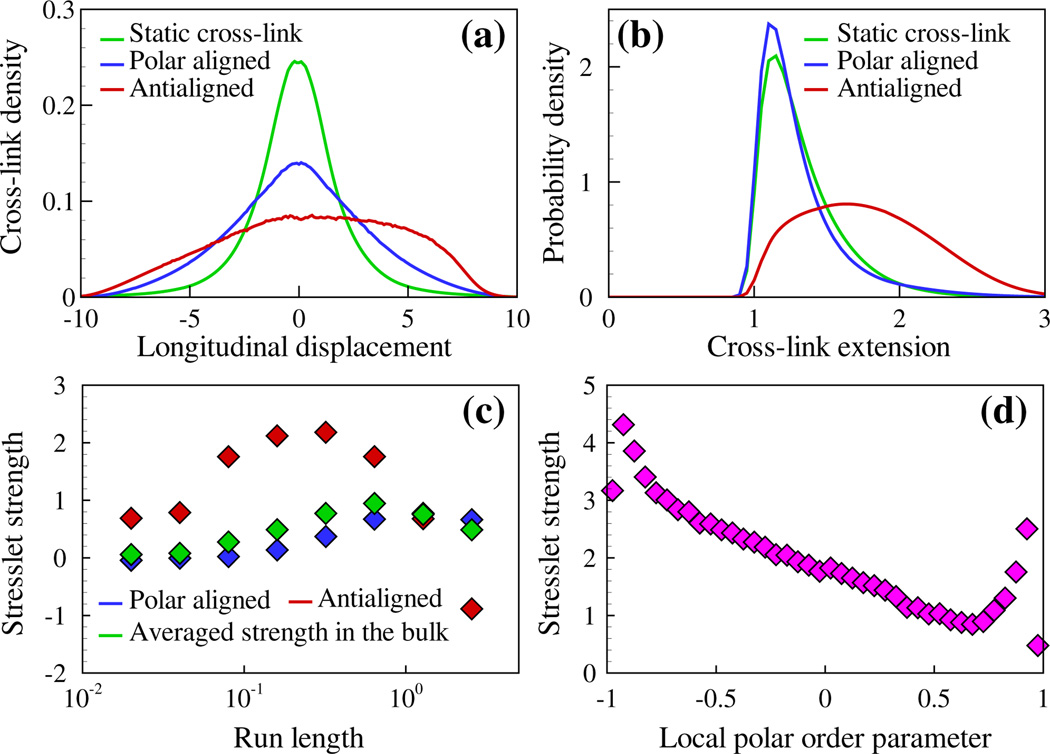
Figure 2 illustrates the long-time behavior of MTs in the BD MC simulations (see video S1 in the Supplemental Material [25]). For two MTs i and j with orientations p_i and p_j and center-of-mass displacement r_ij, the longitudinal displacement is s_ij = (1/2)r_ij · [p_i + sgn(p_i · p_j)p_j]. For antialigned MT pairs (p_i · p_j < 0), s_ij is negative when the MT pair is contracting, and becomes positive when the MT pair is extending (see Fig. 1). When cross-links are static or on polar-aligned MTs (p_i · p_j ≥ 0), the distribution of cross-links is symmetric about s_ij = 0 [Fig. 2(a)]. However, for motors on antialigned MTs, configurations that generate pair extension (those with positive values of s_ij) are more likely.

FIG. 2.

(color online). Results of the BD MC particle simulations. (a) Histogram of cross-link occupancy as a function of the particle pair longitudinal displacement s_ij. (b) Histogram of cross-link extension r_c. (c) Variation of extensile pair stresslet S (unit of force × length) with motor run length ℓ. (d) Typical variation of extensile pair stresslet with local polarity m_i.

Motor motion alters the distribution of cross-link extension r_c [Fig. 2(b)]. The minimum r_c ≈ 1 is due to MT steric interactions. For antialigned (polar-aligned) pairs, cross-link relaxation shifts the distribution toward larger (smaller) extension. The bulk material stress tensor is ${\mathbf{\Sigma }}_b=(N{k}_{B}T/V)\mathbf{I}+(1/V)\langle {\sum }_i^N{\mathbf{W}}_i\rangle$ for N interacting MTs in a volume V, with ${\mathbf{W}}_i=(1/2){\sum }_{j\ne i}^N{\mathbf{r}}_{ij}{\mathbf{F}}_{ij}$ the single-MT virial tensor [25,42]. Over a wide range of motor parameters, the time-averaged bulk stress tensor Σ_b is anisotropic, with larger components in the average MT alignment direction. Denoting the alignment direction by ŷ, the stress difference ${\mathrm{\Sigma }}_b^{yy}-{\mathrm{\Sigma }}_b^{xx}$ is positive, which corresponds to an extensile stress. The stress difference can be expressed as a sum of pair interactions, with each ij pair contributing a stresslet S_ij, prior to division by the bulk volume. The average pair stresslet S [green symbols in Fig. 2(c)] increases with the motor run length ℓ up to a maximum when the typical motor run length is the MT length. Here ℓ = υ_m/k₀l, the typical distance a motor travels during one binding event, with k₀ a base binding rate of motors. Increasing ℓ further leads to decreasing S because the motors rapidly move to the ends of the MTs and unbind.

The extensile stress from antialigned pair interactions arises from asymmetries during polarity sorting. If a MT pair begins sliding when the two minus ends touch and slide with a force proportional to pair overlap until the two plus ends meet, then the total extensile stresslet would be zero. Two effects break this symmetry. First, MTs are unlikely to begin interacting exactly when their minus ends meet, decreasing the range of negative s_ij over which sliding occurs. Second, more motors are bound on average during extension [Fig. 2(a)]. Figure 2(d) shows a typical curve of S as a function of m_i, where the local polar orientational order parameter m_i varies between 1 (all neighboring MTs are polar aligned) and −1 (all neighbors are antialigned). A maximum for m_i occurs near −1 because polarity sorting is the dominant source of pairwise extensile stress. As m_i increases, S drops with approximate linearity, at least away from the two isolated peaks that close examination shows are related to strong steric interactions of nearly parallel MTs: nearly, but not exactly, parallel MTs experience aligning torques due to cross-link-mediated attraction; the resulting steric collisions tend to promote pair extension that increases the extensile stress.

To understand the surprising and counterintuitive result that S remains positive even for polar-aligned pairs, we consider cross-link relaxation on perfectly parallel filaments. When cross-links are active, the force of a longitudinally stretched cross-link opposes the leading motor, slowing it, and pulls forward on the trailing motor. This causes a slight but significant shift in the distribution of cross-link extension toward smaller values relative to the static cross-link case [Fig. 2(b)]. With cross-linking motors, the cross-link-induced contractile stress along the MT alignment direction is decreased, while there is no change in the transverse stress induced by cross-links. This leads to a net anisotropic extensile stress in the alignment direction. When varying system parameters, we find that the extensile stresslet of polar-aligned MT pairs is typically 2–5 times smaller than that of antialigned pairs.

From microscopic to macroscopic models

To coarse grain the BD MC simulation results, we introduce a distribution function Ψ(x, p, t) of MT center-of-mass positions x and polar orientation vectors p (|p| = 1) and describe the particle dynamics in terms of the concentration Φ = ∫_p Ψ, the polarity vector q = ∫_p Ψp/Φ, the second-moment tensor D = ∫_p Ψpp, and the tensor order parameter tensor Q = D/Φ − I/d, with d = 2 or 3 the spatial dimension.

We first consider a nematically ordered local cluster of MTs undergoing polarity sorting (Fig. 1), with n MTs pointing rightwards (labeled R) and m MTs pointing leftwards (labeled L). When the motor ends move at a characteristic speed υ_w, for an antipolar MT pair, a minus-end-directed sliding is induced. Using Stokesian slender-body theory [43], we find the velocities of the left- and rightward pointing MTs [25]: υ^L = 2nυ_w/(n + m), υ^R = −2mυ_w/(n + m). This expression shows that the speed of each population depends on how many opposing MTs there are to pull against, with their drag as the anchor, and their relative velocity fixed at υ^L − υ^R = 2υ_w. When considering a more general orientation distribution, a similar calculation [25] yields ẋ = q − p as the translational flux for MTs.

Slender-body theory also yields the forces each rod exerts on the fluid, and hence, the induced “extra stress” tensor by polarity sorting can be expressed in dimensional form as σ_aa = (ηv_wl²/V_c)α_aa(mn/(m + n))pp [25,44]. Here V_c is the cluster volume and α_aa = s / l with s is the signed distance between the centers of mass of the p and −p oriented subclusters. For the extra stress due to cross-link relaxation, we lack a simple first-principles model of polar-aligned MTs, though the number of polar-pair interactions scales as m² + n². Given that the antialigned and polar-aligned stresses are of the same order [Fig. 2(d)], we assume the form σ_pa = (ηυ_wl²/V_c) (α_pa/2) ((m² + n²)/(m + n))pp. Thus, we are able to extract the (negative) values of α_aa,pa by comparing the antialigned and polar-aligned pair stresslet strengths [S_aa,pa = ηυ_wl²α_aa,pa/(m + n), and υ_w is taken as υ_m] with the BD MC simulations. Again, we construct the dimensionless 3D extra stress from D and Φqq (i.e., the simplest symmetric tensors quadratic in p) as Σ^a = Σ_aa+ Σ_pa = (α_aa/2) (D−Φqq) + (α_pa/2)(D+Φqq). The first (second) term captures active stress production via polarity sorting (cross-link relaxation) and exactly reproduces the form of σ_aa (σ_pa).

We further account for particle rotation as well as steric interactions and couple MT motion with a background flow to study the effect of long-range hydrodynamic interactions absent in the BD MC simulations through a continuum polar fluid model [21,22,24,25,45,46]. Since in the Sanchez et al. experiments [9] the active material is confined to an interface between oil and water, we assume a thin layer of suspension immersed in the bulk viscous liquid and close the system by solving the hydrodynamic coupling between the surface flow U and external fluid motions through a velocity-stress relation in Fourier space: Û = (i/2) (I − k̂ k̂) (Σ̂^ek̂), where k̂ = k/k is the normalized 2D wave vector [25].

Defects and polarity

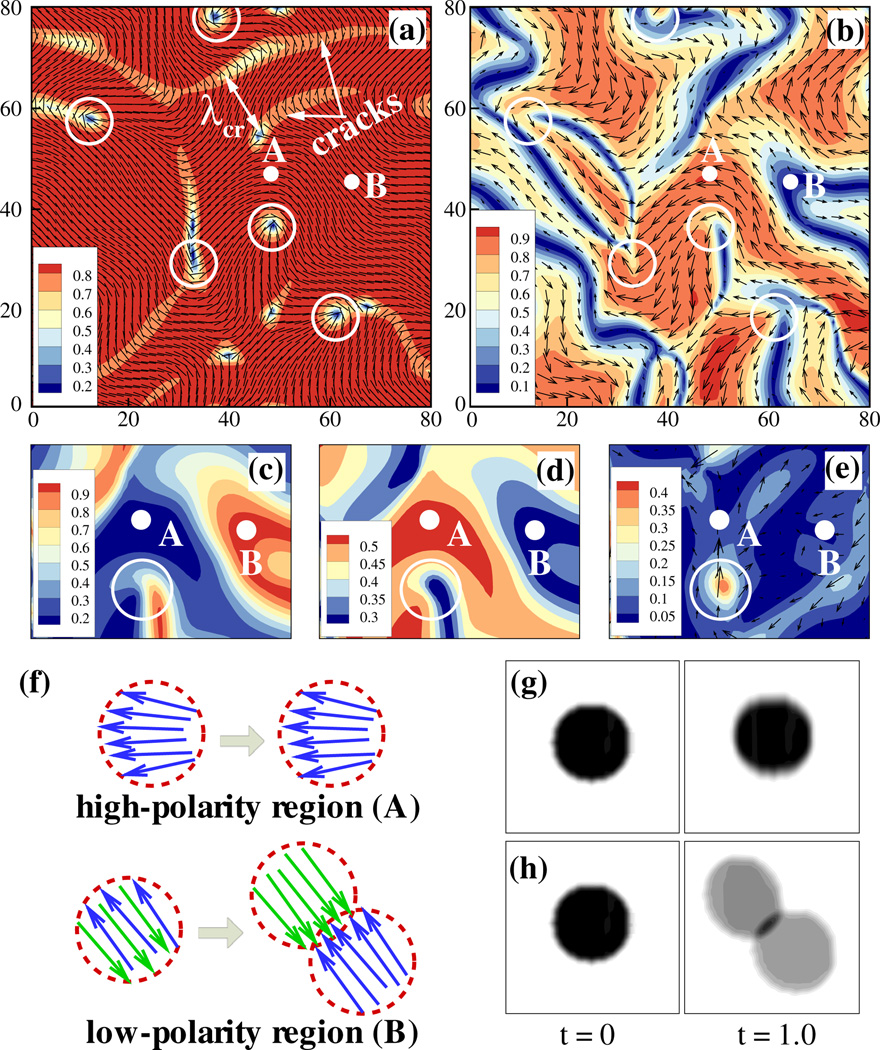
Assuming 2D periodic boundary conditions and using a Fourier pseudospectral numerical method [22,25], we simulated our model over long times. In regions of flow instability, we find persistently unsteady turbulentlike flows that are correlated with continual genesis, propagation, and annihilation of ±1/2 order defect pairs (see videos S2–S5 in the Supplemental Material [25]). In Fig. 3(a), the defects exist in regions of small nematic order (dark blue), and are born as opposing pairs in elongated “incipient crack” regions, qualitatively similar to the structures found in both experiments and apolar models [15–19]. Moreover, as shown in Fig. 3(b), the polarity field develops considerable spatial variation with regions of high and low polar order |q| (video S5 in the SupplementalMaterial [25]). The two active stresses vary in strength depending on the local polarity—the polar-aligned (antialigned) stress is large in regions of high (low) polar order [Figs. 3(c) and 3(d)]— and hence are largest, respectively, in their complementary regions. The circles in Fig. 3(b) encircle +1/2-order defects, showing the sharp variation of the polarity field around them, with the gradients of active stresses there yielding large active force as shown in Fig. 3(e).

FIG. 3.

(color online). Snapshots of streaming MT nematics on an immersed interface. (a) The nematic director field n superimposed on the color map of the scalar order parameter (twice the positive eigenvalue of Q); λ_cr is a calculated characteristic length between the cracks. (b) The polarity vector field q superimposed upon its magnitude. (c),(d) Polarity-dependent active stress magnitudes, showing principal eigenvalues of the active stresses [Σ_aa in (c) and Σ_pa in (d)]. (e) The vector field of the active force f^a = ∇ · Σ^a superimposed upon its magnitude. In (a)–(e), circular areas labeled A and B mark regions of high and low polarity, respectively. Positions of +1/2-order defects are marked by circles. (f)–(h) Predicted results of a photobleaching experiment of fluorescent MTs for a bleached spot in a region of high polar order [(g), area A], and in a region of low polar order [(h), area B]. Arrows represent MTs with arrowheads denoting plus ends. A dimensionless time is used with scale b/νυ_w, where ν is the effective volume fraction.

We further simulated the results of a photobleaching experiment in which a circular region is exposed to high-intensity laser light to inactivate the fluorescent molecules on the corresponding MTs [47] [Figs. 3(f)–3(h)]. In a small high-polarity region (marked A in Fig. 3), little or no polarity sorting occurs, and the photobleached spot remains approximately circular [Fig. 3(f) top, and Fig. 3(g)] over longer times. In a low-polarity region of high nematic order (marked B in Fig. 3), strong polarity sorting of antialigned MTs causes a photobleached spot to separate into two lobes, showing decreased bleaching. This type of experiment probes the local polarity field, and hence the origins of active stress.

Hydrodynamic instabilities and characteristic length

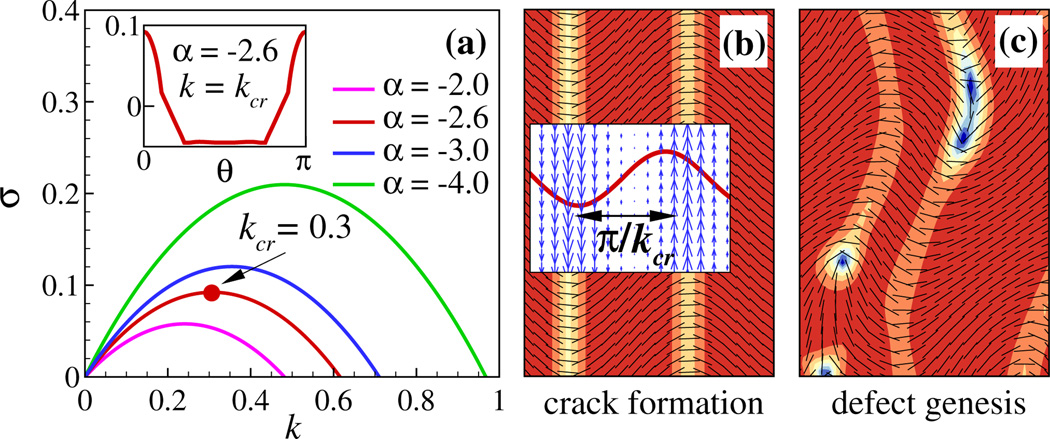
A key observation in our simulations as well as other active fluid systems [18,48–50] is that defect pairs are generated along elongated cracks that themselves develop from regions of high polar order. Here we performed a linear stability analysis for a nematically ordered homogeneous base state [25]. As shown in Fig. 4(a), the analysis reveals a wave number of maximal growth k_cr along this direction, with k_cr growing with approximate linearity in α = α_aa + α_pa. Also the plane wave vector of maximal growth is aligned with the nematic director [θ = 0 in Fig. 4(a) inset]. By contrast, when solving a Stokes equation forced by a bulk stress, the velocity-stress relation in Fourier space becomes û = (i/k) (I − k̂ k̂) (Σ̂^ek̂). Comparing to our surface model, the factor of k in the denominator profoundly changes the nature of system stability, giving that maximal growth occurs at k = 0 for the bulk model, and so not producing a characteristic length scale [22,51]. (This was also noted in Ref. [52] in their study of swimmers confined to immersed thin films, while Ref. [53] shows that adding substrate friction changes length scale selection in 2D active nematic models.)

FIG. 4.

(color online). Linear stability analysis (a) and nonlinear simulation (b),(c) for strongly antialigned MTs. (a) The real part of the growth rate as a function of wave number k for several values of α (α = α_aa + α_pa). Here k_cr corresponds to a maximum growth rate. Inset: Real part of the growth rate as a function of wave angle θ when fixing k = k_cr. (b) Crack formation. Inset: The fluid velocity vector field (blue) and the eigenmode (red line) associated with k_cr. (c) Genesis of defects at late times.

Figure 4(b) shows the nonlinear results of this linear instability. A series of cracks form along ŷ, associated with moving fluid jets and bending of nematic field lines. In Fig. 4(b) inset, the spatial variations of the velocity field are in excellent agreement with the velocity eigenmode associated with k_cr for the linearized system. The distance between these cracks matches the half-wavelength, i.e., λ_cr = π / k_cr, which is in fact representative of the characteristic of the full dynamics of motile defects [Fig. 3(a)]. At late times, Fig. 4(c) shows that these cracks lose stability and eventually “break” to form defect pairs.

Discussion

We have explored other aspects of our model system. For example, when turning off hydrodynamics in our kinetic model, we find polar lanes emerging as in our BD MC model. This arises from a slow instability (consistent with the BD MC model) when compared with hydrodynamic instabilities. We find that either active stress (aa or pa) taken individually will produce qualitatively similar flows and defect dynamics. Hence, the qualitative nature of the large-scale dynamics does not by itself isolate the precise origins of a destabilizing stress. An interesting aspect of our BD MC study is that active stresses are extensile, which is very different from the contractility observed in actin-myosin gels [54]. This is likely related to the rigid MTs being in a nematically ordered state. While we applied our multiscale polar model to study experiments of synthesized active fluids, similar but more elaborated models might serve as a principled basis from which to study biological systems such as the eukaryotic mitotic spindle.