Phylogenetic Analysis of Genome Rearrangements among Five Mammalian Orders

Abstract

Evolutionary relationships among placental mammalian orders have been controversial. Whole genome sequencing and new computational methods offer opportunities to resolve the relationships among 10 genomes belonging to the mammalian orders Primates, Rodentia, Carnivora, Perissodactyla and Artiodactyla. By application of the double cut and join distance metric, where gene order is the phylogenetic character, we computed genomic distances among the sampled mammalian genomes. With a marsupial outgroup, the gene order tree supported a topology in which Rodentia fell outside the cluster of Primates, Carnivora, Perissodactyla, and Artiodactyla. Results of breakpoint reuse rate and synteny block length analyses were consistent with the prediction of random breakage model, which provided a diagnostic test to support use of gene order as an appropriate phylogenetic character in this study. We the influence of rate differences among lineages and other factors that may contribute to different resolutions of mammalian ordinal relationships by different methods of phylogenetic reconstruction.

1. Introduction

A well-resolved mammalian tree is essential for annotation of genetic features in their genomes and sequence evolution within this taxonomic class. However, the phylogenetic relationships of the 18 extant placental mammalian orders are highly contentious (Cannarozzi et al., 2007; Cao et al., 1998; Hallstrom and Janke, 2008; Kullberg et al., 2007; Li et al., 1990; Springer and de Jong, 2001; Wildman et al., 2007). Two major alternative hypotheses have been proposed regarding the evolutionary relationship within placental mammals. One maintains that Rodentia is more closely related to Primates than Perissodactyla, Artiodactyla and Carnivora (three orders of Laurasiatheria), (Fig 1A), while the alternative supports Rodentia as an outgroup to the other four orders (Fig 1B).

Figure 1.

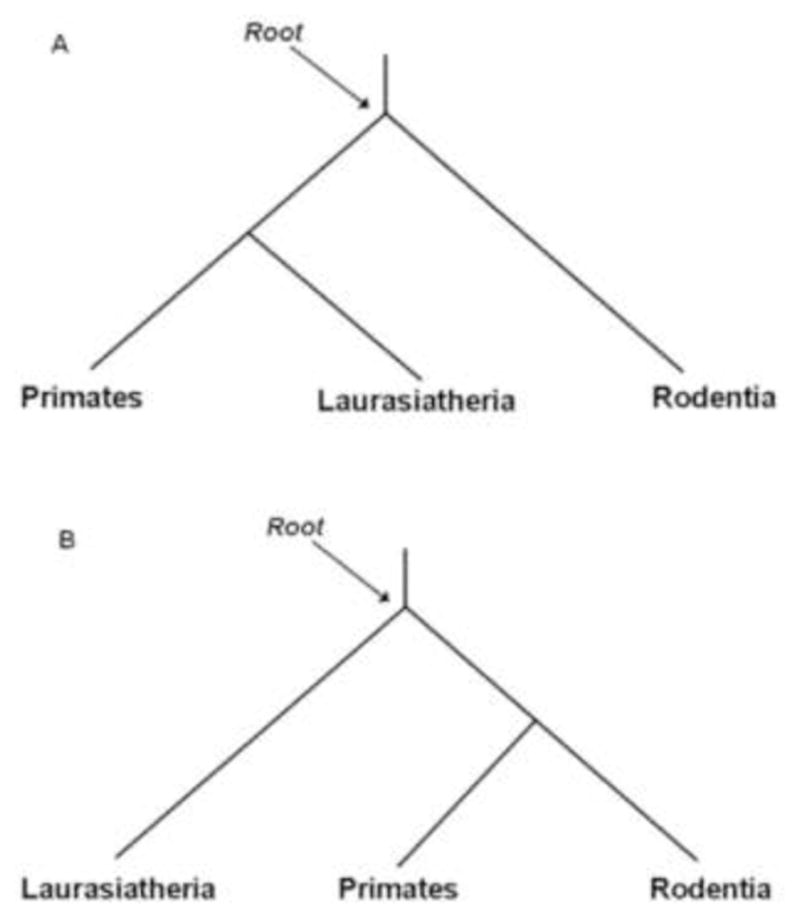
Two alternative hypotheses for the evolutionary relationship among Primates, Laurasiatheria (Artiodactyla, Carnivora, Perissodactyla) and Rodentia. (A) Primates closer to Rodentia than Laurasiatheria; (B) Primates closer to Laurasiatheria than Rodentia.

Earlier studies investigated the placental mammalian relationship with single genes of mitochondrial (Cao et al., 1994; Cao et al., 1998) and nuclear genomes (Easteal, 1988, 1990; Goodman et al., 1985; Li et al., 1990). Single gene analyses frequently created discrepancies in branching order, and it was thought that large molecular data sets of concatenated alignments have the potential to resolve these issues (Madsen et al., 2001; Murphy et al., 2001a; Murphy et al., 2001b). Whole genomic sequences of mammalian mitochondria, each ranging about 16,500 to 17,000 bases (Penny and Hasegawa, 1997), provided more base pairs than single genes. Nevertheless, evidence from mitochondrial genomic analyses is inconsistent. Although a majority of these mitochondrial genomic analyses supported the Primates-Laurasiatheria clade which excluded Rodentia (Arnason et al., 1997; Arnason et al., 1999; Janke et al., 1994; Janke et al., 1997; Mouchaty et al., 2000; Pumo et al., 1998; Reyes et al., 2000; Springer et al., 1997), mitochondrial genomic evidence for Euarchontoglires (Primates-Rodentia clade) also existed (Arnason et al., 2002; Arnason et al., 2008; Reyes et al., 2004). There are other controversies regarding the use of mitochondrial genomic data. A tree derived from first and second codon positions in mitochondrial genes supported the Euarchontoglires hypothesis, whereas another tree of amino acid sequence data suggested a Primates-Laurasiatheria clade (Arnason and Janke, 2002). Further studies showed that complete mitochondrial genomic sequences were valuable for resolving relationships within placental orders, but they appeared inadequate in resolving between-order relationships (Corneli, 2002).

Phylogenomic studies of concatenated alignments of nuclear and mitochondrial genes resolved the 18 extant placental orders into four superordinal groups: Xenarthra, Afrotheria, Laurasiatheria, and Euarchontoglires (Hallstrom et al., 2007; Madsen et al., 2001; Murphy et al., 2001a; Murphy et al., 2001b). Since Artiodactyla, Perissodactyla and Carnivora are three orders of Laurasiatheria and Primates and Rodentia are within Euarchontoglires, these studies favored the Primates and Rodentia as a superordinal clade while excluding Artiodactyla, Perissodactyla and Carnivora (Fig 1B). However, the basal position of Rodentia was again underscored in a recent study of eight housekeeping genes across 22 placental mammals and three marsupials (Kullberg et al., 2006). In addition, another phylogenomic study using distance-, parsimony-, and likelihood-based methods yielded overwhelming support for a Primates-Carnivora clade while excluding Rodentia (Cannarozzi et al., 2007).

The controversial relationships among these mammalian orders have been highlighted by several recent studies. Murphy and others (2001b) claimed that the deep mammalian relationships were resolved by Bayesian-based phylogenetics. Afterwards, Misawa and Nei (2003) showed that Murphy and others’ data (2001b) can lead to two different Bayesian trees, both of which were supported by high posterior probabilities.

Kolaczkowski and Thornton (2004) pointed out that when the substitution rate at a single base or amino acid position varies over evolutionary time (referred to as heterotachy), both Bayesian- and likelihood-based methods are statistically inconsistent, leading to an incorrect partition as the amount of data grows (Nishihara et al., 2007; Wildman et al., 2007). Likewise, Hughes and Friedman (2007) found that genes with different substitution rates yielded a different branching order between Carnivora and Rodentia, but concatenation of these genes yielded a tree supporting Rodentia branching first regardless of the method or model of sequence evolution.

Since several factors can lead to a misleading topology, such as nucleotide or amino acid compositional bias (Nishihara et al., 2007), phylogenetic method (Kullberg et al., 2007), long-branch attraction, and heterotachy, it is desirable to seek whole genome-based phylogenetic characters to resolve the basal relationships in the mammalian tree.

Gene order is a type of rare genomic change, which provides independent ways to evaluate conflicting molecular sequence phylogenies (Rokas and Holland, 2000). It has been demonstrated as a useful phylogenetic character in resolving both shallow and deep prokaryotic relationships (Belda et al., 2005; Luo et al., 2008; Luo et al., 2009). Genome rearrangements include inversion, transposition, block exchange, circularization and linearization, all of which act on a single chromosome, and translocation, fusion, and fission, which act on two chromosomes. All of these operations are subsumed in the double-cut-and-join (DCJ) model, which has formed the basis for much of the algorithmic research on rearrangements over the last few years.

A DCJ operation consists of cutting two adjacencies in the first genome, and rejoining the resulting four unconnected vertices in two new pairs. As a result, it swaps two gene ends in two different vertices of the same genome in the breakpoint graph. Fig. 2 shows an example of a DCJ operation on two adjacencies (a, b) and (c, d). It splits (a, b), (c, d), and can create new adjacencies (a, c), (b, d) or (a, d), (b, c). The DCJ distances between two permutations is defined as the number of minimal DCJ operations needed to transform one permutation into another. If two unichromosomal linear genomes are identical, we can see that there are N cycles in the breakpoint graph (N is the length of the genome). A DCJ operation can increase at most one cycle (Fig. 3), so for unichromosomal linear genomes, DCJ distance is N - C where C is the number of cycles in the breakpoint graph.

Figure 2.

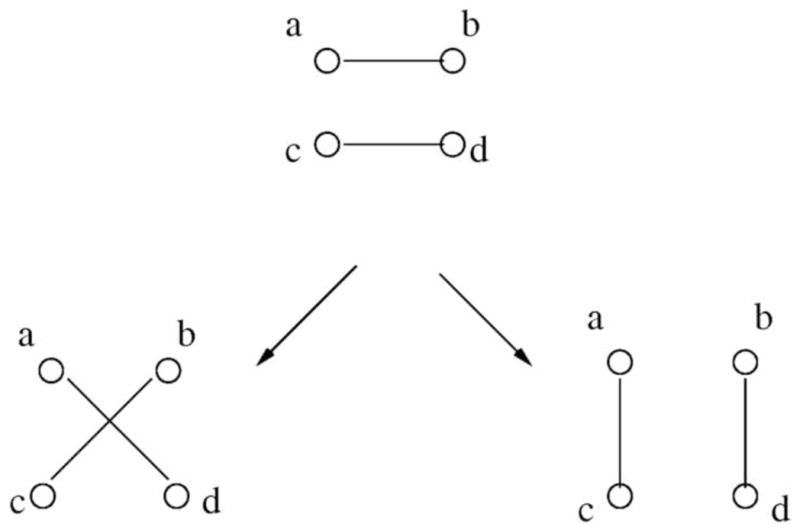
A DCJ operation on adjacencies (a, b) and (c, d) can create two possible results: (a, c), (b, d) or (a, d), (b, c).

Figure 3.

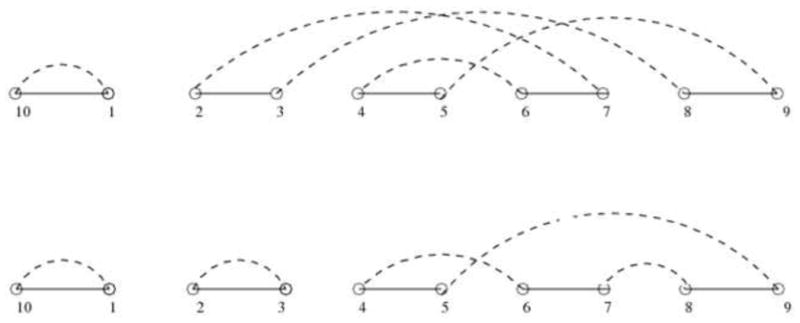
On the top is the breakpoint graph of genome G = 1, 2,-3, 4,-5, with respect to the identity genome G = 1, 2, 3, 4, 5. We can see there are two cycles in the graph. An optimal DCJ operation removes adjacencies (2,7), (3,8) and creates adjacencies (2,3), (7,8) so that the number of cycles increases by one.

Genome rearrangements occur at a much lower rate than that of nucleotide substitution, hence it has the potential to resolve ancient interordinal divergences among mammals (Boore, 2006; Murphy et al., 2004). Applying genome rearrangement data to the Primates-Rodentia-Carnivora controversy, a recent study used the Multiple Genome Rearrangements and Ancestors (MGRA) algorithm, based on a multiple breakpoint graph, which favored the sister relationship between Primates and Carnivora, but did not exclude the possibility of a Primates-Rodentia clade (Alekseyev and Pevzner, 2009). In this present study, we constructed a distance-based gene order phylogeny to resolve the phylogenetic relationship among Primates, Rodentia, Artiodactyla, Perissodactyla and Carnivora.

2. Materials and Methods

2.1 Genome data

10 genomes were used in the analysis, including Homo sapiens (Human), Macaca mulatta (Macaque), Pan troglodytes (Chimpanzee), Pongo pygmaeus (Orangutan), Equus caballus (Horse), Bos Taurus (Bovine), Mus musculus (Mouse), Rattus norvegicus (Rat), Canis familiaris (Canine), and Monodelphis domestica (Opossum). The supersets of all gene translations, both known and predicted, were obtained from Ensembl release 52. Non-nuclear genes and genes that were not mapped to a chromosome were discarded. Some genes encode alternative spliced proteins, and only the longest translation was kept. The final number of protein in each of the 10 mammalian genomes that was used for ortholog prediction was summarized in Table 1. Although some assembly errors occur in the Macaque genome (Karere et al. 2008) and likely to occur in other genomes, simulation studies have shown that gene order phylogenetic approaches are robust against those errors (Lin et al. 2011a and Lin et al. 2011b). By the time of this study, no genomes from Afrotheria (e.g. elephant) were properly assembled. We also analyzed two relevant but unpublished genomes, including Oryctolagus cuniculus (Rabbit) and Sus scrofa (Swine). These lineages are associated with long branches with unknown reasons (Supplementary Figure 1 and Supplementary Table 2).

Table 1.

Size of mammalian proteome

Mammal	Proteome size 1
bovine	19030
canine	19014
horse	20170
human	21165
macaque	21023
mouse	23228
orangutan	18868
chimpanzee	19199
rat	22490
opossum	18641

¹The proteome does not include translations of genes that are not mapped to nuclear chromosomes. For alternative spliced genes with multiple translations, only the longest protein was counted.

2.1. Ortholog identification and data preparation

All pairs of proteomes were assembled by a reciprocal all-versus-all BLASTP search with an E value smaller than 0.1 and by filtering sequenced regions with low complexity. The output file was prepared to include mapped position and strandedness. MSOAR software was then used to identify common orthologs in every pair of genomes. MSOAR is a high-throughput genome-scale ortholog assignment system; it is a two-step procedure where homologous genes were first identified by sequence similarity search and then orthologous genes were identified by corresponding to each other in the most parsimonious evolutionary scenario involving both genome rearrangements and gene duplications (Chen et al., 2005; Jiang, 2007). Then the pairwise ortholog sets were used to identify the common ortholog sets in the subsets of the 10 genomes. The same procedure was applied in a previous study (Luo et al., 2009).

MSOAR identifies orthologs by minimizing the number of rearrangement events, which will have an impact on the distance-based gene order phylogeny only if the distance obtained severely underestimates the true number of events. Based on various simulation studies (Moret et al. 2002; Shi and Tang 2010), distance correction must be performed if the number of events between two genomes exceeds 70% of the number of genes. In this study, the largest DCJ distance is 1450 (between rate and opossum), far smaller than the number of orthologues (9212), thus using DCJ distance based on orthologs identified by MSOAR is still valid.

The genomic positions of all protein-coding regions were extracted by Perl scripts. The order of orthologs in each genome was determined based upon their chromosomal position and strandedness. In this way, each genome was represented by a set of signed permutations for each chromosome where sign indicates strandedness (Moret et al., 2002).

2.2. Gene order phylogeny construction

Evolutionary events that change gene orders include inversion and transposition which act on a single chromosome, and translocation, fusion, and fission which act across chromosomes. Although combining events such as inversion, translocation, fusion and fission have been well studied, handling transpositions is still beyond reach. The “double-cut-and-join” (DCJ) operation was proposed to provide a “universal” operation to account for all rearrangement events. A DCJ operation occurs when two breaks are created in the chromosomes of a genome and the fresh telomeres are reconnected in a new arrangement. Two supplementary DCJ operations are the separation of an adjacency into two telomeres and the attachment of two telomeres to form a single adjacency. As a result, the DCJ operation can simulate each of the rearrangement events in one or two steps.

Bergeron et al. (Bergeron et al., 2006) provided a linear algorithm to compute the edit DCJ distance between two genomes, which can be used to reconstruct phylogenies using distance-based methods such as neighbor-joining (Saitou and Nei, 1987) and FastME (Desper and Gascuel, 2002). Experiments on simulated datasets showed that inversion and DCJ distances return very similar results even on data generated using only transpositions (Kothari and Moret, 2007). Lin and Moret later showed that it is possible to estimate the true number of evolutionary events from the DCJ model (Lin and Moret, 2008), making the DCJ model attractive in phylogenetic reconstruction. The Double Cut and Join (DCJ) distance metric (Yancopoulos et al., 2005) is implemented in GRAPPA (Moret et al., 2002; Zhang et al., 2009), which computed the pairwise DCJ and breakpoint distances from the gene order data and generated a pairwise distance matrix. Next, the FastME (Desper and Gascuel, 2002) software constructed the DCJ and breakpoint phylogenetic trees. The tree topologies were visualized by MEGA4 (Tamura et al., 2007).

To calculate the statistical reliability of the branches of the phylogeny, we applied a jackknife resampling technique that, in each iteration, randomly removed 50% of the initial orthologous gene sets. Note that bootstrapping is not applicable here, because gene order is one character with multiple states (Shi et al., 2010).

1000 jackknife random samples were generated to compute 1000 matrices for both DCJ and breakpoint distances. Each of these 1000 matrices were imported into the FastME program to obtain 1000 DCJ and breakpoint distance-based trees. Finally, the CONSENSE program in the PHYLIP software package (Felsenstein, 1989) calculated a majority-rule consensus tree with percent values at each node. Each value represents the percentage of trees supporting a clade defined by a node. This procedure was applied in a prior study (Luo et al., 2009), and the usefulness of the jackknife technique in gene order phylogeny was illustrated in a recent study (Shi et al., 2010). The elephant genome has not been assembled and hence cannot be used for genome rearrangement-based phylogenetic analysis. Either rabbit or swine or both were included in preliminary analyses, but all had very long branches (Supplementary Fig. 1), perhaps because of errors in assembly.

2.3. Breakpoint reuse rate measurement

We further analyzed the breakpoint reuse rate among the placental mammals. Breakpoints are not exact positions in the genome. Rather, they represent genomic regions whose resolution is dictated by synteny blocks. In rearrangement analysis, genomes are basically represented by sequences of synteny blocks interspaced with breakpoint regions that are typically much shorter than synteny blocks. Synteny blocks hide effects of much more frequent and intractable evolutionary events like mutations and micro-rearrangements and allow one to focus on analysis of large-scale genome rearrangements. Large-scale genome rearrangements are detected from different orderings of synteny blocks in different genomes. The span of such rearrangements is therefore defined in terms of synteny blocks and their actual breakpoints (i.e., positions where rearrangements break the genome) are known only to belong to certain breakpoint regions. So there is no way to determine exact locations of breakpoints which are therefore treated as genomic regions.

In fact, exact locations of breakpoints are not that important for large-scale rearrangement analysis. It is now known that mammalian genomes are formed by mosaic of “solid” and “fragile” regions where the latter are prone to rearrangements (Alekseyev and Pevzner 2007). From this perspective, it does not matter much whether two breakpoints exactly coincide or just colocated within a short breakpoint region. Both cases are treated as breakpoint reuse and simply indicate that the corresponding breakpoint region is “fragile”.

Using the principle of parsimony, the breakpoints reuse rate was computed among genomes (Alekseyev, 2008). Since each gene rearrangement causes two breakpoints, the breakpoint reuse rate is measured by multiplying two by the number of rearrangements which is then divided by the total number of breakpoints (for a 2-genome comparison). The breakpoint reuse rate measurement ranges in between the interval of 1 and 2, where the value 1 implies no breakpoint reuse. One caveat is that a high breakpoint reuse rate may indicate that the parsimony assumption is not valid.

2.4. Synteny block length analysis

The gene order sequence data were used to compute synteny block lengths of all pairwise comparisons among the mammalian genomes. The frequency distribution of the synteny block lengths was fitted to the expected exponential Probability Density Function (Zdobnov and Bork, 2007) and a power law function using MatLab.

2.5. Gene order rate calculation

Each of the 1000 jackknife random samples resulted in a DCJ distance-based phylogenetic tree. Trees with different topologies from the consensus tree were discarded. We then collected the branch lengths from the remaining jackknifing trees. To test that any two branches were of different lengths, the mean values of jackknife-generated branch lengths were compared by a z-test. All statistical analyses were performed using the R statistical software package (R Develop Core Team, 2008).

2.6. Sequence-based phylogenetic tree construction

The shared orthologous amino acid sequences were aligned separately using PRANK software (Loytynoja and Goldman, 2005, 2008). PRANK models insertions and deletions as distinct evolutionary events and thus dramatically reduces bias in sequence alignment (Loytynoja and Goldman, 2005, 2008). In each genome, the orthologous sequences were concatenated together and transformed as a Phylip format. All ambiguous amino acid sites were removed which left 3,873,035 sites per genome.

Phylogenetic trees were constructed using Neighbor-Joining (Saitou and Nei, 1987), Maximum-Likelihood (Schmidt et al., 2002), Maximum-Parsimony (Eck and Dayhoff, 1966), and Bayesian (Huelsenbeck and Ronquist, 2001) methods. To establish the confidence of internal branches of the resulting trees, 1000 bootstrapped replicates were resampled in the NJ and MP trees separately. Likewise, 1000 puzzling steps were applied in the ML tree. The puzzling steps are akin to the bootstrapped random samples in testing the tree topology. In the Bayesian tree, posterior probabilities were calculated by using a Metropolis-coupled Markow chain Monte Carlo approach with sampling according to the Metropolis–Hastings algorithm.

The NJ and MP methods were implemented in MEGA4 software (Tamura et al., 2007). In the NJ tree, the pairwise genomic distances were computed using Jones-Taylor-Thornton (JTT) model (Jones et al., 1992) with gamma correction. The gamma distribution parameter alpha (alpha=0.32) was estimated from the concatenated dataset by TREE-PUZZLE software (Schmidt et al., 2002) implemented by the Mobyle online server (Neron et al., 2009). The ML tree was constructed using TREE-PUZZLE software on the Mobyle online server with JTT model and gamma correction. The Bayesian analysis was implemented in the MPI version of MrBayes software (Altekar et al., 2004). One cold and three heated Markov chain Monte Carlo (MCMC) chains with default chain temperatures were run for a total of 10,000 generations with trees sampled every 10 generations. The first 25% of all runs were discarded as “burn-in”. A majority-rule consensus tree was constructed from the post-burn-in trees. To assess whether rate variation across the tree has an impact on Bayesian tree, the covarion model was invoked in some Bayesian tree reconstructions. Different protein rate variation models, including the gamma-distributed rate model (rates=gamma) and the proportion of invariable sites model combined with the gamma model (rates=invgamma), were used. Average standard deviation of split frequencies = 0.00000 is reached at the end of the calculations.

3. Results

3.1. Gene order trees

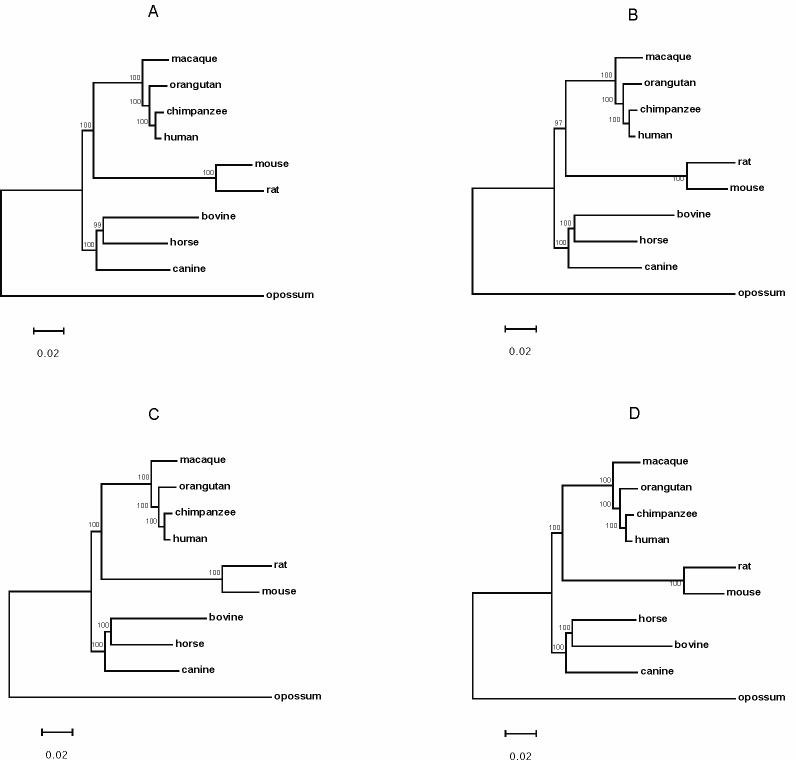
We obtained 9,212 orthologs shared by the 10 organisms (Supplementary Table 1), accounting for 49.4% of the smallest proteome (i.e. opossum; Table 1). These shared orthologous amino acid sequences were used in gene order and sequence-based phylogeny construction. The Double Cut and Join (DCJ, Fig. 4A) and breakpoint (Fig. 4B) distance-based gene order trees of the five mammalian orders were consistent. The distance-based gene order trees resolved the evolutionary relationships among hominid and non-hominid primates with high statistical support (Fig. 4). In addition, the gene order trees supported a Primates-Carnivora-Perissodactyla clade excluding Rodentia. This relationship received high statistical support in the breakpoint tree (Fig. 4B). Moreover, the gene order trees showed that Artiodactyla branched before Perissodactyla and Carnivora (Fig. 4). However, the distance-based gene order trees did not resolve the phylogenetic position of Artiodactyla (Fig. 4).

Figure 4.

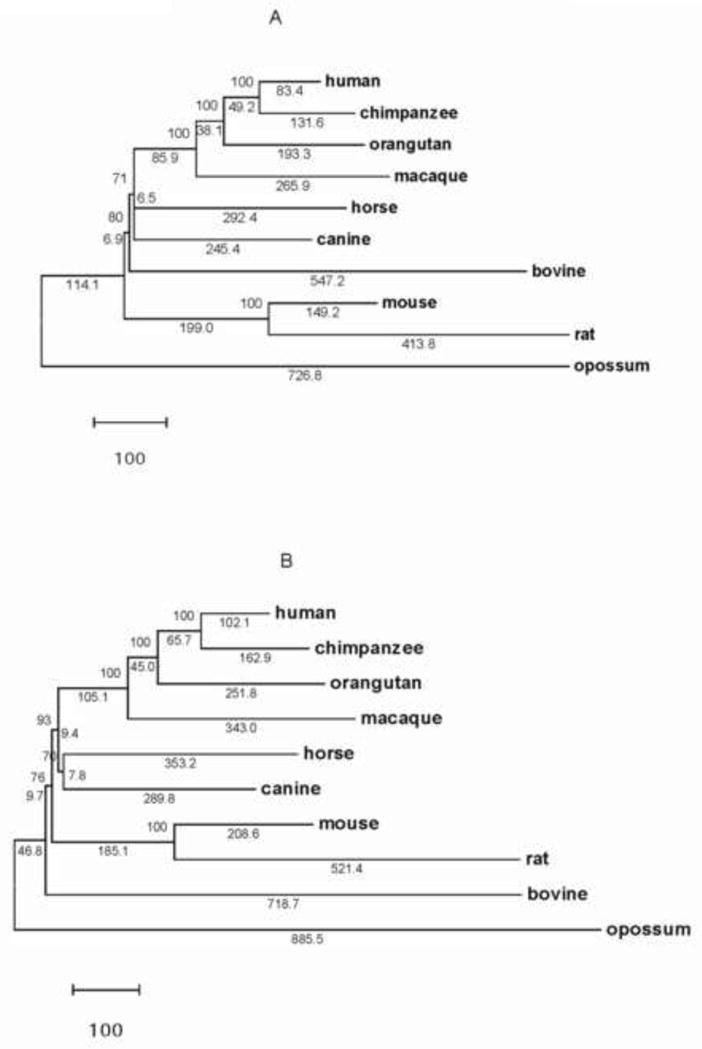
Phylogeny of Primates (human, chimpanzee, orangutan, macaque), Laurasiatheria (canine, horse, bovine) and Rodentia (mouse, rat) inferred from (A) a DCJ distance and (B) a breakpoint distance matrix tree. Values above branches show the number of times that the clade defined by that node was supported by 1000 jackknife trees. Values below branches show number of genome rearrangement events. Opossum is the outgroup.

3.2. Sequence-based trees

The Neighbor-Joining (NJ, Fig. 5A), Maximum-Likelihood (ML, Fig. 5B) and Maximum-Parsimony (MP, Fig. 5C) trees using concatenated amino acid sequences were congruent. With high statistical support, these sequence-based trees unanimously supported Primates, Carnivora, Perissodactyla and Artiodactyla as a monophyletic group and Rodentia as the outgroup. We also analyzed the same concatenated sequences with Bayesian approaches in MrBayes software which implements the covarion model to take heterotachy into account. In contrast to other molecular sequence phylogenies, the Bayesian trees (Fig. 6) consistently supported a Primates-Rodentia clade excluding Carnivora, Perissodactyla and Artiodactyla with high posterior probability, regardless of whether the gamma-distributed model or a combination of a proportion of invariable sites model and the gamma-distributed model was used, and regardless of whether rate variation across the tree (i.e. heterotachy) was considered.

Figure 5.

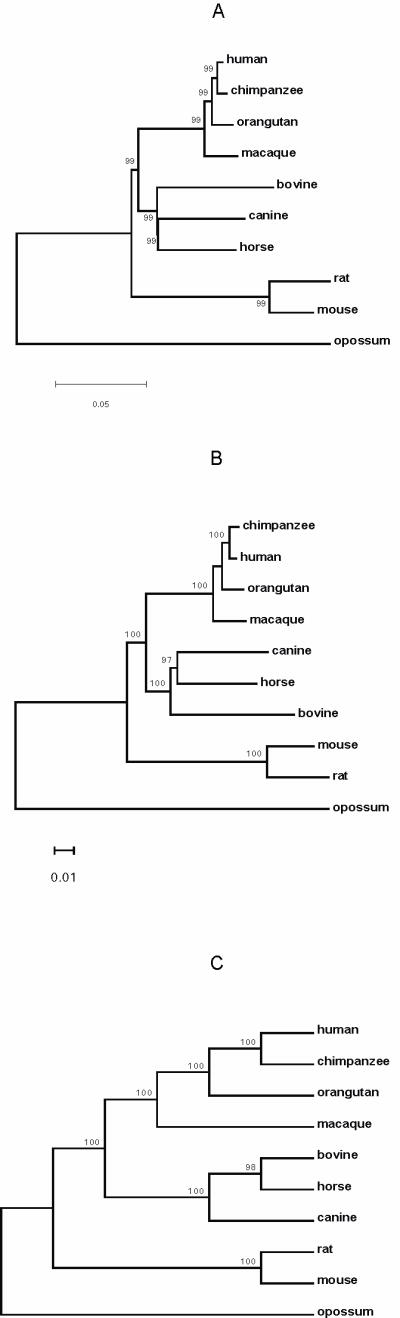
Phylogeny of Primates (human, chimpanzee, orangutan, macaque), Laurasiatheria (canine, horse, bovine) and Rodentia (mouse, rat) inferred from concatenated amino acid sequences: (A) Neighbor-Joining (NJ) method with JTT model and gamma correction, (B) Maximum-Likelihood (ML) with JTT model and gamma correction, and (C) Maximum-Parsimony (MP). Values above branches show the number of times that the clade defined by that node were supported by 1000 bootstrapped pseudoreplicates (NJ, MP) or 1000 puzzling steps (ML).

Figure 6.

Bayesian phylogeny of Primates (human, chimpanzee, orangutan, macaque), Laurasiatheria (canine, horse, bovine) and Rodentia (mouse, rat) inferred from concatenated amino acid sequences, assuming (A) gamma-distributed rate variation across sites (rates=gamma) and rate variation across tree (covarion=yes); (B) a proportion of invariable sites combined with the gamma model (rates=invgamma) and rate variation across tree (covarion=yes); (C) gamma-distributed rate variation across sites (rates=gamma, covarion=no); (D) a proportion of invariable sites combined with the gamma model (rates=invgamma, covarion=no).

The sequence-based trees were also inconsistent regarding the evolutionary relationship among Carnivora, Perissodactyla and Artiodactyla. The ML and NJ tree supported Artiodactyla as an outgroup of the Carnivora-Perissodactyla clade, whereas the MP and Bayesian trees supported Carnivora as an outgroup of the Perissodactyla-Artiodactyla clade.

3.3. Evolutionary rates

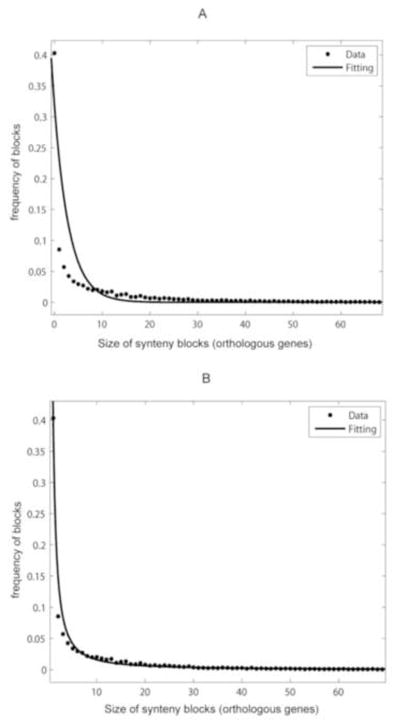
A breakpoint reuse rate analysis showed that there is limited breakpoint reuse in the placental mammals (Table 2). The synteny block lengths in the placental mammals did not follow the expected exponential distribution (Fig. 7A), but it was fit to a power function (Fig. 7B).

Table 2.

Breakpoint re-use rate ¹ in mammalian genomes

	canine	bovine	horse	human	opossum	macaque	mouse	orangutan	chimpanzee	rat
canine		1.15	1.15	1.21	1.6	1.29	1.46	1.3	1.31	1.46
bovine			1.13	1.16	1.53	1.25	1.35	1.25	1.27	1.39
horse				1.19	1.6	1.22	1.41	1.25	1.29	1.46
human					1.61	1.07	1.42	1.2	1.14	1.43
opossum						1.61	1.66	1.61	1.61	1.66
macaque							1.42	1.21	1.24	1.43
mouse								1.46	1.5	1.19
orangutan									1.07	1.47
chimpanzee										1.5
rat

¹Breakpoint re-use rate ranges from 1 without reuse to 2 with extensive reuse.

Figure 7.

Frequency of synteny block lengths. (A) The Probability Density Function (PDF) fits an exponential distribution (f(x)= 0.318*e^−0.318x, R²= 0.6812); (B) The PDF fits a power function (f(x)= 0.381* x^−1.381, R²= 0.9682

We tested whether the evolutionary rates of gene order change were consistent with a molecular clock model. Among the placental mammals analyzed in this study, the bovine and rat lineages had an accelerated gene rearrangement rate as compared to other placental mammals (z-test, P<0.001, in both cases). Although the rat rearranged significantly faster than all Primates (z-test, P<0.001), the mouse had a significantly greater gene rearrangement rate than human (z-test, P<0.001), chimpanzee (z-test, P<0.001), and orangutan (z-test, P<0.05) but no difference from macaque (z-test, N.S.). In addition, significant within-order differences in the gene rearrangement rates were observed in Rodentia separately (z-test, P<0.001 in both cases). In the NJ and ML trees, we also observed the intraordinal differences in the amino acid substitution rates in Rodentia (z-test, P<0.001 in both cases).

Discussion

The effect of choice of outgroup on phylogenetic reconstruction using sequence data was discussed previously (Janke et al., 1994). Since amphibian and bird diverged from the mammalian ancestor about 350 and 300 million years ago, respectively, (Graur and Martin, 2004), multiple substitutions may lead to saturation of nucleotide changes, which will degrade the phylogenetic signal (Janke et al., 1994). However, marsupials diverged from placentals about 130 million years ago based on paleontological evidence, making it suitable as an outgroup for the placental radiation (Janke et al., 1994). In the case of the gene order character, excessive gene rearrangement events lead to reuse of chromosomal breakpoints, making it difficult to resolve the species relationship.

In addition, the chicken (Gallus gallus) genome is reduced in size along with many absent gene families as compared to other vertebrates (Hughes and Friedman, 2008). Inclusion of the chicken genome reduced the dataset size of common orthologous genes, which are the data source for gene order phylogeny construction (Luo et al., 2009). Therefore, a marsupial mammal (i.e. opossum) is a better choice of an outgroup in reconstructing the basal relationship among placental mammals.

The distance-based gene order phylogenetic approach yielded well-resolved evolutionary relationships among some placental mammals. For instance, the relationship among hominid and non-hominid Primates revealed by gene order trees (Fig. 4) were congruent with that shown in the nucleotide substitution trees (Tocheri et al., 2008) and amino acid concatenated sequence-based trees (Fig. 5). In addition, the gene order trees provided an alternative cladistic character to investigate basal interordinal mammalian relationships which have been unresolved by the nucleotide substitution process. For instance, many studies have investigated but not resolved the evolutionary relationship of Primates, Rodentia, and some orders of Laurasiatheria (e.g. Carnivora, Artiodactyla and Perissodactyla) (Hallstrom et al., 2007; Madsen et al., 2001; Misawa and Nei, 2003; Murphy et al., 2001a; Murphy et al., 2001b). Likewise, the relationship among Carnivora, Perissodactyla and Artiodactyla is unclear (Arnason and Janke, 2002; Kullberg et al., 2006; Murphy et al., 2001a). The gene order phylogeny supported that Rodentia is an outgroup of Primates, Carnivora and Perissodactyla, and also supported that Artiodactyla as an outgroup of Carnivora and Perissodactyla. However, Artiodactyla, Carnivora and Perissodactyla were not a monophyletic group in the distance-based gene order phylogeny, and the DCJ tree differed from the breakpoint tree in the phylogenetic position of Artiodactyla.

Analysis of breakpoint reuse is important for reconstruction of ancestral genomes and rearrangement history (Alekseyev and Pevzner, 2009). Unambiguous reconstruction is possible when breakpoint reuse is limited. In contrast, extensive breakpoint reuse eliminates tracks of earlier rearrangements and thus represents a major obstacle to reconstruction of the rearrangement history. The low breakpoint reuse rate obtained in the present study (Table 2) is consistent with a previous report of 20% reuse of breakpoints during mammalian evolution (Murphy et al., 2005), suggesting that chromosomal rearrangements occurred randomly and the gene order sequence is reliable for reconstructing the placental mammalian phylogeny.

The short but well-supported basal branches leading to the Primate-Artiodactyla-Carnivora-Perissodactyla clade (Fig. 4) suggested that only a few synapomorphies joined the Primates-Carnivora-Perissodactyla clade, whereas the long leaf branches (Fig. 4) indicated that most autapomorphies occurred after the divergence of these placental orders. Short basal branches were also revealed in trees using mitochondrial genomic sequences (Corneli, 2002). Note that the branch lengths shown (Fig. 4) were related to the number of the orthologous genes shared by all of the genomes in the phylogenetic tree; with less genomes included in the phylogenetic tree, a greater number of orthologous genes were shared among the genomes in comparison and could be used to compute the gene rearrangements, which would result in longer branches. Preliminary analyses with a smaller number of genomes were consistent with this hypothesis (not shown).

The amino acid sequence-based trees constructed by NJ, ML, and MP methods were generally consistent with the distance-based gene order trees. The former supported a monophyly of Primates-Artiodactyla-Carnivora-Perissodactyla (Fig. 5), which is consistent with the DCJ tree. However, a Bayesian tree from the concatenated amino acid sequences supported the Euarchontoglires hypothesis (i.e. monophyly of Primates and Rodentia). One advantage of the Bayesian method implemented in MrBayes software over NJ, ML, and MP methods is that it provides options to model heterotachy in phylogeny construction. However, because inclusion of heterotachy in our Bayesian analyses did not affect the results, it seems unclear whether heterotachy is responsible for the differences between trees constructed by the Bayesian method and by the NJ, ML, and MP methods.

Another notable difference between the molecular sequence and gene order based trees is whether the Artiodactyla-Carnivora-Perissodactyla forms a monophyletic clade. Whatever method was used, the amino acid sequence trees supported a monophyly of these three orders (Fig. 5 and 6), whereas the gene order trees did not (Fig. 4).

Ohno proposed the random breakage model (Ohno, 1973) which described that chromosomal rearrangements occur randomly and breaks of the ancestral genome are uniformly distributed along the chromosomal length (Zdobnov and Bork, 2007). Several follow-up studies provided evidence supporting the random breakage of chromosomes (International Human Genome Sequencing Consortium, 2001; Mural et al., 2002; Nadeau and Taylor, 1984). It was claimed that an exponential distribution of synteny blocks of a certain length should be expected, provided the random breakage occurred (Zdobnov and Bork, 2007). However, data available in the literature from pairwise comparisons among sequenced genomes suggested that synteny blocks of a certain length fit better to a power function than to an exponential distribution (Zdobnov and Bork, 2007). Other studies suggested that the random breakage model cannot explain closely located breakpoints (i.e. synteny block length < 1 Mbp), and proposed the fragile breakage model could account for a significant number of short synteny blocks observed from genomic sequences (Pevzner and Tesler, 2003). Here, we showed that the distribution of synteny block lengths cannot fit to an exponential function (Fig. 7A), but the power function seems a better fit (Fig. 7B), which is consistent with previous observations (Zdobnov and Bork, 2007). The approximate power law distribution of synteny block lengths is consistent with the finding of a low breakpoint reuse rate, indicating random breakages among chromosomes.

Phylogenomic analysis dated the basal placental mammal divergences at 95–100 million years ago, but many of the interordinal divergences occurred only a few million years later (Hallstrom and Janke, 2008). Paleontological evidence also supported a sudden radiation of placental mammals in the late Cretaceous period (Archibald, 2003; Cannarozzi et al., 2007). The narrow time interval within which basal placental divergences took place renders it problematic in constructing the sequence-based (Hallstrom and Janke, 2008) and short interspersed repetitive elements (SINEs) based phylogenetic relationships (Miyamoto 1999). Although using a large amount of data and improving taxon sampling might have enhanced the resolution of narrow divergences, such efforts did not resolve the deep mammalian relationships (Hallstrom and Janke, 2008).

Many possible causes have been proposed to account for the difficulty in resolving narrow divergences, as in the case of ordinal and higher level divergences among placental mammals (Hallstrom and Janke, 2008). One possible explanation is introgression from species hybridization, a process known as the incorporation of genes from one species into the gene pool of another (Mallet, 2005). This happens where closely related populations hybridize with each other before they become genetically isolated (Hallstrom and Janke, 2008). Another possible cause is lineage sorting which results from fixation of different alleles in the descendant lineages from a speciation event. Lineage sorting jumbles the genomes of species which radiated over a short period of evolutionary time and also gives rise to the inconsistency between gene history and species phylogeny (Hallstrom and Janke, 2008).

Short branches suggest few changes of character states during a rapid taxon radiation (Boore, 2006), indicating that an extremely conserved character is not able to resolve such a rapid radiation and instead that a relatively fast evolving character is required (Corneli, 2002). On the other hand, an ancient relationship suggests that the fast evolving character may accumulate backward mutations, resulting in homoplasy and in turn obscuring the phylogenetic signal (Boore, 2006; Corneli, 2002). Although traditional sequence substitution models have resolved many controversies, resolving short branches remains a notoriously difficult problem (Murphy et al., 2004). For instance, mitochondrial DNA sequences are highly saturated at many positions with respect to ancient interordinal divergences (Corneli, 2002).

However, many properties of gene rearrangements are favorable to resolving rapid radiations. One important characteristic is the lower rate of change of gene order in contrast to nucleotide substitution. Likewise, in a deeper evolutionary relationship, multiple nucleotide substitutions may obscure the phylogenetic signal (Boore, 2006), whereas relatively few chromosomal breakpoints are reused. In addition, the molecular sequence character has only four (nucleotides) or 20 (amino acids) possible character states, hence convergent and parallel substitutions might have occurred among different lineages over a long period of time. In contrast, there are a large number of states in a gene order character, each of which represents a permutation of genes in the genome, so that identical changes are unlikely to occur in two separate lineages (Boore, 2006). The potential usage of genome rearrangement as a powerful evolutionary character to resolve short branches and contested relationships in mammalian phylogeny has already been addressed by Murphy et al. (2004) and Boore (2006). Our results suggest that the genome rearrangement character is useful and complementary to nucleotide substitution in resolving the deeper mammalian relationships.

In mammalian genomes, the order of genes in some genomic regions is more conserved than other regions (Murphy et al., 2004), implying that the various genes and blocks of genes resulting from rearrangement events are not entirely independent of each other. However, by applying a jackknifing technique, we assume that the sequential ordering of genes is arranged by a rearrangement process which occurs uniformly across the genome. A similar assumption is made in a bootstrapping test of a sequence-based phylogeny, in which aligned sites (nucleotides or amino acids) are assumed independent of each other. However, in many cases they are correlated (Felsenstein, 1985). For instance, in a protein-coding gene, a single codon consists of three adjacent sites. In most cases, replacement of the first or second position of a codon results in an amino acid substitution. In another example, when a slightly deleterious mutation is fixed during a bottleneck, afterwards another advantageous mutation that compensates for the deleterious mutation may occur. This compensatory mutation may then be fixed by positive selection. Such compensatory changes usually occurred near to the site of the deleterious mutation (Hughes, 2008). Both examples show that the aligned sites, like that of gene order, are not independent of each other.

Therefore, both bootstrapping and jackknifing techniques generate an approximate statistic rather than a true statistic. The essence of the two techniques is to add perturbation to the data, and to assess whether the original data contain sufficient phylogenetic signal to resist the perturbation. A high jackknifing or bootstrap support value on an internal branch indicates the branch is reliable (Felsenstein, 1985). In fact, the jackknifing test has been used and verified in the gene order phylogenies of prokaryotic species (Belda et al., 2005; Luo et al., 2008; Luo et al., 2009). A recent simulation study demonstrated the jackknifing test is useful in gene order data (Shi et al., 2010).

However, in some cases high bootstrap support in a sequence-based tree may indicate the reinforcement of certain systematic errors contained in the data, which results in an incorrect tree (Gadagkar et al., 2005). Wildman and others (2007) showed that Maximum Parsimony (MP), Maximum Likelihood (ML), and Bayesian methods supported the Euarchontoglires clade, whereas Neighbor Joining (NJ) yielded a basal position of murid rodents from their sampling of Primates, artiodactyls and carnivores. Both of these mutually exclusive topologies were well supported by the bootstrap test (Wildman et al., 2007). The possible systematic errors in molecular sequence data include nucleotide or amino acid compositional bias, long-branch attraction, and heterotachy (Wildman et al., 2007). In gene order data, there is no compositional bias issue, because its character states are not analogous to those of nucleotide and amino acid sites. Long-branch attraction due to parallel changes is less severe in the gene order data than in nucleotide (or amino acid) sequence data, because gene order has many more character states and hence less parallel changes than the other (Boore, 2006). Furthermore, currently there is little evidence for heterotachy in the genome rearrangement process.

Computer simulation suggested that, at the 85% as the threshold of confidence value, only 20% of the jackknife trees contained false positive branches (Shi et al., 2010). The jackknifing test is able to identify 95% of the incorrect branches under the 85% threshold confidence value (Shi et al., 2010). One shortcoming of the jackknifing technique is that a low confidence value could be assigned to correct branches, suggesting that interpretation of branches with low confidence values should be carefully examined (Shi et al., 2010). In the case of the distance-based mammalian gene order phylogeny, the DCJ tree (Fig. 4A) and breakpoint tree (Fig. 4B) have the same topology, but the DCJ tree has lower confidence values than the breakpoint tree for the branches leading to swine, bovine, canine and horse (Fig. 4). The high confidence values of these branches in the breakpoint tree lend additional support for these branches in the DCJ tree.

The question of whether a phylogenetic analysis is reliable based on a limited number of taxa has been much debated (DeBry, 2005; Hillis, 1998; Hillis et al., 2003; Hughes and Friedman, 2007; Mitchell et al., 2000; Poe, 1998; Pollock et al., 2002; Rannala et al., 1998; Rosenberg and Kumar, 2001, 2003; Zwickl and Hillis, 2002). Increased taxon sampling serves to break up long branches and thereby avoids erroneous clustering of fast evolving taxa known as the long-branch attraction problem (Hughes and Friedman, 2007; Pollock et al., 2002). Although there are only 10 taxa included in the gene order phylogenetic analysis (Fig. 4), there is no evidence that supports long-branch attraction as the cause of the basal position of Rodentia in relationship to Carnivora and Perissodactyla. Mouse had a much lower rate than rat in gene rearrangements, and inclusion of mouse avoided the potential long-branch attraction problem. However, it is not clear whether the basal position of Artiodactyla in the breakpoint tree was due to long-branch attraction.

An early study by Wu and Li (1985) showed that the rodent lineages evolved significantly faster than human; they made comparisons of protein-coding regions of 11 nuclear genes, the 5′ and 3′ untranslated regions of five different mRNAs, and the beta-globin gene family of rodents and human. Later, Janke and others (1994) argued the use of Artiodactyla or Carnivora as an outgroup by Wu and Li (1985) was not appropriate, which may account for the observed acceleration of molecular rates in the rodent lineage. They further showed that the majority of mitochondrial genes conformed to a molecular clock model in human and rodents (Janke et al., 1994). In fact, before the publication of Janke et al., other studies using chicken as an outgroup reached the same conclusion that rodent evolved significantly faster than Primates (Bulmer et al., 1991; Li et al., 1990). This conclusion was confirmed by recent studies using large datasets (Huttley et al., 2007).

These conflicting findings may result from the distinctive evolutionary patterns between nuclear and mitochondrial genes. For instance, recombination is common in nuclear genes but not in mitochondrial genes in mammals (Innan and Nordborg, 2002). In mammalian mitochondria, transitions predominate over transversions, while this is not the case for nuclear genes (Belle et al., 2005). These differences indicate that nuclear and mitochondrial genes are not directly comparable in the evolutionary rate analysis, and the rate of the mitochondrial DNA change may not represent that of nuclear genomic change. Although there was evidence that the evolutionary rates of the several nuclear genes are constant across the placental mammals (Easteal, 1988, 1990), a small number of nuclear genes is not sufficient to draw certain conclusions on lineage-specific rates of evolution (Easteal, 1992). The concatenated nuclear amino acid sequence-based phylogenetic analysis using Maximum-Likelihood and Neighbor-Joining methods in the present study supported that Rodentia evolved significantly faster than Primates (z-test, P<0.001).

Our gene rearrangement rate analysis supported that the rat lineage evolved significantly faster than Primates, and the mouse lineage evolved significantly faster than human, chimpanzee, and orangutan, but not macaque. This is consistent with the previous findings that the rearrangement rate of mouse is in-between various Primates (Coghlan et al., 2005). In addition, the rat lineage showed a significantly increased rate of rearrangement as compared to mouse. Other studies detected 180 conserved elements (genomic segments of preserved gene order) shared between human and mouse and 109 shared between human and rat (O’Brien et al., 1999), suggesting that the rearrangement rate of rat is greater than that of mouse. This is also consistent with the concatenated amino acid sequence-based analysis in the present study, but different from several previous reports, which showed that rat had either slightly more neutral substitutions in protein-coding gene regions than in mouse (Rat Genome Sequencing Project Consortium, 2004) or almost identical rates with mouse (Huttley et al., 2007).

A non-clock-like manner of gene order changes has been observed in animal mitochondrial genomes (Boore, 1999; Boore and Brown, 1998), and is a common property of genome-level cladistic characters (Boore, 2006). Clock-like characters (e.g. nucleotide substitution) perform poorly in resolving short basal branches because the signal to noise ratio in the data closely matches the ratio of the time periods of the internal branches to the leaf branches (Boore, 2006). However, non-clocklike characters (e.g. genome rearrangement) may have had some occasional and abrupt changes occurring and being fixed during rapid radiation (Boore, 2006). Although non-clocklike character is not desirable to estimate the time of lineage splitting, it is the non-clocklike behavior that makes a genome-level character such as genome rearrangement especially useful in resolving narrow and ancient divergences (Boore, 2006).

Supplementary Material

01

Supplementary Figure 1. Phylogeny of Primates (human, chimpanzee, orangutan, macaque), Laurasiatheria (canine, horse, bovine) and Rodentia (mouse, rat) inferred from (A, C, E) a DCJ distance (swine or rabbit may or may not be included); (B, D, F) a breakpoint distance matrix tree (swine or rabbit may or may not be included). Values above branches show the number of times that the clade defined by that node was supported by 1000 jackknife trees. Values below branches show number of genome rearrangement events. Opossum is the outgroup.

02

Supplementary Table 1. The 9212 orthologous genes shared by 10 mammalian genomes.

03

Supplementary Table 2. The 6740 orthologous genes shared by 11 mammalian genomes (with rabbit genome included)

• Gene order phylogeny placed rodents outside other orders of placental mammals.

• Rapid radiation in distant past makes phylogenetic reconstruction difficult.

• Gene order may be a good character in mammals because breakpoint re-use is low.