A Sparse Ising Model with Covariates

Summary

There has been a lot of work fitting Ising models to multivariate binary data in order to understand the conditional dependency relationships between the variables. However, additional covariates are frequently recorded together with the binary data, and may influence the dependence relationships. Motivated by such a dataset on genomic instability collected from tumor samples of several types, we propose a sparse covariate dependent Ising model to study both the conditional dependency within the binary data and its relationship with the additional covariates. This results in subject-specific Ising models, where the subject’s covariates influence the strength of association between the genes. As in all exploratory data analysis, interpretability of results is important, and we use ℓ₁ penalties to induce sparsity in the fitted graphs and in the number of selected covariates. Two algorithms to fit the model are proposed and compared on a set of simulated data, and asymptotic results are established. The results on the tumor dataset and their biological significance are discussed in detail.

1. Introduction

Markov networks have been applied in a wide range of scientific and engineering problems to infer the local conditional dependency of the variables. Examples include gene association studies (Peng et al., 2009; Wang et al., 2011), image processing (Hassner and Sklansky, 1980; Woods, 1978), and natural language processing (Manning and Schutze, 1999). A pairwise Markov network can be represented by an undirected graph G = (V, E), where V is the node set representing the collection of random variables, and E is the edge set where the existence of an edge is equivalent to the conditional dependency between the corresponding pair of variables, given the rest of the graph.

Previous studies have focused on the case where an i.i.d. sample is drawn from an underlying Markov network, and the goal is to recover the graph structure, i.e., the edge set E, from the data. Two types of graphical models have been studied extensively: the multivariate Gaussian model for continuous data, and the Ising model (Ising, 1925) for binary data. In the multivariate Gaussian case, the graph structure E is completely specified by the off-diagonal elements of the inverse covariance matrix, also known as the precision matrix. Therefore, estimating the edge set E is equivalent to identifying the non-zero off-diagonal entries of the precision matrix. Many papers on estimating the inverse covariance matrix have appeared in recent years, with a focus on the high-dimensional framework, for example, Meinshausen and Bühlmann (2006); Yuan and Lin (2007); Rothman et al. (2008); d’Aspremont et al. (2008); Rocha et al. (2008); Ravikumar et al. (2008); Lam and Fan (2009); Peng et al. (2009); Yuan (2010); Cai et al. (2011). Most of these papers focus on penalized likelihood methods, and many establish asymptotic properties such as consistency and sparsistency. Many have also proposed fast computational algorithms, the most popular of which is perhaps glasso by Friedman et al. (2008), which was recently improved further by Witten et al. (2011) and Mazumder and Hastie (2012).

In the Ising model, the network structure can be identified from the coefficients of the interaction terms in the probability mass function. The problem is, however, considerably more difficult due to the intractable normalizing constant, which makes the penalized likelihood methods popular for the Gaussian case extremely computationally demanding. Ravikumar et al. (2010) proposed an approach in the spirit of Meinshausen and Bühlmann (2006)’s work for the Gaussian case, fitting separate ℓ₁-penalized logistic regressions for each node to infer the graph structure. A pseudo-likelihood based algorithm was developed by Höeing and Tibshirani (2009) and analyzed by Guo et al. (2010c).

The existing literature mostly assumes that the data are an i.i.d. sample from one underlying graphical model, although the case of data sampled from several related graphical models on the same nodes has been studied both for the Gaussian and binary cases (Guo et al., 2010b,a). However, in many real-life situations, the structure of the network may further depend on other extraneous factors available to us in the form of explanatory variables or covariates, which result in subject-specific graphical models. For example, in genetic studies, deletion of tumor suppressor genes plays a crucial role in tumor initiation and development. Since genes function through complicated regulatory relationships, it is of interest to characterize the associations among various deletion events in tumor samples. However, in practice we observe not only the deletion events, but also various clinical phenotypes for each subject, such as tumor category, mutation status, and so on. These additional factors may influence the regulatory relationships, and thus should be included in the model. Motivated by situations like this, here we propose a model for the conditional distribution of binary network data given covariates, which naturally incorporates covariate information into the Ising model, allowing the strength of the connection to depend on the covariates. With high-dimensional data in mind, we impose sparsity in the model, both in the network structure and in covariate effects. This allows us to select important covariates that have influence on the network structure.

There have been a few recent papers on graphical models that incorporate covariates, but they do so in ways quite different from ours. Yin and Li (2011) and Cai et al. (2013) proposed to use conditional Gaussian graphical models to fit the eQTL (gene expression quantitative loci) data, but only the mean is modeled as a function of covariates, and the network remains fixed across different subjects. Liu et al. (2010) proposed a graph-valued regression, which partitions the covariate space and fits separate Gaussian graphical models for each region using glasso. This model does result in different networks for different subjects, but lacks interpretation of the relationship between covariates and the graphical model. Further, there is a concern about stability, since the so built graphical models for nearby regions of the covariates are not necessarily similar. In our model, covariates are incorporated directly into the conditional Ising model, which leads to straightforward interpretation and “continuity” of the graphs as a function of the covariates, since in our model it is the strength of the edges rather than the edges themselves that change from subject to subject.

The rest of the paper is organized as follows. In Section 2, we describe the conditional Ising model with covariates, and two estimation procedures for fitting it. Section 3 establishes asymptotic properties of the proposed estimation method. We evaluate the performance of our method on simulated data in Section 4, and apply it to a dataset on genomic instability in breast cancer samples in Section 5. Section 6 concludes with a summary and discussion.

2. Conditional Ising Model with Covariates

2.1 Model set-up

We start from a brief review of the Ising model, originally proposed in statistical physics by Ising (1925). Let y = (y₁, …, y_q) ∈ {0, 1}^q denote a binary random vector. The Ising model specifies the probability mass function P_θ(y) as

$$P_{\mathit{\theta }}(\mathit{y})=\frac{1}{Z(\mathit{\theta })}\text{exp}(\sum _j{\theta }_{jj}{y}_j+\sum _{k>j}{\theta }_{jk}{y}_j{y}_k),$$

where θ = (θ₁₁, θ₁₂, …, θ_q−1q, θ_qq) is a q(q + 1)/2-dimensional parameter vector and Z(θ) is the partition function ensuring the 2^q probabilities summing up to 1. Note that from now on we assume θ_jk equals to θ_kj unless otherwise specified. The Markov property is related to the parameter θ via

$${\theta }_{jk}=0\iff y_j\perp y_k\Vert {\mathit{y}}_{\backslash (j,k)},\forall j\ne k,$$ (1)

i.e., y_j and y_k are independent given all other y’s if and only if θ_jk = 0.

Now suppose we have additional covariate information, and the data are a sample of n i.i.d. points 𝒟_n = {(x¹, y¹), …, (xⁿ, yⁿ)} with xⁱ ∈ ℝ^p and yⁱ ∈ {0, 1}^q. We assume that given covariates x, the binary response y follows the Ising distribution given by

$$P(\mathit{y}|\mathit{x})=\frac{1}{Z(\mathit{\theta }(\mathit{x}))}\text{exp}(\sum _{j=1}^q{\mathit{\theta }}_{jj}(\mathit{x})y_j+\sum _{(j,k):1\le k<j\le q}{\mathit{\theta }}_{jk}(\mathit{x})y_j{y}_k).$$ (2)

We note that for any covariates xⁱ, the conditional Ising model is fully specified by the vector θ(xⁱ) = (θ₁₁(xⁱ)θ₁₂(xⁱ), …, θ_q−1q(xⁱ), θ_qq(xⁱ)), and by setting θ_kj(x) = θ_jk(x) for all j > k, the functions θ_jk(x) can be connected to conditional log-odds in the following way,

$$\text{log}\left(\frac{P(y_j=1|{\mathit{y}}_{\backslash j},\mathit{x})}{1-P(y_j=1|{\mathit{y}}_{\backslash j},\mathit{x})}\right)={\mathit{\theta }}_{jj}(\mathit{x})+\sum _{k:k\ne j}{\mathit{\theta }}_{jk}(\mathit{x})y_k,$$ (3)

where, y_\j = (y₁, …, y_j−1, y_j+1, …, y_q). Further, conditioning on y_\{j,k} being 0, we have

$$\text{log}\left(\frac{P(y_j=1,y_k=1|{\mathit{y}}_{\backslash \{j,k\}},\mathit{x})P(y_j=0,y_k=0|{\mathit{y}}_{\backslash \{j,k\}},\mathit{x})}{P(y_j=1,y_k=0|{\mathit{y}}_{\backslash \{j,k\}},\mathit{x})P(y_j=0,y_k=1|{\mathit{y}}_{\backslash \{j,k\}},\mathit{x})}\right)={\mathit{\theta }}_{jk}(\mathit{x}).$$

Similarly to (1), this implies y_j and y_k are conditionally independent given covariates x and all other y’s if and only if θ_jk(x) = 0.

A natural way to model θ_jk(x) is to parametrize it as a linear function of x. Specifically, for 1 ≤ j ≤ k ≤ q, we let

$${\mathit{\theta }}_{jk}(\mathit{x})={\theta }_{jk0}+{\mathit{\theta }}_{jk}^T\mathit{x},\hspace{1em}\text{where}{\mathit{\theta }}_{jk}^T=({\theta }_{jk1},\dots ,{\theta }_{jkp})$$

$${\mathit{\theta }}_{jk}(\mathit{x})={\mathit{\theta }}_{kj}(\mathit{x}),\hspace{1em}\hspace{1em}\forall j>k$$

The model can be expressed in terms of the parameter vector θ as follows:

$$P_{\mathit{\theta }}(\mathit{y}|\mathit{x})=\frac{1}{Z(\mathit{\theta }(\mathit{x}))}\text{exp}(\sum _{j=1}^q({\theta }_{jj0}+{\mathit{\theta }}_{jj}^T\mathit{x})y_j+\sum _{k>j}({\theta }_{jk0}+{\mathit{\theta }}_{jk}^T\mathit{x})y_j{y}_k).$$ (4)

Instead of (3), we now have the log-odds that depend on the covariates, through

$$\text{log}\left(\frac{P(y_j=1|{\mathit{y}}_{\backslash j},\mathit{x})}{1-P(y_j=1|{\mathit{y}}_{\backslash j},\mathit{x})}\right)={\theta }_{jj0}+{\mathit{\theta }}_{jj}^T\mathit{x}+\sum _{k:k\ne j}({\theta }_{jk0}+{\mathit{\theta }}_{jk}^T\mathit{x})y_k.$$ (5)

Note that for each j, the conditional log-odds in (5) involves (p+1)q parameters; taking into account the symmetry, i.e. θ_jk0 = θ_kj0 and θ_jk = θ_kj, we thus have a total of (p+1)q(q+1)/2 parameters in the fully parametrized model.

The choice of linear parametrization for θ_jk(x) has several advantages. First, (5) mirrors the logistic regression model when viewing the x_ℓ’s, y_k’s and x_ℓy_k’s (k ≠ j) as predictors. Thus the model has the same interpretation as the logistic regression model, where each parameter describes the size of the conditional effect of that particular predictor. Specifically, for continuous covariates, θ_jkℓ (ℓ ≥ 1) describes the effect of covariate x_ℓ on the conditional log-odds of y_j when y_k is 1, and θ_jk0 simply describes the main effect of y_k on the conditional log-odds of y_j. For categorical covariates, the interpretation is almost the same except that now the covariate would be represented by several dummy variables, and the parameter θ_jkℓ represents the effect of each level of the covariate relative to the reference level. Second, this parametrization has a straightforward relationship to the Markov network. One can tell which edges exist and on which covariates they depend by simply looking at θ. Specifically, the vector $({\theta }_{jk0},{\mathit{\theta }}_{jk}^T)$ being zero implies that y_k and y_j are conditionally independent given any x and the rest of y_ℓ’s, and θ_jkℓ being zero implies that the conditional association between y_j and y_k does not depend on x_ℓ. Third, the continuity of linear functions ensures the similarity among the conditional models for similar covariates, which is a desirable property. Finally, the linear formulation promises the convexity of the negative log-likelihood function, allowing efficient algorithms for fitting the model discussed next.

2.2 Fitting the model

The probability model P_θ(y|x) in (4) includes the partition function Z(θ(x)), which requires summation of 2^q terms for each data point and makes it intractable to directly maximize the joint conditional likelihood $\sum _{i=1}^n\text{log}{P}_{\mathit{\theta }}({\mathit{y}}^i|{\mathit{x}}^i)$. However, (5) suggests we can use logistic regression to estimate the parameters, an approach in the spirit of Ravikumar et al. (2010). The idea is essentially to maximize the conditional log-likelihood of $y_j^i$ given ${\mathit{y}}_{\backslash j}^i$ and xⁱ rather than the joint log-likelihood of yⁱ.

Specifically, the negative conditional log-likelihood for y_j can be written as follows

$${\ell }_j(\mathit{\theta };{𝒟}_n)=-\frac{1}{n}\sum _{i=1}^n\text{log}P(y_j^i|{\mathit{x}}^i,{\mathit{y}}_{\backslash j}^i)=-\frac{1}{n}\sum _{i=1}^n(\text{log}(1+e^{{\eta }_j^i})-y_j^i{\eta }_j^i),$$ (6)

where

$${\eta }_j^i=\text{log}\left(\frac{P(y_j^i=1|{\mathit{y}}_{\backslash j}^i,{\mathit{x}}^i)}{1-P(y_j^i=1|{\mathit{y}}_{\backslash j}^i,{\mathit{x}}^i)}\right)={\theta }_{jj0}+{\mathit{\theta }}_{jj}^T{\mathit{x}}^i+\sum _{k\ne j}({\theta }_{jk0}+{\mathit{\theta }}_{jk}^T{\mathit{x}}^i)y_k^i.$$

Note that this conditional log-likelihood involves the parameter vector θ only through its subvector ${\mathit{\theta }}_j=({\theta }_{j10},{\mathit{\theta }}_{j1}^T,\dots ,{\theta }_{jq0},{\mathit{\theta }}_{jq}^T)\in {ℝ}^{(p+1)q}$, thus we sometimes write ℓ_j(θ_j; 𝒟_n) when the rest of θ is not relevant.

There are (p + 1)q(q + 1)/2 parameters to be estimated, so even for moderate p and q the dimension of θ can be large. For example, with p = 10 and q = 10, the model has 605 parameters. Thus there is a need to regularize θ. Empirical studies of networks as well as the need for interpretation suggest that a good estimate of θ should be sparse. Thus we adopt the ℓ₁ regularization to encourage sparsity, and propose two approaches to maximize the conditional likelihood (6).

2.2.1 Separate regularized logistic regressions

The first approach is to estimate each θ_j, j = 1, …, q separately using the following criterion,

$$\underset{{\mathit{\theta }}_j\in {ℝ}^{(p+1)q}}{\text{min}}{\ell }_j({\mathit{\theta }}_j;{𝒟}_n)+\lambda {\Vert {\mathit{\theta }}_{j\backslash 0}\Vert }_1,$$

where θ_j\0 = θ_j\{θ_jj0}, that is, we do not penalize the intercept term θ_jj0.

In this approach, θ_jk and θ_kj are estimated from the jth and kth regressions, respectively, thus the symmetry θ̂_jk = θ̂_kj is not guaranteed. To enforce the symmetry in the final estimate, we post-process the estimates following Meinshausen and Bühlmann (2006), where the initial estimates are combined by comparing their magnitudes. Specifically, let θ̂_jkℓ denote the final estimate and ${\hat{\theta }}_{jk\ell }^0$ denote the initial estimate from the separate regularized logistic regressions. Then for any 1 ≤ j < k ≤ q and any ℓ = 0, …, p, we can use one of the two symmetrizing approaches:

$$\text{separate}-\text{max}:{\hat{\theta }}_{jk\ell }={\hat{\theta }}_{kj\ell }={\hat{\theta }}_{jk\ell }^0{𝕀}_{(|{\hat{\theta }}_{jk\ell }^0|>|{\hat{\theta }}_{kj\ell }^0|)}+{\hat{\theta }}_{kj\ell }^0{𝕀}_{(|{\hat{\theta }}_{jk\ell }^0|<|{\hat{\theta }}_{kj\ell }^0|)}$$

$$\text{separate}-\text{min}:{\hat{\theta }}_{jk\ell }={\hat{\theta }}_{kj\ell }={\hat{\theta }}_{jk\ell }^0{𝕀}_{(|{\hat{\theta }}_{jk\ell }^0|<|{\hat{\theta }}_{kj\ell }^0|)}+{\hat{\theta }}_{kj\ell }^0{𝕀}_{(|{\hat{\theta }}_{jk\ell }^0|>|{\hat{\theta }}_{kj\ell }^0|)}$$

The separate-min approach is always more conservative than separate-max in the sense that the former provides more zero estimates. It turns out that when q is relatively small, the separate-min approach is often too conservative to effectively identify non-zero parameters, while when q is relatively large, the separate-min approach performs better than the separate-max approach.. More details are given in Section 4.

2.2.2 Joint regularized logistic regression

The second approach is to estimate the entire vector θ simultaneously instead of estimating the θ_j’s separately, using the criterion,

$$\underset{\mathit{\theta }\in {ℝ}^{(p+1)q(q+1)/2}}{\text{min}}\sum _{j=1}^q{\ell }_j({\mathit{\theta }}_j;{𝒟}_n)+\lambda {\Vert {\mathit{\theta }}_{\backslash 0}\Vert }_1,$$

where θ_\0 = θ\{θ₁₁₀, θ₂₂₀, …, θ_qq0}. One obvious benefit of the joint approach is that θ̂ can be automatically symmetrized by treating θ_jk and θ_kj as the same during estimation. The price, however, is that it is computationally much less efficient than the separate approach.

To fit the model using either the separate or the joint approach, we adopt the coordinate shooting algorithm in Fu (1998), where we update one parameter at a time and iterate until convergence. The implementation is similar to the glmnet algorithm of Friedman et al. (2010), and we omit the details here.

3. Asymptotics: Consistency of Model Selection

In this section we present the model selection consistency property for the separate regularized logistic regression. Results for the joint approach can be derived in the same fashion. The spirit of the proof is similar to Ravikumar et al. (2010), but since their model does not include covariates x, both our assumptions and conclusions are different.

In this analysis, we treat the covariates x_i’s as random vectors. With a slight change of notation, we now use θ_j to denote θ_j\0, dropping the intercept which is irrelevant for model selection. The true parameter is denoted by θ*. Without loss of generality we assume that ${\theta }_{jj0}^{*}=0,$, and we also assume that θ̂_jj0 = 0.

First, we introduce additional notation to be used throughout this section. Let

$${\mathit{I}}_j^{*}={𝔼}_{{\theta }^{*}}({\nabla }^2\text{log}{P}_{\mathit{\theta }}(y_j|\mathit{x},{\mathit{y}}_{\backslash j}))={𝔼}_{{\theta }^{*}}(p_j(1-p_j)(\mathit{x}\otimes {\mathit{y}}_{\backslash j}){(\mathit{x}\otimes {\mathit{y}}_{\backslash j})}^T)(\text{Information matrix})$$ (7)

$${\mathit{U}}_j^{*}={𝔼}_{{\theta }^{*}}((\mathit{x}\otimes {\mathit{y}}_{\backslash j}){(\mathit{x}\otimes {\mathit{y}}_{\backslash j})}^T)$$ (8)

where

$$p_j=p_j(\mathit{x},{\mathit{y}}_{\backslash j})=P_{{\mathit{\theta }}^{*}}(y_j=1|\mathit{x},{\mathit{y}}_{\backslash j}),$$

$$\mathit{x}\otimes {\mathit{y}}_{\backslash j}={(1,x_1,\dots ,x_p)}^T\otimes {(y_1,\dots ,y_{j-1},1,y_{j+1},\dots ,y_q)}^T\backslash \{1\}.$$

Let 𝒮_j denote the index set of the non-zero elements of ${\mathit{\theta }}_j^{*}$, and let ${\mathit{I}}_{{𝒮}_j{𝒮}_j}^{*}$ be the submatrix of ${\mathit{I}}_j^{*}$ indexed by 𝒮_j. Similarly defined are ${\mathit{I}}_{{𝒮}_j^c{𝒮}_j}$ and ${\mathit{I}}_{{𝒮}_j^c{𝒮}_j^c}$, where ${𝒮}_j^c$ is the complement set of 𝒮_j. Moreover, for any matrix A, let ‖A‖_∞ = max_i ∑_j |A_ij | be the matrix L_∞ norm, and let Λ_min(A) and Λ_max(A) be the minimum and maximum eigenvalues of A, respectively.

For our main results to hold, we make the following assumptions for all q logistic regressions.

• A1
  There exists a constant α ∈ (0, 1], such that

  $${\Vert {\mathit{I}}_{{𝒮}_j^c{𝒮}_j}^{*}{\left({\mathit{I}}_{{𝒮}_j{𝒮}_j}^{*}\right)}^{-1}\Vert }_{\infty }\le (1-\alpha ).$$
• A2
  There exist constants Δ_min > 0 and Δ_max > 0, such that

  $${\mathrm{\Lambda }}_{\text{min}}\left({\mathit{I}}_{{𝒮}_j{𝒮}_j}^{*}\right)\ge {\mathrm{\Delta }}_{\text{min}}$$

  $${\mathrm{\Lambda }}_{\text{max}}({\mathit{U}}_j^{*})\le {\mathrm{\Delta }}_{\text{max}}$$
• A3
  There exists δ > 0, such that

  $$P({\Vert \mathit{x}\Vert }_{\infty }\ge M)\le \text{exp}(-M^{\delta }),\text{for all}M\ge M_0>0.$$ (9)

These assumptions bound the correlation among the effective covariates, and the amount of dependence between the group of effective covariates and the rest. Under these assumptions, we have the following result:

Theorem 1

For any j = 1, …, q, let θ̂_j be a solution of the problem

$$\underset{{\mathit{\theta }}_j}{\text{min}}{\ell }_j({\mathit{\theta }}_j;{𝒟}_n)+{\lambda }_n{\Vert {\mathit{\theta }}_j\Vert }_1.$$ (10)

Assume A1, A2 and A3 hold for ${\mathit{I}}_j^{*}$ and ${\mathit{U}}_j^{*}$. Let d = max_j ‖ 𝒮_j‖₀ and C > 0 be a constant independent of (n, p, q). If

$$M_n=M\ge {(C{\lambda }_n^{2}n)}^{\frac{1}{1+\delta }},$$ (11)

$${\lambda }_n\ge C{M}_n\sqrt{\frac{\text{log}p+\text{log}q}{n}},$$ (12)

$$n\ge C{M}_n^2{d}^3(\text{log}p+\text{log}q),$$ (13)

then the following hold with probability at least $1-{\text{exp}}^{-C{({\lambda }_n^{2}n)}^{{\delta }^{*}}}$ (δ* is a constant in (0, 1)),

1. Uniqueness: θ̂_j is the unique optimal solution for any j ∈ {1, …, q}.

2. ℓ₂ consistency: ${\Vert {\hat{\mathit{\theta }}}_j-{\mathit{\theta }}_j^{*}\Vert }_2\le 5{\lambda }_n\sqrt{d}/{\mathrm{\Delta }}_{\text{min}},\mathit{\text{for any}}j\in \{1,\dots ,q\}$ for any j ∈ {1, …, q}

3. Sign consistency: θ̂_j correctly identifies all the zeros in ${\mathit{\theta }}_j^{*}$ for any j ∈ {1, …, q}; moreover, θ̂_j identifies the correct sign of non-zeros in ${\mathit{\theta }}_j^{*}$ whose absolute value is at least $10{\lambda }_n\sqrt{d}/{\mathrm{\Delta }}_{\text{min}}$.

Theorem 1 establishes the consistency of model selection allowing both of the dimensions p(n) and q(n) to grow to infinity with n. The extra condition A3, which requires the distribution of x to have a fast decay on large values, was not in Ravikumar et al. (2010) as the paper does not consider covariates. The new condition is, however, quite general; for example, it is satisfied by the Gaussian distribution and all categorical covariates. The proof of the theorem can be found in the Online Supplementary Materials Appendix A.

Note that the properties in Theorem 1 hold on the original fit for each separate regression; in practice, we still need to post-process the fitted parameters by symmetrizing them using either the separate-max or the separate-min approach described earlier in section 2.2.1. Here we briefly investigate the three properties after this symmetrization. For property (1), the symmetrized estimates might not necessarily be the optimal solution for each regression, thus it is not sensible to consider uniqueness anymore; next, it is not difficult to see that property (3) still holds for both sets of symmetrized estimates since it characterizes the relationship between the fitted value and the true value and the true value remains the same for different fits of the same parameters; as for property (2), we will have to enlarge the upper bound on the right hand side by a factor of d^1/2, i.e,

$${\Vert {\hat{\mathit{\theta }}}_j^{\text{max}}-{\mathit{\theta }}_j^{*}\Vert }_2\le 5{\lambda }_{n}d/{\mathrm{\Delta }}_{\text{min}},{\Vert {\hat{\mathit{\theta }}}_j^{\text{min}}-{\mathit{\theta }}_j^{*}\Vert }_2\le 5{\lambda }_{n}d/{\mathrm{\Delta }}_{\text{min}},\text{for any}j\in \{1,\dots ,q\}.$$ (14)

A simple proof of this adapted results can be found in the Online Supplementary Materials Appendix B.

4. Empirical Performance Evaluation

In this section, we present four sets of simulation studies designed to test the model selection performance of our methods. We vary different aspects of the model, including sparsity, signal strength and proportion of relevant covariates. The results are presented in the form of ROC curves, where the rate of estimated true non-zero parameters (sensitivity) is plotted against the rate of estimated false non-zero parameters (1-specificity) across a fine grid of the regularization parameter. Each curve is smoothed over 20 replications.

The data generation scheme is as follows. For each simulation, we fix the dimension of the covariates p, the dimension of the response q, the sample size n and a graph structure E in the form of a q × q adjacency matrix (randomly generated scale-free networks (Barabási and Albert, 1999); in the Online Supplementary Materials Appendix E, we also study the effect of sparsity for k-nearest neighbor graphs). For any (j, k), 1 ≤ j ≤ k ≤ q, $({\theta }_{jk0},{\mathit{\theta }}_{jk}^T)$ consists of (p + 1) independently generated and selected from three possible values: β > 0 (with probability ρ/2), −β (with probability ρ/2), and 0 (with probability 1−ρ). An exception is made for the intercept terms θ_jj0, where ρ is always set to 1. Covariates xⁱ’s are generated independently from the multivariate Gaussian distribution N_p(0, I_p). Given each xⁱ and θ, we use Gibbs sampling to generate the yⁱ, where we iteratively generate a sequence of $y_j^i’\mathrm{s}$ (j = 1, …, q) from a Bernoulli distribution with probability $P_{\mathit{\theta }}(y_j^i=1|{\mathit{y}}_{\backslash j}^i,{\mathit{x}}^i)$ and take the last value of the sequence when a stopping criterion is satisfied.

We compared three estimation methods: the separate-min method, the separate-max method and the joint method. Our simulation results indicate that performance of the separate-min method is substantially inferior to that of the separate-max method when the dimension of the response is relatively small (results omitted for lack of space). Thus we only present results for the separate-max and the joint methods for the first three simulation studies.

4.1 Effect of sparsity

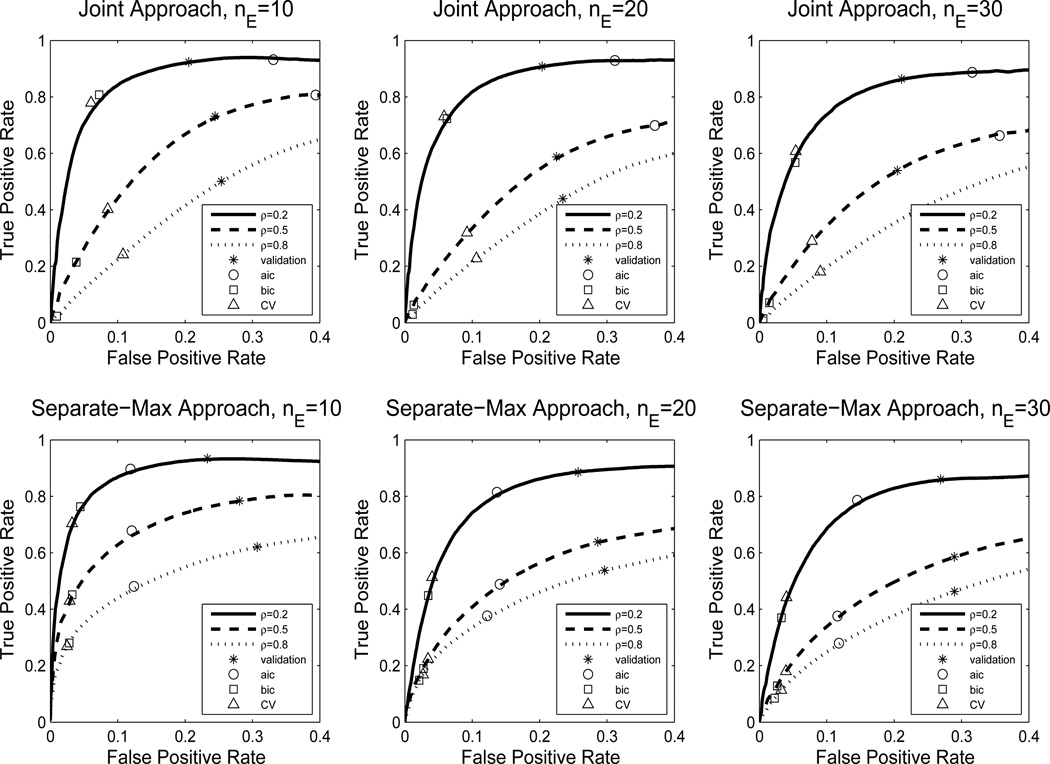
First, we investigate how the selection performance is affected by the sparsity of the true model. The sparsity of θ can be controlled by two factors: the number of edges in E, denoted by n_E, and the average proportion of effective covariates for each edge, ρ. We fix the dimensions q = 10, p = 20 and the sample size n = 200, and set the signal size to β = 4. Under this setting, the total number of parameters is 1155. The sparsity parameter n_E takes values in the set {10, 20, 30}, and ρ takes values in {0.2, 0.5, 0.8}. The resulting ROC curves are shown in Figure 1.

Figure 1.

ROC curves for varying levels of sparsity, as measured by the number of edges (n_E) and expected proportion of non-zero covariates (ρ). Optimal points are marked for different model selection methods.

The first row shows the results of the joint approach and the second row of the separate-max approach. As the true model becomes less sparse, the performance of both the joint and the separate methods deteriorates, since sparse models have the smallest effective number of parameters to estimate and benefit the most from penalization. Note that the model selection performance seems to depend on the total number of non-zero parameters ((q+n_E)(p+1)ρ), not just on the number of edges (n_E). For example, both approaches perform better in case n_E = 20, ρ = 0.2 than n_E = 10, ρ= 0.5, even though the former has a more complicated network structure. Comparing the separate-max method and the joint method, we observe that the two methods are quite comparable, with the joint method being slightly less sensitive to increasing the number of edges.

In practice, one often needs to select a value for the tuning parameter. We compared different methods for selecting the optimal tuning parameter: validating the conditional likelihood on a separate data set of the same size, cross-validation, AIC and BIC. The selected models corresponding to each method are marked on the ROC curves. As we can see, cross-validation seems to provide a reasonable choice in terms of balancing the true positive rate and the false positive rate.

4.2 Effect of signal size

Second, we assess the effect of signal size. The dimensions are set to be the same as in the previous simulation, that is, q = 10, p = 20 and n = 200, and underlying network is the same. The expected proportion of effective covariates for each edge is ρ = 0.5. The signal strength parameter β takes values in the set {0.5, 1, 2, 4, 8, 16}. For each setting, the non-zero entries of the parameter vectors θ are at the same positions with the same signs, only differing in magnitude. The resulting ROC curves are shown in Figure 2.

Figure 2.

ROC curves for varying levels of signal strength, as measured by the parameter β. Optimal points are marked for different model selection methods.

As the signal strength β increases, both the separate and the joint methods show improved selection performance, but the improvement levels off eventually. The separate-max method performs better overall given that the optimal points selected by cross-validation have lower false discovery rate.

4.3 Effect of noise covariates

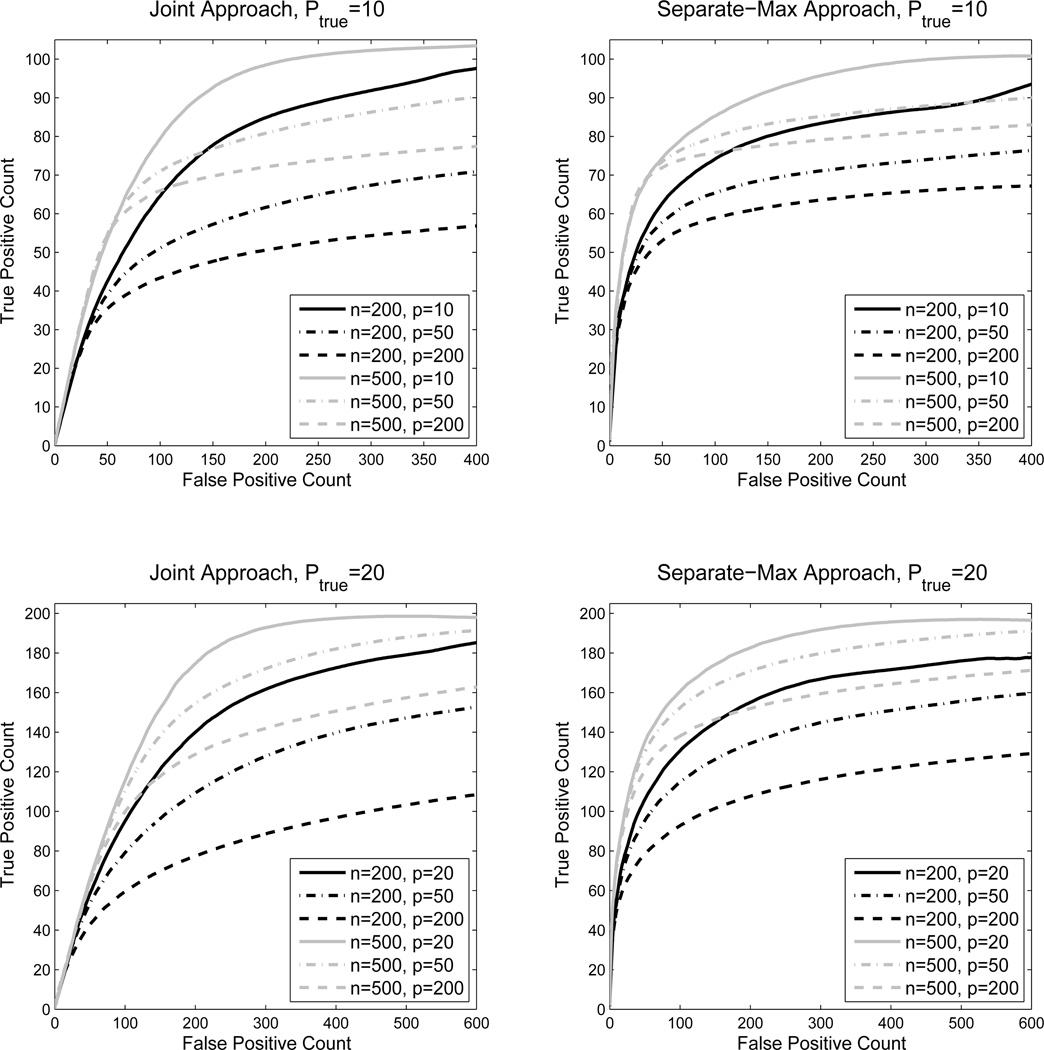
In this set of simulations, we study how the model selection performance is affected by adding extra uninformative covariates. At the same time, we also investigate the effect of the number of relevant covariates p_true and the sample size n. The dimension of the response is fixed to be q = 10 and the network structure remains the same as in the previous simulation. We take p_true ∈ {10, 20} and n ∈ {200, 500}. For each combination, we first fit the model on the original data and then on augmented data with extra uninformative covariates added. The total number of covariates p_total ∈ {p_true, 50, 200}. The non-zero parameters are generated the same way as before with β = 4 and ρ = 0.5. With the changes in p_total, the total number of non-zero parameters remains fixed for each value of p_true, while the total number of zeros is increasing.

To make the results more comparable across setting, we plot the counts rather than rates of true positives and false positives. The resulting curves are shown in Figure 3. Generally, performance improves when the sample size grows and deteriorates when the number of noise covariates increases, particularly with a smaller sample size. The separate-max method dominates the joint method under these settings, but the difference is not large.

Figure 3.

ROC curves for varying dimension, number of noise covariates, and sample size.

4.4 Stability selection when q is large

Stability selection was proposed by Meinshausen and Bühlmann (2010) to improve potential lack of stability of a solution and to quantify the significance of a selected structure under high-dimensional settings. It is based on subsampling in combination with (high-dimensional) selection algorithms. Benefits of stability selection includes its insensitiveness to the amount of the regularization in the original selection algorithms and its improvement of model selection accuracy over them. Specifically, we repeatedly fit the model 100 times on random subsamples (without replacement) of half of the original data size. For each tuning parameter λ from a fixed grid of values, we record the frequency of θ̂_jkℓ being non-zero respectively for each covariate X_ℓ, ℓ = 0, …, p on all pairs of (j, k), 1 ≤ j < k ≤ q, and denote it by f_jkℓ(λ). Then we use $f_{jk\ell }^{*}={\text{max}}_{\lambda }{f}_{jk\ell }(\lambda )$ as a measure of importance of covariate X_ℓ for the edge (j, k). Finally, for each covariate X_ℓ, we rank the edges based on the selection frequencies $\{f_{jk\ell }^{*}:1\le j<k\le q\}$. At the top of the list are the edges that depend on X_ℓ most heavily.

We note that in previous simulation settings, even though the dimensions of the variables are not large, the number of parameters far exceeds the sample size. We applied stability selection coupled with the proposed methods, and found that the results of stability selection are comparable with those of not using stability selection without much improvement. (See the Online Supplementary Materials Appendix C.)

In this subsection, we mimic the real data example and increase the dimension of the binary responses q to a large value. Specifically, we set the sample size n = 100, the dimension of the covariates p = 5 and vary the dimension of binary responses q = {50, 100, 200}. The total number of non-zero parameters is fixed to be 150. The magnitude of the model parameters are set to be β = 8. We then compare the three proposed methods with stability selection. The results are shown in Figure 3 of the Online Supplementary Materials. We found that as the dimension q increases, coupling stability selection with the joint approach and the separate-max approach significantly improve model selection performance over the respective original methods. Since the separate-min approach coupled with stability selection had the best performance overall, we adopted it for our data example in Section 5.

5. Application to Tumor Suppressor Genes Study

In breast cancer, deletion of tumor suppressor genes plays a crucial role in tumor initiation and development. Since genes function through complicated regulatory relationships, it is of interest to characterize the associations among various deletion events in tumor samples, and at the same time to investigate how these association patterns may vary across different tumor subtypes or stages.

Our data set includes DNA copy number profiles from cDNA microarray experiments on 143 breast cancer specimens (Bergamaschi et al., 2006). Among them, 88 samples are from a cohort of Norwegian patients with locally advanced (T3/T4 and/or N2) breast cancer, receiving doxorubicin (Doxo) or 5 uorouracil/mitomycin C (FUMI) neoadjuvant therapy (Geisler et al., 2003). The samples were collected before the therapy. The other 55 are from another cohort of Norwegian patients from a population-based series (Zhao et al., 2004). Each copy number profile reports the DNA amounts of 39,632 probes in the sample. The array data was preprocessed and copy number gain/loss events were inferred as described in Bergamaschi et al. (2006). To reduce the spatial correlation in the data, we bin the probes by cytogenetic bands (cytobands). For each sample, we define the deletion status of a cytoband to be 1 if at least three probes in this cytoband show copy number loss. 430 cytobands covered by these probes show deletion frequencies greater than 10% in this group of patients, and they were retained for the subsequent analysis. The average deletion rate for all the 430 cytobands in 143 samples is 19.59%. Our goal is to uncover the association patterns among these cytoband-deletion events and how the association patterns may change with different clinical characteristics, including TP53 mutation status (a binary variable), estrogen receptors (ER) status (a binary variable), and tumor stage (an ordinal variable taking values in {1, 2, 3, 4}).

For our analysis, denote the array data by y_143×430, where $y_j^i$ indicates the deletion status of the j^th cytoband in the i^th sample. Let xⁱ denote the covariate vector containing the three clinical phenotypes of the i^th sample, and x_ℓ the ℓth covariate vector. We first standardize the covariate matrix x_143×3 and then fit our Ising model with covariates with the separate-min fitting method. We then apply stability selection (Meinshausen and Bühlmann, 2010) to infer the stable set of important covariates for each pairwise conditional association. We are primarily interested in the pairs of genes belonging to different chromosomes, as the interaction between genes located on the same chromosome is more likely explained by strong local dependency. The results are shown in Table 1 of the Online Supplementary Materials, where the rank list of the edges depending on different covariates are recorded. The first two columns of each covariate-related columns are the node names and the third column records the selection frequency.

There are 348 inter-chromosome interactions (between cytobands from different chromosomes) with selection probabilities at least 0.3. Among these, 75 interactions change with the TP53 status; 51 change with the ER status; and another 58 change with the tumor grade (see details in Table 1 of the Online Supplementary Materials). These results can be used by biologists to generate hypotheses and design relevant experiments to better understand the molecular mechanism of breast cancer. The most frequently selected pairwise conditional association is between deletion on cytoband 4q31.3 and deletion on 18q23 (83% selection frequency). Cytoband 4q31.3 harbors the tumor suppressor candidate gene SCFFbw7, which works cooperatively with gene TP53 to restrain cyclin E-associated genome instability (Minella et al., 2007). Previous studies also support the existence of putative tumor suppressor loci at cytoband 18q23 distal to the known tumor suppressor genes SMAD4, SMAD2 and DCC (Huang et al., 1995; Lassus et al., 2001). Thus the association between the deletion events on these two cytobands is intriguing.

Another interesting finding is that the association between deletion on cytoband 9q22.3 region and cytoband 12p13.31 appears to be stronger in the TP53 positive group than in the TP53 negative group. A variety of chromosomal aberrations at 9p22.3 have been found in different malignancies including breast cancer (Mitelman et al., 1997). This region contains several putative tumor suppressor genes (TSG), including DNA-damage repair genes such as FANCC and XPA. Alterations in these TSGs have been reported to be associated with poor patient survival (Sinha et al., 2008). On the other hand, cytoband 12p13.31 harbors another TSG, namely ING4 (inhibitor of growth family member 4), whose protein binds TP53 and contributes to the TP53-dependent regulatory pathway. A recent study also suggests involvement of ING4 deletion in the pathogenesis of HER2-positive breast cancer. In light of these previous findings, it is interesting that our analysis also found the association between the deletion events of 9p22.3 and 12p13.31, as well as the changing pattern of the association under different TP53 status. This result suggests potential cooperative roles for multiple tumor suppressor genes in cancer initiation and progression.

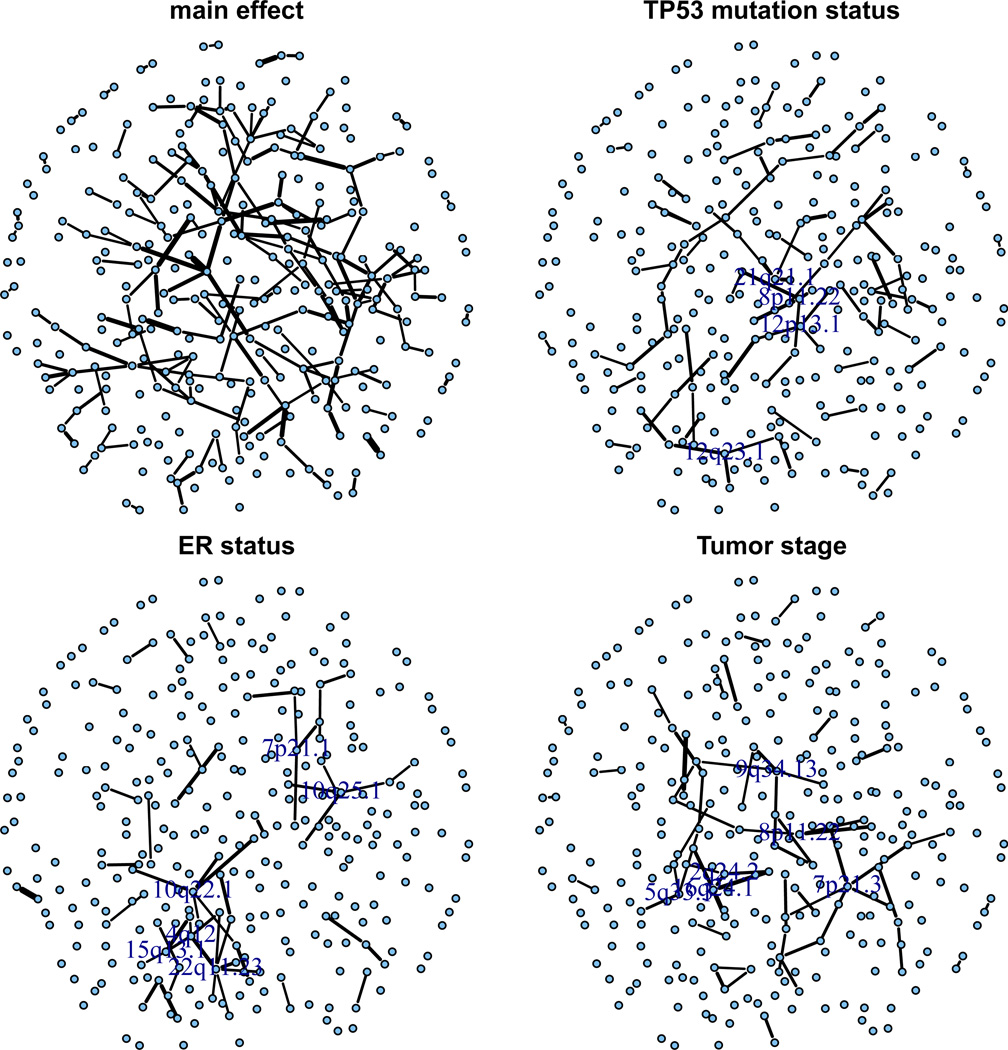
For visualization, we constructed separate graphs for each covariate, where each graph includes all the edges depending on that covariate with selection frequency at least 0.3. Specifically, we use the results from Table 1 of the Online Supplementary Materials to create Figure 4. In Figure 4, the “main effect” subplot shows all edges in the first two columns of Table 1 of the Online Supplementary Materials, which correspond to non-zero θ̂_jk0 parameters and the edges are weighted by their selection frequency as shown in the same table. The remaining three subplots are created in the same fashion. For nodes that have at least 3 neighbors in the covariate dependent plots, we also mark the names of them. To make the graph readable, we did not include all 430 nodes but only the nodes with edges.

Figure 4.

Graphs of edges depending on each covariate (based on Table 1 of the Online Supplementary Materials).

Since there are obvious hubs (highly connected nodes) in the graph, which often have important roles in genetic regulatory pathways, we also did extra analysis to confirm the findings. As there can be different hubs associated with different covariates, we separate them as follows. For each node j, covariate ℓ, and stability selection subsample m, let the “covariate-specific” degree of node j be $d_{j,\ell }^m=\#\{k:{\hat{\theta }}_{jk\ell }\ne 0\}$. A ranking of nodes can then be produced for each covariate ℓ and each replication m, with $r_{j,\ell }^m$ being the corresponding rank. Finally, we compute the median rank across all stability selection subsamples $r_{j,\ell }=\text{median}\{r_{j,\ell }^m,m=1,\dots ,100\}$, and order nodes by rank for each covariate. The results are listed in Table 2 of the Online Supplementary Materials. Interestingly, cytoband 8p11.22 was ranked close to the top for all three covariates. The 8p11–p12 genomic region plays an important role in breast cancer, as numerous studies have identified this region as the location of multiple oncogenes and tumor suppressor genes (Yang et al., 2006; Adélaïde et al., 1998). High frequency of loss of heterozygosity (LOH) of this region in breast cancer has also been reported (Adélaïde et al., 1998). Particularly, cytoband 8p11.22 harbors the candidate tumor suppressor gene TACC1 (transforming, acidic coiled-coil containing protein 1), whose alteration is believed to disturb important regulations and participate in breast carcinogenesis (Conte et al., 2002). From Table 1 of the Online Supplementary Materials, we can also see that the deletion of cytoband 8p11.22 region is associated with the deletion of cytoband 6p21.32 with relatively high confidence (selection frequency = 0.46); and these associations change with both TP53 status. This finding is interesting because high frequency LOH at 6q in breast cancer cells are among the earliest findings that led to the discovery of recessive tumor suppressor genes of breast cancer (Ali et al., 1987; Devilee et al., 1991; Negrini et al., 1994). These results together with the associations we detected confirm the likely cooperative roles of multiple tumor suppressor genes involved in breast cancer.

6. Summary and Discussion

We have proposed a novel Ising graphical model which allows us to incorporate extraneous factors into the graphical model in the form of covariates. Including covariates into the model allows for subject-specific graphical models, where the strength of association between nodes varies smoothly with the values of covariates. One consequence of this is that if all covariates are continuous, then when the value of a covariate changes, only the strength of the links is affected, and there is zero probability for the graph structure to change. In principle this could be seen as a limitation. On the other hand, this is a necessary consequence of continuity, and small changes in the covariates resulting in large changes in the graph, as can happen with the approach of Liu et al. (2010), make the model interpretation difficult. With binary covariates, which is the case in our motivating application, the situation is different; for example, since edge (j, k) depends on the value ${\theta }_{jk0}+{\mathit{\theta }}_{jk}^T\mathit{x}$, the graph structure can change in the following situation: when θ_jk0 = 0 and ${\mathit{\theta }}_{jk}^T\ne \mathbf{0}$, for a subject at the reference level where the entire x is 0, edge (j, k) does not exist, but edge (j, k) will exist if any of the “important“ covariate is at the non-reference level. It is the same case with categorical covariates with more than two levels. Further, our approach has the additional advantage of discovering exactly which covariates affect which edges, which can be more important in terms of scientific insight.

While here we focused on binary network data, the idea can be easily extended to categorical and Gaussian data, and to mixed graphical models involving both discrete and continuous data. Another direction of interest is understanding conditions under which methods based on the neighborhood selection principle of running separate regressions are preferable to pseudo-likelihood type methods, and vice versa. This comparison arises frequently in the literature, and understanding this general principle would have applications far beyond our particular method.