Abstract
Droplet-based microfluidic technologies are powerful tools for applications requiring high-throughput, for example, in biochemistry or material sciences. Several systems have been proposed for the high-throughput production of monodisperse emulsions by parallelizing multiple droplet makers. However, these systems have two main limitations: (1) they allow the use of only a single disperse phase; (2) they are based on multiple layer microfabrication techniques. We present here a pipette-and-play solution offering the possibility of manipulating simultaneously 10 different disperse phases on a single layer device. This system allows high-throughput emulsion production using aqueous flow rates of up to 26 ml/h (>110 000 drops/s) leading to emulsions with user-defined complex chemical composition. We demonstrate the multiplex capabilities of our system by measuring the kinetics of β-galactosidase in droplets using nine different concentrations of a fluorogenic substrate.
I. INTRODUCTION
Miniaturization and automation are key features in technology developments. Over the past ten years, droplet-based microfluidics has emerged as a groundbreaking technology for the miniaturization and automation of biochemical assays:1–6 it provides essential elements to both miniaturize assays down to the scale of single microorganisms or even single molecules7–9,11–16 and automatize sample processing.17,18 In many biochemical applications, high-throughput droplet generation with a precise control of the size is required. For this purpose, the capabilities offered by microfluidics in terms of throughput and volume control led to quantitative analysis in biochemistry for drug screening,7,9,18 molecular diagnostics,16,19,20,22 cell screening,8,11,13,23,24 or enzymology.12,25,26 Although the throughput of droplet production and manipulation is already very high,27 microfluidics offers in addition unprecedented capabilities for parallelization.28 The parallelization at droplet production combines the fine control on size, frequency, and monodispersity with ultra-high-throughput.29–33 Although commercial apparatus based on droplet-based microfluidics already provide tools for parallel droplet generation and sensitive detection,20,21 the measurement of kinetic processes at ultra-high-throughput has not been described to date.
In order to reduce the number of inlets and outlets for parallel production, microfluidic systems based on multiple layer microfabrication were proposed.31,34 A large number of inlets and outlets can be merged by connecting them with a single channel from a second superimposed layer, usable for the mass-production of emulsions. To date, these approaches have limitations for applications in which the number of samples to be emulsified is large. Increasing the number of test samples results in practical obstacles with regard to the loading of the samples as it requires the use of several pumps as well as numerous syringes and tubing connections which can be responsible for dead volumes resulting in a loss of samples.9
We present here a parallel droplet maker system implemented on a microfluidic chip and a pressure chamber10 usable to load and emulsify samples from standard pipette sampling. The microfluidic “pipette-and-play” chip is composed of one inlet for the continuous phase, and ten parallel flow-focusing droplet makers, each comprising a loading milli-well having the size of a microtiter plate well and one outlet. The flow rate of the disperse phase is controlled by the air pressure in the chamber applied from a single pressure controller, and the flow rate of the continuous phase is controlled independently. In order to control the homogeneity of the droplet sizes over the whole chip we analyzed the monodispersity of the droplets produced in parallel with a different fluorescent dye concentration in each disperse phase. We demonstrate the versatility of our system to perform standard automatized biological assays: We measured the steady-state kinetics of β-galactosidase with a fluorogenic substrate (FDG, Fluorescein di-β-D-Galactopyranoside) using nine different substrate concentrations and one reference in parallel. We demonstrate that in a single analysis the characteristic kinetic constants kcat and Km of the biocatalyst can be obtained and quantitatively match the values previously reported for the catalyst.
II. RESULTS
A. Microfluidic platform for the multiplexed production of emulsions
Traditionally in droplet-based microfluidics, single emulsion producers are used, which limits both achievable production throughputs and multiplexing possibilities. Indeed, with a single production system, the production throughput is ruled by the dripping regime that defines a range of flow rates for which droplets are monodisperse. Moreover, depending on the nature of the material of the microfluidic system, the pressures at which the fluids are injected into the system need to be limited to avoid delamination effects. In practical operation of droplet production with conventional methods, each fluid has to be loaded in syringes or vials and connected with a microfluidic chip through tubings. When a single type of emulsion is needed, the throughput of the droplet production can be improved without increasing the number of syringes or vials by installing a parallelized droplet producer sharing flow inlets. However, the previously developed microfluidic systems for parallel droplet production30–32,34 allow the use of only a single disperse phase and thus have strong limitations in many applications in which a large number of different contents have to be emulsified in parallel such as in material sciences and biochemistry. A second limitation of these systems is due to the fact that they are based on multiple layer microfabrication techniques requiring a large number of inlets and outlets that are merged through connection to a single channel from a superimposed layer.
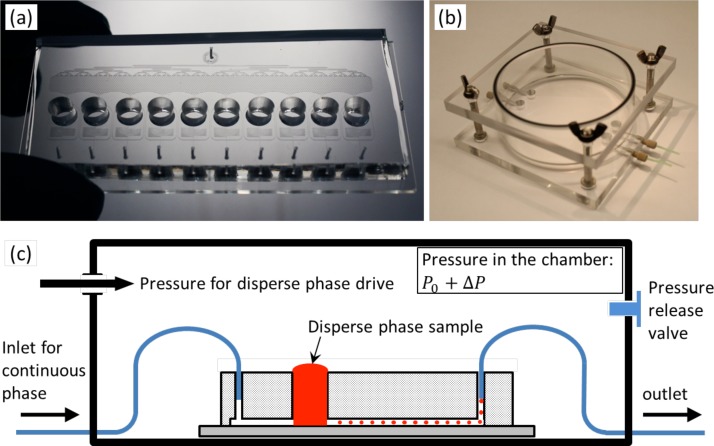
We developed a system composed of two parts: (i) a microfluidic chip and (ii) a pressure chamber. The microfluidic chip was fabricated in polydimethylsiloxane (PDMS) using standard soft lithography processes. It integrates one oil phase inlet (used for the continuous phase) split to feed ten parallel flow-focusing droplet makers. The continuous phase, actuated by a syringe pump at constant flow rate, is first divided into 128 flow splitters, and merged in a fluidic buffer space upstream to the flow-focusing nozzles in order to ensure that the flow of oil at each flow focusing junction is stabilized at one tenth of the total flow. This design is relevant as in the oil distribution region of the device the hydraulic resistance at the edges of the PDMS walls is larger than the resistance in the center of the device. The dispersed phase of each flow-focusing junction is flowing from ten independent millimeter-sized wells (Figure 1(a)). A wide range of volumes can be handled with the system as the diameter and the thickness of these wells can be varied, and if a further increase of the sample volume is necessary, several layers of punched PDMS slabs can be superimposed and assembled on the chip to increase the volumes used for each disperse phase. Moreover, this system has the advantage of being highly flexible regarding the range of emulsion volumes and the number of different emulsions required by the specific experimental conditions as the number of milli-wells can be increased as a function of the number of disperse phases needed. The only main limitation regarding the number of available wells is the size of the pressure chamber which constrains the size of the chip sealed inside it, but its dimensions can be customized. The well is manufactured with a diameter of 5 mm for the loading of the dispersed phase. As the channels are hydrophobic, there is no flow of liquid from the well to the nozzle at atmospheric pressure P0. In addition, a fluidic resistance was implemented between the well and the flow-focusing droplet maker to minimize the outflow of the oil towards the well. The flow of the dispersed phase towards the nozzle is achieved by increasing the pressure above the milli-wells as the chip is embedded in a pressure chamber where the pressure P0 + ΔP is controlled above the atmospheric pressure. Hence, the number of pump controllers required for the driving of the dispersed phase is drastically reduced as compared to conventional systems, which contributes to the uniformity of produced emulsions as there are no flow inhomogeneities induced by differences of pumping stability. The chamber body is made of polymethylmethacrylate (PMMA) in two separate parts (Figure 1(b)). The bottom part carries four through-holes from the side wall of the bottom plate for conventional finger-tight fitting (Upchurch Scientific) which enables the tubing connection from the outside of the chamber to the microfluidic chip without any pressure leakage. As depicted in the schematic diagram (Figure 1(c)), the microfluidic chip is placed in the pressure chamber, and the tubings introduced into the pressure chamber were connected through the fingertight fittings for inlets and outlets. The pressure ΔP is controlled by a pressure controller (Fluigent) between 0 and 1 bar (100 kPa).
FIG. 1.
Description of the microfluidic system. (a) Photograph of the fabricated microfluidic chip for parallel droplet production. (b) Assembled pressure chamber with the finger-tight fittings for tubing connections. (c) Schematic diagram for the principle of the proposed system.
Since the parallel droplet makers share a single continuous phase inlet, the oil flow rate at each junction is determined by the hydrodynamic resistance of each arm. In the plane, a symmetrical system is simply achieved by design. In the vertical dimension, the variability in the device thickness will then determine the flow in each arm. The geometrical characteristics of the microfluidic chip are mainly governed by the quality of the photoresist patterned silicon wafer. With optimized patterning process, the averaged thickness of the photoresist was 34.9 μm with a standard deviation of 0.05 μm over the chip. With variations of less than 1% in thickness, the flow is split equally at each nozzle.
We first demonstrate that the system produces monodisperse emulsions from the ten nozzles. To initiate droplet generation, we apply the continuous phase flow and the pressure to the chamber at the same time. Given the volume of air within the pressure chamber, a delay of approximately 20 s was observed between the activation of flows and droplet production for all tested conditions. The droplet production started in a synchronous manner over the ten channels qualitatively showing that microfabrication inaccuracies are negligible. Droplet size and droplet production frequencies are a function of both the applied pressure ΔP and the oil flow rate Qc. Scanning both parameters, we obtained a range of conditions to prepare droplets of volumes ranging from 68 to 256 pl (Table I).
TABLE I.
Production regimes. Five production regimes were studied. For each regime we give: the applied pressure (ΔP), the oil flow rate (Qc), the mean droplet diameter (D), the coefficient of variation over diameter (CV), the production frequency (f), the mean droplet volume (V), and the aqueous flow rate (Qw).
| Condition | ΔP (kPa) | Qc (μl/min) | D (μm) | CV (%) | f (Hz) | V (pl) | Qw (μl/min) |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 10 | 103.5 | 1.4 | 425 | 256 | 65 |
| 2 | 40 | 20 | 92.1 | 1.9 | 1000 | 195 | 117 |
| 3 | 50 | 40 | 75.1 | 1.8 | 3200 | 128 | 246 |
| 4 | 80 | 60 | 64.7 | 1.1 | 6400 | 88 | 338 |
| 5 | 100 | 90 | 54.1 | 1.5 | 10 600 | 68 | 432 |
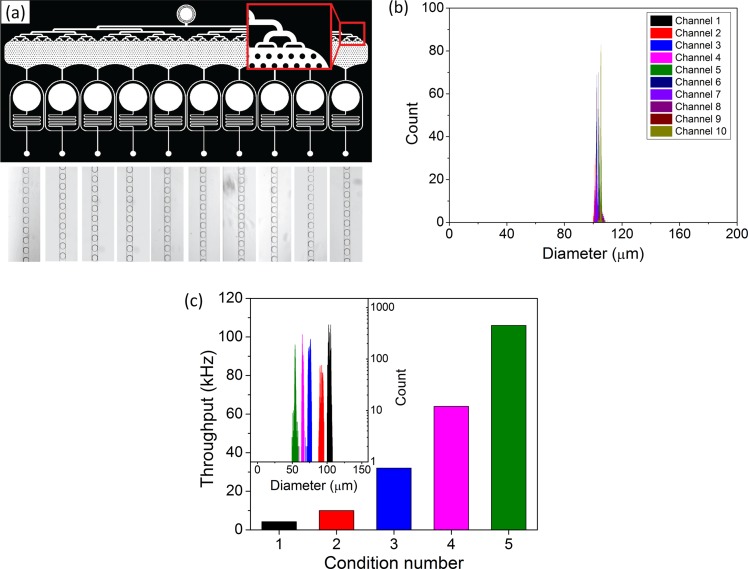
To further address the capabilities and spatial variability of the droplet production over the chip, the droplet size dispersion was evaluated by image processing of the frames recorded at high-speed for each individual droplet producer (Figure 2(a)). 18 400 droplets were detected (approximately 1840 droplets/movie), and the measured diameters of droplets from each channel were plotted in a histogram (Figure 2(b)). We used five different conditions, from low throughput and large droplets to ultra-high-throughput and small droplets. The flow and pressure conditions were characterized for each condition (Table I). We obtained the aqueous flow rate in each channel as the product of the droplet volume by the droplet frequency f, both obtained by image processing
| (1) |
The droplet volume V is determined from the apparent radius of the droplet, using the approximation of a nodoid shape for the droplet (see supplementary material46).35–37 The nodoid is relevant as it guarantees a constant mean curvature for the droplet (valid at low capillary number) and a contact angle of 180°. We discuss in the supplementary material, the various approximations that can be made on the droplet shape and their accuracy for determining the droplet volume. We show that the toroidal approximation provides an excellent analytical estimate for the droplet volume with less than 2.5% error compared to the nodoid. The relationship between the aqueous flow rate Qw and ΔP is given in a first approximation by the hydraulic resistance of the channel upstream of the nozzle. The length of the channel is L = 35 mm, its width w = 100 μm, and depth d = 35 μm, the Poiseuille flow calculated for a rectangular channel leads to a hydraulic resistance R = 1.5 × 1014 mPas/m3 for an oil viscosity of 1.2 mPas. This value closely matches the experimental value of 1.4 × 1014 ± 0.4 mPas/m3 (supplementary material46). The modification of the resistance and pressure distribution by the other channels and by the presence of droplets come as a correction factor marginally affecting the flow. This condition is crucial to avoid hydrodynamic coupling between the nozzles through the flow of droplets that could affect the distribution of oil.38 We evaluated the monodispersity and throughput of the droplet production for each condition. The different droplet populations had a very narrow size distribution (Figure 2(c)) showing the ability to produce emulsions from different streams with a high level of control on the droplet sizes. The coefficient of variations (CVs) over the diameter of the produced droplets in different conditions is listed in Table I. The maximum throughput reached more than 110 000 droplets/s for condition 5 (i.e., 432μl/min and 90 μl/min for disperse phase and oil phase, respectively). Larger throughputs might even be reachable but were not attempted in this study. Typically, we expect our device to be reliable as long as the hydrodynamic conditions in each individual nozzle are compatible with the dripping production mode.
FIG. 2.
Droplet production analysis performed with the developed image analysis tool. (a) Example of the recorded high-speed movies from each droplet producer from condition number 1 (channel width: 100 μm). (b) Histogram of the detected droplet diameter. 18 400 droplets were analyzed from ten droplet producers from condition 1. (c) Measured throughput for each of the five conditions; inset: histogram of droplet diameter for each condition.
The agreement of the data with a simple hydrodynamic model provides insights into the limits of the system. Fixing the oil flow rate, we find a lower limit of ΔP for which droplets are produced. This point is recovered in a minimal model, considering the pressure at the nozzle PN. In the outlet channel, the pressure - flow rate relationship is given by
| (2) |
where Rout is the hydraulic resistance of the channel of length 5 mm and considering the outlet at atmospheric pressure Rout = 2 × 1013 mPas/m3. The closure relationship is given by the Poiseuille flow in the arm upstream
| (3) |
Combining both leads to
| (4) |
Neglecting Rout compared to R, we recover the Poiseuille expression for Qw and we see that Qw becomes negative if ΔP is smaller than a critical pressure RoutQoil. In all cases tested above, we worked at pressure three to six times larger than this critical value. Reducing the pressure closer to the limit will hence destabilize the flow and also decrease significantly the throughput of droplet production. Obviously, for a more accurate modeling, the pressure of the two phase flows should be computed38,39 but this simple model provides elementary design rules for such a microfluidic system.
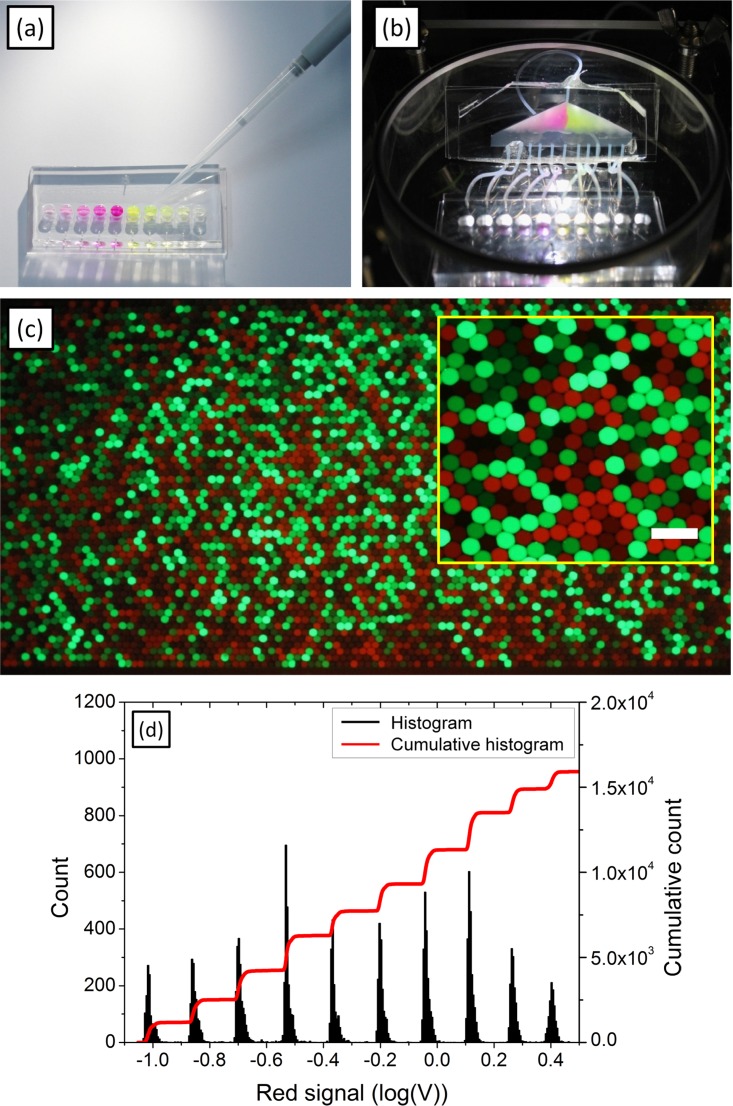
In order to collect the produced emulsions, a reservoir is integrated either inside or outside the pressure chamber. The storage in the pressure chamber is possible through a trapping mechanism similar to the one described in Ref. 45. We loaded and emulsified two different fluorescent dyes (Sulforhodamine-B for a red signal and Fluorescein for a green signal) using five different concentrations of each (Figures 3(a) and 3(b)). The collected emulsions were introduced into a reservoir chip for wide-field imaging with a height of 75 μm to confine the droplets to a monolayer, and imaged with a fluorescent microscope. No coalescence of the droplets was observed (Figure 3(c) and movie in the supplementary material46). To quantify the measurement, we labeled each droplet population with ten different concentrations of Sulforhodamine-B, and reinjected the droplets to a laser-induced fluorescence setup to measure the fluorescent signal intensity of each droplet, and plotted the results as a histogram (Figure 3(d)). We obtained ten separated fluorescence peaks on the reinjected emulsion, demonstrating the robustness of the system for the preparation of compound libraries and end-point measurements. We further show that our system is compatible with multiplex kinetic measurements.
FIG. 3.
Parallel emulsification and analysis of ten different samples. (a) Loading of ten aqueous phases (Five different concentrations of Fluorescein and Sulforhodamine-B, respectively) into the chip milli-wells. (b) Droplet production and collection. (c) Droplet observation using fluorescence microscopy. Scale bar: 300 μm. (d) Histogram and cumulative histogram of detected fluorescent signals for 10 concentrations of sulforodamine (the concentration are 3.9, 5.8, 8.8, 13.2, 19.7, 29.6, 44.4, 66.7, 100 et 150 μM).
B. Enzymology: Michaelis-Menten constants in a single analysis
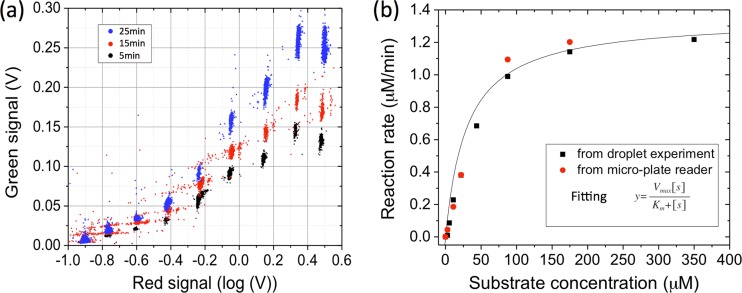
In order to demonstrate the potential of the developed system for a kinetic measurement, we performed an enzymatic assay to measure the kinetics of β-galactosidase from Escherichia coli (E. coli) using the fluorogenic substrate FDG. Typically, the characteristic kinetic parameters of an enzyme catalyzed reaction are obtained following the Michaelis-Menten kinetic model. Here, reaction rates were measured for ten different conditions in parallel. As the velocity saturation curve for the enzyme shows a hyperbolic relationship between the reaction rate and the substrate concentration, the Michaelis constant (Km) and the turnover number (kcat) can be determined. We prepared substrate dilutions in phosphate buffered saline (PBS) with 9 different concentrations of FDG ranging from 0 to 350 μM, and one solution containing fully converted 350 μM of FDG as a reference. Each solution was labeled with ten different concentrations of Sulforhodamine-B. The prepared substrate dilutions were kept on ice. The enzyme was added to a final concentration of 2 nM, and subsequently the mixture was loaded in the prepared chip. The emulsion was introduced through the reservoir into the two-color laser-induced fluorescence detector. The reinjection rate was controlled to be approximately 500 Hz by the control pump which was connected with the reservoir. We measured the fluorescent signal increasing over time (Figure 4(a)) and the reaction rates were calculated based on the average values of the detected droplet populations (Figure 4(b)). The values determined in droplets were in very good agreement with those obtained in bulk using a microplate reader (Figure 4(b)). The derived Km = 30 μM and kcat = 12.1 s−1 are in good agreement with the previously reported values Km = 18 μM and kcat = 17 s−1, respectively.40,41
FIG. 4.
Measurement of β-galactosidase kinetics in continuous mode with different substrate concentrations. (a) Laser read-out of 9 droplet populations containing 2 nM β-galactosidase and increasing concentrations of FDG substrate (0, 2.73, 5.47, 10.94, 21.88, 43.75, 87.5, 175, and 350 μM) over time. Each droplet population was labeled with a different concentration of Sulforhodamine B. The black points correspond to the first measured points after reinjection. (b) The measured kinetics follows the Michaelis-Menten equation. Derived Km and kcat constants were 30 μM and 12.1 s−1, respectively.
III. CONCLUSIONS
We have demonstrated a pipette-and-play like technology solution which combines a microfluidic chip and a pressure chamber, offering the possibility of simultaneously manipulating ten different disperse phases on a single-layer device. The microfluidic chip is composed of one inlet for the continuous phase and ten parallel flow focusing droplet makers, each comprising a loading well for the disperse phases and for the outlet. The dispersed phases are loaded directly into the microfluidic chip milli-wells by simple pipetting. The pressure chamber enables controlled driving of the loaded samples without the need of complex connections. This system allows the ultra-high-throughput production (up to 110 000 droplets/s) of highly monodisperse emulsions with user-defined chemical composition. Our experimental setup provides a reliable and versatile system to manipulate biomolecules. We demonstrate a multiplex approach usable for kinetic measurements on multiple samples. Parallelization has already been demonstrated for end-point measurements, for example, in diagnostics,16,20,22 and we show here that a multiplex operation is also achievable with a kinetic process. In this study, we demonstrated the application of the described system to a biologically relevant enzymatic reaction by measuring the kinetics of β-galactosidase in droplets with nine different concentrations of the fluorogenic substrate FDG and one internal reference. This leads in one single analysis step to the determination of the Michaelis constant and the turnover number, which proved to be similar to previously reported values obtained from steady-state kinetics assays performed in bulk solutions. In a more general perspective, we believe that our platform has applications for analysis in biochemistry requiring a broad spectrum of reaction conditions and for dynamic multiplex assays which can now be measured in a single analysis.
IV. MATERIALS AND METHODS
A. Pressure chamber fabrication
A cylindrical PMMA tube with an outer diameter of 110 mm and a thickness of 3 mm was assembled into the micro-machined groove in the middle of the bottom plate and glued with an epoxy adhesive (3 M). The thickness of the bottom plate was 10 mm to allow for imaging with 4× objective lens (numerical aperture of 0.16, working distance of 13 mm), and cut in 120 mm × 120 mm squares. The cover part has a circular groove in which a sealing rubber O-ring is integrated. The cover part was pressed onto the cylindrical tube integrated on the bottom plate and supported by four hex-head socket bolts fixed on the bottom plate and sealed with butterfly nuts. Figure 1(b) shows the assembled pressure chamber.
B. Microfluidic chip fabrication
The microfluidic device was designed with conventional computer aided design (CAD) tool (AutoCAD, AutoDesk), and it was printed on an optical grade transparent film (Selba, Switzerland). We used SU8-100 (Microchem) to achieve a resist thickness of 35 μm by optimizing the spin-coating process for the photoresist. We spun the substrate at 5000 rpm for 50 s instead of the standard protocol used for producing 100 μm thickness. The thicknesses of the photoresist at each flow focusing region were measured by using a white light interferometer (Wyko NY1100, Veeco). The average thickness of the patterned resist was 34.5 μm with a standard deviation of 0.05 μm. The fabricated master pattern was then replicated in PDMS (Sylgard 184). The base and the cross-linker were mixed in a 10:1 ratio by weight and degassed. The prepared mixture was then poured onto the patterned silicon master and cured, the outlets were punched by using a 0.75 mm biopsy puncher (Harris Uni-Core), and the holes for the sample loading wells were punched by using a biopsy puncher with a diameter of 5 mm (Harris Uni-Core). The PDMS block was then bonded to a glass substrate after oxygen plasma treatment. Finally, the microchannel surfaces were hydrophobized using a commercial reagent (Aquapel, PPG Industries).
C. Emulsion reservoir
We fabricated a reservoir with ten collecting connections to the outlets of the chip, one tubing for the control pump to pump liquid into (for reinjection) or out (for collection) of the reservoir, and one outlet. First, a PDMS slab was cast on a bare wafer with a thickness of approximately 2 mm. The middle part of the PDMS slab was cut in a triangular shape, one hole was punched at the vertex of the triangle from the side wall of the PDMS and 11 holes were punched at the opposite side wall, 1 for the control pump connection and ten for the outlet connections of the parallel producer chip. The prepared PDMS slab was then bonded between two slide glasses in a sandwich-like structure after oxygen plasma treatment.
D. Emulsification system
For the water-in-oil droplet production, we used water as dispersed phase and a solution made of 0.5% (w/w) block-polymer surfactant KJ1000 solubilized in HFE-7500 fluorinated oil (3 M) as the continuous phase. KJ1000 was prepared from the commercially available carboxylic acid Krytox157-FSH (Dupont) and Jeffamine polyetheramines (M 1000, Huntsmann) following the synthesis route based on the one described by Holtze et al.42 With this surfactant concentration, the aqueous droplets are stabilized against coalescence.
E. Device operation
A precision syringe pump (neMESYS, cetoni GmbH) was used to control the continuous phase flow rate. Before loading the aqueous phases into the wells, the microfluidic channel of the chip was filled with the oil phase to remove the trapped air bubbles that can disturb the synchronization of droplet production (see supplementary material46). Finally, the dispersed phases were loaded in the wells using a standard pipette which usually serves for loading a microtiter plate, and the pressure chamber was sealed. The pressure-driven pump (MFCS-8C, Fluigent) was connected through the tubing to the pressure chamber. The other through hole was used as a valve to release the pressure in the chamber by using blocked fitting or additional tubing connection. The device was mounted on an inverted microscope (Olympus, IX71) for visualization. Droplet production movies were recorded using a high-speed camera (Phantom V411, Vision Research).
F. Image analysis
Videos were recorded from each channel and frame rates were varied from 5000 to 20 000 fps depending on the droplet production frequency. The analysis area was centered on a 1 mm section of the channel taken approximately 1 mm from the droplet production. For each frame, a Hough circle detection algorithm43 was used to roughly localize droplet center and size. This rough detection was then refined using Virtual Image Correlation44 based on a gray level distribution along one cross-section of the droplet shape. This refinement allows for a sub-pixel estimation of the 2D droplet section imaged by the high-speed camera. A projection model (described in Supporting Information) was then used to estimate the diameter and the volume of the detected droplet. Tracking of the droplets along the analysis area enables to define the droplet physical characteristics which can suffer from local variations due to channel irregularities or pixel alignment. The number of occurrences for each droplet which can be observed varied between 20 and 40 depending on the spacing between droplets and the camera frame rates. The tracking also enables to assess droplet speed, frequency, and throughput. Approximately 2000 droplets were processed for each one of the ten channels to measure droplet size dispersion amongst channels. The developed tool facilitates automatic statistical analysis of droplet size distribution from a large number of measurements with a high precision.
G. Enzymatic assay
Kinetic properties of β-galactosidase from E. coli were measured using the developed system as a model biological reaction. The enzymatic activity was measured by using the fluorogenic substrate FDG. The β-galactosidase and the FDG were purchased from Sigma-Aldrich. β-galactosidase hydrolyzes FDG in two successive steps resulting in the highly fluorescent free fluorescein (absorption maximum at 494 nm and emission maximum at 521 nm) and two galactose molecules.40 PBS was used as a buffer solution. The droplet fluorescence was measured using a laser-induced fluorescence system as described in Ref. 45. Droplets were reinjected to a microchannel with a height of 35 μm and a width of 70 μm at a frequency of 500 Hz with an oil flow rate of 15 μl/min and an emulsion flow rate of 5 μl/min.
ACKNOWLEDGMENTS
We thank the Max Planck Society and the CNRS for financial support. J.-C.B. acknowledges the support of the Initiative of Excellence “IdEx Bordeaux” and of the “Région Aquitaine.” O. Caen thanks ITMO National Cancer Alliance for Life Sciences and Health (AVIESAN, INSERM, no. HAP_2012001) for a fellowship within the Frontiers in Life Science Ph.D. program (FdV). We thank W. Keiderling, A. Gerke, and W. Schubert from the Workshop facility of the MPIds for technical support.
References
- 1.Thorsen T., Roberts R. W., Arnold F. H., and Quake S. R., “ Dynamic pattern formation in a vesicle-generating microfluidic device,” Phys. Rev. Lett. 86, 4163–4166 (2001). 10.1103/PhysRevLett.86.4163 [DOI] [PubMed] [Google Scholar]
- 2.Squires T. M. and Quake S. R., “ Microfluidics: Fluid physics at the nanoliter scale,” Rev. Mod. Phys. 77, 977–1026 (2005). 10.1103/RevModPhys.77.977 [DOI] [Google Scholar]
- 3.See the series of papers in the “Lab on a Chip” supplement in Nature 442, 367–418 (2006), available at http://www.nature.com/nature/supplements/insights/labonachip/index.html. [Google Scholar]
- 4.Kelly B. T., Baret J.-C., Taly V., and Griffiths A. D., “ Miniaturizing chemistry and biology in microdroplets,” Chem. Commun. 2007, 1773–1788 10.1039/B616252E [DOI] [PubMed] [Google Scholar]
- 5.Seemann R., Brinkmann M., Pfohl T., and Herminghaus S., “ Droplet-based microfluidics,” Rep. Prog. Phys. 75, 016601 (2012). 10.1088/0034-4885/75/1/016601 [DOI] [PubMed] [Google Scholar]
- 6.Guo M. T., Rotem A., Heyman J. A., and Weitz D. A., “ Droplet microfluidics for high-throughput biological assays,” Lab Chip 12, 2146–2155 (2012). 10.1039/c2lc21147e [DOI] [PubMed] [Google Scholar]
- 7.Brouzes E., Medkova M., Savenelli N., Marran D., Twardowski M., Hutchison J. B., Rothberg J. M., Link D. R., Perrimon N., and Samuels M. L., “ Droplet microfluidic technology for single-cell high-throughput screening,” Proc. Natl. Acad. Sci. U.S.A. 106, 14195–14200 (2009). 10.1073/pnas.0903542106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baret J.-C., Miller O. J., Taly V., Ryckelynck M., El-Harrak A., Frenz L., Rick C., Samuels M. L., Hutchison J. B., Agresti J. J.et al. , “ Fluorescence-activated droplet sorting (FADS): Efficient microfluidic cell sorting based on enzymatic activity,” Lab Chip 9, 1850–1858 (2009). 10.1039/b902504a [DOI] [PubMed] [Google Scholar]
- 9.Baret J.-C., Beck Y., Billas-Massobrio I., Moras D., and Griffiths A. D., “ Quantitative cell-based reporter gene assays using droplet-based microfluidics,” Chem. Biol. 17, 528–536 (2010). 10.1016/j.chembiol.2010.04.010 [DOI] [PubMed] [Google Scholar]
- 10.Satoh T., Kodama K., Ichikawa S., Sugiura S., and Kanamori T., “ Pressure-driven microfluidic device for droplet formation with minimized dead volume,” J. Chem. Eng. Jpn. 47, 841–847 (2014). 10.1252/jcej.14we103 [DOI] [Google Scholar]
- 11.Debs B. E., Utharala R., Balyasnikova I. V., Griffiths A. D., and Merten C. A., “ Functional single-cell hybridoma screening using droplet-based microfluidics,” Proc. Natl. Acad. Sci. U.S.A. 109, 11570–11575 (2012). 10.1073/pnas.1204514109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sjostrom S. L., Bai Y., Huang M., Liu Z., Nielsen J., Joensson H. N., and Svahn H. A., “ High-throughput screening for industrial enzyme production hosts by droplet microfluidics,” Lab Chip 14, 806–813 (2014). 10.1039/C3LC51202A [DOI] [PubMed] [Google Scholar]
- 13.Wang B. L., Ghaderi A., Zhou H., Agresti J., Weitz D. A., Fink G. R., and Stephanopoulos G., “ Microfluidic high-throughput culturing of single cells for selection based on extracellular metabolite production or consumption,” Nat. Biotechnol. 32, 473–478 (2014). 10.1038/nbt.2857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Joensson H. N., Samuels M. L., Brouzes E. R., Medkova M., Uhlén M., Link D. R., and Andersson-Svahn H., “ Detection and analysis of low-abundance cell-surface biomarkers using enzymatic amplification in microfluidic droplets,” Angew. Chem. Int. Ed. 48, 2518–2521 (2009). 10.1002/anie.200804326 [DOI] [PubMed] [Google Scholar]
- 15.Arayanarakool R., Shui L., Kengen S. W. M., van den Berg A., and Eijkel J. C. T., “ Single-enzyme analysis in a droplet-based micro- and nanofluidic system,” Lab Chip 13, 1955–1962 (2013). 10.1039/c3lc41100a [DOI] [PubMed] [Google Scholar]
- 16.Pekin D., Skhiri Y., Baret J.-C., Corre D. L., Mazutis L., Salem C. B., Millot F., Harrak A. E., Hutchison J. B., Larson J. W.et al. , “ Quantitative and sensitive detection of rare mutations using droplet-based microfluidics,” Lab Chip 11, 2156–2166 (2011). 10.1039/c1lc20128j [DOI] [PubMed] [Google Scholar]
- 17.Clausell-Tormos J., Griffiths A. D., and Merten C. A., “ An automated two-phase microfluidic system for kinetic analyses and the screening of compound libraries,” Lab Chip 10, 1302–1307 (2010). 10.1039/b921754a [DOI] [PubMed] [Google Scholar]
- 18.Miller O. J., Harrak A. E., Mangeat T., Baret J.-C., Frenz L., Debs B. E., Mayot E., Samuels M. L., Rooney E. K., Dieu P.et al. , “ High-resolution dose-response screening using droplet-based microfluidics,” Proc. Natl. Acad. Sci. U.S.A. 109, 378–383 (2012). 10.1073/pnas.1113324109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhong Q., Bhattacharya S., Kotsopoulos S., Olson J., Taly V., Griffiths A. D., Link D. R., and Larson J. W., “ Multiplex digital PCR: Breaking the one target per color barrier of quantitative PCR,” Lab Chip 11, 2167–2174 (2011). 10.1039/c1lc20126c [DOI] [PubMed] [Google Scholar]
- 20.Taly V., Pekin D., Benhaim L., Kotsopoulos S. K., Corre D. L., Li X., Atochin I., Link D. R., Griffiths A. D., Pallier K.et al. , “ Multiplex picodroplet digital PCR to detect KRAS mutations in circulating DNA from the plasma of colorectal cancer patients,” Clin. Chem. 59, 1722–1731 (2013). 10.1373/clinchem.2013.206359 [DOI] [PubMed] [Google Scholar]
- 21.Pinheiro L. B., Coleman V. A., Hindson C. M., Herrmann J., Hindson B. J., Bhat S., Emslie K. R.et al. , “ Evaluation of a droplet digital polymerase chain reaction format for DNA copy number quantification,” Anal. Chem. 84, 1003–1011 (2012). 10.1021/ac202578x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Didelot A., Kotsopoulos S. K., Lupo A., Pekin D., Li X., Atochin I., Srinivasan P., Zhong Q., Olson J., Link D. R.et al. , “ Multiplex picoliter-droplet digital PCR for quantitative assessment of DNA integrity in clinical samples,” Clin. Chem. 59, 815–823 (2013). 10.1373/clinchem.2012.193409 [DOI] [PubMed] [Google Scholar]
- 23.Agresti J. J., Antipov E., Abate A. R., Ahn K., Rowat A. C., Baret J.-C., Marquez M., Klibanov A. M., Griffiths A. D., and Weitz D. A., “ Ultrahigh-throughput screening in drop-based microfluidics for directed evolution,” Proc. Natl. Acad. Sci. U.S.A. 107, 4004–4009 (2010). 10.1073/pnas.0910781107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mazutis L., Gilbert J., Ung W. L., Weitz D. A., Griffiths A. D., and Heyman J. A., “ Single-cell analysis and sorting using droplet-based microfluidics,” Nat. Protoc. 8, 870–891 (2013). 10.1038/nprot.2013.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ristenpart W. D., Wan J., and Stone H. A., “ Enzymatic reactions in microfluidic devices: Michaelis-Menten kinetics,” Anal. Chem. 80, 3270–3276 (2008). 10.1021/ac702469u [DOI] [PubMed] [Google Scholar]
- 26.Ahn K., Agresti J., Chong H., Marquez M., and Weitz D. A., “ Electrocoalescence of drops synchronized by size-dependent flow in microfluidic channels,” Appl. Phys. Lett. 88, 264105 (2006). 10.1063/1.2218058 [DOI] [Google Scholar]
- 27.Shim U. K., Ranasinghe R. T., Smith C. A., Ibrahim S. M., Hollfelder F., Huck W. T. S., Klenerman D., and Abell C., “ Ultrarapid generation of femtoliter microfluidic droplets for single-molecule-counting immunoassays,” ACS Nano 7, 5955–5964 (2013). 10.1021/nn401661d [DOI] [PubMed] [Google Scholar]
- 28.Lim J., Gruner P., Konrad M., and Baret J.-C., “ Micro-optical lens array for fluorescence detection in droplet-based microfluidics,” Lab Chip 13, 1472–1475 (2013). 10.1039/c3lc41329b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Abate A. R. and Weitz D. A., “ Syringe-vacuum microfluidics: A portable technique to create monodisperse emulsions,” Biomicrofluidics 5, 14107 (2011). 10.1063/1.3567093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li W., Young E. W. K., Seo M., Nie Z., Garstecki P., Simmons C. A., and Kumacheva E., “ Simultaneous generation of droplets with different dimensions in parallel integrated microfluidic droplet generators,” Soft Matter 4, 258–262 (2008). 10.1039/B712917C [DOI] [PubMed] [Google Scholar]
- 31.Nisisako T. and Torii T., “ Microfluidic large-scale integration on a chip for mass production of monodisperse droplets and particles,” Lab Chip 8, 287–293 (2008). 10.1039/B713141K [DOI] [PubMed] [Google Scholar]
- 32.Nisisako T., Ando T., and Hatsuzawa T., “ High-volume production of single and compound emulsions in a microfluidic parallelization arrangement coupled with coaxial annular world-to-chip interfaces,” Lab Chip 12, 3426–3435 (2012). 10.1039/c2lc40245a [DOI] [PubMed] [Google Scholar]
- 33.Mulligan M. K. and Rothstein J. P., “ Scale-up and control of droplet production in coupled microfluidic flow-focusing geometries,” Microfluid. Nanofluid. 13, 65–73 (2012). 10.1007/s10404-012-0941-7 [DOI] [Google Scholar]
- 34.Conchouso D., Castro D., Khan S. A., and Foulds I. G., “ Three-dimensional parallelization of microfluidic droplet generators for a litre per hour volume production of single emulsions,” Lab Chip 14, 3011–3020 (2014). 10.1039/C4LC00379A [DOI] [PubMed] [Google Scholar]
- 35.Langbein D., Capillary Surfaces, Springer Tracts in Modern Physics Series (Springer, 2002), Vol. 178. [Google Scholar]
- 36.Brinkmann M., “ Benetzung lateral strukturierter Oberflaechen,” Ph.D. dissertation, Potsdam, 2002. [Google Scholar]
- 37.Baret J.-C. and Brinkmann M., “ Wettability control of droplet deposition and detachment,” Phys. Rev. Lett. 96, 146106 (2006). 10.1103/PhysRevLett.96.146106 [DOI] [PubMed] [Google Scholar]
- 38.Fuerstman M. J., Lai A., Thurlow M. E., Shevkoplyas S. S., Stone H. A., and Whitesides G. M., “ The pressure drop along rectangular microchannels containing bubbles,” Lab Chip 7, 1479–1489 (2007). 10.1039/b706549c [DOI] [PubMed] [Google Scholar]
- 39.Sullivan M. T. and Stone H. A., “ The role of feedback in microfluidic flow-focusing devices,” Philos. Trans. A: Math. Phys. Eng. Sci. 366, 2131–2143 (2008). 10.1098/rsta.2008.0003 [DOI] [PubMed] [Google Scholar]
- 40.Huang Z., “ Kinetic fluorescence measurement of fluorescein di-beta-D-galactoside hydrolysis by beta-galactosidase: Intermediate channeling in stepwise catalysis by a free single enzyme,” Biochemistry 30, 8535–8540 (1991). 10.1021/bi00099a006 [DOI] [PubMed] [Google Scholar]
- 41.Sakakihara S., Araki S., Iino R., and Noji H., “ A single-molecule enzymatic assay in a directly accessible femtoliter droplet array,” Lab Chip 10, 3355–3362 (2010). 10.1039/c0lc00062k [DOI] [PubMed] [Google Scholar]
- 42.Holtze C., Rowat A. C., Agresti J. J., Hutchison J. B., Angile F. E., Schmitz C. H. J., Koester S., Duan H., Humphry K. J., Scanga R. A.et al. , “ Biocompatible surfactants for water-in-fluorocarbon emulsions,” Lab Chip 8, 1632–1639 (2008). 10.1039/b806706f [DOI] [PubMed] [Google Scholar]
- 43.D'Orazio T., Guaragnella C., Leo M., and Distante A., “ A new algorithm for ball recognition using circle Hough transform and neural classifier,” Pattern Recognit. 37, 393–408 (2004). 10.1016/S0031-3203(03)00228-0 [DOI] [Google Scholar]
- 44.Schreier H., Orteu J.-J., and Sutton M. A., Image Correlation for Shape, Motion and Deformation Measurements ( Springer Science+Business Media, 2009). [Google Scholar]
- 45.Skhiri Y., Gruner P., Semin S., Brosseau Q., Pekin D., Mazutis L., Goust V., Kleinschmidt F., Harrak A. E., Hutchison J.et al. , “ Dynamics of molecular transport by surfactants in emulsions,” Soft Matter 8, 10618–10627 (2012). 10.1039/c2sm25934f [DOI] [Google Scholar]
- 46.See supplementary material at http://dx.doi.org/10.1063/1.4919415E-BIOMGB-9-025502 for more details about the methodology and the microfluidic platform.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4919415E-BIOMGB-9-025502 for more details about the methodology and the microfluidic platform.