Accelerated statistical reconstruction for C-arm cone-beam CT using Nesterov’s method

Abstract

Purpose:

To accelerate model-based iterative reconstruction (IR) methods for C-arm cone-beam CT (CBCT), thereby combining the benefits of improved image quality and/or reduced radiation dose with reconstruction times on the order of minutes rather than hours.

Methods:

The ordered-subsets, separable quadratic surrogates (OS-SQS) algorithm for solving the penalized-likelihood (PL) objective was modified to include Nesterov’s method, which utilizes “momentum” from image updates of previous iterations to better inform the current iteration and provide significantly faster convergence. Reconstruction performance of an anthropomorphic head phantom was assessed on a benchtop CBCT system, followed by CBCT on a mobile C-arm, which provided typical levels of incomplete data, including lateral truncation. Additionally, a cadaveric torso that presented realistic soft-tissue and bony anatomy was imaged on the C-arm, and different projectors were assessed for reconstruction speed.

Results:

Nesterov’s method provided equivalent image quality to OS-SQS while reducing the reconstruction time by an order of magnitude (10.0 ×) by reducing the number of iterations required for convergence. The faster projectors were shown to produce similar levels of convergence as more accurate projectors and reduced the reconstruction time by another 5.3 ×. Despite the slower convergence of IR with truncated C-arm CBCT, comparison of PL reconstruction methods implemented on graphics processing units showed that reconstruction time was reduced from 106 min for the conventional OS-SQS method to as little as 2.0 min with Nesterov’s method for a volumetric reconstruction of the head. In body imaging, reconstruction of the larger cadaveric torso was reduced from 159 min down to 3.3 min with Nesterov’s method.

Conclusions:

The acceleration achieved through Nesterov’s method combined with ordered subsets reduced IR times down to a few minutes. This improved compatibility with clinical workflow better enables broader adoption of IR in CBCT-guided procedures, with corresponding benefits in overcoming conventional limits of image quality at lower dose.

1. INTRODUCTION

Advances in model-based iterative reconstruction (IR) methods for x-ray CT and cone-beam CT (CBCT) imaging have led to numerous studies demonstrating the benefits of improved image quality and/or reduced radiation dose over conventional analytic reconstruction methods.^1–6 However, the increased reconstruction time (up to several hours, even on commercial systems) is a major drawback that limits the use of IR in many applications, especially those that require timely images as a part of the clinical workflow.^7–10 For example, potential applications of IR for CBCT include the use of C-arms in image-guided surgery for verifying device placement (e.g., pedicle screws in spine surgery) and providing high-quality, low-dose intraoperative checks against complications in healthy tissue (e.g., intracranial hemorrhage in neurosurgery).^11–14 Such applications demand image reconstructions on the order of minutes rather than hours.

Further compounding the challenge, C-arm CBCT data are typically incomplete and missing information due to the failure to satisfy Tuy’s condition with a cone-beam acquisition and a circular orbit^15–19 (which yields so-called cone-beam artifacts), longitudinal truncation (i.e., the long-object problem), an incomplete orbit (e.g., if 180°+ the fan angle is not acquired), sparse sampling (i.e., fewer projections acquired), and/or lateral truncation [due to the relatively small field of view (FOV)].^20–24 Therefore, the problem is generally ill-conditioned, leading to slow convergence. In particular, for truncated acquisitions, expanding the reconstruction FOV beyond the C-arm imaging FOV to encompass the object support is important in IR methods to enforce consistency of the line integral of the reconstruction with the measurements, but convergence is slow in the expanded FOV due to the lack of data. Although image regularization can improve conditioning of the problem, truncated projections and other forms of incomplete data remain a challenge for CBCT IR convergence speed.

Accelerating IR is an active area of research and can be addressed using a number of possible solutions, including hardware and/or algorithmic improvements.^25–29 A common acceleration technique divides the projections into ordered subsets (OS) to accelerate the reconstruction by a factor approximately equal to the number of subsets.^28,30 The acceleration is achieved by using one subset of projections per subiteration to update the volume, which correspondingly reduces the number of forward and backprojections per update. For example, the penalized-likelihood (PL) reconstruction problem, which leverages a statistical model of the measured data combined with a priori assumptions on the image such as local smoothness, can be solved iteratively by combining OS with the separable quadratic surrogates (SQS) algorithm (previously referred to as separable paraboloidal surrogates, SPS),³⁰ although other algorithms for maximum-likelihood (ML) and PL problems have been developed as well, including expectation maximization (EM), iterative coordinate descent, and grouped coordinate ascent.^28,31–33 OS-SQS uses a highly parallelizable approach that can leverage advances in parallel computing on hardware such as general-purpose graphics processing units (GPUs). Even so, convergence can still be slow, typically requiring hundreds of iterations and upward of several hours to perform the reconstruction. This is in part due to conventional OS-SQS updating the image without any “memory” of previous updates. Therefore, if the algorithm can be modified to carry “momentum” from previous updates, it can better inform the current update and achieve faster convergence.^34,35 Such a method, known as Nesterov acceleration or Nesterov’s method,³⁴ was first applied to total-variation (TV)-based CT image reconstruction by Jørgensen et al.³⁶ and Jensen et al.³⁷ TV reconstruction is similar to PL in that accelerated convergence of the optimization problem is desired and the objective function is smooth, enabling the development of an accelerated method called unknown parameter Nesterov (UPN), which has also been applied to CBCT reconstruction by others.^38,39 Kim et al. also recently demonstrated the use of Nesterov’s method,^40,41 combining it with OS-SQS for penalized weighted least squares (PWLS) CT reconstructions. A number of alternative approaches have been investigated for accelerating PWLS reconstructions, including work by Ramani and Fessler²⁹ that compared the fast iterative shrinkage-thresholding algorithm (FISTA)⁴² and split-Bregman^43,44 methods with a splitting-based alternating direction method of multipliers (ADMM) algorithm accelerated by a preconditioning filter. Additionally, the linearized augmented Lagrangian method with ordered subsets (OS-LALM) was recently developed.⁴⁵ Such methods could possibly be extended to PL reconstructions, but are not considered within the scope of this work. The work below applies Nesterov’s method with OS-SQS to acceleration of PL reconstruction similar to the approach by Kim et al.^40,41 and applies the algorithm to C-arm CBCT in the context of image-guided surgery, with a particular emphasis on how acceleration can help to overcome convergence speed issues associated with truncated data. Performance is assessed relative to SQS in an anthropomorphic head phantom for truncated and untruncated data and demonstrated in a cadaveric torso emulating a scenario of CBCT-guided abdominal surgery.

2. METHODS

2.A. Statistical reconstruction algorithms

The PL framework³⁰ enables statistical image reconstruction by first applying a basic Poisson statistics model to the data

$${\displaystyle y_i\sim \text{Poisson}\left(b_i{e}^{-l_i}\right),}$$ (1)

where y are the noisy measured projection data, b are the number of incident photons, l = Aμ are the line integrals computed for system matrix A (forward-projection) and image volume μ, and i indexes the rays. PL then formulates the reconstruction as the solution to an optimization problem, where the objective Φ(μ; y) comprises the log-likelihood function $L\left(\mu ;y\right)$ of the data and image regularization by a roughness penalty R(μ) with strength β,

$${\displaystyle \hat{\mu }=\underset{\mu }{\mathrm{argmax}}\mathrm{\Phi }(\mu ;y)\text{s.t.}\mu \ge 0.}$$ (2)

$${\displaystyle \mathrm{\Phi }(\mu ;y)=L\left(\mu ;y\right)-\beta R\left(\mu \right).}$$ (3)

Ignoring constant terms, the log-likelihood function is

$${\displaystyle L\left(\mu ;y\right)\cong -\sum _i{b}_i{e}^{-l_i}+y_i{l}_i}$$ (4)

and the image roughness penalty³⁰ is calculated as

$${\displaystyle R\left(\mu \right)=\sum _j\sum _{k\in {\mathcal{N}}_j}{w}_{\mathit{jk}}\psi \left({\mu }_j-{\mu }_k\right),}$$ (5)

where j indexes all voxels, k indexes the voxels in a neighborhood N_j about voxel j (first-order neighborhood in this work), w_jk are the weights within a neighborhood (unity in this work), and ψ is the penalty function.

The OS-SQS method³⁰ is often employed to solve Eq. (2) and utilizes highly parallelizable voxel-wise operations on volumes. Additionally, the forward and backprojection operators are performed on the entire volume and subsets of projections, respectively, which are tasks well-suited for implementation on parallel hardware architectures such as GPUs. OS-SQS leverages a separable quadratic “surrogate” function that locally approximates the PL objective function, and the surrogate function is maximized during each update to increase the objective value of the reconstructed volume. The starting image μ⁽⁰⁾ can be initialized by the filtered backprojection (FBP) reconstruction (although a common alternative is a zero image). When M subsets are used (providing acceleration by approximately a factor of M), the algorithm is run for N iterations as follows (Algorithm I, denoted SQS-M):

ALGORITHM I.

SQS with M ordered subsets (SQS-M).

Initialize μ = μ(0)

Precompute γm = Am1, for m = 1, 2, 3, …, M

For n = 1, 2, 3, …, N

For m = 1, 2, 3, …, M $${\displaystyle l={\mathbf{A}}_m\mu }$$ (6) $${\displaystyle {\dot{h}}_i=y_i-b_i{e}^{-l_i},\forall i\in S_m}$$ (7) $${\displaystyle \dot{L}=M{\mathbf{A}}_m^T\dot{h}}$$ (8) $${\displaystyle c_i\left(l_i\right)=\left\{\begin{array}{ll}2b_i\left(1-e^{-l_i}-l_i{e}^{-l_i}\right)/l_i^2\hfill & l_i>0\hfill \\ b_i\hfill & l_i=0\hfill \end{array}\right.}$$ (9) $${\displaystyle d=M{\mathbf{A}}_m^T({\gamma }_m\cdot c\left(l\right))}$$ (10) $${\displaystyle {\mathrm{\Delta }}_j=-\frac{{\dot{L}}_j+\beta \sum _{k\in \underset{j}{\mathcal{N}}}{w}_{\mathit{jk}}\dot{\mathit{\Psi }}({\mu }_j-{\mu }_k)}{d_j+\beta \sum _{k\in \underset{j}{\mathcal{N}}}2w_{\mathit{jk}}{\omega }_{\psi }({\mu }_j-{\mu }_k)}}$$ (11) $${\displaystyle \mu ={\left[\mu +\mathrm{\Delta }\right]}_{+}}$$ (12)

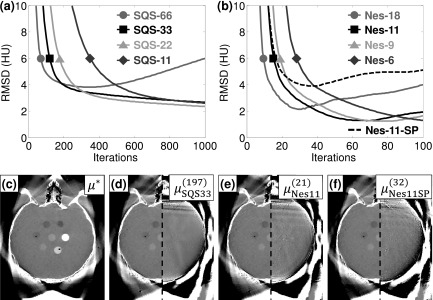
where A_m and A_m^T are the forward and backprojection operators, respectively, for subset m; γ _m are the projections of a volume of all ones for the mth subset; S_m are the projections in subset m; i and j index detector pixels and volume voxels, respectively; $\dot{L}$ and d are the gradient and curvature of the likelihood surrogates, respectively; ⋅ denotes an element-wise product of two vectors; $\dot{\psi }$ and ω_ψ are the derivative and curvature of the penalty function surrogates, respectively; Δ is the image update; and ${\left[\cdot \right]}_{+}$ is a thresholding operation at 0 that enforces a non-negativity constraint. The reconstructed image after N iterations of M subsets is denoted as ${\mu }_{\text{SQS}M}^{\left(N\right)}$. In this work, the edge-preserving Huber penalty was used, with

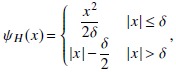(13)

$${\displaystyle {\omega }_{{\psi }_H}\left(x\right)=\frac{1}{max\left(\left|x\right|,\delta \right)},}$$ (14)

where δ is used to control the degree of edge preservation by controlling the width of the quadratic penalty region around x = 0.

Despite the OS acceleration, SQS-M convergence can be very slow. Kim et al.^40,41 demonstrated significant acceleration can be achieved by adapting Nesterov’s original method³⁴ with a modified and improved set of momentum weights [Eq. (17), below]⁴⁶ to accumulate momentum from image updates Δ [denoted $-D^{-1}M\nabla {\mathrm{\Psi }}_m\left(\mu \right)$ in Refs. 40 and 41], where the improved weights provide faster convergence. The algorithm is run for N iterations and M subsets as follows (Algorithm II, denoted Nes-M): where z is the current image estimate; v is the cumulative momentum from all image updates; t is a scalar momentum weight that increases approximately linearly with each subiteration; and the image μ is now a state variable that linearly combines the current image estimate with a momentum-based image (the cumulative momentum added to the initial image). Note that after each iteration, the current image estimate is now z rather than μ, with this redefinition of μ enabling the same definition of image update Δ with relation to μ [Eqs. (6)–(11)].

ALGORITHM II.

Nesterov acceleration of SQS-M (Nes-M).

Initialize z = μ = μ(0), v = 0, t = 1

For n = 1, 2, 3, …, N

For m = 1, 2, 3, …, M

Compute Δ in (6)–(11)

$${\displaystyle z={\left[\mu +\mathrm{\Delta }\right]}_{+}}$$ (15) $${\displaystyle v=v+t\mathrm{\Delta }}$$ (16) $${\displaystyle t=\left(1+\sqrt{1+4t^2}\right)/2}$$ (17) $${\displaystyle \mu =\left(1-\frac{1}{t}\right)z+\frac{1}{t}{\left[{\mu }^{\left(0\right)}+v\right]}_{+}}$$ (18)

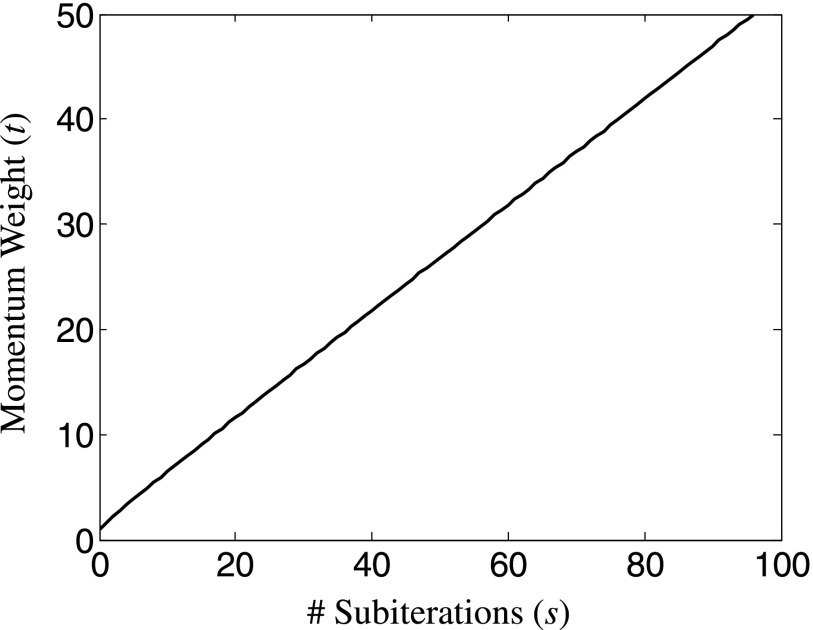
The additional computational expense of Nesterov’s method is minimal: it requires just one additional volume v in memory storage (an implementation that eliminates the intermediate variable z), and the additional computation of v and μ are multiply-and-add, voxel-wise operations of volumes that can be performed in parallel. Because t ≥ 1 and is an increasing function (Fig. 1), the momentum-based term in Eq. (18) takes larger steps in the combined direction of the previous updates, but does so in a controlled manner due to the 1/t weight. The selection of momentum weights is key to the acceleration and stability of the method;^34,46–48 for example, as a special case, if the weights were fixed at t = 1 for all subiterations, the Nes algorithm would be equivalent to the SQS algorithm. In the case of Nesterov’s method, the momentum weight t asymptotically approaches s/2, where s is the number of subiterations,

$${\displaystyle s=\left(n-1\right)M+m.}$$ (19)

FIG. 1.

Momentum weight t for Nesterov acceleration increases approximately linearly with the number of subiterations [despite the nonlinear recursive definition, Eq. (17)] and asymptotically approaches s/2.

2.B. Experimental setup

The performance of the SQS-M and Nes-M algorithms was compared using CBCT data acquired with an x-ray test bench and a prototype mobile C-arm capable of CBCT (modified PowerMobil, Siemens Healthcare). Studies employed an anthropomorphic head phantom containing a natural skeleton and simulated soft-tissue inserts as well as a cadaveric torso emulating an abdominal surgery scenario. The test bench incorporated a 43 × 43 cm² flat-panel detector with 0.278 × 0.278mm² pixel size (PaxScan 4343CB, Varian Medical Systems, Palo Alto, CA) providing little or no lateral truncation of the head phantom. The C-arm employed a 30 × 30 cm² detector with 0.388 × 0.388 mm² pixel size (PaxScan 3030+, Varian Medical Systems, Palo Alto, CA) with realistic lateral truncation (Fig. 2). The acquisition technique and geometry of the test bench replicated that of the C-arm—100 kVp tube voltage, 80 mA s total exposure (3.3 mGy head dose), 198 projections over ∼180° orbit, 60 cm source-axis distance (SAD), and 120 cm source-detector distance (SDD). Additionally, a separate study emulating a scenario of CBCT-guided abdominal surgery was conducted on the C-arm using a fresh, unfixed cadaveric torso presenting realistic anatomical structures and an acquisition technique of 100 kVp, 120 mA s (3.1 mGy body dose).⁵

FIG. 2.

(a) Benchtop system with anthropomorphic head phantom. (b) Mobile C-arm system with phantom on operating table. (c) The bench and C-arm FOV are depicted with respect to a CT image of the phantom, display window [−400 400] HU.

The SQS and Nes algorithms were implemented using custom CUDA libraries (Nvidia, Santa Clara, CA) to leverage the parallel computing capabilities of GPUs. Unless otherwise noted, the voxel-based separable footprints with trapezoidal basis functions (SF-TT) projector was used due to its greater accuracy⁴⁹—the forward projector was previously defined as matrix operator A and the backprojector by A^T. As described in Ref. 5, the original SF-TT approach was extended from a circular trajectory (five degrees of freedom, DOF) to handle an arbitrary 9-DOF geometry represented by projection matrices. The extension changed computation of the “amplitude” (i.e., height of the trapezoid function of the footprint of each voxel) to calculating the intersection length between the voxel and a ray connecting the source and the center of the voxel,⁵⁰ followed by determining the detector pixels intersecting the trapezoidal footprint by projecting the eight vertices of the voxel to compute the trapezoid vertices. Each voxel was projected by a single thread on the GPU, enabling a highly parallelized implementation.

While the high-fidelity but relatively slow SF-TT projector was used by default, reconstructions with faster, less accurate projectors were also evaluated—in particular, the ray-driven Siddon forward projector⁵¹ and voxel-driven Peters backprojector,⁵² denoted SP. The use of mismatched forward and backprojectors (sometimes referred to as dual-matrix reconstruction) to reduce computation time has been previously proposed and empirically shown to accelerate the reconstruction process with little penalty on image quality, despite convergence no longer necessarily being guaranteed, even for SQS-1.^53–55 We therefore assessed the impact of the faster SP projectors on both reconstruction time and convergence speed. The GPU-based implementation assigned each ray to a computational thread for the Siddon projector, while each voxel was assigned to a computational thread for the Peters backprojector, and both projectors were found to be substantially faster than the SF-TT projectors due to faster computation and efficient memory access. An additional modification was made to better match the voxel size (0.6 mm isotropic at isocenter with a magnification of ∼2.0) with the pixel size (0.388 mm at the detector): prior to each backprojection, the projection was convolved with a 3 × 3 averaging window to approximately match the pixel and (magnified) voxel size. A number of other projection methods have been developed, and the topic remains an active area of research.^56–58 Comparison to other projectors, such as distance-driven,⁵⁹ blobs,⁶⁰ and B-splines,⁶¹ and their tradeoffs between computation time and accuracy for PL reconstruction can be considered in future work.

Reconstruction parameters were set at b = 8000 quanta, β = 200 (for the bench data, and β = 80 for the C-arm data to compensate for the smaller detector array, which results in a smaller log-likelihood magnitude [Eq. (4)] relative to the image roughness [Eq. (5)]), δ = 10 ⁻⁴ mm⁻¹, and 0.6 × 0.6 × 0.6 mm³ voxel size. The effect of M was quantified for integer divisors of the number of projections—thus, M ∈ {66, 33,  …,  1}. Different reconstruction algorithms (e.g., Nes-11 vs SQS-1) were compared by assessing how many iterations n_A were required for Algorithm A to achieve the same objective value as n_B iterations of Algorithm B,

$${\displaystyle min{n}_A\text{s}.\text{t}.\mathrm{\Phi }\left({\mu }_A^{\left(n_A\right)};y\right)\ge \mathrm{\Phi }\left({\mu }_B^{\left(n_B\right)};y\right).}$$ (20)

In this way, the acceleration factor (AF) of Algorithm A could be determined in relation to Algorithm B,

$${\displaystyle {\text{AF}}_B^{\text{A}}\left(n_B\right)=n_B/n_A.}$$ (21)

For example, the acceleration of SQS-M relative to SQS-1 is expected to produce the familiar ${\text{AF}}_{\text{SQS}-1}^{\text{SQS}-M}\left(n\right)\approx M$. The work below exclusively computes the AF for SQS-M and Nes-M (Algorithm A) relative to SQS-1 (Algorithm B), so the algorithm names are dropped from the AF notation for simplicity. Additionally, the root mean square difference (RMSD) between μ⁽ⁿ⁾ and a “converged” reconstruction μ^* was used to quantify image accuracy as a function of iteration. Conversion from reconstructed units of mm⁻¹ to Hounsfield units (HU) was approximated as 5 × 10⁴ HU/mm⁻¹.

3. RESULTS

3.A. Untruncated reconstructions of the head

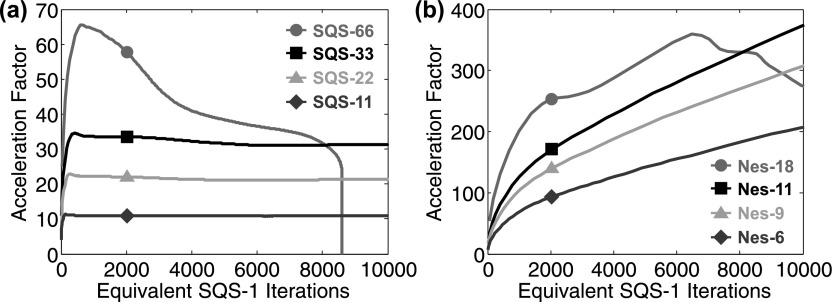
Test bench images of the head phantom were reconstructed using the SQS-M algorithm run for 1000 iterations for each M and the acceleration factors relative to SQS-1 demonstrated the speedups associated with SQS-M (Fig. 3). As expected, SQS-M achieved AF up to M (although the AF tends to fall off due to suboptimal limit cycles,^28,62 as seen with SQS-66). The Nes-M algorithm was run for 100 iterations each and demonstrated much greater AF than SQS-M. For example, Nes-11 exhibited AF = 357 at 10⁴ equivalent SQS-1 iterations and the AF continued to monotonically increase with more iterations, suggesting a faster rate of convergence than SQS and increasingly more benefit from additional iterations. The AF also appeared to be proportional to M (for M ≤ 11). For M > 11, the reconstruction may not converge due to limit-cycle issues or instability, since momentum from each subset only contains information from a few projections, which may lead the reconstruction to false local optima.

FIG. 3.

Acceleration factor for SQS and Nes relative to SQS-1 (note the different y-axis scaling). (a) SQS-66 reaches a suboptimal limit cycle and cannot further improve the objective, while SQS-{33, 22, 11} achieve the same objective as 10⁴ iterations of SQS-1 in {321, 469, 922} iterations, respectively, and provide AF approximately equal to M. (b) On the other hand, Nes-18 (and greater M) exhibits unstable, nonmonotonic acceleration, while Nes-{11, 9, 6} achieve the same objective as 10⁴ iterations of SQS-1 in only {28, 34, 50} iterations, giving AF of {357, 294, 200}, respectively.

A converged reference volume μ^* was achieved with 3000 iterations of Nes-1 followed by 3000 iterations of convergent SQS-1 and was confirmed to have greater objective value than any of the other reconstructions. Although the Nes-1 iterations appeared to be convergent, the behavior of the Nes algorithm has not been thoroughly investigated. The 3000 iterations of Nes-1 produced an objective value that appeared to be within the numerical accuracy limits of the computations (performed in single-precision floating-point format), with numerical errors potentially accumulating in the momentum term. Therefore, the additional 3000 iterations of SQS-1 were performed to verify the Nes-1 solution and found to slightly increase the objective value. The RMSD before and after the additional SQS-1 iterations was only 0.0025 HU, suggesting that the Nes-1 solution was already very close to μ ^*. Alternatively, SQS-1 alone could have been run for tens of thousands of iterations to provide μ ^*, requiring an extremely long run time (weeks).

The convergence speed of SQS-M and Nes-M was assessed by the RMSD with μ^* in a region encompassing soft-tissue simulating inserts (Fig. 4). For SQS reconstructions, SQS-66 most rapidly reduced RMSD in early iterations but quickly leveled out after achieving 2.0 HU accuracy in 140 iterations, while SQS-33 was capable of RMSD = 1.0 HU after 260 iterations. On the other hand, Nes-18 only required 15 iterations to achieve RMSD = 2.0 HU (9.3 × acceleration vs SQS-66) and continued to reduce the error, achieving RMSD = 1.0 HU in 28 iterations (9.3 × acceleration vs SQS-33). Although the difference images contain some dissimilarities due to the different algorithms and subsets, they have the same RMSD and illustrate the most challenging aspect of convergence in the central axial slice—high frequency structure at edges and residual streaks at the posterior of the skull arising from the incomplete orbit (180°). Both SQS-M and Nes-M are capable of reducing the residual errors and streak artifacts beyond what is shown in Fig. 4 through a combination of lower M and more iterations, although this comes at the expense of higher run times, as indicated by the RMSD plots. For SQS-M, this requires using fewer subsets, since SQS-66 reaches a limit-cycle and converges to a RMSD = 1.9 HU. On the other hand, more iterations could be applied to Nes-18 (eventually achieving RMSD = 0.9 HU), or Nes-11 could be used to achieve even lower RMSD.

FIG. 4.

Accuracy of image reconstructions. (a) For RMSD = 2.0 HU, the fewest iterations required for SQS were M = 66, N = 140 and (b) for Nes were M = 18, N = 15. (Note the different x-axis scalings.) (c) Reference volume μ* and region used for RMSD evaluation annotated in the white dashed circle, display window [−400 400] HU. The SQS and Nes reconstructed images are shown on the left half of (d) and (e), respectively, for RMSD = 2.0 HU, while the right half shows the difference image with μ^*, display window [−20 20] HU.

3.B. Truncated reconstructions of the head

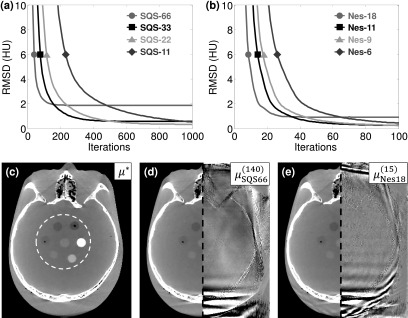
For the truncated C-arm projections, the AF followed a similar trend as the untruncated bench data, with Nes-11 providing a stable, monotonic increase in AF up to 345 × for 10⁴ equivalent SQS-1 iterations. However, analysis of RMSD illustrated the challenge of truncated projections, particularly due to missing data outside the C-arm FOV and the slow convergence in those regions (Fig. 5). Both SQS and Nes were unable to achieve RMSD as low as their counterparts in the untruncated data, in large part due to influence from the large errors outside the C-arm FOV (RMSD > 180 HU outside the C-arm FOV). The algorithms therefore require more iterations even for a higher RMSD than in untruncated data, with SQS-33 achieving 4.0 HU RMSD in 197 iterations and Nes-11 in 21 iterations. Even so, Nes-11 provided a 9.4 × reduction in the number of iterations required with SQS-33. Additionally, large M (e.g., SQS-66, Nes-18) resulted in unstable reconstructions and was susceptible to divergence from the optimal solution with too many iterations, possibly due to the missing data in truncated projections. For example, SQS-66 only utilizes three truncated projections per subset and errors from each update begin to accumulate, especially in regions of the reconstructed volume outside the C-arm FOV. Similarly, errors can accumulate in the cumulative momentum term for Nes-M—even moderate values of M for Nes exhibited some degree of divergent behavior. The stability of both SQS-M and Nes-M as a function of the number of subsets is the subject of ongoing work by others⁴⁷ and can continue to be investigated further.

FIG. 5.

Convergence and accuracy in truncated data. (a) SQS and (b) Nes reconstructions of truncated projections provided reconstructions with RMSD < 4 HU but were subject to divergence at a large number of iterations. (c) The converged solution μ^∗ shows a reasonably accurate reconstruction inside the C-arm FOV. A RMSD = 4.0 HU was achieved by (d) 197 iterations of SQS-33, (e) 21 iterations of Nes-11, and (f) 32 iterations of Nes-11 with the simpler SP projectors. In (d)-(f), the reconstructed result is shown in the left half (display window [−400 400] HU), while the difference image with μ^* is shown in the right half (display window [−40 40] HU).

Reconstruction with the modified, faster SP projectors was also able to yield RMSD = 4.0 HU compared to the SF-TT-based μ^* but required a greater number of iterations [32 iterations for Nes-11-SP, Fig. 5(f)]. It should be noted that Nes-11-SP barely achieved RMSD = 4.0 HU, so the stopping criterion is essential to any potential advantage of using the SP projectors. For example, if a lower RMSD were desired, fewer subsets would have to be used (e.g., Nes-6-SP), resulting in slower convergence speed. Much of the increased RMSD is attributable to inherent differences between the SP and SF-TT projectors, with a converged, SP-based μ^* having a RMSD = 3.7 HU relative to the SF-TT-based μ^*. Although SF-TT has been shown to be more accurate for projecting voxels,⁴⁹ neither set of projectors produces the “true” image. Stability remains a concern for Nes-M-SP since the error begins increasing shortly after reaching a minimum. In the case of Nes-11-SP, the target RMSD was reached in 32 iterations and the minimum was soon reached at 38 iterations before increasing again, demonstrating the need for a carefully chosen stopping criterion, whereas Nes-11 reached the target RMSD in 21 iterations and continued to lower the error until RMSD = 1.3 HU at 70 iterations. Nonetheless, despite the mismatched projectors, the RMSD = 4.0 HU error level was achievable without introducing noticeable artifact due to the addition of the smoothing step (convolving the projection with a 3 × 3 averaging window) prior to backprojection as well as the image regularization innate to PL. Therefore, the SP projectors may be useful if the benefit of increased speed outweighs the cost of additional iterations—e.g., in near-real-time CBCT for image-guided surgery.

3.C. Reconstruction time with GPU implementation

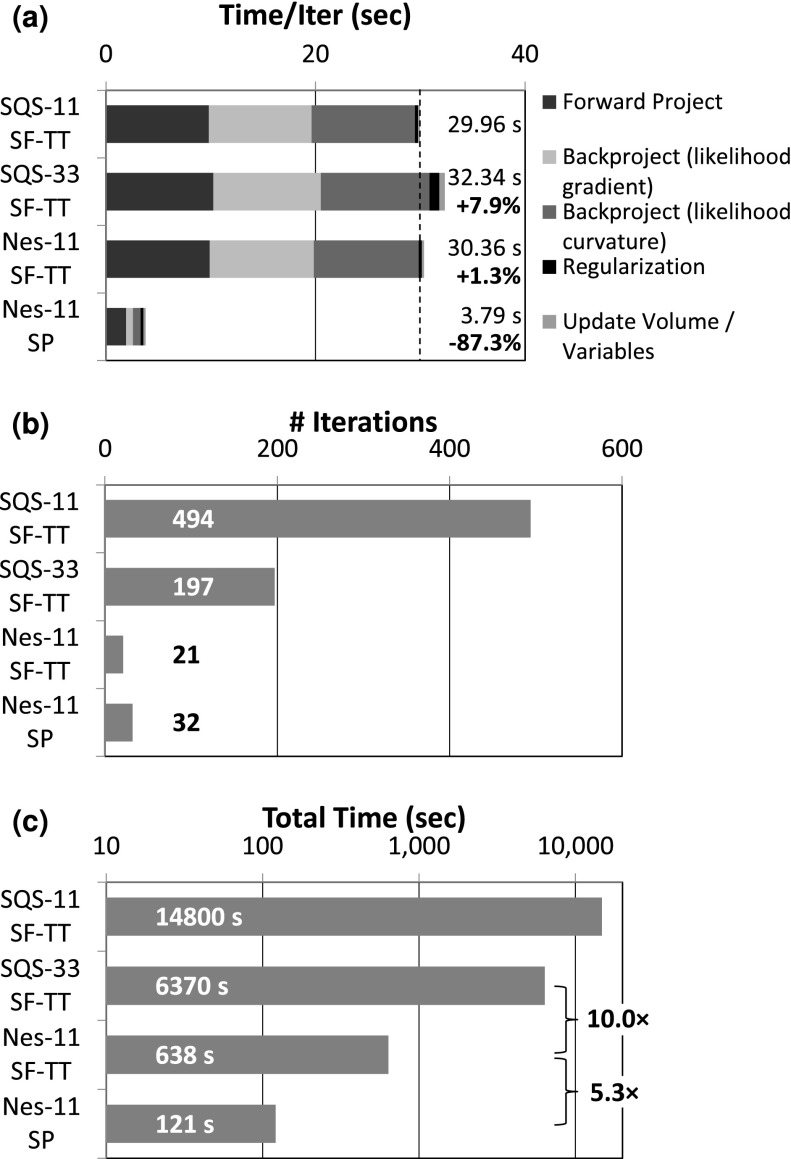
Reconstruction times for C-arm CBCT (768 × 768 × 198 data) were measured for the full head volume (300 × 360 × 300 voxels) on a PC workstation with a single GPU (GeForce GTX Titan Black, Nvidia, Santa Clara, CA). The vast majority of the reconstruction time is spent in the forward and backprojection operations (Fig. 6). Relative to the SQS-11 time per iteration, SQS-33 added an additional 7.94% computational time cost (primarily due to regularizing and updating the volume for each subset), while Nes-11 only added 1.34% cost [Fig. 6(a)]. Conversely, the faster SP projectors dramatically reduced the time per iteration by almost a factor of 8 since they are particularly well-suited for efficient parallel implementation. When the time per iteration is multiplied by the number of iterations required, a RMSD = 4 HU could be accomplished in ∼11 min for Nes-11 SF-TT (cf. 106 min for SQS-33), while the faster SP projectors allowed reconstruction in just over 2 min (121 s). Therefore, Nesterov’s method (Nes-11) alone reduced reconstruction time by 10.0 × over SQS (SQS-33), and faster projectors enabled an additional speedup of 5.3 × over SF-TT with the same RMSD.

FIG. 6.

Reconstruction time for a full head volume (300 × 360 × 300 voxels) at fixed RMSD = 4 HU. (a) The time per iteration for each algorithm shows that Nesterov’s method only adds a negligible amount of computation and that the SP projectors are substantially faster. (b) Nesterov’s method reduces the number of iterations required to achieve the same RMSD = 4 HU by an order of magnitude over SQS. (c) The combined effect of Nesterov’s method and fast projectors yields a reconstruction time of ∼2 min for Nes-11-SP.

3.D. Truncated reconstructions of the abdomen

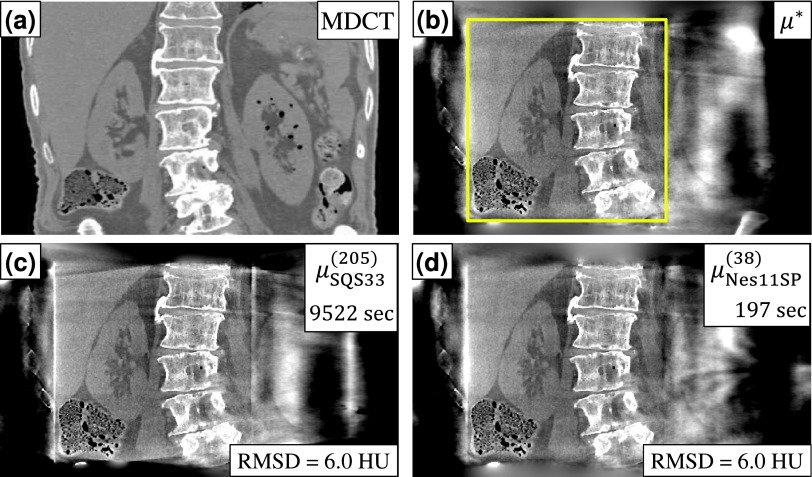
The same analysis of SQS and Nes algorithms was performed in reconstructions of fully truncated C-arm projections of a cadaveric torso (Fig. 7). Because of the larger object size, the reconstructed volume was increased to 500 × 350 × 330 voxels and a balance between reconstruction time and RMSD was found with SQS-33 providing 6.0 HU RMSD in 205 iterations (9522 s = 2.6 h), while Nes-11-SP was able to do so in only 38 iterations (197 s = 3.3 min). Compared to the head reconstruction, the abdomen reconstruction required more iterations even for a higher RMSD due to the greater degree of truncation and missing data. However, the acceleration of Nes-M-SP relative to SQS-M was just as pronounced, with a 48.3 × reduction in reconstruction time, demonstrating the applicability of the algorithm to objects with even more severe truncation.

FIG. 7.

Accelerated reconstruction of a cadaveric torso in CBCT-guided surgery. (a) Coronal slice of the multidetector CT volume, provided for visualization purposes only. (b) CBCT reference reconstruction μ ^*. The reconstruction FOV encompassed the axial extent of the abdomen, while the C-arm FOV (outlined in the figure) covered the right kidney, liver, spine, and small pockets of gas in the bowels. (c) SQS-33 provided RMSD = 6.0 HU (measured in a ROI around the kidney) in 205 iterations (9522 s), while (d) Nes-11-SP provided the same RMSD in 38 iterations (197 s). Display window [−500 500] HU.

4. DISCUSSION AND CONCLUSIONS

Nesterov’s method offers dramatic reduction in reconstruction time by accelerating convergence of the conventional ordered-subsets SQS algorithm by an order of magnitude (∼10 ×) for typical reconstructions. With faster Siddon-Peters type projectors, a GPU implementation of Nesterov-accelerated SQS was capable of providing a volumetric reconstruction of the head in ∼2 min, despite the challenges of fully truncated C-arm CBCT projections and/or other forms of incomplete data that lead to ill-conditioning and slower convergence. Of course, conventional FBP reconstruction is still faster than iterative reconstruction since by definition it requires only a single backprojection (cf. multiple forward/backprojections for IR). For example, FBP reconstruction of the head volume only required 19.3 s [18.0 s for filtering (implemented on GPU, but not yet fully optimized for run time) and 1.3 s for backprojection]. Nonetheless, reconstruction speeds accomplished by Nesterov acceleration further facilitates incorporation of IR methods in image-guided interventions, with corresponding benefits to image quality and reduced radiation dose.

Ongoing work includes integration of other methods for addressing lateral truncation, e.g., a fit of projection data to an elliptical model of the volume.^63,64 Using coarser voxels outside the C-arm FOV (i.e., a multiresolution volume) could provide further acceleration, since accuracy outside the C-arm FOV is not as critical despite comprising up to 68% of the total voxels in the reconstructed FOV. Simultaneous use of multiple GPUs has been investigated to reduce forward and backprojection time for the SF-TT projector by distributing the projections within each subset among the GPUs, whereas the already fast SP projectors were unable to take advantage of multiple GPUs due to the overhead cost of transferring data between GPUs. For example, a GPU workstation with 3 × GTX Titan’s reduced the time per iteration of the head volume to 15.52 s [2.1 × reduction, cf. Figure 6(a)] for Nes-11, but increased the time to 6.84 s (1.8 × increase) for Nes-11-SP. Further acceleration is also possible by using precomputed likelihood curvatures to eliminate one backprojection per iteration,³⁰ applying spatially nonuniform updates,⁶⁵ and applying different momentum techniques that increase stability or optimize convergence speed.^41,47,48 The impact of these modifications on convergence properties deserves further study, including whether the precomputed likelihood curvatures converge at the same rate and whether the curvatures should be updated every few iterations. Future work includes determining a method for selecting M a priori to maximize acceleration and minimize instability for a given level of RMSD as well as incorporation of a convergence criterion for terminating the reconstruction at an appropriate number of iterations. Additionally, comparison to other Nesterov-accelerated methods, such as the TV-based UPN method^36,37 applied to accelerated barrier optimization compressed sensing (ABOCS),³⁹ could be made. Future work includes comparison of the growing number of such momentum-based methods, not only in terms of reconstruction performance but also in obtaining the converged reference, which requires numerical stability and can benefit from a better understanding of convergence behavior. In conclusion, the increased compatibility of an accelerated reconstruction with the clinical workflow has the potential to increase adoption and the routine use of IR methods for C-arm CBCT.