Fine-resolution maps of acoustic properties at 250 MHz of unstained fixed murine retinal layers

Abstract

Ex vivo assessment of microscale tissue biomechanical properties of the mammalian retina could offer insights into diseases such as keratoconus, and macular degeneration. A 250-MHz scanning acoustic microscope (7-μm resolution) has been constructed to derive two-dimensional quantitative maps of attenuation (α), speed of sound (c), acoustic impedance (Z), bulk modulus (B), and mass density ($\rho$). The two-dimensional maps were compared to coregistered hematoxylin-and-eosin stained sections. This study is the first to quantitatively assess $\hspace{0.17em}\alpha$, c, Z, B, and $\rho$ of individual retinal layers of mammalian animals at high ultrasound frequencies. Significant differences in these parameters between the layers were demonstrated.

1. Introduction

The mammalian retina is highly heterogeneous and anisotropic at the micrometer scale (Nag and Wadhwa, 2012). Retinal disease is generally associated with structural changes such as loss of photoreceptors or degeneration of retinal layers (Nag and Wadhwa, 2012). Glaucoma is associated with degeneration of the ganglion cell and nerve-fiber layers of the retina. In retinitis pigmentosa and other inherited retinopathies, the photoreceptors and retinal pigment epithelium undergo progressive damage. Therefore, most retinal diseases are expected to occur concomitantly with changes in the local mechanical properties of the retina, as demonstrated in recent studies (Friedman et al., 1989; Worthington et al., 2014). Specifically, Worthington et al. (2014) found a significant change in the compressive modulus associated with rapid degeneration of mouse retinas.

Although these cited studies emphasize the necessity for assessing the mechanical properties of ocular components in ophthalmology diagnostics, only a few studies directly assess elastic properties using novel technologies, such as acoustic radiation force impulse imaging or sequential ultrasound imaging (Shahbazi et al., 2012; Silverman et al., 2013). However, data for ocular tissue at this scale are rare.

Scanning acoustic microscopy (SAM) has become a reliable tool for assessing acoustical properties, such as speed of sound (c), attenuation (α), and acoustic impedance (Z). These properties are directly related to the elastic properties of the tissue such as the bulk modulus (B). SAM has been applied successfully to characterize various soft tissues (Daft and Briggs, 1989; Hozumi et al., 2004; Saijo et al., 1997). These studies revealed significant variations in the acoustic properties, e.g., in cancerous tissue or atherosclerosis, indicating that structural changes of soft tissues are manifested in the mechanical properties of tissue at the micron level. Few studies have reported SAM measurements for ocular tissues (Beshtawi et al., 2013; Marmor et al., 1977). Beshtawi et al. (2013) found a 5% increase of c of corneal tissue using SAM and Marmor et al. (1977) found significant variations of acoustic properties of retinal layers.

These cited studies demonstrated that ocular tissues manifest a high variation of structural and mechanical properties at the micron level that, in many instances, can be accurately estimated using SAM. The transducer frequency and bandwidth determine the structural sizes that can be assessed by SAM. Studies report a wide range of utilized frequencies ranging from 100 MHz (Sasaki et al., 2003) to 1 GHz (Marmor et al., 1977) providing lateral resolutions ranging from approximately 15 to 1.5 μm.

However, although SAM potentially can assess c, α, and Z in a single measurement, and therefore can provide a means for estimating mechanical properties, such as B, most of the cited studies overlook some of these parameters or lack a full description of the processing procedures. Our aim was to develop a quantitative ultrasound signal-processing approach for ex vivo micron-scale assessment of the mechanical properties of slide-mounted tissue sections, and to apply this methodology to characterizing the murine retina.

2. Methods

In this pilot study, we conducted SAM measurements on two retinal sections derived from pigmented rdh4 knockout mice. All animal experiments were performed in accordance with the ARVO Statement for the use of Animals in Ophthalmic and Visual Research under a research protocol approved by the Columbia University Medical Center Institutional Animal Care and Use Committee.

The mice were euthanized and enucleated, and the eyes were processed for histology. The two animals are referred to as animal 1 (A1) and animal 2 (A2). Mouse eyes were fixed and embedded in paraffin. Adjacent sections at a thickness of 3 and 12 μm were taken and the sections were transferred to glass microscope slides pre-coated in poly-l-lysine. When the slides were ready for examination, they were deparaffinized and rehydrated in series of Histoclear ethanol (100%, 75%) and saline (each 2 × 5 min). After SAM imaging, 12 and 3-μm sections were counterstained using hematoxylin and eosin (H&E), and retinal histology was analyzed by light microscopy.

The samples were scanned using a custom-designed SAM. A photo of the apparatus and a block diagram of the working principle are depicted in Figs. 1(a) and 1(b), respectively. The microscope slides were mounted on a three-axis, high-precision scanning stage (Newport, Irvine, CA), and 2D raster-scanned in increments of 2 μm in an “upside down” configuration. A drop of degassed and filtered water was used as a coupling fluid. Ultrasonic signals were generated and received using a 300-MHz monocycle pulser (GEOZONDAS, Vilnius-09, Lithuania) and an F-1.16, 250-MHz transducer (Fraunhofer, Ingbert, Germany) with a 160-MHz bandwidth and a 450-μm radius of curvature. The lateral resolution (−6-dB beam width) of the transducer was 7 μm and depth of field was 72 μm. The amplified (MITEQ, Hauppauge, NY) radio-frequency signals were digitized at 2.5 GHz using a 12-bit HD oscilloscope (Teledyne Lecroy, Chestnut Ridge, NY).

Fig. 1.

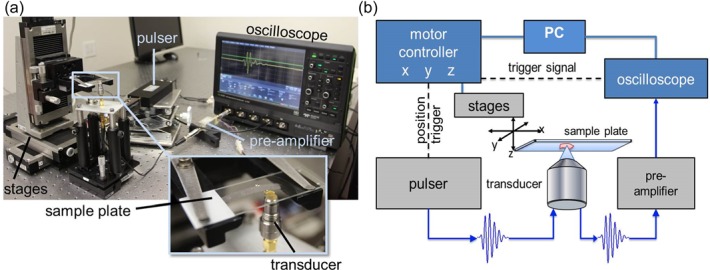
(Color online) (a) Photograph of microscope setup with labeled components. (b) Block diagram of SAM measurement principle. The sample is mounted on the scanning stages while the transducer is fixed.

Two-dimensional maps of acoustic amplitude used for overview and reference purposes were obtained by calculating the maximum of the envelope of each time-domain signal using the Hilbert transform. Maps of quantitative acoustic properties were derived from the frequency-domain representation of each recorded signal using a model-based approach similar to the procedures described by Hozumi et al. (2004). A fast Fourier transform was applied to the recorded radiofrequency data and normalized (i.e., divided) by the Fourier transform of a reference signal. The reflected signals from the sample surface and sample-glass-plate-interface can be modeled in the time domain by a summation of two reference signals with different phase, frequency-dependent attenuation effects, and amplitude. By normalizing this theoretical model using the experimentally measured reference signal, and fitting this normalized model to the normalized measured signals in the frequency domain, sample thickness, c, $\alpha$, and Z can be directly derived. The resulting 2D maps of acoustical parameters were post processed using a median filter with a $3\times 3$ pixel (i.e., 6 μm × 6 μm) square kernel. All signal processing was implemented using matlab (The MathWorks, Inc., Natick, MA). The material properties, mass density ($\rho$ in ${\mathrm{g}/\text{cm}}^3$) and bulk modulus (B in GPa), were calculated from $c$ and Z for each pixel location using $\rho =Z/c$ and $B=c\cdot Z$, respectively (Briggs, 1992).

Histology photomicrographs were digitized and manually registered to the amplitude maps and six regions of interest (ROIs) per animal were selected according to the different retinal layers. The selected ROIs were assigned to the ganglion cell layer (GCL), the inner plexiform layer (IPL), the inner nuclear layer (INL), the outer plexiform layer (OPL), the outer nuclear layer (ONL) and the outer segment (i.e., OS, a combination of inner and outer segments). The ROIs identified on the amplitude maps were used to derive descriptive statistics (i.e., mean and standard deviation) for all maps of acoustical parameters (i.e., $\hspace{0.17em}\alpha$, $\hspace{0.17em}c,\hspace{0.17em}\hspace{0.17em}Z,\hspace{0.17em}\hspace{0.17em}B,\hspace{0.17em}\hspace{0.17em}\rho$). Figure 2(b) depicts the ROI selection for sample A1 together with a cartoon illustrating the cellular structure of the retinal layers.

Fig. 2.

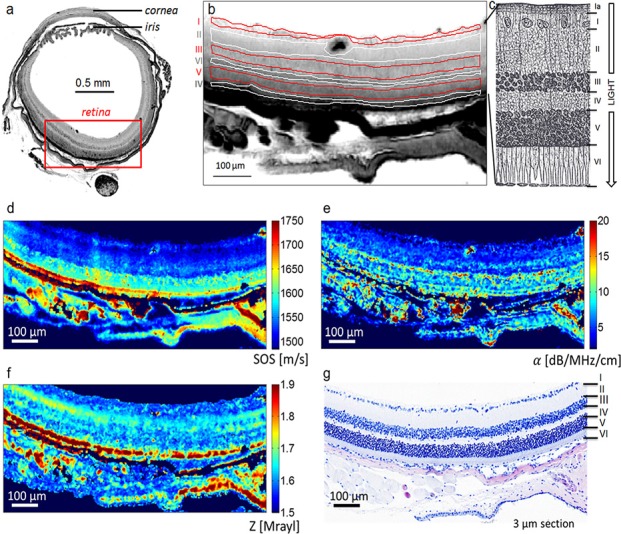
(Color online) (a) Map of ultrasound signal amplitude of a whole mouse cross section. Retina layers are clearly visible. (b) Amplitude image of sample A1 illustrating the definition of the ROI for the retinal layers with I = GCL, II = IPL, III = INL, IV = OPL, V = ONL, and VI = IS + OS. (c) Scheme illustrating the different structures of the retina including Ia = Nerve Fiber Layer Modified from (Gray and Lewis, 2000). (d)–(f) Maps of acoustic properties $\hspace{0.17em}c$, $\hspace{0.17em}\alpha$, and Z of the mouse retina in comparison with site-matched H&E histology slide (g).

Nonparametric Kruskal–Wallis tests followed by post hoc multi-comparison tests with Bonferroni correction were used to evaluate the impact of retinal layers and sample specific effects on the derived acoustical properties. Statistical results were considered significant for p-values less than 0.05. All pixels from each ROI were used as an input for the statistical tests. Relationships between the acoustical properties were assessed using linear-regression analysis with a significance level of 0.05. All data points of the 2D parameter maps were included in the regression analysis. Statistical test were conducted using Statistics Toolbox, matlab.

3. Results

Ultrasound amplitude maps were successfully registered to the H&E-stained photomicrographs [Fig. 2(g)]. In addition, the spatial resolution of the ultrasound amplitude maps was sufficient to resolve the six retinal layers which were first identified on the histology images. The identified layers were OS, ONL, OPL, INL, IPL, and GCL.

The signal processing procedures successfully yielded 2D maps of quantitative acoustic properties. Figures 2(d)–2(f) show an example of three 2D maps of derived parameters (i.e., $c$, $\hspace{0.17em}\alpha$, and Z) with the coregistered H&E-stained histology photomicrograph.

The three 2D parameter maps (i.e. $,\hspace{0.17em}\hspace{0.17em}\alpha ,\hspace{0.17em}c,$ and Z) are in good agreement with the registered 3-μm histology image [Fig. 2(g)]. Although several structures, such as the retinal layers, are visible, the contrast between these structures in the three parameter maps $\hspace{0.17em}(\mathrm{i}.\mathrm{e}.,\hspace{0.17em}\hspace{0.17em}\alpha ,\hspace{0.17em}c,$ and Z) varies. For instance, the OS has much higher values of $c$ [Fig. 2(d)] and $Z$ [Fig. 2(e)] when compared to the other layers whereas $\alpha$ of the OS is in the same range as ONL [Fig. 2(f)]. With larger values when compared to OPL, INL, IPL, and GCL, the ONL layer is easily seen in the $\hspace{0.17em}c$ and $\hspace{0.17em}\alpha$ maps but not in the $\hspace{0.17em}Z\hspace{0.17em}\text{map}$.

Table 1 gives an overview of the standard deviation and average values of both animals for each layer and every acoustic parameter. Boxplots showing the distribution of the parameters for the two animals together with the results of the Kruskal–Wallis tests are shown in Fig. 3. Kruskal–Wallis tests revealed significant inter-specimen and inter-layer variations for all five parameters (i.e., $\alpha ,$ c, Z, $\rho$, and B). The average c of both specimens is successively increasing from the GCL layer with 1507 m/s to the OS layer with 1620 m/s. The average difference in c values between adjacent layers is about 23 m/s. A similar behavior was observed for $\alpha$ values with $\alpha$ = 4.22 dB/MHz/cm for the GCL layer and increasing to $\alpha$ = 15.93 dB/MHz/cm for the OS layer. Variations of Z and B values did not show a clear trend from GCL to OS although the lowest values were found for GCL (Z ∼ 1.6 Mrayl, B ∼ 2.42 GPa) as well. Z was about 0.04 Mrayl higher in IPL, INL, and ONL compared to GCL and OPL. The highest standard deviations were found in the OS for all parameters.

Table 1.

Average parameters over both animals for each retinal layer. Values are presented in mean ± standard deviation.

	Z [Mrayl]	c [m/s]	B [GPa]	$\alpha$ [dB/MHz/cm]	$\rho$ [g/cm3]
GCL	1.60 ± 0.03	1507 ± 20	2.42 ± 0.06	4.22 ± 1.47	1.06 ± 0.02
IPL	1.64 ± 0.03	1520 ± 20	2.49 ± 0.06	4.38 ± 0.97	1.08 ± 0.02
INL	1.65 ± 0.05	1556 ± 22	2.57 ± 0.09	7.64 ± 2.00	1.06 ± 0.03
OPL	1.61 ± 0.03	1562 ± 25	2.51 ± 0.06	8.28 ± 2.96	1.03 ± 0.03
ONL	1.64 ± 0.04	1596 ± 30	2.62 ± 0.08	8.75 ± 2.29	1.03 ± 0.03
OS	1.71 ± 0.10	1620 ± 47	2.77 ± 0.21	15.93 ± 6.25	1.05 ± 0.06

Fig. 3.

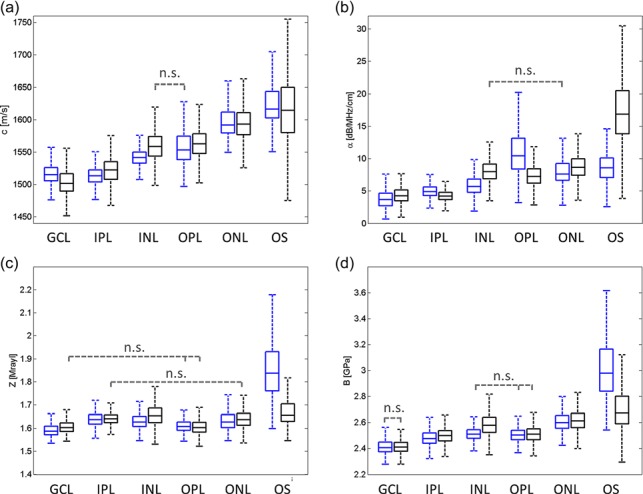
(Color online) Statistical analysis showing Kruskal–Wallis boxplots of (a) c, (b) α, (c) Z, and (d) B. Dashed bars indicate non-significant (n.s.) differences between the groups of OS, ONL, OPL, INL, IPL, and GCL.

The Kruskal–Wallis test also revealed inter-group interactions between the two animals and retinal layers (p < 0.01). For instance, in A1 the OPL ($\alpha$ ∼ 10.4 dB/MHz/cm) showed an about 1.6 times higher attenuation compared to INL ($\alpha$ ∼ 5.6 dB/MHz/cm) and ONL [$\alpha$ ∼ 7.6 dB/MHz/cm; Fig. 3(b), blue boxes] whereas A2 showed slightly lower values for OPL ($\alpha$ ∼ 7.2 dB/MHz/cm) compared to INL ($\alpha$ ∼ 8.0 dB/MHz/cm) and ONL ($\alpha$ ∼ 8.7 dB/MHz/cm). However, although significant differences in the mean values between the two animals were found, it can be seen that in most cases these differences are smaller for the same retinal layer compared to adjacent layers. For instance, the difference between the two animals in the Z value of IPL was about 0.004 and 0.01 Mrayl for GCL but the differences of Z values between IPL and GCL were 0.05 and 0.04 Mrayl for A1 and A2, respectively. Moreover the variation of the parameters was found to be similar for the same layer. Nevertheless, for some layers the difference between the two animals was found to be larger compared to adjacent layers. For example, this is the case at the OS for $\hspace{0.17em}\alpha$, Z, and B, at the INL and OPL for c; at the IPL and INL for Z; or at the INL and OPL for B.

Spearman correlations between the parameters were statistically significant, but were weak to nonexistent with R²= 0.53 between c and $\alpha$, R²= 0.07 between c and Z, and R²= 0.1 between Z and $\alpha$.

4. Discussion

In this study we report for the first time the quantitative assessment of five acoustic properties ($\alpha ,\hspace{0.17em}\hspace{0.17em}c,\hspace{0.17em}$Z, B, and $\rho$) of mouse retinas with a very fine resolution. B is related to the Young's modulus together with the Poisson's ratio or shear modulus. The results of the current study strongly suggest that these maps can be derived at a high resolution from thin ocular tissue sections using a 250-MHz transducer. To the best knowledge of the authors, only one acoustic microscopy study was conducted with two human retinas by Marmor et al. (1977). The authors used a 1-GHz transducer (approximately 1.5-μm spot size) in a through transmission configuration and found good agreement with histology. However, only amplitude and phase rather than appropriate quantitative measures of $\alpha$ and c were reported. Nevertheless, different ultra-structural features such as cell nuclei, rod, and cone outer segments or ocular pigments could be related to a variation of material properties. High loss in signal amplitude for tissues containing large molecules such as collagen, melanin, or hemoglobin was reported. Moreover, Marmor et al. (1977) found an advanced phase shift and a larger loss in intensity of the nuclear layers compared to the plexiform layers. This is in good agreement with our findings where $c_{\text{ONL}}$ was significantly larger than $c_{\text{OPL}}$ and ${\alpha }_{\text{ONL}}$ significantly larger than $\hspace{0.17em}{\alpha }_{\text{OPL}}$. Interestingly, the outer and inner segments containing the photoreceptors showed significantly higher values of α, c, and Z. Similar effects were observed by Marmor et al. (1977) who explained it by a higher concentration of intracellular organelles or a greater thickness of the cones in the inner segments.

In another study performed with a 761-MHz transducer, Beshtawi et al. (2013) compared c at the μm-scale of human cross-linked corneas with controls and found a significant 5% increase in c for the treated specimens. The study did not assess $\alpha$ or Z. Moreover, c was directly compared to the elastic modulus of other studies using the strip extensiometery method, which measures the global Young's modulus. For an accurate comparison, values would have needed to be converted to B first, which requires the measurement of Z or density.

The elastic B is directly dependent on c and Z. However, no correlation between c and Z was found (R²= 0.07), which suggests that both parameters contribute independently to B of the mouse retina. We therefore hypothesize that a more comprehensive assessment of material properties rather than estimations from single parameters such as c, will lead to a more precise and realistic characterization of the elastic properties of ocular tissues at small length scales. These material properties are for example required for in-silico studies involving numerical models such as the finite-element modeling used by Basinger et al. (2009). Moreover, ocular tissue elastic properties may be associated with several disease conditions such as keratoconus (Andreassen et al., 1980) and high myopia and straphyloma (McBrien et al., 2009).

The contrast in Z and $c$ between the retinal layers are in good agreement with the findings of Jolly et al. (2005). In their ex vivo study, they were able to distinguish between the different retinal layers because of the significant inter-layer variations of material properties. No other SAM study focusing on the retina and reporting Z, $\alpha$, B, $\rho$, and $c$ can be found in literature which makes a direct comparison of the values impossible. A few studies measured c and α at much lower frequencies between 10 MHz (Thijssen et al., 1985) and 20 MHz (de Korte et al., 1994). The values for $c$ ranged from 1532 m/s (Thijssen et al., 1985) to 1576 m/s (de Korte et al., 1994) in pig eyes and averaged 1538 m/s (Thijssen et al., 1985) in human eyes. α in the human eye was found to be 1.15 dB/cm/MHz (de Korte et al., 1994). These parameters correspond very well to the overall average c of 1560 m/s. α, however, was much higher in our study with an overall average of 8.2 dB/cm/MHz. This can be explained by the likely nonlinear behavior of α between 10 and 250 MHz. Briggs, Daft, and coworkers (Daft and Briggs, 1989) established an approach similar to the approach described in this study which also allowed the estimation of α at 425 MHz. The authors measured various soft tissue types of mammals and their estimated α values were consistent with our values (i.e., ranging between 4 dB/MHz/cm to 12 dB/MHz/cm).

The statistical tests revealed significant parameter variations among the retinal layers although the differences were relatively small. Our findings support the studies of Jolly et al. (2005) and Marmor et al. (1977) whose results also suggest significant variations in the values of acoustical properties among different layers. The boxplots of Fig. 3 demonstrate that, in most cases, the differences among layers in a given animal are greater than the differences of a given layer between animal. This is further supported by Table 1, where the average acoustical-parameter variation among several layers is larger than the standard variation within the layer (e.g., c_GCL = 1507 ± 20 < c_NL  = 1556 ± 22, Z_GCL = 1.60 ± 0.03 < Z_IPL = 1.64 ± 0.03). Moreover, the 2D maps show apparent contrast for the different layers. Therefore, we hypothesize that differences in material properties among the retinal layers are small but relevant.

The material properties of the thin sections are easily altered by the irreversible effects of dehydration or long exposures in saline; changes include cell shrinkage, cell swelling, and other forms of cell damage. To prevent dehydration, the samples were measured immediately after immersion in the saline bath. We also expect the embedding and de-paraffinization process to cause alterations in properties. Hence, the reported absolute values should be viewed with caution. Further investigations are required to assess the effects more fully.

In conclusion, the results of this pilot study demonstrate a suitable method for ex vivo assessment of the material properties of thin-sectioned ocular tissues. As expected from the theoretical 7-μm lateral resolution of its 250-MHz transducer, our system is able to resolve the different retinal layers. An advantage of the acoustic approach is its ability to image soft tissues without the need for staining, which may, in addition to fixation, alter the properties of the investigated tissue.