Continuous Shear Wave Elastography: a New Method to Measure in-vivo Viscoelastic Properties of Tendons

Abstract

Viscoelastic mechanical properties are frequently altered after tendon injuries and during recovery. Therefore, non-invasive measurements of shear viscoelastic properties may help evaluate tendon recovery and compare the effectiveness of different therapies. The objectives of this study are to present an elastography method to measure localized viscoelastic properties of tendon and to present initial results in healthy and injured human Achilles and semitendinosus tendons. The technique used an external actuator to generate the shear waves in the tendon at different frequencies and plane wave imaging to measure shear wave displacements. For each of the excitation frequencies, maps of direction specific wave speeds were calculated using Local Frequency Estimation. Maps of viscoelastic properties were obtained using a pixel wise curve-fit of wave speed and frequency. The method was validated by comparing measurements of wave speed in agarose gels to those obtained using magnetic resonance elastography. Measurements in human healthy Achilles tendons revealed a pronounced increase in wave speed as function of frequency that highlights the importance of tendon viscoelasticity. Additionally, the viscoelastic properties of the Achilles tendon were larger than those reported for other tissues. Measurements in a tendinopathic Achilles tendon showed that it is feasible to quantify local viscoeasltic properties. Similarly, measurement in the semitendinosus tendon showed a substantial differences in viscoelastic properties between the healthy and contralateral tendons. Consequently, this technique has the potential of evaluating localized changes in tendon viscoelastic properties due to injury and during recovery in a clinical setting.

Introduction

Tendon injuries, such as tendinopathy and ruptures, often result in local increase of tendon cross-sectional area, abnormal collagen-fiber structure, and hydration (Arya and Kulig 2010; Helland et al. 2013; Józsa and Kannus 1997; Lui 2013; Soslowsky et al. 2000). These compositional and structural changes result in local changes of viscoelastic properties (e.g., elasticity and viscosity) (Lin et al. 2004; Soslowsky et al. 2000). Therefore, tendon injuries can be diagnosed and monitored by measuring tendon viscoelastic properties non-invasively. Elastic properties of tendon have been measured in-vivo using ultrasound elastography (Aubry et al. 2013; Chen et al. 2013b). However, the elasticity modulus of tendons often exceeds the range of commercial scanners (Chen et al. 2013b; DeWall et al. 2014). Additionally, commercial systems do not provide measurements of viscosity or other viscoelastic properties. Recently, an experimental method to measure tendon viscoelastic properties was proposed using transient shear wave and dispersion analysis where representative values of the viscoelastic properties in a region of interest were obtained (Brum et al. 2014). Although Brum’s method was used to get an overall value of viscoelastic properties, it is possible to use local windows to measure local shear wave viscosity. However, the spatial resolution of such method would be limited by the local window size. Therefore, there is a need of a technique to measure spatial variations of viscoelastic properties in tendons.

Treatments for tendinopathy and rupture aim to promote remodeling of the tendon structure with the goal of recovering function (Aspenberg 2007; de Vos et al. 2010). However, the original structure and mechanical properties of the tendons are often not recovered (Schepull et al. 2012; Silbernagel et al. 2012). Evaluating and comparing the effect of treatments on the tendon structure is difficult since current metrics are based on pain sensation, activity levels and ultrasound imaging that only evaluates tendon morphology. Research in animal models have shown strong correlation between altered viscoelastic mechanical properties and structural and compositional changes often observed in tendon injuries (Lin et al. 2 004; Soslowsky et al. 2000). Therefore, viscoelastic properties may be used as biomarkers to evaluate the structural integrity, and ultimately function, of tendons, to compare the effectiveness of available treatments, and to optimize a patient-specific physical therapy program for a faster return of function and decreased risk of re-injury.

Ultrasound elastography is a tool that has enabled measurement of mechanical properties of soft tissue, but has limitations for tendons. Elastography methods can be broadly divided in two groups: quasi-static and dynamic elastography (Greenleaf et al. 2003). Quasi-static methods compare pre- and post-compression ultrasound images. Analysis of these images result in relative of tissue stiffness (Hall et al. 2003). However, quasi-static techniques available in commercial systems do not provide absolute values of stiffness and therefore cannot be used to track the tendon remodeling during the healing process. Dynamic methods, such as shear wave elastography (SWE), detect the velocity of a transverse wave propagating through a soft tissue (Bercoff et al. 2004; Nightingale et al. 2003; Parker et al. 1998; Sarvazyan et al. 1998; Taylor et al. 2000). In SWE, a single shear wave, usually generated by the ultrasound probe, travels through the region of interest (ROI). The shear modulus map is generated by calculating the wave speed at each point of the ROI. Although SWE has widely used in many applications, this technique does not measure viscoelastic properties. SWE has been used to measure elastic properties of tendons (Aubry et al. 2013; Chen et al. 2013b; Zhang and Fu 2013). Chen et al. (2003) and DeWall et al. (2014) reported that healthy tendons measured in-vivo may be stiffer than the measurement range of commercial ultrasound systems. Therefore, there is a need for elastography methods for tissues with high stiffness. Additionally, commercial systems do not provide measurement of viscoelastic properties. Overall values of viscoelastic properties have been measured in the Achilles tendon using dispersion analysis (Brum et al. 2014). Therefore, there is a need of an ultrasound-based technique to measure maps of viscoelastic properties for stiff tissues such as tendons.

The objective of this study is to present an elastography method to measure viscoelastic mechanical properties of tendons. The proposed technique, named continuous Shear Wave Elastography (cSWE), calculates viscoelastic properties by applying continuous shear waves using an external actuator and measuring the wave speed at different excitation frequencies. The technique presented in this study introduces a combination of methods to analyze raw radiofrequency (RF) data for measuring displacements, wave speed, and viscoelastic properties. Although each of these methods has been used in previous studies (Ballyns et al. 2012; Chen et al. 2009; Chen et al. 2013a; Clayton et al. 2013; Gennisson et al. 2010; Manduca et al. 2003; Muthupillai et al. 1995; Streitberger et al. 2012; Sumanaweera and Liu 2005), the combination of these methods was chosen to measure maps of viscoelastic properties in tendons. Measurements of viscoelastic properties in healthy and injured Achilles and hamstring tendons are presented to demonstrate the feasibility of the proposed ultrasound method.

Methods

Overview

cSWE is a technique designed to measure local variations, or maps, of viscoeasltic properties. To do this, shear waves at several frequencies are excited in the tissue using an external actuator (Ballyns et al. 2012; Muthupillai et al. 1995; Sack et al. 2008). Displacements in the tissue are measured using ultrasound plane wave imaging (Bercoff et al. 2004; Gennisson et al. 2010). From the measured displacements, maps of shear wave speed are calculated for each of the applied frequencies using a method called Local Frequency Estimation (LFE) (Knutsson et al. 1994; Manduca et al. 1996; Manduca et al. 2003). Pixel-wise viscoelastic properties are obtained by curve-fitting a viscoelastic model to the wave speed as function of frequency (Chen et al. 2009; Urban et al. 2009). This technique was validated by comparing the values of wave speed to those measured using Magnetic Resonance Elastography (Cortes et al. 2014). Measurements in human Achilles and hamstring tendons are presented as possible applications of the technique. Each subject read and signed and informed consent approved by the institutional review board of the University of Delaware.

Equipment

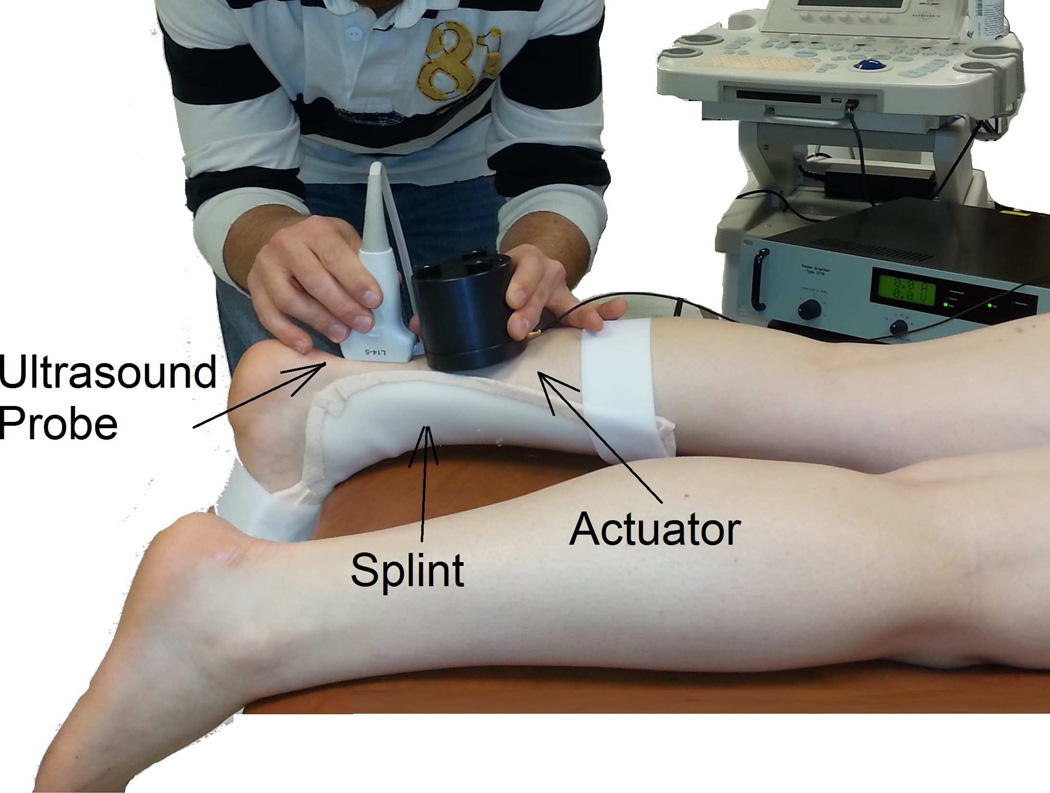
The cSWE experiment consisted of applying a mechanical vibration at the surface of the tissue/sample and simultaneously collecting RF data (Figure 1). An Ultrasonix MDP ultrasound scanner with an L14-5/38 transducer (Ultrasonix, Vancouver, Canada) and a 128 channel data acquisition device (DAQ) were used to collect RF data. Each of the 128 channels of the DAQ recorded a single RF line of the frame. Therefore, each frame consisted of 128 RF lines. Since the size of the field of view in the lateral direction is 38 mm, the lateral spacing is 0.29 mm. Plane wave imaging is necessary to achieve the high frame rate needed to acquire the several frames within one cycle of the mechanical vibration. A frame rate of 6240 frames/second was used in this study. The transmission frequency was set a 10 MHz and the sampling rate was 40 MHz. The shear wave was generated by a mini-shaker type 4810, small vibration exciter (Bruel & Kjaer, Norcross, GA), which has frequency range from DC to 18 kHz. The actuator was hand held next to ultrasound probe (Figure 1).

Figure 1.

Continuous shear wave elastography set-up consists of a hand-held mechanical actuator that generates shear waves that propagate through the tendon. Shear wave velocity is measured using the proposed ultrasound analysis. A splint is used to keep the ankle at a consistent angle between subjects.

Shear Wave Generation

Shear waves were excited in the tendon by an external actuator in contact with the tendon via the skin (Figure 1). The choice of the vibration frequency was based on the frame rate. Choosing a vibration frequency that is an integer fraction of the frame rate gives the best accuracy when the Fourier transformation is applied to the displacements in the time dimension (see Directional Filtering and Speed Calculation section below). When the vibration frequencies are an integer fraction of the frame rate, the number of frames per time period of the mechanical vibration is an integer number. This allows analyzing a number of frames corresponding to a given number of time periods. In these conditions, the main vibration frequency is exactly one of the frequencies in the discrete Fourier spectrum. This give a very precise calculation of the motion at the excitation frequency. If the number of analyzed frames does not correspond to a number of entire time periods, the vibration frequency is going to be located in between discrete points of the frequency spectrum. This means that the peak in the frequency spectrum corresponds to a frequency that is not the vibration frequency. This is particularly important for low frequencies where the number of analyzed time periods is low. For instance, for a frame rate of 6240 frame/sec, an excitation frequency of 624 Hz will produce of an acquisition of 10 frames per wave period. If 60 frames are considered, 6 complete wave cycles be used in the analysis. After Fourier transformation, the main frequency will correspond exactly to the 7^th frequency frame.

Plane wave imaging

Plane wave imaging allows high frame rate acquisition which is necessary for calculating the wave speed (Bercoff et al. 2004; Couture et al. 2012; Montaldo et al. 2009; Sandrin et al. 2002; Tanter et al. 2002; Tanter and Fink 2014). However, a disadvantage of plane wave imaging is the reduced lateral resolution and contrast due to the hyperbolic diffraction effect. This effect occurs when echoes, in the form of spherical waves generated by scatter points, are recorded by elements of the transducer at different times. These different times are proportional to the distance from the scatter point to the element of the transducer. This effect makes points to appear in the field of view as curved lines (Figure 2a). Several methods have been proposed to suppress the diffraction effects (Garcia et al. 2013; Montaldo et al. 2009; Sumanaweera and Liu 2005). However, due to its simplicity a method based on remapping the RF data was used in this study (Sumanaweera and Liu 2005). This method consists on applying 2D Fourier transform to each frame of RF data from the time and distance domain to the time and space frequency domains, respectively (r(t, x) → R(f_t, f_x)). The data are then remapped based on the following relation:

$$\mathrm{\Gamma }(f_{\tau },f_x)=-\pi R(f_t,f_x)\sqrt{\frac{{f_t}^2}{c^2}-{f_x}^2}$$ (1)

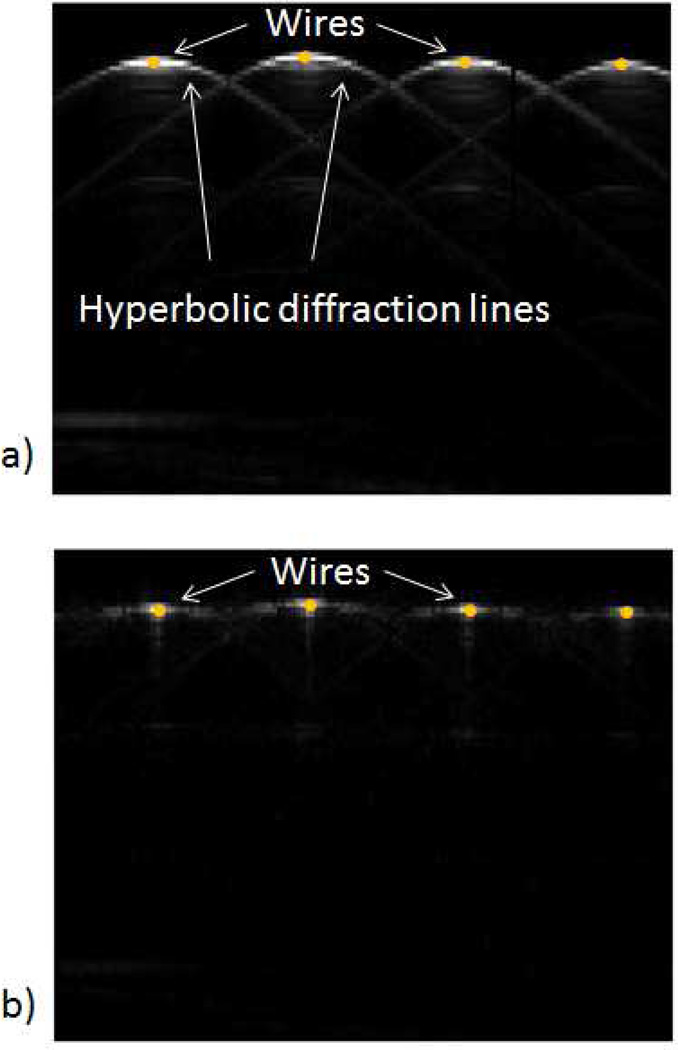
Where $f_t=\frac{c}{2f_{\tau }}({f_x}^2+{f_{\tau }}^2)$ and c is the speed of sound. Notice that the remap is applied in the direction of the RF lines. The remapped RF data (ϱ(z, x)) is obtained by inverse Fourier transformation of Γ(f_τ, f_x). To evaluate the remap of RF data, a plane wave image of 4 steel wires (0.6 mm of diameter) separated 10 mm from each other. The wires were immersed in water. The raw RF data was analyzed without remapping of RF data (Figure 2a). The remapped image shows a significant reduction of the hyperbolic diffraction effect (Figure 2b).

Figure 2.

RF remap decreases the diffraction artifacts commonly observed in plane wave imaging. The effect of RF remap can be observed on the images of 4 wires separated by 10 mm and immersed in water: A) reconstructed image from raw RF data, B) reconstructed image using remapped RF data.

Compounding is a common technique to reduce the hyperbolic effect on plane wave imaging that consists on averaging several frames acquired with different tilt angles. Since several frames are used to obtain a single corrected frame, the effective frame rate is reduced. Although compounding is the typical method used to suppress diffraction artifacts, it would have reduced the effective frame rate from 6240 to 1560 frames/sec in the case of 4-angle spatial compounding. This effective frame rate is low to analyze high frequency excitations. An advantage of the RF remap method chosen for this study is that effective frame rate is not reduced. This is especially important to test tissues at high mechanical frequencies, since the maximum frequency for the mechanical excitation is limited number of RF frames collected during one vibration cycle, i.e., frame rate. For instance, in our case the frame rate achieved from the ultrasound system was 6240 frames/sec. By collecting a minimum of four frames per vibration cycle, a maximum mechanical excitation frequency of 1560 Hz can be applied to the tissue. It is worth noting that there are other diffraction correction methods that may also preserve the effective frame rate (Montaldo et al. 2009, Garcia et al. 2013). Additionally, Tanter and co-workers proposed a compounding method, based on a sliding-window approach, which could also preserve the frame rate (Tanter et al. 2002). A comparison of different diffraction correction methods is out of the scope of this study.

Envelop and Phase Difference Calculation

The displacements in the tissue cause changes in the phase of the raw RF data. The In-phase/Quadrature (IQ) demodulation is commonly used to find the phase of the RF signal at a known transmission frequency. Due to losses in the tissue, high frequencies are more attenuated. Therefore, the frequency of the received signal is lower than that of the transmitted signal (Urban et al. 2009). To calculate the frequency of the received signals, a Hann window and Fourier transform were applied to each RF line and the main frequency was obtained as the maximum of the frequency spectrum (Urban et al. 2009). The Hann window used in this study had a length of 20 samples (0.38 mm) and was shifted in steps of 10 samples (0.19 mm). For each step of the Hann window, a value of the phase difference between two consecutive frames was calculated at the main frequency. The phase difference is proportional to the velocity of a tissue point at a given time (Zheng et al. 2007). This velocity should not be confused to the shear wave speed or the speed of sound. Since the calculation of the phase difference involves two RF lines, this method improves the signal to noise ratio of the phase difference (Zheng et al. 2007). A 3×3 median filter was applied to eliminate noise spike points (Song et al. 2012).

Directional Filtering and Speed Calculation

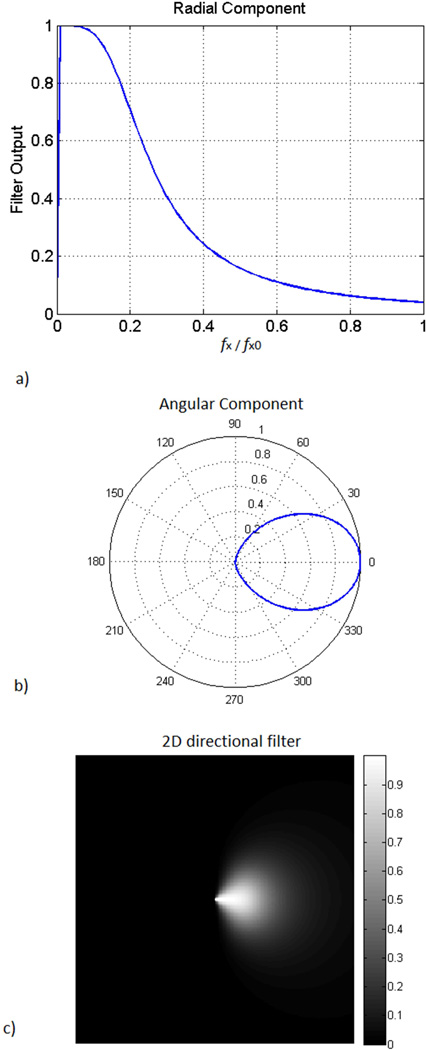
Since the external vibration may reflect from different surfaces close to field of view, the displacement field may be composed of waves travelling in different directions. The superposition of waves causes inaccuracies in the calculation of the shear wave speed. This phenomena has been observed in magnetic resonance elastography and other ultrasound elastography methods (Manduca et al. 2003; Song et al. 2012). Consequently, it is necessary to apply a directional filter to isolate the wave component travelling away from the external actuator in the direction of the tendon. In this study, directional filtering was used to isolate waves propagating in the direction of the tendon (Manduca et al. 2003). To achieve this, the phase difference data was Fourier transformed into the k_x, k_y, and k_t space. The filter was applied to the main temporal plane (actuator frequency) and all the other planes were zeroed. A 2D filter was applied to the main temporal plane. The radial component was a Butterworth low-pass filter (Figure 3a) and the directional component had a cos² dependence (Figure 3b). The product of the radial and directional components resulted in the 2D directional filter (Figure 3c). Finally, inverse Fourier transformed was applied resulting in waves travelling in a single direction along the length of the tendon.

Figure 3.

Directional filter used to isolate shear waves travelling in one direction: A) the radial component is a Butterworth filter with cutoff frequency ω/ω_max = 0.1. B) Angular component is cos². C) 2D directional filter is calculated by multiplying the radial and angular components.

The shear wave speed is obtained using the Local Frequency Estimation method (Knutsson et al. 1994; Manduca et al. 1996). This technique has been successfully used in magnetic resonance elastography (Manduca et al. 1996; Muthupillai et al. 1995). LFE is an image processing technique that combines local estimates of instantaneous frequency over several scales calculated with a bank of spatially oriented lognormal quadrature filters (Knutsson et al. 1994). Since the phase difference data was directionally filtered, in this study, LFE was slightly modified to use a bank of 10 quadrature filters oriented only in the tendon direction.

Calculation of shear modulus and viscoelastic properties

The shear modulus can be easily calculated using an isotropic linear elastic model:

$$\mu =\rho {c_s}^2.$$ (2)

Where μ is the shear modulus, ρ is the tissue density, and c_s is the shear-wave velocity. Due to viscoelastic effects, the shear-wave velocity changes with frequency. Therefore, the shear modulus calculated in Eq. (2) also depends on the frequency. To describe the frequency dependency, a viscoelastic model must be used (Urban et al. 2012). In this study, the Voigt model was used due to its comprehendible analog to biological tissue with the fibers acting as the spring and the interstitial fluid acting as the damper in parallel to one another (Chen et al. 2009; Urban et al. 2012).

$$c_s({\omega }_s)=\sqrt{\frac{2({\mu }_1^2+{\omega }_s^2{\mu }_2^2)}{\rho ({\mu }_1+\sqrt{{\mu }_1^2+{\omega }_s^2{\mu }_2^2})}}$$ (3)

where ω_s is the angular frequency of the mechanical excitation, and μ₁ and μ₂ are the shear elasticity and shear viscosity, respectively. The maps of viscoelastic parameters for the Voigt model can be calculated by fitting the model to the shear-wave velocity as a function of frequency in pixel-wise basis. Notice that equations (2) and (3) are identical when ω_s = 0.

Validation with Agarose Gels

The analysis of the raw RF data and calculation of the shear-wave velocity was validated by comparing the shear-wave velocity to that obtained using magnetic resonance elastography (Cortes et al. 2014). Agarose gels of difference concentrations (1% 1.5% and 2% w/w) were mixed with MgCO₃ (0.5% w/w) which was used as scatter generator. The stiffness of the gels increases with concentration. The number of excitation frequencies that can be used in the MRE method used for this comparison is limited (Cortes et al. 2014). The frequency that produced wavelengths suitable for the analysis with both technics was 625 Hz. An image depth of 20 mm was used. A region of 10 × 10 mm from the wave speed map was considered for the comparisons. A Pearson correlation analysis was applied between shear modulus obtained from the two techniques.

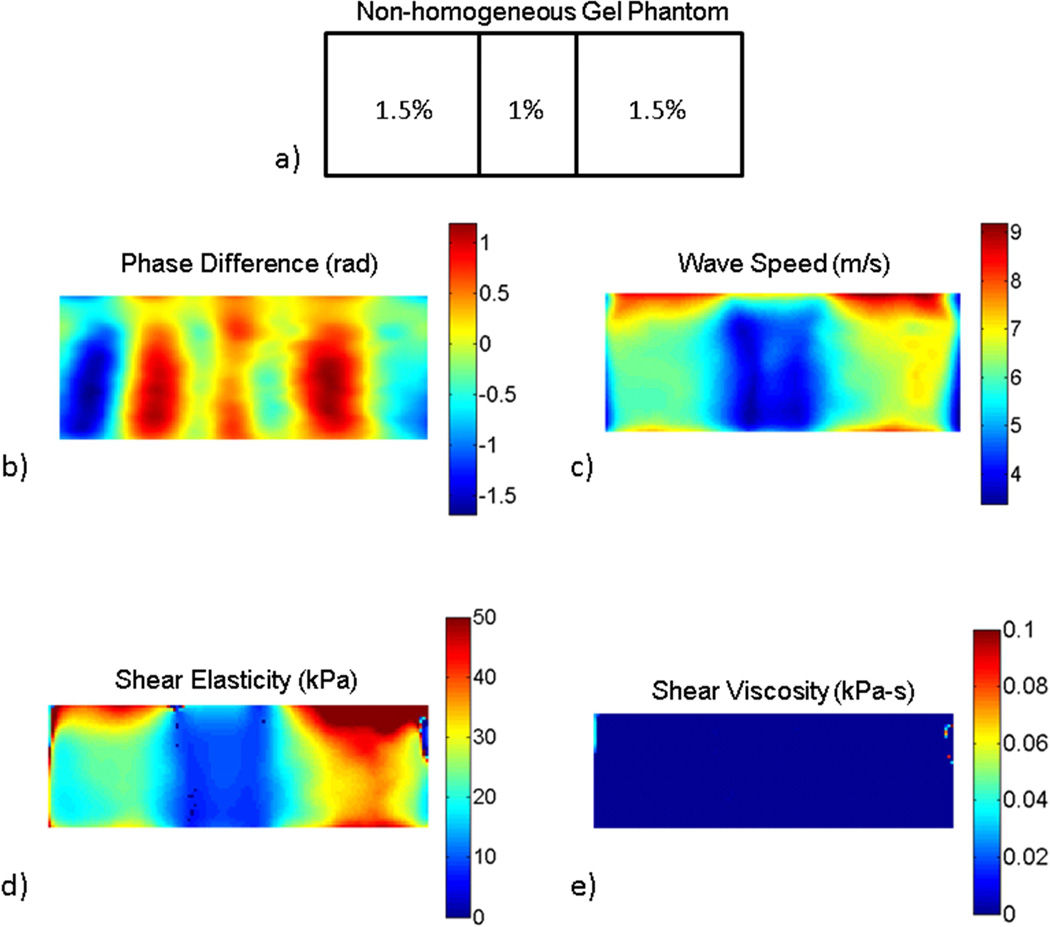
A non-homogeneous gel phantom was used to demonstrate the ability of the technique to detect local changes in viscoelastic properties. The phantom was made by inserting a slab of 12.7 mm of 1% agarose in an otherwise homogeneous block of 1.5% agarose. The lower concentration of the inclusion was intended to mimic the lower stiffness and approximate size of tendinopathy injuries. For this phantom, the frame rate used was 6440 frames/sec and the mechanical excitation was applied at 280, 293, 307, 322, 340, and 358 Hz. The reason for this choice was to obtain a full wave length in all the regions of the gel phantom.

Viscoelastic properties of human tendons

Viscoelastic properties of human Achilles and were measured in healthy volunteers (n = 7). Subjects read and signed an informed consent approved by the University of Delaware institutional review board. The age range of the subjects was 18 – 48 years old (mean 28.8, standard dev = 9.6 years old). Subjects were lying prone with the hip and knee in full extension and the ankle hanging outside the treatment table. The ankle was immobilized using a splint to keep the foot at a consistent angle between subjects (Figure 1). Imaging was applied in a longitudinal view along the length of the tendon. Shear waves were excited at 208, 312, 416, and 624 Hz. Shear modulus and viscoelastic maps were calculated using Voigt model (Eqs 2 and 3).

In addition to healthy Achilles tendons, measurements were applied to two patients with injured tendons. The first patient was 61 year old male with chronic tendinopathy in the right Achilles tendon. Both tendons (injured and contralateral) were imaged using cSWE. The region imaged corresponded to the location of the injury as indicated by a physical therapist. The contralateral Achilles tendon was imaged in a region distal to the soleus junction. The second patient was a 19 year old female whose right hamstring tendon was recovering after being used as a graft of an ACL reconstruction were imaged. The mid-portion was imaged in both tendons. The excitation frequencies used for these measurements were 323, 340, 358, 379, 403 and 430 Hz. The excitation frequencies were chosen based on a frame rate of 6450 frames/sec.

Results

Validation with Agarose Gels

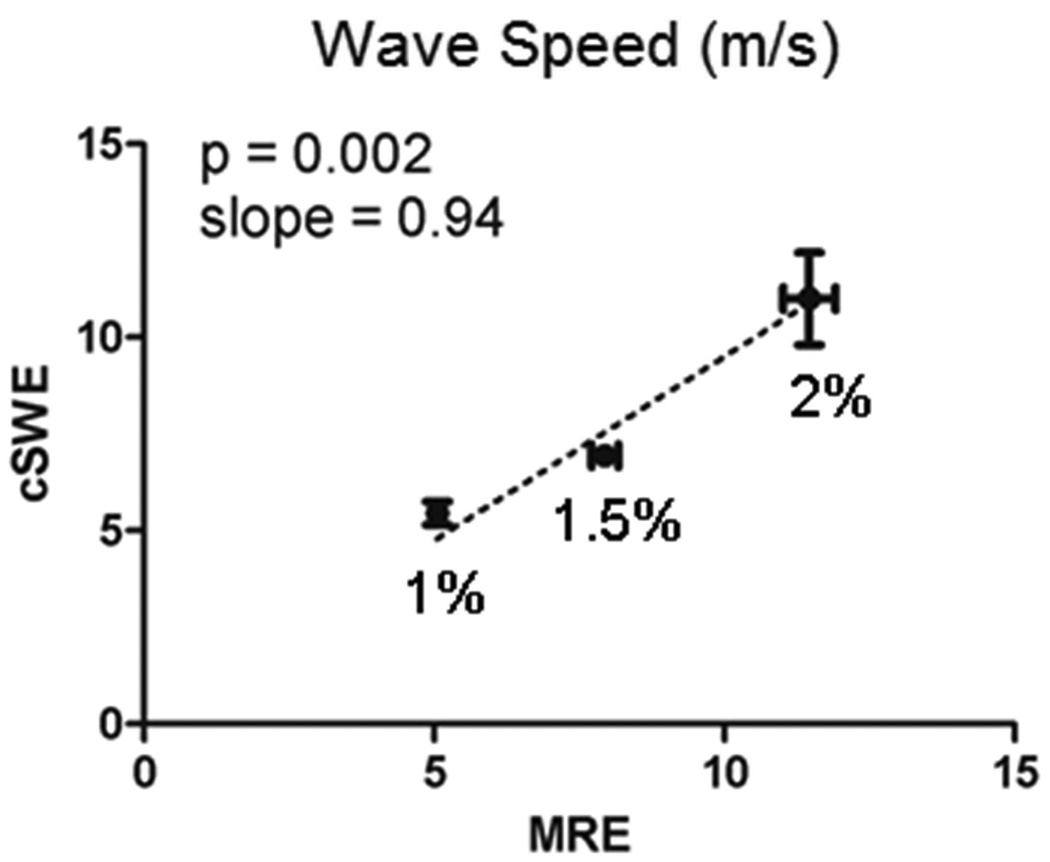
An excellent agreement between cSWE and MRE was obtained for each of the gels (Figure 4). The error bars correspond to standard deviation of the wave speed within the region of interest used in the comparison. This agreement was expected since cSWE and MRE rely on the generation and measurement of shear wave displacements and the same frequency for the mechanical excitation was used. This comparison validates the accuracy of our proposed method for calculating the shear wave speed from the RF raw data. This comparison is sufficient to validate the technique since the calculation of viscoelastic properties is simply a curve-fit of a model to the measured wave speed.

Figure 4.

Shear wave speed measured using continuous Shear-Wave Elastography (cSWE) was similar to that measured using Magnetic Resonance Elastography (MRE) for agarose gels of different concentrations.

The inclusion gel was also clearly identified using this technique. A map of the phase difference, at a frequency of 340 Hz, for the inhomogeneous phantom shows a ‘snap-shot’ of the wave field in a gel (Figure 5b). As expected, the soft inclusion has a lower wave speed compared to that of the surrounding stiffer gel (Figures 5c). The values of wave speed obtained for each the gels were similar to those obtained for the homogeneous gels (Figure 4). The maps of viscoelastic properties (μ₁ and μ₂) are shown in Figures 5d and 5e. The low values of the shear viscosity (μ₂) indicate that viscoelastic effect is negligible for these gels at the frequency range used in the study. Consequently, the map of shear elasticity (μ₁) closely resembles the map of wave speed shown in Figure 5c.

Figure 5.

cSWE applied to a non-homogeneous gel phantom: a) the phantom was composed of a ‘soft’ 1% agarose inclusion of 12 mm embedded in a ‘stiff’ 1.5% agarose gel, b) phase difference which is proportion to the displacements in the phantom, c) wave speed map calculated from the phase difference map, d) and e) maps of the viscoelastic parameters μ₁ and μ₂, respectively.

Viscoelastic properties of human tendon

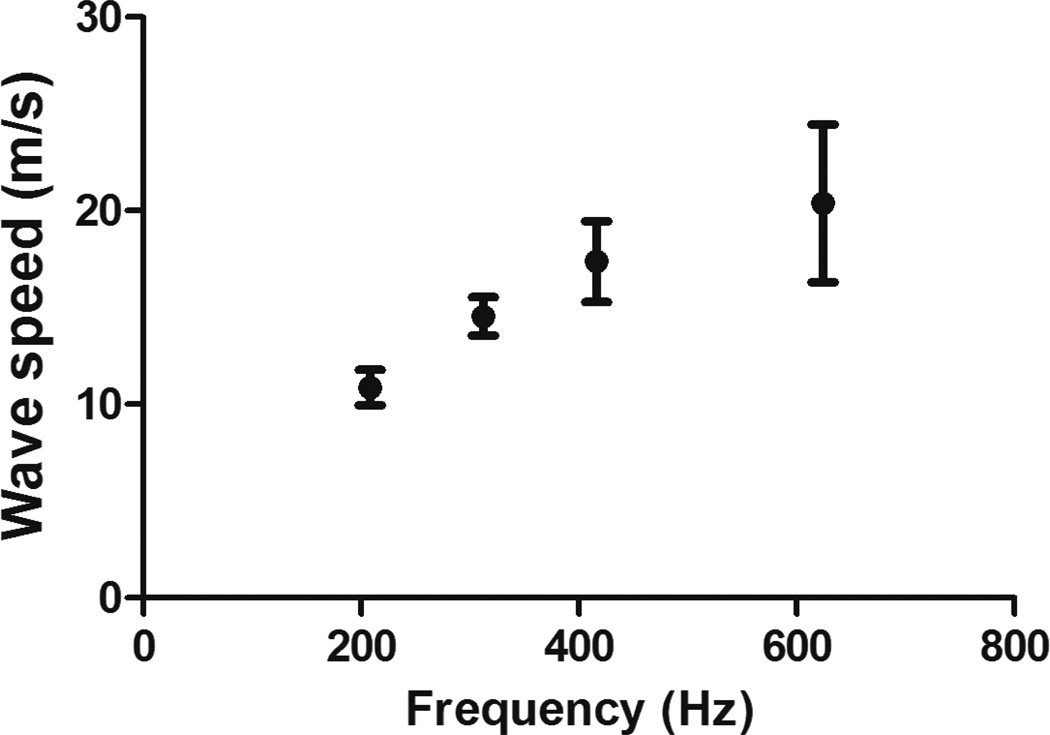
A strong viscoelastic effect was observed in the tendons as the wave speed substantially increased with frequency (Figure 6). The increase in wave speed reported in this study suggests that the shear stiffness of the tendon increases 4-fold when the frequency increases 3-fold. An average value of viscoelastic properties was calculated for each of the tendons. Averages of the average value of the viscoelastic properties of the Achilles tendons are μ₁ = 71.7±49.2 kPa and μ₂ = 64.6±13.3 Pa·s.

Figure 6.

Achilles tendon exhibits a strong viscoelastic behavior as shown in the change of wave speed as function of frequency.

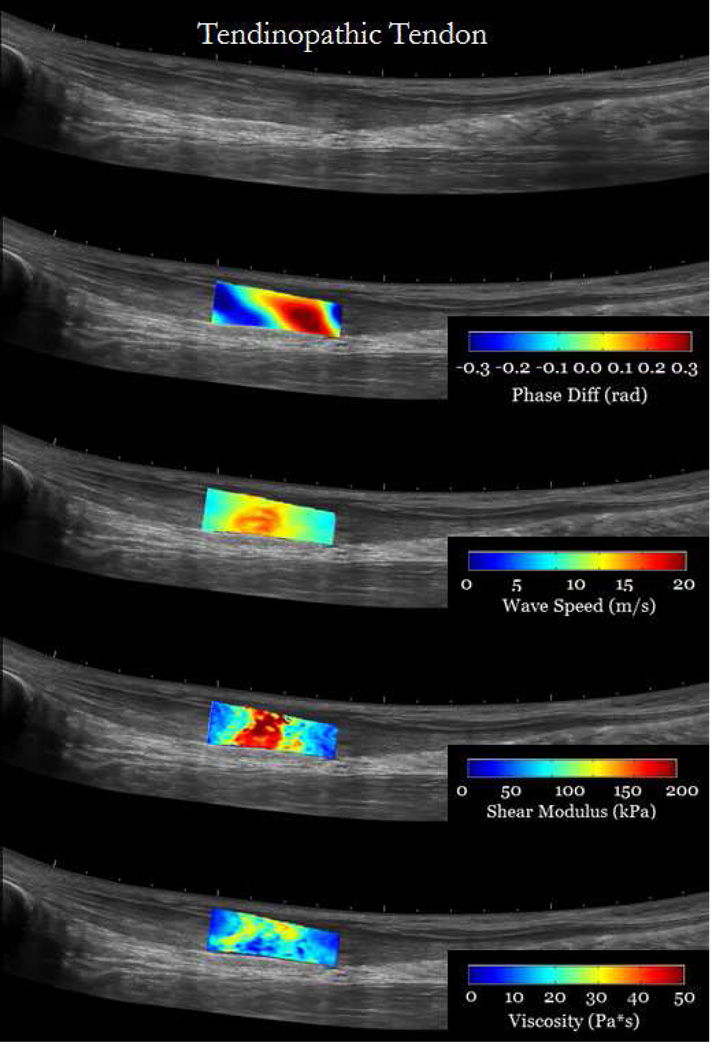
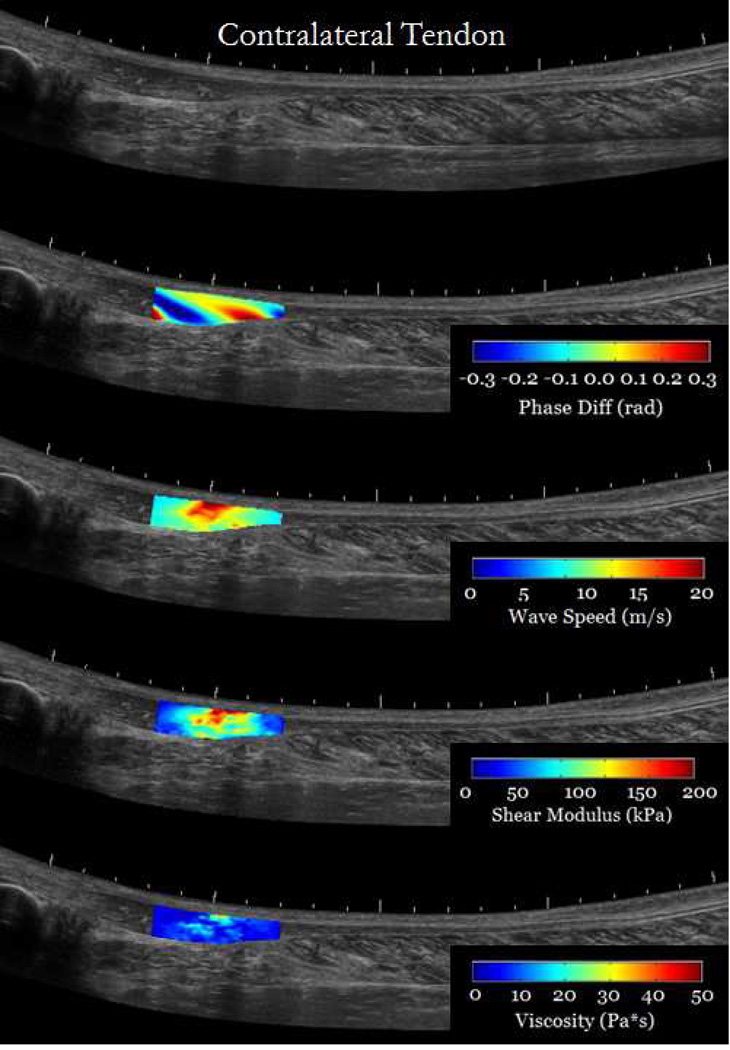
Results from in-vivo injured tendons showed that it is feasible to use cSWE to measure viscoelastic properties in regions affected by the injury. Figure 7 shows an overlay of the cSWE measurements (phase difference, wave speed, shear elasticity and viscosity) on a panoramic B-mode image of the tendons. It can be observed, in the case of chronic tendinopathy, that the size of the injury is larger than the field of view. The phase difference map, which corresponds to the lowest applied frequency of 323 Hz, shows that at least one full wavelength was captured. The corresponding speed map and the maps for shear elasticity and viscosity show substantial variation the in the imaged region. In average the shear modulus and viscosity were 105.5 kPa and 35.5 Pa*s, respectively. The lower viscoelastic properties at the edges of the field of view are partially caused by of inaccuracies of the LFE method that occur at the boundaries of the speed map. For the patient with re-growing hamstring tendon, the maps of wave speed and viscoelastic properties are more homogeneous (Figure 8). This was expected for the contralateral tendon since it is a healthy tendon. The re-growing tendon had much lower wave speeds, lower viscoelastic properties and the distribution seemed homogeneous. The average shear modulus of the re-growing hamstring and contralateral tendons were 32.4 kPa and 59.1 kPa, respectively. The average viscosity of the re-growing hamstring and contralateral tendons were 8.9 Pa*s and 18.4 Pa*s, respectively. These results are meant to show possible applications of the technique, but conclusions should not be drawn from one single case. Several studies will be performed to measure changes in viscoelastic properties in injured tendons.

Figure 7.

cSWE was applied to both tendons of a tendinopathy patient (Male, 61 years old) with chronic tendinopathy in the right Achilles tendon (a). The region imaged corresponded to the location identified by a clinician as the location of the injury. The contralateral tendon was images for comparison (b). Maps of phase difference, wave speed, and viscoelastic properties were overlaid on panoramic image of the tendons for better visualization.

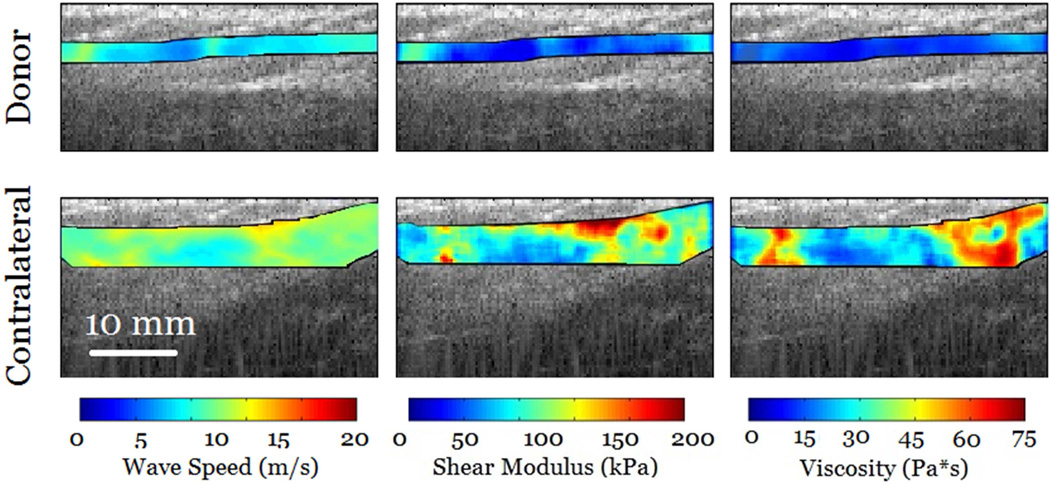
Figure 8.

cSWE was applied to a re-growing hamstring tendon that was used as a graft to reconstruct a ACL-rupture patient (female, 19 years old). The contralateral tendon is also shown for comparison. The values of wave speed, shear elasticity and viscosity were higher in the contralateral tendon.

Discussion

This study presents a novel ultrasound method, continuous Shear Wave Elastography, designed to measure local viscoelastic properties of tendons. This technique was validated by comparing the wave speed to that measured with magnetic resonance elastography in agarose gels of different concentrations. Results from in-vivo measurement in healthy and injured tendons were shown. One advantage of cSWE compared to other elastographic techniques used for tendons is that parameters such as excitation frequency can be tuned to evaluate tissues with high stiffness such as the Achilles tendon. Previous studies have shown that healthy Achilles tendon often exceeds the upper limit of commercial systems. cSWE overcomes this limitation by adjusting the frequency of the external excitation to higher values. Another advantage of cSWE is that maps of viscoelastic properties can be measured to show local variation of viscoelastic properties due to injury. Therefore, it is feasible to evaluate healthy tendons as well as localized lesions such as tendinopathy, tears or ruptures using cSWE.

The method proposed to analyze the raw RF data presented in this study uses a unique combination of procedures to ensure accuracy in calculation of shear wave speed. One of these procedures is the use of windowed Fourier transformation for the calculation of phase differences. As shown by (Urban et al. 2009), the main frequency of the received RF signal is not the same as that of the transmitted pulse. Therefore, IQ demodulation may result in small error in the calculation of the phase. However, in this study we calculate the phase difference between two consecutive frames. Therefore, the phase difference may not be directly affected by altered attenuation since it is calculated at the same pixel. This suggests that using IQ demodulation is also a possibility for the proposed technique. However, the strongest signal is received at a frequency different than that used in the IQ demodulation which may slightly decrease the SNR of the phase difference data. To the best of our knowledge, this is the first time the windowed Fourier transformation has been used for the analysis of plane wave elastography data.

The external mechanical excitation used in cSWE is paramount for calculating viscoelastic maps. In cSWE, the motion is continuously applied at known frequency using an external actuator. Therefore, the speed map corresponds to a single, known frequency which allows the pixel-wise curve-fitting of a viscoelastic model. This process is a crucial step for the measurement of maps of viscoelastic properties. In previous studies, shear wave has been generated using acoustic radiation force induction which produces two shear wave-fronts propagating in opposite directions away from the focal axis. The shear wave-fronts are composed of a broad range of frequencies. Therefore, the speed maps calculated using that method are not associated to a particular frequency. Fourier analysis has been used to calculate viscoelastic properties by taking advantage of the dispersion effect (Brum et al. 2014). In that technique, a map of displacement as function of time and distance along the tendon was analyzed using 2D-Fourier transform. The wave speed as function of frequency (dispersion) was calculated by multiplying the wave length by time frequency. Viscoelastic properties were calculated by curve fitting the dispersion using the guided-wave model (Brum et al. 2014). Although there are several methods to find maps of viscoelastic properties of soft tissues (Muller et al. 2009; Tanter et al. 2008), this is the first time maps of viscoelastic properties are obtained in healthy and injured tendons.

The constitutive mechanical models presented in Eqs (2) and (3) have several advantages and disadvantages compared to other models used to calculated mechanical properties in tendons. One advantage of using Eq. (2) and (3) is that values of the elastic and viscoelastic parameters can be calculated in a pixel-wise basis. This is particularly important to analyze localized injuries such as tendinopathy, lesions and ruptures. However, a disadvantage is the assumption of tissue isotropy and wave propagation in an infinite medium without boundaries. A sophisticated constitutive model for the analysis of wave propagation considering anisotropy and finite dimension have been proposed for tendons (Brum et al. 2014). However, this model has a high number of elastic and viscoelastic properties (7 properties) that are required to define the model. Many of those parameters have to be assumed, so that the only parameters obtained by analysis of experimental data are the shear elastic modulus and viscosity. Another disadvantage of the method proposed by Brum et al., (2014) is the assumption of constant cross-section or thickness. This is a major limitation to analyze injuries such as tendinopathy and ruptures since they often cause a localized increase in the tendon area and thickness.

The shear wave velocity measured in human Achilles tendon using cSWE compares well with other techniques (Aubry et al. 2013; Brum et al. 2014; Chen et al. 2013b). This study reports shear wave velocity values between 10 and 20 m/s for frequencies between 200 and 600 Hz. These values are similar to those measured by Aubry et al. (15.5±0.9 m/s) and Chen et al. (~16 m/s) using Acoustic Radiation Force Impulse (ARFI). Brum et al. used dispersion analysis and found shear wave velocity values of 12 – 16 m/s for frequencies between 300 and 800 Hz. However, it is worth noticing that maximum wave speed measurable with Aixplorer ultrasound scanner used in previous tendon studies is 16.3 m/s. Therefore, this limit may affect the range of values reported in previous studies. It is difficult to exactly determine the wave speed limit in cSWE. The wave speed, in general, is limited by the wavelength of the shear wave. If wavelength is larger than the field of view, LFE will under-predict the wave speed. However, the wavelength can be shortened by increasing the vibration frequency. Due to viscoelastic effects, increasing the vibration frequency also increases the wave speed (and wavelength) and increasing vibration frequency also increases the attenuation of shear waves. Consequently, the wave speed limit when using cSWE is sample specific.

Shear viscoelastic properties of the Achilles tendon have not been previously measured using the Voigt model. However, viscoelastic properties of other tissues have been calculated using 1D ultrasound techniques (Urban et al. 2012). For the liver, the viscoelastic parameters were μ₁ = 2.6 kPa and μ₂ = 1.52 Pa·s. Similarly, the reported viscoelastic parameters for muscle were μ₁ =29 kPa and μ₂ = 9.9 Pa·s. The Achilles tendon shows higher values of μ₁ and μ₂ compared to other tissues, which agrees with the idea of tendon having a greater stiffness than other soft tissues, thus revealing the importance of using a technique that can measure fast wave speeds and large values of viscoelastic properties.

This study showed the feasibility of applying this technique to the evaluatation of viscoelastic changes within an injured tendons. cSWE was applied to a patient with chronic Achilles tendinopathy and a patient with a re-growing hamstring tendon, resulting from a resection as part of an ACL autograft. In both cases, the size of the affected region was larger than the lateral field of view (38 mm). This indicates that multiple data collection with different ultrasound probe locations may be required to fully characterize injuries in the Achilles tendon. Additionally, it suggests that other methods based on transient shear waves, such as that proposed by Brum et al., (2014), can also characterize the overall change in viscoelastic properties due to tendinopathy. However, cSWE provides more localized quantification of viscoelastic properties which may be useful for other pathologies such as ruptures or tears.

The proposed technique has some limitations. The spatial resolution of cSWE is limited by capability of the LFE technique to detect spatial variations in wave speed. This implies that the size of local variation in properties that can be detected depend on the applied frequencies and wavelengths. It has been suggested that the minimum inclusion size that can be accurately detected by LFE is half of a wavelength. Therefore, it is convenient to decrease the wavelength by increasing the frequency to levels allowed by attenuation of the wave in the tissue. Other techniques, such as autocorrelation of the time variation of the phase difference between two pixels, may help to obtain a better estimation of wave speeds in small regions of the field of view. Another limitation is the wave speed of the shear wave may be affected by the anisotropy and the shape and size of the cross-section of the tendon. Future studies will evaluate this dependency by analyzing the wave propagation using guided wave analysis. Finally, the maximum frame rate of the ultrasonix MDP system was 6450 frames/sec for 20 mm depth which could only be increased with a reduction in viewing depth. It still remains that 6450 frames/sec is much lower than the theoretical limit. However, this frame rate is enough to measure wave speeds at the frequencies used in this study.

In conclusion, this study presents an ultrasound technique to measure viscoelastic properties of tendons. The use of an external actuator and a novel combination of methods to analyze the raw RF data enable the pixel-wise measurement of viscoelastic properties of the tissue. An important characteristic of the technique is that parameters such as excitation frequency can be adjusted to measure properties in stiff tissues such as tendons. As a first application of the developed technique, viscoelastic properties of the Achilles tendon were measured in healthy individuals. The feasibility of applying cSWE to injured tendons was shown by measuring properties in tendons with different pathologies. This technique has the potential of evaluating localized changes in tendon viscoelastic properties due to injury, provide insights on the relations between mechanical properties of tendon and clinical, functional and patient-reported outcomes, and evaluate the effect of treatments on the mechanics and function of tendons.