Abstract
Purpose
In the last decade several different radiotherapy treatment plan evaluation and optimization schemes have been proposed as viable approaches, aiming in dose escalation or in an increase of healthy tissue sparing. In particular it has been argued that dose-mass plan evaluation and treatment plan optimization might be viable alternatives to the standard of care, which is realized through dose-volume evaluation and optimization. The purpose of this investigation is to apply dose-mass optimization to a cohort of lung cancer patients and compare the achievable healthy tissue sparing to the one achievable through dose-volume optimization.
Materials and Methods
Fourteen non-small cell lung cancer (NSCLC) patient plans were studied retrospectively. The range of tumor motion was below 0.5 cm and motion management in the treatment planning process was not considered. For each case dose-volume (DV) based and dose-mass (DM) based optimization was carried out. Nine-field step-and-shoot IMRT was used, where all of the optimization parameters were kept the same between DV and DM optimizations. Commonly used dosimetric indices (DIs) such as dose to 1% the spinal cord volume, dose to 50% of the esophageal volume, doses to 20% and 30% of healthy lung volumes, were used for cross-comparison. Similarly, mass-based indices (MIs), such as doses to 20% and 30% of healthy lung masses, 1% of spinal cord mass, 33% of heart mass, were also tallied. Statistical equivalence tests were performed to quantify the findings on the entire patient cohort.
Results
Both DV and DM plans for each case were normalized such that 95% of the planning target volume received the prescribed dose. DM optimization resulted in more organs at risk (OAR) sparing than DV optimization. The average sparing of cord, heart, and esophagus is 23%, 4%, and 6%, respectively. For the majority of the DIs, DM optimization resulted in lower lung doses. On average the doses to 20% and 30% of healthy lung were lower by about 3% and 4%, while lungs volumes receiving 2000 cGy and 3000 cGy are lower by 3% and 2%, respectively. The behavior of MIs was very similar. The statistical analyses of the results again indicated better healthy anatomical structures sparing with DM optimization.
Conclusions
The presented findings indicate that dose-mass based optimization results in statistically significant OAR sparing as compared to dose-volume based optimization for NSCLC. However, the sparing is case dependent and it is not observed for all tallied dosimetric endpoints.
Keywords: dose, mass, volume, IMRT, lung, optimization
1. Introduction
Lung cancer is the most common cause of cancer-related deaths worldwide. Two major types are small or non-small cell lung cancer. Non-small cell lung cancer (NSCLC) comprises about 84% of the diagnosed cases.(American Cancer Society, 2014) Definitive radiotherapy is suitable for approximately 40% of NSCLC cases.(Perez et al., 2004) It has been demonstrated that 70 Gy is a significant threshold in terms of survival benefits,(Kong et al., 2005) while doses of ~85 Gy are required to achieve 30 months of local progression-free survival.(Martel et al., 1999) Phase I RTOG 0117 trial demonstrated that 74 Gy is the maximum tolerated dose in combined chemo-radiotherapy for that disease, indicating the detrimental effects of chemo-radiotherapy combination which prohibit dose escalation.(Auperin et al., 2006; Bradley et al.; Gopal et al., 2003a; Meadors et al., 2006) Healthy tissue tolerance is very often the dose limiting factor for a definitive lung cancer treatment. Symptomatic radiation-induced lung injury occurs in ~30% of the patients, while radiologic evidence occurs in ~50% of the NSCLC cases.(Mathew et al.; Movsas et al., 1997; Kocak et al., 2005; McDonald et al., 1995; Rodrigues et al., 2004; Evans et al., 2007; Graham et al., 1999; Marks et al., 2000; Fan et al., 2001; Fu et al., 2001; Anscher et al., 2003; Marks et al.; Ma et al., 2009)
Human respiration includes changes in both lung volumes and lung masses.(Wei et al., 2005; Brecher and Hubay, 1955; Vermeire and Butler, 1968) While the changes in lung volumes are intuitive, the changes in lung masses are not obvious, and they have not been adequately explored and accounted for.(Nioutsikou et al., 2005; Butler et al., 2004) To date, mass information has been utilized only in evaluation of treatment plans and radiobiological modeling for NSCLC.(Butler et al., 2004; Forster et al., 2001; Mavroidis et al., 2006; Nioutsikou et al., 2005; Tucker et al., 2006; Wei et al., 2005) Dose-mass histograms (DMHs) were introduced for evaluation and review of thoracic treatment plans.(Butler et al., 2004; Forster et al., 2001) Shortly after, the analytic rationale (not complete in our opinion) for their application was outlined.(Mavroidis et al., 2006; Nioutsikou et al., 2005) More recently a conceptual study, shedding more light on the mathematical formalism of dose-mass inverse optimization, was published.(Mihaylov and Moros, 2014)
The purpose of the present work is to retrospectively evaluate treatment plans generated through conventional dose-volume inverse optimization and newly developed dose-mass inverse optimization paradigm.
2. Materials and Methods
According to published data,(Keall et al., 2006a; Stevens et al., 2001; Mihaylov et al., 2010) in nearly half of the lung cases the lesions move less than 0.5 cm in superior-inferior direction. The investigation herein is targeted toward those minimally moving lung lesions, since the effect of motion would not play a role in the treatment planning and the treatment motion management.(Keall et al., 2006b; Keall et al., 2001)
2.1. Patients
Fourteen lung cancer patients, who had time-resolved (4D) computed tomography (CT) simulations, were retrospectively evaluated. The 4D CT scans were performed on a Philips Big Bore Brilliance multi-slice CT scanner (Philips Medical Systems, Cleveland, OH) interfaced with a Varian (Varian Medical Systems, Palo Alto, CA) real-time position management (v. 1.62) respiratory gating system(Kubo et al., 2000). The patients were scanned under normal respiration without coaching. The tumor motion range was estimated from the reconstructed 4D CT data. In all patients selected for this study the tumor motion was within 0.5 cm, where the 0.5 cm threshold was determined from a sagittal projection on the 4D CT. In other words if motion in superior-inferior and anterior-posterior was less than 0.5 cm, the patients were selected for the study. The disease stages are T2 (3 patients), T3 (8 patients), and T4 (3 patients) with different nodal involvement from N0 to N3.
2.2. Phase Selection and Contouring
A mid-ventilation phase, representing an average phase over the entire breathing cycle, was selected for external beam inverse treatment planning.(Wolthaus et al., 2008) The GTV was contoured in the mid-ventilation phase of the breathing cycle by using anatomical correlation between CT simulation data set and available diagnostic imaging studies (i.e. CT, MRI or PET-CT). A Planning target volume (PTV) was generated by a uniform expansion of 1 cm around the GTV. The lungs were contoured on mid-ventilation phase CT data sets with the automatic lung contouring tools in Pinnacle3 (Philips Medical Systems, Fitchburg, WI) treatment planning system (TPS). The lung contours were visually verified on each slice.
2.3. Treatment Planning
For each patient an IMRT deliverable(Dogan et al., 2006; Mihaylov and Siebers, 2008; Siebers and Mohan, 2003; Siebers et al., 2002) optimization was performed. Two plans were generated – one with newly proposed dose-mass (DM) optimization,(Mihaylov and Moros, 2014) and another one based on the standard of care realized through dose-volume (DV) optimization.(Fredriksson, 2012; Shipley et al., 1979; Wu and Mohan, 2000) The treatment plans consisted of 9 co-planar 6MV beams. DM and DV plans for each patient were normalized such that 95% of the PTV received the prescription dose. Once prescription was achieved, the doses to organs at risk (OARs) such as spinal cord, heart, esophagus, and lungs were iteratively lowered until standard deviation of the dose across the PTV in each plan became ~ 4%.(Aaltonen et al., 1997) For the targets with either optimization scheme pure dose objectives were used. The objectives included minimum, maximum, and uniform desired doses to the target. For the OARs the IMRT objectives were dose-volume and dose-mass based, depending on the optimization scheme.
2.4. Analysis
The dose distributions computed with the DM optimization were used as a reference to which the dose distributions computed with the DV optimization were compared. The metric used to perform the comparison was based on dose-volume indices (DVI), isovolumes (volumes encompassed by certain isodose line), dose-mass indices (DMI) derived from dose-mass histograms,(Butler et al., 2004; Nioutsikou et al., 2005) and isomasses (mass of healthy tissue receiving greater than pre-specified dose). The evaluated DVIs were DVIPTV 95% (dose to 95% of the PTV), DVICord 1%, DVIHeart 33%, DVIEsophagus 50%, DVILung 20%, and DVILung 30%. The compared DMIs were for 1% of the mass of the cord, 33% of the heart, 50% of the esophagus, and 20% and 30% of the lungs. DMIs are represented by the dose covering certain mass of an OAR while DVIs are doses covering a certain volume of an OAR.
A statistical equivalence test was used to determine the minimum dose, volume, or mass interval around the reference DIs, MIs, isovolumes, and isomasses, such that the reference and the compared index values were equivalent.(Mihaylov and Siebers, 2008; Mihaylov et al., 2010) The test was performed for each index using two one-tailed paired t-tests(Rosner, 1986). The dose/fractional volume/mass interval was initially set to zero and the t- and p-values computed. Subsequently, the dose/fractional volume interval was progressively increased in 1 cGy/1 g steps until equivalence between the indices with p < 0.05 was reached.
3. Results
Both DV and DM plans were normalized such that 95% of the PTV received the prescription dose. Therefore, with either optimization scheme the therapeutic effects of the plans are supposed to be the same and dosimetric indices for the targets would not be evaluated further
3.1. OAR DIs, MIs, Isovolumes and Isomasses
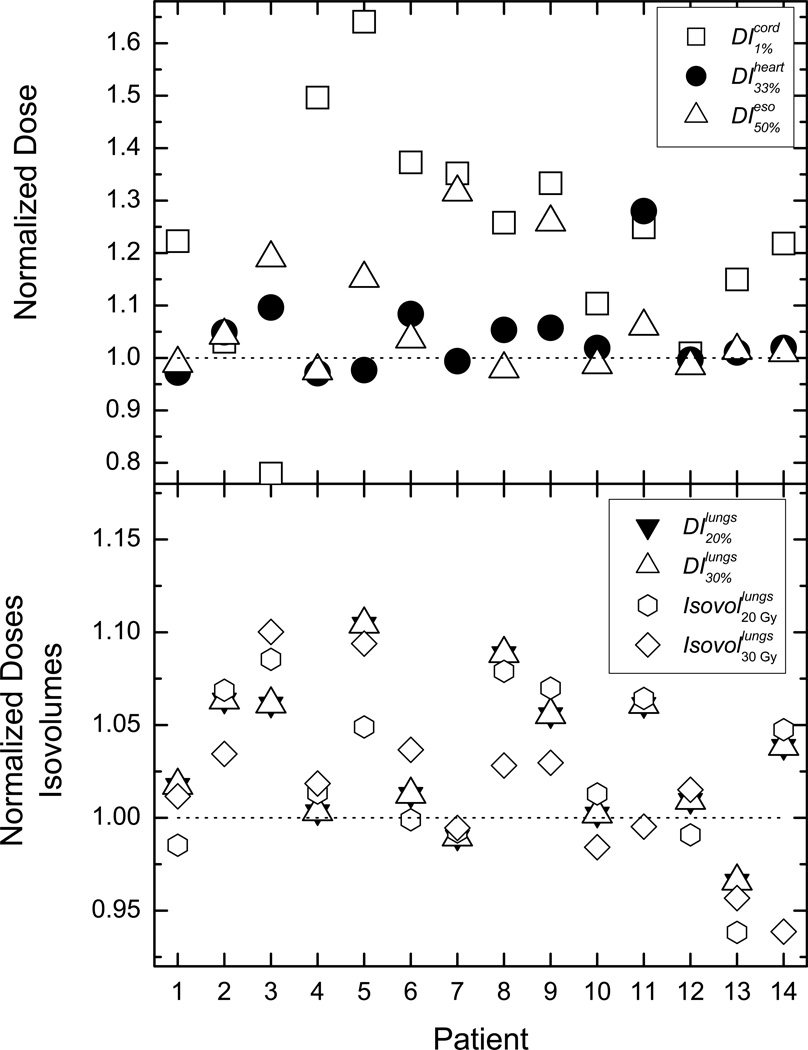
The results from the per-patient evaluation of the OAR normalized DVIs and isovolumes are presented in Figure 1. In the normalization of the tallied indices, the quantities obtained from the DM plans were used as a reference. Therefore, doses for different DVIs or isovolumes for different patients could be visualized together on a single plot.(Mihaylov et al., 2007; Mihaylov and Siebers, 2008) In order to aid the evaluation of the obtained differences unity is denoted on the figure by a dotted line. If a normalized DV or isovolume is greater than unity then the DM optimization results in lower absolute value for that quantity and vice versa. Majority of DVIs for spinal cord, heart end esophagus demonstrate that DM optimization results in more OAR sparing than DV optimization (cf. top panel of Figure 1). The differences range from −23% (dose to 1% of the spinal cord for patient 3) to more than 60% (dose to 1% of the spinal cord for patient 5) with average sparing of cord, heart, and esophagus of 23%, 4%, and 6% respectively. Negative difference corresponds to better lower dosimetric values with DV optimization. Bottom panel of the figure represents the healthy lung indices. The behavior is very similar to the spinal cord, heart and esophagus DVIs. For majority of the indices DM optimization yields lower lung doses. On average the doses to 20% and 30% of healthy lung are lower by about 3% and 4%, while lungs volumes receiving 2000 cGy and 3000 cGy are lower by 3% and 2% respectively.
Figure 1.
Normalized dose indices and isodose volumes for all patients. In the top panel the indices for the heart, spinal cord, and esophagus are presented, while in the bottom panel the lung data is plotted.
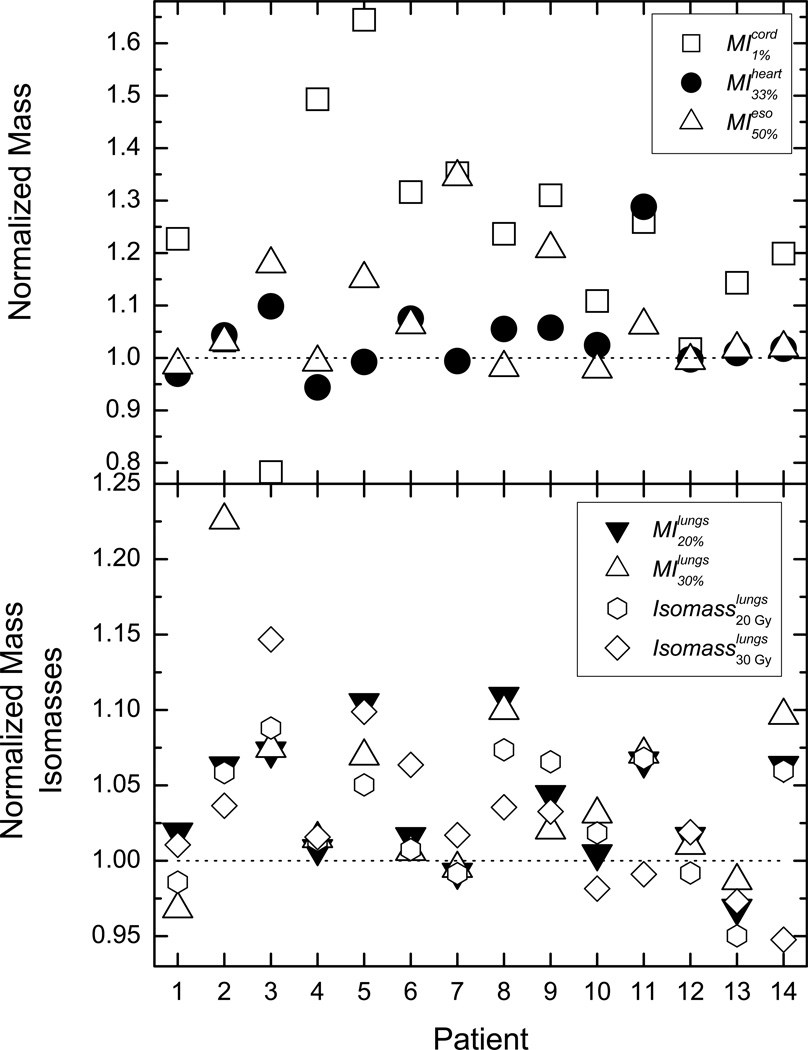
Figure 2 represents the corresponding MIs and isomasses. For all OARs, the majority of the tallied indices indicate more healthy tissue sparing with DM optimization. The average DMIs for the spinal cord, the heart, and the esophagus have values very close to the average DVI differences. Doses to 20% and 30% mass of lung tissue differ between DM and DV optimization by 4% and 4.8%, while lung mass receiving more than 2000 cGy and 3000 cGy differ by 3% and 2.6% respectively.
Figure 2.
The presented data is the same as in Figure 1, but in this case the dose data has been extracted from the dose-mass histograms. In the top panel are the normalized doses to 1% mass of the spinal cord, 33% of the heart mass, and 50% of the esophagus mass. In the bottom panel the presented data is for doses to 20% and 30% of lung mass, as well as the lung tissue mass receiving 2000 and 3000 cGy.
3.2. Statistical analyses
Table 1 contains the average value of the DVIs (estimated from the doses derived by the DM optimization) in cGy, the statistical equivalence in cGy, and the percent change in the dose index necessary to establish statistical equivalence. In addition, the bottom two rows of the table contain the lung volumes encompassed by 2000 and 3000 cGy isodose lines in cm3, as well as the statistical equivalence interval and the percent change with respect to the average. The statistical equivalence tests demonstrate that the DVIs percent change for equivalency for the lungs range from 3.5% to 5.4%. However, the DIs to heart, cord, and esophagus differ from 8% to more than 40%. Table 2 is the counterpart of Table 1, with the only difference that the tallied quantities were derived from the dose-mass histograms. The statistically significant sparing of lung mass varies from 4% to almost 6.5%. The statistically significant differences in sparing of heart, esophagus, and spinal cord tissue are from 8% to 40%. Table 3 presents the statistical significance test results for generalized equivalent uniform doses for (gEUDs) for the OARs of interest.(Niemierko, 1997, 1999) The parameters a used in the calculation of the gEUDs is based on the available published values.(Wu and Mohan, 2000; Burman et al., 1991; Cella et al., 2014; Belderbos et al., 2005) The percent change with respect to the average gEUDs calculated from the DM plans again range from about 4% for the heart to nearly 100% for the spinal cord.
Table 1.
Dose intervals at which statistical equivalence test indicates that the differences between DM and DV derived DVIs are statistically significant (p<0.05). The average doses or volumes are derived from the DM optimization.
| Dose Volume Index |
Average Value of Tallied Index [cGy or cm3] |
Statistical Equivalence Interval [cGy or cm3] |
Percent change for equivalency (% Sparing) [%] |
|---|---|---|---|
| heart DI33% | 981.3 | 79 | 8.0 |
| cord DI1% | 1366.0 | 571 | 41.2 |
| esophagus DI50% | 443.8 | 81 | 18.3 |
| lungs DI20% | 2421 | 126 | 5.2 |
| lungs DI30% | 1708.5 | 93 | 5.4 |
| Isovolume 2000 cGy | 819.1 | 31 | 3.8 |
| Isovolume 3000 cGy | 510.8 | 17.1 | 3.5 |
Table 2.
The same as Table 1 but for the dose intervals derived from the dose-mass histograms.
| Dose Mass Index |
Average Value of Tallied Index [cGy or g] |
Statistical Equivalence Interval [cGy or g] |
Percent change for equivalency (% Sparing) [%] |
|---|---|---|---|
| heart MI33% | 967.7 | 77 | 8 |
| cord MI1% | 1387.8 | 559 | 40.3 |
| esophagus MI50% | 442.7 | 74 | 16.8 |
| lungs MI20% | 2285 | 128 | 5.6 |
| lungs MI30% | 1572 | 101 | 6.4 |
| Isomass 2000 cGy | 253.5 | 9.8 | 3.9 |
| Isomass 3000 cGy | 159.5 | 7.0 | 4.4 |
Table 3.
The same as Table 1 but for generalized equivalent uniform doses derived from the dose-volume histograms.
| gEUD | Average Value of Tallied Index [cGy] |
Statistical Equivalence Interval [cGy] |
Percent change for equivalency (% Sparing) [%] |
|---|---|---|---|
| heart (a = 6.0) | 3058 | 118 | 4 |
| cord (a = 7.4) | 758 | 736 | 97 |
| esophagus (a = 1.5) | 1200 | 569 | 47.5 |
| lungs (a = 1.2) | 1533 | 93 | 6.1 |
4. Discussion and Conclusion
Radiation toxicity and normal tissue injury is a common problem in radiotherapy.(Marks and Ma, 2007) Several studies have demonstrated that chemo-radiotherapy combination in cancer treatments has rather detrimental effects on normal tissue.(Bentzen and Trotti, 2007; Bradley et al.; Gopal et al., 2003b) In case of NSCLC phase I RTOG 0117 trial demonstrated that combined chemo-radiation prevents dose escalation,(Bradley et al., 2010) while single institution studies have reported on decreased total lung capacity and lung diffusing capacity as a result of chemo-radiotherapy combination.(Gopal et al., 2003a) Those findings indicate that new approaches, allowing reduction of radiation induced toxicity in normal tissue, would benefit those patients who need radiation therapy as part of their standard of care.
The findings herein show that on average DM based optimization results in better OAR sparing than DV optimization for lung cancer patients. This has been demonstrated by both comparing the observed differences on point-by-point basis as well as performing paired statistical analyses on the data. The statistical equivalence tests indicate sparing ranging from 4% to more than 40%. In case of the seventy individual DIs presented on Figure 1 twenty of them showed percent differences larger than the statically equivalent values quoted in Table 1. Therefore, in more than one quarter of the observed points the DM optimization results were at least as large as the quoted significant differences. In case of the gEUDs, the observed differences were in excess of the relative levels reported in Table 3 in eighteen out of fifty six individual data points for all patient, thereby indicating that in almost one third of all tallied gEUDs DM optimization outperforms DV optimization. Those lower doses can be used for normal tissue sparing or alternatively isotoxic dose escalation may be exploited.
Notably, target dose differences of 3% and more have observable clinical significance.(Bentzen, 2004; Dutreix, 1984; Mijnheer, 1996) It should be noted however, that the sparing is case dependent and it is not observed for all tallied dosimetric endpoints. The combined plots evaluating all of compared dosimetric quantities indicate that the most modest healthy tissue sparing is observed in the lungs and in the heart, while significantly better sparing is achieved in the spinal cord and the esophagus with dose-mass based inverse optimization. Investigation of DM optimization on an idealized simulated phantom indicated that DV optimization is a special case of DM optimization, where in homogeneous media there is no difference between the cost functions.(Mihaylov and Moros, 2014) The simple example presented therein also demonstrated the fact that in DM optimization dose is delivered to the target through lower density regions where the attenuation is lower.
In order to shed some light on the significance of the observed differences through Figures 1 and 2 as well as Tables 1 through 3 an normal tissue complication probability (NTCP) model based on the original work by Kutcher et. al. was developed.(Kutcher et al., 1991) The organ dependent model parameters n, m and TD50 for the different anatomical structures have been derived from published studies. (Belderbos et al., 2005; Burman et al., 1991; Cella et al., 2014; Semenenko and Li, 2008; Schultheiss, 2008) According to the model the differences in the gEUDs of an OAR may result in substantial change in the expected complication probability. If lung gEUD is 20 Gy, then 6% increase in dose will result in modest 3% increase of the NTCP. Similarly, if heart gEUD is 20 Gy, a change of 4% will result only in 2.5% increase of the NTCP. A change of 47.5% in esophageal gEUD of 20 Gy will result in about 9.5% increase in the NTCP predicted by the model. Obviously change in cord gEUD of ~100% for 20 Gy would result in rather small increase of the NTCP, but a change of that magnitude for gEUD of 30 Gy will result in NTCP increase of over 25%. Nonetheless, dose reduction to normal tissue, for adequate therapeutic dose to the tumors, would always benefit patients regardless of the model derived numbers.
It is possible that the advantages afforded by dose-mass inverse optimization over dose-volume inverse optimization can be attributed to further personalizing the dose optimization to a given patient by weighting the cost function components by the variable mass in every voxel (density).(Mihaylov and Moros, 2014) In dose-volume optimization voxels are usually all of the same volume so the weighting is uniform.
Acknowledgments
This work was supported NIH grant R01 CA163370.
References
- Aaltonen P, Brahme A, Lax I, Levernes S, Naslund I, Reitan JB, Turesson I. Specification of dose delivery in radiation therapy. Recommendation by the Nordic Association of Clinical Physics (NACP) Acta oncologica (Stockholm, Sweden) 1997;36(Suppl 10):1–32. doi: 10.1080/0284186X.1997.11835454. [DOI] [PubMed] [Google Scholar]
- American Cancer Society. Cancer Facts and Figures 2014. American Cancer Society. 2014 [Google Scholar]
- Anscher MS, Marks LB, Shafman TD, Clough R, Huang H, Tisch A, Munley M, Herndon JE, Garst J, Crawford J, Jirtle RL. Risk of long-term complications after TFG-beta1-guided very-high-dose thoracic radiotherapy. International journal of radiation oncology, biology, physics. 2003;56:988–995. doi: 10.1016/s0360-3016(03)00184-6. [DOI] [PubMed] [Google Scholar]
- Auperin A, Le Pechoux C, Pignon JP, Koning C, Jeremic B, Clamon G, Einhorn L, Ball D, Trovo MG, Groen HJ, Bonner JA, Le Chevalier T, Arriagada R. Concomitant radio-chemotherapy based on platin compounds in patients with locally advanced non-small cell lung cancer (NSCLC): a meta-analysis of individual data from 1764 patients. Ann oncol. 2006;17:473–483. doi: 10.1093/annonc/mdj117. [DOI] [PubMed] [Google Scholar]
- Belderbos J, Heemsbergen W, Hoogeman M, Pengel K, Rossi M, Lebesque J. Acute esophageal toxicity in non-small cell lung cancer patients after high dose conformal radiotherapy. Radiother oncol. 2005;75:157–164. doi: 10.1016/j.radonc.2005.03.021. [DOI] [PubMed] [Google Scholar]
- Bentzen SM. High-tech in radiation oncology: should there be a ceiling? International journal of radiation oncology, biology, physics. 2004;58:320–330. doi: 10.1016/j.ijrobp.2003.09.057. [DOI] [PubMed] [Google Scholar]
- Bentzen SM, Trotti A. Evaluation of early and late toxicities in chemoradiation trials. J clin oncol. 2007;25:4096–4103. doi: 10.1200/JCO.2007.13.3983. [DOI] [PubMed] [Google Scholar]
- Bradley JD, Bae K, Graham MV, Byhardt R, Govindan R, Fowler J, Purdy JA, Michalski JM, Gore E, Choy H. Primary analysis of the phase II component of a phase I/II dose intensification study using three-dimensional conformal radiation therapy and concurrent chemotherapy for patients with inoperable non-small-cell lung cancer: RTOG 0117. J Clin Oncol. 28:2475–2480. doi: 10.1200/JCO.2009.27.1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley JD, Bae K, Graham MV, Byhardt R, Govindan R, Fowler J, Purdy JA, Michalski JM, Gore E, Choy H. Primary analysis of the phase II component of a phase I/II dose intensification study using three-dimensional conformal radiation therapy and concurrent chemotherapy for patients with inoperable non-small-cell lung cancer: RTOG 0117. J clin oncol. 2010;28:2475–2480. doi: 10.1200/JCO.2009.27.1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brecher GA, Hubay CA. Pulmonary blood flow and venous return during spontaneous respiration. Circulation research. 1955;3:210–214. doi: 10.1161/01.res.3.2.210. [DOI] [PubMed] [Google Scholar]
- Burman C, Kutcher GJ, Emami B, Goitein M. Fitting of normal tissue tolerance data to an analytic function. International journal of radiation oncology, biology, physics. 1991;21:123–135. doi: 10.1016/0360-3016(91)90172-z. [DOI] [PubMed] [Google Scholar]
- Butler LE, Forster KM, Stevens CW, Bloch C, Liu HH, Tucker SL, Komaki R, Liao Z, Starkschall G. Dosimetric benefits of respiratory gating: a preliminary study. Journal of applied clinical medical physics / American College of Medical Physics. 2004;5:16–24. doi: 10.1120/jacmp.26.146. [DOI] [PubMed] [Google Scholar]
- Cella L, Palma G, Deasy JO, Oh JH, Liuzzi R, D'Avino V, Conson M, Pugliese N, Picardi M, Salvatore M, Pacelli R. Complication probability models for radiation-induced heart valvular dysfunction: do heart-lung interactions play a role? PloS one. 2014;9:e111753. doi: 10.1371/journal.pone.0111753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogan N, Siebers JV, Keall PJ, Lerma F, Wu Y, Fatyga M, Williamson JF, Schmidt-Ullrich RK. Improving IMRT dose accuracy via deliverable Monte Carlo optimization for the treatment of head and neck cancer patients. Medical physics. 2006;33:4033–4043. doi: 10.1118/1.2357835. [DOI] [PubMed] [Google Scholar]
- Dutreix A. When and how can we improve precision in radiotherapy? Radiother oncol. 1984;2:275–292. doi: 10.1016/s0167-8140(84)80070-5. [DOI] [PubMed] [Google Scholar]
- Evans ES, Hahn CA, Kocak Z, Zhou SM, Marks LB. The role of functional imaging in the diagnosis and management of late normal tissue injury. Seminars in radiation oncology. 2007;17:72–80. doi: 10.1016/j.semradonc.2006.11.003. [DOI] [PubMed] [Google Scholar]
- Fan M, Marks LB, Hollis D, Bentel GG, Anscher MS, Sibley G, Coleman RE, Jaszczak RJ, Munley MT. Can we predict radiation-induced changes in pulmonary function based on the sum of predicted regional dysfunction? J clin oncol. 2001;19:543–550. doi: 10.1200/JCO.2001.19.2.543. [DOI] [PubMed] [Google Scholar]
- Forster KM, Starkschall G, Butler LE, Keall P, Liu H, Travis EL, Komaki R, Stevens CW. The dose-mass histogram: a tool for evaluating thoracic treatment plans. Medical physics. 2001;28:1228–1229. [Google Scholar]
- Fredriksson A. Automated improvement of radiation therapy treatment plans by optimization under reference dose constraints. Physics in medicine and biology. 2012;57:7799–7811. doi: 10.1088/0031-9155/57/23/7799. [DOI] [PubMed] [Google Scholar]
- Fu XL, Huang H, Bentel G, Clough R, Jirtle RL, Kong FM, Marks LB, Anscher MS. Predicting the risk of symptomatic radiation-induced lung injury using both the physical and biologic parameters V(30) and transforming growth factor beta. International journal of radiation oncology, biology, physics. 2001;50:899–908. doi: 10.1016/s0360-3016(01)01524-3. [DOI] [PubMed] [Google Scholar]
- Gopal R, Starkschall G, Tucker SL, Cox JD, Liao Z, Hanus M, Kelly JF, Stevens CW, Komaki R. Effects of radiotherapy and chemotherapy on lung function in patients with non-smallcell lung cancer. International journal of radiation oncology, biology, physics. 2003a;56:114–120. doi: 10.1016/s0360-3016(03)00077-4. [DOI] [PubMed] [Google Scholar]
- Gopal R, Tucker SL, Komaki R, Liao Z, Forster KM, Stevens C, Kelly JF, Starkschall G. The relationship between local dose and loss of function for irradiated lung. International journal of radiation oncology, biology, physics. 2003b;56:106–113. doi: 10.1016/s0360-3016(03)00094-4. [DOI] [PubMed] [Google Scholar]
- Graham MV, Purdy JA, Emami B, Harms W, Bosch W, Lockett MA, Perez CA. Clinical dose-volume histogram analysis for pneumonitis after 3D treatment for non-small cell lung cancer (NSCLC) International journal of radiation oncology, biology, physics. 1999;45:323–329. doi: 10.1016/s0360-3016(99)00183-2. [DOI] [PubMed] [Google Scholar]
- Keall P, Mageras G, Balter J, Emery R, Forster K, Jiang S, Kapatoes J, Kubo H, Low D, Murphy M, Murray B, Ramsey C, van Herk M, Vedam S, Wong J, Yorke E. American Association of Physicists in Medicine Radiation Therapy Committee Task Group 76: the management of respiratory motion in radiation oncology. Medical physics. 2006a doi: 10.1118/1.2349696. [DOI] [PubMed] [Google Scholar]
- Keall PJ, Kini VR, Vedam SS, Mohan R. Motion adaptive x-ray therapy: a feasibility study. Physics in medicine and biology. 2001;46:1–10. doi: 10.1088/0031-9155/46/1/301. [DOI] [PubMed] [Google Scholar]
- Keall PJ, Mageras GS, Balter JM, Emery RS, Forster KM, Jiang SB, Kapatoes JM, Low DA, Murphy MJ, Murray BR, Ramsey CR, Van Herk MB, Vedam SS, Wong JW, Yorke E. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Medical physics. 2006b;33:3874–3900. doi: 10.1118/1.2349696. [DOI] [PubMed] [Google Scholar]
- Kocak Z, Evans ES, Zhou SM, Miller KL, Folz RJ, Shafman TD, Marks LB. Challenges in defining radiation pneumonitis in patients with lung cancer. International journal of radiation oncology, biology, physics. 2005;62:635–638. doi: 10.1016/j.ijrobp.2004.12.023. [DOI] [PubMed] [Google Scholar]
- Kong FM, Ten Haken RK, Schipper MJ, Sullivan MA, Chen M, Lopez C, Kalemkerian GP, Hayman JA. High-dose radiation improved local tumor control and overall survival in patients with inoperable/unresectable non-small-cell lung cancer: long-term results of a radiation dose escalation study. International journal of radiation oncology, biology, physics. 2005;63:324–333. doi: 10.1016/j.ijrobp.2005.02.010. [DOI] [PubMed] [Google Scholar]
- Kubo HD, Len PM, Minohara S, Mostafavi H. Breathing-synchronized radiotherapy program at the University of California Davis Cancer Center. Medical physics. 2000;27:346–353. doi: 10.1118/1.598837. [DOI] [PubMed] [Google Scholar]
- Kutcher GJ, Burman C, Brewster L, Goitein M, Mohan R. Histogram reduction method for calculating complication probabilities for three-dimensional treatment planning evaluations. International journal of radiation oncology, biology, physics. 1991;21:137–146. doi: 10.1016/0360-3016(91)90173-2. [DOI] [PubMed] [Google Scholar]
- Ma J, Zhang J, Zhou S, Hubbs JL, Foltz RJ, Hollis DR, Light KL, Wong TZ, Kelsey CR, Marks LB. Association between RT-induced changes in lung tissue density and global lung function. International journal of radiation oncology, biology, physics. 2009;74:781–789. doi: 10.1016/j.ijrobp.2008.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marks LB, Bentzen SM, Deasy JO, Kong FM, Bradley JD, Vogelius IS, El Naqa I, Hubbs JL, Lebesque JV, Timmerman RD, Martel MK, Jackson MA. Radiation dose-volume effects in the lung. International journal of radiation oncology, biology, physics. 76:S70–S76. doi: 10.1016/j.ijrobp.2009.06.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marks LB, Fan M, Clough R, Munley M, Bentel G, Coleman RE, Jaszczak R, Hollis D, Anscher M. Radiation-induced pulmonary injury: symptomatic versus subclinical endpoints. International journal of radiation biology. 2000;76:469–475. doi: 10.1080/095530000138466. [DOI] [PubMed] [Google Scholar]
- Marks LB, Ma J. Challenges in the clinical application of advanced technologies to reduce radiation-associated normal tissue injury. International journal of radiation oncology, biology, physics. 2007;69:4–12. doi: 10.1016/j.ijrobp.2007.05.010. [DOI] [PubMed] [Google Scholar]
- Martel MK, Ten Haken RK, Hazuka MB, Kessler ML, Strawderman M, Turrisi AT, Lawrence TS, Fraass BA, Lichter AS. Estimation of tumor control probability model parameters from 3-D dose distributions of non-small cell lung cancer patients. Lung cancer (Amsterdam, Netherlands) 1999;24:31–37. doi: 10.1016/s0169-5002(99)00019-7. [DOI] [PubMed] [Google Scholar]
- Mathew L, Gaede S, Wheatley A, Etemad-Rezai R, Rodrigues GB, Parraga G. Detection of longitudinal lung structural and functional changes after diagnosis of radiation-induced lung injury using hyperpolarized 3He magnetic resonance imaging. Medical physics. 37:22–31. doi: 10.1118/1.3263616. [DOI] [PubMed] [Google Scholar]
- Mavroidis P, Plataniotis GA, Gorka MA, Lind BK. Comments on 'Reconsidering the definition of a dose-volume histogram'--dose-mass histogram (DMH) versus dose-volume histogram (DVH) for predicting radiation-induced pneumonitis. Physics in medicine and biology. 2006;51:L43–L50. doi: 10.1088/0031-9155/51/24/L01. [DOI] [PubMed] [Google Scholar]
- McDonald S, Rubin P, Phillips TL, Marks LB. Injury to the lung from cancer therapy: clinical syndromes, measurable endpoints, and potential scoring systems. International journal of radiation oncology, biology, physics. 1995;31:1187–1203. doi: 10.1016/0360-3016(94)00429-O. [DOI] [PubMed] [Google Scholar]
- Meadors M, Floyd J, Perry MC. Pulmonary toxicity of chemotherapy. Seminars in oncology. 2006;33:98–105. doi: 10.1053/j.seminoncol.2005.11.005. [DOI] [PubMed] [Google Scholar]
- Mihaylov IB, Fatyga M, Moros EG, Penagaricano J, Lerma FA. Lung dose for minimally moving thoracic lesions treated with respiration gating. International journal of radiation oncology, biology, physics. 2010;77:285–291. doi: 10.1016/j.ijrobp.2009.08.021. [DOI] [PubMed] [Google Scholar]
- Mihaylov IB, Lerma FA, Fatyga M, Siebers JV. Quantification of the impact of MLC modeling and tissue heterogeneities on dynamic IMRT dose calculations. Medical physics. 2007;34:1244–1252. doi: 10.1118/1.2712413. [DOI] [PubMed] [Google Scholar]
- Mihaylov IB, Moros EG. Mathematical Formulation of DMH-Based Inverse Optimization. Frontiers in oncology. 2014;4:331. doi: 10.3389/fonc.2014.00331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihaylov IB, Siebers JV. Evaluation of dose prediction errors and optimization convergence errors of deliverable-based head-and-neck IMRT plans computed with a superposition/convolution dose algorithm. Medical physics. 2008;35:3722–3727. doi: 10.1118/1.2956710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mijnheer BJ. The clinical basis for dosimetric accuracy in radiotherapy. In: Faulkner K, Harrison RM, editors. Radiation Incidents. 1996. pp. 16–20. [Google Scholar]
- Movsas B, Raffin TA, Epstein AH, Link CJ., Jr Pulmonary radiation injury. Chest. 1997;111:1061–1076. doi: 10.1378/chest.111.4.1061. [DOI] [PubMed] [Google Scholar]
- Niemierko A. Reporting and analyzing dose distributions: a concept of equivalent uniform dose. Medical physics. 1997;24:103–110. doi: 10.1118/1.598063. [DOI] [PubMed] [Google Scholar]
- Niemierko A. A generalized concept of Equivalent Uniform Dose (EUD) Medical physics. 1999;26:1100. doi: 10.1118/1.598063. [DOI] [PubMed] [Google Scholar]
- Nioutsikou E, Webb S, Panakis N, Bortfeld T, Oelfke U. Reconsidering the definition of a dose-volume histogram. Physics in medicine and biology. 2005;50:L17–L19. doi: 10.1088/0031-9155/50/11/l01. [DOI] [PubMed] [Google Scholar]
- Perez CA, Brady LW, Halperin EC, Schmidt-Ullrich R. Principles and Practice of Radiation Oncology. 4 edition. Lippincott Williams & Wilkins; 2004. [Google Scholar]
- Rodrigues G, Lock M, D'Souza D, Yu E, Van Dyk J. Prediction of radiation pneumonitis by dose - volume histogram parameters in lung cancer--a systematic review. Radiother oncol. 2004;71:127–138. doi: 10.1016/j.radonc.2004.02.015. [DOI] [PubMed] [Google Scholar]
- Rosner B. Fundamentals of biostatistics. Boston: Duxberry; 1986. pp. 54–58. [Google Scholar]
- Schultheiss TE. The radiation dose-response of the human spinal cord. International journal of radiation oncology, biology, physics. 2008;71:1455–1459. doi: 10.1016/j.ijrobp.2007.11.075. [DOI] [PubMed] [Google Scholar]
- Semenenko VA, Li XA. Lyman-Kutcher-Burman NTCP model parameters for radiation pneumonitis and xerostomia based on combined analysis of published clinical data. Physics in medicine and biology. 2008;53:737–755. doi: 10.1088/0031-9155/53/3/014. [DOI] [PubMed] [Google Scholar]
- Shipley WU, Tepper JE, Prout GR, Jr, Verhey LJ, Mendiondo OA, Goitein M, Koehler AM, Suit HD. Proton radiation as boost therapy for localized prostatic carcinoma. Jama. 1979;241:1912–1915. [PubMed] [Google Scholar]
- Siebers J, Mohan R. Monte Carlo and IMRT. In: Palta JR, Mackie TR, editors. Intensity-Modulated Radiation Therapy. The State of the Art. Colorado Springs, Colorado: Medical Physics Publishing; 2003. pp. 531–561. [Google Scholar]
- Siebers JV, Lauterbach M, Keall PJ, Mohan R. Incorporating multi-leaf collimator leaf sequencing into iterative IMRT optimization. Medical physics. 2002;29:952–959. doi: 10.1118/1.1477230. [DOI] [PubMed] [Google Scholar]
- Stevens CW, Munden RF, Forster KM, Kelly JF, Liao Z, Starkschall G, Tucker S, Komaki R. Respiratory-driven lung tumor motion is independent of tumor size, tumor location, and pulmonary function. International journal of radiation oncology, biology, physics. 2001;51:62–68. doi: 10.1016/s0360-3016(01)01621-2. [DOI] [PubMed] [Google Scholar]
- Tucker SL, Liu HH, Wang S, Wei X, Liao Z, Komaki R, Cox JD, Mohan R. Dose-volume modeling of the risk of postoperative pulmonary complications among esophageal cancer patients treated with concurrent chemoradiotherapy followed by surgery. International journal of radiation oncology, biology, physics. 2006;66:754–761. doi: 10.1016/j.ijrobp.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Vermeire P, Butler J. Effect of respiration on pulmonary capillary blood flow in man. Circulation research. 1968;22:299–308. doi: 10.1161/01.res.22.2.299. [DOI] [PubMed] [Google Scholar]
- Wei X, Liu H, Jang S, Jauregui M, Dong L, Liao Z, Komaki R, Mohan R. Dose mass histogram and its application for 4D treatment planning. Medical physics. 2005;32:2038. [Google Scholar]
- Wolthaus JW, Sonke JJ, van Herk M, Belderbos JS, Rossi MM, Lebesque JV, Damen EM. Comparison of different strategies to use four-dimensional computed tomography in treatment planning for lung cancer patients. International journal of radiation oncology, biology, physics. 2008;70:1229–1238. doi: 10.1016/j.ijrobp.2007.11.042. [DOI] [PubMed] [Google Scholar]
- Wu Q, Mohan R. Algorithms and functionality of an intensity modulated radiotherapy optimization system. Medical physics. 2000;27:701–711. doi: 10.1118/1.598932. [DOI] [PubMed] [Google Scholar]