Conspiracist Ideation as a Predictor of Climate-Science Rejection

Reanalysis of the survey data sets of Lewandowsky, Oberauer, and Gignac (2013) and Lewandowsky, Gignac, and Oberauer (2013) indicates that the conclusions of those articles—that conspiracist ideation predicts skepticism regarding the reality of anthropogenic climate change—are not supported by the data. Nonlinear relationships were overlooked in both analyses, and this resulted in model misspecification. The authors used structural equation modeling (SEM) assuming linear relationships between the variables, and it is essential to test this assumption (Bentler & Chou, 1987, p. 86; Ullman, 2007, p. 683). In this Commentary, we show, using nonparametric local regression, that this assumption does not hold for the relationship between conspiracist ideation and views on climate science, the relationship that produced one of the central claims of both articles and the majority of the press interest (e.g., Corner, 2012; Pearlman, 2012).

The Data Sets and Variables

The invitation to one of the surveys (Lewandowsky, Oberauer, & Gignac, 2013) appeared on climate-related blogs from August through October 2010 (we refer to this as the blogs survey). In this survey, responses were on a 4-point scale from strongly disagree (1) to strongly agree (4); all 1,145 responses in the data set were analyzed. The second survey (Lewandowsky, Gignac, & Oberauer, 2013) involved U.S. citizens drawn from an Internet panel in June 2012 (we refer to this as the panel survey). In this survey, responses were on a 5-point scale from strongly disagree (1) to strongly agree (5), with a neutral option at the midpoint (3); all 1,001 responses in the data set were analyzed. The data sets are available through the publications page of Lewandowsky’s Web site, http://www.cogsciwa.com/. We provide further details of the surveys and questions relating to the present analysis in Table S1 in the Supplemental Material available online.

We calculated composite variables for conspiracist ideation (CY) and endorsement of climate-change science (CLIM) for each data set by averaging the numerical responses to the relevant questions. Higher scores denoted higher levels of ideation or endorsement.

Analysis and Results

We initially analyzed the data from the blogs survey using ordinary least squares (OLS) fitting (see the left-hand plot in Fig. S1 in the Supplemental Material). For the linear model predicting CLIM from CY, the coefficient of the linear term was −0.310, 95% confidence interval (CI) = [−0.438, −0.182]. Although this coefficient was significantly negative, CY predicted less than 2% of the variance in CLIM (adjusted R² = .018). Furthermore, by far the largest group of respondents (41%) expressed maximum agreement with all five propositions relating to climate change (i.e., CLIM = 4.0), whereas only 15% were “more skeptical than not” (CLIM in the range of 1.0–2.4). This self-selected data set was therefore too skewed on the variable of interest to test the relationship properly. Figure S2 in the Supplemental Material shows the distribution of cases for both variables in both data sets and clearly demonstrates the extreme skew of the blogs data set along CLIM (upper right-hand plot). Berk (1983) showed that nonrandom selection on an endogenous variable compromises both external and internal validity of a model (i.e., the results are not applicable even to the sample). We therefore turned to the population-sampled data set from the panel survey.

That sample was far less decided about climate change, having a median CLIM only slightly toward the “convinced” side. For the complete data set, simple linear regression (see the right-hand plot in Fig. S1) showed that CY marginally predicted CLIM, linear term = −0.062, 95% CI = [−0.118, −0.007], but accounted for much less than 1% of the variance (adjusted R² = .0039). However, there were 35 respondents who had responded “neutral” to all 11 questions relating to CLIM and CY. These respondents contributed to spikes at CY = 3 and CLIM = 3 (see the lower two panels of Fig. S2 in the Supplemental Material). To test the effect of these satisficing respondents (Krosnick, 1991; Kulas, Stachowski, & Haynes, 2008) on the results, we performed a regression excluding their data (i.e., using data from the remaining 966 respondents). Excluding these cases resulted in the linear relationship between CY and CLIM becoming nonsignificant; the linear term was −0.056, 95% CI = [−0.113, 0.001]. This emphasizes the marginality of the original result.

Given the very weak nature of the linear relationship identified by OLS, we turned to the possibility of a nonlinear relationship between CY and CLIM, which we investigated using loess nonparametric local regression (Cleveland & Devlin, 1988). With nonlinear models, it is important to explore relationships in both directions, as nonlinear models cannot be easily transposed. In particular, a relationship that is nonmonotonic in one direction will be multivalued in the other, and loess fits are single-valued functions. Figure 1 therefore shows loess fits for both CY predicting CLIM and CLIM predicting CY in the data from the panel survey. These plots were calculated using the R function loess (R Development Core Team, 2011) with default parameters (degree = 2, span = 0.75) and include estimated 95% CIs.

Fig. 1.

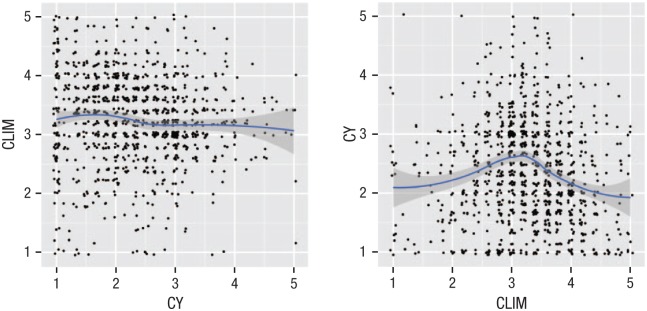
Loess plots (with 95% confidence intervals) for the relationship between average conspiracist ideation (CY) and average endorsement of climate-change science (CLIM) in the data from Lewandowsky, Gignac, and Oberauer (2013). Data points have been jittered (Chambers, Cleveland, Kleiner, & Tukey, 1983, pp. 106–108).

Figure 1 shows that CY had very little predictive power for CLIM, but the fit in the transposed plot has an obvious bell-shaped curve. Respondents with high and low CLIM scores had very similar CY scores, and the highest conspiracist ideation was observed for respondents whose CLIM scores were neutral. It is therefore inappropriate to use a linear function of CY to predict CLIM, as the underlying relationship in that direction is multivalued.

Corresponding plots for the blogs-survey data are in the top row of Figure S3 in the Supplemental Material. These plots are similar to Figure 1 but less clear because of the extreme skew in the blogs data set. The middle row of Figure S3 shows the effect of omitting from this data set the 18 cases with CY scores greater than 2.5, which was the sensitivity test that Lewandowsky et al. reported for the blogs survey. The original analysis of Lewandowsky et al. was robust to the removal of those cases, but we found that the nonparametric fits were substantially altered when those cases were removed, such that CY was no longer a significant predictor of CLIM, and the curvilinear relationship for CLIM as a predictor of CY became more prominent. (Plots of the panel-survey data set, as in Fig.1, are included in the bottom row of Fig. S3 for comparison.) As implemented in both surveys, SEM does not produce meaningful results from multivalued functions (see Bentler & Chou, 1987, p. 86).

Given the multivalued curved relationship, one might wonder why a linear correlation between CY and CLIM was seen in both data sets. It arose from an imbalance in responses along the CLIM scale in both cases: The preponderance of respondents on the right-hand side of the bell curve meant that this downward-sloping part of the curve prevailed in a linear fit, which led to an overall negative linear term in the OLS fit. This imbalance was subtle in the case of the panel survey, but very pronounced for the blogs survey, and consequently led to a more significant fit for that highly skewed data set and hence the misidentification of a linear term in the original SEM analyses.

Conclusion

This analysis highlights the fact that a skewed sample can easily mask a nonlinear relationship and lead to serious misinterpretation of modeled relationships (Berk, 1983; Groves, 2006; MacCallum & Mar, 1995). Techniques such as SEM should not be used as a “black box” without thorough initial exploration of the data set to check for nonlinearities (Bentler & Chou, 1987; Cumming, 2014). The curvilinear relationship identified in both the panel-survey data of Lewandowsky, Gignac, and Oberauer (2013) and the blogs-survey data of Lewandowsky, Oberauer, and Gignac (2013) suggests that both respondents convinced of anthropogenic climate change and respondents skeptical about such change were less likely to accept conspiracy theories than were those who were less decided about climate change.