Abstract
In addition to the excretion of metabolic waste and toxin, the kidney plays an indispensable role in regulating the balance of water, electrolyte, acid-base, and blood pressure. For the kidney to maintain proper functions, hemodynamic control is crucial. In this review, we describe representative mathematical models that have been developed to better understand the kidney's autoregulatory processes. We consider mathematical models that simulate glomerular filtration, and renal blood flow regulation by means of the myogenic response and tubuloglomerular feedback. We discuss the extent to which these modeling efforts have expanded the understanding of renal functions in health and disease.
Keywords: kidney, blood flow, myogenic response, tubuloglomerular feedback, glomerular filtration, nonlinear dynamics
1. Introduction
As part of the excretory system, the kidney's functions are to remove waste products from the bloodstream, to maintain the balance of body water and electrolytes, and to control blood volume and blood pressure. Renal dysfunction is often associated with serious health conditions such as diabetes, hypertension, and congestive heart failure.
Despite their small size, the kidneys receive a substantial fraction of the cardiac output [1]. Blood enters kidney's circulation through the renal artery and, following successive branching, reaches the arcuate arteries [2]. The arcuate arteries traverse through the boundary between the cortex and the medulla and branch into interlobular arteries that give rise to the afferent arterioles that supply the glomeruli (see Fig. 1, left panel).
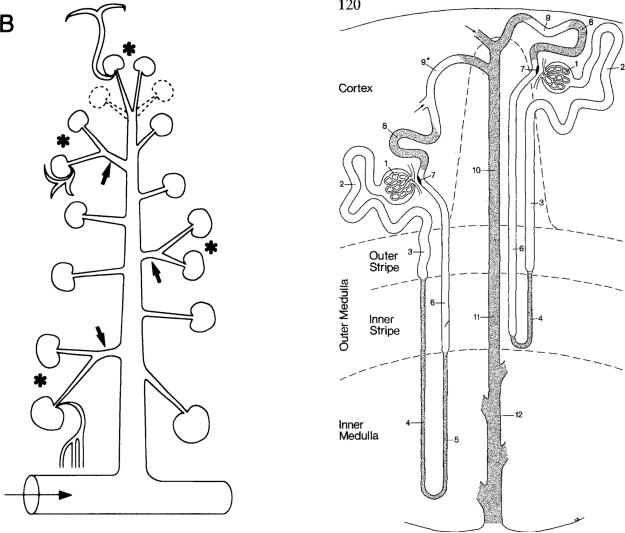
Figure 1.
Left: Structure of the pre-glomerular vasculature. Diagram shows an arcuate artery (main horizontal vessel), which splits into a cortical radial artery (main vertical vessel), from which afferent arterioles (smaller vessels) branch off either alone or in pairs. A glomerulus is located at the end of each afferent arteriole. Right: Two representative nephrons and part of the collecting duct system. 1: glomerulus; 2–3, proximal tubule; 4–7, loop of Henle; 8–9, distal tubule; 10–12, collecting duct. Figures reproduced from Refs. [3] and [4].
The glomeruli feed into the nephrons, which are the functional units of the kidney. A kidney contains a large number of nephrons, ranging from 30,000–40,000 in rats to ~1 million in humans. A nephron is a long tubular structure made up of a single layer of epithelial cells; it is divided into four distinct segments: a glomerulus, a proximal tubule, a loop of Henle, and a distal tubule (Fig. 1, right panel). At the proximal end, nephrons are separated from the vasculature by a semi-permeable membrane that allows plasma filtrate to pass from the bloodstream. As the filtrate flows through the nephron segments, its composition changes through reabsorption and secretion of fluid and solutes by the tubular epithelia. The nephron's distal end is connected to the collecting duct system, which delivers the remaining tubular fluid to the ureter. The composition of the final urine is adjusted so that daily intake equals urinary excretion.
2. Glomerular filtration
Each nephron consists of an initial filtering component called the glomerulus. The glomerulus is formed by a network of capillaries enclosed by a capsule that is connected to the nephron's proximal tubule. The capillaries of a glomerulus are supplied by a single afferent arteriole and drained by a single efferent arteriole.
In the glomerulus, urine formation begins with the filtration of blood plasma across the capillary walls. The capillary walls permit the filtration of large amounts of fluid and small solutes while preventing the passage of large proteins and blood cells. The filtrate is collected by the enclosing capsule and delivered to the proximal tubule. The volume of plasma filtered per unit time is referred to as single-nephron glomerular filtration rate (SNGFR), which is a key determinant of nephron and, more generally, kidney function.
The first quantitative analysis of glomerular function is attributed to Starling, who in 1899 showed that the forces governing fluid transport across capillary walls could explain the formation of the glomerular filtrate [6]. Many decades later, in the early 1970s, progress in experimental techniques (e.g., micropuncture) gave rise to a wave of glomerular modeling efforts [7, 8, 9]. The principal objective of mathematical modeling of glomerular function is to better understand the relationship between renal hemodynamics (i.e., blood pressure and flow) and SNGFR, both in health and disease.
In mathematical models of glomerular filtration, the network of capillaries are commonly idealized as a number of identical tubes connected in parallel, in spite of their actual tortuosity. A schematic diagram is shown in Fig. 2. Along each tubule, filtration is driven by the Starling forces developed between the capillary's lumen and the surrounding space.
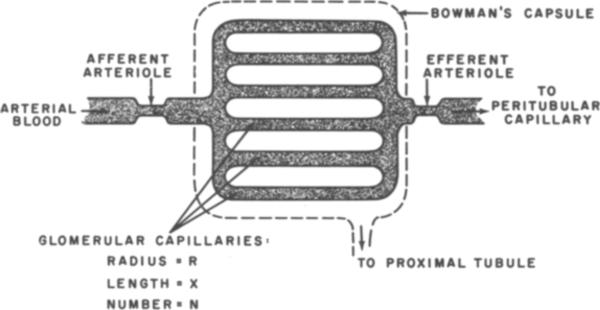
Figure 2.
Glomerular filtration model. Capillary bed is represented by a network of parallel, identical tubes. Blood enters through the afferent arteriole and exits through the efferent arteriole. Filtrate is collected by the surrounding capsule and delivered to the proximal tubule. Figure adapted from Ref. [5].
To derive model equations for glomerular filtration, consider a capillary network of n parallel tubes. Given the sufficiently fast glomerular transit time (~0.1 s), model equations are formulated for quasi-steady state. Let x denote the position along the tube, where x = 0 and x = LGL mark the connections with afferent and efferent arterioles, respectively. Conservation of plasma and protein is given by
| (1) |
| (2) |
where Qp and Cp denote plasma flow and protein concentration, respectively. The parameters S and k are tube's surface area and water permeability, respectively. The Starling forces are given by the hydrostatic pressure in the capillary lumen and the surrounding space (denoted by PGL and PT, respectively), and by the colloid osmotic pressure π in the capillary lumen.
SNGFR is given by the total plasma flux across the network of capillaries
| (3) |
Equation (3) can be simplified by assuming uniform pressure and protein concentration profiles, which yields
| (4) |
In Eq. (4), Kf = nSk is the ultrafiltration coefficient, which is determined by total network surface area and permeability.
In a stand-alone glomerular filtration model, e.g. [8], Qp(0), PGL(x), PT are assumed known a priori. When a glomerular filtration model is incorporated into a more comprehensive model of renal hemodynamics, e.g., [10, 11, 12, 13], Qp(0) and PGL(x) are typically determined by the vascular component, whereas PT is determined by the tubular component, which takes into account tubular flow and tubular compliance.
3. Renal autoregulation
Normal renal function requires that the fluid flow through the nephron be kept within a narrow range. When tubular flow rate falls outside of that range, the ability of the nephron to operate may be compromised. Tubular flow rate depends, in large part, on SNGFR, which is stabilized by the autoregulatory mechanisms discussed below.
Blood flow is commonly modeled by the Poiseuille's law [14]
| (5) |
where ΔP denotes pressure drop along the vessel, and Q denotes volumetric flow. Due to the analogy with Ohm's law (e.g., ΔV = IR), the factor R in Eq. (5) is termed vascular resistance. Resistance is related to the vessel's luminal radius r by an inverse 4-th power law
| (6) |
where L is the vessel's length, and μ is blood viscosity.
In the renal vasculature, nearly all of the pressure drop between the renal artery PA and renal vein PV occurs along the afferent and efferent arterioles. As a first approximation, one may assume that pressure drop along the preafferent arteriole, glomerulus, and post-efferent arteriole segments, as well as fluid loss due to filtration, are negligible; see Fig. 3. In other words, SNGFR, which is typically ~10% of blood flow, is assumed negligible in this approximation. This yields
| (7) |
| (8) |
where Q and PGL denote blood flow and glomerular capillary pressure, respectively, and RAA and REA denote the afferent and efferent arteriolar resistance.
Figure 3.
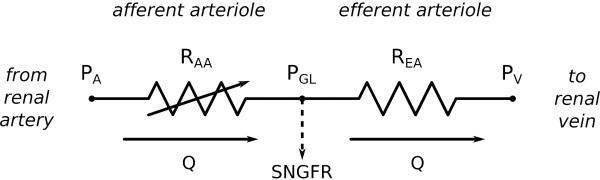
Equivalent circuit of renal vasculature. PA, renal arterial pressure; PV, renal vein pressure. Pressure drop and fluid loss in the glomerulus are assumed negligible, so glomerular capillary pressure PGL equals both afferent arteriole outlet and efferent arteriole inlet pressures, and blood flow Q is the same in both vessels.
Due to heart beat, breathing, movement, excitement, etc., PA is constantly under perturbations. If these perturbations were transmitted to PGL and Q without attenuation, glomerular capillaries would be susceptible to barotrauma and SNGFR would be destabilized, thereby negatively impacting proper nephron and kidney functions. To buffer these perturbations, the afferent arteriole responds by adjusting its radius rAA (and consequently arteriolar resistance RAA) to compensate for changes in PA, thereby shielding Q and PGL from fluctuations in PA. This phenomenon is known as renal autoregulation and is mediated primarily by two mechanisms: myogenic response and tubuloglomerular feedback (TGF). The events underlying renal autoregulation are summarized in Fig. 4.
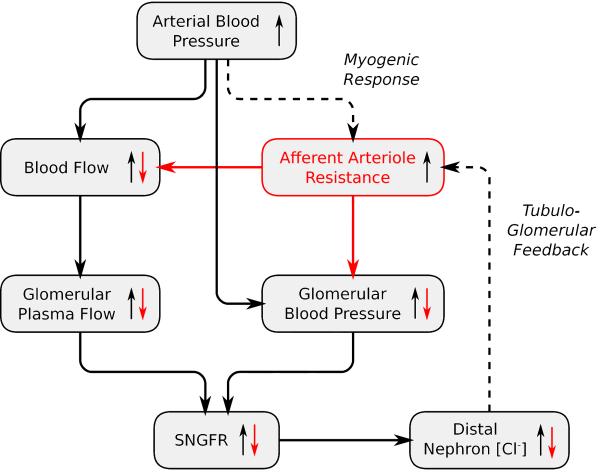
Figure 4.
Renal autoregulation. An increase in arterial blood pressure (black arrows) leads to increase of glomerular plasma flow and blood pressure, which elevates SNGFR. Activation of the autoregulatory mechanisms (dashed arrows) increases afferent arteriole resistance, which decreases glomerular plasma flow, blood pressure, and SNGFR (red arrows)
The myogenic response and tubuloglomerular feedback respond to different signals and exhibit their own frequency characteristics [15, 16, 17]. In rat, the myogenic response is activated by local blood pressure perturbations and buffers fluctuations up to ~200 mHz. Tubuloglomerular feedback is activated by variations in chloride concentration of the fluid reaching the distal nephron, and buffers fluctuations up to ~30 mHz. Both mechanisms share a common effector: the smooth muscles of the afferent arteriole, [15, 16, 17, 18].
Over the past decades, a series of mathematical models have been developed to study the functions and interactions of autoregulatory mechanisms. Below we focus on comprehensive models that provide dynamic representations. Earlier studies that account only for steady state, e.g., models in Refs. [19, 20, 21, 22, 23, 24, 25], are not discussed.
4. Myogenic response
The smooth muscles that form the afferent arteriole walls respond to pressure elevation by vasoconstriction and to pressure drop by vasodilation. The phenomenon, known as the myogenic response, is found in nearly all terminal vessels of the body. Two characteristics distinguish the myogenic response of the renal afferent arteriole from that of most other vascular beds: its ability to buffer large pressure perturbation (up to 80 mmHg), and its short response times (as low as 10 s).
Based on the observed kinetics and steady-state characteristics of afferent arteriole vasoresponse, Loutzenhiser et al. formulated models of the renal myogenic response [27, 28] that utilize pressure–radius relations. Effectively, at any t, a target vascular radius is determined by arterial pressure at an earlier time t − τm, where τm represents the response delay. Arteriolar radius rAA(t) follows by an exponential decay
| (9) |
The vasoresponse time courses have been reported to be asymmetric. Loutzenhiser et al. reported faster vasoconstriction activation times and kinetics in the hydronephrotic rat kidney [27]. In contrast, Just and Arendshorst observed stronger and faster dilator response than constrictor response [29] in rats. To represent the asymmetries of myogenic response, one may set τm and km in Eq. (9) to be pressure rate sensitive, i.e., different τm and km values can be specified for responses triggered by pressure increases and decreases. When a faster vasoconstrictive response is assumed [27, 28], models predict sustained vasoconstriction at sufficiently fast pressure fluctuations (see Fig. 5), owing to the cumulative effect of the faster contractile response. As a result, in these models, arteriolar radius is sensitive to peak rather than mean blood pressure.
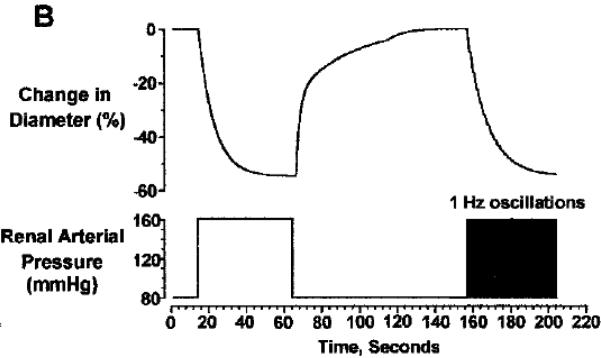
Figure 5.
Myogenic responses to a step pressure perturbation and to fast pressure oscillations. Afferent arteriole constricts at elevated arterial pressure. Due to the asymmetries in the activation times and rate constants induced by increasing/decreasing pressure, the afferent arteriole responds to rapid oscillations with sustained vasoconstriction with a radius that is determined by peak rather than mean pressure. Reproduced from [26].
The above models [27, 28] are formulated phenomenologically and do not represent intracellular dynamics. Gonzalez-Fernandez and Ermentrout developed a mathematical model of the myogenic mechanism of the cerebral arteriole that captures cellular processes [30]. That model represents muscle membrane potential, Ca2+ and K+ transmembrane fluxes, and cytosolic [Ca2+] handling. Below we summarize key model equations.
The rate of change of cytosolic [Ca2+], denoted Cai, depends on the influx from the extracellular space ICa and is given by
| (10) |
where α is a constant converting charge to mass flux; kCa is a first-order rate constant for cytosolic calcium extrusion; Kd is the ratio of the forward and backward reaction rates of the calcium-buffer system; and BT is the total buffer concentration. Calcium influx is provided by voltage gated membrane channels
| (11) |
where gCa is the maximum whole-cell membrane conductance for the calcium current, and m∞ is the equilibrium distribution of open calcium channel states which is a function of membrane potential (v)
| (12) |
where v1 is the voltage at which half of the channels are open, and v2 determines the spread of the distribution.
The opening of potassium channels induces a transmembrane K+ efflux. To represent the K+ flux, one may describe the rate of change of the fraction of K+ channel open states, denoted n, by first-order kinetics
| (13) |
where n∞ denotes the equilibrium distribution of open K+ channel states, given by
| (14) |
where v3 is a function of Cai, and v4 is a measure of the spread of the distributions of n∞.
The opening of the Ca2+ and K+ channels depends on the membrane potential v (Eqs. (12) and (14)). The rate of change of v is the sum of the transmembrane currents
| (15) |
where Cap denotes the capacitance of the cell membrane. The transmembrane leak, potassium, and calcium currents are denoted IL, IK, and ICa, respectively.
Cytosolic [Ca2+] determines the formation of crossbridges, which in turn determines the muscle tone. Muscle tone, together with luminal pressure, gives rise to hoop forces, the balance of which determines the luminal radius.
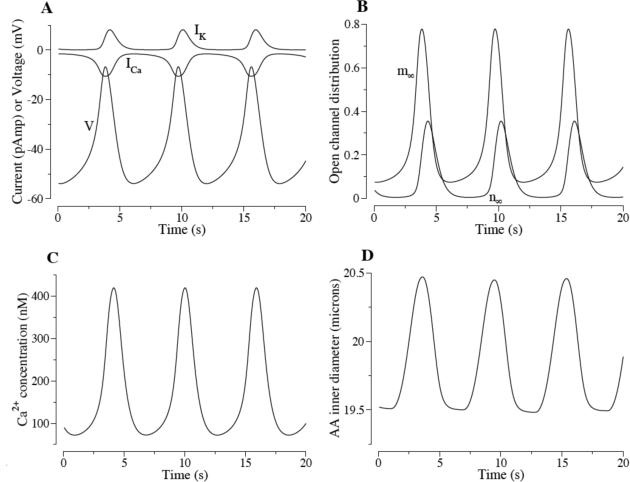
The model [30] predicts that the smooth muscle cell exhibits periodic oscillations in luminal radius even in the absence of external stimuli, i.e., spontaneous vasomotion. Those oscillations, shown in Fig. 6, are triggered by a limit cycle developed between membrane potential and ion channels. The inward-directed Ca2+ current depolarizes the cell, which results in an increase in v that triggers the opening of K+ channels. The subsequent outward-directed K+ current re-polarizes the cell, i.e., v decreases. The fluctuations in ICa drive cytosolic calcium, which in turn drives muscle tone.
Figure 6.
Afferent arteriole spontaneous vasomotion. A, oscillations in Ca2+ and K+ currents (denoted ICa and IK, respectively) and membrane potential v. B, oscillations in equilibrium distribution of open Ca2+ and K+ channel states (denoted m∞ and n∞, respectively). C and D, oscillations in intracellular free Ca2+ concentrations and arteriolar diameter. Reproduced from [31].
The model of Ref. [30] has been adapted to represent the renal myogenic mechanism by Marsh and co-workers [32, 10, 33, 34, 35] and by Layton and co-workers [31, 36, 12]. The latter of these models represents the afferent arteriole's myogenic response based on the hypothesis that changes in hydro-static pressure induce changes in the activity of non-selective cation channels [36, 12]. Such changes are modeled by a modification of Eq. (15)
| (16) |
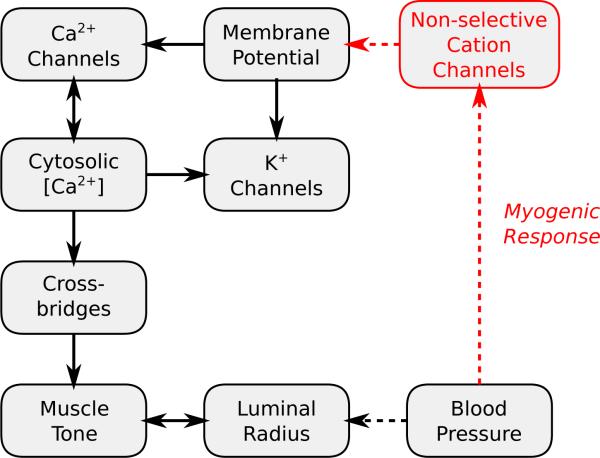
where Iions represents the currents induced by transmembrane ionic fluxes (e.g., potassium, calcium, leak currents), and IMR is the current mediating the myogenic response; e.g., IMR induces depolarization at elevated pressures and polarization at lower pressures. The resulting changes in membrane potential affect Ca2+ influx through the voltage-gated Ca2+ channels, thereby inducing appropriate myogenic vasoresponses. More specifically, vasoconstriction is initiated by membrane depolarization, which stimulates the opening of voltage-gated Ca2+ channels (Eq. (12)), leading to elevations in cytosolic [Ca2+], muscle tone, and vasoconstriction. Membrane polarization has the opposite effects and yields vasodilation. The events leading to myogenic vasoresponse are summarized in Fig. 7.
Figure 7.
A erent arteriole myogenic mechanism. Membrane depolarization leads to opening of Ca2+ channels and increase of cytosolic [Ca2+]. Increased [Ca2+] leads to crossbridge phosphorylation, increased muscle tone, and vasoconstriction. Membrane polarization, having the opposite effects, leads to vasodilation. The myogenic response (red arrows) senses blood pressure and adjusts membrane potential accordingly through the activity of non-selective cation channels.
The models in [30, 31] were originally developed for a single smooth muscle cell. To study renal autoregulation at the vascular level, one may develop a vessel model using an ensemble of single-cell models, as done by Sgouralis and Layton [36, 12] and by Marsh and co-workers [32, 10, 33, 34, 35]. Such an extension requires the representation of intercellular communication provided by gap-junctions [37]. For example, in [36, 12] gap-junctional coupling is provided directly through the muscle layer as well as indirectly through an endothelium layer; see Fig. 8. Let the cell models of the ensemble be indexed by i. The membrane potential of the i-th smooth muscle and the associated endothelium (denoted by subscripts ‘m’ and ‘e’, respectively) are given by
| (17) |
| (18) |
The four terms scaled by g's represent gap-junctional coupling, which allows for spreading of local (de)polarizations.
Figure 8.
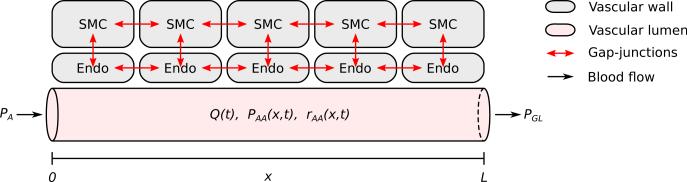
A erent arteriole segment model. Vascular wall consists of a linear ensemble of smooth muscle cells (SMC) augmented with an endothelial layer (Endo). Intercellular communication is mediated by three types of gap-junctional interfaces: SMC–SMC, SMC– Endo, Endo–Endo. In the diagram, afferent arteriole is shown with a reduced number of SMC. Figure modified from Ref. [36].
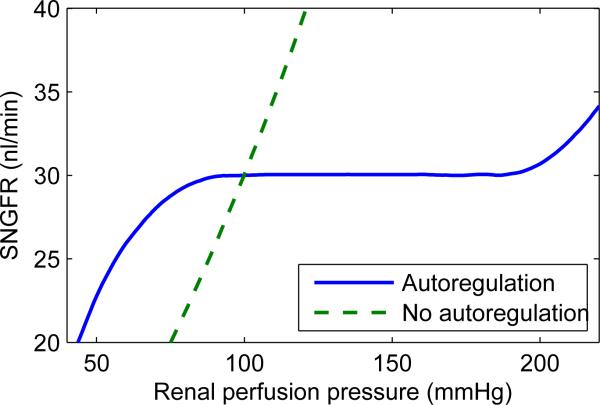
SNGFR is known to remain relatively stable over a wide range of arterial pressure values, e.g., Ref. [15]. The model in Ref. [12] was used to determine the extent to which the myogenic response alone can provide such stability. The model, which does not represent the tubuloglomerular feedback, predicts a hemodynamic “plateau” for arterial pressure ranging from 80 to 180 mmHg, within which glomerular blood pressure, blood flow, and SNGFR remain close to baseline values; see Fig. 9. For arterial pressures outside of that range, arteriolar diameter fails to adjust sufficiently. As a result, some of the pressure perturbation is transmitted downstream. Because the model afferent arteriole fails to adequately compensate, outflow delivery deviates noticeably from the baseline value. When the myogenic response is disabled, the model predicts a steady increase in vascular and tubular fluid pressure and flow as arterial pressure is increased.
Figure 9.
Autoregulatory plateau. Autoregulatory mechanisms maintain a stable SNGFR for perfusion pressure between ~90–180 mmHg (blue solid curve). In the absence of autoregulation, SNGFR increases along with perfusion pressure (green dashed curve). Figure modified from Ref. [12].
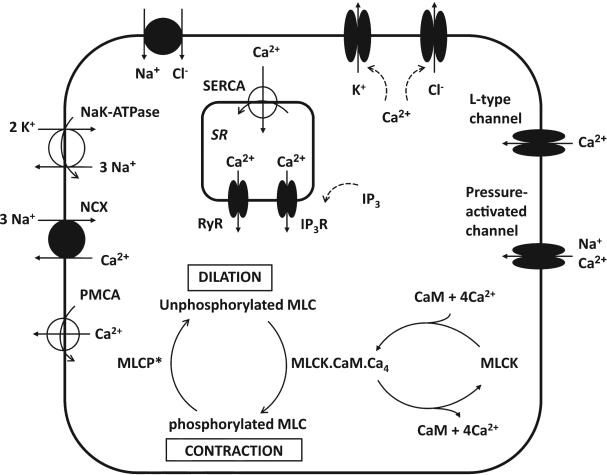
Recently, Edwards and Layton developed a highly detailed model of the intracellular Ca2+ signaling of the afferent arteriole smooth muscle cells to study the mechanisms underlying the myogenic response [38]. In addition to detailed transmembrane ionic transport, the model also represents intra-cellular Ca2+ dynamics, including Ca2+ trafficking between the cytosol and the sarcoplasmic reticulum, which involves the release of Ca2+ by ryanodine receptors (RyR) and the inositol triphosphate receptors (IP3R). Figure 10 summarizes the channels and currents represented in the model. A large number of model equations are used to represent these processes; interested readers are referred to Ref. [38]. The model represents the kinetics of myosin light chain (MLC) phosphorylation and the mechanical behavior of the cell. The contractile force (myogenic tone) depends on the fraction of MLC that are phosphorylated. An increase in luminal pressure generates an influx of cations in to the cytosol via pressure-induced changes in channel opening probability. The subsequent increase in cytosolic Ca2+ levels enhances the formation of the MLCK.CaM.Ca4 complex, i.e., the active form of myosin light chain kinase. As a result, the contractile force increases, leading to vasoconstriction.
Figure 10.
Detailed model of afferent arteriole intracellular dynamics [38]. The model distinguishes the sarcoplasmic reticulum Ca2+ store from the cytosolic Ca2+, and tracks the trafficking of Ca2+ between the two compartments. MLCP, myosin light chain phosphatase; CaM, calmodulin; PMCA, plasma membrane Ca2+ pump; NCX, Na+/Ca2+ exchanger, SERCA, sarco/endoplasmic Ca2+ pump; RyR, ryanodine receptor; IP3R, inositol triphosphate receptor. Figure adopted from Ref. [38].
The model in Ref. [38] reveals new details that explain the emergence of spontaneous vasomotion. Model results suggest that the time-periodic oscillations stem from the dynamic exchange of Ca2+ between the cytosol and the sarcoplasmic reticulum, coupled to the stimulation of Ca2+-activated potassium and chloride channels, and the modulation of voltage-activated L-type channels. Blocking sarco/endoplasmic reticulum Ca2+ pumps, RyR, Ca2+-activated potassium and chloride channels, or L-type channels abolishes these oscillations. These details were not seen in less comprehensive models, e.g., [30, 31].
5. Tubuloglomerular feedback
Tubuloglomerular feedback (TGF) is a negative feedback system, specific to the kidney, in which SNGFR is adjusted according to the chloride concentration of the fluid reaching the distal nephron [15]. Distal chloride concentration is sensed by a specialized cluster of cells, known as the macula densa, that are located in the tubular wall in the region where it comes in contact with the terminal part of the afferent arteriole that feeds the stemming glomerulus. Anatomically, the macula densa marks the end of the loop of Henle and the beginning of the distal tubule.
An important tubular segment for TGF function is the thick ascending limb of the loop of Henle. The epithelial cells of the thick ascending limb vigorously pump NaCl from the tubular fluid into the surrounding interstitium by means of active transport. Because the thick ascending limb walls are water impermeable, water does not follow. As a result, the active reabsorption of NaCl dilutes the tubular fluid.
If SNGFR increases above its normal, baseline rate, then tubular fluid flow in the thick ascending limb increases. The resulting shorter transit time of a given fluid packet along the thick ascending limb implies that a smaller fraction of filtered NaCl is reabsorbed. As a result, the chloride concentration in the tubular fluid alongside the macula densa is increased above its target value. This concentration increase, through a sequence of signaling events, results in a constriction of the afferent arteriole and a corresponding reduction in glomerular blood pressure and thus a reduction in SNGFR. Conversely, if SNGFR decreases below its base-line rate, the chloride concentration in tubular fluid alongside the macula densa is decreased below its target value, and TGF acts to increase SNGFR by signaling the afferent arteriole to relax. The resulting higher flow rate reduces transit time along the thick ascending limb and raises tubular fluid chloride concentration.
Some of the earliest dynamical models of TGF were developed by Holstein-Rathlou and co-workers [11, 39, 40, 41]. A common feature of these models is the representation of the afferent arteriole by a damped linear oscillator upon which TGF acts as external forcing. For example, in Ref. [11] afferent arteriole resistance RAA is given by
| (19) |
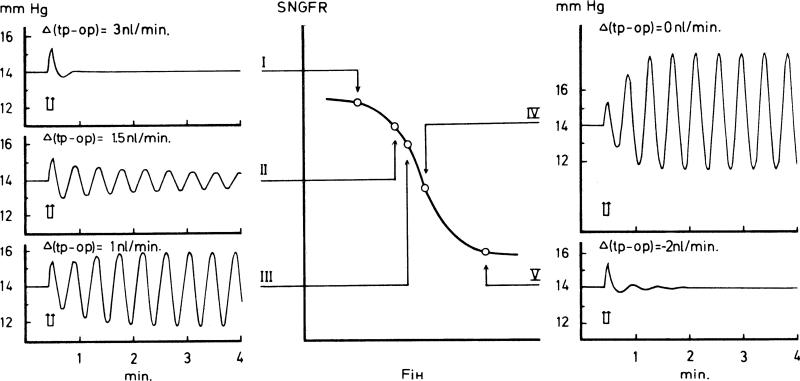
where ωn denotes the natural frequency of the oscillator and ξ the damping coefficient. For all time, RAA is used to evaluate blood flow and glomerular capillary pressure. SNGFR is obtained by imposing conservation of plasma across the glomerulus as in Eq. (3). SNGFR then passes to a tubular component which accounts for a simplified representation of water transport along the proximal tubule and loop of Henle. TGF is represented by the forcing term Φ(FiH) in Eq. (19), which has a sigmoidal dependence on Henle's loop flow, FiH. For physiologically relevant parameter values, this model predicts one equilibrium point (SNGFR* , RAA* , FiH*), the stability of which depends on its position on the Φ(FiH) curve. Specifically, equilibria falling on the flat parts of Φ(FiH) are stable (Fig. 11), and therefore a transient perturbation of the TGF system results in a steady state. In contrast, equilibria falling on the steep part of Φ(FiH) are unstable, therefore a transient perturbation results in sustained oscillations.
Figure 11.
TGF-mediated oscillations. Driven by the forcing term Φ(FiH), afferent arteriole resistance develops a sigmoidal dependence upon Henle's loop flow FiH. Such sigmoidal dependence is transmitted to SNGFR. For a given set of parameter values, one equilibrium point is predicted. The stability of the equilibrium depends on its location on the response curve: flat parts stable (I and V), steep part unstable (cases II–IV). Reprinted from Ref. [11].
The model in [11] contains a simplified representation of nephron tubular flow. Motivated by the observation that tubular fluid [Cl−], the key signal for TGF, changes most substantially along the thick ascending limb of the loop of Henle, Layton and co-workers developed a family of TGF models that represent tubular transport in more detail [42, 43, 44, 45, 46, 47, 48, 49]. This class of models explicitly represent tubular fluid and solute reasborption along the thick ascending limb; more recently these models have been extended to include the representation of the descending limb and proximal tubule [50, 51, 52]. Conservation of Cl− along the thick ascending limb is given by
| (20) |
where CT is tubular fluid [Cl−], Cext is interstitial fluid [Cl−], QT is volume flow, rT is tubular radius, and rss is the steady-state tubular radius. Chlo-ride transport involves active transport, characterized by Michaelis-Menten kinetics with parameters Vmax and KM, and passive diffusion, characterized by chloride permeability κ. Because the thick ascending limb is water impermeable, fluid flow QT (t) varies in time but not in space. TGF activation is provided by [Cl−] at the site of macula densa, CT (LT , t), where LT denotes the length of the thick ascending limb. Specifically, TGF is incorporated by assuming a sigmoidal relationship between QT (t) and CT (LT , t) of the form
| (21) |
The TGF delay τ represents the response time of the afferent arteriole; Cop denotes the macula densa [Cl−] at the operating point; K1 and K2 determine the maximum range of flow that is affected by TGF and the feedback loop gain γ. The feedback loop gain γ is a measure of the response strength: for a given macula densa [Cl−] deviation, low/higher γ values lead to weak/strong SNGFR adjustment.
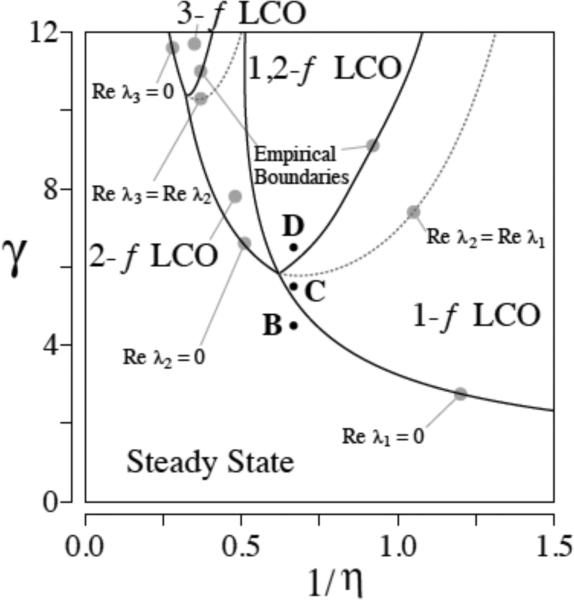
Stability of the model TGF system depends on a number of parameters, including feedback gain γ, feedback delay τ, and the thick ascending limb cross-sectional area (which impacts tubular transit time) denoted η. Figure 12 shows a bifurcation diagram, obtained via numerical solution of the model equations (20)–(21), which indicates the stability of the TGF system in the γ –1/ plane. For sufficiently small feedback gain γ and sufficiently long transit time (equivalently small 1/η ), the system is in a stable equilibrium. Thus, for any initial conditions, or for any transient perturbation of a steady-state solution, the model solutions closely approximate the time-independent steady-state. See Fig. 13, panels B1 and B2.
Figure 12.
TGF bifurcation analysis. Diagram indicates parameter regions that correspond to qualitatively different model solutions: (1) a region having one stable, time-independent steady-state solution (“Steady State”); (2) a region having one stable oscillatory solution only, with fundamental frequency f (“1-f LCO”); (3) a region having one stable oscillatory solution only, with fundamental frequency ~ 2f (“2-f LCO”); (4) a region having two possible stable oscillatory solutions, of frequencies ~ f and ~ 2f (“1,2-f LCO”). The λ's correspond to eigenvalues of the characteristic equation derived from a linear stability analysis of the model equation; that analysis is not discussed. Reprinted from Ref. [53].
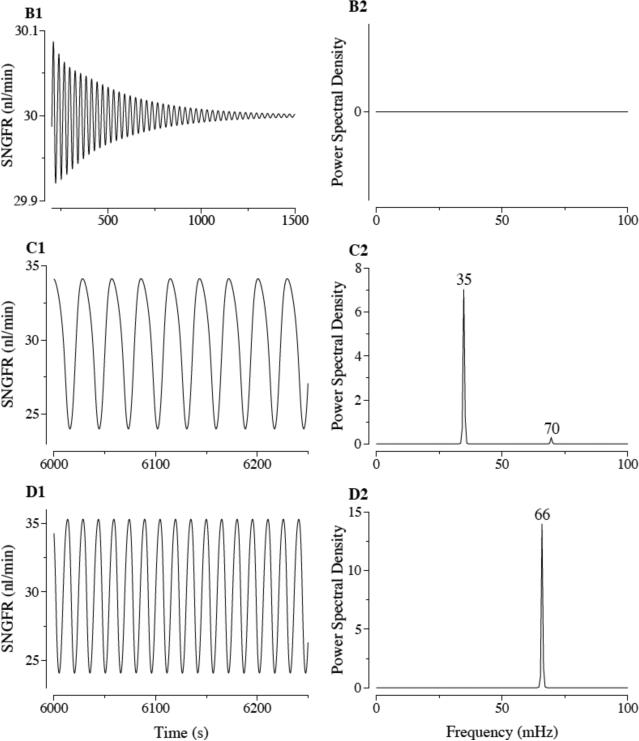
Figure 13.
Observed behavior of stable solutions corresponding to the bifurcation diagram in Fig. 12. Response to perturbation (B1) and power spectrum (B2) for stable solution (a time-independent steady state) corresponding to point B in Fig. 12. Stable single-frequency oscillation (C1) and corresponding power spectrum (C2) for point C in Fig. 12. Stable double-frequency oscillation and corresponding power spectrum (D2) for point D in Fig. 12. Reprinted from Ref. [53].
In the region marked “1-f LCO,” which corresponds to larger values of γ and 1/η , the only stable solution is a regular oscillation that converge to a limit cycle with a frequency f. The limit-cycle solution for SNGFR, obtained using parameters at the point labeled “C,” and the corresponding power spectrum, are shown in Fig. 13, panels C1 and C2. In the parameter region marked “2-f LCO,” the solutions are stable limit-cycle oscillations that have a frequency approximately twice that of the 1-f LCO. Simulations also revealed a region where LCO with frequency f and ~ 2f are potentially both stable; this region is marked “1,2-f LCO.” Simulated oscillations in SNGFR, obtained using parameters corresponding to point D, and the resulting power spectrum are shown in Fig. 13, panels D1 and D2.
The model described above, (20) and (21), assumes that the renal tubule is rigid. If the tubular walls were compliant, increases in fluid pressure would expand the tubule, thereby slowing the flow and increasing transit time. Thus, tubular wall compliance is expected to have a significant impact on the response time and dynamic behaviors of TGF. TGF models that represent compliant tubular walls have been developed [49, 54]. Model results suggest that tubular compliance reduces the stability of the TGF system.
Coupled nephrons
As previously noted, the mammalian kidney contains a large number of nephrons. These nephrons do not act autonomously. Electrotonic conduction and hemodynamics along the pre-glomerular vasculature provide coupling of the TGF systems of nearby nephrons [15, 17]. A system of coupled oscillators can yield complex dynamic behaviors, including synchronization and a heightened tendency to oscillate. TGF models previously discussed have been extended to networks of two or more nephrons, e.g., Refs. [54, 55, 47, 33, 34, 35].
A model of coupled TGF nephrons (Fig. 14) can be constructed by extending the model described by Eqs. (20)–(21). Consider N coupled nephrons (indexed by i = 1, . . . , N). Conservation of Cl− for the i-th nephron, analogous to Eq. (20), is given by
| (22) |
where we allow for different parameters among the nephrons. Coupling is represented by the flow Q̃T i(t), which incorporates inputs from nearby nephrons
| (23) |
| (24) |
Equation (23) expresses Q̃T i(t) as the sum of a nephron's own TGF mediated response QT i(t), given by Eq. (24) that is similar to the single nephron case (e.g., Eq. (21)), and a coupling term incorporating contributions from the nearby nephrons’ TGF responses. Each summand in the coupling term is a weighted difference between the nearby nephron's TGF response QT j(t) and the time-independent steady-state flow Q0. The coupling coefficient ϕij is a non-negative constant in [0, 1] that scales the influence of the j-th nephron on the i-th nephron.
Figure 14.
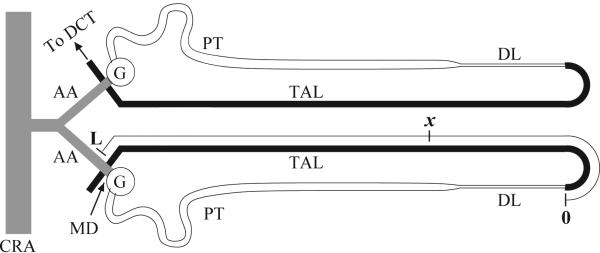
Schematic diagram of two coupled nephrons, shown with the corresponding afferent arterioles, along which tubuloglomerular signals initiated in one of the nephrons is transmitted to the other. Reprinted from Ref. [54].
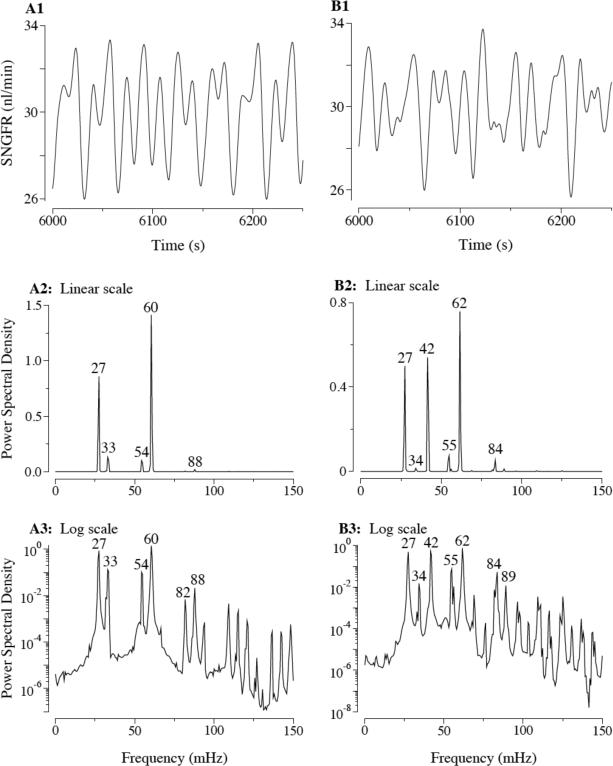
TGF mediated oscillations of tubular fluid pressure and flow in spontaneously hypertensive rats can exhibit highly irregular oscillations similar to deterministic chaos [56, 57]. Layton et al. used a model of coupled nephrons to investigate potential sources of those irregular oscillations and the associated complex power spectra. Their results suggest that spectral complexity may be explained by the inherent complexity of TGF dynamics, which may include bifurcation, modest time-variation in TGF parameters, and coupling between small numbers of neighboring nephrons. Figure 15, panels A1–A3, shows oscillations in SNGFR for two coupled model nephrons having different parameters and distinct fundamental frequencies. Figure 15, panels B1–B3, shows oscillations for three coupled nephrons, also having distinct fundamental frequencies. Both configurations yield irregular oscillations in SNGFR and complexities in the corresponding power spectra, a result that suggests that the irregular oscillations observed in spontaneously hypertensive rats may be explained, in part, by internephron coupling.
Figure 15.
Oscillations in SNGFR for two (A1) coupled nephrons and corresponding power spectra with linear (A2) and logarithmic (A3) ordinates. Oscillations in SNGFR for three (B1) coupled nephrons and corresponding power spectra with linear (B2) and logarithmic (B3) ordinates. Reprinted from Ref. [53].
Marsh et al. constructed a vascular tree consisting of 22 nephrons supplied with blood from a common cortical radial artery [58]. The model nephrons interact via hemodynamic and electrical coupling, both of which are mediated by vascular connections. For parameters that generate simple limit cycle dynamics in the pressure and flow regulation of single nephrons, the ensemble of coupled nephrons show stationary, quasiperiodic, or chaotic dynamics, depending on the coupling strengths and the arterial blood pressure. For oscillatory solutions, the nephrons may synchronize to form clusters, with each cluster characterized by a distinct frequency.
6. Applications to health and disease
Mathematical models of renal hemodynamics have been used to investigate aspects of kidney functions, both in physiology and pathophysiology. Below we highlight some examples.
The renal autoregulatory mechanisms are believed to simultaneously insulate kidney function from variations in blood pressure and to protect the glomerular structure, which is a high-pressure capillary bed prone to physical injury. Models of renal afferent arteriole myogenic response [27, 31] have revealed the mechanisms by which autoregulation preserve the glomerular structure. Strong correlations have been identified between transmission of high systolic pressure to the glomerulus and renal injury [59]. Loutzenhiser et al. [27] suggested that, owing to the asymmetry in vasoconstriction/vasodilation myogenic response times and activations delays, the afferent arteriole may sense systolic pressure at heart-beat frequency and respond with a sustained vasoconstriction when systolic pressure is elevated. Model simulations have confirmed that hypothesis [27, 31]. This protective function of autoregulation differs from its other function, which is to regulate SNGFR that is determined primarily by mean arterial pressure, and not peak pressure. Under physiologic conditions, where mean and systolic blood pressures vary in tandem, a myogenic response determined by systolic pressure would also regulate renal blood flow and glomerular filtration rate.
However, under pathophysiologic conditions, where changes in systolic and mean blood pressures are decoupled, an elevation in systolic pressure could result in a myogenic vasoconstriction, even if mean perfusion pressure is unchanged or decreased (which is possible with a sufficient reduction in diastolic pressure). One implication is that pathophysiological processes that may alter the kinetics of the myogenic response, even in the absence of a significant impairment of steady-state autoregulatory responses, could result in an increased transmission of the systolic pressure transients to the glomerular capillaries and enhanced susceptibility to hypertension-induced renal damage. The validity of this hypothesis can be assessed using a model of the afferent arteriole that represents the kinetics of the myogenic response in sufficient details.
Together, the myogenic response and TGF maintain a generally stable SNGFR and protect the glomerular capillaries from excessive intravascular pressure and shear stress. To assess the individual contributions of the two mechanisms to SNGFR regulation, Sgouralis and Layton developed an integrated model of renal autoregulation [13] that represents both autoregulatory mechanisms, which, as previously noted, share a common effector in the afferent arteriole. The integrated model combines an afferent arteriole, a glomerulus, and a renal tubule; a schematic diagram is shown in Fig. 16. The model afferent arteriole consists of a linear ensemble of smooth muscle cells that react to stimulation by the myogenic response and TGF. The two mechanisms are modeled by applying to the smooth muscles transmembrane currents and that depend on local blood pressure and macula densa chloride concentration, respectively
| (25) |
TGF is believed to be mediated predominantly via adenosine and A1-adenosine receptors, which induce the release of Ca2+ primarily from the sarcoplasmic reticulum [60]. The representation of the TGF signal as a current across the cell membrane is an approximation that increases intracellular [Ca2+] without requiring an explicit representation of the sarcoplasmic reticulum. The model predicts that a stable SNGFR is maintained within a physiological range of perfusion pressure (80–180 mmHg). The contribution of TGF to overall autoregulation is significant only within a narrow band of arterial pressure values (80–110 mmHg).
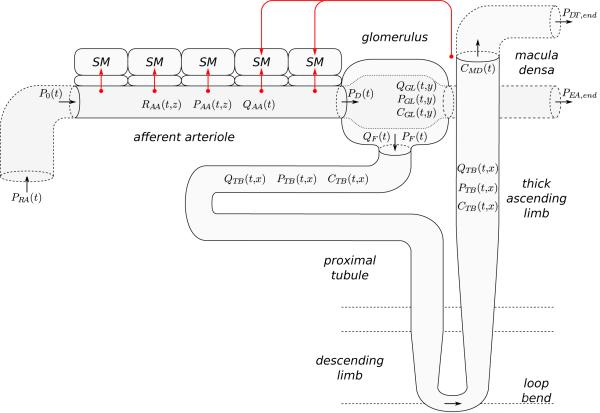
Figure 16.
Integrated model of renal autoregulation. Model consists of a vascular (afferent arteriole), a filtering (glomerulus), and a tubular component (proximal tubule, descending limb, thick ascending limb). Afferent arteriole is shown with a reduced number of smooth muscles (SM). Red arrows indicate sensor and effector sites of the autoregulatory mechanisms. Figure adopted from Ref. [13].
Simulations have been conducted to assess the extent to which structural changes and functional impairment observed in diabetic rats cause glomerular hyperfiltration. The model in Ref. [13] was adjusted to simulate: (i) functional impairment in afferent arteriole voltage-gated Ca2+ channels, Eq. (12), which diminishes the vasoconstrictive response, (ii) proximal tubule hyper-trophy [61], (iii) TGF resetting [62, 63], i.e., changes in the macula densa operating point, Cop in Eq. (21), and (iv) increase in the ultrafiltration coefficient Kf, Eq. (4). With these modifications, the model predicts hyperfiltration in diabetes, with a SNGFR that is ~60% above baseline value. Each of these changes tends to elevate SNGFR, and from a clinical perspective, it is important to understand the relative contribution of each change. Model simulations suggest that functional impairment in the afferent arteriolar constrictive response is the most important contributing factor.
Most of the autoregulation models discussed above are single-nephron models. As previously noted, the nephrons do not function autonomously. Thus, a complete understanding of kidney function in health and disease may be better gleaned from autoregulation models that represent the heterogeneity among nephrons, as well as their interactions. Given that there are 30,000–40,000 nephrons in a rat kidneys, and ~1 million in a human kidney, how to accurately model a whole kidney while avoiding a prohibitive computational cost is a challenge, albeit a highly worthwhile one.
Highlights.
Hemodynamic control is essential to the maintenance of proper kidney functions.
We describe mathematical models developed to study renal autoregulation.
Models have been applied to understand kidney functions in health and disease.
Acknowledgments
This research was supported in part by the National Institutes of Health: National Institute of Diabetes and Digestive and Kidney Diseases, grant R01DK089066 to Layton. Part of the work was conducted while Sgouralis was a Postdoctoral Fellow at the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation through NSF Award #DBI-1300426, with additional support from The University of Tennessee, Knoxville.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Botti R, Razzak M, MacIntyre W, Pritchard W. The relationship of renal blood flow to cardiac output in normal individuals as determined by concomitant radioisotopic measurements. Cardiovas Res. 1968;2:243–246. doi: 10.1093/cvr/2.3.243. [DOI] [PubMed] [Google Scholar]
- 2.Nordsletten DA, Blackett S, Bentley MD, Ritman EL, Smith NP. Structural morphology of renal vasculature. Am J Physiol Heart Circ Physiol. 2006;291(1):H296–309. doi: 10.1152/ajpheart.00814.2005. [DOI] [PubMed] [Google Scholar]
- 3.Casellas D, Dupont M, Bouriquet N, Moore LC, Artuso A, Mimran A. Anatomic pairing of afferent arterioles and renin cell distribution in rat kidneys. Am J Physiol. 1994;267(6 Pt 2):F931–6. doi: 10.1152/ajprenal.1994.267.6.F931. [DOI] [PubMed] [Google Scholar]
- 4.Kriz W, Bankir L. A standard nomenclature for structures of the kidney. the renal commission of the international union of physiological sciences (iups) Kidney Int. 1988;33(1):1–7. doi: 10.1038/ki.1988.1. [DOI] [PubMed] [Google Scholar]
- 5.Huss RE, Marsh DJ, Kalaba RE. Two models of glomerular filtration rate and renal blood flow in the rat. Ann Biomed Eng. 1975;3(1):72–99. doi: 10.1007/BF02584490. [DOI] [PubMed] [Google Scholar]
- 6.Starling E. The glomerular functions of the kidney. J Physiol. 1899;24:317–330. doi: 10.1113/jphysiol.1899.sp000760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brenner BM, Troy JL, Daugharty TM. The dynamics of glomerular ultrafiltration in the rat. J Clin Invest. 1971;50(8):1776–80. doi: 10.1172/JCI106667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Deen WM, Robertson CR, Brenner BM. A model of glomerular ultrafiltration in the rat. Am J Physiol. 1972;223(5):1178–83. doi: 10.1152/ajplegacy.1972.223.5.1178. [DOI] [PubMed] [Google Scholar]
- 9.Chang R, Robertson C, Deen W, Brenner B. Permselectivity of the glomerular capillary wall to macromolecules. I. Theoretical considerations. Biophys J. 1975:861–886. doi: 10.1016/S0006-3495(75)85862-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Marsh DJ, Sosnovtseva OV, Chon KH, Holstein-Rathlou N-H. Nonlinear interactions in renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol. 2005;288(5):R1143–59. doi: 10.1152/ajpregu.00539.2004. [DOI] [PubMed] [Google Scholar]
- 11.Holstein-Rathlou NH, Leyssac PP. Oscillations in the proximal intratubular pressure: a mathematical model. Am J Physiol. 1987;252(3 Pt 2):F560–72. doi: 10.1152/ajprenal.1987.252.3.F560. [DOI] [PubMed] [Google Scholar]
- 12.Sgouralis I, Layton AT. Control and modulation of fluid flow in the rat kidney. Bull Math Biol. 2013;75(12):2551–74. doi: 10.1007/s11538-013-9907-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sgouralis I, Layton AT. Theoretical assessment of renal autoregula-tory mechanisms. Am J Physiol Renal Physiol. doi: 10.1152/ajprenal.00649.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Milnor WR. Hemodynamics. 2nd Edition Williams & Wilkins; Baltimore: 1989. [Google Scholar]
- 15.Holstein-Rathlou NH, Marsh DJ. Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol Rev. 1994;74(3):637–81. doi: 10.1152/physrev.1994.74.3.637. [DOI] [PubMed] [Google Scholar]
- 16.Just A. Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am J Physiol Regul Integr Comp Physiol. 2007;292(1):R1–17. doi: 10.1152/ajpregu.00332.2006. [DOI] [PubMed] [Google Scholar]
- 17.Cupples WA, Braam B. Assessment of renal autoregulation. Am J Physiol Renal Physiol. 2007;292(4):F1105–23. doi: 10.1152/ajprenal.00194.2006. [DOI] [PubMed] [Google Scholar]
- 18.Casellas D, Carmines PK. Control of the renal microcirculation: cellular and integrative perspectives. Curr Opin Nephrol Hypertens. 1996;5(1):57–63. doi: 10.1097/00041552-199601000-00011. [DOI] [PubMed] [Google Scholar]
- 19.Lush DJ, Fray JC. Steady-state autoregulation of renal blood flow: a myogenic model. Am J Physiol. 1984;247(1 Pt 2):R89–99. doi: 10.1152/ajpregu.1984.247.1.R89. [DOI] [PubMed] [Google Scholar]
- 20.Moore LC, Rich A, Casellas D. Ascending myogenic autoregulation: interactions between tubuloglomerular feedback and myogenic mechanisms. Bull Math Biol. 1994;56(3):391–410.. doi: 10.1007/BF02460464. [DOI] [PubMed] [Google Scholar]
- 21.Feldberg R, Colding-Jørgensen M, Holstein-Rathlou NH. Analysis of interaction between tgf and the myogenic response in renal blood flow autoregulation. Am J Physiol. 1995;269(4 Pt 2):F581–93. doi: 10.1152/ajprenal.1995.269.4.F581. [DOI] [PubMed] [Google Scholar]
- 22.Cupples WA, Wexler AS, Marsh DJ. Model of tgf-proximal tubule interactions in renal autoregulation. Am J Physiol. 1990;259(4 Pt 2):F715–26.. doi: 10.1152/ajprenal.1990.259.4.F715. [DOI] [PubMed] [Google Scholar]
- 23.Aukland K, Oien AH. Renal autoregulation: models combining tubuloglomerular feedback and myogenic response. Am J Physiol. 1987;252(4 Pt 2):F768–83.. doi: 10.1152/ajprenal.1987.252.4.F768. [DOI] [PubMed] [Google Scholar]
- 24.Oien AH, Aukland K. A multinephron model of renal blood flow autoregulation by tubuloglomerular feedback and myogenic response. Acta Physiol Scand. 1991;143(1):71–92. doi: 10.1111/j.1748-1716.1991.tb09203.x. [DOI] [PubMed] [Google Scholar]
- 25.Jensen PK, Christensen O, Steven K. A mathematical model of fluid transport in the kidney. Acta Physiol Scand. 1981;112(4):373–85. doi: 10.1111/j.1748-1716.1981.tb06833.x. [DOI] [PubMed] [Google Scholar]
- 26.Loutzenhiser R, Griffin K, Williamson G, Bidani A. Renal autoregulation: new perspectives regarding the protective and regulatory roles of the underlying mechanisms. Am J Physiol Regul Integr Comp Physiol. 2006;290(5):R1153–67. doi: 10.1152/ajpregu.00402.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Loutzenhiser R, Bidani A, Chilton L. Renal myogenic response: kinetic attributes and physiological role. Circ Res. 2002;90(12):1316–24. doi: 10.1161/01.res.0000024262.11534.18. [DOI] [PubMed] [Google Scholar]
- 28.Williamson GA, Loutzenhiser R, Wang X, Griffin K, Bidani AK. Systolic and mean blood pressures and afferent arteriolar myogenic response dynamics: a modeling approach. Am J Physiol Regul Integr Comp Physiol. 2008;295(5):R1502–11. doi: 10.1152/ajpregu.00490.2007. [DOI] [PubMed] [Google Scholar]
- 29.Just A, Arendhorst W. Nitric oxide blunts myogenic autoregulation in rat renal but not skeletal muscle circulation via tubuloglomerular feedback. J Physiol. 2005;569:959–974. doi: 10.1113/jphysiol.2005.094888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gonzalez-Fernandez JM, Ermentrout B. On the origin and dynamics of the vasomotion of small arteries. Math Biosci. 1994;119(2):127–67. doi: 10.1016/0025-5564(94)90074-4. [DOI] [PubMed] [Google Scholar]
- 31.Chen J, Sgouralis I, Moore LC, Layton HE, Layton AT. A mathematical model of the myogenic response to systolic pressure in the afferent arteriole. Am J Physiol Renal Physiol. 2011;300(3):F669–81. doi: 10.1152/ajprenal.00382.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Marsh DJ, Sosnovtseva OV, Pavlov AN, Yip K-P, Holstein-Rathlou N-H. Frequency encoding in renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol. 2005;288(5):R1160–7.. doi: 10.1152/ajpregu.00540.2004. [DOI] [PubMed] [Google Scholar]
- 33.Marsh DJ, Toma I, Sosnovtseva OV, Peti-Peterdi J, Holstein-Rathlou N-H. Electrotonic vascular signal conduction and nephron synchronization. Am J Physiol Renal Physiol. 2009;296(4):F751–61.. doi: 10.1152/ajprenal.90669.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Laugesen JL, Sosnovtseva OV, Mosekilde E, Holstein-Rathlou N-H, Marsh DJ. Coupling-induced complexity in nephron models of renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol. 2010;298(4):R997–R1006. doi: 10.1152/ajpregu.00714.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marsh DJ, Wexler AS, Brazhe A, Postnov DE, Sosnovtseva OV, Holstein-Rathlou N-H. Multinephron dynamics on the renal vascular network. Am J Physiol Renal Physiol. 2013;304(1):F88–F102. doi: 10.1152/ajprenal.00237.2012. [DOI] [PubMed] [Google Scholar]
- 36.Sgouralis I, Layton AT. Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am J Physiol Renal Physiol. 2012;303(2):F229–39.. doi: 10.1152/ajprenal.00589.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Brink PR. Gap junctions in vascular smooth muscle. Acta Physiol Scand. 1998;164(4):349–56. doi: 10.1046/j.1365-201X.1998.00439.x. [DOI] [PubMed] [Google Scholar]
- 38.Edwards A, Layton AT. Calcium dynamics underlying the myogenic response of the renal afferent arteriole. Am J Physiol Renal Physiol. 2014;306(1):F34–48. doi: 10.1152/ajprenal.00317.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Holstein-Rathlou NH, Wagner AJ, Marsh DJ. Tubuloglomerular feedback dynamics and renal blood flow autoregulation in rats. Am J Physiol. 1991;260(1 Pt 2):F53–68. doi: 10.1152/ajprenal.1991.260.1.F53. [DOI] [PubMed] [Google Scholar]
- 40.Barfred M, Mosekilde E, Holstein-Rathlou N-H. Bifurcation analysis of nephron pressure and flow regulation. Chaos. 1996;6(3):280–287. doi: 10.1063/1.166175. [DOI] [PubMed] [Google Scholar]
- 41.Holstein-Rathlou NH, Marsh DJ. A dynamic model of the tubuloglomerular feedback mechanism. Am J Physiol. 1990;258(5 Pt 2):F1448–59. doi: 10.1152/ajprenal.1990.258.5.F1448. [DOI] [PubMed] [Google Scholar]
- 42.Layton HE, Pitman EB, Moore LC. Bifurcation analysis of tgf-mediated oscillations in sngfr. Am J Physiol. 1991;261(5 Pt 2):F904–19.. doi: 10.1152/ajprenal.1991.261.5.F904. [DOI] [PubMed] [Google Scholar]
- 43.Layton HE, Pitman EB, Moore LC. Nonlinear filter properties of the thick ascending limb. Am J Physiol. 1997;273(4 Pt 2):F625–34. doi: 10.1152/ajprenal.1997.273.4.F625. [DOI] [PubMed] [Google Scholar]
- 44.Layton HE, Pitman EB, Moore LC. Spectral properties of the tubuloglomerular feedback system. Am J Physiol. 1997;273(4 Pt 2):F635–49.. doi: 10.1152/ajprenal.1997.273.4.F635. [DOI] [PubMed] [Google Scholar]
- 45.Layton HE, Pitman EB, Moore LC. Limit-cycle oscillations and tubuloglomerular feedback regulation of distal sodium delivery. Am J Physiol Renal Physiol. 2000;278(2):F287–301. doi: 10.1152/ajprenal.2000.278.2.F287. [DOI] [PubMed] [Google Scholar]
- 46.Layton HE, Pitman EB, Moore LC. Instantaneous and steady-state gains in the tubuloglomerular feedback system. Am J Physiol. 1995;268(1 Pt 2):F163–74.. doi: 10.1152/ajprenal.1995.268.1.F163. [DOI] [PubMed] [Google Scholar]
- 47.Bayram S, Stepien TL, Pitman EB. Tgf-mediated dynamics in a system of many coupled nephrons. Bull Math Biol. 2009;71(6):1482–506. doi: 10.1007/s11538-009-9410-1. [DOI] [PubMed] [Google Scholar]
- 48.Layton AT, Moore LC, Layton HE. Signal transduction in a compliant thick ascending limb. Am J Physiol Renal Physiol. 2012;302(9):F1188–202. doi: 10.1152/ajprenal.00732.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Layton A. Feedback-mediated dynamics in a model of a compliant thick ascending limb. Math Biosci. 2010;228:185–194. doi: 10.1016/j.mbs.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Layton AT, Pham P, Ryu H-Y. Signal transduction in a compliant short loop of henle. Int j numer method biomed eng. 2012;28(3):369–383.. doi: 10.1002/cnm.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ryu H, Layton AT. Tubular fluid flow and distal nacl delivery mediated by tubuloglomerular feedback in the rat kidney. J Math Biol. 2014;68(4):1023–49.. doi: 10.1007/s00285-013-0667-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ryu H, Layton AT. Effect of tubular inhomogeneities on feedback-mediated dynamics of a model of a thick ascending limb. Math Med Biol. 2013;30(3):191–212. doi: 10.1093/imammb/dqs020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Layton AT, Moore LC, Layton HE. Multistability in tubuloglomerular feedback and spectral complexity in spontaneously hyper-tensive rats. Am J Physiol Renal Physiol. 2006;291(1):F79–97. doi: 10.1152/ajprenal.00048.2005. [DOI] [PubMed] [Google Scholar]
- 54.Layton AT, Bowen M, Wen A, Layton HE. Feedback-mediated dynamics in a model of coupled nephrons with compliant thick ascending limbs. Math Biosci. 2011;230(2):115–27. doi: 10.1016/j.mbs.2011.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Layton AT, Moore LC, Layton HE. Multistable dynamics mediated by tubuloglomerular feedback in a model of coupled nephrons. Bull Math Biol. 2009;71(3):515–55. doi: 10.1007/s11538-008-9370-x. [DOI] [PubMed] [Google Scholar]
- 56.Holstein-Rathlou N, Leyssac P. TGF-mediated oscillations in the proximal intratubular pressure: Differences between spontaneously hypertensive rats and Wistar-Kyoto rats. Acta Physiol Scand. 1986;126:333–339. doi: 10.1111/j.1748-1716.1986.tb07824.x. [DOI] [PubMed] [Google Scholar]
- 57.Yip K, Holstein-Rathlou N, Marsh D. Chaos in blood flow control in genetic and renovascular hypertensive rats. Am J Physiol (Renal Fluid Electrolyte Physiol 30) 1991;261:F400–F408. doi: 10.1152/ajprenal.1991.261.3.F400. [DOI] [PubMed] [Google Scholar]
- 58.Marsh D, Sosnovtseva O, Mosekilde E, Rathlou NH. Vascular coupling induces synchronization, quasiperiodicity, and chaos in a nephron tree. Chaos. 2007;17:015114–1—015114–10. doi: 10.1063/1.2404774. [DOI] [PubMed] [Google Scholar]
- 59.He J, Whelton P. Elevated systolic blood pressure and risk of cardiovascular and renal disease: overview of evidence from observational epidemiologic studies and randomized controlled trials. Am Heart J. 1999;138:211–219. doi: 10.1016/s0002-8703(99)70312-1. [DOI] [PubMed] [Google Scholar]
- 60.Hansen P, Frils U, Uhrenholt T, Briggs J, Schnermann J. Intracellular signalling pathways in the vasoconstrictor response of mouse afferent arterioles to adenosine. Acta Physiol. 2007;191:89–97. doi: 10.1111/j.1748-1716.2007.01724.x. [DOI] [PubMed] [Google Scholar]
- 61.Vallon V. The proximal tubule in the pathophysiology of the diabetic kidney. Am J Phyysiol Regu Int Comp Physiol. 1996;300:R1009–R1022. doi: 10.1152/ajpregu.00809.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Thomson SC, Vallon V, Blantz RC. Resetting protects efficiency of tubuloglomerular feedback. Kidney Int Suppl. 1998;67:S65–70. doi: 10.1046/j.1523-1755.1998.06713.x. [DOI] [PubMed] [Google Scholar]
- 63.Vallon V, Thomson SC. Renal function in diabetic disease models: the tubular system in the pathophysiology of the diabetic kidney. Annu Rev Physiol. 2012;74:351–75. doi: 10.1146/annurev-physiol-020911-153333. [DOI] [PMC free article] [PubMed] [Google Scholar]