Abstract
Objectives
To measure the inter-expert and intra-expert agreement in sleep spindle scoring, and to quantify how many experts are needed to build a reliable dataset of sleep spindle scorings.
Methods
The EEG dataset was comprised of 400 randomly selected 115 s segments of stage 2 sleep from 110 sleeping subjects in the general population (57±8, range: 42-72 years). To assess expert agreement, a total of 24 Registered Polysomnographic Technologists (RPSGTs) scored spindles in a subset of the EEG dataset at a single electrode location (C3-M2). Intra-expert and inter-expert agreements were calculated as F1-scores, Cohen’s kappa (κ), and intra-class correlation coefficient (ICC).
Results
We found an average intra-expert F1-score agreement of 72±7 % (κ: 0.66±0.07). The average inter-expert agreement was 61±6 % (κ: 0.52±0.07). Amplitude and frequency of discrete spindles were calculated with higher reliability than the estimation of spindle duration. Reliability of sleep spindle scoring can be improved by using qualitative confidence scores, rather than a dichotomous yes/no scoring system.
Conclusions
We estimate that 2-3 experts are needed to build a spindle scoring dataset with ‘substantial’ reliability (κ: 0.61-0.8), and 4 or more experts are needed to build a dataset with ‘almost perfect’ reliability (κ: 0.81-1).
Significance
Spindle scoring is a critical part of sleep staging, and spindles are believed to play an important role in development, aging, and diseases of the nervous system.
Keywords: sleep spindles, agreement, reliability, inter-rater, inter-expert, intra-rater, intra-expert, electroencephalography, polysomnography, event detection, sleep staging, sleep scoring
Introduction
Sleep spindles are discrete events observed in the scalp electroencephalogram (EEG) signal that are generated as a result of interactions between several regions of the brain including thalamic and cortico-thalamic networks (De Gennaro and Ferrara, 2003). They are observed as brief 11-16 Hz bursts that are distinct from the background activity, typically last less than a second, are maximal at central scalp locations, and have a characteristic waxing and waning amplitude (Iber et al., 2007). Spindles are a defining EEG feature of non-REM stage 2 (N2) sleep, although they can also occur in N3 (Iber et al., 2007). The gold standard to detect spindles is visual scoring by a trained sleep technologist. However, the EEG is a noisy signal, making the process of identifying individual spindle events very time consuming and subjective. Spindle density (counts/min), amplitude and duration decrease with age (Crowley et al., 2002, Martin et al., 2013), which might make spindle identification a more difficult task in older subjects. The purpose of this study was to estimate intra-expert and inter-expert reliabilities of spindle scoring using EEG data from middle-to-older aged subjects in the general population.
Identification of sleep spindles is of great clinical and biological interest because they are believed to play an important role in development, aging, and diseases of the nervous system. Spindle density (Bodizs et al., 2005, Fogel et al., 2007), frequency (Geiger et al., 2011, Gruber et al., 2013), and activity (Schabus et al., 2006, Schabus et al., 2008) have been correlated with both intelligence and general mental ability. Moreover, increased sleep spindle density following learning predicts improved memory consolidation (Bergmann et al., 2012, Eschenko et al., 2006, Gais et al., 2002, Genzel et al., 2012, Schabus et al., 2006, Schabus et al., 2008, Tamminen et al., 2010, Wamsley et al., 2012). Pharmacological interventions that increase spindle density have been found to correlate with improvements in specific types of memory (Kaestner et al., 2013, Mednick et al., 2013) and spindle density has been associated with selective attention (Forest et al., 2007). Numerous studies have found alterations in sleep spindle density in patients with psychiatric (Ferrarelli et al., 2007, Ferrarelli et al., 2010, Limoges et al., 2005, Miano et al., 2004, Seeck-Hirschner et al., 2010, Wamsley et al., 2012) and neurologic disease (Comella et al., 1993, Emser et al., 1988, Montplaisir et al., 1995, Myslobodsky et al., 1982, Silvestri et al., 1995, Wiegand et al., 1991).
One common limitation in research studies is that they focused only on spindle density, and ignored spindle characteristics like oscillation frequency, amplitude and duration, possibly because this information is more difficult to obtain. However, elegant modeling on how various neuronal networks are involved in the initiation, amplification, maintenance, or termination of sleep spindle bursts suggest that spindle characteristics may reflect an important role in the function of the spindle (Bazhenov et al., 2002, Bonjean et al., 2012, Bonjean et al., 2011, Fuentealba et al., 2005, Olbrich and Achermann, 2008). For example, specific types of memory consolidation have been associated with specific topographical locations (Martin et al., 2013) and oscillation frequencies (Fogel et al., 2012, Molle et al., 2011). The amplitude and duration of spindles also appears to be important for age-related changes (Nicolas et al., 2001), and are altered by benzodiazepines (Kaestner et al., 2013). The analysis of spindle characteristics requires precise determination of the beginning and end of spindle events in the EEG time series. Therefore, we previously tested several automatic sleep spindle detection algorithms and found their performance for detecting discrete spindle events to be significantly different from human experts. Further, the average inter-algorithm agreement was low (F1-score = 32±16 %), suggesting that spindle detection was not consistent between automated detectors (Warby et al., 2014).
Identifying sleep spindles is also important because it is a critical part of sleep stage scoring. Spindles and K-complexes are the two EEG features that are used to differentiate stage 2 from stage 1. Despite detailed rules and guidelines however, inter-expert agreement for sleep stage scoring is not perfect. Studies from the last decade report an overall stage scoring agreement between observers of 76-82 % (κ: 0.63-0.76) both in healthy subjects and patients with various sleep pathologies (Anderer et al., 2005, Danker-Hopfe et al., 2009, Danker-Hopfe et al., 2004, Magalang et al., 2013, Malinowska et al., 2009, Pittman et al., 2004). The agreement in scoring stage 2 is in the same range (κ: 0.60-0.72), whereas scoring stage 1 has considerably lower agreement (κ: 0.31-0.46) (Danker-Hopfe et al., 2009, Danker-Hopfe et al., 2004, Magalang et al., 2013). Furthermore, agreement in stage scoring has shown to worsen in subjects with increasing age and sleep disorder severity (Anderer et al., 2005). Improving the agreement of sleep spindle scoring, particularly in the transition of stage 1 to stage 2 in the EEG of older subjects may be important for improving the overall reliability of sleep stage scoring.
Very few studies have looked specifically at the agreement between human spindle scorers. In these studies, there were between 6-12 subjects (21-59 years old), and at most three experts were used to score spindles. In general, results were consistent with sleep stage scoring agreement, except that spindle scoring reliability in most cases deteriorated more rapidly with age and sleep pathologies. In healthy subjects, Huupponen et al. and Campbell et al. estimated 81 % and 86 % inter-expert agreement in sleep spindle identification, respectively (Campbell et al., 1980, Huupponen et al., 2007). Using three annotators, Zygierewicz et al. estimated an average agreement of 70±8 % in spindle identification in healthy subjects (Zygierewicz et al., 1999). In contrast, Devuyst et al. did not find the agreement in spindle scoring between two experts measured by F1-score to be more than 46 % when using slightly older patients with various sleep pathologies (Devuyst et al., 2011). To the best of our knowledge, no studies evaluating the intra-expert reliability in sleep spindle scoring have been reported.
The purpose of this study was to assess the intra-expert and inter-expert agreement of sleep spindle scoring averaged over multiple pairs of experts to find the mean pair-wise reliability. In addition to measuring the reliability of identifying spindle events in the EEG signal, we also assess the reliability of estimating spindle characteristics of the events, such as duration. Finally, based on our calculation of mean inter-expert reliability, we estimate how many experts are needed to build a reliable dataset of spindle scorings in EEG of older subjects.
Methods
Subjects and the EEG dataset
The EEG data used in the study was 110 middle aged and older subjects (mean±SD: 57±8 years, range: 42-72 years, 47 % male). These subjects were selected as a random subset of the Wisconsin Sleep Cohort (Peppard et al., 2013), which is a representative sample of the general population. In-clinic overnight polysomnography (PSG) was collected on these subjects following standardized protocols (Peppard et al., 2009), including 18-channels in a referential montage to record sleep stage, breathing, heart rate and rhythm, leg movements, snoring, arterial oxygenation, and body position. EEG data were collected with a sampling frequency of 100 Hz and band-pass filtered between 0.3-35 Hz. Sleep staging was conducted using standard criteria according to Rechtschaffen & Kales (Kales and Rechtschaffen, 1968). In total, the dataset consisted of 400 randomly selected, artifact-free, 115 s segments of stage 2 sleep. Each 115 s segment was broken into 5 epochs of 25 s each, overlapping by 2.5 s. The segments were extracted from the 110 subjects in the following manner: 2 segments (10 epochs) were randomly selected from 100 subjects and 20 segments (100 epochs) from 10 subjects. We chose to sample a lot of data from few subjects and little data from many subjects to estimate both intra-subject and inter-subject spindle variations, thereby getting most information from a dataset with only 400 segments. In total, there were 2,000 epochs of EEG data. Sleep spindle density is maximal at central scalp locations, so a single central EEG electrode placement (C3-M2) was used to reduce complexity and difficulty of the spindle detection task. All subjects provided written consent, and data collection and usage was approved by the Review Boards of the University of Wisconsin-Madison and Stanford University.
Experts
To assess expert reliability, we collected spindle scorings from Registered Polysomnographic Technologists (RPSGTs) who were tested on their ability to identify sleep spindles as part of their certification. Each expert was required to have a RPSGT number, have several years of experience, or actively (or retired from) working in a sleep clinic. Experts were recruited by word-of-mouth, email lists, or via an online PSG forum. Experts received a small remuneration for their work, including gifts or donations on their behalf. In total 24 RPSGTs were recruited from United States and Canada.
Spindle data collection
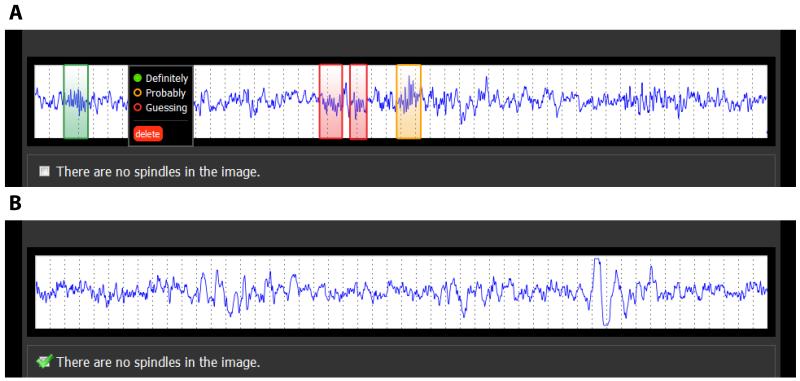
To allow the remote collection of spindle scorings by the experts, we created a web interface to present the EEG data over the internet in a standardized fashion, as described previously (Warby et al., 2014). EEG data were presented one epoch at a time with an aspect ratio that is consistent with the presentation of data in a sleep clinic (10 mm/s) (Kales and Rechtschaffen, 1968). Epochs (25 s in duration, voltage rage −50 to 50 μV) were converted to 90×900 pixel images for display. A 25 s epoch length was used to ensure that the entire epoch would fit in the width of a standard-size internet browser window. Experts were asked to review the epoch and identify spindle events by drawing a box around them in the browser window. Spindles were scored according to a set of instructions based on the American Academy of Sleep Medicine (AASM) standard. They were also asked to assign a confidence score of either ‘definitely’, ‘probably’ or ‘guessing’ to each detected spindle corresponding to high, medium and low confidence (Figure 1). Not all epochs contained spindles, and experts could indicate that ‘There are no spindles in the image’. The EEG data was arranged in blocks of 5 epochs from one subject, and the blocks of epochs were presented to the experts in random order. To prevent edge effects where spindles fall on an epoch boundary, we overlapped the EEG data between images by 2.5 s, using a procedure described previously (Warby et al., 2014). To assess intra-expert reliability, one expert scored the same data three times, and a second expert scored the same data twice (in both cases re-scorings were separated by several months).
Figure 1.
Two examples of the web interface used for the spindle identification task. (A) Experts identified spindles by drawing boxes around them, and then indicated their confidence in the scores as ‘Definitely’, ‘Probably’ or ‘Guessing’. (B) Alternatively, if no spindles were found in the epoch, the expert could indicate ‘There are no spindles in the image’.
Assessment of intra-expert and inter-expert agreements
The agreement between two scorers was assessed on a sample-by-sample (each data point in the EEG time series), event-by-event (each spindle), or epoch-by-epoch (each 25 s epoch) basis. In the sample-by-sample analysis, each sample point was considered a true positive or true negative if there was agreement. Sample points where there was not agreement were considered false positives or false negatives, depending on which scoring was arbitrarily selected as the reference. In the event-by-event analysis, spindle events in a scoring-pair were ‘matched’ (i.e. in agreement; true positive) if the events overlapped by at least 20 %, otherwise an event was a false positive or negative depending on which scoring was arbitrarily used as reference. Overlap (O) was defined as intersecting duration divided by the united duration of the paired events (E) (Equation 1). See Warby et al.2014 for pseudo-code explaining the event-by-event matching:
| (1) |
One-to-many or many-to-one spindle events were not allowed and were consolidated to one-to-one comparisons only. If one event overlapped more than 20 % with two or more events, the event-pair with highest overlap score was matched as the true positive, and the remaining events classified as false positive or negative if they could not be matched to other events. In case of tied overlap scores, the temporally first event was matched as the true positive. In the epoch-by-epoch domain a true positive was counted when both scorings within an epoch contained one or more spindles; it was a true negative if both experts scored no spindles within an epoch. Two experts viewed portions of the dataset more than once (separated by several months), and the intra-expert reliability was only evaluated on the portion of the dataset the expert viewed multiple times. Not all experts viewed the entire dataset, and inter-expert agreement was only evaluated on data both of the compared experts viewed. In cases where multiple confidence scores are being pooled (H+M+L, H+M), spindles do not have to have the same confidence scores in order to be considered a match. Thus when considering H+M spindles, a spindle with medium confidence can be matched perfectly with a spindle of high confidence or another spindle with medium confidence.
Report of intra-expert and inter-expert agreements
The agreements within an expert and between experts are summarized using F1-score (Equations 2a-b; true positive (TP), false negative (FN), false positive (FP)) or Cohen’s Kappa (κ) (Equations 3a-b):
| (2a) |
| (2b) |
| (3a) |
| (3b) |
However, κ cannot be calculated in the event-by-event analysis, as true negative events cannot be counted. Since we are primarily interested in the detection of individual spindle events, we focus first on F1-score which is the harmonic mean between recall (sensitivity) and precision (selectivity) and is not biased by TN counts. When possible, we also present κ, which modifies the observed accuracy according to the accuracy expected by chance. Both F1-score and κ are symmetric regarding false detections and the two formulas therefore yield the same result for a pair of experts regardless of which expert is being used as the reference. F1-score ranges from 0 (no agreement) to 100 % (perfect agreement), whereas κ ranges from −1 (no agreement) to 1 (perfect agreement). When accuracy is equal to what is expected by chance, κ is 0. The relative strength of reliability associated with κ is defined as ‘poor’ (<0.00), ‘slight’ (0.00-0.20), ‘fair’ (0.21-0.40), ‘moderate’ (0.41-0.60), ‘substantial’ (0.61-0.80) and ‘almost perfect’ (0.81-1.00) (Landis and Koch, 1977). To estimate the number of experts needed to build a dataset with a certain level of reliability, we used the Spearman-Brown formula (Equation 4) (Brown, 1910, Spearman, 1910):
| (4) |
In this formula, r is the number of experts with inter-expert reliability of κ, thus κr is the reliability of a dataset build from scores of r experts.
Assessment of reliability in spindle characteristics
There were two scenarios that could result in expert agreement; two experts could detect the same spindle event or the same expert could detect the same event twice. Therefore, we were able to investigate how well different spindle characteristics like duration, amplitude, and oscillation frequency agreed between the matched scorings. Since spindle characteristics vary on a continuous scale, we use intra-class correlation coefficient (ICC) to estimate the reliability in spindle characteristics within or between expert pairs (Equation 5a-b; (Fisher, 1925)):
| (5a) |
| (5b) |
In these equations, N is the total number of paired events and x refers to the characteristic of the event. ICC range from 0 to 1 where 0 is no consistency and 1 is perfect correlation between the two sets of scorings. Further, we could calculate the average amount of overlap between matched spindle events, using the intersection over union overlap rule (Equation 1). Events are not matched if the overlap score is less than 20 %, thus the average overlap score ranges from 0.2 to 1. While duration is directly determined by the expert, spindle amplitude and oscillation frequency are calculated from the detected spindle event, and not estimated by the expert directly. Spindle duration is compared between detections on a sample-by-sample basis. Spindle amplitude is calculated as the maximum peak to peak amplitude in the 11-16 Hz band measured in microvolts. Spindle oscillation frequency is calculated from the sampling frequency (100Hz) divided by the average peak to peak interval (minima to minima and maxima to maxima) in the 11-16 Hz band (Warby et al., 2014).
Results
Data Collection
The amount of work each expert performed varied (mean: 442 scored epochs/expert, range: 5-1946 scored epochs/expert). Despite this variation, several experts scored large proportions of the data and this yielded an average coverage of 5.3 unique expert views per epoch. We restricted the calculations of inter-expert agreement to expert pairs having viewed more than 300 of the same epochs (i.e. approximately 125 minutes). Among the 24 experts, 24 expert pairs out of 276 possible pairs matched this criterion. Experts assigned a confidence score to each identified spindle: H (high = ‘definitely’), M (medium = ‘probably’), and L (low = ‘guessing’). During analysis, spindles were divided in five groups based on their assigned confidence scores: H (including only high confidence spindles), M (including only medium confidence spindles), L (including only low confidence spindles), H+M (pooling high and medium confidence spindles together) and H+M+L (pooling high, medium and low confidence spindles together).
Intra-expert agreement
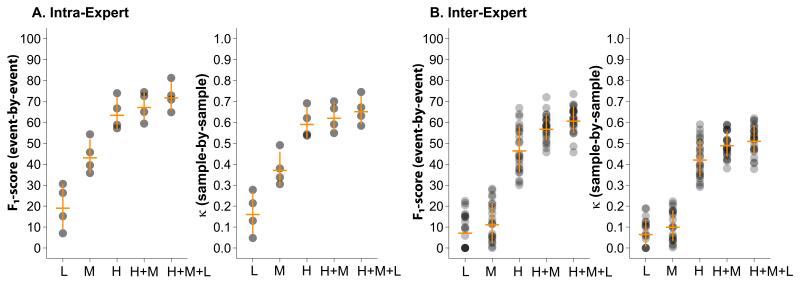
One expert scored the same data three times and another expert scored the same data twice independently, allowing calculation of intra-expert reliability for those experts. The intra-expert agreements were calculated pairwise and averaged results are presented in Tables 1 and 2. Spindles were divided in groups based on their assigned confidence scores. Using only high confidence spindles, intra-expert reliability of 64.1±7.7 % event-by-event (κ: 0.60±0.07 sample-by-sample) was obtained. Including all spindles in the analysis increased intra-expert agreement to 72.4±6.7 % event-by-event (κ: 0.66±0.07 sample-by-sample). Figure 2A shows that the average intra-expert agreement is increasing with increasing spindle confidence scores, and increases further when spindles of all confidence scores are pooled (p= 7.17·10−07 for F1-score; one way ANOVA across all confidence scores). Compared to the event-by-event analysis, intra-expert reliability using all spindles increased for the epoch-by-epoch analysis to 85.7±1.8 % (F1-score: p=0.02; paired t-test, Table 1), but was unchanged from sample-by-sample to epoch-by-epoch analysis (κ: p=n.s.; paired t-test, Table 2).
Table 1.
Mean F1-score agreement (event-by-event and epoch-by-epoch).
| Event | Epoch | ||||||
|---|---|---|---|---|---|---|---|
| L | M | H | H+M | H+M+L | H+M+L | p-value2 | |
|
|
|
||||||
| Intra-expert | 19.8±10.7 | 43.8±8.1 | 64.1±7.7 | 67.9±6.9 | 72.4±6.7 | 85.7±1.8 | 0.02 |
| Inter-expert | 7.8±8.2 | 11.9±9.6 | 47.1±11.0 | 57.5±6.2 | 61.4±6.4 | 74.8±5.8 | 6.5·10−17 |
|
|
|
||||||
| p-value1 | 0.04 | 2.2 10−6 | |||||
The intra-expert and inter-expert agreement is averaged (mean ± SD) over 4 and 24 pairwise agreements, respectively. Spindles are divided in groups based on their assigned confidence scores: H (high = ‘definitely’), M (medium = ‘probably’) and L (low = ‘guessing’). Intra-expert versus inter-expert agreement is tested with student t-tests (p-value1) while event-by-event versus epoch-by-epoch agreement is tested with paired t-tests for the H+M+L category (p-value2). All pairwise agreements are listed in Supplementary Tables S1 and S2.
Table 2.
Mean κ reliability (sample-by-sample and epoch-by-epoch).
| Sample | Epoch | ||||||
|---|---|---|---|---|---|---|---|
| L | M | H | H+M | H+M+L | H+M+L | p-value2 | |
|
|
|
||||||
| Intra-expert | 0.17±0.10 | 0.38±0.08 | 0.60±0.07 | 0.63±0.07 | 0.66±0.07 | 0.72±0.11 | n.s. |
| Inter-expert | 0.06±0.07 | 0.09±0.08 | 0.43±0.09 | 0.50±0.06 | 0.52±0.07 | 0.51±0.09 | n.s. |
|
|
|
||||||
| p-value1 | 0.02 | 0.02 | |||||
The intra-expert and inter-expert reliability is averaged (mean ± SD) over 4 and 24 pairwise reliabilities, respectively. Spindles are divided in groups based on their assigned confidence scores: H (high = ‘definitely’), M (medium = ‘probably’) and L (low = ‘guessing’). Intra-expert versus inter-expert reliability is tested with student t-tests (p-value1) while sample-by-sample versus epoch-by-epoch reliability is tested with paired t-tests for the H+M+L (p-value2). All pairwise reliabilities are listed in Supplementary Tables S3 and S4.
Figure 2.
(A) Intra-expert and (B) inter-expert reliability as a function of spindle confidence scores. Each dot represents one pairwise comparison. The intensity of the dot indicates the density of pairwise comparisons with the given reliability. The horizontal orange bars represent the means and the vertical bars the standard deviations.
Inter-expert agreement
Inter-expert agreements for each expert pair were calculated using spindles from each of the confidence groups and averaged results presented in Tables 1 and 2. Inter-expert agreements for group H (only spindles given the highest confidence score by both experts) yielded an average inter-expert agreement of 47.1±11.0 % event-by-event (κ: 0.43±0.09 sample-by-sample). Similar to the intra-expert agreement, the average inter-expert agreement was significantly different between the spindle confidence groups L, M, H, H+M and H+M+L (p=1.46·10−52 for F1-score; one-way ANOVA across all confidence scores). Average inter-expert agreement increased for spindles with increasing confidence score and was maximal for the pooled group including all spindles (F1-score: 61.4±6.4 % event-by-event, κ: 0.52±0.07 sample-by-sample), suggesting that reliability increases as more spindles are added to the comparison, despite their lower confidence scores. The F1-score obtained in the epoch-by-epoch analysis using all spindles, 74.8±5.8 %, increased significantly relative to event-by-event agreement (F1-score: p=6.5·10−17; paired t-test). However, reliability was unchanged between epoch-by-epoch and sample-by-sample analysis (κ: p=n.s.; paired t-test).
Reliability of spindle characteristics
Using the ICC formula we calculated the reliability of spindle duration estimates, as well as the mean overlap of events within an expert and between experts. The averaged results using spindles with high, medium and low confidence scores pooled together are listed in Table 3. We found that confidence scores did not have a significant impact on estimating spindle duration (results not shown) and we therefore only report the reliability results of group H+M+L. However, the ICC of spindle duration differed significantly when measured within or between experts (0.68±0.14 versus 0.43±0.16, p=0.03; student t-test), showing higher reliability in spindle duration within an expert than between experts. The average amount of overlap between matched spindle events was 0.81 within an expert and 0.75 between experts (Table 4). Despite these differences in the estimation of spindle duration and overlap, we found that this did not have a significant impact on the reliability of spindle amplitude or oscillation frequency calculation from the matched spindle events. The ICC of spindle amplitude was 0.95±0.03 versus 0.91±0.04 (p=n.s., student t-test) whereas ICC of spindle frequency was 0.89±0.03 versus 0.88±0.04 (p=n.s.; student t-test) for intra-expert and inter-expert, respectively.
Table 3.
Mean ICC for the measurement of spindle characteristics.
| Duration | Amplitude | Frequency | |
|---|---|---|---|
|
|
|||
| Intra-expert | 0.68±0.14 | 0.95±0.03 | 0.89±0.03 |
| Inter-expert | 0.43±0.16 | 0.91±0.04 | 0.88±0.04 |
|
|
|||
| p-value | 0.03 | n.s. | n.s. |
The intra-expert and inter-expert ICC is averaged (mean ± SD) across 4 and 24 pairwise comparisons, respectively. Spindle characteristics reliability is calculated using matched spindle detections (see Methods). All reported values are calculated from the pooled group containing spindles with H+M+L confidence scores. Intra-expert versus inter-expert reliability is tested with student t-tests. All pairwise ICCs are listed in Supplementary tables S5 and S6. Spindle duration is measured directly by the expert; amplitude and frequency are calculated from the resulting detected event.
Table 4.
Mean overlap score of matched spindle detections.
| Mean | SD | |
|---|---|---|
|
|
||
| Intra-expert | 0.81 | 0.12 |
| Inter-expert | 0.75 | 0.14 |
|
|
||
| p-value | 1.6·10−4 | n.s. |
The intra-expert and inter-expert average overlap and SD of overlap are calculated using matched events and reported as mean values across 4 and 24 pairwise comparisons, respectively. All reported values are calculated from the pooled group containing spindles with H+M+L confidence scores. Intra-expert versus inter-expert results are tested with student t-tests. Each expert pair has an average overlap and SD, and the mean of all of the pairs is reported here. All pairwise average overlaps and corresponding SDs are listed in Supplementary tables S7 and S8.
We investigated whether the different amount of data (10-epochs from 100 subjects and 100-epochs from 10 subjects) had biased any of the reliability results to favor the greater amount of data from few subjects rather than little amount of data from many subjects. We found no difference in reliability between the subject groups (p=n.s.; paired t-test) suggesting that our calculations of reliability are not biased by the data sampling. Furthermore, we divided the subjects according to age (42-51, 52-61 and 62-72 years) to investigate if the inter-expert reliability decreased with increasing age. We found no age effect on any of the reliability measures (p=n.s.; ANOVA).
Number of experts needed to build a reliable dataset
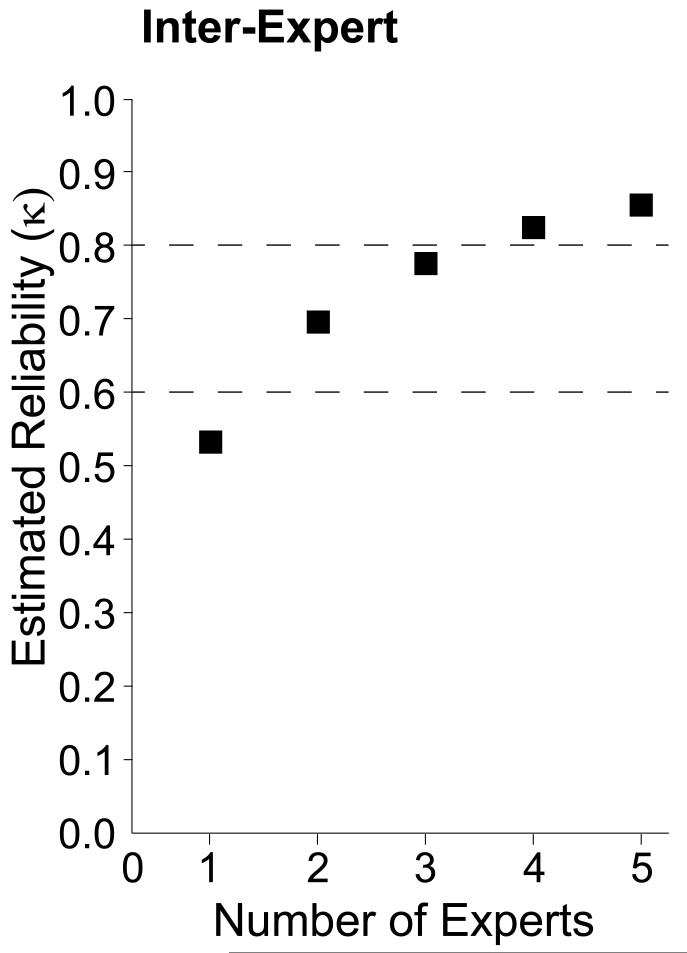
Using the Spearman-Brown formula and the average inter-expert reliability (κ: 0.52), we calculated the theoretically expected reliability of datasets build using 2-5 experts (Figure 3). We found that to build a spindle scoring dataset with ‘substantial’ reliability 2-3 experts are needed. Building a dataset using 4 or more experts results in a dataset with ‘almost perfect’ reliability. Simply using two experts to build the dataset instead of one improves the reliability by 32 %, and using three experts instead of one theoretically improves the reliability of the dataset by 47 %.
Figure 3.
κ reliability of datasets build using spindle scorings from 1 - 5 experts theoretically estimated using Spearman-Brown formula. Dashed lines indicate the limits between ‘moderate-substantial’ and ‘substantial-almost perfect’ reliability.
Discussion
In this paper we calculated intra-expert and inter-expert agreement in sleep spindle scoring in the EEG of middle aged to older subjects from the general population. For the intra-expert analysis we averaged the pairwise agreement of two experts having scored the same data 2 or 3 times, and found event-by-event F1-score reliability of 72±7 % (κ: 0.66±0.07). In the inter-expert analysis we averaged the agreement among 24 pairs of experts having scored a minimum of 300 epochs in common, and found event-by-event F1-score reliability of 61±6 % (κ: 0.52±0.07). As expected, we found the intra-expert agreement to be consistently higher than inter-expert agreement on all measurements. The results indicate that experts do not agree perfectly with themselves, although they agree more consistently with themselves than with other experts.
We also investigated how reliably sleep spindle characteristics like duration, amplitude and oscillation frequency could be estimated either directly or indirectly by the experts. The mean ICC for spindle duration measurements was moderate (0.68 intra-expert; 0.43 inter-expert), despite relatively high average event-by-event overlap between matched detections (average overlap 0.81 intra-expert; 0.75 inter-expert). However, maximum peak-to-peak amplitude and spindle oscillation frequency can be calculated from a detected spindle event, and our data suggest that these calculations are not affected by inconsistency in the estimation of spindle duration. The ICC of spindle amplitude and frequency were both near 0.9, suggesting that calculations of these characteristics are very robust, despite individual disagreement associated with identifying the beginning and ending of spindles (Table 3). The somewhat low agreement on the duration of spindles is not surprising considering that clear rules describing when spindles begin and end have not been defined.
We discovered that intra-expert and inter-expert agreements were dependent on assigned spindle confidence scores. As expected, agreement increased with increasing spindle confidence scores. However, overall agreement increased further when spindles of all confidence scores (H+M+L) were pooled together, suggesting that there was some inconsistency within an expert and between experts in assigning identical confidence scores to the same detected spindle event. Supplementary figure S1 demonstrates how pooling spindle events with varying confidence scores together leads to improved agreement. Our results show that experts identify the same spindles but have different subjective confidence in one particular spindle, thus assigning different confidence scores to the same spindle event. Interestingly, one study in detecting epileptiform spikes (Webber et al., 1993) also found that pooling events with mixed confidence scores resulted in improved inter-expert agreement, which is similar to our findings with spindles (Figure 2).
Our data suggest that we were able to obtain higher reliability scores because we allowed the expert scorers to use confidence scores, rather than forcing them to use a dichotomous yes/no spindle scoring system. We left it up to the expert to decide how to categorize the spindles within the qualitative confidence scores that were broadly defined as high, medium or low confidence. One expert’s ability to assign the same confidence score to a detected spindle reflects the subjectivity in perception of spindles, possibly associated with level of skill and expertise. We found that allowing the experts to assign confidence scores to the spindle detections to be very useful, because it allows experts to identify putative spindle events that may have a degree of uncertainty; conservative experts could take risks in calling spindles by assigning a low confidence score to a spindle they otherwise would not have marked. As our data shows, allowing the experts to use confidence scores produces more reliable data. If we had forced a dichotomous scoring system, we would expect the results to be similar to using only the ‘H’ category alone (for example), resulting in lower reliability than the combined H+M+L. We recommend that future studies allow experts to assign confidence scores to detected sleep spindles to maximize the agreement for spindle event identification within and between experts.
To our knowledge, no other studies exploring the intra-expert agreement in sleep spindle scoring have been published and so we wanted to provide an initial estimate. We are aware that calculating intra-expert reliability based on only two experts is not as valid as calculating inter-expert reliability based on 24 expert pairs. As expected, we find the intra-expert reliability to be significantly higher than inter-expert reliability, but far from perfect. Intra-expert reliability will likely vary between experts probably due to level of skills and alertness, among other factors. However, a dataset produced from a large number of unique experts will compensate for deficits in intra-expert reliability given the intra-expert reliability is greater than the inter-expert reliability. For producing high quality sleep spindle data, we consider multiple different experts to be more important than multiple scorings from the same expert. In addition, other event detection tasks like detection of epileptiform spikes have shown highly varying intra-expert agreement (Halford et al., 2013, Hostetler et al., 1992, Webber et al., 1993). Previous studies on inter-expert agreement in spindle scoring have found agreements ranging from 46-86 %. The agreement appears to be heavily dependent on the age and disease status of the subjects. Three studies using 2-3 experts and healthy subjects (aged 21-59 years) found average inter-expert agreements of 86 % (Campbell et al., 1980), 70±8 % (Zygierewicz et al., 1999) and 81 % (Huupponen et al., 2007). However, it is unclear what measurements of agreement are reported. One study using patients with various sleep pathologies of age 31-54 years found considerably lower inter-expert agreement of 46 % in sleep spindle scoring (Devuyst et al., 2011). Our estimate of 61±6 % inter-expert agreement (averaged over 24 pairs of experts) falls in the middle of this range and our range of pair-wise inter-expert agreement of 46-74 % fits well with previously reported numbers of agreement between one expert pair. Previous results vary largely since they are often only a reflection of the agreement between a single expert pair. Our observed inter-expert agreement is also consistent with studies that found inter-expert agreements of 53 % (Bremer et al., 1970) and 66 % (O. Sherif, 1977) for K-complexes, which is a similar event scoring task to sleep spindles. Other sleep events like limb movements, arousals and respiratory events have much higher inter-expert agreements of 96 %, 84 %, and 95 % (Pittman et al., 2004). The increased agreement in identifying these events might be due to the events’ longer durations, larger magnitudes and distinctness from the background signal. Our study population is a middle- to older-aged (42-72 years) sample of the general population. Spindle amplitude (Crowley et al., 2002) and duration (Crowley et al., 2002, Nicolas et al., 2001) are known to decrease with age, reducing the signal to background activity ratio of spindles in older subjects. It is therefore not surprising that our estimates of agreement in older subjects are less than previous studies with younger subjects, as spindle scoring is a more difficult task in older subjects. However, assessing the reliability of sleep spindle detection in older subjects is important, because of the possible role of spindles in age-related cognitive decline and neurological diseases (Christensen et al., 2014, Fogel et al., 2012, Peters et al., 2008, Plante et al., 2013, Westerberg et al., 2012).
In the sleep clinic, spindles are particularly important for the scoring of stage 2 sleep. Therefore, we also investigated the inter-expert agreement in spindle scoring on an epoch-by-epoch basis. This modification makes the spindle scoring task more similar to scoring sleep stages since experts do not have to agree on the number of spindles or location within the epoch, but only decide if an epoch contains spindles or not. The higher F1-score agreement we achieved evaluating spindles on an epoch-by-epoch basis (intra: 86±2 %; inter: 75±6 %) compared to event-by-event basis reflects this simplification in the detection task (Table 1). However, we did not see an improvement in κ for the epoch-by-epoch analysis (Table 2), likely due to the large increase in the prevalence of spindle events when counted by-epoch rather than by-sample (spindle events are rare in the sample-by-sample analysis, but epochs containing spindles are very common in the epoch-by-epoch analysis). High event prevalence is known to negatively influence the κ estimation of agreement (Feinstein and Cicchetti, 1990, Sim and Wright, 2005).
Interestingly, our inter-expert F1-score agreement in spindle scoring epoch-by-epoch of 75±6 % corresponds very well to previous studies on inter-expert agreement in stage 2 scoring which ranges from 71 % to 86 % (Anderer et al., 2005, Danker-Hopfe et al., 2009, Danker-Hopfe et al., 2004, Malinowska et al., 2009, Pittman et al., 2004). Our estimate of agreement by κ is also consistent with previous findings in inter-expert stage 2 scoring agreement (Danker-Hopfe et al., 2009, Danker-Hopfe et al., 2004, Magalang et al., 2013). Importantly, the scoring of stage 1 is particularly unreliable. Studies found κ agreements in stage 1 scoring as low as 0.31-0.46 (Danker-Hopfe et al., 2009, Danker-Hopfe et al., 2004, Magalang et al., 2013). Since the presence of sleep spindles and K-complexes are the defining features that are used to discriminate stage 2 from stage 1, difficulties in the identification of spindles are likely to play an important role in the unreliability of scoring these stages. Improving spindle detection may therefore improve sleep stage scoring reliability.
We present the intra-expert and inter-expert agreements using two common methods of reporting agreement: F1-score and κ. When evaluating event detections we find it most informative to perform the analysis on an event-by-event basis. Since spindles are of variable length, we cannot appropriately count true negative events (and therefore cannot calculate κ for events). We favor the F1-score as a measure of agreement for event detection. Further, F1-score has the advantage that it is the mean of recall and precision, which are focused on quantifying event detections, rather than quantifying non-event detections, and are therefore not biased by the prevalence of events in the data. Kottner et al. recommends reporting multiple measures of agreement when investigating reliability (Kottner et al., 2011). We also present κ when possible (sample-by-sample and epoch-by-epoch), because it is a commonly used measurement and allows for additional comparison. Additionally, we assessed the F1-score and κ agreement at an epoch-by-epoch basis with the one goal of comparing to stage scoring agreement. Although these epoch-by-epoch agreements may parallel sleep stage scoring, they are not a good assessment of the reliability of scoring individual spindle events. It is also important to note that at all levels of analysis (sample-by-sample, event-by-event, and epoch-by-epoch), agreements among different expert pairs are calculated on different subsets of the data. Not all experts viewed the entire dataset. Therefore, we assessed agreement between a pair of experts only on the data they both viewed; the viewed portion of the dataset may be different for each pair. It cannot be ruled out that some sub-datasets may have been easier to score than others which could lead to artificially increased variance in agreement. Moreover, all spindle scorings were restricted to stage 2, simplifying the task compared to detection of spindles among slow waves in stage 3. We choose to only collect data from C3-M2 to ensure there was enough power to make intra-expert and inter-expert reliability calculations. In this study we have not collected data to study inter-expert reliabilities in scoring slow/fast, left/right hemispheric or frontal/central spindles, although this will be important in future studies.
Finally, we used the inter-expert reliability to theoretically estimate how many experts are needed to build a reliable dataset of sleep spindle scorings. A dataset built from the scores of multiple unique experts will converge towards generalizable and valid group consensus scores (Kraemer, 1979). We found that if a single expert scores the dataset that dataset will only be 52 % similar to the scores of another expert measured by inter-expert κ reliability. The similarity of the datasets increases if more than one expert is used to build each of the datasets being compared. We found that 2-3 experts are needed to build a dataset with ‘substantial’ reliability, and 4 or more are needed to build an ‘almost perfectly’ reliable dataset (Figure 3).
Automated methods of sleep spindle detection have perfect test-retest reliability and therefore provide an attractive solution to the problems of reliability in human scoring. However, before automated methods can be considered the gold standard method for spindle detection, there are two important issues that need to be addressed. The first issue is to identify and resolve the discrepancy between automated and manually scored spindles. This is particularly important for clinical applications such as sleep stage scoring where there is an important historical context to spindles. While the automated detectors are perfectly reliable, thus they will return the same result each time they are applied to the same data, the validity of many automated detectors against the current gold standard is low, even using EEG from healthy subjects (maximum F1-score= 53 %) (Warby et al., 2014). While automated detectors reliably identify specific events in the EEG, it is important to measure and quantify the agreement with human-identified spindles if we wish to claim they are the same thing. Based on our data, if only one expert is used to score spindles in a dataset you would expect agreement of approximately 61% with another single expert, corresponding to the average inter-expert agreement. Therefore, if an automatic algorithm is compared to scores from a single expert it would be unreasonable to expect the performance of the algorithm to be higher than 61%. However, the reliability of individual experts against a gold standard formed by consensus among a group of experts (in which individual expert errors have been reduced or eliminated), is higher than the reliability between two individual experts; previously we reported the average F1-score performance of these experts against a gold standard to be 0.75± 0.06 (Warby et al., 2014). We therefore argue that it is important that the performance of spindle detectors is assessed against a gold standard compiled from the scores of many experts. Second, there are several methodological approaches to automatic spindle scoring and differences in the results of these different methods need to be resolved. The average inter-detector agreement of 6 previously published automated detectors was found to be quite low (F1-score = 32±16 %) (Warby et al., 2014). It is therefore not clear which of the automated methods should replace human-detected spindles as the gold standard, as each detector produced different results. While it is clear that automated detection will eventually surpass manual methods, it is important to first assess the limits of spindle detection by the human eye. We have presented data to help define the limits of human detected spindles to assist with the overall goal of developing reliable and valid automated spindle detectors.
Supplementary Material
Highlights.
-
-
Spindle identification is a difficult task, and more than one sleep expert is needed to reliably score spindles in EEG data.
-
-
The reliability of sleep staging may be improved by improving the reliability of spindle scoring, particularly for the discrimination of stage N1 and N2 sleep.
-
-
Reliability of sleep spindle scoring can be improved by using qualitative confidence scores, rather than a dichotomous yes/no scoring system.
Acknowledgements
We thank the RPSGT experts who participated in the spindle identification task, and the participants of the Wisconsin Sleep Cohort who provided the polysomnography data. Also, thanks to Eileen B Leary for valuable comments and edits that helped improve the clarity of the manuscript. SCW is supported by the Canadian Institutes of Health Research and the Brain and Behavior Research Foundation. EM is supported by National Institutes of Health (grant NS23724). EEG data collection was supported by grants from the National Heart, Lung, and Blood Institute (grant R01HL62252) and the National Center for Research Resources (grant 1UL1RR025011) at the National Institutes of Health.
Footnotes
All authors report no conflicts of interest for this work.
References
- Anderer P, Gruber G, Parapatics S, Woertz M, Miazhynskaia T, Klosch G, et al. An E-health solution for automatic sleep classification according to Rechtschaffen and Kales: validation study of the Somnolyzer 24 × 7 utilizing the Siesta database. Neuropsychobiology. 2005;51:115–33. doi: 10.1159/000085205. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Model of thalamocortical slow-wave sleep oscillations and transitions to activated States. J Neurosci. 2002;22:8691–704. doi: 10.1523/JNEUROSCI.22-19-08691.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmann TO, Molle M, Diedrichs J, Born J, Siebner HR. Sleep spindle-related reactivation of category-specific cortical regions after learning face-scene associations. Neuroimage. 2012;59:2733–42. doi: 10.1016/j.neuroimage.2011.10.036. [DOI] [PubMed] [Google Scholar]
- Bodizs R, Kis T, Lazar AS, Havran L, Rigo P, Clemens Z, et al. Prediction of general mental ability based on neural oscillation measures of sleep. J Sleep Res. 2005;14:285–92. doi: 10.1111/j.1365-2869.2005.00472.x. [DOI] [PubMed] [Google Scholar]
- Bonjean M, Baker T, Bazhenov M, Cash S, Halgren E, Sejnowski T. Interactions between core and matrix thalamocortical projections in human sleep spindle synchronization. J Neurosci. 2012;32:5250–63. doi: 10.1523/JNEUROSCI.6141-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonjean M, Baker T, Lemieux M, Timofeev I, Sejnowski T, Bazhenov M. Corticothalamic feedback controls sleep spindle duration in vivo. J Neurosci. 2011;31:9124–34. doi: 10.1523/JNEUROSCI.0077-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremer G, Smith JR, Karacan I. Automatic detection of the K-complex in sleep electroencephalograms. IEEE Trans Biomed Eng. 1970;17:314–23. doi: 10.1109/tbme.1970.4502759. [DOI] [PubMed] [Google Scholar]
- Brown W. Some Experimental Results in the Correlation of Mental Abilities. Br J Psychol. 1910;3:296–322. [Google Scholar]
- Campbell K, Kumar A, Hofman W. Human and automatic validation of a phase-locked loop spindle detection system. Electroencephalogr Clin Neurophysiol. 1980;48:602–5. doi: 10.1016/0013-4694(80)90296-5. [DOI] [PubMed] [Google Scholar]
- Christensen JA, Kempfner J, Zoetmulder M, Leonthin HL, Arvastson L, Christensen SR, et al. Decreased sleep spindle density in patients with idiopathic REM sleep behavior disorder and patients with Parkinson’s disease. Clin Neurophysiol. 2014;125:512–9. doi: 10.1016/j.clinph.2013.08.013. [DOI] [PubMed] [Google Scholar]
- Comella CL, Tanner CM, Ristanovic RK. Polysomnographic sleep measures in Parkinson’s disease patients with treatment-induced hallucinations. Ann Neurol. 1993;34:710–4. doi: 10.1002/ana.410340514. [DOI] [PubMed] [Google Scholar]
- Crowley K, Trinder J, Kim Y, Carrington M, Colrain IM. The effects of normal aging on sleep spindle and K-complex production. Clin Neurophysiol. 2002;113:1615–22. doi: 10.1016/s1388-2457(02)00237-7. [DOI] [PubMed] [Google Scholar]
- Danker-Hopfe H, Anderer P, Zeitlhofer J, Boeck M, Dorn H, Gruber G, et al. Interrater reliability for sleep scoring according to the Rechtschaffen & Kales and the new AASM standard. J Sleep Res. 2009;18:74–84. doi: 10.1111/j.1365-2869.2008.00700.x. [DOI] [PubMed] [Google Scholar]
- Danker-Hopfe H, Kunz D, Gruber G, Klosch G, Lorenzo JL, Himanen SL, et al. Interrater reliability between scorers from eight European sleep laboratories in subjects with different sleep disorders. J Sleep Res. 2004;13:63–9. doi: 10.1046/j.1365-2869.2003.00375.x. [DOI] [PubMed] [Google Scholar]
- De Gennaro L, Ferrara M. Sleep spindles: an overview. Sleep Med Rev. 2003;7:423–40. doi: 10.1053/smrv.2002.0252. [DOI] [PubMed] [Google Scholar]
- Devuyst S, Dutoit T, Stenuit P, Kerkhofs M. Automatic sleep spindles detection--overview and development of a standard proposal assessment method. Conf Proc IEEE Eng Med Biol Soc. 2011;2011:1713–6. doi: 10.1109/IEMBS.2011.6090491. [DOI] [PubMed] [Google Scholar]
- Emser W, Brenner M, Stober T, Schimrigk K. Changes in nocturnal sleep in Huntington’s and Parkinson’s disease. J Neurol. 1988;235:177–9. doi: 10.1007/BF00314313. [DOI] [PubMed] [Google Scholar]
- Eschenko O, Molle M, Born J, Sara SJ. Elevated sleep spindle density after learning or after retrieval in rats. J Neurosci. 2006;26:12914–20. doi: 10.1523/JNEUROSCI.3175-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinstein AR, Cicchetti DV. High agreement but low kappa: I. The problems of two paradoxes. J Clin Epidemiol. 1990;43:543–9. doi: 10.1016/0895-4356(90)90158-l. [DOI] [PubMed] [Google Scholar]
- Ferrarelli F, Huber R, Peterson MJ, Massimini M, Murphy M, Riedner BA, et al. Reduced sleep spindle activity in schizophrenia patients. AJ Psychiatry. 2007;164:483–92. doi: 10.1176/ajp.2007.164.3.483. [DOI] [PubMed] [Google Scholar]
- Ferrarelli F, Peterson MJ, Sarasso S, Riedner BA, Murphy MJ, Benca RM, et al. Thalamic dysfunction in schizophrenia suggested by whole-night deficits in slow and fast spindles. AJ Psychiatry. 2010;167:1339–48. doi: 10.1176/appi.ajp.2010.09121731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. Statistical Methods for Research Workers. Oliver and Boyd; Edinburgh: 1925. Intraclass correlations and the analysis of variance; pp. 177–210. [Google Scholar]
- Fogel S, Martin N, Lafortune M, Barakat M, Debas K, Laventure S, et al. NREM Sleep Oscillations and Brain Plasticity in Aging. Front Neurol. 2012;3:176. doi: 10.3389/fneur.2012.00176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogel SM, Nader R, Cote KA, Smith CT. Sleep spindles and learning potential. Behav Neurosci. 2007;121:1–10. doi: 10.1037/0735-7044.121.1.1. [DOI] [PubMed] [Google Scholar]
- Forest G, Poulin J, Daoust AM, Lussier I, Stip E, Godbout R. Attention and non-REM sleep in neuroleptic-naive persons with schizophrenia and control participants. Psychiatry Res. 2007;149:33–40. doi: 10.1016/j.psychres.2005.11.005. [DOI] [PubMed] [Google Scholar]
- Fuentealba P, Timofeev I, Bazhenov M, Sejnowski TJ, Steriade M. Membrane bistability in thalamic reticular neurons during spindle oscillations. J Neurophysiol. 2005;93:294–304. doi: 10.1152/jn.00552.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gais S, Molle M, Helms K, Born J. Learning-dependent increases in sleep spindle density. J Neurosci. 2002;22:6830–4. doi: 10.1523/JNEUROSCI.22-15-06830.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiger A, Huber R, Kurth S, Ringli M, Jenni OG, Achermann P. The sleep EEG as a marker of intellectual ability in school age children. Sleep. 2011;34:181–9. doi: 10.1093/sleep/34.2.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genzel L, Kiefer T, Renner L, Wehrle R, Kluge M, Grozinger M, et al. Sex and modulatory menstrual cycle effects on sleep related memory consolidation. Psychoneuroendocrinology. 2012;37:987–98. doi: 10.1016/j.psyneuen.2011.11.006. [DOI] [PubMed] [Google Scholar]
- Gruber R, Wise MS, Frenette S, Knaauper B, Boom A, Fontil L, et al. The association between sleep spindles and IQ in healthy school-age children. Int J Psychophysiol. 2013;89:229–40. doi: 10.1016/j.ijpsycho.2013.03.018. [DOI] [PubMed] [Google Scholar]
- Halford JJ, Schalkoff RJ, Zhou J, Benbadis SR, Tatum WO, Turner RP, et al. Standardized database development for EEG epileptiform transient detection: EEGnet scoring system and machine learning analysis. J Neurosci Methods. 2013;212:308–16. doi: 10.1016/j.jneumeth.2012.11.005. [DOI] [PubMed] [Google Scholar]
- Hostetler WE, Doller HJ, Homan RW. Assessment of a computer program to detect epileptiform spikes. Electroencephalogr Clin Neurophysiol. 1992;83:1–11. doi: 10.1016/0013-4694(92)90126-3. [DOI] [PubMed] [Google Scholar]
- Huupponen E, Gomez-Herrero G, Saastamoinen A, Varri A, Hasan J, Himanen SL. Development and comparison of four sleep spindle detection methods. Artif Intell Med. 2007;40:157–70. doi: 10.1016/j.artmed.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Iber C, Ancoli-Israel S, Chesson A, Quan SF, American Academy of Sleep Medicine . The AASM manual for the scoring of sleep and associated events : rules, terminology, and technical specifications. American Academy of Sleep Medicine; Westchester, IL: 2007. [Google Scholar]
- Kaestner EJ, Wixted JT, Mednick SC. Pharmacologically increasing sleep spindles enhances recognition for negative and high-arousal memories. J Cogn Neurosci. 2013;25:1597–610. doi: 10.1162/jocn_a_00433. [DOI] [PubMed] [Google Scholar]
- Kales A, Rechtschaffen A. A manual of standardized terminology, techniques and scoring system for sleep stages of human subjects. Bethesda, Md.: 1968. [DOI] [PubMed] [Google Scholar]
- Kottner J, Audige L, Brorson S, Donner A, Gajewski BJ, Hrobjartsson A, et al. Guidelines for Reporting Reliability and Agreement Studies (GRRAS) were proposed. J Clin Epidemiol. 2011;64:96–106. doi: 10.1016/j.jclinepi.2010.03.002. [DOI] [PubMed] [Google Scholar]
- Kraemer HC. Ramifications of a population model forκ as a coefficient of reliability. Psychometrika. 1979;44:461–72. [Google Scholar]
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–74. [PubMed] [Google Scholar]
- Limoges E, Mottron L, Bolduc C, Berthiaume C, Godbout R. Atypical sleep architecture and the autism phenotype. Brain. 2005;128:1049–61. doi: 10.1093/brain/awh425. [DOI] [PubMed] [Google Scholar]
- Magalang UJ, Chen NH, Cistulli PA, Fedson AC, Gislason T, Hillman D, et al. Agreement in the scoring of respiratory events and sleep among international sleep centers. Sleep. 2013;36:591–6. doi: 10.5665/sleep.2552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinowska U, Klekowicz H, Wakarow A, Niemcewicz S, Durka PJ. Fully parametric sleep staging compatible with the classical criteria. Neuroinformatics. 2009;7:245–53. doi: 10.1007/s12021-009-9059-9. [DOI] [PubMed] [Google Scholar]
- Martin N, Lafortune M, Godbout J, Barakat M, Robillard R, Poirier G, et al. Topography of age-related changes in sleep spindles. Neurobiol Aging. 2013;34:468–76. doi: 10.1016/j.neurobiolaging.2012.05.020. [DOI] [PubMed] [Google Scholar]
- Mednick SC, McDevitt EA, Walsh JK, Wamsley E, Paulus M, Kanady JC, et al. The critical role of sleep spindles in hippocampal-dependent memory: a pharmacology study. J Neurosci. 2013;33:4494–504. doi: 10.1523/JNEUROSCI.3127-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miano S, Bruni O, Leuzzi V, Elia M, Verrillo E, Ferri R. Sleep polygraphy in Angelman syndrome. Clin Neurophysiol. 2004;115:938–45. doi: 10.1016/j.clinph.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Molle M, Bergmann TO, Marshall L, Born J. Fast and slow spindles during the sleep slow oscillation: disparate coalescence and engagement in memory processing. Sleep. 2011;34:1411–21. doi: 10.5665/SLEEP.1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montplaisir J, Petit D, Lorrain D, Gauthier S, Nielsen T. Sleep in Alzheimer’s disease: further considerations on the role of brainstem and forebrain cholinergic populations in sleep-wake mechanisms. Sleep. 1995;18:145–8. doi: 10.1093/sleep/18.3.145. [DOI] [PubMed] [Google Scholar]
- Myslobodsky M, Mintz M, Ben-Mayor V, Radwan H. Unilateral dopamine deficit and lateral eeg asymmetry: sleep abnormalities in hemi-Parkinson’s patients. Electroencephalogr Clin Neurophysiol. 1982;54:227–31. doi: 10.1016/0013-4694(82)90164-x. [DOI] [PubMed] [Google Scholar]
- Nicolas A, Petit D, Rompre S, Montplaisir J. Sleep spindle characteristics in healthy subjects of different age groups. Clin Neurophysiol. 2001;112:521–7. doi: 10.1016/s1388-2457(00)00556-3. [DOI] [PubMed] [Google Scholar]
- Sherif BP O, Mahmoud S, Broughton R. Automatic Detection of K-complex in the Sleep EEG. Int Electrical and Electronic Conf and Exp. 1977;81:204–5. [Google Scholar]
- Olbrich E, Achermann P. Analysis of the temporal organization of sleep spindles in the human sleep EEG using a phenomenological modeling approach. J Biol Phys. 2008;34:241–9. doi: 10.1007/s10867-008-9078-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peppard PE, Ward NR, Morrell MJ. The impact of obesity on oxygen desaturation during sleep-disordered breathing. Am J Respir Crit Care Med. 2009;180:788–93. doi: 10.1164/rccm.200905-0773OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peppard PE, Young T, Barnet JH, Palta M, Hagen EW, Hla KM. Increased prevalence of sleep-disordered breathing in adults. Am J Epidemiol. 2013;177:1006–14. doi: 10.1093/aje/kws342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters KR, Ray L, Smith V, Smith C. Changes in the density of stage 2 sleep spindles following motor learning in young and older adults. J Sleep Res. 2008;17:23–33. doi: 10.1111/j.1365-2869.2008.00634.x. [DOI] [PubMed] [Google Scholar]
- Pittman SD, MacDonald MM, Fogel RB, Malhotra A, Todros K, Levy B, et al. Assessment of automated scoring of polysomnographic recordings in a population with suspected sleep-disordered breathing. Sleep. 2004;27:1394–403. doi: 10.1093/sleep/27.7.1394. [DOI] [PubMed] [Google Scholar]
- Plante DT, Goldstein MR, Landsness EC, Peterson MJ, Riedner BA, Ferrarelli F, et al. Topographic and sex-related differences in sleep spindles in major depressive disorder: a high-density EEG investigation. J Affect Disord. 2013;146:120–5. doi: 10.1016/j.jad.2012.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schabus M, Hodlmoser K, Gruber G, Sauter C, Anderer P, Klosch G, et al. Sleep spindle-related activity in the human EEG and its relation to general cognitive and learning abilities. Eur J Neurosci. 2006;23:1738–46. doi: 10.1111/j.1460-9568.2006.04694.x. [DOI] [PubMed] [Google Scholar]
- Schabus M, Hoedlmoser K, Pecherstorfer T, Anderer P, Gruber G, Parapatics S, et al. Interindividual sleep spindle differences and their relation to learning-related enhancements. Brain Res. 2008;1191:127–35. doi: 10.1016/j.brainres.2007.10.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeck-Hirschner M, Baier PC, Sever S, Buschbacher A, Aldenhoff JB, Goder R. Effects of daytime naps on procedural and declarative memory in patients with schizophrenia. J Psychiatr Res. 2010;44:42–7. doi: 10.1016/j.jpsychires.2009.05.008. [DOI] [PubMed] [Google Scholar]
- Silvestri R, Raffaele M, De Domenico P, Tisano A, Mento G, Casella C, et al. Sleep features in Tourette’s syndrome, neuroacanthocytosis and Huntington’s chorea. Neurophysiol Clin. 1995;25:66–77. doi: 10.1016/0987-7053(96)81034-3. [DOI] [PubMed] [Google Scholar]
- Sim J, Wright CC. The kappa statistic in reliability studies: use, interpretation, and sample size requirements. Phys Ther. 2005;85:257–68. [PubMed] [Google Scholar]
- Spearman C. Correlation Calculated from Faulty Data. Br J Psychol. 1910;3:271–95. [Google Scholar]
- Tamminen J, Payne JD, Stickgold R, Wamsley EJ, Gaskell MG. Sleep spindle activity is associated with the integration of new memories and existing knowledge. J Neurosci. 2010;30:14356–60. doi: 10.1523/JNEUROSCI.3028-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wamsley EJ, Tucker MA, Shinn AK, Ono KE, McKinley SK, Ely AV, et al. Reduced sleep spindles and spindle coherence in schizophrenia: mechanisms of impaired memory consolidation? Biol Psychiatry. 2012;71:154–61. doi: 10.1016/j.biopsych.2011.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warby SC, Wendt SL, Welinder P, Munk EG, Carrillo O, Sorensen HB, et al. Sleep-spindle detection: crowdsourcing and evaluating performance of experts, non-experts and automated methods. Nat Methods. 2014;11:385–92. doi: 10.1038/nmeth.2855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webber WR, Litt B, Lesser RP, Fisher RS, Bankman I. Automatic EEG spike detection: what should the computer imitate? Electroencephalogr Clin Neurophysiol. 1993;87:364–73. doi: 10.1016/0013-4694(93)90149-p. [DOI] [PubMed] [Google Scholar]
- Westerberg CE, Mander BA, Florczak SM, Weintraub S, Mesulam MM, Zee PC, et al. Concurrent impairments in sleep and memory in amnestic mild cognitive impairment. J Int Neuropsychol Soc. 2012;18:490–500. doi: 10.1017/S135561771200001X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiegand M, Moller AA, Lauer CJ, Stolz S, Schreiber W, Dose M, et al. Nocturnal sleep in Huntington’s disease. J Neurol. 1991;238:203–8. doi: 10.1007/BF00314781. [DOI] [PubMed] [Google Scholar]
- Zygierewicz J, Blinowska KJ, Durka PJ, Szelenberger W, Niemcewicz S, Androsiuk W. High resolution study of sleep spindles. Clin Neurophysiol. 1999;110:2136–47. doi: 10.1016/s1388-2457(99)00175-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.