Steady-state functional MRI using spoiled small-tip fast recovery (STFR) imaging

Abstract

Purpose

To determine whether a recently-proposed steady-state magnetic resonance imaging (MRI) sequence, “small-tip fast recovery” (STFR), can be used for functional brain imaging. Compared to existing functional MRI (fMRI) based on T2*-contrast and long echo time (TE), STFR has the potential for high-resolution imaging with reduced B0 artifacts such as geometric distortions, blurring, or local signal dropout.

Methods

We used Monte Carlo Bloch simulations to calculate the voxel-averaged steady-state signal during rest and activation, for BOLD and STFR. STFR relies on a tailored “tip-up” radiofrequency (RF) pulse to align the spins with the longitudinal axis after each data readout segment, and here we performed proof-of-concept in vivo STFR fMRI experiments using a tip-up pulse tailored to a 2D region-of-interest (ROI) in motor cortex. Experiments were performed on multiple subjects to test reliability of the functional activation maps.

Results

Bloch simulations predict a detectable functional signal that depends mainly on intra-voxel dephasing, and only weakly on spin diffusion. STFR produces similar activation maps and signal change as BOLD in finger-tapping experiments, and shows reliability comparable to BOLD.

Conclusion

STFR can produce functional contrast (even with short TE), and is a potential alternative to long-TE (T2*) fMRI. The functional contrast arises primarily from the interaction between T2*-like dephasing and the tailored tip-up pulse, and not from spin diffusion.

Introduction

The majority of functional magnetic resonance imaging (fMRI) studies in the brain use T2*-weighted gradient-echo sequences with single-shot readout (blood oxygen level dependent (BOLD) fMRI) (1). The long echo time (TE) required to build up sufficient functional contrast makes BOLD fMRI susceptible to background B0 inhomogeneity unrelated to oxygenation, leading to signal dropout near air/tissue boundaries and geometric distortions or blurring. Steady-state fMRI based on passband balanced steady-state free precession (passband bSSFP) uses segmented readouts and can produce high resolution functional maps with reduced geometric distortions (2–8), but is susceptible to dark “banding” artifacts in regions of high B0 inhomogeneity and generally has lower functional contrast than BOLD (3).

Small-tip fast recovery (STFR) imaging is a recently-proposed steady-state imaging sequence (9). STFR relies on a tailored “tip-up”, or “fast recovery”, RF pulse to align the spins with the longitudinal axis after each data readout segment, such that the magnetization is preserved for the next TR and a T2 dependence is introduced. The design of the tip-up pulse is based on a separately acquired B0 map. STFR can provide bSSFP-like image contrast, but with reduced signal variations due to B0 inhomogeneity. However, it is not yet known whether STFR is suitable for fMRI, and whether the functional contrast mechanism is the same as in passband bSSFP.

Here we investigate the possibility of using STFR for steady-state fMRI, using Monte Carlo Bloch simulations and proof-of-concept in vivo functional imaging experiments. We first review the STFR imaging concept, and discuss potential functional contrast mechanisms. We then describe our steady-state Monte Carlo Bloch simulations that account for spin diffusion in a realistic microvascular environment. We continue by describing our STFR functional experiments, including the design of the tailored tip-up RF pulse. Our results indicate that STFR can produce reliable functional contrast(even with near-zero TE), and that diffusion plays only a minor role.

Theory

Small-tip fast recovery imaging

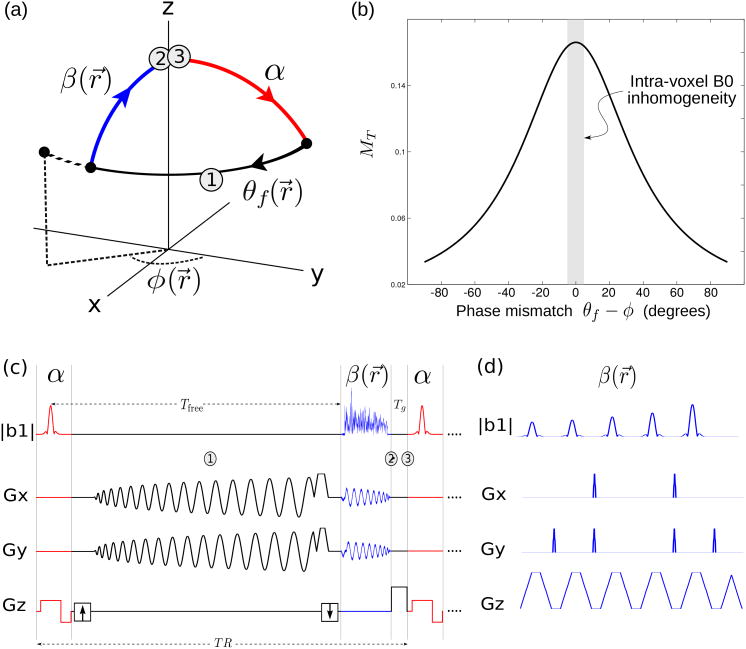
The STFR imaging principle is illustrated in Fig. 1. As in most conventional imaging sequences, a tip-down pulse α is first played out, and the signal is acquired during a free precession interval of duration T_free. During this interval, the spin precesses in the transverse plane by an angle

Figure 1.

Proposed STFR functional imaging sequence. (a) Steady-state spin path for a single spin isochromat. The tip-up pulse (blue) is tailored to the local free precession angle. In general, there will be a mismatch θ_f –φ between the spin phase at the end of the free precession interval (θ_f), and the phase (direction) of the tip-up pulse (φ). In STFR imaging, the goal is to design a tip-up pulse that minimizes θ_f –φ within the ROI. (b) Steady-state STFR transverse magnetization for a single spin isochromat as a function of phase mismatch θ_f –φ, calculated from Eq. [2]. The observed voxel-averaged signal is obtained by weighted integration of the signal profile over the B0 distribution within a voxel (Eq. [3], illustrated with shaded gray column). (c) Pulse sequence diagram for the STFR sequence used in the in vivo functional experiments (spiral tip-up pulse). (d) fast-kz tailored tip-up pulse (only 5 subpulses are shown).

$$\theta \left(\overrightarrow{r}\right)=\omega \left(\overrightarrow{r}\right){\mathrm{T}}_{\text{free}},$$ [1]

where ω(r⃗) is the spatially varying local B0 off-resonance frequency. After data readout, spins within the desired imaging region are tipped back toward the longitudinal axis (m_z) by a spatially-tailored tip-up pulse β(r⃗) that depends on θ(r⃗). The residual transverse magnetization remaining after the tip-up pulse can be spoiled using RF-spoiling, i.e., by inserting an unbalanced gradient area and cycling the RF phase quadratically (10). RF-spoiling has the additional benefit that it suppresses signal from outside the field-of-view (FOV) in the slice-select direction, and hence allows a thin slab (or slice) to be imaged by using a slab-selective tip-down pulse and a non-slice-selective tip-up pulse (9). The transverse magnetization for an isochromat is (9)

$$M_T=M_{0}sin\alpha \frac{e^{-T_g/T1}\left(1-e^{-{\mathrm{T}}_{\text{free}}/T1}\right)cos\beta +\left(1-e^{-T_g/T1}\right)}{1-e^{-T_g/T1}{e}^{-{\mathrm{T}}_{\text{free}}/T2}sin\alpha sin\beta cos\left({\theta }_f-\varphi \right)-e^{-T_g/T1}{e}^{-{\mathrm{T}}_{\text{free}}/T1}cos\alpha cos\beta }$$ [2]

where T_free is the free procession time, T_g is the duration of the gradient crusher, ϕ is the phase of the tip-up pulse, and α and β are the flip angle of tip-down pulse and tip-up pulse, respectively. Based on this equation, when there is no phase mismatch (φ = θ_f), the transverse magnetization would be close to passband bSSFP (see plot in (9)). Although STFR is a spoiled sequence, it still has T2 dependence since the transverse magnetization recovered by the tip-up pulse is a function of T2, and this magnetization will contribute to the final steady-state signal.

Possible functional contrast mechanisms in STFR: Diffusion and T2*

Increased brain activation is generally assumed to be accompanied by reduced B0 inhomogeneity within a voxel, due to decreased deoxyhemoglobin concentration resulting from overcompensatory arterial blood flow increases in response to increased oxygen demand (1). In conventional BOLD fMRI, these intra-voxel inhomogeneity changes are detected as changes in T2* using single-shot imaging with long TE. In passband bSSFP, on the other hand, functional contrast is believed to be driven at least in part by the interaction between spin diffusion and intra-voxel B0 inhomogeneity: during activation, diffusion-related deviations in spin free precession angle between RF excitations are reduced, leading to a signal change that can be modeled as a change in “apparent” T2 (6,8). The functional contrast mechanism is therefore (at least in part) decoupled from the choice of TE, enabling segmented readouts and hence reduced geometric distortions. Given the similarity between STFR and passband bSSFP (9), one might expect STFR to exhibit a similar diffusion-driven functional contrast.

In addition to spin diffusion, STFR has a second possible source of functional contrast, which arises from the dependence of the steady-state transverse magnetization on the mismatch between the spin phase after data readout (θ_f) and the phase (φ) of the tailored tip-up pulse (Fig. 1(a)). Fig. 1(b) plots the transverse magnetization for a spin isochromat as a function of the phase mismatch θ_f — φ, using Eq. [2]. The tip-up pulse is tailored to the mean phase of spins within a voxel, therefore, different spins in a voxel experience different phase mismatch and the total voxel signal must be obtained by weighted integration of the isochromat signal profile over the B0 distribution within a voxel (illustrated in Fig. 1(b)):

$$S\left(\overrightarrow{r}\right)=\int M_T\left({\theta }_f-\varphi \left(\overrightarrow{r}\right)\right)f_{\overrightarrow{r}}\left({\theta }_f\right)d{\theta }_f$$ [3]

where r⃗ is the voxel position, f_r⃗(θ_f) is the intra-voxel phase distribution for a voxel at r⃗, which is often modeled as a Lorentzian distribution. It is therefore possible that the interaction between the activation-induced change in the intra-voxel phase distribution and the tailored tip-up pulse can lead to a measurable signal change in spoiled STFR imaging.

It is not immediately clear (i) which of these mechanisms dominate, and (ii) whether they are sufficient to produce detectable functional signal. In this paper we use numerical Bloch simulations and in vivo functional experiments to address these questions.

Methods

Monte Carlo Bloch simulations

To investigate the functional contrast behavior of STFR, we performed time-resolved Bloch simulations similar to those in (6,8). We constructed a 1mm³ numerical 3D voxel model containing cylindrical vessels with random orientations. The simulated vessel diameters were in the range 5.6-60 μm (11). We assumed a constant blood fraction f_b = 7.3% (6), and venous oxygenation of 67% and 81% during rest and activation, respectively (12). We calculated the intra- and extravascular field according to Eqs. [4-6] in (6). To keep memory requirements manageable, only a 2D plane through the 3D numerical voxel was simulated, as in (6). Figure 2(a) shows the resulting 2D intra-voxel B0 field map.

Figure 2.

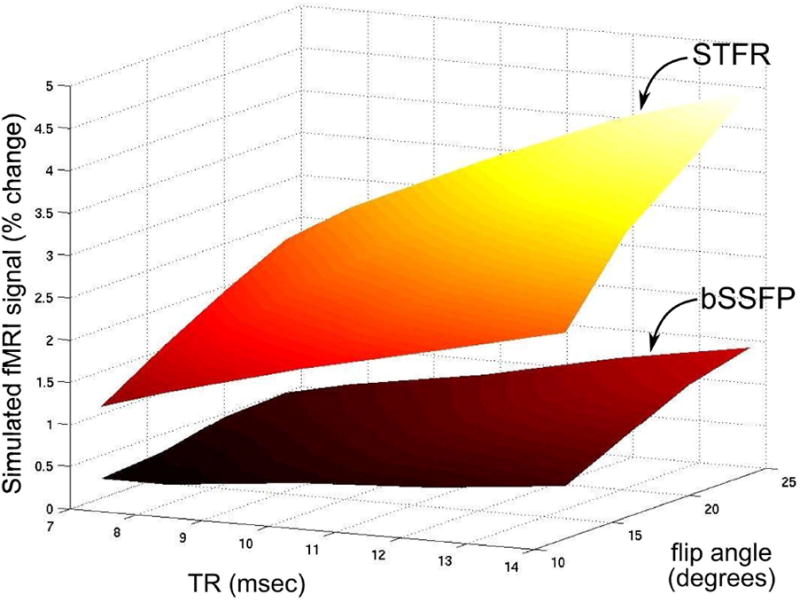
Monte Carlo Bloch simulation results. (a) Calculated microscopic B0 inhomogeneity (Hz) in the numerical voxel used in our Monte Carlo Bloch simulations. A 2D cut through the 1×1×1 mm³ voxel is shown. (b) Absolute functional signal change for STFR over a range of TRs and flip angles with and without diffusion. (c) Absolute functional signal change for STFR with respect to flip angle for several TRs used in our experiment. These simulations predict that STFR can produce a functional signal. The absolute signal change is maximized around 20°. “Turning off” spin diffusion has a relatively small impact on the functional signal, indicating that functional contrast in STFR arises primarily from the interaction between microscopic off-resonance and the tailored tip-up pulse, and not from spin diffusion. (d) The absolute signal change when the mean phase mismatch in a voxel is not 0 (equivalent to the weighted integration over a narrow spectrum off the center in Fig. 1-(b)). The functional signal change is maximized when mean phase mismatch for a voxel is 0.

We simulated the steady-state signals for STFR, both with and without diffusion. In each simulation, 2500 spins were randomly placed into the 2D numerical voxel. Spins were assigned a 2D random walk using diffusion coefficient of 0.001 mm²/s with 50μs simulation step size (6). We assumed circular voxel edge conditions (i.e., spins leaving the voxel at one edge were allowed to enter the voxel through the opposite edge). We used T1/T2=1470/71 ms in simulation (13). In the non-diffusion case, we fixed all spin locations and repeated the simulations. We simulated a range of TRs (8–24 ms) and flip angles (8°– 45°). We assumed non-selective 1.5 ms hard pulses, TE=1.8 ms (to match our STFR experiments), and 1.2 ms gradient crusher for STFR. We ran the simulations for a duration of 5.5×T₁ prior to “recording” the signal to establish a steady state.

For reference, we also simulated the spoiled gradient echo (GRE) BOLD with 16° flip angle, 44 ms TR, and 32 ms TE, which is matched to our experiments. For computational efficiency, we assumed ideal RF spoiling for STFR and BOLD in the simulation, in other words, the transverse magnetization is set to 0 prior to each tip-down pulse. We implemented the Bloch simulator in Matlab using C-mex files, available online (http://www.eecs.umich.edu/∼sunhao).

Functional imaging

To establish whether STFR can produce useful functional contrast, we performed fMRI experiments in 5 healthy volunteers. Table 1 summarizes these experiments. We performed all imaging experiments on two different GE 3T scanners equipped with quadrature transmit/receive head coils. The subjects performed bilateral finger-tapping, using 5 cycles of a 20 second on, 20 second off, block paradigm. We used checkerboard visual stimulation to cue the subject to begin/end finger tapping.

Table 1.

Summary of fMRI experiments.

Subject	A, Session 1	A, Session 2	B to E
Region	Motor	Motor	Motor
Sequence(s)	STFR/BOLD	STFR	STFR/BOLD
No. Repetitions	5	1	3 to 5
Tip-up pulse	fast-kz (7 ms)	spiral (4.5 ms)	fast-kz (7 ms)
TR (ms)	20.2/43.4	18	24/44
Frame rate (s)	1.62/3.47	1.44	1.92/3.52
TE (ms)	1.8/32	1.8	1.8/32
Flip-angle (°)	16/16	16 and 8	16/16
Results	Fig. 3, Fig. 4	Fig. 5	Fig. 4

We repeated the fMRI run 3-5 times for each subject, to quantitatively compare STFR and BOLD in terms of test-retest reliability (14,15). The number of repeated scans varied across subjects (from 3 to 5) depending on how long the volunteer could comfortably stay in the scanner. One subject was scanned in a second session to demonstrate: (1) the effect of varying flip angle, and (2) the use of an alternative tip-up pulse design (spiral).

We acquired time-series image volumes using the sequence shown in Fig. 1(c,d), which consists of a 3 cm axial slab-selective Shinnar-Le Roux tip-down pulse (16), a balanced 3D stack-of-spirals readout, and a tailored tip-up pulse. Other sequence parameters were: 5 cm FOV with 10 partitions in z; 8 spiral kx-ky segments supporting 128×128 matrix size; in-plane FOV 24 cm. To suppress out-of-slab steady-state signal formation (primarily a concern when using non-slice-selective tip-up pulses such as spiral), we used RF-spoiling with 117° linear phase increment, as described in (9).

To minimize the possible influence of eddy-currents on the steady-state, we minimized the frequency of large jumps in k-space (caused, e.g., by rotating the spiral leafs) by acquiring all z partitions in linear fashion before moving to the next spiral leaf, and by alternating the direction of kz-space traversal when jumping to the next spiral leaf (17,18).

In each scan session, we tailored the tip-up pulse to a 2D region-of-interest (ROI) containing most of the central slice, but excluding regions with severe B0 inhomogeneity if present (such as the frontal sinus). To design the pulse, we acquired an axial 2D B0 map ω(x, y) located at the center of the 3D fMRI image volume (z=0). We calculated the 2D B0 map from two spoiled gradient-echo (SPGR) images with echo time difference of 2.3 ms to minimize the contribution of fat to the measured image phase difference (flip angle 16°; 64×64 matrix size).

We designed the tailored tip-up pulses using two different RF designs: fast-kz (19) and spiral. The fast-kz (spoke) pulse is longer and can be tailored to only relatively smooth in-plane phase patterns, but it has the advantage that there is no out-of-slice signal. The fast-kz tailored tip-up pulse duration was 7 ms, and consisted of 10 slice-selective subpulses at different kx-ky locations. We designed the kx-ky locations and RF waveform jointly using a greedy approach as in (20). The spiral non-slice-selective tailored tip-up RF waveform was 4.5 ms, designed as in (9). We used the small-tip (Fourier) approximation (21) and the discretized design method in (22), implemented with the IRT Matlab toolbox (http://www.eecs.umich.edu/∼fessler). In our current experimental setting, after we acquire the B0 map, the system will automatically trigger the pulse design code and then transfer the pulse to the scanner. The total overhead for the B0 acquisitions and RF pulse creation was ∼2 min.

We designed a 2D, rather than 3D, tip-up pulse to ensure accurate tip-up pulses in the center slice with acceptable pulse duration. Hence, these functional experiments were designed as proof-of-concept experiments, i.e., to investigate whether STFR can in fact produce functional contrast; A true 3D functional experiment would require a tip-up pulse tailored to a 3D ROI, which would extend the RF pulse duration significantly unless using transmit coil arrays. We also note that we could in principle have performed single-slice functional experiments for our purposes here; however this could have introduced slice-profile errors and blood in-flow effects that could have confounded the results.

fMRI processing and analysis

We reconstructed 3D image volumes using iterative nonuniform fast Fourier transform (NUFFT) (23,24) in the axial plane with second order roughness penalty and no B0 correction, and FFT in the through-slab (z) direction. The iterative algorithm was run for 15 iterations. We performed 2D image co-registration along the temporal dimension for each slice. We then applied linear time drift removal for each pixel. We correlated the resulting filtered time-series with the block stimulus to obtain a correlation value for each voxel.

We estimated test-retest reliability following (14, 15). Specifically, this analysis is based on calculating activation maps using multiple activation thresholds, and obtaining a maximum likelihood estimate (MLE) of sensitivity and false positive rate at each threshold. These rates are then plotted to form a receiver operating characteristic (ROC) curve for each subject, which gives a quantitative reliability measure for each acquisition method (STFR and BOLD). The MATLAB code is available on line (http://www.eecs.umich.edu/∼jfnielse).

Results

Bloch simulation results

Figure 2 shows the simulated functional signal change for STFR (both with and without diffusion) over a range of TRs (8 ms – 24 ms) and flip angles (8° – 45°). Figure 2(b) shows the absolute signal change, i.e., as a fraction of M₀, over a range of TR and flip angles, which predicts that STFR can in fact produce a functional signal. Figure 2(c) shows the absolute signal versus flip angle for several TRs, to investigate the optimal flip angle for different TR. The absolute signal change is maximized around 20° flip angle, and increases with increasing TR. “Turning off” spin diffusion in the simulation has a relatively small impact on the functional signal, indicating that functional contrast in STFR is primarily driven by the interaction between microscopic off-resonance and the tailored tip-up pulse (as illustrated schematically in Fig. 1(b)). As a reference, the simulated percent and absolute functional signal change of the spoiled GRE BOLD sequence (TR = 44 ms, TE = 32 ms, flip angle = 16°) is 5.2 % and 0.0037 respectively. Note that the percent signal change of conventional BOLD is 44% higher than STFR with TR = 20 ms, flip angle = 16°, but the absolute signal change is 10% lower.

The simulation was performed assuming the tip-up pulse perfectly matches the mean accumulated phase of each voxel, which corresponds to a weighted integration over a narrow spectrum located in the center of Fig. 1(b). We also simulated the absolute signal change when the mean phase mismatch is not 0 (that would correspond to a weighted integration over a narrow spectrum off the center), and the result is shown in Fig. 2(d), which predicts that the functional signal change is maximized when mean phase mismatch is 0°.

Functional imaging

Figure 3(a) shows the thresholded correlation maps of STFR and BOLD imaging for 5 scans in one subject (A, Session 1). Both STFR and BOLD show high correlation in the motor cortex areas. To quantitatively evaluate the functional signal, we first selected a region of interest (ROI) by choosing all the pixels that show activations in at least 4 scans in both STFR and BOLD (see Fig. 3(b)), and then obtained the signal time course for voxels within that ROI. The absolute signal change is shown in Fig. 3(c), which was obtained by normalizing each time course by its corresponding background noise, and then taking the mean within the ROI. The percent signal change is shown in Fig. 3(d). STFR shows slightly smaller percent signal change than BOLD, but larger absolute signal change, as predicted in simulation. The measured percent signal change is reported in Table 2, and is in good agreement with simulation results, scaled by an arbitrary factor (1.2 times). Also, the measured result agrees with the simulation prediction that STFR has higher absolute signal change than BOLD.

Figure 3.

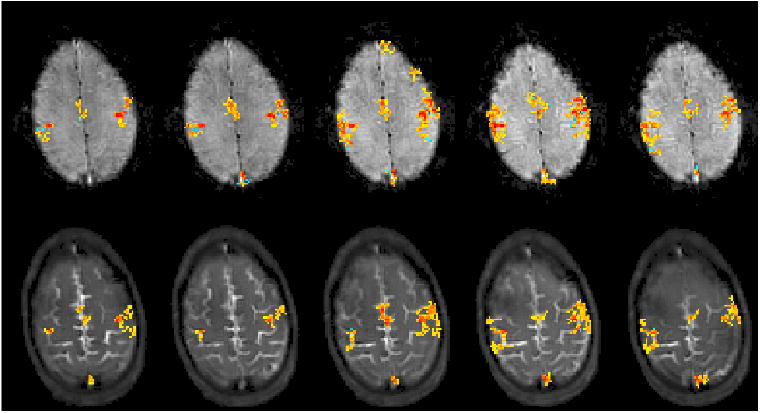
Repeated motor cortex imaging using STFR and BOLD in one subject (A, Session 1). (a) Activation maps with correlation threshold 0.3 and cluster size 10 (28). All five scans demonstrate that STFR can produce similar activation maps as BOLD, which are well localized to the motor cortex area. (b) ROI used to calculate the mean time course for each sequence, obtained by selecting the pixels showing activations in at least 4 scans in both BOLD and STFR. (c,d) One cycle of the mean time course signal over the ROI, shown as absolute (c) and relative (d) changes. In (c) the signal level is scaled by the corresponding background noise, and in (d) the rest state signal is normalized to be 1. STFR has slightly lower relative signal change than BOLD, but higher absolute signal change (i.e., higher CNR), as predicted in simulation. The calculated functional signal change is reported in Table 2.

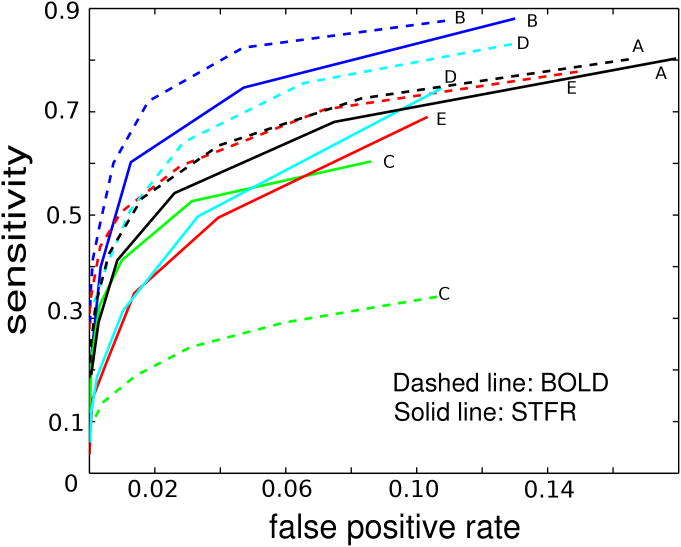
Figure 4 shows ROC curves for STFR and BOLD in 5 subjects (A-E). STFR functional imaging shows good reliability in general, but slightly lower than conventional BOLD. One BOLD curve had very low reliability, which may be due to motion artifact (observed in the functional maps for that subject).

Figure 4.

Summary of test-retest reliability results for 5 different subjects (Subjects A–E), calculated using the method in (14,15) from motor cortex imaging data. The ROC curves for STFR are generally slightly lower than BOLD, but still demonstrate that it is a reliable sequence for detecting functional activity. One BOLD curve (C) is much lower than other curves, which is probably due to the motion artifact we observed in that set of data.

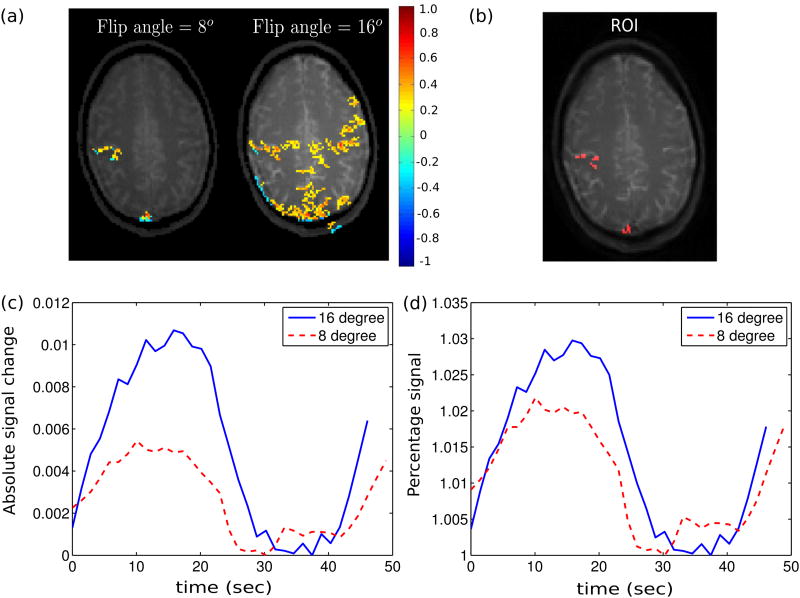
Finally, Fig. 5 shows STFR functional imaging results of one subject for two different flip angles (8° and 16°). Imaging with 16° flip angle results in more active voxels in the expected region compared to 8°. To quantitatively compare the results for different flip angles, we plotted the mean time course over an ROI in Figs. 5(c) and 5(d). The ROI is chosen by selecting the voxels that are classified as active in both flip angle acquisitions. Higher flip angle has more absolute and percent signal change, which agrees with the simulation.

Figure 5.

Effect of flip angle on functional signal in STFR. (a) Correlation map obtained with STFR fMRI, using flip angles 16° and 8°. Threshold and cluster size are 0.22/12 for both flip angle acquisitions. (b) ROI used to calculate the mean time course for each flip angle, which includes pixels showing activation in both flip angle acquisitions. (c,d) One cycle of mean time course within ROI. 16° flip angle produces higher absolute and percent functional signal change compared to 8° flip angle, as predicted in simulation.

Discussion

The Bloch simulation results suggest that the STFR functional signal arises primarily from interactions between the intra-voxel dephasing and the tip-up pulse. If we ignore the relatively small diffusion effect, we can obtain the STFR functional signal by numerical weighted integration of the steady-state signal over the intra-voxel frequency distribution as in Eq. [3], instead of performing a full Monte Carlo Bloch simulation. Using this method, we predict a 3.3% signal change, which is close to the Monte Carlo simulation result of 3.6%.

The dephasing effect in STFR is similar, but not exactly the same as the T2* effect in the conventional BOLD sequence. We can not simply replace T2 in Eq. [2] with a conventionally defined T2*, i.e., 1/T2* = 1/T2 + 2πγ, where γ is the half-width at half-maximum (HWHM) of the intra-voxel Lorentzian distribution, to obtain the voxel signal. Fitting a Lorentzian line shape to the simulated frequency distribution with T2 = 71 ms (13) yields T2* values of 62 ms and 68 ms in rest and active conditions, respectively (we have not found literature supporting those T2* values but we believe T2* change of this size is reasonable, as it would produce a ∼ 4% BOLD functional change assuming TE=30 ms, which is within the commonly observed range). By replacing T2 with T2* in Eq. [2] we obtain a percentage signal change of 7.0%, which is almost twice the contrast obtained from Monte Carlo simulation or numerical integration, supporting the idea that the functional contrast mechanism is not quite the same as T2* decay. In addition, from Eq. [2], we note that T2 is paired with T_free, not TE, which decouples the main source of functional signal from TE.

In our Monte Carlo Bloch simulations, we observed that the effect of diffusion is to increase the image signal and decrease the functional contrast compared to the result without diffusion (see Fig. 2). We think the reason for this change is that with diffusion, spins effectively experience different frequencies during the free precession interval, and that the accumulated phase therefore tends to be closer to the mean phase of that voxel. This effectively narrows the line spread of the intra-voxel distribution, which increases the image signal but decreases the functional contrast.

Flip angle and TE are two other variables that affect the signal contrast. We used 16 degrees in most of our experiments, which is approximately the Ernst angle for the BOLD acquisitions (assuming a T1 of about 1.1 sec). According to the simulation in Fig. 2(b), a flip angle around 20 degrees generates the maximum absolute signal change. We used the minimum available TE for STFR in our experiments, but we found later in simulation that the functional signal increases with increasing TE (not shown here), probably due to the normal T2* effect. This suggests that a spiral-in readout rather than a spiral-out readout could be used to increase the effective TE and therefore the functional signal.

Physiological fluctuations in B0 (e.g., due to respiration) would shift the voxel signal as a whole along the curve in Fig. 2(d), which would reduce the functional contrast. We expect the B0 shift due to respiration to be of order 1-2 Hz at 3T (fluctuations of 1.45-4 Hz have been reported at 7T (25)), which would not shift the voxel signal significantly (e.g., 5-11 degrees assuming T_free = 15 ms) along the curve in Fig. 2(d). In the experiments presented here we have not observed significant physiological noise increases in STFR compared to BOLD.

A potential advantage of STFR compared to BOLD is that it can achieve high resolution segmented 3D imaging with reduced signal loss and image distortion. However, to achieve this across the whole brain, a 3D tailored tip-up pulse would be necessary, which may be prohibitively long. We have suggested methods for improving 3D tailored pulse design (26), but it is still challenging to tailor to the whole brain including regions with high field inhomogeneity (e.g., near frontal sinus). A potential solution is to use parallel transmission to reduce the pulse duration, and we plan to explore the feasibility of 3D STFR functional protocol using an 8-channel parallel transmit head array (27).

Conclusions

Taken together, the work presented here indicates that STFR has the potential to become a sensitive functional imaging modality. The functional contrast mechanism is decoupled from the echo time, enabling segmented readouts and high image quality. Our Monte Carlo Bloch simulations indicate that STFR fMRI can produce observable functional contrast, and proof-of-concept in vivo STFR fMRI observations using a 2D tailored tip-up pulse support this prediction. Our simulations also indicate that the functional contrast in STFR is driven primarily by the interaction between microscopic off-resonance and the tailored tip-up pulse, and that diffusion plays a relatively minor role. In the future, we plan to evaluate the feasibility of whole-brain STFR fMRI, using 3D tailored tip-up pulses. We expect the design of such 3D pulses to benefit greatly from parallel transmission systems, high-order gradient shimming, and novel RF pulse design approaches.

Table 2.

Simulated and measured functional signal change.

	Percent Signal Change (BOLD / STFR)	Absolute Signal Change (BOLD / STFR)
Simulation	5.2 % / 3.6 %	0.9
Measurement	4.1 % / 3.1 %	0.75