Heterogeneity of functional groups in a metal–organic framework displays magic number ratios

Significance

Arranging multiple component types in a controlled manner within solid frameworks may one day allow us to combine the heterogeneity characteristic of biological materials with the robustness characteristic of synthetic ones. Here, we report the synthesis of a metal–organic framework whose two component types are incorporated within it in a manner that is robust with respect to changes of solution composition. Calculations done on a model system suggest that this robustness occurs because component types become kinetically trapped during framework growth. Our calculations also show how different controlled arrangements of component types might be obtained by varying their noncovalent interactions, or by varying the topology of the covalent framework within which they are housed.

Abstract

Multiple organic functionalities can now be apportioned into nanoscale domains within a metal-coordinated framework, posing the following question: how do we control the resulting combination of “heterogeneity and order”? Here, we report the creation of a metal–organic framework, MOF-2000, whose two component types are incorporated in a 2:1 ratio, even when the ratio of component types in the starting solution is varied by an order of magnitude. Statistical mechanical modeling suggests that this robust 2:1 ratio has a nonequilibrium origin, resulting from kinetic trapping of component types during framework growth. Our simulations show how other “magic number” ratios of components can be obtained by modulating the topology of a framework and the noncovalent interactions between component types, a finding that may aid the rational design of functional multicomponent materials.

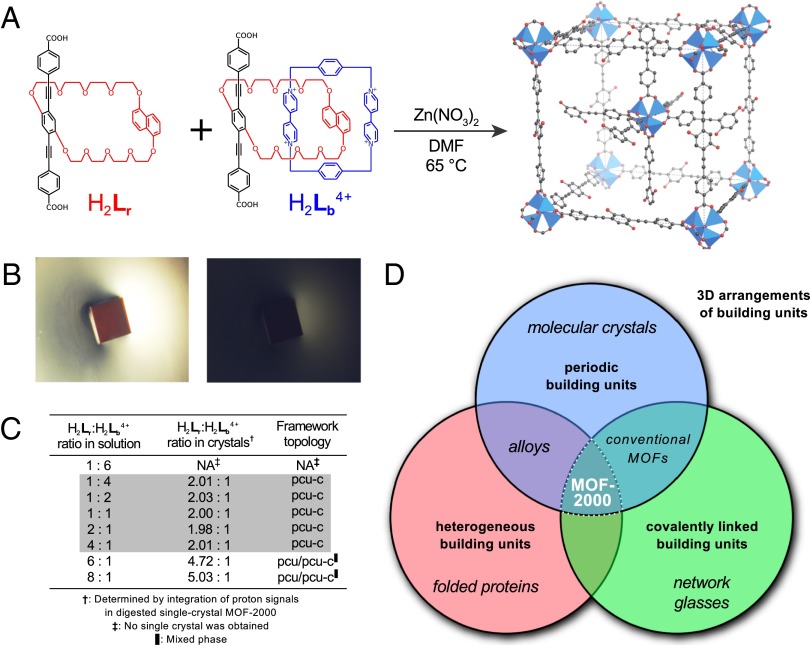
The assembly of multiple types of component offers a potential route to the precise control of component heterogeneity within ordered 3D frameworks. Metal–organic frameworks (MOFs) (1–5) possessing well-defined connectivities (6, 7) and tunable pore sizes (8–10) can assemble from a variety of building blocks (11–17). Recently, a MOF harboring two components distributed in a heterogeneous fashion on an ordered framework was demonstrated (1, 2). There exists no framework, however, whose component heterogeneity remains controlled in the face of changes of environment. Here, we report the creation of a material with exactly this property. MOF-2000 is assembled from two types of organic struts, called L_r and L_b (Fig. 1A). These struts have identical rigid backbones but bear either a crown ether (L_r) or [2]catenane (L_b) side chain attached at their center. X-ray diffraction of MOF-2000 single crystals revealed that struts form a twofold interpenetrated cubic framework of pcu-c topology (Fig. 1A, Right, and SI Appendix, section S1.3; structure available in Dataset S1). As a result of optical investigations, we confirmed that the two struts are distributed in the crystalline framework in an isotropic manner (Fig. 1B), suggesting that the two components are not distributed in a simple periodic way throughout the framework (because such arrangements would give rise to optical anisotropy; SI Appendix, section S1.5).

Fig. 1.

MOF-2000 is a periodic framework harboring controlled component heterogeneity. (A) Chemical structures of organic struts H₂L_r and H₂L_b⁴⁺ incorporated in MOF-2000 (Methods Summary), and the MOF-2000 crystal structure [key: carbon, black; oxygen, red; Zn₄O(CO₂)₆ polyhedra, blue; all hydrogen atoms have been omitted for clarity]. (B) Optical images of MOF-2000 single crystal: without polarizer (up) and in between crossed polarizers (down). The lack of birefringence indicates that MOF-2000 is optically isotropic. The edge of the crystal is about 0.1 mm. (C) As determined by ¹H-NMR and powder X-ray diffraction measurements (SI Appendix, sections S1.3 and S1.4), MOF-2000 consists of a twofold interpenetrated crystalline framework (of topology pcu-c) of 2:1 L_r:L_b ratio (estimated 5% error), for a wide range of solution ratios (shaded region). (D) MOF-2000 therefore combines the regularity of a covalent framework with controlled irregularity of its components.

Even though the arrangement of the two components in MOF-2000 is indiscernible by X-ray crystallography, presumably as a result of the positional disorder of the two strut types within the framework, and the rotational (11, 18) and conformational (11) disorder of the side chains, the presence of the two organic struts can be clearly determined by ¹H-NMR (SI Appendix, section S1.4). Strikingly, MOF-2000 displays a 2:1 ratio of L_r and L_b struts, even when the ratios of components in the parent solution are varied by over an order of magnitude (Fig. 1C). This feature makes MOF-2000 unique among multicomponent extended frameworks, whose struts are usually incorporated in ratios determined largely by initial solution conditions (1, 19). Thus, MOF-2000 incorporates environmentally robust component heterogeneity within a regular covalent framework (Fig. 1D).

The robust 2:1 composition does not have an obvious thermodynamic origin, in contrast to common organic cocrystals or ionic systems such as CsCl (20). The latter possess robust compositions as a consequence of charge complementarity. In MOF-2000, the L_b strut bears a charge of +4 (neutralized in the assembly by counterions), whereas the L_r strut is uncharged. Thus, charge complementarity alone does not suggest a 2:1 component ratio. Simple packing arguments suggest that it is reasonable that L_b is not the majority species within the framework (because it is bulky), but likewise do not offer a simple explanation for the 2:1 ratio.

Modeling MOF-2000

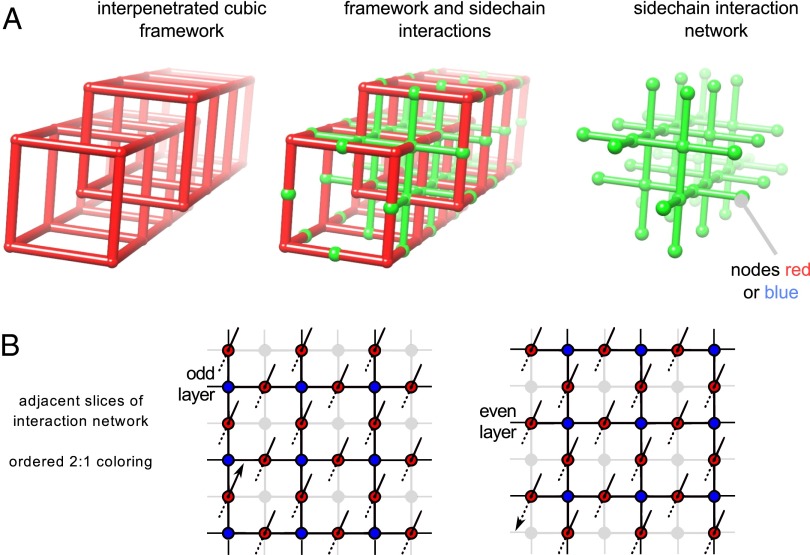
To make further progress in understanding this robust ratio, we built a simple and physically motivated computer model of MOF-2000. As its degrees of freedom, the model considers the type of strut at a given spatial location (a “node”) within the framework (Fig. 2A, Left). Each node is colored red or blue, representing the struts L_r or L_b, respectively. Because the physically interpenetrated cubic lattices that comprise MOF-2000 present each node with four nearest-neighbor nodes, all on the adjacent cubic lattice, we allowed each node to interact energetically with its four nearest neighbors (green bonds between nodes; Fig. 2A, Middle). The nodes and noncovalent interactions between nearest neighbors comprise a “virtual” side-chain interaction network with nbo topology (Fig. 2 A, Right, and B). Because side chains likely possess considerable conformational and rotational freedom, we assume they do not interact in a directional manner. We therefore considered only isotropic interaction energies between nodes. As an additional simplifying assumption, we made these interactions pairwise: bonds between red nodes have energy ε_r-r; bonds between blue nodes have energy ε_b-b; and red–blue bonds have energy ε_b-r. For the purposes of structure sampling, we considered only fully populated lattices, and without loss of generality we set ε_r-r to zero. The resulting description of MOF-2000 is equivalent to the Ising model on an nbo framework (SI Appendix, section S2.1).

Fig. 2.

MOF-2000 simulation model. (A) Mapping of the physical framework pcu-c onto an nbo network of interacting side chains. L_r (respectively, L_b) side chains are represented by red (respectively, blue) nodes. Nearest-neighbor nodes interact energetically. (B) Adjacent 2D slices of the interaction network, with in-plane and out-of-plane interactions marked (the two arrows connect one particular out-of-plane interaction). The network is colored in a regular 2:1 fashion for the purposes of illustration. The corresponding experimental side-chain arrangement is ruled out by MOF-2000’s optical isotropy.

Local Energy Minima of the MOF-2000 Interaction Network Display “Magic Number” Component Ratios for Particular Hierarchies of Interaction Energies

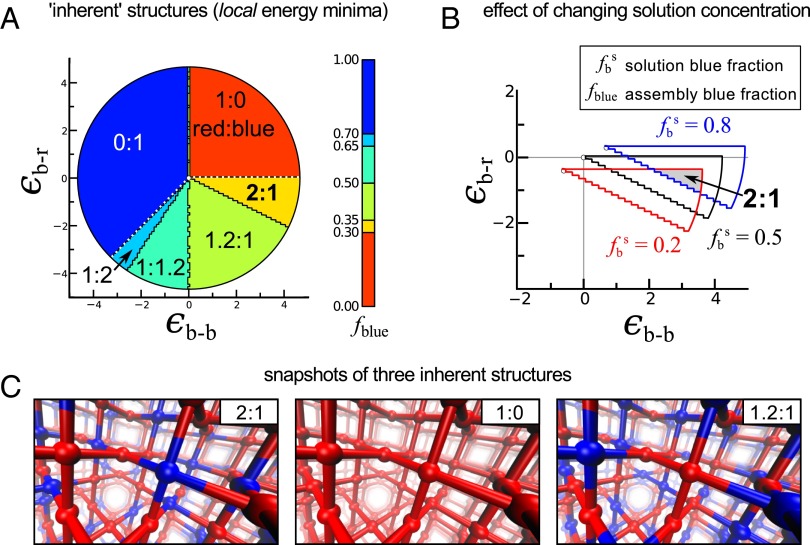
Standard Monte Carlo simulations (Methods Summary) of this model revealed no thermodynamically stable 2:1 red:blue phase at any temperature (SI Appendix, Figs. S10 and S11). As shown in Fig. 3, however, there does exist a set of nonequilibrium states of the model that display such a ratio. These nonequilibrium states correspond to “inherent structures” (or “local energy minima”) of the model Hamiltonian (21, 22). To generate these structures, we started with a framework whose nodes were colored randomly red or blue (SI Appendix, Fig. S13), and we repeatedly accepted proposed changes of color, of randomly chosen single nodes, that did not increase the system’s energy. Although this procedure does not correspond to a physical dynamics, it reveals the energy minimum “closest” (in the sense of distance in phase space) to a starting “solution” of randomly mixed red and blue components. This closeness suggests that such states may be kinetically accessible during growth from solution; we shall see later that simplified growth simulations indeed reproduce these inherent structures in certain regimes of parameter space.

Fig. 3.

Local energy minima (inherent structures) of the MOF-2000 simulation model have a 2:1 red:blue ratio for a particular hierarchy of interaction energies. (A) MOF-2000 interaction networks were simulated for a range of red–blue (ε_r-b) and blue–blue (ε_b-b) node interaction energies. Inherent structures (local energy minima) possess well-defined magic number component ratios; these depend in an abrupt way on the hierarchy of interaction energies (SI Appendix, Fig. S14). Below the dotted white line, node–node interaction energies are antiferromagnetic, in Ising model language, meaning that red and blue nodes attract; this is a necessary condition for nontrivial component ratios (i.e., 1:0 and 0:1 are trivial ratios). The 2:1 structures (yellow sector) are found in a region of phase space for which the thermodynamic structure is a binary 1:1 coloring (SI Appendix, Fig. S11), and are made of a patchwork of binary domains (Fig. 4). (B) Magic number ratios are robust to solution conditions: here, we vary the fraction f_b^s of blue nodes in implicit solution from 0.2 to 0.8. (C) Snapshots of the three inherent structures seen for this framework.

The 2:1 kinetic traps obtained by the inherent structure procedure are found in a region of parameter space in which red and blue nodes attract, and blue nodes repel (Fig. 3A). The noncovalent side-chain–side-chain interactions implied by these parameters appear to be physically reasonable: molecular considerations suggest that L_r and L_b struts may engage in aromatic donor–acceptor attractions (23)—and the fact that they become incorporated within the same framework indicates that they attract each other—and L_b struts are bulky and may repel in an entropic sense. It is important to note, however, that there is no direct mapping between our simulation interactions and those of the real framework. Our simulated 2:1 structures are robust to changes of “solution composition” (Fig. 3A, Right), which we mimicked computationally by including a chemical potential term [μ_C(i)] in our energy minimization procedure (Methods Summary).

In addition to the 2:1 local energy minima, there also exist local energy minima with 1:0 and 1.2:1 component ratios, as well as the corresponding reverse ratios (Fig. 3A). These ratios are “magic” numbers in the sense that we observe abrupt “transitions” between them as we vary the magnitudes of component interaction energies (SI Appendix, Fig. S14). A requirement for nontrivial ratios (here, 2:1 and 1.2:1) is that blue and red nodes prefer to be neighbors within a framework, rather than to be apart. A necessary condition for such correlation is that model energetics are, in Ising model language, “antiferromagnetic” (meaning that “red–blue” interactions have lower energy than “blue–blue” and “red–red” ones; see dotted white line in Fig. 3A). This observation suggests that one requirement for robust component ratios away from equilibrium is a particular hierarchy of noncovalent interactions between component types.

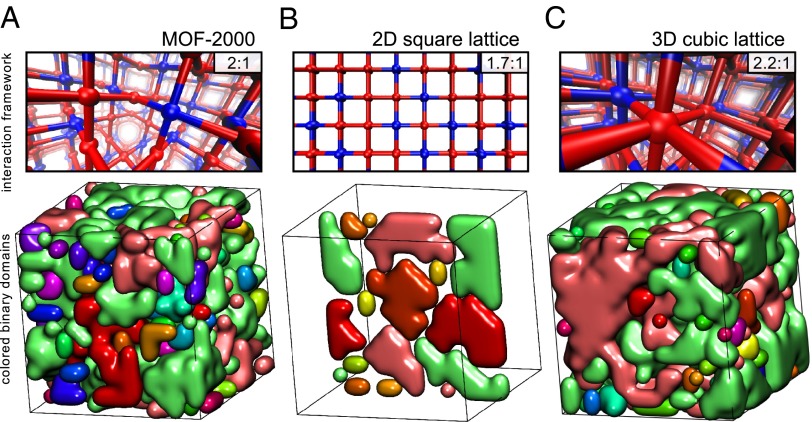
The 2:1 Local Energy Minima Are “Compositional Polycrystals” That Possess Spatial Properties Consistent with Those Seen in Experiment

The 2:1 local energy minima are aperiodic and isotropic, consistent with structures seen in experiment (Fig. 1B), and can be thought of as compositional polycrystals (Fig. 4A). These we define as materials whose physical structures are periodic, but whose compositional degrees of freedom, i.e., component types, are distributed within those structures as a patchwork of domains of particular composition that meet at grain boundaries of different composition. The 2:1 structures are found in a region of phase space in which the thermodynamic ground state (“global energy minimum”) is an ordered 1:1 antiferromagnetic lattice (meaning that each node has four nearest neighbors of the other color). If we color the 2:1 structures according to their antiferromagnetic order, by identifying domains in which all nodes have only unlike nodes as neighbors, then the resulting pictures are a patchwork of domains or “grains” that are separated by all-red regions that we call “grain boundaries” (Fig. 4A, Bottom). Although an anisotropic and ordered 2:1 decoration of the nbo lattice exists (Fig. 2B and SI Appendix, Figs. S6 and S15), it is not accessible via this simulation procedure.

Fig. 4.

The 2:1 inherent structures are compositional polycrystals of binary order, and the numerical red:blue ratio depends on framework topology. (A) Simulated 2:1 structures are compositional polycrystals, sections of 1:1 thermodynamically preferred order that meet at red grain boundaries (SI Appendix, Figs. S16 and S22). The lower panel shows distinct regions of 1:1 order in different colors. (B) The corresponding structures on a 2D square lattice possess a red:blue ratio of 1.7:1, demonstrating that the component magic number ratio depends on the topology of the framework, not just its local connectivity. (C) The corresponding ratio is 2.2:1 on a 3D cubic lattice, showing that dimensionality alone does not control the magic number ratio. Magic numbers obtained for a range of local connectivity and dimensionality (SI Appendix, Fig. S20) further support the idea that magic number ratios may be tuned by the choice of framework topology.

The 2:1 ratio of the model local energy minima emerges from a combination of 1:1 ordered domains and all-red (1:0) grain boundaries. The exact numerical ratio of red:blue nodes found in simulation agrees with the value measured experimentally (Fig. 1C) and is a property of the overall topology of the nbo graph, not just its local connectivity. When we repeated the inherent structure procedure for a 2D square lattice (Fig. 4B)—which shares nbo’s fourfold local connectivity but not its nonlocal connectivity (SI Appendix, Fig. S19)—we found that structures in the corresponding region of phase space look qualitatively similar, but possess a red:blue ratio of 1.70:1 (Fig. 4B and SI Appendix, Fig. S18). The corresponding ratio for the 3D cubic lattice (a possible interaction network of, e.g., MOF-5) is different again, 2.2:1 (SI Appendix, Fig. S21). The precise magic number ratio appears therefore to be a function of both the noncovalent interactions between side chains, and the framework topology.

Growth Simulations Reveal That Magic Number Component Ratios Emerge for Particular Hierarchies and Scales of Component Interaction Energies

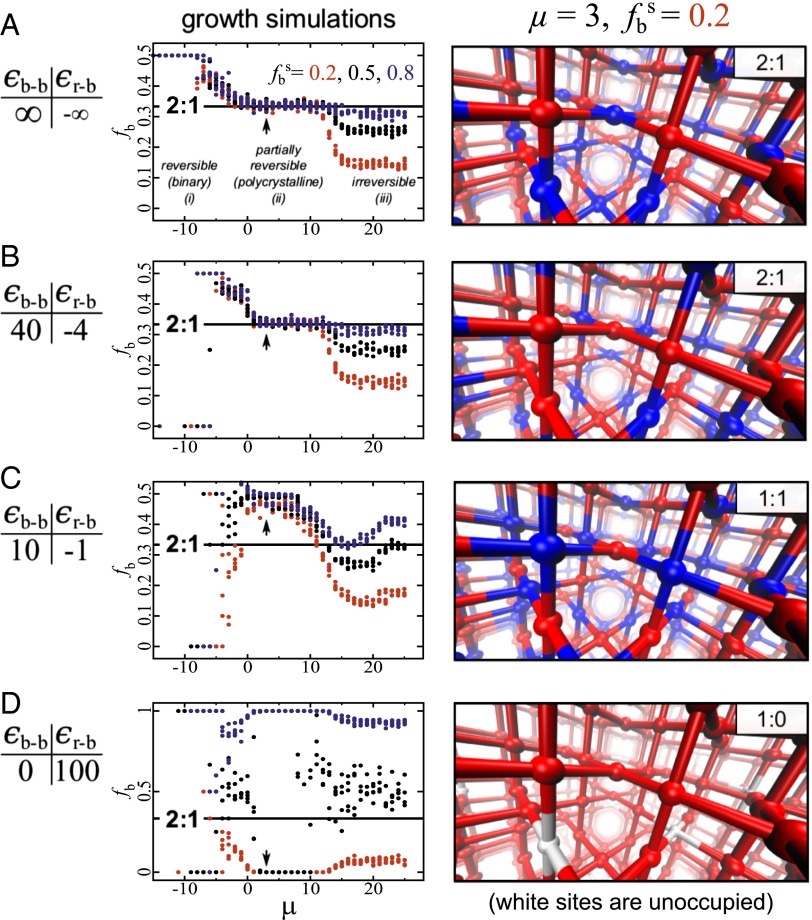
With the objective of connecting our simulation approach more closely to a possible assembly pathway of MOF-2000, we carried out a simple Monte Carlo growth protocol (Methods Summary). In this protocol, all nodes in the system were unoccupied (colored white) initially and were allowed to become occupied (blue or red) under a standard grand-canonical Monte Carlo protocol. Rates of binding of red and blue nodes then depend on node–node interaction energies. The overall growth rate of a red–blue structure is controlled by a term μ, related to the chemical potential of side chains in the parent solution, which sets the relative energetics of unoccupied and occupied nodes. Our growth protocol assumes implicitly that rates of establishment of covalent linkages are modulated by side-chain–side-chain noncovalent interaction energies. Experiment indicates that this assumption must be true, because otherwise the two component types—which form identical covalent linkages—would simply be incorporated into the framework at the ratio at which they are present in the parent solution.

In Fig. 5A, we show the results of growth simulations done using node interaction energies taken from the regime in which 2:1 inherent structures (Fig. 3A) were found. For simplicity, we arranged for a clear separation in scales of node interaction energies (and hence binding rates). We set ε_b-r large and negative, and ε_b-b large and positive (with ε_b-r/ε_b-b → 0), so forbidding blue–blue contacts and making red–blue contacts effectively unbreakable. We set ε_r-r = 0 and k_BT = 1. The thermodynamically stable structure in this regime is the 1:1 antiferromagnetic coloring, in which each node possesses four neighboring nodes of the other color.

Fig. 5.

The nonequilibrium 2:1 structures seen in simulations can be generated by simple “growth” simulations, provided that noncovalent interaction energies possess a certain hierarchy and scale. (A) Grand-canonical growth simulations of the model as a function of basic rate of growth (controlled by a chemical potential μ) show three distinct regimes, of which the partially irreversible regime recapitulates the 2:1 structure (a snapshot is shown to the Right). This regime is also robust to a range of relative concentrations of blue nodes in implicit solution (colored lines). (B and C) Growth simulations done using the same hierarchy of interaction energies but reduced interaction energy scales show the plateau region to shrink (B) and eventually vanish (C). (D) Similarly, a different (ferromagnetic) hierarchy of interaction energies shows no solution-invariant magic number regime.

As seen in Fig. 5A, the nature of the structure generated dynamically depends on μ, the growth chemical potential. When μ is large and negative, only blue–red contacts form. They do so readily, and the structure that results is the thermodynamically stable 1:1 coloring. When μ is large and positive, both blue–red and red–red contacts form readily, and the result is a coloring whose red:blue ratio depends on the red:blue ratio present in implicit solution (we call this regime “irreversible”). Between these extremes, we find a large range of growth rates that give rise to spatially disordered 2:1 structures, independent of the red:blue fraction in solution. This regime is one of “partially reversible” growth: “native” (red–blue) contacts form readily and do not break; “defect” (red–red) contacts can form and break readily. The combination of these microscopic processes leads to growth of structures similar to the 2:1 inherent structures seen in energy minimization simulations, namely compositional polycrystals of thermodynamically favored 1:1 domains, separated by red grain boundaries (SI Appendix, Fig. S22).

This growth procedure reveals that the inherent structures described earlier can be obtained when a pattern of thermodynamically desirable red–blue bonds is infiltrated by red–red bond “mistakes” that occur because of the stochastic nature of assembly (SI Appendix, Fig. S22). Simple although our growth protocol is, it provides, in concert with the inherent structure analysis, one possible explanation for the 2:1 ratio seen experimentally: according to this analysis, the ratio results from kinetic trapping of MOF-2000s components during their attempt to assemble into a 1:1 thermodynamic structure. The resulting component arrangements are consistent with those seen in experiments: a 2:1 component ratio, without apparent anisotropy, obtained over a wide range of solution component concentrations.

Finally, in Fig. 5 B and C, we show that growth simulations done using the same hierarchy but reduced scale of noncovalent interaction energies causes this solution-robust growth regime to shrink (Fig. 5B) and eventually disappear (Fig. 5C). Similarly, adopting a “ferromagnetic” hierarchy of energy scales (meaning that red and blue nodes prefer to form like-color contacts; this appears to be the case for the components of the MTV-MOF in ref. 1) results in no regime of solution-robust component ratios (Fig. 5D); none was seen in those experiments. Note that model side-chain interactions cannot be mapped directly to experimental parameters, because the former represent effective free energies of interaction that in experiment are mediated by solvent, etc. The difference between the energetic parameters displayed in Fig. 5 and the parameter μ would correspond roughly to side-chain–side-chain equilibrium binding affinities, given a set of component concentrations.

We have reported the assembly of a MOF whose two components are incorporated in a 2:1 ratio, robust to changes in relative concentration of struts in the initial solution. Components are distributed throughout the framework in a manner that is apparently isotropic and nonperiodic, making MOF-2000 unique among extended frameworks. Our simulations of a simple and physically motivated model of MOF-2000 identify a set of nonequilibrium structures that correspond to our experimental observations. The simulated structures, which are local energy minima and are also accessible to a microscopically reversible growth process, display a 2:1 ratio of components distributed isotropically and nonperiodically, and emerge in a region of phase space that corresponds to a physically reasonable side-chain chemistry.

Although we cannot rule out a thermodynamic origin for the 2:1 disordered regime, our findings suggest a possible nonequilibrium origin for MOF-2000s robust composition ratio. Previous work has demonstrated that kinetic trapping of multiple component types during self-assembly can occur in a variety of contexts (20, 24–29). Our simulations also suggest a set of requirements for generating nontrivial magic number ratios of components within covalent frameworks generally. First, the hierarchy of noncovalent interactions between components must be such that “local” energy minima are nontrivial, i.e., not 1:0 (meaning that nodes must prefer energetically to be adjacent to nodes of another color) (Fig. 3A). Second, the scale of interaction energies must be such that “nonnative” (here red–red) contacts can form but do so reversibly; otherwise, the outcome of growth is the thermodynamic structure (if nonnative contacts cannot form) or a structure whose composition is sensitive to solution concentration (if nonnative contacts form irreversibly). If these conditions hold, then solution-robust ratios can be generated; the precise numerical values of these ratios are a consequence of the particular topology of the MOF (Fig. 4). Together, this set of observations suggests a strategy for making multicomponent covalent frameworks with solution-robust ratios of component types. The utility of such frameworks awaits exploration.

Methods Summary

Synthesis of MOF-2000.

Methylamine solution (Aldrich Chemical; 40 wt % in H₂O; 40 μL) was mixed with anhydrous N,N-dimethylformamide (DMF) (EM Science) (2 mL) to make a stock solution. H₂L_r (1.20 mg, 1.37 × 10⁻³ mmol), H₂L_b•4PF₆ (2.71 mg, 1.37 × 10⁻³ mmol), and Zn(NO₃)₂•6H₂O (EM Science; 5.97 mg, 20 μmol) were dissolved in anhydrous DMF solution (1 mL). The mixture was filtered and injected in a 4-mL vial. After the methylamine stock solution (20 μL) was added, the vial was capped and placed in an isothermal oven at 65 °C for 3 d. Dark red crystals of MOF-2000 were collected and rinsed with DMF (4 × 1.0 mL) after the vial was removed from the oven and cooled to room temperature.

Monte Carlo Simulation Algorithm 1: Inherent Structure Production (Fig. 3A).

Each edge in our interaction network (nbo) describes a noncovalent node–node interaction energy, whose value we define as a function of the colors of two nearest-neighbor nodes. The energy of the system is as follows:

$$E={\displaystyle \sum _{i,j}^{\text{interactions}}{\epsilon }_{C\left(i\right)-C\left(j\right)}}-{\displaystyle \sum _i^{\text{sidechains}}{\mu }_{C\left(i\right)}}.$$

The first sum runs over all distinct nearest-neighbor interactions; the second runs over all nodes. Here, C(i) = b if node i is blue, and r if node i is red. ε_C(i)-C(j) is the pairwise interaction energy between two adjacent side chains i and j, and so is ε_b-b, ε_r-b, or ε_r-r. The chemical potential term μ_C(i) is 0 and μ for red and blue side chains, respectively. The fraction of blue nodes in implicit solution is then f_b^s = e^μ/(1 + e^μ).

Monte Carlo simulations were performed as follows. We selected a node at random, proposed a change of color of that node (r↔b), and accepted the change with the Metropolis probability min(1, exp(–ΔE/T)), where ΔE = E_new – E_old is the energy change resulting from the proposal. Inherent structures were identified by setting the system temperature T to zero.

Monte Carlo Simulation Algorithm 2: Growth (Fig. 5).

Keeping the interaction network (nbo) the same as for the previous protocol, we introduced a third color, white (w), describing the solvent. The energy of this extended system is as follows:

$$E={\displaystyle \sum _{i,j}^{\text{interactions}}{\epsilon }_{C\left(i\right)-C\left(j\right)}}-{\displaystyle \sum _i^{\text{sidechains}}{\mu }_{C\left(i\right)}}.$$

Here, C(i) = b, r, or w, depending on the color of the node i, ε_C(i)-C(j) describes the interaction potential between colors C(i) and C(j), and the chemical potential μ_C(i) is μ, −ln($f_{\mathrm{b}}^{\mathrm{s}}$), and −ln(1 − $f_{\mathrm{b}}^{\mathrm{s}}$) for w, b, and r, respectively. Here, $f_{\mathrm{b}}^{\mathrm{s}}$ is the relative fraction of reds versus blues in implicit solution, while μ is the chemical potential associated with removing/adding a colored site to the system, and therefore controls the combined concentration of reds and blues in solution. The latter is distinct from the relative fraction $f_{\mathrm{b}}^{\mathrm{s}}$ of reds versus blues in solution.

Monte Carlo simulations were performed as follows. We selected a node at random and proposed a change of color of that node. If the chosen node was white, we attempted to make it colored; if the chosen node was colored, we attempted to make it white. If the chosen node was white, then we proposed to make it blue with probability f_b^s; otherwise, we proposed to make it red. No red–blue interchange was allowed, mimicking the idea that unbinding events are required to relax configurational degrees of freedom. Starting configurations were all white.

To maintain detailed balance with respect to the stated energy function, the acceptance rates for these moves were as follows (ΔE is the energy change resulting from the proposed move):

$$\begin{array}{lllll}\mathrm{r}\hfill & \Rightarrow \hfill & \mathrm{w}\hfill & \text{:}\hfill & \min \left(1,\exp \left[-\mathrm{\Delta }E/T\right]\left[1-f_{\mathrm{b}}^{\mathrm{s}}\right]\right)\hfill \\ \mathrm{b}\hfill & \Rightarrow \hfill & \mathrm{w}\hfill & \text{:}\hfill & \min \left(1,\exp \left[-\mathrm{\Delta }E/T\right]\left[f_{\mathrm{b}}^{\mathrm{s}}\right]\right)\hfill \\ \mathrm{w}\hfill & \Rightarrow \hfill & \mathrm{r}\hfill & \text{:}\hfill & \min \left(1,\exp \left[-\mathrm{\Delta }E/T\right]/\left[1-f_{\mathrm{b}}^{\mathrm{s}}\right]\right)\hfill \\ \mathrm{w}\hfill & \Rightarrow \hfill & \mathrm{b}\hfill & \text{:}\hfill & \min \left(1,\exp \left[-\mathrm{\Delta }E/T\right]/\left[f_{\mathrm{b}}^{\mathrm{s}}\right]\right).\hfill \end{array}$$